Elasticity of CaSiO₃–CaTiO₃ perovskite at lower-mantle pressures

Calcium silicate perovskite (named davemaoite, Ca-Pv for short) is believed to be the third most abundant mineral in Earth's lower mantle. Knowledge of its elasticity is important to constrain velocities of pyrolite and basalt models in lower-mantle conditions and then decipher the origins of seismic signatures via comparison with observed seismic velocities. Here elasticities and sound velocities of cubic CaSiO₃–CaTiO₃ perovskites at lower-mantle pressures have been investigated by first-principles calculations. The incorporation of titanium into cubic Ca-Pv increases C₁₁ but decreases C₁₂ and C₄₄ at high pressures. As a result, elastic moduli (K_S and G) and wave velocities (V_P and V_S) decrease with increasing Ti content. Cubic CaSiO₃ exhibits high-seismic-velocity anisotropies at low pressures, which gradually decrease with increasing pressure, reaching minimum values near the lowermost mantle. In contrast, Ti-bearing Ca-Pv shows an initial decrease in velocity anisotropies, followed by a progressive increase at higher pressures. Compositional effects on elastic properties and velocity anisotropies of cubic CaSiO₃–CaTiO₃ perovskites are significant at lower-mantle pressures. Considering the amounts of Ca-Pv in pyrolite and basalt models, Ti-bearing Ca-Pv may be responsible for the observed seismic velocity anomalies associated with subducted oceanic crust and a potential source of seismic anisotropies in the lower mantle.

1 Introduction

Knowledge of structures and physical properties of constituent minerals in the lower mantle is essential to model the density and sound velocities of pyrolite and subducted oceanic crust models. Comparisons between predicted seismic velocities and geophysical observations are crucial to discussions of the causes of seismic anomalies and dynamic processes in the lower mantle. However, a major source of uncertainty in the predicted seismic velocities of pyrolite has been the influence of davemaoite, also called cubic CaSiO₃ perovskite (Ca-Pv hereafter), on velocity (Murakami et al., 2012; Tschauner et al., 2021). Cubic Ca-Pv is believed to be the third most abundant mineral, as it comprises 5 vol. %–10 vol. % and 24 vol. %–29 vol. % of pyrolite and basalt models in the lower mantle, respectively (Ricolleau et al., 2010; Irifune et al., 2010). However, there are few reliable measurements of its sound velocities in lower-mantle conditions because it is technically challenging to carry out static compression experiments in lower-mantle conditions.

As shown in Fig. S1 in the Supplement, CaSiO₃ is stable in the wollastonite structure in ambient conditions and transforms into breyite at pressures above ∼4 GPa (Essene, 1974). Breyite decomposes into larnite (Ca₂SiO₄) and titanite (CaSi₂O₅) at pressures exceeding ∼8 GPa (Gasparik et al., 1994). These two phases subsequently react to form the perovskite phase above ∼ 13 GPa (Sueda et al., 2006), where tetragonal Ca-Pv is stable below ∼500 K, and the cubic Ca-Pv becomes stable above this temperature (Komabayashi et al., 2007; Sagatova et al., 2021; Yin et al., 2023). Experimental studies at high pressure and room temperature on the elasticity of tetragonal Ca-Pv (space group: I4/mcm) propose that it might explain the seismic anomalies observed in the deep mantle (Li et al., 2004; Kudo et al., 2012). However, both experimental and theoretical studies on the phase stability of CaSiO₃ show that CaSiO₃ adopts a cubic perovskite structure (space group: Pm$\overline{\mathrm{3}}m)$ in lower-mantle conditions (Komabayashi et al., 2007; Stixrude et al., 2007). Since cubic Ca-Pv is unquenchable in ambient conditions, in situ experimental studies at high pressure and high temperature on its elasticity are technically challenging. As recently as 2019, Gréaux et al. (2019) reported in situ X-ray diffraction and sound velocity measurements on cubic Ca-Pv of up to 23 GPa and 1700 K. They found that cubic Ca-Pv has a smaller shear modulus than the tetragonal phase, which leads to substantially lower sound velocities of subducted basalt. This further supports the hypothesis of accumulation of basaltic crust in the uppermost lower mantle, which is associated with the observed low-seismic-velocity signatures. Soon after, Thomson et al. (2019) reported sound velocities of (Ti-bearing) Ca-Pv at ∼12 GPa and up to 1500 K. By combining the new results with literature data and extrapolating, they proposed that seismic velocities of Ca-Pv can explain large low-shear-velocity provinces observed in the lower mantle (Garnero et al., 2016).

Since it is difficult to experimentally investigate the elastic properties of Ca-Pv in lower-mantle conditions, it is essential to employ computational methods. Karki and Crain (1998) reported elastic properties of cubic Ca-Pv by first-principles calculations in static (0 K) conditions. Stixrude et al. (2007) investigated elasticities of cubic and tetragonal Ca-Pv using static calculations and mean field theory. They proposed that tetragonal Ca-Pv has a much smaller shear modulus than cubic Ca-Pv. Additionally, Li et al. (2006) reported the elasticity of tetragonal Ca-Pv in lower-mantle conditions by means of first-principles molecular dynamics simulations. Later, the elasticity of cubic Ca-Pv in lower-mantle conditions was also studied using first-principles molecular dynamics. Kawai and Tsuchiya (2015) demonstrated that cubic Ca-Pv had a smaller shear modulus and slower sound velocities than bridgmanite. This suggests that Ca-Pv-rich material can produce low-seismic-velocity anomalies in the lower mantle. Both theoretical results and experimental extrapolations show that Ca-Pv with a small shear modulus may contribute to low seismic velocity in subducted basalt.

Ca-Pv in mid-ocean ridge basalt (MORB) contains up to 28 wt % TiO₂ in lower-mantle conditions (Litasov and Ohtani, 2005; Hirose and Fei, 2002; Ricolleau et al., 2010; Ono et al., 2001). In contrast, Ca-Pv in pyrolite contains a maximum of 3 wt % TiO₂ in the lower mantle (Hirose, 2002; Kesson et al., 1998). Additionally, up to 2.9 wt % TiO₂ has been reported in Ca-Pv inclusions found in deep diamond (Nestola et al., 2018; Walter et al., 2011). Notably, the incorporation of Ti stabilizes the tetragonal phase of CaSi_0.6Ti_0.4O₃ up to 1200 K at 12 GPa (Thomson et al., 2019). This indicates that tetragonal–cubic phase transition in Ti-bearing Ca-Pv occurs in higher-P–T conditions than it does in pure CaSiO₃ and may be associated with elastic anomalies of Ca-Pv. The incorporation of Ti in Ca-Pv may have a significant effect on its elastic properties. However, there are limited experimental studies on the elasticity of Ti-bearing Ca-Pv, and direct measurements of sound velocity under lower-mantle conditions remain challenging. Therefore, theoretical investigations into the elastic properties of CaSiO₃–CaTiO₃ perovskites are both essential and significant for advancing our understanding of the mineralogy and dynamics of Earth's lower mantle.

2 Computational methods

First-principles calculations based on density functional theory (DFT) were performed using the Vienna ab initio simulation package (VASP) in static conditions (Kresse and Furthmüller, 1996; Kresse and Joubert, 1999). The interaction between ions and electrons was described by the projector augmented-wave (PAW) method (Blöchl, 1994). The Ceperley–Alder exchange correlation potential of the local density approximation (LDA) parametrized by Perdew and Zunger was selected in this study (Ceperley and Alder, 1980; Perdew and Zunger, 1981), since it yields better agreement with the experimental equation of state (Stixrude et al., 2007). The kinetic energy cut-off was set to 1000 eV, and the energy convergence criterion was 10⁻⁶ eV. The Monkhorst–Pack scheme was used for Brillouin zone sampling (Monkhorst and Pack, 1976).

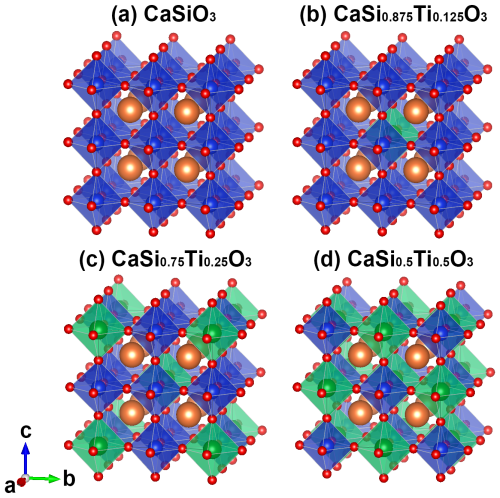
According to phase diagram of the CaSiO₃–CaTiO₃ system (Kubo et al., 1997), cubic Ca-Pv (Pm$\overline{\mathrm{3}}m$) is considered in this study. A $\mathrm{2}\times \mathrm{2}\times \mathrm{2}$ supercell (40 atoms) of the conventional cubic unit cell is built (Tschauner et al., 2021). Four structural configurations, 8CaSiO₃–0CaTiO₃ (CaSiO₃), 7CaSiO₃–1CaTiO₃ (CaSi_0.875Ti_0.125O₃), 6CaSiO₃–2CaTiO₃ (CaSi_0.75Ti_0.25O₃), and 4CaSiO₃–4CaTiO₃ (CaSi_0.5Ti_0.5O₃), were considered (Fig. 1). For all structural configurations, Si atoms are substituted by Ti atoms in the most dispersed way possible to lower total energy. The k-points grid was set to $\mathrm{4}\times \mathrm{4}\times \mathrm{4}$ for cubic Ca-Pv. Structural relaxations were performed at various unit-cell volumes, where unit-cell parameters and atomic positions were allowed to relax to obtain the minimum total energy. The obtained minimum total energies (E) at different volumes (V) were fitted to the third-order finite strain equation to obtain unit-cell volume (V₀), isothermal bulk modulus (K_T0), its pressure derivative ($K_{\mathrm{T}\mathrm{0}}^{\prime }$), and energy (E₀) at zero pressure (Birch, 1978; Davies, 1974). Once the equilibrium structure at a given volume was obtained, the structure was strained by applying compressional and shear strains of ±0.01, then the stress tensor in the strained structure was calculated. The elastic constants were determined by the ratios of deviatoric stress to applied strain.

It is noteworthy that the method of determining elastic constants described above assumes that the Ca-Pv has a Pm$\overline{\mathrm{3}}m$ symmetry. Strictly, this assumption is incorrect as some of Si atoms have been replaced by Ti atoms. The magnitude of the effect of the broken symmetry on elastic constants has been assessed by examination of the stress tensor matrices. The deviations from the expected cubic symmetry are sufficiently small (Table S1 in the Supplement).

Figure 1 Four structural configurations of cubic CaSiO₃–CaTiO₃ perovskites with compositions of CaSiO₃, CaSi_0.875Ti_0.125O₃, CaSi_0.75Ti_0.25O₃, and CaSi_0.5Ti_0.5O₃.

3 Results and discussion

Three independent elastic constants, C₁₁, C₁₂, and C₄₄ for the cubic Ca-Pv, are determined up to 130 GPa. The calculated elastic constants are analyzed using finite strain theory as follows (Birch, 1978; Davies, 1974):

$$\begin{array}{}\text{(1)}& {\displaystyle }{C}_{ij}=(\mathrm{1}+\mathrm{2}f{)}^{\frac{\mathrm{7}}{\mathrm{2}}}\left[C_{ij\mathrm{0}}+a_{\mathrm{1}}f+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{a}_{\mathrm{2}}{f}^{\mathrm{2}}\right]+a_{\mathrm{3}}P,\text{(2)}& {\displaystyle }{a}_{\mathrm{1}}=\mathrm{3}{K}_{\mathrm{0}}\left(C_{ij}^{\prime }-a_{\mathrm{3}}\right)-\mathrm{7}{C}_{ij\mathrm{0}},\text{(3)}& {\displaystyle }\begin{array}{rl}{a}_{\mathrm{2}}& =\mathrm{9}{K}_{\mathrm{0}}^{\mathrm{2}}{C}_{ij}^{\prime \prime }+\mathrm{9}{K}_{\mathrm{0}}^{\prime }{K}_{\mathrm{0}}\left(C_{ij}^{\prime }-a_{\mathrm{3}}\right)\\ & -\mathrm{48}{K}_{\mathrm{0}}\left(C_{ij}^{\prime }-a_{\mathrm{3}}\right)+\mathrm{63}{C}_{ij\mathrm{0}},\end{array}\text{(4)}& {\displaystyle }f={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}[{\left({\displaystyle \frac{V_{\mathrm{0}}}{V}}\right)}^{\frac{\mathrm{2}}{\mathrm{3}}}-\mathrm{1}],\end{array}$$

where subscript 0 denotes values at zero pressure and prime denotes pressure derivatives; f is the finite strain; a₃ equals 3 for C₁₁ and 1 for C₁₂ and C₄₄; and the parameters K₀, K₀', and V₀ are taken from the E–V fitting of third-order finite strain equation. A third-order equation is used for C₁₁ and C₁₂ assuming $C_{ij}^{\prime \prime }=\mathrm{0}$, while a fourth-order equation is used for C₄₄. The adiabatic bulk (K) and shear (G) moduli of cubic Ca-Pv are calculated by means of Voigt–Reuss–Hill approximation (Hill, 1952):

$$\begin{array}{}\text{(5)}& {\displaystyle }K={\displaystyle \frac{K_{\mathrm{V}}+K_{\mathrm{R}}}{\mathrm{2}}},\text{(6)}& {\displaystyle }G={\displaystyle \frac{G_{\mathrm{V}}+G_{\mathrm{R}}}{\mathrm{2}}},\text{(7)}& {\displaystyle }{K}_{\mathrm{V}}=K_{\mathrm{R}}={\displaystyle \frac{C_{\mathrm{11}}+\mathrm{2}{C}_{\mathrm{12}}}{\mathrm{3}}},\text{(8)}& {\displaystyle }{G}_{\mathrm{V}}={\displaystyle \frac{\left(C_{\mathrm{11}}-C_{\mathrm{12}}\right)+\mathrm{3}{C}_{\mathrm{44}}}{\mathrm{5}}},\text{(9)}& {\displaystyle }{G}_{\mathrm{R}}={\displaystyle \frac{\mathrm{5}{C}_{\mathrm{44}}(C_{\mathrm{11}}-C_{\mathrm{12}})}{\mathrm{4}{C}_{\mathrm{44}}+\mathrm{3}(C_{\mathrm{11}}+C_{\mathrm{12}})}},\end{array}$$

where subscripts “V” and “R” denote Voigt and Reuss, respectively. The obtained shear modulus is analyzed using the fourth-order finite strain equation:

$$\begin{array}{}\text{(10)}& {\displaystyle }G=(\mathrm{1}+\mathrm{2}f{)}^{\frac{\mathrm{5}}{\mathrm{2}}}\left[G_{\mathrm{0}}+b_{\mathrm{1}}f+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{b}_{\mathrm{2}}{f}^{\mathrm{2}}\right],\text{(11)}& {\displaystyle }{b}_{\mathrm{1}}=\mathrm{3}{K}_{\mathrm{0}}{G}_{\mathrm{0}}^{\prime }-\mathrm{5}{G}_{\mathrm{0}},\text{(12)}& {\displaystyle }{b}_{\mathrm{2}}=\mathrm{9}\left\{K_{\mathrm{0}}^{\mathrm{2}}\left[G_{\mathrm{0}}^{\prime \prime }+{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{0}}}}\left(K_{\mathrm{0}}^{\prime }-\mathrm{4}\right)G_{\mathrm{0}}^{\prime }\right]+{\displaystyle \frac{\mathrm{35}}{\mathrm{9}}}{G}_{\mathrm{0}}\right\}.\end{array}$$

Since calculations are performed in static conditions (0 K), the adiabatic bulk modulus (K_S) is equal to the isothermal bulk modulus (K_T). Thus, parameter K without a subscript is used in these equations. The calculated K_S0 via Voigt–Reuss–Hill approximation is very close to K_T0 (Table 2). The isotropic aggregate compressional (V_P) and shear (V_S) wave velocities of Ca-Pv are then evaluated from the bulk and shear moduli and the density ρ as follows:

$$\begin{array}{}\text{(13)}& {\displaystyle }{V}_{\mathrm{P}}=\sqrt{{\displaystyle \frac{K+\frac{\mathrm{4}}{\mathrm{3}}G}{\mathit{\rho }}}},\text{(14)}& {\displaystyle }{V}_{\mathrm{S}}=\sqrt{{\displaystyle \frac{G}{\mathit{\rho }}}}.\end{array}$$

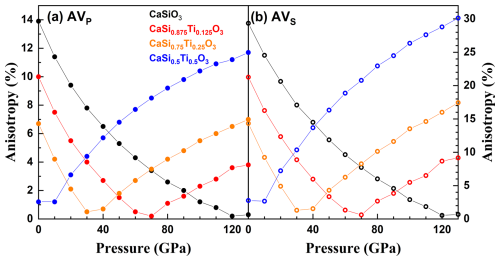
Figure 2 Elastic moduli of cubic CaSiO₃–CaTiO₃ perovskites at high pressures. Black, red, orange, and blue symbols represent CaSiO₃, CaSi_0.875Ti_0.125O₃, CaSi_0.75Ti_0.25O₃, and CaSi_0.5Ti_0.5O₃, respectively. The dotted curves are the results of fitting finite strain equations to the data (Birch, 1978; Davies, 1974).

Table 1 The elastic moduli and their pressure derivatives of cubic Ca-Pv at zero pressure.

All elastic constants increase with increasing pressure, and no elastic instability is found up to 130 GPa (Fig. 2). For different compositions, the individual elastic constants follow similar trends with pressure. The elastic constants at zero pressure and their pressure derivatives are listed in Table 1. The $C_{\mathrm{11}}^{\prime }$ increases but $C_{\mathrm{12}}^{\prime }$ and $C_{\mathrm{44}}^{\prime }$ decrease with an increasing molar fraction of CaTiO₃. This indicates that increasing Ti content in cubic Ca-Pv has an opposite effect on C₁₁ and C₁₂ (C₄₄). As a result, the elastic moduli (K_S and G) and wave velocities (V_P and V_S) increase at high pressures (Figs. 2b and 3b). The elastic moduli and wave velocities of cubic Ca-Pv with different compositions have similar trends with pressure. In general, the addition of Ti in cubic Ca-Pv makes elastic moduli (except for C₁₁) and wave velocities smaller with respect to pure cubic CaSiO₃.

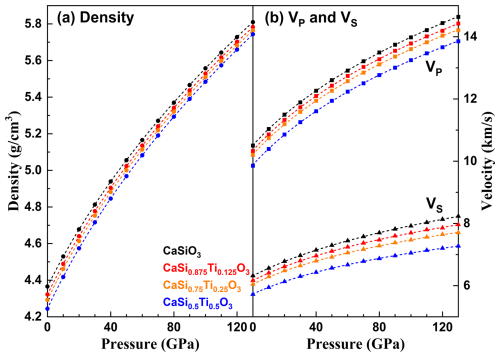
Figure 3 Densities (a) and wave velocities (b) of cubic CaSiO₃–CaTiO₃ perovskites at high pressures. Black, red, orange, and blue symbols represent CaSiO₃, CaSi_0.875Ti_0.125O₃, CaSi_0.75Ti_0.25O₃, and CaSi_0.5Ti_0.5O₃, respectively. The dashed curves are the best fit of the Eulerian finite strain equation (Birch, 1978; Davies, 1974).

Table 2 Density, volume per formula, and elastic moduli at zero pressure and their pressure derivatives of Ca-Pv from this study and the previous literature.

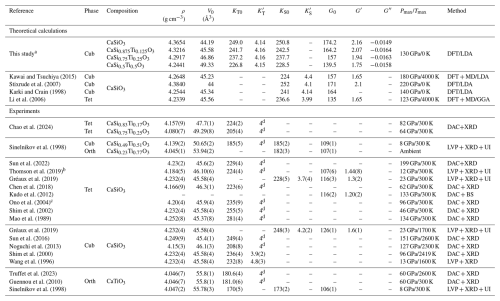
^a K_S0 is calculated by means of Voigt–Reuss–Hill approximation. ^b Equation-of-state parameters from data of Thomson et al. (2019), Shim et al. (2000), and Chen et al. (2018). ^c The chemical composition is inferred from the unit-cell volume in ambient conditions. ^d $K_{\mathrm{T}}^{\prime }$ is fixed to 4. Cub, Tet, and Orth represent cubic, tetragonal, and orthorhombic Ca-Pv. DFT: density functional theory. MD: molecular dynamics. LDA: local density approximation. GGA: generalized gradient approximation. DAC: diamond anvil cell. LVP: large-volume press. XRD: X-ray diffraction. UI: ultrasonic interferometry. BS: Brillouin scattering.

The calculated density, unit-cell volume, and elastic moduli and their pressure derivatives, together with previous literature values of Ca-Pv, are summarized in Table 2. The volume per formula of Ca-Pv increases with an increasing molar fraction of CaTiO₃. However, it is important to mention that these Ca-Pv phases have different crystal structures. The Ks₀ and $K_{\mathrm{S}}^{\prime }$ of cubic CaSiO₃ obtained in this study are comparable to those of theoretical calculations and experimental measurements considering the trade-off between K_T0 and $K_{\mathrm{T}}^{\prime }$ (Karki and Crain, 1998; Kawai and Tsuchiya, 2015; Stixrude et al., 2007; Li et al., 2006; Gréaux et al., 2019). The values of G₀ and G^′ of cubic CaSiO₃ derived in this study are in good agreement with those of other computational studies but larger than those reported by Gréaux et al. (2019) based on experiments because of the systematic overestimations of elastic moduli by LDA calculations. The values of K_S0 and G₀ of cubic CaSi_0.5Ti_0.5O₃ obtained with our computations are also larger than those of experimental studies due to the same reason as mentioned before (Sinelnikov et al., 1998). In general, both K_S0 (K_T0) and G₀ of Ca-Pv decrease with an increasing molar fraction of CaTiO₃ demonstrated by both experimental measurements and first-principles calculations.

Table 3 The compositional derivatives of density, elastic constants, elastic moduli, and wave velocities of cubic Ca-Pv at 20, 30, 80, and 100 GPa.

X is the molar fraction of CaTiO₃.

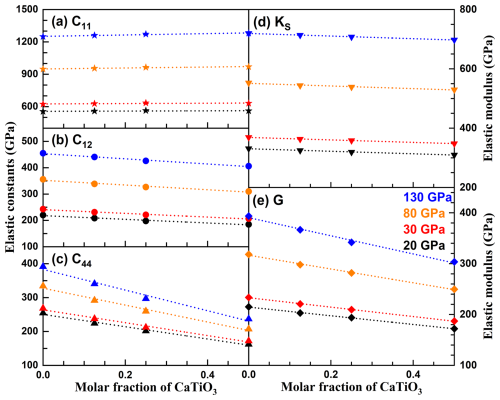
Figure 4 Elastic moduli of cubic CaSiO₃–CaTiO₃ perovskites at 20 GPa (black), 30 GPa (red), 80 GPa (orange), and 130 GPa (blue). Symbols and dotted lines are calculated values and linear fitting results, respectively.

The density as a function of the molar fraction of CaTiO₃ has been fitted with a second-order polynomial, whereas the elastic moduli and wave velocities exhibit linear relationships with CaTiO₃ content. The compositional derivatives of density (dρ $/$ dX and d²ρ $/$ dX²), elastic constants (dC_ij $/$ dX), elastic moduli (dK $/$ dX and dG $/$ dX), and wave velocities (dV_P $/$ dX and dV_S $/$ dX) at 20, 30, 80, and 100 GPa are summarized in Table 3, where X denotes the molar fraction of CaTiO₃. The density of Ca-Pv increases with pressure but decreases with increasing CaTiO₃ content (Figs. 3a and 5a). Among the elastic constants, dC₁₁ $/$ dX is positive, while dC₁₂ $/$ dX and dC₄₄ $/$ dX are negative at all four pressures, indicating that C₁₁ increases while C₁₂ and C₄₄ decrease with the addition of CaTiO₃ (Fig. 4). Both K_S and G decrease with increasing CaTiO₃ content. Notably, cubic CaSi_0.5Ti_0.5O₃ has a lower K_S (∼3.1 %) and significantly lower G (∼23 %) than cubic CaSiO₃ at 130 GPa (Fig. 4b). This suggests that the incorporation of Ti into cubic Ca-Pv has a more pronounced effect on shear properties than on compressional properties, primarily due to the strong compositional influence on C₄₄. Consequently, the wave velocities of cubic Ca-Pv decrease with increasing Ti content (Fig. 5b). At 130 GPa, the V_P and V_S of cubic CaSi_0.5Ti_0.5O₃ are reduced by approximately 5.3 % and 12 %, respectively, compared to those of cubic CaSiO₃.

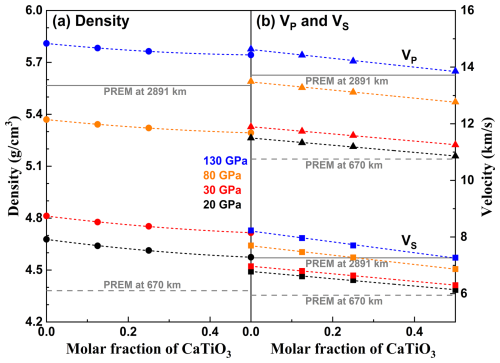
Figure 5 Densities and wave velocities of cubic CaSiO₃–CaTiO₃ perovskites at 20 GPa (black), 30 GPa (red), 80 GPa (orange), and 130 GPa (blue). Symbols and dashed curves are calculated values and fitting results, respectively. Dashed and solid grey lines represent the density and velocities of the preliminary reference Earth model at 670 and 2891 km, respectively.

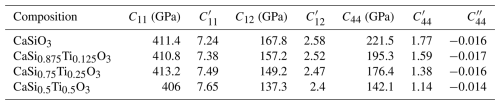
To understand the evolution of velocity anisotropy in cubic Ca-Pv at high pressures, the anisotropy for V_P (AV_P) and the maximum anisotropy for V_S (AV_S) are defined as follows (Mainprice, 1990):

$$\begin{array}{}\text{(15)}& {\displaystyle }A{V}_{\mathrm{P}}={\displaystyle \frac{V_{\mathrm{P},\max }-V_{\mathrm{P},\min }}{V_{\mathrm{P},\max }+V_{\mathrm{P},\min }}}\times \mathrm{200}\mathit{\%},\text{(16)}& {\displaystyle }A{V}_{\mathrm{s}}={\left({\displaystyle \frac{V_{\mathrm{S}\mathrm{1}}-V_{\mathrm{S}\mathrm{2}}}{V_{\mathrm{S}\mathrm{1}}+V_{\mathrm{S}\mathrm{2}}}}\right)}_{\max }\times \mathrm{200}\mathit{\%},\end{array}$$

where V_P,max and V_P,min represent the maximum and minimum compressional velocities, respectively, and V_S1 and V_S2 are two orthogonally polarized shear velocities in a given propagation direction. As shown in Fig. 6, both AV_P and AV_S of cubic CaSiO₃ decrease with pressure and have trends consistent with those of previous theoretical studies (Karki and Crain, 1998; Kawai and Tsuchiya, 2015). Cubic CaSiO₃ has small AV_P and AV_S values at 130 GPa (AV_P=0.3 % and AV_S=0.7 %). There is an enhanced composition effect on velocity anisotropies of cubic Ca-Pv at high pressures. The anisotropies of V_P and V_S in CaSi_0.875Ti_0.125O₃ and CaSi_0.75Ti_0.25O₃ initially decrease with increasing pressure, reaching minimum values at approximately 70 and 30 GPa, respectively, before increasing again at higher pressures. In contrast, AV_P and AV_S values of CaSi_0.5Ti_0.5O₃ continuously increase with pressure, reaching ∼12 % and ∼30 %, respectively, at 130 GPa. The elastic anisotropy of cubic crystals can also be quantified using the Zener ratios, defined as $A=\mathrm{2}{C}_{\mathrm{44}}/(C_{\mathrm{11}}-C_{\mathrm{12}})$, where A=1 indicates elastic isotropy. As shown in Fig. S2, the Zener ratio of cubic CaSiO₃ decreases with increasing pressure and approaches unity at ∼125 GPa. For Ti-bearing Ca-Pv (CaSi_0.875Ti_0.125O₃, CaSi_0.75Ti_0.25O₃, and CaSi_0.5Ti_0.5O₃), the Zener ratios also decrease with pressure, crossing the isotropic value of 1 at approximately 5, 25, and 65 GPa, respectively. The transition from A>1 to A<1 significantly alters the directional dependence of V_S. Specifically, the fastest V_S, which propagates along the [100] direction when A>1, shifts to the [111] direction when A<1. Conversely, the slowest V_S, initially along [111] for A>1, shifts to the [100] direction for A<1.

Figure 6 Velocity anisotropies of cubic CaSiO₃–CaTiO₃ perovskites at high pressures. Black, red, orange, and blue circles represent CaSiO₃, CaSi_0.875Ti_0.125O₃, CaSi_0.75Ti_0.25O₃, and CaSi_0.5Ti_0.5O₃, respectively. Solid and open circles stand for AV_P and AV_S, respectively.

4 Implications

Our results suggest that the acoustic wave velocities of cubic Ca-Pv significantly decrease with increasing Ti content (Fig. 5). Considering the temperature effect predicted by Kawai and Tsuchiya (2015), the cubic Ca-Pv's velocity profiles can be substantially reduced with the addition of Ti in lower-mantle conditions. Thus, it is expected that cubic Ti-bearing Ca-Pv can reduce the seismic velocity of subducted oceanic crust in the lower mantle because the amount of Ca-Pv in basalt is up to ∼ 29 vol. % (Ricolleau et al., 2010). In addition, Ca-Pv in subducted MORB assemblages has a composition of CaSi_1−xTi_xO₃ with $\mathrm{0}<x<\mathrm{0.45}$ (Litasov and Ohtani, 2005; Hirose and Fei, 2002; Ricolleau et al., 2010). Ca-Pv discovered in “super-deep” diamonds has a detectable content of Ti (Nestola et al., 2018; Walter et al., 2011). However, although our theoretical results in static conditions demonstrate that incorporation of Ti into Ca-Pv significantly reduces its wave velocities at lower-mantle pressures, further experimental or computational studies of the temperature effect on elasticities and velocities of Ti-bearing Ca-Pv are required to determine whether or not its sound velocities explain observed seismic velocity anomalies associated with subducted oceanic crust in Earth's lower mantle (Garnero et al., 2016).

Although Ca-Pv adopts a cubic structure in the lower mantle, it exhibits significant seismic velocity anisotropy in the transition zone and the uppermost lower mantle. Kawai and Tsuchiya (2015) have proposed that cubic CaSiO₃ has the largest anisotropy at the lower part of the mantle transition zone; even a small amount of cubic CaSiO₃ could produce detectable anisotropy. Our calculations confirm this point of view. Thus, seismic anisotropy observed in the mantle transition zone associated with the subducted slabs may be derived from highly anisotropic Ca-Pv (Foley and Long, 2011). More importantly, it is noteworthy that there is an enhanced composition effect on velocity anisotropies of cubic CaSiO₃–CaTiO₃ with Ti content. Incorporation of Ti into Ca-Pv significantly increases its velocity anisotropies, especially for shear velocity, at lower-mantle pressures. Cubic CaSi_0.5Ti_0.5O₃ is highly anisotropic with AV_P and AV_S values of up to ∼12 % and ∼30 %, respectively, at the lowermost mantle pressure. These values are larger than those of ferropericlase (AV_P: ∼10 % and AV_S: ∼23 %) and bridgmanite (AV_P: ∼12 %; AV_S: ∼16 %) (Yang et al., 2016; Kawai and Tsuchiya, 2015; Kurnosov et al., 2017; Fu et al., 2018) and comparable with those of MgSiO₃ post-perovskite (Mg-PPv) (AV_P: ∼ 15 %; AV_S: ∼30 %) (Tsuchiya et al., 2004). The anisotropies of Ti-bearing Ca-Pv in lower-mantle conditions can be much larger than results in static conditions, taking into account the temperature effect based on the results by Kawai and Tsuchiya (2015). Although Mg-PPv is believed to be the major origin of seismic anisotropies in the lowermost mantle and D^′′ layer (Wu et al., 2017; Garnero and Mcnamara, 2008), our results indicate that Ti-bearing Ca-Pv is highly anisotropic and may be an additional source of seismic anisotropies in the lowermost mantle.