Elasticity of mixtures and implications for piezobarometry of mixed-phase inclusions

Elastic thermobarometry (or piezobarometry) is the process of determining the P (pressure) and T (temperature) of entrapment of inclusions from their pressure, stress or strain measured when their host mineral is at room conditions. The methods and software used for piezobarometry are currently restricted to inclusions consisting of single phases. In this contribution we describe the theory of the elasticity of mixtures of different phases and combine it with the existing isotropic analysis of the elastic interactions between single-phase inclusions and their hosts to calculate the inclusion pressures of mixed-phase inclusions. The analysis shows that the reliability of calculated entrapment conditions for mixed-phase inclusions, including those containing fluid plus minerals, depends in a complex way upon the contrasts between the elastic properties of the host and the phases in the inclusion. The methods to calculate the entrapment conditions of mixed-phase inclusions have been incorporated into the EosFit7c program (version 7.6) that is available as freeware from http://www.rossangel.net.

1 Introduction

Elastic thermobarometry (or piezobarometry) is the process of determining the P (pressure) and T (temperature) of entrapment of inclusions from the pressure measured in them when their host mineral is at room conditions. It has recently provided new constraints on the P–T conditions attained during metamorphism (e.g. Zhong et al., 2018; Gonzalez et al., 2019; Korsakov et al., 2020; Kosminska et al., 2020) and on the environments in which lithospheric and mantle diamonds grow (e.g. Izraeli et al., 1999; Sobolev et al., 2000; Nestola et al., 2011; Anzolini et al., 2018, 2019). Current applications of elastic thermobarometry rely on several fundamental assumptions. At the time of entrapment of the inclusion it is assumed that the host and inclusion both experience the same temperature and the same homogeneous isotropic stress (i.e. hydrostatic pressure) and that, once sealed, there is no void space in the inclusion. The standard analysis (e.g. Angel et al., 2017b; Mazzucchelli et al., 2021; Angel et al., 2022a; Cisneros and Befus, 2020) is based on the assumption that the host and inclusion behave entirely elastically from entrapment until the time of measurement of the residual pressure of the inclusion, P_inc, in the laboratory. Partial or complete resetting of P_inc during exhumation by plastic flow or cracking of the host mineral is therefore not considered in the calculations, although plastic flow in the host mineral during its post-entrapment exhumation history (e.g. Ferrero and Angel, 2018; Anzolini et al., 2019; Campomenosi et al., 2021) can reset the inclusion stress state so that the measured P_inc may indicate the conditions of resetting rather than entrapment (Zhong et al., 2018; Campomenosi et al., 2023). The standard analysis also assumes that the inclusion is spherical and is elastically isolated within the host and that the host and inclusion are both elastically isotropic. With these assumptions the measured P_inc can be used with the equations of state (EoSs) of the inclusion and host phases to calculate an entrapment isomeke, a line in P–T space that represents possible entrapment conditions (Adams et al., 1975; Rosenfeld and Chase, 1961). Several programs are available that perform this calculation (e.g. Kohn, 2014; Angel et al., 2017b; Mazzucchelli et al., 2021; Cisneros and Befus, 2020).

Minerals are not elastically isotropic, which means that even if they are trapped in cubic mineral hosts they will be under non-hydrostatic stress when measured in the laboratory (e.g. Bonazzi et al., 2019; Murri et al., 2022). But it has been shown for common inclusion minerals such as zircon and quartz that the biggest influence of this deviatoric stress is on the frequencies of Raman bands used to determine the inclusion “pressure” (Bonazzi et al., 2019). If the mode Grüneisen tensor (Angel et al., 2019b) of the inclusion mineral is used to determine its strain state from the measured Raman frequencies and then its stress state (Gilio et al., 2021a), the average normal stress can then be used as a good approximation of P_inc from which a reliable entrapment isomeke can be calculated (Bonazzi et al., 2019). Corrections to the measured P_inc of non-spherical inclusions can be calculated so that the model can still be used to calculate their entrapment conditions (Mazzucchelli et al., 2018). A full analysis of systems in which both the host and the inclusion are elastically anisotropic is currently under development (Mazzucchelli et al., 2019; Gonzalez et al., 2021).

All of this analysis has been focused on single-phase inclusions. But many inclusions contain more than one phase, some of the most obvious being the multiphase “nanogranitoid” inclusions derived from the crystallisation of melt inclusions (Cesare et al., 2015) and those containing two phases together as a result of partial back transformation of a high-pressure polymorph (e.g. quartz and coesite; Chopin, 1984; Ye et al., 2001). Fluid films are often found around silicate inclusions in diamonds (Nimis et al., 2016) and around diamond inclusions in silicates along with graphite (e.g. Perraki et al., 2006; Kotková et al., 2021). Diamonds are also found in fluid-dominated inclusions (Frezzotti et al., 2011). Rims of amorphous material occur around diamond inclusions in silicate hosts (e.g. Kotková et al., 2021; Jakubová et al., 2022) and oxide inclusions in silicates (Alifirova et al., 2022). In this paper we therefore describe the theory of the elasticity of mixtures of different phases to calculate the elastic properties of mixed-phase inclusions. We start with an analysis of the elastic properties of multiphase inclusions that contain sufficient fluid to ensure hydrostatic pressure conditions throughout the inclusion and use this in the isotropic analysis of host–inclusion systems, as described above, to calculate the effect of the fluid on inclusion pressures. We then extend this analysis to multiphase inclusions without fluids. This allows us to determine when the P_inc of various types of multiphase inclusions can be used to reliably calculate their entrapment conditions and when they cannot.

2 Methods

In the context of this work we use the term “fluid” to indicate any material that cannot support significant shear stress because it has small or zero shear moduli. Thus fluid can indicate a gas, liquid or melt, with or without dissolved species. If there is sufficient fluid in an inclusion, then there will be no elastic interactions between the solid mineral grains, and all of the minerals within the fluid and the fluid itself will be under the same hydrostatic pressure. In such situations (e.g. Fig. 1a, b) the fluid is said to “percolate”, which means that it occupies a single continuous connected volume. The temperature is also assumed to be uniform across the inclusion and the host mineral at all times. All other situations, especially those in which the fluid is not a continuous phase in the inclusion or the mineral grains form a continuous network (e.g. Fig. 1c), lead to stress gradients within the solid phases, and no simple thermodynamic analysis with EoS can be made. For the purposes of making the presentation of the thermodynamics straightforward, we further assume that there are no reactions between the minerals and the fluid or between the minerals themselves, there is no precipitation of solid from the fluid and no dissolution of the minerals or the host mineral into the fluid, and there is no loss of volatiles (e.g. Ni et al., 2017) from the inclusion. Thus, we assume that the chemical composition and amount of each mineral phase and that the fluid remains constant. Under these conditions the P–V–T relation of each mineral phase in the inclusion is defined by its own hydrostatic EoS. Note that this approach can incorporate the effects of isochemical phase transitions in the solid mineral phases (e.g. the α–β transition in quartz) as well as in the fluid. Under these constraints and assumptions the P–V–T relationship of a composite inclusion can be derived from the individual EoS of the solid and fluid phases in the inclusion. The expressions that we derive here also apply in general to any mixture of phases in a closed system under uniform P and T. For extension to closed systems in which there are chemical reactions between the phases, see Stixrude and Lithgow-Bertelloni (2022).

Figure 1 Various configurations of fluid (blue) and solid (white and grey) in composite inclusions. In (a) and (b) the fluid occupies a single continuous volume, and the solid does not form a continuous network across the inclusion. The pressure of the fluid will be hydrostatic and the same as the solid phase or phases. This situation is exactly analogous to experiments in a diamond anvil pressure cell with a hydrostatic pressure medium. (c) Examples in which the solid phases form a continuous network so there will be stress gradients in the solid and the stress state in the inclusion will not be hydrostatic.

2.1 EoS of mixtures

The derivation of the elastic properties and EoS of a composite inclusion is easiest to follow if we use the molar volumes of the phases, $V_{m_i}$, and define the number of moles of each phase i in the inclusion as m_i (see Appendix). The total volume V_i of each phase in the inclusion is then $m_i{V}_{m_i}$, where m_i remains constant in a given inclusion, and $V_{m_i}$ at any P and T is given by the EoS of the phase i. The total volume, V, of the mixture of the phases in the inclusion at any P and T is the sum of the volumes of the individual phases:

$$\begin{array}{}\text{(1)}& V=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{m}_i{V}_{m_i}.\end{array}$$

The volume fraction f_i of any phase in the inclusion is given by

$$\begin{array}{}\text{(2)}& f_i={\displaystyle \frac{m_i{V}_{m_i}}{V}}.\end{array}$$

It is important to note that while the number of moles of each phase m_i remains constant because the inclusion is a closed system that does not undergo chemical exchange between the phases, the volume fractions f_i will vary with P and T because the phases have different elastic properties. We will show below how the volume fractions f_i vary with pressure.

The volume thermal expansion coefficient α of the mixture of the phases in the inclusion is obtained by taking the temperature derivative of Eq. (1):

$$\begin{array}{}\text{(3)}& \mathit{\alpha }={\displaystyle \frac{\mathrm{1}}{V}}{\displaystyle \frac{\partial V}{\partial T}}={\displaystyle \frac{\mathrm{1}}{V}}\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{m}_i{\displaystyle \frac{\partial V_{m_i}}{\partial T}}.\end{array}$$

The thermal expansion coefficient of a single phase is ${\mathit{\alpha }}_i=\frac{\mathrm{1}}{V_{m_i}}\frac{\partial V_{m_i}}{\partial T}$, so substitution into Eq. (3) shows that the thermal expansion of the mixture is the sum of the individual thermal expansion coefficients of the phases weighted by their volume fractions but not by the molar fractions of the phases:

$$\begin{array}{}\text{(4)}& \mathit{\alpha }=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{m}_i{\displaystyle \frac{V_{m_i}}{V}}{\mathit{\alpha }}_i=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{f}_i{\mathit{\alpha }}_i.\end{array}$$

The volume compressibility $\mathit{\beta }=\frac{\mathrm{1}}{V}\frac{\partial V}{\partial P}$ of the inclusion can be obtained in the same way by taking the derivative of Eq. (1) with respect to pressure:

$$\begin{array}{}\text{(5)}& \mathit{\beta }=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{\displaystyle \frac{m_i{V}_{m_i}}{V}}{\mathit{\beta }}_i=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{f}_i{\mathit{\beta }}_i.\end{array}$$

Equations of state are normally expressed not in terms of the compressibility but in its inverse, the bulk modulus $K=-V\frac{\partial P}{\partial V}=\frac{-\mathrm{1}}{\mathit{\beta }}$. From Eq. (5) the bulk modulus of the mixture of phases in the inclusion is thus

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{1}}{K}}=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{{\displaystyle \frac{f_i}{K}}}_i.\end{array}$$

This is the well-established result that the Reuss bound on the elastic properties of a mixture of phases all under the same hydrostatic pressure is determined, in general, as a linear sum of the compliances or compressibilities of the components and not as a linear sum of the moduli (e.g. Hill, 1963). The latter is the Voigt bound, which is appropriate for situations when all of the components of the mixture are subject to the same isotropic strain but not the same pressure. Although the Voigt bound is appropriate for the composite properties of a host and inclusion in the fictive “unrelaxed state” (Angel et al., 2014b) where the inclusion is subject to the volume strain imposed by the host mineral, the Voigt bounds are not relevant for the properties of a mixture including a fluid and are therefore not discussed further in this work.

The rate of change of the bulk modulus with pressure $K^{\prime }=\partial K/\partial P$ is also an important parameter of EoS. It can be obtained for the mixture of phases in the inclusion by taking the pressure derivative of Eq. (5); thus,

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\partial \mathit{\beta }}{\partial P}}=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{\displaystyle \frac{\partial \left(f_i{\mathit{\beta }}_i\right)}{\partial P}}=\sum _{i=\mathrm{1}}^{n\mathrm{phase}}\left[f_i{\mathit{\beta }}_i^{\prime }+{\mathit{\beta }}_i{\displaystyle \frac{\partial f_i}{\partial P}}\right],\end{array}$$

in which we use ${\mathit{\beta }}_i^{\prime }=\partial {\mathit{\beta }}_i/\partial P$. Equation (7) shows that the change in the compressibility of a mixture with pressure is more complicated than might be expected. It is made up of two contributions. The first, $f_i{\mathit{\beta }}_i^{\prime }$, is the sum over the compressibility derivatives of the individual phases, weighted by their volume fractions, and it represents the change in the total compressibility with pressure if the volume fractions of the phases f_i do not change with pressure. The second term represents the contribution from the changing volume fractions of the phases as pressure is changed and can lead to some unexpected properties. It can be evaluated by taking the pressure derivative of Eq. (2):

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\displaystyle \frac{\partial f_i}{\partial P}}& ={\displaystyle \frac{m_i}{V}}\left[{\displaystyle \frac{\partial V_{m_i}}{\partial P}}-{\displaystyle \frac{V_{m_i}}{V}}{\displaystyle \frac{\partial V}{\partial P}}\right]\\ & ={\displaystyle \frac{m_i{V}_{m_i}}{V}}\left[{\displaystyle \frac{\mathrm{1}}{V_{m_i}}}{\displaystyle \frac{\partial V_{m_i}}{\partial P}}-{\displaystyle \frac{\mathrm{1}}{V}}{\displaystyle \frac{\partial V}{\partial P}}\right]\\ & =f_i\left[{\mathit{\beta }}_i-\mathit{\beta }\right].\end{array}\end{array}$$

This shows that the volume fractions of the phases in mixtures remain constant only if their compressibilities (or bulk moduli) are the same as the compressibility of the mixture. If there are only two phases in the mixture, this would require the two phases to have identical compressibilities and thus EoSs. Substituting the result of Eq. (8) back into Eq. (7) and using Eq. (5) gives the pressure derivative of the Reuss bound on the compressibility:

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\partial \mathit{\beta }}{\partial P}}=-{\mathit{\beta }}^{\mathrm{2}}+\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{f}_i{\mathit{\beta }}_i^{\prime }+\sum _{i=\mathrm{1}}^{n\mathrm{phase}}{f}_i{\mathit{\beta }}_i^{\mathrm{2}},\end{array}$$

from which the pressure derivative of the Reuss bulk modulus of the mixture follows as

$$\begin{array}{}\text{(10)}& K^{\prime }={\displaystyle \frac{\partial K}{\partial P}}=K^{\mathrm{2}}{\displaystyle \frac{\partial \mathit{\beta }}{\partial P}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\beta }}^{\mathrm{2}}}}{\displaystyle \frac{\partial \mathit{\beta }}{\partial P}}.\end{array}$$

The form of these relationships between the properties of the individual phases and those of the mixture shows that, while the molar proportions of the phases in a mixture remain constant in a closed system such as an inclusion, the elastic properties of the mixture depend (Eqs. 4, 6, 10) on the volume fractions that change (Eq. 8) with P and T. This has the important consequence that it is not possible to define the parameters of an EoS for a mixture by simply taking an average of the EoS parameters of the phases at reference conditions weighted by either volume or molar fractions. Instead, the properties of a mixture can only be defined as the appropriate sums, given above, of the properties of the individual phases calculated at P and T from their individual EoS.

2.2 Mixtures in inclusions

Apart from the calculation of the elastic properties of the mixed-phase inclusion outlined in the previous section, host–inclusion calculations for multiphase inclusions can be based on the standard idealised model of an isotropic isolated spherical inclusion embedded within an isotropic homogeneous host phase (Angel et al., 2017b). The effect of the shapes of non-spherical multiphase inclusions on measured P_inc values can be corrected by a shape factor (Mazzucchelli et al., 2018). The final measured inclusion pressure P_inc can then be considered to arise from two contributions, P_thermo and ΔP_relax:

$$\begin{array}{}\text{(11)}& P_{\mathrm{inc}}=P_{\mathrm{thermo}}+\mathrm{\Delta }{P}_{\mathrm{relax}}.\end{array}$$

The first term, P_thermo, is the pressure generated in the inclusion due to the volume change imposed upon it by the volume change of the host on exhumation from entrapment to room conditions (Angel et al., 2017b). This is easily calculated from the EoSs of the host and the inclusion phases (e.g. Angel et al., 2014b, 2017b). However, it is a fictive pressure that is never actually measurable because an inclusion at P_thermo cannot be in mechanical equilibrium with its host at room pressure. If P_thermo is greater than room pressure, the inclusion therefore expands within the host and the inclusion pressure decreases. This has been described as the mutual elastic relaxation of the system and is denoted ΔP_relax (e.g. Angel et al., 2014b, 2017b; Zhang, 1998). In general, when P_thermo is more positive than the external final pressure, then ΔP_relax<0, and vice versa. This means that the final measured inclusion pressure P_inc always lies between P_thermo and the external pressure.

The magnitude of ΔP_relax can be calculated in several ways by relying on various assumptions. One approach uses the concept of the entrapment isomeke (Rosenfeld and Chase, 1961; Adams et al., 1975; Angel et al., 2014b), which is the line through entrapment conditions along which the volume ratios $V/V_{\mathrm{trap}}$ of a free host crystal and a free inclusion crystal would be equal. The pressure of the isomeke can be determined at any T from the EoS of the host and inclusion by finding the pressure at which their two $V/V_{\mathrm{trap}}$ curves cross (Fig. 2). The pressure of the entrapment isomeke at the temperature at which P_inc is measured is denoted P_foot. The entrapment isomeke is a thermodynamic concept whose position depends only upon the entrapment P and T and the EoSs of the host and inclusion. The change in inclusion volume along the entrapment isomeke is the same as for a free crystal under the same change in P and T. Therefore the inclusion pressure remains equal to the external pressure on the entrapment isomeke. Hence, the entrapment isomeke is useful because it separates the areas of P and T space where the inclusion is at higher pressures than the external pressure applied to the host from areas where the inclusion pressure is lower than the external pressure (e.g. Rosenfeld and Chase, 1961; Angel et al., 2015b).

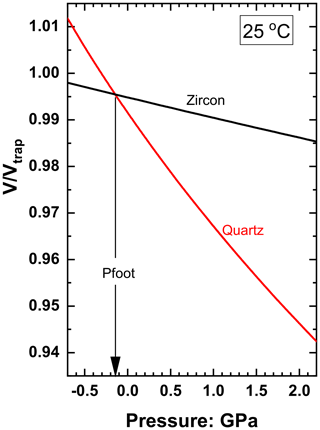
Figure 2 Plot of $V/V_{\mathrm{trap}}$ against pressure at 25 ^∘C for quartz and zircon for entrapment at 1.5 GPa and 900 ^∘C. The crossing point of these two curves corresponds to the pressure on the entrapment isomeke at 25 ^∘C, denoted as P_foot. EoS from Angel et al. (2017a) and Ehlers et al. (2022).

The slope of an isomeke between the host and inclusion can be calculated from their elastic properties:

$$\begin{array}{}\text{(12)}& {\left({\displaystyle \frac{\partial P}{\partial T}}\right)}_{\mathrm{isomeke}}={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{I}}-{\mathit{\alpha }}_{\mathrm{H}}}{{\mathit{\beta }}_{\mathrm{I}}-{\mathit{\beta }}_{\mathrm{H}}}},\end{array}$$

in which the subscripts “H” and “I” indicate the properties of the host and inclusion phases respectively. Because the inclusion pressure remains equal to the external pressure on the entrapment isomeke, the inclusion is in mechanical equilibrium with its host, and there is no relaxation. The isomeke therefore provides a reference state of uniform stress P_foot at room T from which ΔP_relax can be calculated isothermally (Angel et al., 2014b, 2017b). The effects of mixtures on ΔP_relax can be understood by using a linearised approximation of the approach of Angel et al. (2014b):

$$\begin{array}{}\text{(13)}& \mathrm{\Delta }{P}_{\mathrm{relax}}\sim {\displaystyle \frac{K_{\mathrm{I}}}{K_{\mathrm{H}}}}{K}_{\mathrm{21}}{P}_{\mathrm{foot}},\end{array}$$

in which $K_{\mathrm{21}}=\frac{K_{\mathrm{I}}-K_{\mathrm{H}}}{K_{\mathrm{I}}-\frac{\mathrm{4}}{\mathrm{3}}{G}_{\mathrm{H}}}$ is a function of the bulk moduli as well as the shear modulus G_H of the host.

2.3 Implementation in EosFit

The equations given in Sect. 2.1 have been coded into the EoS module of the CrysFML Fortran subroutine library (Rodriguez-Carvajal and Gonzalez-Platas, 2003) that underlies the EosFit suite of programs (Angel et al., 2014a; Gonzalez-Platas et al., 2016) for EoS calculations. While the properties of a mixture can be calculated at any P and T directly through these equations from the EoS of the individual phases, it is not possible to invert Eq. (1) in order to directly calculate the P at a known V and T. To overcome this problem the calculation of P is done in two steps within the EoS module of the CrysFML. First, a simple search in P at constant T is performed until the calculated volume V_cal is approximately equal to the specified V. Then V_cal−V is calculated for a series of P values, and the array of values is fitted with a spline to determine the pressure at which $V_{\mathrm{cal}}-V=\mathrm{0}$. The use of a spline interpolation means that the precision of the resulting pressure value is not significantly limited by numerical precision.

Calculations at any P and T of the elastic properties (K, K^′ and α), volume and pressure of mixtures of phases from their individual EoS can be performed in a dedicated utility, named mphase (for multiphase calculations), within the EosFit7c console program (Angel et al., 2014a). The program is freely available at http://www.rossangel.net in compiled form for Windows™, Linux™ and MacOS™ operating systems. The architecture of the EosFit7c program also allows it to be called from other software such as MATLAB™ to perform EoS calculations, including those in the mphase utility, without the need to cross-compile code directly with the CrysFML library.

The EoS parameters of individual phases can be loaded into the mphase utility from the standard “.eos” files used throughout the EosFit program suite. For convenience, the file format has been extended to allow the EoSs of several phases to be stored together in a single file. The mphase utility also includes the common EosFit7c commands to input the EoS directly or to modify EoS parameters and associated metadata. The EoS of fluid phases can be imported directly from tables of V at P and T values in text files. The elastic properties of fluid EoSs provided in this way are calculated by numerical differentiation and interpolation on the table values. In order for calculations in mphase to be meaningful, the pressure units for the bulk moduli of the various phases must all be in the same units (e.g. kbar or GPa) and the reference volume given for the EoS of each phase must be the molar volume in consistent units (e.g. cm³ mol⁻¹). This is checked by the mphase utility before calculations can be made, and inconsistencies are clearly reported to the user.

Within mphase the molar quantities of each phase, denoted m_i above, are termed the “stoichiometries” of the phases. Properties can be calculated and listed for both a fixed stoichiometry of a mixture over ranges of P and T or for ranges of stoichiometry and volume fractions at a single P and T. Isochors of mixtures can also be calculated. The use of negative stoichiometries for some phases enables the variation of ΔV of reactions to be calculated as a function of P and T. In studies of multiphase inclusions the stoichiometries of the phases within the inclusion are typically not known, but the volume fractions of the phases when the host is at room conditions can be measured or estimated. Therefore, mphase includes a command to calculate the stoichiometries from the volume fractions of the phases specified by the user.

Apart from the calculation of the elastic properties of the mixed-phase inclusion, all of the calculations for host and inclusion systems use the same methods as the EosFit-Pinc program (Angel et al., 2017b). Specifically, mphase allows the calculation of isomekes between a multiphase inclusion and its host, the entrapment isomeke given an observed final inclusion pressure P_inc and the P_inc from known entrapment conditions P_trap and T_trap. The value of ΔP_relax (Eq. 13) is calculated by the iterative method described in Angel et al. (2017b) which uses the elastic properties of the host at the final room conditions and the bulk modulus of the inclusion at the final P_inc. In the cases in which the calculation of P_foot fails, for reasons we discuss below, the relaxation is approximated by $\mathrm{\Delta }{P}_{\mathrm{relax}}\sim \frac{-\mathrm{3}{K}_{\mathrm{I}}}{\mathrm{4}{G}_{\mathrm{H}}}{P}_{\mathrm{inc}}$ (from Eq. 21 in Zhang, 1998), which is a linear-elastic approximation to our Eq. (13) (Appendix in Angel et al., 2014b). As we will show below, the cases in which P_foot cannot be calculated normally correspond to relatively small values of P_thermo and P_inc, and this approximation does not introduce any significant discontinuity in the trends of P_inc with inclusion composition.

3 Mixed fluid–solid inclusions

3.1 Properties of fluid plus solid mixtures

The properties of fluid and solid mixtures are most easily demonstrated with a simple mixture of one fluid and one solid mineral. We express the properties in terms of the volume fraction f_fluid in the mixture, with the volume fraction of the solid therefore being (1−f_fluid). Equations (3) and (5) clearly show that the thermal expansion coefficient and the compressibility of this mixture are linear in the volume fraction of fluid. However, EoSs are normally parameterised in terms of the bulk modulus, which is the inverse of the compressibility. As a consequence, the fact that fluids are typically much softer than solids means that the variation in the bulk modulus is very non-linear (Fig. 3a) and that the bulk modulus decreases very rapidly as small amounts of fluid are added to the solid; the properties of a mixture with small amounts of fluid are therefore very sensitive to the exact volume fraction of the fluid. At larger volume fractions of fluid the bulk modulus becomes close to that of the pure fluid. Thus, adding a small amount of solid to a fluid has no significant effect on the bulk modulus (Fig. 3a). The magnitude of the effects of adding fluid depends on the contrast in the bulk moduli of the fluid and solid. As Fig. 3a shows, the reduction in the bulk modulus upon mixing CO₂ with olivine is much more rapid than adding water, because CO₂ at room conditions is a gas and thus its bulk modulus is several orders of magnitude less than that of water. For practical applications to inclusions, the effects of less than a few volume percent of any fluid will not be those shown in Fig. 3 because the solid will remain as a connected network of crystals (e.g. Fig. 1c). Thus, the properties of the inclusion will remain between those of the minerals and the fluid until the solid phases no longer form a continuous network, at which point the properties will rapidly change to those shown in Fig. 3.

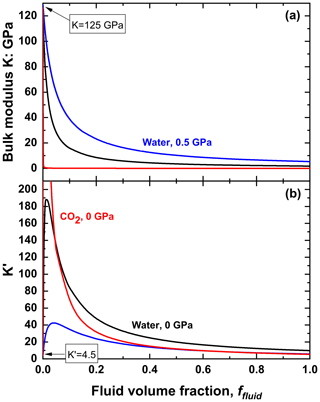
Figure 3 The variation of the (a) bulk modulus and (b) its pressure derivative K^′ of solid–fluid mixtures. Properties are shown for olivine with water at 0 GPa and 25 ^∘C (black lines) and 0.5 GPa and 25 ^∘C (blue lines). Properties for olivine plus CO₂ mixtures are shown as red lines. The EoSs used to calculate these properties are the BM3 isothermal model (Angel et al., 2018) for mantle composition (Fo90-92) olivine, the water EoS of Zhang and Duan (2005), and the CO₂ EoS of Pitzer and Sterner (1994).

The variation of the pressure derivative of the compressibility $\frac{\partial \mathit{\beta }}{\partial P}$ (Eq. 9) is almost linear in f_fluid because only the first term (in β²) is non-linear. But the behaviour of the pressure derivative K^′ of the bulk modulus is more complex in mixtures (Fig. 3b) and deserves some detailed explanation. It also arises from the much lower bulk modulus of the fluid compared to that of the solid. This means that there is a rapid decrease in the volume fraction f_fluid as pressure is increased, and this contributes to an increase in the bulk modulus of the mixture (Eq. 6, Fig. 3a) in addition to the normal stiffening of the individual phases with increasing pressure. This behaviour of K^′ can be simply expressed as

$$\begin{array}{}\text{(14)}& K^{\prime }={\displaystyle \frac{\partial K}{\partial f_{\mathrm{fluid}}}}\times {\displaystyle \frac{\partial f_{\mathrm{fluid}}}{\partial P}}.\end{array}$$

Both derivatives in Eq. (14) are negative, the value of $\frac{\partial K}{\partial f_{\mathrm{fluid}}}$ being the slope of the lines shown in Fig. 3a and $\frac{\partial f_{\mathrm{fluid}}}{\partial P}$ because the compressibility of the fluid is larger and thus more negative than the mixture of fluid plus solid (Eq. 8). Thus, the value of K^′ increases rapidly with the first addition of the fluid to the solid because $\frac{\partial K}{\partial f_{\mathrm{fluid}}}$ is very large and negative for small amounts of fluid. At much larger fluid fractions, corresponding to mixtures dominated by the fluid, $\frac{\partial K}{\partial f_{\mathrm{fluid}}}$ is smaller, so the value of K^′ is smaller, although it always remains higher than the K^′ of the stiffer solid (Fig. 3b). This significant non-linearity (Fig. 3b) can also be considered to be arising from the factor of $\frac{\mathrm{1}}{{\mathit{\beta }}^{\mathrm{2}}}$ (Eq. 10) relating K^′ to $\frac{\partial \mathit{\beta }}{\partial P}$. Differentiation with respect to f_fluid of the expression for β² (from Eq. 5) shows that β² has a minimum value at

$$\begin{array}{}\text{(15)}& f_{\mathrm{fluid}}^{max}={\displaystyle \frac{{\mathit{\beta }}_{\mathrm{solid}}}{{\mathit{\beta }}_{\mathrm{fluid}}-{\mathit{\beta }}_{\mathrm{solid}}}},\end{array}$$

at which point K^′ has a maximum value (Fig. 3b). The value of β² can never become zero because the bulk modulus must always be positive, so the maximum value of K^′ always remains finite. As pressure is increased the compressibility of the fluid increases faster than that of the solid, so β_fluid−β_solid (Eq. 15) becomes smaller, and the maximum in K^′ therefore shifts towards larger fluid fractions as shown in Fig. 3b for olivine plus water at 0.5 GPa. At the same time, the increase in $f_{\mathrm{fluid}}^{max}$ means that the maximum value of K^′ is reduced (Eq. 14) by increasing pressure. Conversely, if the contrast in the compressibilities between the solid and fluid is increased, for example on changing the fluid from water to CO₂, the maximum value of K^′ is increased and it occurs at smaller fluid fractions (Fig. 3b). This pattern of variation in elastic properties for a simple mixture of a fluid with a single solid will also occur for mixtures of several solid phases with a single fluid phase provided the fluid remains much softer than the solid minerals.

3.2 Effect of fluids on inclusions in a stiff host

In the absence of fluid, and assuming similar thermal expansion coefficients for the host and the inclusion, an inclusion that has a lower bulk modulus than its host would exhibit a positive P_inc when measured in the laboratory at room conditions. We will use olivine in diamond as an example because olivine inclusions in gem-quality diamonds are surrounded by a thin film of hydrous silicic fluid (Nimis et al., 2016). Such films seem to be almost ubiquitous around silicate and oxide inclusions in lithospheric diamonds (e.g. Nestola et al., 2018; Nimis et al., 2019), and their existence may explain the hydrostatic stress state of some of the inclusions (Angel et al., 2022a). Although there is evidence that the fluid has precipitated material after entrapment and that the fluid is not pure water, we will use the properties of water (Zhang and Duan, 2005) to illustrate the possible effects on P_inc of the presence of fluids in these inclusions.

The final pressures P_inc of inclusions can be understood in terms of how their isochors compare to their host and their isomekes with their host (e.g. Rosenfeld and Chase, 1961; Adams et al., 1975; Angel et al., 2014b). The slopes of isochors of a single phase i are given by ${\left(\partial P/\partial T\right)}_{V_i}={\mathit{\alpha }}_i{K}_i$. Although water has a much lower bulk modulus than olivine (Fig. 3a), it also has a much larger thermal expansion coefficient in this range of P and T, and, as a consequence, the isochors of both phases are very similar (Fig. 4).

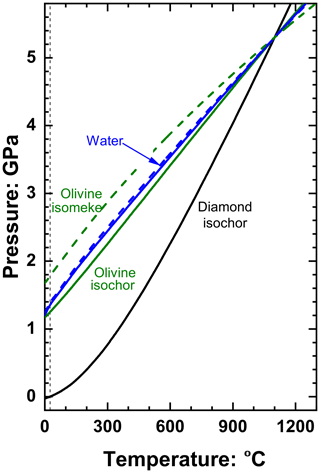
Figure 4 The isochors (solid lines) of diamond (Angel et al., 2015a), olivine (Angel et al., 2018) and water (Zhang and Duan, 2005) that all pass through 5.3 GPa and 1100 ^∘C. Dashed lines are the isomekes of water and olivine with diamond and represent the P and T required for the inclusion phase to have the same pressure as the external pressure applied to the diamond host after entrapment at 5.3 GPa and 1100 ^∘C.

The isochor of diamond through P=5.3 GPa and T=1100 ^∘C also passes through P=0.0 GPa and T=25 ^∘C. Thus, the volume of diamond would not change from entrapment at these conditions to the examination at room conditions. In this special case the volume of an inclusion phase trapped in the diamond at P=5.3 GPa and T=1100 ^∘C would not change on exhumation (apart from the mutual elastic relaxation), and therefore the P_thermo of the inclusion will be defined by the isochor of the inclusion phase through entrapment conditions. The similarity of the isochor pressures of water and olivine at 25 ^∘C (1.365 and 1.249 GPa respectively) therefore qualitatively suggests that the effect of water on the inclusion pressures of olivine may be smaller than might be expected from their great contrast in bulk moduli. The contrast between the elastic properties of diamond and water is extreme with α_H≪α_I and β_H≪β_I, so the slope of their isomeke is, from Eq. (12), very similar to that of the isochor of water (Fig. 4):

$$\begin{array}{}\text{(16)}& {\left({\displaystyle \frac{\partial P}{\partial T}}\right)}_{\mathrm{isomeke}}\sim {\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{I}}}{{\mathit{\beta }}_{\mathrm{I}}}}={\left({\displaystyle \frac{\partial P}{\partial T}}\right)}_{V_{\mathrm{inc}}}={\mathit{\alpha }}_{\mathrm{I}}{K}_{\mathrm{I}}.\end{array}$$

This is why the isochors of fluid inclusions in minerals can be used to estimate their conditions of entrapment (e.g. Roedder and Bodnar, 1980). By contrast, the much stiffer compressibility of olivine compared to that of water means that the isomeke of olivine with diamond for entrapment at P=5.3 GPa and T=1100 ^∘C lies at pressures significantly above those of its isochor (Fig. 4). The consequence is that, as water is added to an inclusion of olivine trapped at these conditions, the P_foot decreases quite rapidly. This contributes to a decrease in ΔP_relax (Eq. 13). The bulk modulus of the composite inclusion also falls rapidly (Fig. 3a), so $\frac{K_{\mathrm{I}}}{K_{\mathrm{H}}}$ also decreases and the amount of relaxation becomes smaller at larger fluid fractions (Fig. 5) and almost zero for a pure fluid inclusion. The result, for these entrapment conditions, is that P_inc increases with fluid content (Fig. 5). For lower entrapment pressures, such as P=4 GPa and T=1100 ^∘C, the P_foot of olivine is lower than that of pure water inclusions, so P_foot also increases with increasing fluid content, but the value of ΔP_relax is less than the previous entrapment example (Fig. 5). Quite surprisingly, this means the presence of pure water will increase the measured inclusion pressures of olivine inclusions in diamond when they have been trapped in the lithosphere or upper mantle.

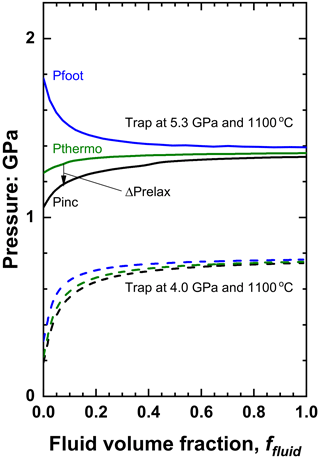
Figure 5 The variation of pressures of olivine plus water inclusions in diamond as a function of the fluid volume fraction for two different entrapment conditions. The value of $\mathrm{\Delta }{P}_{\mathrm{relax}}=P_{\mathrm{inc}}-P_{thermo}$ is indicated by the arrow. Note that although lower entrapment pressures lead to P_foot for olivine inclusions being less than for water, the trend of increasing inclusion pressure P_inc applies for all entrapment conditions.

Figures 5 and 6 show that the difference in P_thermo of pure solid inclusion compared to that of the pure fluid inclusion trapped at the same conditions is the primary control on whether fluid increases or decreases P_inc. For solid inclusions in diamond P_thermo tends to decrease as the bulk modulus of the solid increases, so inclusions of garnet (K₀ ∼ 170 GPa) and spinels (K₀ ∼ 190–200 GPa) have lower P_thermo and P_inc than olivines (K₀ ∼ 125 GPa) trapped at the same conditions, and thus the presence of fluid also raises their inclusion pressures. Coesite (K₀=101 GPa; Angel et al., 2001) and orthoenstatite (K₀=105 GPa; Angel and Jackson, 2002) are sufficiently soft that P_thermo and P_inc are significantly higher than water trapped at the same conditions, and thus the presence of fluid will, in contrast to the case of olivine, garnets and spinels, reduce the inclusion pressures (Fig. 6). The effect is particularly strong for coesite whose isomekes with diamond are approximately horizontal in P–T space (Angel et al., 2022a) as a result of its thermal expansion coefficient being very small (Kulik et al., 2018) and similar to that of diamond (see Eq. 12).

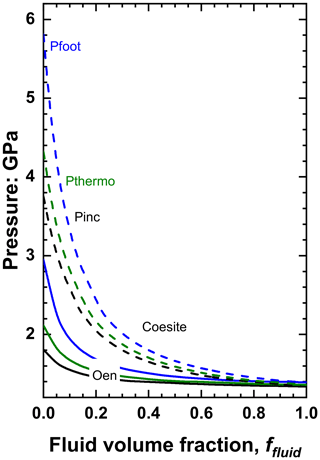
Figure 6 The variation of pressures of coesite plus water (dashed lines) and orthoenstatite plus water (solid lines) inclusions in diamond as a function of the fluid volume fraction for the same entrapment conditions as Fig. 4 (P=5.3 GPa and T=1100 ^∘C). The value of P_thermo for both minerals is higher than for pure water, so addition of fluid decreases the measured inclusion pressure P_inc in contrast to stiffer inclusion minerals such as olivine (Fig. 5).

3.3 Effect of fluids on inclusions in a soft host

The effect of the addition of the fluid to a solid inclusion phase that is stiffer than the host (the fluid always remaining softer than the host mineral) follows the same principles illustrated in Sect. 3.2. For zircon trapped in pyrope at metamorphic conditions, the effect of fluid is relatively minor, but this system serves to show how the effect of fluid can be reversed as entrapment conditions change. For entrapment at 3 GPa and 800 ^∘C the P_inc of pure water and pure zircon inclusions differ by less than 0.1 GPa, so the effect of adding water to a zircon inclusion is minimal (Fig. 7). For lower entrapment pressures (e.g. 2 GPa; Fig. 7) and/or higher entrapment temperatures, the addition of water lowers the P_inc, while P_inc is increased by the presence of water at higher pressures and lower temperatures of entrapment.

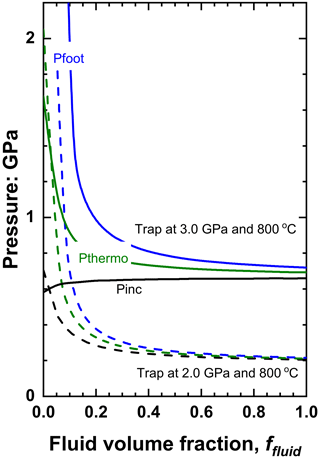
Figure 7 The variation of pressures of zircon plus water inclusions in pyrope as a function of the fluid volume fraction for two different entrapment conditions. Note that for entrapment at 3 GPa and 800 ^∘C the effect of water on the P_inc is small. Lower entrapment pressures (or higher temperatures) lead to water decreasing the P_inc.

Also note in Fig. 7 the divergence of P_foot to extreme values for low fluid contents in this system in which the solid inclusion phase is stiffer than the host. This arises because the addition of fluid to the solid inclusion reduces the bulk modulus of the inclusion and it becomes very similar to that of the host over a range of P, T and f_fluid. The resulting problems for host–inclusion calculations are difficult to illustrate with zircon in garnet because of the similarity of the bulk moduli of garnet and zircon (K₀ ∼ 170 and 225 GPa respectively), which means that the amount of fluid required to make the bulk modulus of the inclusion equal to that of the garnet is very small, around 1 vol %. Calculations at such low water contents are very sensitive to numerical round-off errors. We can better illustrate the concepts and difficulties with the system of zircon plus water in a quartz host, in which the much larger contrast in the bulk moduli moves the critical compositions to ∼ 6.5 vol % water at room conditions and ∼ 20 vol % at 1.5 GPa and 900 ^∘C (Fig. 8a).

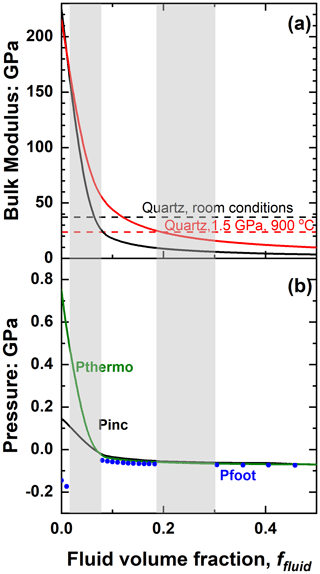
Figure 8 (a) The variation of the bulk modulus of zircon plus water mixtures as a function of fluid content (solid lines) for room conditions (black) and 1.5 GPa and 900 ^∘C (red). The values of the bulk modulus of quartz at the same conditions of P and T are indicated by the horizontal dashed lines. (b) Calculated inclusion pressures of zircon plus water inclusions in quartz trapped at 1.5 GPa and 900 ^∘C. The grey areas indicate where P_foot is not defined, corresponding to inclusion compositions whose bulk moduli are close to that of the quartz host at room conditions (left) and entrapment conditions (right). Note that the x axis only extends to 50 % water by volume. Pressures for more water-rich inclusions are very similar to those of an inclusion with 50 vol % water; see also the isomekes in Fig. 9.

Fluid-dominated inclusions in the system of zircon plus water in quartz with f_fluid > 0.3 (30 vol % fluid) have thermoelastic properties of the inclusion dominated by the properties of the fluid (Fig. 8a), so the entrapment isomeke closely follows that for pure water inclusions (Fig. 9). The resulting P_foot and P_inc are therefore very similar to those of pure water (Fig. 8b). As the f_fluid is reduced towards 0.2, the bulk moduli of the inclusion and the host become very similar near to the entrapment conditions, so the entrapment isomeke becomes very steep in P–T (Eq. 12) and does not extend to room T at reasonable or finite pressures. Therefore P_foot cannot be calculated, and ΔP_relax has to be approximated by the alternative expression of Zhang (1998). This does not introduce significant error because for these amounts of fluid P_thermo remains small and therefore ΔP_relax is small. At slightly lower f_fluid (in this case 0.08 to 0.18) the bulk moduli are sufficiently different at entrapment (Fig. 8a) for the entrapment isomeke (Fig. 9) to be well-defined. However, with decreasing P and T along the entrapment isomeke, the difference between the bulk moduli of the host and inclusion decreases and the isomeke steepens. In this example, this steepening is additionally modified by the softening of quartz associated with its α–β transition (Angel et al., 2017a), and the isomeke terminates. For other hosts without phase transitions, the isomeke would become vertical (Eq. 12). In both cases the entrapment isomekes do not extend continuously to room T. Nonetheless, the entrapment isomeke can still exist at lower T and still represents conditions under which the fractional volume change of the host and the inclusion from entrapment are equal (Fig. 9). At these lower temperatures it is not unusual to find the isomeke so strongly curved that there are two isomeke pressures for each T as shown for f_fluid=0.16 and 0.10 in Fig. 9. This arises from the composite inclusion being softer than the host while its K^′ is larger than the host due to the rapid decrease in fluid volume fraction with increasing pressure (Fig. 3b, Eqs. 7–10, 14). Consequently, the P–V line of the inclusion is strongly curved compared to that of the normal EoS of the host, so the curves of $V/V_{\mathrm{trap}}$ for the host and inclusion cross twice for a single pressure (see 10 vol % water curve in Fig. 10). Both crossing points represent the entrapment isomeke and thus possible values of P_foot. But the relevant isomeke pressure can be identified by interpolation or extrapolation from adjacent inclusion compositions with more normal isomekes and single values of P_foot from the same entrapment conditions. For this example, it is obvious that the correct P_foot to be used in the range f_fluid = 0.08–0.18 is the lower value that is very similar to that of the more water-rich inclusions. This can also be verified by comparing the final P_inc calculated from the two P_foot values to the Zhang (1998) approximation. At even lower fluid contents (f_fluid=0.02 to 0.06) the bulk modulus of the inclusion differs significantly from the host at entrapment conditions but instead becomes very similar to that of the host at room conditions (Fig. 8a), and, as a result, the curves of $V/V_{\mathrm{trap}}$ for the host and inclusion against P can become parallel, or not cross at all (see 4 vol % water curve in Fig. 10), so that P_foot is not defined. For these compositions, relaxation must be calculated with the approximation of Zhang (1998). Finally, at very low f_fluid (<0.02 for this example) the properties of the composite inclusion and thus the entrapment isomeke, P_foot and P_inc approach those of a pure zircon inclusion (Figs. 2, 9).

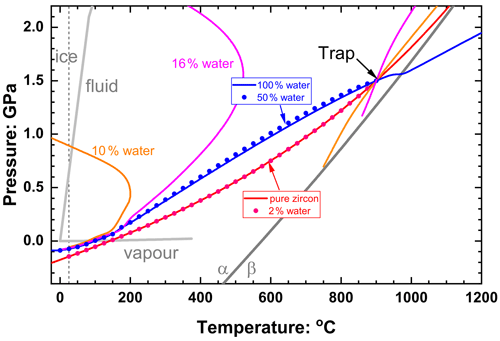
Figure 9 Entrapment isomekes for zircon plus water inclusions in quartz, entrapped at 1.5 GPa and 900 ^∘C. Inclusion compositions in volume percent fluid at entrapment conditions are indicated in the same colours as the isomekes. The red dots show that the entrapment isomeke for 2 % water is very similar to that of pure zircon, and the blue dots for 50 % water show that the entrapment isomekes for water-rich inclusions are indistinguishable from those of pure water. Note that the entrapment isomekes for 10 % and 16 % water are terminated below entrapment by the α–β phase transition in quartz (dark grey line) but exist as separate line segments at lower temperatures. The phase boundaries for water and quartz are shown in light grey. The transformation from α to β quartz is responsible for the deflection of the isomeke for pure water at ca. 1000 ^∘C.

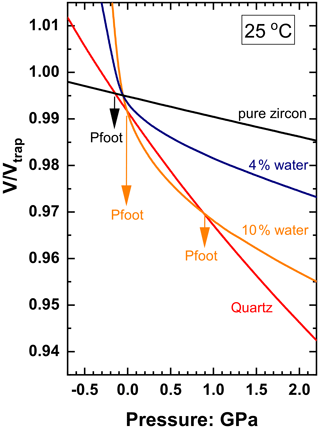
Figure 10 Plot of $V/V_{\mathrm{trap}}$ against pressure at 25 ^∘C for quartz and zircon plus water for entrapment at 1.5 GPa and 900 ^∘C to illustrate potential problems in calculating P_foot for systems in which the solid inclusion phase is stiffer than the host. Normally, the host and inclusion EoSs define a single crossing point and a unique value for P_foot as for pure zircon (black line). However, the curve for 10 vol % water plus zircon (at entrapment) crosses the curve for quartz twice, defining two values for P_foot. This is caused by the severe curvature of the $V/V_{\mathrm{trap}}$ line of the mixture due to its large value of K^′ (Eqs. 7–10, 14) compared to that for pure quartz. At lower water contents (e.g. 4 vol %) the large value of K^′ means that its $V/V_{\mathrm{trap}}$ line does not intersect the line for quartz, so P_foot is not defined.

So far, we have only considered the effects of a fluid for systems and entrapment conditions that would lead to the pure solid having a positive P_inc. When P_inc for a solid inclusion falls below P=0, this corresponds to a stretched state of the inclusion being kept in tension by bonding to the surrounding host mineral that has expanded more from entrapment than a free crystal of the inclusion phase would. Measured examples include quartz trapped in metamorphic garnet at high T and low P (Gilio et al., 2021b), apatite in olivine (Cisneros and Befus, 2020), and synthetic zircon in quartz (Gonzalez et al., 2022). If the P_inc of a pure fluid inclusion trapped at the same conditions would be positive, the addition of small amounts of fluid to the solid-phase inclusion would result in the calculated P_inc first becoming less negative and then positive. However, while EoSs of solids at negative pressures in the extensional regime are valid, at least for small negative pressures (Angel et al., 2019a), they are not valid for fluids or gases. Instead, P_inc will be buffered to the fluid–vapour equilibrium curve by the formation of a vapour bubble in the fluid phase, which for water lies below 0.02 GPa at temperatures below the critical point 374 ^∘C (near-horizontal grey line in Fig. 9). In these circumstances the entrapment isomeke should not be calculated from the measured P_inc. Instead, the P and T of homogenisation of the fluid component in the inclusion will define a point on the entrapment isomeke (Fig. 9).

3.4 Implications of fluids in inclusions

The examples discussed above show that the practical consequences of fluid contents of inclusions for the calculation of their entrapment conditions strongly depend on the elastic contrast between the solid phases within the inclusion and the fluid phase and between both of them and the host phase, as well as the entrapment conditions themselves. Together these control the dependence of P_inc on fluid content (e.g. Figs. 5, 6, 7 and 8). As an example, the influence of water on the pressures of olivine inclusions in diamonds is not as serious as might be expected from the contrast in elastic properties shown in Fig. 3. A 1 µm thick rim of water on an olivine-containing inclusion of 100 µm diameter represents ∼ 6 % of the total volume of the inclusion. The measured P_inc of such a water-containing inclusion trapped at 4 GPa and 1100 ^∘C will be almost 0.3 GPa higher than a pure dry olivine trapped at the same conditions (Fig. 5). If the P_trap is then calculated from the measured P_inc by ignoring the presence of fluid and using only the EoS for olivine, the P_trap will be 0.4 GPa too high at 1100 ^∘C. This error decreases with increasing depth of entrapment and is approximately zero for entrapment above 6.5–7 GPa. Therefore, failure to allow for the fluid content of olivine inclusions will result in estimates of depth of their entrapment that are in error by less than 12 km. This is probably significantly less than the errors introduced by not modelling the effects on P_inc of either the precipitation of solids from the fluid in these inclusions after their entrapment (Nimis et al., 2016) or the escape of fluids into cracks around the inclusions (e.g. Angel et al., 2022a). Similar levels of error, but in the opposite direction (Fig. 6), will arise from ignoring fluids in pyroxene inclusions. In contrast, the much stronger variation in P_inc with fluid content in coesite inclusions (Fig. 6) means that ignoring 6 vol % water leads to a larger underestimate of entrapment pressures, of the order of 1 GPa. This serves to illustrate that the potential errors due to low fluid contents must be carefully evaluated for each host–inclusion system in turn over the range of expected entrapment conditions. In addition, the contributions from uncertainties in the EoS of the fluid should also be evaluated by calculation with alternative EoSs when they are available.

4 Multiphase solid inclusions

4.1 Properties of solid mixtures

In the absence of a percolating fluid completely surrounding the solid crystals, the stress (and pressure) distribution in a mixture of solid phases, or indeed in a polycrystalline aggregate of one anisotropic phase, is inhomogeneous (e.g. Chap. 6 in Pollard and Fletcher, 2006) because the stress state at any point depends on how the crystal grains interact with one another (e.g. Fig. 1c). In this case the local distribution of the stress must be calculated from full mechanical calculations (e.g. Schmalholz et al., 2020). The average elastic response of an aggregate of a very large number of randomly oriented crystals falls between the Reuss and Voigt bounds. The latter corresponds to a state of uniform strain applied to each of the constituent crystals and leads to unequal pressures or stresses in each of them. The Reuss bound corresponds to what we have already described for fluid-dominated mixtures, in which all of the grains of solid are subject to the same uniform hydrostatic pressure, and it also implies that the boundaries between the grains are completely free to slip so that there are no coherency-induced strains when P or T are changed. In an inclusion the number of crystals is very limited, and it may be that neither bound applies. In principle, the stress state of inclusions containing multiple phases can be determined by measuring the stress or strain states of the individual component crystals by diffraction or spectroscopy. If the crystals are all at the same pressure, the elastic properties will be determined by the Reuss bound and the equations presented in Sect. 2.2, and they will be independent of the internal microstructure of the inclusion.

Under these assumptions, the calculations for multiphase solid inclusions are the same as for those involving a fluid, with the difference that the contrast in elastic properties will, in general, be much less because no mineral has elastic properties close to those of fluids such as water. Thus, the variation in the bulk modulus with volume fraction of solid phases is less curved than for fluids (e.g. compare Fig. 11a with Figs. 3 and 8), which means that the value of K^′ shows a much weaker maximum than found for mixtures with fluids in agreement with Eq. (14). This also means that the volume fractions of phases in a purely solid mixture change much less with P and T than those of a solid plus fluid. Similarly, the variation in thermal expansion coefficient in a mixture of solids will be much less than for a mixture of solid plus liquid (Eq. 4). Consequently, for inclusions containing phases that are either all more stiff or all less stiff than the host there are no difficulties in calculating inclusion pressures which will lie between those expected for the individual phases. Problems arise, as for fluids, when the bulk modulus of the host lies between those of the individual phases within the inclusion.

4.2 Hosts of intermediate stiffness

This case can be illustrated (Fig. 11a) by composite rutile plus amphibole (cummingtonite) inclusions that have been found in eclogitic garnets (e.g. Musiyachenko et al., 2021). Rutile is stiffer than garnet, and therefore pure rutile inclusions trapped in the eclogite field are calculated to have P_inc<0, while amphibole is considerably softer than garnet (Fig. 11a), so pure amphibole inclusions should therefore show positive P_inc. With the addition of amphibole to rutile inclusions the calculated P_inc will therefore initially become less negative, then zero, and then positive as shown in Fig. 11b. This figure also demonstrates a significant difference in the pressures of mixed-phase solid inclusions from those including fluids. The trend of P_inc for a mixture of solids is far closer to linear (Fig. 11b) than the trends seen with fluids (e.g. Figs. 5, 6, 7, 8), so the addition of a small amount of the stiffer solid component to the softer solid has an effect on P_inc that is similar in magnitude (but opposite in sign) to that of adding the soft component to the stiffer mineral (Fig. 11b).

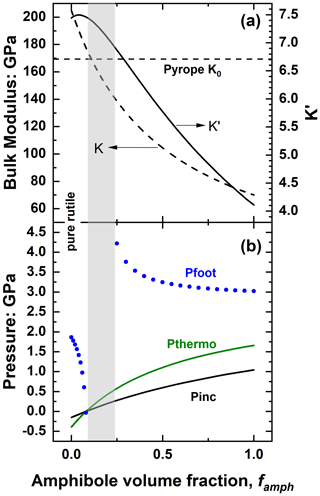
Figure 11 (a) The variation of the bulk modulus and K^′ of rutile–amphibole mixtures at room conditions as a function of the volume fraction of amphibole. (b) Calculated pressures of rutile plus amphibole inclusions trapped in pyrope garnet at 3 GPa and 800 ^∘C. The grey area indicates the compositions for which P_foot is either not defined or exceeds ±10 GPa. Calculations with the EoSs of pyrope (Angel et al., 2022b), rutile (Angel et al., 2020) and cummingtonite (Holland and Powell, 2011).

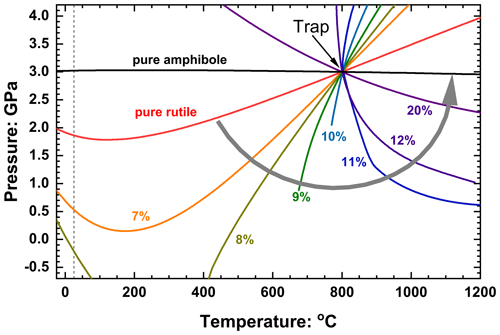
Figure 12 Entrapment isomekes for rutile plus amphibole inclusions trapped in pyrope garnet at 3 GPa and 800 ^∘C. Isomekes are labelled with the volume percent of amphibole in each inclusion, and the grey arrow indicates how the entrapment isomekes rotate with increasing amphibole content. The intersection of the entrapment isomekes with 25 ^∘C (vertical dashed line) correspond to the P_foot values shown in Fig. 11; note that the entrapment isomekes for inclusion with 9 vol %–12 vol % amphibole do not arrive to 25 ^∘C and therefore do not have a P_foot. Calculated with the EoSs of pyrope (Angel et al., 2022b), rutile (Angel et al., 2020) and cummingtonite (Holland and Powell, 2011).

The absence of P_foot values at intermediate compositions (Fig. 11b) can, as for the example of zircon plus water in quartz, be explained with calculations of the entrapment isomekes (Fig. 12) and the elastic properties of the phases. At entrapment conditions of 3 GPa and 800 ^∘C both rutile and amphibole have lower thermal expansion coefficients than pyrope, so any mixture of the two in an inclusion will similarly have a lower α (Eq. 4). Rutile is stiffer than pyrope over the entire P–T range of interest, which means that β_pyrope>β_rutile, and thus the entrapment isomeke of pure rutile in pyrope has a positive slope at these entrapment conditions. However, at low pressures at ambient T, α_pyrope is significantly less than that of rutile and amphibole, so the slope of the isomeke must become negative, leading to a minimum in the isomeke pressure at some intermediate T. As amphibole is added to a rutile inclusion, the bulk modulus of the inclusion at entrapment conditions is reduced towards that of the pyrope host, and the entrapment isomekes become steeper. The thermal expansion coefficient of rutile plus amphibole mixtures at any given P and T does not vary significantly with volume fraction, so the addition of amphibole to rutile leads to both a depression of the minimum of the entrapment isomeke and a decrease in P_foot, as shown for 7 vol % and 8 vol % amphibole in Fig. 12. Further small increases in amphibole content (e.g. 9 vol % and 10 vol %) continue to reduce the bulk modulus of the inclusion towards that of the host pyrope, leading to even steeper isomekes that become undefined at lower pressures because the $V/V_{\mathrm{trap}}$ curves of the host and inclusion no longer have a crossing point, a situation similar to that shown in Fig. 10 for the inclusion containing 4 vol % water. For such compositions, the entrapment isomeke also exists at temperatures far below room T but not at room T, and thus a P_foot at room T does not exist. At ca. 11 vol % amphibole, the isomeke becomes vertical at entrapment conditions. At pressures just below entrapment the bulk modulus of the host is greater than that of the inclusion, so β_pyrope<β_inc, leading to an isomeke with a negative slope. But the larger K^′ of the inclusion mixture (Fig. 11a) causes the bulk modulus of the inclusion to increase more rapidly than that of the pyrope host with increasing pressure, with the result that above the entrapment pressure the situation is reversed with K_pyrope<K_inc and β_pyrope>β_inc, so the entrapment isomeke has a positive slope. Thus, the entrapment isomeke is curved towards higher temperatures (Fig. 12), with the P–V curves at any temperature resembling those of the inclusion of 10 vol % water shown in Fig. 10. With a further increase in amphibole content the bulk modulus of the inclusion mixture falls below that of the host, so the isomeke slope at entrapment has a negative slope. By 20 vol % the slope is sufficiently shallow that the higher K^′ of the inclusion no longer has the effect of curving the isomeke back on itself, so P_foot at room T exists but is larger than 10 GPa. Further increase in amphibole content decreases the contrast between the bulk moduli of the inclusion and host (Fig. 11a), making the isomekes shallower until that for 100 % amphibole is almost flat because of the similarity of the thermal expansion coefficients of amphibole and pyrope at 3 GPa for all temperatures. Note that this anti-clockwise rotation of the isomekes as amphibole is added to rutile means that the isomekes for mixtures of the two phases never lie between those of the pure phases (Fig. 12).

This example also shows that the exact behaviour of entrapment isomekes is very sensitive to the details of the EoSs of both the host and inclusion phases and the relative change in their elastic properties with P and T, especially at compositions for which the thermal expansion and/or compressibility of the inclusion are very similar to those of the host mineral. As one example, if the EoS of Milani et al. (2015) for pyrope is used instead of that of Angel et al. (2022b), then the isomekes for 10 vol %–12 vol % amphibole have the opposite curvature to those shown in Fig. 12 and instead curve back to yield two values of P_foot at room temperature. P_inc for these entrapment conditions is calculated to be zero not at ∼ 11 vol % but at ∼ 14 vol % amphibole (Musiyachenko et al., 2021). Nonetheless, the comparison of Fig. 11 with Fig. 9 of Musiyachenko et al. (2021) shows that while relatively small changes in mineral elastic properties can significantly change the isomekes for compositions whose properties are close to those of the host, the values of P_thermo and P_inc vary much less and are therefore more robust. Conversely, the calculation of entrapment isomekes from measured values of P_inc becomes less reliable as the properties of the inclusion approach that of the host, whether at the final conditions or at conditions around entrapment.

The example of rutile inclusions in garnet also serves to illustrate one further point. Measurements of pure rutile inclusions generally show them to be at room pressure (Musiyachenko et al., 2021; Cisneros and Befus, 2020) instead of having negative P_inc expected from calculations. This does not indicate that the calculations described here are incorrect but shows that instead of being “stretched” into tension by bonding to the surrounding host garnet, the rutile inclusion crystals have been released by the host. The inclusions must therefore include either a void space due to contraction of the rutile back to the volume of a free rutile crystal at room conditions or an interface region of a lower-density material (Alifirova et al., 2022). In such cases we then expect P_inc=0 for amphibole–rutile mixtures for which the calculated P_inc<0 and then increasing positive values of P_inc as the amphibole content is increased further. The measured P_inc=0 for inclusions that have undergone contraction cannot be used to infer entrapment conditions using the methods described in this paper.

5 Summary

Mixtures of mineral phases are, of course, common as rocks. The thermodynamic properties of a mixed-phase inclusion, which are the same as those of the same mixture in a rock closed to chemical exchange, are not simple sums of the properties of the individual phases. This means that it is not possible to define the parameters of a single EoS for a mixture by simply taking an average of the EoS parameters of the phases at reference conditions weighted by either volume or molar fractions. Thermodynamic calculations of phase equilibria in rocks normally also consider that the P and T are externally imposed and that the volume of the system is free to respond to changes in these two intensive variables and is not modified by elastic interaction between the phases. Multiphase inclusions obviously differ from mixtures of phases in rocks in two important respects; the volume of the system is imposed by the host mineral (in response to the external P and T) which also interacts elastically with the inclusion. When the host–inclusion system is subject to uniform temperature, the inclusion pressure then becomes the dependent variable and can be calculated as the sum of two contributions (Eq. 11). The first, P_thermo, arises from the imposition of the change in the volume of the host mineral on the closed inclusion and is calculated without ambiguity from the EoS of the host and that of the phases comprising the composite inclusion. The second, ΔP_relax, arises from the elastic interaction between the inclusion and the host (e.g. Angel et al., 2014b, 2017b; Zhang, 1998). Calculations for multiphase inclusions have been implemented in the EoS module of the CrysFML Fortran subroutine library (Rodriguez-Carvajal and Gonzalez-Platas, 2003) and made available to users in the EosFit7c program (Angel et al., 2014a). If it is assumed that the properties of a solid solution are ideal and the coefficients of volume compressibility and thermal expansion vary linearly with molar proportions of the end-members (but see Myhill, 2018), then the equations given here and the mphase utility of EosFit7c can also be used to calculate the EoS of any composition in the solid solution.

We have shown that, as for single-phase inclusions, it is the contrast in the bulk moduli and the thermal expansivities between the host and the inclusion that determines P_thermo, which is quite often more important than the relaxation in determining the final inclusion pressure. Problems and uncertainties arise when the properties of the inclusion become similar to those of the host. This will always occur for certain volume fractions in two-phase inclusions when one phase is stiffer than the host and the other softer, whether the softer phase is a fluid or a solid. At these inclusion compositions the entrapment isomekes can become vertical in P–T space and can become undefined, as illustrated by a zircon plus 4 vol % water inclusion in quartz (Fig. 10). Often associated with such behaviour is the occurrence of entrapment isomekes that are so strongly curved that two P_foot are defined for a given temperature (Fig. 10), creating difficulties for the calculation of ΔP_relax. A third possibility that we have not illustrated is when the curves of $V/V_{\mathrm{trap}}$ for both the host and inclusion become identical over a pressure range because both K and K^′ of host and inclusion are the same. For this last case there is no unique P_foot. These situations only affect the ability to calculate the entrapment isomeke and P_foot, while P_thermo remains well-defined in all cases and the relaxation can be approximated by other methods not involving P_foot. This can be understood in another way by considering a small portion of a single mineral grain as an inclusion with exactly the same composition and EoS as its surrounding host. Then the “inclusion”, which is really part of the host crystal, will always be at the same P and T as the host. Therefore, the host and inclusion have the same fractional volume change from entrapment to any other P and T, the isomeke is no longer a unique line in P–T space, and P_foot cannot be defined. Nonetheless, in this special case P_thermo=P_inc are always the same as the external pressure, and thus P_thermo can be calculated from the EoS of the mineral. In the cases where P_foot cannot be determined, an alternative method of calculating ΔP_relax must be employed. We have found that a linear-elastic approximation to Eq. (13) provides a good estimate of ΔP_relax as $\frac{-\mathrm{3}{K}_{\mathrm{I}}}{\mathrm{4}{G}_{\mathrm{H}}}{P}_{\mathrm{inc}}$, but there are other alternative methods (e.g. Gonzalez et al., 2021; Zhong et al., 2021; Morganti et al., 2020) that should converge to very similar values of P_inc.

The calculated inclusion pressures depend on the volume fractions of the phases in the inclusion, which can be measured or estimated by a variety of methods including 3D Raman mapping (e.g. Musiyachenko et al., 2021), diffraction or optical imaging of the entrapped inclusion, or mapping of an inclusion exposed for further analysis, for example by microprobe. The sensitivity, and hence reliability, of calculated entrapment pressures to the volume fractions of the constituent phases depends on the contrast in the elastic properties of the inclusion phases themselves. For inclusions containing two or more solid phases the calculated P_inc values for the same entrapment conditions are approximately linear with the volume fractions of the phases (e.g. Fig. 11), and the same applies to P_trap values calculated from measured P_inc. The uncertainty in P_trap for mixed solid inclusions therefore depends on the contrast in elastic properties, and especially bulk moduli, of the phases involved. If this contrast is small, then P_trap values will be insensitive to estimates of the volume fractions of the phases in the inclusion. Conversely, although it might be thought that the large contrast between the bulk moduli of solids and fluids would always lead to very strong variations in P_inc values with the amount of fluid in the inclusion, this is not always the case because there can be a compensating effect of the contrast in thermal expansion coefficients (e.g. Fig. 4). For example, the variation in P_inc values with fluid fraction in silicate inclusions in diamond differs considerably between olivine, coesite and orthopyroxene (Figs. 5, 6). Therefore, no general guidelines can be given for the sensitivity of P_trap values to volume fractions of fluids, but we have provided the tools for calculations to be made for any inclusion system.

The examples that we have discussed illustrate that the measured P_inc of mixed-phase inclusions must be interpreted with care. In addition to considering the uncertainties that may be introduced into host–inclusion calculations by uncertainties in phase fractions in the inclusion, and when the properties of the two become similar, one also should consider whether the inclusion has undergone reactions or transformations of any sort between the phases. Such changes would affect both the volumes of the phases due to changes in composition and their elastic properties and cannot be easily generalised. They are therefore excluded from our current analysis because they should be analysed on a case-by-case basis. One can, however, make the general statement that any reactions or transformations in the inclusion that would lead to an increase in the volume of an unconstrained system will result in the inclusion pressure being buffered to a higher value than expected had the reaction or transformation not occurred (Gillet et al., 1984; Perrillat et al., 2003; Anzolini et al., 2016; Arlt and Angel, 2000).

Lastly, careful consideration must be given to the microstructure of the inclusion before applying the analysis described in this paper. Our analysis strictly only applies to inclusions in which there are no significant elastic interactions between the solid phases, a situation which occurs when the crystals are bathed in sufficient fluid (Fig. 1); one can say that the fluid percolates across the inclusion but the solids do not. As the amount of fluid is decreased there will be a point at which the solids also percolate and form a continuous network (e.g. Fig. 1c). This will lead to stress gradients within the solid grains, and the methods presented here should be used with caution unless it can be demonstrated that the mineral grains are, on average, all at the same pressure and that the stress gradients are limited either in magnitude or extent within the grains. Otherwise, the stress state of multiphase inclusions must be analysed explicitly to account for the elastic interaction between the grains, especially for microstructures in which the elastic interactions are expected to be significant and the stress state is unlikely to be isotropic and hydrostatic. Examples would include inclusions within inclusions or grains containing coherently exsolved phases.

Appendix A: Definition of symbols used in this paper

Equation of state parameters, single phases
$V_{m_i}$	Molar volume of phase i
αi	Thermal expansion coefficient of phase i
βi	Volume compressibility of phase i
Ki	Bulk modulus (inverse of volume compressibility) of phase i
$K_i^{\prime }$	Pressure derivative of the bulk modulus of phase i;
	a subscript 0, as in V0 or K0, indicates the property at reference conditions
Parameters for mixtures of phases
mi	Number of moles of phase i in a mixture (constant in a given mixture)
fi	Volume fraction of phase i in a mixture (varies with P and T)
V,K, K′, α, β	Equation of state parameters of a mixture
Inclusion pressures
Ptrap	The pressure of entrapment of the inclusion
Ttrap	The temperature of entrapment of the inclusion
Pinc	The final measured pressure of the inclusion, normally when the host mineral is at room conditions
Pfoot	The pressure of the entrapment isomeke at the temperature of measurement of the inclusion pressure Pinc
Pthermo	The pressure the inclusion would have if there was no elastic relaxation; it is the pressure of the inclusion subject to the volume change in the host
ΔPrelax	The pressure change in the inclusion due to the mutual elastic relaxation: $\mathrm{\Delta }{P}_{\mathrm{relax}}=P_{\mathrm{inc}}-P_{\mathrm{thermo}}$
KH,αH	Bulk modulus and thermal expansion coefficient of the host mineral
GH	Shear modulus of the host mineral
KI, αI	Bulk modulus and thermal expansion coefficient of the inclusion