Relatively oxidized conditions for diamond formation at Udachnaya (Siberia)

Thanks to the physical strength of diamonds and their relatively unreactive chemical nature, their mineral inclusions may remain exceptionally preserved from alteration processes and chemical exchanges with surrounding minerals, fluids and/or melts following diamond formation. Cr-bearing spinels are relatively common inclusions found in peridotitic diamonds and important oxybarometers providing information about the oxygen fugacity (fO₂) of their source mantle rocks. Here, we investigated a magnesiochromite–olivine touching pair in a diamond from the Udachnaya kimberlite (Siberia) by in situ single-crystal X-ray diffraction and energy-domain synchrotron Mössbauer spectroscopy, aiming to constrain the physical–chemical conditions of diamond formation and to explore the redox state of this portion of the Siberian craton when the diamond was formed.

The P–T–fO₂ entrapment conditions of the inclusion pair, determined by thermo- and oxybarometric analyses, are ∼ 5.7(0.4) GPa and ∼ 1015(50) ^∘C (although entrapment at higher T and re-equilibration during subsequent mantle storage are also possible) and fO₂ near the enstatite–magnesite–olivine–diamond (EMOD) buffer. The determined fO₂ is similar to, or slightly more oxidized than, those of xenoliths from Udachnaya, but whilst the xenoliths last equilibrated with the surrounding mantle just prior to their entrainment in the kimberlite at ∼ 360 Ma, the last equilibration of the inclusion pair is much older, occurring at 3.5–3.1, ∼ 2 or ∼ 1.8 Ga before final encapsulation in its host diamond. Hence, the similarity between xenoliths and inclusion fO₂ values indicates that the modern redox state of this portion of the Siberian lithosphere was likely attained relatively early after its formation and may have persisted for billions of years after diamond formation, at least at the local scale. Moreover, the oxygen fugacity determination for the inclusion pair provides direct evidence of diamond formation near the EMOD buffer and is consistent with recent models suggesting relatively oxidized, water-rich CHO fluids as the most likely parents for lithospheric diamonds.

1 Introduction

Virtually all mineral inclusions in diamond (98 %) formed beneath cratons at depths between about 130 and 230 km (i.e. lithospheric), with the remainder forming in the asthenosphere, transition zone or lower mantle (i.e. sub-lithospheric) (e.g. Kaminsky et al., 2001; Stachel and Harris, 2008; Shirey et al., 2013; Stachel et al., 2022). Once trapped in their diamond hosts, these inclusions remain uncorrupted over geological time and represent key geological samples from otherwise inaccessible regions of our planet. Furthermore, these minerals can reveal the physical–chemical environment in which their host diamonds were formed (Bulanova et al., 2010; Stachel and Luth, 2015; Jean et al., 2016; Nimis et al., 2016; Nestola et al., 2018).

Cr-bearing spinels (Mg, Fe²⁺)(Cr, Al, Fe³⁺)₂O₄ (mainly magnesiochromites, hereafter mchr in the singular) are among the more common inclusions found in the peridotitic suite of lithospheric diamonds (e.g. Sobolev, 1977; Meyer, 1987; Stachel and Harris, 2008) as well as a recurrent accessory phase in ultramafic rocks. Despite their accessory nature (Cr-bearing spinels are disseminated in quantities of less than 3 % in on- and off-craton peridotite xenoliths; Pearson et al., 2003), they are important petrogenetic and oxybarometric indicators, providing information about the physical–chemical conditions under which their host rocks formed (e.g. O'Neill and Wall, 1987; Ballhaus et al., 1991; Barnes and Roeder, 2001; Miller et al., 2016). Oxygen fugacity, fO₂, is the thermodynamic variable that allows quantification of the chemical potential of oxygen in reactions where at least one element changes its oxidation state between the reagents and products. In mantle peridotites, fO₂ is estimated from the compositions of coexisting Fe-rich minerals, such as olivine, orthopyroxene, spinel and garnet. Essentially, fO₂ reflects Earth's mantle oxidation state, which can control the speciation of carbon in fluids or melts and governs the stability of carbon-bearing phases, such as diamond and carbonate minerals (e.g. Frost and McCammon, 2008; Stagno et al., 2013).

Here, we provide the first oxygen fugacity estimate for a mchr–olivine touching inclusion pair still trapped in a diamond (Oli-CHR1) from the Udachnaya kimberlite (Siberia, Russia). The diamond, previously investigated by Nestola et al. (2014) and Nimis et al. (2016, 2019), was recovered from the run-of-mine production, the vast majority of which is from kimberlite and most unlikely from any rare accompanying xenoliths. The colourless diamond is octahedral in shape with most faces showing bevelled edges. As seen in Fig. 1, mchr dominates the inclusion pair, which is situated in a peripheral position in the diamond. Thermo-/oxybarometric analysis of the inclusion pair determined the P–T–fO₂ conditions at the time of its entrapment in the host diamond, and from this result, the physical conditions under which the crystallization of Oli-CHR1 diamond occurred could be inferred, and additionally information about the redox state of this portion of the Siberian craton at the time of diamond formation could be provided. Our knowledge of the redox and thermal state of the mantle under Udachnaya largely relies on data obtained from mantle xenoliths in the kimberlite (Ionov et al., 2010; Goncharov et al., 2012; Yaxley et al., 2012; Doucet et al., 2013; Miller et al., 2016; Liu et al., 2022). These data are supposed to constrain the physical–chemical conditions of the cratonic mantle at the time of kimberlite eruption (360 ± 7 Ma; Kinny et al., 1997) but do not generally probe the redox state of the Siberian craton at an early stage of its geological history. Despite the age of our diamond being unknown, previous geochronological work on Udachnaya diamonds has suggested two major peaks of diamond formation, dated to 3.5–3.1 and ∼ 2 Ga (Richardson and Harris, 1997; Pearson et al., 1999a, b), although slightly younger ages, 1.8(5) Ga, were also obtained (Wiggers de Vries et al., 2013). Therefore, the fO₂ recorded by inclusions in Udachnaya diamonds allows the earlier redox state of the source mantle to be evaluated. By comparing fO₂ for this inclusion pair with those of xenoliths from the same depth (ca. 180 km), we will place constraints on the redox state evolution of the Siberian cratonic lithosphere from diamond formation to kimberlite eruption. The determined fO₂ for our inclusion pair also establishes a direct link to the redox conditions for diamond formation in the lithospheric mantle and will be compared with theoretical predictions based on thermodynamic modelling of CHO fluids (Luth and Stachel, 2014).

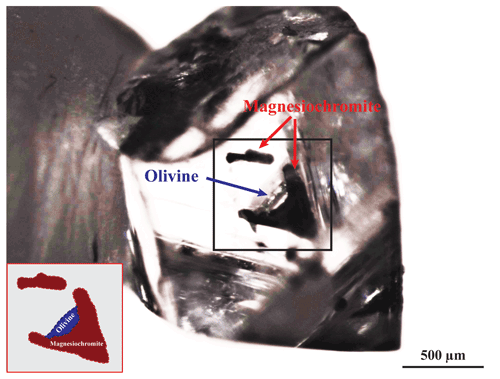
Figure 1 Close-up photograph of the Oli-CHR1 diamond shows the studied mchr–olivine inclusion pair (see also the simplified sketch of the inclusion pair, bottom left corner) and a separate elongated mchr inclusion. The larger crystal is principally cuboctahedral in shape, and both mchr inclusions are deep cherry red. The colourless olivine inclusion is attached to the larger mchr crystal, as shown. Photograph from Fabrizio Nestola's lab.

2 Experimental approach

In this work, an in situ characterization of the inclusion chemical composition was carried out by using non-destructive techniques. The sample (see Fig. 1) was analysed by (i) energy-domain synchrotron Mössbauer spectroscopy (SMS) and (ii) single-crystal X-ray diffraction (SCXRD).

2.1 Synchrotron Mössbauer spectroscopy

The SMS measurements were conducted at the nuclear resonance beamline ID18 (Rüffer and Chumakov, 1996) at the European Synchrotron Radiation Facility (ESRF), Grenoble, during operation in multibunch mode ($\mathrm{7}/\mathrm{8}+\mathrm{1}$ filling). This source provides ⁵⁷Fe resonant radiation at 14.4 keV within a bandwidth of 15 neV which is tuneable in energy over a range of ±0.6 µeV (i.e. ±12 mm s⁻¹) (Potapkin et al., 2012). The X-ray beam emitted by the SMS was focused to a 16 vertical × 15 horizontal µm spot size using Kirkpatrick–Baez mirrors. Before and after sample measurement, the SMS linewidth was controlled using a K₂Mg⁵⁷Fe(CN)₆ reference single-line absorber. The velocity scale (±5 mm s⁻¹) was calibrated relative to a 25 µm thick natural α-Fe foil. For locating the inclusion in the X-ray beam, the dedicated experimental protocol described in Nestola et al. (2016) was followed.

The acquired spectrum was fitted with a full transmission integral and a normalized Lorentzian-squared source line shape, using the software package MossA (Prescher et al., 2012). A linear function was applied to model the background.

2.2 Single-crystal X-ray diffraction

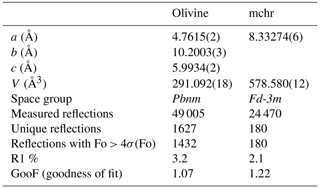
The SCXRD measurements for both minerals were conducted at the Department of Geosciences, University of Padua, with a Rigaku Oxford Diffraction SuperNova diffractometer, equipped with a Mo-target X-ray micro-source operating at 50 kV and 0.8 mA and a PILATUS 200 K Dectris hybrid pixel array detector (HPAD). The sample-to-detector distance was 68 mm, and the X-ray beam size was 0.12 mm. Data reduction was performed using the CrysAlisPro software (Rigaku Oxford Diffraction, version 40.64.67a), which allows the integration of the measured intensities and applies corrections for Lorentz-polarization effects. Unit-cell parameters along with information related to data collection and refinement details (see below) are reported in Table 1.

Table 1 Unit-cell parameters, data collection information and refinement details for the touching olivine and mchr inclusion in the studied diamond. Note the remarkable agreement factors of the determined crystal structures of both the olivine (R1 % = 3.2 %) and mchr (R1 % = 2.1 %) inclusions.

3 Results

3.1 Synchrotron Mössbauer spectroscopy

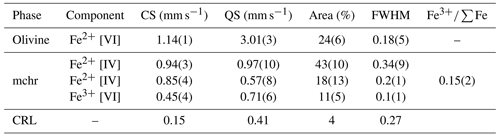
The resulting spectral model for the mchr (Fig. 2) shows three doublets with equal relative peak widths and areas: two are assigned to tetrahedrally coordinated Fe²⁺ and the remaining one to octahedrally coordinated Fe³⁺. This result indicates a typically ordered distribution of Fe²⁺ and Fe³⁺ in the chromite, consistent with current crystal–chemical models (see Li et al., 2002). The spectral model for the olivine (e.g. Canil and O'Neill, 1996) includes two doublets related to the two octahedrally coordinated Fe²⁺ in the non-equivalent M1 and M2 sites, there being negligible or no Fe³⁺ content. However, only one doublet with equal relative peak widths and areas can be used to fit the olivine spectrum (e.g. Dyar et al., 2006) (Fig. 2). Also shown in Fig. 2 is the low-velocity component represented by the compound refractive lens (CRL), which is used to decrease the divergence of the beam incident to the synchrotron Mössbauer source (Potapkin et al., 2012). As it contains some iron, CRL hyperfine parameters (known from independent measurements) are accounted for in the SMS spectrum. Hyperfine parameters obtained for each specific iron structural site are reported in Table 2.

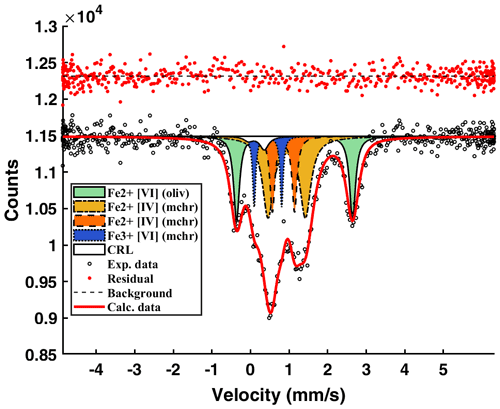
Figure 2 Energy-domain SMS spectrum of the studied mchr–olivine inclusion pair showing the contribution of both crystals. Fe²⁺ [VI] (oliv) denotes octahedrally coordinated Fe²⁺ in olivine; Fe²⁺ [IV] (mchr) denotes tetrahedrally coordinated Fe²⁺ in mchr; Fe³⁺ [VI] (mchr) denotes octahedrally coordinated Fe³⁺ in mchr; CRL denotes compound refractive lens; Exp. data denotes experimental data; Calc. data denotes calculated data. Total absorption ∼ 22 %.

Table 2 Hyperfine parameters determined from the fitting of the SMS spectrum. CS (mm s⁻¹) denotes centre shift; QS (mm s⁻¹) denotes quadrupole splitting; FWHM denotes full width half maximum; Fe²⁺ [VI] denotes octahedrally coordinated Fe²⁺; Fe²⁺ [IV] denotes tetrahedrally coordinated Fe²⁺; Fe³⁺ [VI] denotes octahedrally coordinated Fe³⁺; CRL denotes compound refractive lens.

3.2 Single-crystal X-ray diffraction

Structure refinement was performed using the SHELX program in the WinGX package (Farrugia, 2012; Sheldrick, 2015) in the Fd-3m space group for mchr and Pbnm space group for olivine, starting from published atomic coordinates (Nestola et al., 2011, 2019). CIF files with full refinement details are available in the Supplement. Ionic scattering curves were taken from the International Tables for X-ray Crystallography (Wilson, 1995), and anisotropic thermal parameters were refined for all atoms following Angel and Nestola (2016). The cationic distribution at the two different crystallographic sites for each inclusion was indirectly retrieved by refining the site occupancy factor of these sites (see Nestola et al., 2011, for a detailed review).

For olivine, this yielded the chemical composition (Mg${}_{\mathrm{0.925}\left(\mathrm{2}\right)}^{\mathrm{2}+}$Fe${}_{\mathrm{0.075}\left(\mathrm{2}\right)}^{\mathrm{2}+}$)₂SiO₄, corresponding to Fo_92.5. Possible contributions from Ca, Ni, Ti, Mn, Na, Cr and K were not considered, as these elements altogether typically account for ca. 0.01 atoms per unit formula (a.p.f.u.) in mantle olivines. For example, based on 831 reviewed samples of olivine inclusions in diamonds, Stachel and Harris (2008) showed the typical content of Ni was ca. 0.007 a.p.f.u. and the total content of other minor elements amounted to a negligible average of 0.007 a.p.f.u. The chemical composition determined is well within the compositional field for olivine inclusions in diamond from Russian (Yakutian) kimberlites (Fo₉₁ to Fo₉₄; Sobolev et al., 2009).

The mchr has a more complex crystal chemistry than olivine and is expected to host Mg²⁺ and Fe²⁺ in the tetrahedral site and Cr³⁺; Al³⁺; Fe³⁺; and, among others, traces of Ti⁴⁺ in the octahedral site. In this study, the cation distribution at the tetrahedral site was retrieved by refining the site occupancy factor, but for the octahedral site, the Fe³⁺ content was calculated from the synchrotron Mössbauer ${\mathrm{Fe}}^{\mathrm{3}+}/\sum \mathrm{Fe}$ ratio. The Ti⁴⁺ content was fixed to 0.004 a.p.f.u, which corresponds to the average of 815 reviewed samples of mchr inclusions in diamonds (Stachel and Harris, 2008); this value well defines an average Ti⁴⁺ content of mchr specifically from Yakutian diamonds (Sobolev et al., 2004). Finally, Cr³⁺ and Al³⁺ were calculated by refining the site occupancy factor. These calculations yielded the formula (Mg${}_{\mathrm{0.58}\left(\mathrm{1}\right)}^{\mathrm{2}+}$Fe${}_{\mathrm{0.42}\left(\mathrm{1}\right)}^{\mathrm{2}+}$)(Cr${}_{\mathrm{1.75}\left(\mathrm{3}\right)}^{\mathrm{3}+}$Al${}_{\mathrm{0.17}\left(\mathrm{3}\right)}^{\mathrm{3}+}$Fe${}_{\mathrm{0.074}\left(\mathrm{12}\right)}^{\mathrm{3}+}$Ti${}_{\mathrm{0.004}\left(\mathrm{7}\right)}^{\mathrm{4}+}$)O₄. If Ti⁴⁺ is varied within 1 standard deviation, according to Stachel and Harris (2008), the corresponding variations in Cr³⁺ and Al³⁺ contents are less than 0.005 a.p.f.u. (i.e. largely within their uncertainty). Even though minor elements other than Ti⁴⁺ were not considered, the calculated chemical composition is well within the compositional field of mchr from Yakutian diamonds reported in Sobolev et al. (2004). Cation distributions for the different crystallographic sites for both inclusions are reported in Table 3.

Table 3 Cation distribution at each crystallographic site for the touching olivine and mchr inclusion in the studied diamond.

4 Discussion

4.1 Thermobarometric analysis of the inclusion pair and thermal state of the mantle

The strong dependence of fO₂ on temperature and pressure means that thermobarometric data are required to convert ${\mathrm{Fe}}^{\mathrm{3}+}/\sum \mathrm{Fe}$ ratios and mineral chemical compositions into fO₂ values. Whilst several thermometers are available for temperature estimates of mantle samples (e.g. Brey and Kohler, 1990; Ryan et al., 1996; Taylor, 1998; Nimis and Grütter, 2010), comparatively few barometers are available for assessing pressures. This disparity is further exacerbated in mineral assemblages involving spinel, for which geobarometers are particularly limited.

In this study, the Ballhaus et al. (1991) olivine–spinel thermometer was used to calculate the last equilibration temperature of the mchr–olivine pair. Due to the slight dependence of this thermometer on pressure, values in the range 3.5 to 6 GPa were used as input for the thermometric calculations. Accordingly, the calculated temperatures varied between ca. 980 and 1020 ^∘C (with an estimated error of ±50 ^∘C). These temperatures do not necessarily indicate the conditions of diamond formation because touching inclusions may re-equilibrate during long-term mantle storage (e.g. Phillips et al., 2004; Stachel and Harris, 2008; Stachel and Luth, 2015; Viljoen et al., 2018).

With the present inclusion pair, an estimate of the entrapment pressure cannot be directly made from its chemical composition because there are no suitable geobarometers for coexisting olivine and mchr. However, assuming negligible vertical movement of the diamond in the rigid cratonic lithosphere, an approximate estimate of the entrapment pressure can be obtained by projecting thermometric estimates for the inclusion pair onto the local xenolith geotherm (Korolev et al., 2018; Nimis et al., 2020). Studies of mantle xenoliths from the Udachnaya kimberlite (Ionov et al., 2010; Goncharov et al., 2012; Yaxley et al., 2012; Doucet et al., 2013; Miller et al., 2016; Liu et al., 2022) indicate a deep lithospheric root (∼ 230 km) but show a relatively large range of geothermal gradients, spanning between the 35 and 40 mW m⁻² model conductive geotherms of Hasterok and Chapman (2011) (see Fig. 3). To account for this geotherm range, Griffin et al. (1996) suggested that the mantle beneath Udachnaya initially experienced cold conditions as testified by ca. 35 mW m⁻² equilibrated xenoliths (Fig. 3) but was later affected by thermal perturbations which raised the temperature of the mantle locally, especially in the deeper parts. Griffin et al. (1996) and earlier researchers (Pokhilenko et al., 1991, 1993) also noted a correlation between xenolith grain size and thermal conditions, with the fine-grained and sheared peridotite xenoliths recording higher temperatures (a feature which is commonly observed also in other cratons, e.g. Woodland and Koch, 2003), whereas the coarse-grained and megacrystalline peridotite xenoliths largely recorded lower T values falling close to a ca. 35 mW m⁻² conductive geotherm. Liu et al. (2022) showed that heating and deformation in the deep lithospheric portion were variable, not strictly concurrent, and likely controlled by local small-scale processes. Pokhilenko et al. (1991, 1993) proposed that megacrystalline peridotite xenoliths constituted the principal host rocks of Siberian diamonds and, by extension, that the formation and storage of diamonds occurred under cold conditions consistent with a 35 mW m⁻² conductive geotherm. Further evidence for an old, cold conductive geotherm was provided by Nestola et al. (2019), who estimated, based on elastic geobarometry and nitrogen thermometry, the P–T formation conditions for a mchr-bearing diamond from Udachnaya to be 6.5(0.2) GPa and 1125(32)–1140(33) ^∘C. These conditions fall right on the 35 mW m⁻² geotherm (Fig. 3), consistent with the establishment of a cold geothermal gradient over the whole Udachnaya lithosphere at the time of diamond formation. Considering the ages of diamonds at Udachnaya (3.5–3.1, ∼ 2 and ∼ 1.8 Ga; Richardson and Harris, 1997; Pearson et al., 1999a, b; Wiggers de Vries et al., 2013), these cold conditions persisted for billions of years in some portions of the Udachnaya lithosphere, particularly in the 140–190 km depth interval (Liu et al., 2022). Based on these lines of evidence, our diamond Oli-CHR1 also most likely formed and equilibrated under conditions close to a 35 mW m⁻² geotherm. Projection of the thermometric estimates for diamond Oli-CHR1 on this geotherm (Fig. 3) yields formation conditions of P ∼ 5.7(0.4) GPa and T ∼ 1015(50) ^∘C that are within the largely unperturbed depth interval (Liu et al., 2022). These results are fairly consistent with thermodynamic modelling in multicomponent, natural peridotitic systems (Ziberna et al., 2013), which predicts that in very depleted (highly refractory) harzburgite with bulk Cr# = 0.32 and along a 35 mW m⁻² geotherm, spinel is stable up to 5.5 GPa and 1000 ^∘C, where it reaches a Cr#_spinel of ca. 0.9, similar to that of mchr in the Oli-CHR1 diamond. Therefore, we propose that the inclusion pair did not experience any significant thermal perturbations and did not re-equilibrate after incorporation (Fig. 3); hence it records the P–T conditions of the ambient cratonic mantle at the time of its entrapment by the host diamond. Although the evidence presented above and the data reported in the literature suggest that this is the most reasonable scenario, we are aware that available age constraints suggest multi-stage diamond formation beneath Udachnaya. Consequently, if Oli-CHR1 and the diamond investigated by Nestola et al. (2019) have different ages, this implies that they may not necessarily have formed under the same geothermal gradient. An important aspect linked to different diamond ages is secular cooling of the cratonic lithosphere, which is supported both by thermal models for the formation of the cratonic roots (e.g. Michaut et al., 2009) and by the temporal change in reconstructed geotherms from xenoliths found in Proterozoic kimberlites (Grütter, 2009). Further corroborating evidence for secular lithosphere cooling has been found in comparative studies of non-touching and touching inclusions (e.g. Phillips et al., 2004; Stachel et al., 2022). Such data show that touching inclusions generally record lower average temperatures (∼ 100 ^∘C less) than non-touching inclusions, and this is attributed to re-equilibration in a cooling mantle until the time of eruption. However, in other cases no discrepancy exists, suggesting that diamonds formed when the lithospheric mantle had already attained a thermal regime comparable to or even colder than that existing at the time of emplacement of the host kimberlite or lamproite (Nimis, 2002). Considering all these uncertainties, we will also address a scenario in which our inclusion pair was trapped at a ∼ 100 ^∘C higher temperature, i.e. ∼ 1115 ^∘C, and eventually re-equilibrated to ∼ 1015 ^∘C during long-term mantle storage (Fig. 3). To provide any meaningful inference, such as calculating the fO₂ for the inclusion pair (see next section), the chemical compositions of olivine and mchr and specifically their $\mathrm{Fe}/(\mathrm{Fe}+\mathrm{Mg})$ ratios have to be recalculated to 1115 ^∘C. This can be done by means of the Ballhaus et al. (1991) olivine–spinel exchange thermometer, using a trial-and-error procedure. Considering that the olivine inclusion is much smaller than the mchr inclusion, the Mg–Fe²⁺ exchange between the two inclusions would have mostly modified the olivine composition, while that of the mchr would have remained approximately constant. Accordingly, the back-calculated compositions yield χMg ∼ 0.909 and χFe ∼ 0.091 in olivine and χMg ∼ 0.582 and χFe²⁺ ∼ 0.418 in mchr. With respect to the entrapment pressure, we will assume it to be 5.7(1.0) GPa, the larger uncertainty being related to the uncertainties in the geothermal gradient.

Figure 3 Pressure–temperature diagram showing the distribution of well-equilibrated mantle xenoliths from Udachnaya kimberlite (data source: Tables S1–S2). Red squares indicate the most recent P–T data from Liu et al. (2022), which include a new suite of garnet peridotite xenoliths as well as literature data (see Table S1); these data are based on a carefully selected set of well-equilibrated samples and robust thermobarometers. Yellow rhombi show the data from Goncharov et al. (2012) and Yaxley et al. (2012), for which robust P–T estimates were re-determined following Liu et al. (2022) (see Table S2). P–T conditions for the MgCr2 diamond–mchr pair from Nestola et al. (2019) and 35 mW m⁻² equilibrated xenoliths from Griffin et al. (1996, and references therein) are also reported. The gradient bar indicates the P–T equilibration curve (see text) for the studied mchr–olivine inclusion pair; the diamond marker shows the suggested interpretation for our Oli-CHR1 diamond (see text), although entrapment at higher (∼ 100 ^∘C) T and re-equilibration during mantle storage cannot be excluded a priori. The 35, 40 and 45 mW m⁻² conductive geotherms for the lithospheric mantle and the 1300 ^∘C mantle adiabat are from Hasterok and Chapman (2011); the graphite–diamond (G–D) transition is from Day (2012).

4.2 fO₂ analysis of the inclusion pair and oxidation state of the mantle

Oxygen fugacity in cratonic mantle has been mostly explored using xenoliths from the Kaapvaal craton in South Africa (Woodland and Koch, 2003; Creighton et al., 2009; Lazarov et al., 2009), the Slave craton in northern Canada (McCammon and Kopylova, 2004; Creighton et al., 2010) and the Siberian craton (e.g. Ashchepkov et al., 2014, 2016). These studies showed that fO₂ is close to the fayalite–magnetite–quartz (FMQ) buffer at the top of the lithospheric mantle and progressively decreases with increasing depth. These data also showed that fO₂ exhibits important lateral variations, which are commonly attributed to either melt extraction or oxidation/reduction induced by fluid or melt-driven metasomatism.

Oxybarometric data for mantle peridotite xenoliths from the Udachnaya kimberlite (Goncharov et al., 2012; Yaxley et al., 2012; Miller et al., 2016; Table S2 in the Supplement) also show this global trend with progressively lower Δlog fO₂ (FMQ) values (ΔFMQ ≃ −1 to $\simeq -\mathrm{3}$, excluding outliers) with increasing depths (Fig. 4). Most of the xenoliths equilibrated at P > 3.5 GPa, i.e. beyond the graphite–diamond (G–D) transition, and at oxygen fugacity conditions more reduced than the enstatite–magnesite–olivine–diamond (EMOD) buffer. The EMOD buffer marks the highest oxygen fugacity at which diamonds could form and be preserved within carbonated peridotite assemblages. For calculating Δlog fO₂ (FMQ) values for our inclusion pair, the two available calibrations are from Ballhaus et al. (1991) (hereafter B91) and Nikolaev et al. (2016) (hereafter N16), both sharing the same formalism. The N16 calibration is a revision of the B91 oxybarometer based on independent experimental data and inherits much from the previous work. Here, Δlog fO₂ (FMQ) values for our inclusion pair were calculated using both the B91 and the N16 calibrations. Results for our preferred model, i.e. entrapment of the pair at P ∼ 5.7(0.4) GPa and T ∼ 1015(50) ^∘C without re-equilibration after incorporation, gave Δlog fO₂ (FMQ) values of −1.4(0.8) and −1.0(0.5), respectively, whereas we obtained −1.7(0.8) and −1.6(0.5) for the scenario in which the inclusions were trapped at higher T, ∼ 1115(50) ^∘C, and P ∼ 5.7(1.0) GPa (Fig. 4). The uncertainties in the calculated fO₂ values reported here are the nominal uncertainties for the two calibrations used. However, we are aware that our estimated chemical compositions derived from X-ray diffraction site occupancies are certainly affected by larger uncertainties than those obtained through standard electron microprobe analysis. To evaluate the uncertainties in the calculated fO₂ values which solely derive from the input parameters (i.e. statistical errors in site occupancy factors refined from SCXRD and in the ${\mathrm{Fe}}^{\mathrm{3}+}/\sum \mathrm{Fe}$ ratio obtained from the SMS and estimated errors in thermobarometry), we applied a Gaussian error propagation function taking into account all possible error sources. In the case of entrapment of the pair at P ∼ 5.7(0.4) GPa and T ∼ 1015(50) ^∘C, error propagation for both calibrations yielded ±0.3 log units. Of all error sources, the most critical one appears to be the uncertainty in the ${\mathrm{Fe}}^{\mathrm{3}+}/\sum \mathrm{Fe}$ ratio of mchr, which already propagates ca. ±0.3 log units on the final fO₂ estimate for both calibrations. If the input T is changed by ±50 ^∘C and P by ±0.4 GPa (i.e. the P–T estimate is moved within uncertainties along the 35 mW m⁻² geotherm), the fO₂ change is only ±0.1 log units for the B91 calibration and ±0.2 log units for the N16 calibration. In the case of post-entrapment re-equilibration, an allowance for a larger pressure uncertainty (±1 GPa, due to the uncertainties in the geothermal gradient) has to be made and then taken into account with all the other possible error sources. This yielded ±0.4 log units for both calibrations. The small total uncertainty (±0.3–0.4 log units) deriving from all possible uncertainties in the input parameters is well within the nominal uncertainty in the two oxybarometer calibrations (i.e. ±0.8 log units for B91 and ±0.5 log units for N16). Additional errors probably derive from the extrapolation of both oxybarometers outside their calibration ranges (i.e. 0.3–2.7 GPa for B91 and 0.0001–2.5 GPa for N16), but these errors are difficult to estimate. Although we recognize that the extrapolation of the B91 and N16 oxybarometers at higher pressures will likely introduce further errors, the most critical issue in both cases was claimed to be the application of the corresponding formulation to some specific settings. In the case of the B91 oxybarometer, the authors advised caution when applying it to orthopyroxene-undersaturated systems or where Cr²⁺ may partially substitute in spinel, while its application to a suite of high-pressure spinels from the Archean cratonic lithosphere gave logical results (Ballhaus, 1993). Ballhaus et al. (1991) have already pointed out that the correction for orthopyroxene-undersaturated rocks rarely exceeds −0.2 log units, which falls largely within the error of the model, while significant Cr²⁺ substitution in spinel may only occur at relatively low oxygen fugacity. In the case of the N16 oxybarometer, the authors warranted caution when applying their oxybarometer to intrusive cumulus rocks, which however is not relevant in our case.

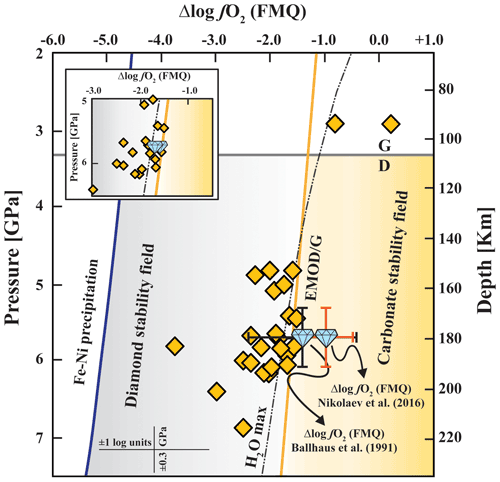
Figure 4 Δlog fO₂ (FMQ)–pressure diagram showing the distribution of well-equilibrated xenoliths from Udachnaya (yellow rhombi) (data source: Tables S2) and the calculated Δlog fO₂ (FMQ) value for the studied inclusion pair (diamond). Δlog fO₂ (FMQ) values and associated uncertainties for mantle xenoliths were calculated with the Miller et al. (2016) oxybarometer (see Table S2); typical uncertainties are shown for reference. Inset: the same data but assuming that the inclusion was trapped at ∼ 100 ^∘C higher T and then re-equilibrated during long-term mantle storage. Δlog fO₂ (FMQ) values calculated for the inclusion pair suggest diamond formation at relatively oxidized conditions near the EMOD buffer, for both the scenarios in which the inclusion did not re-equilibrate after incorporation or was trapped at higher T. EMOD/G buffer is calculated for a 35 mW m⁻² geotherm from the thermodynamic dataset of Holland and Powell (2011) (see Luth and Stachel, 2014, their Appendix 1); the Fe–Ni precipitation curve is from O'Neill and Wall (1987); the graphite–diamond (G–D) transition is from Day (2012) based on a 35 mW m⁻² geotherm; the water maximum curve (labelled “H₂O max”) is calculated for a 35 mW m⁻² geotherm using the GFluid model of Zhang and Duan (2010).

Figure 4 also shows that the EMOD line, calculated for a 35 mW m⁻² geotherm, varies between about ΔFMQ −1.2 and −1.8 in the pressure interval 2–7 GPa. While Δlog fO₂ (FMQ) (B91) values of −1.4(0.8) and −1.7(0.8) are close to that of the EMOD line and fall, within error, in the diamond stability field, only the Δlog fO₂ (FMQ) (N16) of −1.6(0.5) is compatible with diamond (scenario of post-entrapment re-equilibration for the inclusion), while −1.0(0.5) is more oxidized than the EMOD line values. Nonetheless, considering all possible uncertainties, both the B91 and the N16 estimates point to relatively oxidized redox conditions comparable to, or slightly more oxidized than, those of xenoliths from the same depth (Fig. 4, Table S2), regardless of the assumed scenario. The calculated Δlog fO₂ (FMQ) values for our inclusion pair are also found to be good indicators of the fO₂ conditions of diamond formation. In fact, resetting of fO₂ in mantle rocks may be effective and fast, given the very limited oxygen buffering capacity of depleted cratonic peridotites (Luth and Stachel, 2014; Stachel and Luth, 2015). How efficiently the fO₂ of inclusions in diamond is reset during entrapment processes will depend on the time needed for diamond formation. Although the time required for a diamond to form in Earth's mantle is poorly known, evidence from natural diamonds and diamond growth studies suggest that this time may be geologically long. For example, monocrystalline diamonds reveal episodic growth and resorption features, indicating the presence of fluid over several millions of years (Gress et al., 2018). Experimental studies show that diamonds may grow efficiently in the presence of water and within the timescale of the experiments (e.g. Sokol and Pal'yanov, 2008; Sokol et al., 2009; Bureau et al., 2016), which were however conducted at temperatures well above those of the subcratonic lithosphere. Hence, although the time spans required for individual growth episodes and, therefore, for encapsulation of an inclusion are shorter, they are likely to be sufficiently long to allow fO₂ resetting of the inclusion during its incorporation in the growing diamond. Based on this evidence, the inclusion pair shall record fO₂ conditions of diamond formation, regardless of its syngenetic or protogenetic origin (cf. Nestola et al., 2014; Nimis et al., 2019). Hence, both the B91 and the N16 estimates suggest relatively oxidized conditions for diamond formation, probably falling near the upper limit for diamond stability in peridotite.

4.3 Implications for the redox state evolution and diamond formation

Archean and early Proterozoic cratons are stable regions of continental rocks with basement ages of at least 2.5 Ga (e.g. de Wit and Hart, 1993), which preserve the oldest bodies of Earth's lithosphere and contain an extensive record of its ancient history. In this context, mantle xenoliths and inclusion-bearing diamonds hosted in kimberlites are the only known direct samples of the basal lithosphere, which can deliver rare information on the nature of the lithospheric mantle and a unique perspective on the processes, conditions and evolution of the craton (Pearson and Wittig, 2014).

While the palaeo-redox state of the convecting mantle has been investigated by many researchers (e.g. Canil, 2002; Li and Lee, 2004; Aulbach and Stagno, 2016; Nicklas et al., 2019; O'Neill and Aulbach, 2022; Gao et al., 2022), suggesting a statistically significant secular increase in the mantle fO₂ across the Archean–Proterozoic boundary, the oxygen fugacity evolution of the cratonic lithosphere has been less explored. It is well accepted that the cratonic mantle has formed by extensive melt extraction during the Archean, which left highly refractory and reducing residua because of the incompatibility of Fe³⁺ during melting (Frost and McCammon, 2008). This was later followed by percolation of oxidizing melts/fluids that metasomatized most of the lithospheric mantle and increased its fO₂ over time (e.g. Foley, 2011; Foley and Fischer, 2017). However, gauging the timing of these processes is difficult because cratonic xenoliths remained open systems until the time of their entrainment in the host kimberlite. In contrast, once formed, diamonds are chemically inert containers for inclusions, which are protected from alteration/re-equilibration processes with the surrounding mantle. Therefore, the concurrent occurrence of both inclusions in diamonds, with presumably old ages, and xenoliths from the same locality allows the redox state evolution of the cratonic mantle to be unravelled.

The oxygen fugacities recorded by mantle xenoliths from Udachnaya constrain the physical–chemical conditions of the cratonic mantle at the time of xenolith entrainment in the host kimberlite (360 ± 7 Ma; Kinny et al., 1997). In contrast, the inclusion pair last equilibrated with the surrounding mantle before being encapsulated in its host diamond. Although the age of our diamond is unknown, diamonds from Udachnaya have been dated to 3.5–3.1, ∼ 2 and ∼ 1.8 Ga (Richardson and Harris, 1997; Pearson et al., 1999a, b; Wiggers de Vries et al., 2013), which means that the inclusion of our diamond reflects an earlier state of the cratonic lithosphere. Considering this difference in time, the similarity between Δlog fO₂ (FMQ) values for mantle xenoliths from the Udachnaya kimberlite and the inclusion pair studied in this work (Fig. 4) describes a scenario in which the modern redox state of the cratonic lithosphere below Udachnaya would have likely been attained relatively early after its formation. Although the cratonic mantle has been the sink for metasomatic fluids/melts which could certainly change its redox conditions (e.g. Foley, 2011), our determination suggests that the modern redox state of this portion of the Siberian craton, once set, may have persisted for billions of years, at least at the local scale. This also agrees with evidence from multicomponent carbon isotope modelling data coupled with the prominent mode in δ¹³C values for diamonds worldwide at about −5 ± 1 ‰, which indicate that this range can be accounted for by a variation in fO₂ of only 0.4 log units (Howell et al., 2020; Stachel et al., 2017), implying a near-constant fO₂ through time for the mantle from which these fluids derived. Corroborating evidence was also recently observed from a comparative study of worldwide inclusions in eclogitic diamonds and eclogite xenoliths showing no systematic changes in the fO₂ of the cratonic eclogite reservoir subsequent to diamond formation (Aulbach and Stachel, 2022), although the extrapolation of these findings to the dominant peridotite lithology should be treated with care, in the context of its poorer oxygen buffering capacity (Luth and Stachel, 2014).

It was also recently proposed that due to the very limited oxygen buffering capacity of depleted cratonic peridotites, diamond formation in peridotites is unlikely related to rock-buffered redox reactions (Luth and Stachel, 2014; Stachel and Luth, 2015; Stachel et al., 2017). These works indicate that small amounts of O₂ (less than 200 ppm) are required to shift a peridotite from the IW (iron wüstite) to the EMOD buffer, implying that peridotites have virtually no ability to act as a source or sink for O₂ and that their oxidation state can be employed as a faithful indicator of the redox state of the last interacting metasomatic fluid. This may also apply to inclusions in diamonds, as their fO₂ is probably efficiently reset during entrapment processes (see above). Based on the poor redox buffering capacity of cratonic peridotites, Luth and Stachel (2014) have suggested that isochemical precipitation of carbon from CHO fluids under subsolidus mantle conditions may provide an efficient mode for diamond formation, especially in refractory (harzburgitic–dunitic) substrates. This would occur in response to either isobaric cooling or combined cooling and decompression as the fluid migrates upwards along a cratonic geothermal gradient. According to these models, this process can be particularly efficient if the fluid speciation is close to the water maximum, $\mathrm{O}/(\mathrm{O}+\mathrm{H}{)}_{\mathrm{mol}}$ ∼ 0.33, implying that low carbon concentrations in the fluid and high fluid $/$ rock ratios are needed to grow diamonds. This takes place at ΔFMQ between about −1 and −2, conditions which lie very close to the EMOD buffer along a cold geotherm (Luth and Stachel, 2014) and are remarkably consistent with the relatively oxidized conditions estimated for our inclusion pair (Fig. 4). Evidence from experimental work (e.g. Sokol and Pal'yanov, 2008; Sokol et al., 2009; Bureau et al., 2016) also indicates that CHO-fluid-bearing systems at fO₂ near the water maximum promote efficient diamond growth. Nimis et al. (2020) further explored the efficiency of diamond formation processes versus depth by combining CHO-fluid modelling with various P–T paths for the ascending fluid. Their results further confirm that conditions comparable to the Udachnaya cold geotherm at 5.7 GPa at the water maximum would have good potential for diamond formation. The fO₂ estimate for our inclusion pair provides direct evidence of diamond formation under relatively oxidized conditions near the EMOD buffer, i.e. under conditions in which CHO fluids are water-rich.

We are aware that the existence of diamonds with inclusions of methane (e.g. Thomassot et al., 2007; Smit et al., 2016), carbonate or CO₂ (Schrauder and Navon, 1993; Wang et al., 1996) demonstrates that diamond formation may occur over a wide range of oxygen fugacities, in keeping with the record of deep-seated xenoliths (e.g. Yaxley et al., 2017). Although independent evidence from mantle xenoliths and carbon isotope data suggests that very reducing conditions and CH₄-rich parent media are not the norm for diamonds (Luth and Stachel, 2014; Stachel et al., 2017), more data on inclusions in diamonds similar to those provided in this work are required to determine the systematics of fO₂ conditions at which diamonds form. These data should ideally be combined with diamond age estimates to unravel the long-term redox state evolution of the cratonic lithospheric mantle.

5 Summary and conclusions

In this study, we presented the first oxygen fugacity determination of a mchr–olivine touching inclusion pair still trapped in its host diamond from the Paleozoic Udachnaya kimberlite. Thermobarometric analyses and the measured ${\mathrm{Fe}}^{\mathrm{3}+}/\sum \mathrm{Fe}$ ratio in mchr indicate the P–T–fO₂ conditions of the inclusion pair at the time of the entrapment to be ∼ 5.7(0.4) GPa and ∼ 1015(50) ^∘C (although entrapment at higher T and re-equilibration during subsequent mantle storage cannot be excluded) and fO₂ near the EMOD buffer. The estimated redox conditions are similar to, or slightly more oxidized than, those of xenoliths from the same depth. However, while the xenoliths last equilibrated with the surrounding mantle before their entrainment in the kimberlite at ∼ 360 Ma, the inclusion pair retains the signature of a mantle as old as 3.5–3.1 Ga, ∼ 2 or ∼ 1.8 Ga, i.e. the known peaks of diamond formation at Udachnaya, corresponding to the time at which the mchr–olivine pair became trapped in its host diamond. Based on the similarity between xenoliths and inclusion fO₂ values, we propose that the modern redox state of this portion of the Siberian lithosphere was attained relatively early after its formation and may have persisted for billions of years, at least at the local scale, until the time of kimberlite eruption.

Moreover, the oxygen fugacity determination for our inclusion pair provides the first direct evidence for diamond formation under relatively oxidized conditions. These conditions are consistent with recent models of diamond formation suggesting water-rich CHO fluids as the most likely parents for lithospheric diamonds (Luth and Stachel, 2014).