Ab initio thermal expansion and thermoelastic properties of ringwoodite (γ-Mg₂SiO₄) at mantle transition zone conditions

Thermal convection in the Earth's mantle is driven by lateral variations in temperature and density, which are substantially controlled by the local volume thermal expansion of the constituent mineral phases. Ringwoodite is a major component of the lower mantle transition zone, but its thermal expansivity and thermoelastic properties are still affected by large uncertainties. Ambient thermal expansion coefficient (${\mathit{\alpha }}_{V_{\mathrm{0}}}$​​​​​​​), for instance, can vary as much as 100 % according to different experimental investigations available from the literature. In this work, we perform ab initio density functional theory calculations of vibrational properties of spinel-structured Mg₂SiO₄ ringwoodite in order to provide reliable thermophysical data up to mantle transition zone conditions. Temperature- and pressure-dependent thermal expansivity has been obtained by phonon dispersion calculations in the framework of quasi-harmonic approximation (QHA) up to 25 GPa and 2000 K. Theoretical analysis of vibrational spectra reveals that accurate prediction of IR and silent modes, along with their relative mode Grüneisen parameters, is crucial to define thermal expansivity. A six-parameter analytical function is able to reproduce ab initio values fairly well in the whole investigated P–T range, i.e., ${\mathit{\alpha }}_V(P,T)=(\mathrm{1.6033}\times {\mathrm{10}}^{-\mathrm{5}}+\mathrm{8.839}\times {\mathrm{10}}^{-\mathrm{9}}T+\mathrm{11.586}\times {\mathrm{10}}^{-\mathrm{3}}{T}^{-\mathrm{1}}-\mathrm{6.055}{T}^{-\mathrm{2}}+\mathrm{804.31}{T}^{-\mathrm{3}})$ $\times \exp (-\mathrm{2.52}\times {\mathrm{10}}^{-\mathrm{2}}P)$, with temperature in kelvin and pressure in gigapascal. Ab initio static and isothermal bulk moduli have been derived for ringwoodite along with their P, T and cross derivatives, i.e., K₀ = 184.3 GPa, K_T,300 K = 176.6 GPa, $K_{\mathrm{0}}^{\prime }$ = 4.13, $K_{T,\mathrm{300}\mathrm{K}}^{\prime }$ = 4.16, ${\left(\frac{\partial K_T}{\partial T}\right)}_P$ = −0.0233 GPa K⁻¹ and ${\left(\frac{{\partial }^{\mathrm{2}}{K}_T}{\partial P\partial T}\right)}_{\mathrm{0}}=\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}$ K⁻¹. Computed thermal expansivity and thermoelastic properties support the evidence that QHA performs remarkably well for Mg₂SiO₄ ringwoodite up to mantle transition zone temperatures. Since volume thermal expansion of ringwoodite is strongly pressure-dependent and its pressure dependence becomes more marked with the increasing temperature, internally consistent assessments and empirical extrapolation of thermoelastic data to deep mantle conditions should be taken with care to avoid inaccurate or spurious predictions in phase equilibrium and mantle convection numerical modeling.

1 Introduction

Despite the development of internally consistent databases for planetary materials, thermodynamic properties of deep mantle minerals are still poorly constrained or even completely lacking at high pressure and temperature conditions (HP–HT). Relevant geophysical properties like volume thermal expansion and isothermal bulk modulus can be derived from experimental measurements at ambient pressure in the low- to medium-temperature range, but they are usually less defined at higher temperatures (and pressures) due to technical problems or conditions of the samples, especially when melting or decomposition may occur (Thieblot et al., 1998; Fiquet et al., 1999). For these reasons large extrapolation of thermophysical data is often invoked at HP–HT without any warranty of physical soundness (Helffrich, 1999). Inaccurate thermodynamic properties could in turn strongly affect the prediction of phase equilibrium and stability relations of mantle minerals at deep Earth conditions.

Ringwoodite is a major constituent phase of the lowermost mantle transition zone (MTZ), between ∼ 520 and 660 km depths, where its relative amount is estimated to be between ∼ 40 % vol and 60 % vol according to different compositional models of the Earth's mantle (Ringwood, 1975; Bass and Anderson, 1984). It is now generally accepted that spinel and post-spinel phase transformations of olivine play a key role in determining global mantle discontinuities in the middle and bottom part of the transition zone (Bina and Helffrich, 1994; Sinogeikin et al., 2003; Ishii et al., 2019), although the ultimate origin, sharpness and seismic signature of the 520 and 660 km discontinuities are still a matter of debate (e.g., Deuss and Woodhouse, 2001; Deuss et al., 2006; Saikia et al., 2008). This basically reflects the still unconstrained abundance of olivine versus non-olivine mineral phases (majoritic garnet above all) in this part of the mantle and the fact that their stability field, density and thermoelastic properties are roughly compatible with seismic impedance contrasts and velocity jumps observed by global seismology (Shearer, 1996; Deuss et al., 2006; Schmerr and Garnero, 2007). In any case, the thermodynamic behavior of ringwoodite has a significant impact on physicochemical processes of the mantle transition zone (Akaogi et al., 2007; Kojitani et al., 2016). The natural occurrence of ringwoodite with normal spinel structure in many shocked chondritic meteorites (e.g., Chen et al., 2004) and as a mineralogical inclusion in ultradeep diamonds from Juína, Brazil (Pearson et al., 2014), further supports this evidence. Structural inversion may have a potential effect (Kiefer et al., 1999; Panero, 2008; Bindi et al., 2018), but thermodynamic considerations suggest that Mg-endmember ringwoodite is unlikely to be stable in the inverse spinel phase in the Earth's transition zone.

In this work we perform ab initio density functional theory calculations of vibrational properties and volume thermal expansion of spinel-structured Mg₂SiO₄ ringwoodite in the framework of quasi-harmonic approximation (QHA) in order to provide reliable thermophysical data up to mantle transition zone conditions. This study is part of a broader project aimed at setting up a comprehensive high-pressure thermodynamic database for solid-state and solid-liquid phase equilibrium calculations in geochemically relevant multi-component systems by “ab initio assisted” computational thermodynamics (Belmonte et al., 2017a, b). A detailed survey of the available experimental and theoretical data on Raman and IR spectra, isothermal bulk modulus, volume thermal expansion, and thermal expansivity of Mg₂SiO₄ ringwoodite is carried out to show how relevant current uncertainties on the physicochemical behavior of this important building block of planetary interiors might be. By giving a theoretical constraint to the extrapolation of thermodynamic data at MTZ depths, ab initio calculations performed in this work allow us to infer some relevant insights into the role of ringwoodite in mantle dynamics, as briefly discussed in the implications section.

2 Computational method

Ab initio calculations in this work have been performed by using the LCAO (linear combination of atomic orbitals) approach with an all-electron Gaussian-type basis set as implemented in the CRYSTAL code (Dovesi et al., 2014). The hybrid B3LYP density functional, which contains 20 % of exact Hartree–Fock exchange mixed with generalized gradient approximation (GGA) exchange–correlation (Becke, 1993; Lee et al., 1988), has been employed due to its high performance on vibrational, elastic and thermodynamic properties of a large variety of insulating crystalline phases (e.g., Ottonello et al., 2010; Belmonte et al., 2013; Erba et al., 2014; Belmonte et al., 2016). The basis set for Mg, Si and O atoms and computational parameters are the same as those used in our previous investigations on dense magnesium silicates and oxides and can be found elsewhere (see De La Pierre and Belmonte, 2016 and Belmonte, 2017, for full details).

Phonon dispersion calculations at q points other than Γ have been performed on large isotropic or anisotropic supercells with the direct method (see Parlinski et al., 1997; Evarestov and Losev, 2009). In order to check numerical convergence on calculated thermal expansion and thermoelastic properties, a total of 18 q points in the first Brillouin zone have been sampled by using 2 × 2 × 2, 3 × 1 × 1, 1 × 3 × 1, 1 × 1 × 3, 3 × 2 × 1 and 3 × 1 × 2 supercells and exploiting the cubic symmetry of the ringwoodite structure (space group $Fd\stackrel{\mathrm{‾}}{\mathrm{3}}m)$. Once phonon modes have been computed on the fully relaxed equilibrium structure, their volume dependence has been defined in the framework of quasi-harmonic approximation (QHA) (e.g., Wallace, 1972). Mode Grüneisen parameters of phonon modes (γ_i) are thus obtained as follows:

$$\begin{array}{}\text{(1)}& {\mathit{\gamma }}_i\left(\mathbf{q},V\right)=-{\displaystyle \frac{\partial \ln {\mathit{\nu }}_i(\mathbf{q},V)}{\partial \ln V}},\end{array}$$

where ν_i is the wavenumber of the ith vibrational mode of the crystal lattice sampled at discrete q points in the first Brillouin zone, and V is the volume of the unit cell. Thus, also the effect of phonon dispersion on mode Grüneisen parameters has been defined by the supercell approach in this work. Least-square fitting of vibrational frequencies computed at five different volume conditions (i.e., $V/V_{\mathrm{0}}\cong \mathrm{0.89}$, 0.92, 0.96, 0.98 and 1.00) gives the values of γ_i for all modes. Linear or second-order polynomial fitting accurately describes the volume dependence of all the vibrational frequencies in the investigated compression range. The calculated equation of state (EOS) for Mg₂SiO₄ ringwoodite allows us to convert volume dependence of vibrational frequencies into pressure dependence for a direct comparison with experimental measurements (see Sect. 3).

3 Results and discussion

3.1 Vibrational properties at ambient and high-pressure conditions

The experimental characterization of the full vibrational spectra of deep mantle minerals at ambient and non-ambient conditions is still challenging. One of the reasons for the overwhelming success of theoretical investigations based on density functional theory (DFT) combined with the quasi-harmonic approximation (QHA) is that the full vibrational density of state (vDOS) of crystalline solids can be directly provided by phonon dispersion calculations. Physically consistent thermodynamic and thermoelastic properties can then be predicted for a broad range of P–T conditions by statistical mechanics (Wallace, 1972).

Even though there are several IR and Raman spectroscopic studies on ringwoodite, most of them have been performed to characterize natural samples of shocked meteorites (e.g., Guyot et al., 1986; Chen et al., 2004; Feng et al., 2011; Acosta-Maeda et al., 2013) or mineral inclusions in diamonds (Pearson et al., 2014), while only a few experimental investigations focused on the Mg end-member (Akaogi et al., 1984; McMillan and Akaogi, 1987; Chopelas et al., 1994).

The zone-center optic vibrational modes of ringwoodite with cubic spinel structure (space group $Fd\stackrel{\mathrm{‾}}{\mathrm{3}}m$, point group $m\stackrel{\mathrm{‾}}{\mathrm{3}}m)$ can be classified by symmetry analysis as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathrm{\Gamma }}_{\mathrm{optic}}& =A_{\mathrm{1}g}\oplus \mathrm{2}{A}_{\mathrm{2}u}\oplus E_g\oplus \mathrm{2}{E}_u\oplus T_{\mathrm{1}g}\oplus \mathrm{4}{T}_{\mathrm{1}u}\oplus \mathrm{3}{T}_{\mathrm{2}g}\\ & \oplus \mathrm{2}{T}_{\mathrm{2}u},\end{array}\end{array}$$

where A_1g, E_g and T_2g modes (symmetric with respect to inversion) are Raman active; T_1u modes (anti-symmetric with respect to inversion) are IR active; and A_2u, E_u, T_1g and T_2u modes are silent. Due to the high symmetry of the structure, E_g and E_u modes are doubly degenerate, while T_1g, T_1u, T_2g and T_2u modes are triply degenerate in the irreducible representations of Eq. (2). Vibrational frequencies as computed in this work by ab initio B3LYP calculations are compared to experimental results and other DFT calculations (Piekarz et al., 2002; Yu and Wentzcovitch, 2006; Li et al., 2009; Hernández et al., 2015) in Table S1 (see Supplement). Only transverse optic (TO) modes have been computed, as LO–TO splitting is relevant just for the IR-active T_1u modes (Piekarz et al., 2002), and its effect on thermodynamic properties as determined by phonon dispersion calculations is negligible.

The experimental Raman spectrum of Mg₂SiO₄ ringwoodite shows two strong bands at 794–796 and 834–836 cm⁻¹ (assigned to T_2g and A_1g modes and corresponding to asymmetric and symmetric stretching of ${\mathrm{SiO}}_{\mathrm{4}}^{\mathrm{4}-}$ tetrahedra, respectively), along with weaker peaks at 302, 370–372 and 600 cm⁻¹ (McMillan and Akaogi, 1987; Chopelas et al., 1994). Ab initio B3LYP calculations predict the position of the two most intense Raman peaks within 3–5 cm⁻¹ and with the correct symmetry analysis. It is interesting to note that mode assignment in experimental studies could be rather difficult. McMillan and Akaogi (1987) assigned the Raman band at 794 cm⁻¹ to the symmetric stretching vibration of Si–O tetrahedra with A_1g symmetry in their unpolarized powder spectrum, while Chopelas et al. (1994) correctly assigned it to asymmetric stretching with T_2g symmetry based on single-crystal oriented spectra. This mode assignment is confirmed also by other DFT studies (Piekarz et al., 2002; Yu and Wentzcovitch, 2006; Li et al., 2009; Hernández et al., 2015). The weaker Raman peaks are also accurately predicted, with a partial disagreement (∼ 20 cm⁻¹) for the T_2g mode at 619 cm⁻¹ (see Table S1 in the Supplement). By comparing experimental and theoretical investigations, the position of this peak is the most uncertain in the Raman spectrum, located in the region between ∼ 570 and 620 cm⁻¹.

Four infrared bands are expected to be present in the IR spectrum of cubic silicate spinels (White and DeAngelis, 1967; Preudhomme and Tarte, 1971), although additional features could be present possibly due to some deviation from the cubic symmetry, structural disorder or vibrational coupling between octahedral and tetrahedral lattice modes (Jeanloz, 1980). Akaogi et al. (1984) observed only two major bands centered near 830 and 445 cm⁻¹ for Mg₂SiO₄ ringwoodite, along with minor features corresponding to weak bands or shoulders at 920, 785, 510, 395 and 350 cm⁻¹. The broadness of the major infrared bands found in experiments makes a direct comparison with our ab initio calculations, which correctly predict four IR-active T_1u modes with wavenumbers 341, 396, 545 and 802 cm⁻¹ (Table S1) difficult. B3LYP results are quite different from those obtained by other GGA calculations (Piekarz et al., 2002; Hernández et al., 2015), except for the predicted IR modes in the low-frequency range, which may differ by less than 10 cm⁻¹. The same consideration roughly applies to computed frequencies for the silent modes.

In order to test the performance of ab initio B3LYP calculations, theoretical and experimental frequencies are compared by means of a global statistical index, which is defined as follows (see De La Pierre and Belmonte, 2016):

$$\begin{array}{}\text{(3)}& \left|\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\right|=M^{-\mathrm{1}}\sum _{i=\mathrm{1}}^M\left|{\mathit{\nu }}_i^{\mathrm{calc}}-{\mathit{\nu }}_i^{\exp }\right|,\end{array}$$

where M is the number of data considered in the statistics and $\left|\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\right|$ is the mean absolute difference between calculated $\left({\mathit{\nu }}_i^{\mathrm{calc}}\right)$ and experimentally observed frequencies $\left({\mathit{\nu }}_i^{\exp }\right)$. Only the frequencies of the five Raman-active modes (i.e., A_1g, doubly degenerate E_g and triply degenerate T_2g modes) have been included in the statistics, since two different experimental studies give nearly coincident results (McMillan and Akaogi, 1987; Chopelas et al., 1994), and a direct comparison between ab initio and experimental data is not straightforward for the IR-active modes. In that case, M=12 and $\left|\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\right|=\mathrm{7}$ cm⁻¹ if frequencies computed in this work at the B3LYP level of theory are compared with either the experimental dataset by McMillan and Akaogi (1987) or that by Chopelas et al. (1994) (Table S1). The agreement with observed Raman spectra is thus excellent and markedly better than ab initio local density approximation (LDA) or GGA results, which give $\left|\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\right|=\mathrm{10}$–12 cm⁻¹ and $\left|\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\right|=\mathrm{24}$–25 cm⁻¹, respectively. The improved performance of hybrid density functionals on vibrational properties of Mg silicates, supported by several dedicated studies in the literature (Prencipe et al., 2009; Demichelis et al., 2010; De La Pierre et al., 2011; De La Pierre and Belmonte, 2016), is thus also confirmed in this work.

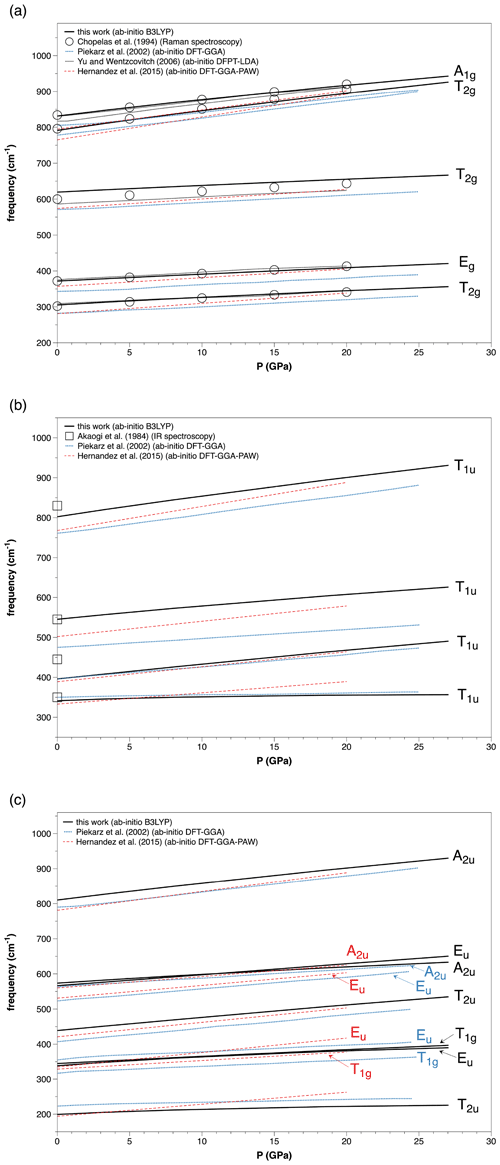
Figure 1 Pressure dependence of vibrational frequencies of Mg₂SiO₄ ringwoodite. (a) Raman-active modes, (b) IR-active modes and (c) silent modes.

The volume (or pressure) dependence of vibrational frequencies in the framework of QHA is defined by the mode Grüneisen parameters (γ_i), which allow in turn the determination of fundamental thermodynamic properties such as thermal expansion and P–V–T equation of state (e.g., Belmonte, 2017). Ab initio mode Grüneisen parameters of Raman-active modes calculated in this work show an excellent agreement with the few spectroscopic data available from the literature in the pressure range from 0 to 20 GPa (Chopelas et al., 1994; Chopelas, 2000). As far as we know, there are no experimental data for IR spectra of Mg₂SiO₄ ringwoodite at high-pressure conditions. A comparison between theoretical and experimental results is shown in Fig. 1 and Table S2. The calculated γ_i values for the two most intense Raman bands in the 790–796 and 830–836 cm⁻¹ frequency range are 1.4 and 1.1, respectively, compared to observed values of 1.3 and 0.9 (Chopelas et al., 1994). The predicted average mode Grüneisen parameter is 〈γ〉​​​​​​​ = 1.19, very close to the experimental value of 1.11 derived from high-pressure Raman spectra. By comparing different DFT simulations, although Raman frequencies change in terms of wavenumbers (see Table S2), their mode Grüneisen parameters turn out to be quite similar to each other. However, this is not the case for the IR-active and silent modes. The pressure dependences of some of the T_1u modes (for instance that in the 330–350 cm⁻¹ region) and some of the silent modes as well (e.g., the low-frequency T_2u mode) are sensibly different if B3LYP results are compared to other GGA calculations (Piekarz et al., 2002; Hernández et al., 2015). This is one of the reasons why marked differences are also observed in the computed values of volume thermal expansion coefficients (see Sect. 3.3 below). It is interesting to note, finally, that the width of the phonon band gap predicted in this work at Γ point is about 170 cm⁻¹ at P = 0, thus sensibly narrower than that obtained by previous ab initio LDA and GGA investigations (Yu and Wentzcovitch, 2006; Piekarz et al., 2002; Hernández et al., 2015). The splitting between upper and lower phonon bands increases up to 260 cm⁻¹ at P = 27 GPa. This likely occurs because the highest-frequency A_1g and T_2g vibrational modes, which are mostly related to stretching of Si–O stiff bonds in tetrahedral sites, display a steep pressure gradient (see Fig. 1 and Table S2 in the Supplement). Therefore the high-frequency modes are affected by pressure more than the medium- and low-frequency modes, as observed also by Yu and Wentzcovitch (2006).

3.2 Thermoelastic properties

Thermoelastic properties of insulating and fixed-composition crystalline phases can be defined solely by the statistical mechanics analysis of vibrational modes of the crystal lattice (Born and Huang, 1954). The key entity is represented by the αK_T product, which can be derived from the Helmholtz free energy F(V,T) by applying the thermodynamic identity:

$$\begin{array}{}\text{(4)}& \mathit{\alpha }{K}_T={\left({\displaystyle \frac{\partial P}{\partial T}}\right)}_V=-{\displaystyle \frac{\partial }{\partial V}}{\left[{\left({\displaystyle \frac{\partial F}{\partial T}}\right)}_V\right]}_T,\end{array}$$

where α and K_T are the volume thermal expansion coefficient (usually referred to as thermal expansivity) and the isothermal bulk modulus, respectively. The statistical mechanics expression is the following (see Belmonte, 2017):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathit{\alpha }{K}_T(V,T)& ={\displaystyle \frac{R}{ZV}}{\sum }_{\mathbf{q},i=\mathrm{1}}^{\mathrm{3}n}{\mathit{\gamma }}_i(\mathbf{q},V)\\ & \times e^{X_i(\mathbf{q},V)}{\left({\displaystyle \frac{X_i(\mathbf{q},V)}{e^{X_i(\mathbf{q},V)}-\mathrm{1}}}\right)}^{\mathrm{2}},\end{array}\end{array}$$

where R is the universal gas constant, Z is the number of unit formula in the unit cell, V is the molar volume, and γ_i(q,V) and X_i(q,V) are the mode Grüneisen parameter and the adimensional frequency of the ith vibrational mode, respectively, which both depend on the q point sampling and the volume of the crystal. The adimensional frequency can be simply obtained by converting the vibrational frequency wavenumbers ν_i(q,V) in angular frequencies ω_i(q,V) via the speed of light in vacuum (c), i.e., ${\mathit{\omega }}_i(\mathbf{q},V)=\left(\mathrm{2}\mathit{\pi }c\right)\times {\mathit{\nu }}_i(\mathbf{q},V)$ and then applying

$$\begin{array}{}\text{(6)}& X_i(\mathbf{q},V)={\displaystyle \frac{\mathrm{\hslash }{\mathit{\omega }}_i(\mathbf{q},V)}{kT}},\end{array}$$

where ℏ and k are the Planck and Boltzmann constants, respectively. By following a fully analytical approach, once the values of αK_T have been computed by Eq. (5), thermal expansivity α_V at given P–T conditions can be defined if the values of the isothermal bulk modulus K_T are also known.

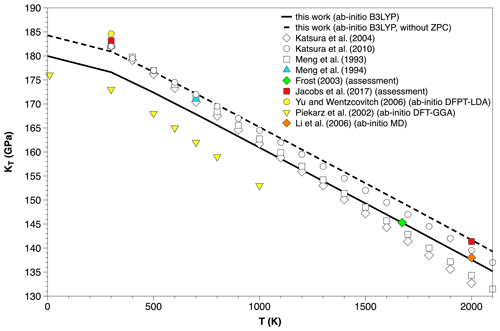
Figure 2 Temperature dependence of the isothermal bulk modulus (K_T) of Mg₂SiO₄ ringwoodite at zero or ambient pressure. Ab initio B3LYP results (with or without zero-point correction) are compared with available experimental data (Meng et al., 1993, 1994; Katsura et al., 2004, 2010), thermodynamic assessments (Frost, 2003; Jacobs et al., 2017) and previous ab initio DFT or MD simulations (Piekarz et al., 2002; Yu and Wentzcovitch, 2006; Li et al., 2006).

Table 1 Ab initio B3LYP thermal EOS parameters, as calculated in this work at P = 0 and different T conditions. Results obtained by experiments (M'94 – Meng et al., 1994; K'04 – Katsura et al., 2004; K'10 – Katsura et al., 2010), thermodynamic assessments (D'15 – Dorogokupets et al., 2015; J'17 – Jacobs et al., 2017) and different ab initio DFT (P'02 – Piekarz et al., 2002; YW'06 – Yu and Wentzcovitch, 2006) and first-principle molecular dynamics calculations (Li'06 – Li et al., 2006) are also shown. K_T is the isothermal bulk modulus (in GPa); $K_T^{\prime }$ and ${\left(\frac{\partial K_T}{\partial T}\right)}_P$ are the first derivatives of K_T with respect to P and T, respectively; ${\left(\frac{{\partial }^{\mathrm{2}}{K}_T}{\partial P\partial T}\right)}_{\mathrm{0}}$ is the mixed P–T derivative of K_T at T = 298.15 K.

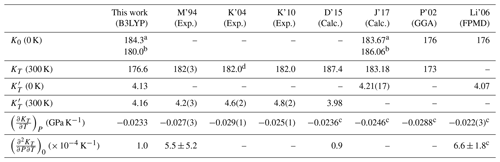
^a Static values. ^b Values at T = 0 K including zero-point correction (ZPC). ^c Results given by linear fitting of published data. ^d Fixed value.

First-principle Mie–Grüneisen equation of state (FPMG-EOS) allow us to define thermoelastic parameters (i.e., K_T and $K_T^{\prime }$) by fitting ab initio P–V–T (or F–V–T) data obtained from phonon dispersion calculations (see Belmonte, 2017, for details). The ab initio B3LYP results of K_T, $K_T^{\prime }={\left(\frac{\partial K_T}{\partial P}\right)}_T$, ${\left(\frac{\partial K_T}{\partial T}\right)}_P$ and $\left(\frac{{\partial }^{\mathrm{2}}{K}_T}{\partial P\partial T}\right)$ as computed in this work for Mg₂SiO₄ ringwoodite are shown in Fig. 2 and Table 1. Static values have been obtained by fitting energy–volume data (E–V) with a third-order Birch–Murnaghan EOS.

Static values calculated in this work for bulk modulus (i.e., K₀ = 184.3 GPa) are in remarkable agreement with experimental results, with the observed isothermal values being around 182–185 GPa at ambient conditions (Hazen, 1993; Meng et al., 1994; Katsura et al., 2004, 2010; see also Table 1). On the other hand, literature values of $K_{\mathrm{0}}^{\prime }$ seem to be more scattered, ranging from 4.2 up to almost 5.0. Our calculated values for the bulk modulus pressure derivative (i.e., $K_{\mathrm{0}}^{\prime }$ = 4.13 at the static level, $K_{T,\mathrm{300}}^{\prime }$ = 4.16 at T = 300 K and ambient pressure) are much closer to the experimental values of Meng et al. (1994) and to some vibrationally constrained thermodynamic assessments as well (e.g., Jacobs et al., 2017) (Table 1). A thorough comparison between different ab initio DFT simulations shows that B3LYP results are intermediate between those obtained by LDA and GGA, respectively, as expected from previous theoretical studies on the elasticity and EOS of several high-pressure minerals with hybrid density functionals (e.g., Erba et al., 2014; Prencipe et al., 2014; Ulian and Valdrè, 2018). In particular, LDA calculations give an upper bound to the calculated static or room-temperature bulk moduli, yielding values in the range 184–208 GPa (Kiefer et al., 1997, 1999; Yu and Wentzcovitch, 2006; Panero, 2008; Núñez-Valdez et al., 2011), while a lower bound of 175–178 GPa is provided by GGA-based DFT or MD simulations (Piekarz et al., 2002; Li et al., 2006, 2009; Panero, 2008; Hernández et al., 2015). It is interesting to note that vibrational effects on EOS parameters are relevant as K_T and $K_T^{\prime }$ at T = 300 K are rather different from static values. The former is lowered by ∼ 8 GPa (i.e., about 4 %), and the latter increases from 4.13 to 4.16 (Table 1). The effect of zero-point motions alone decreases the bulk modulus by ∼ 2.5 % over the entire temperature range (see Fig. 2). Those outcomes on ringwoodite are thus consistent with that observed for other high-pressure Mg silicates, like for instance bridgmanite (Oganov et al., 2001), suggesting that vibrational effects on thermoelastic properties cannot be disregarded in DFT simulations even at ambient P–T conditions (see Belmonte, 2017).

The temperature dependence of the isothermal bulk modulus of Mg₂SiO₄ ringwoodite at P = 0 GPa is shown in Fig. 2. Ab initio B3LYP results compare favorably with literature values, especially in the medium- to high-temperature range. The value inferred for ${\left(\frac{\partial K_T}{\partial T}\right)}_P$ by linear fitting of ab initio data is −0.0233 GPa K⁻¹, which is not far from the available experimental results (Meng et al., 1993, 1994; Katsura et al., 2010). The only exception is represented by the markedly negative value given by Katsura et al. (2004) (see Table 1). Interestingly, the computed ${\left(\frac{\partial K_T}{\partial T}\right)}_P$ is in excellent agreement with that obtained by some thermodynamic assessments based on the Helmholtz free energy, hence constrained by vibrational theory (Dorogokupets et al., 2015; Jacobs et al., 2017). Furthermore, the isothermal bulk modulus values computed by ab initio B3LYP at HT conditions are nearly coincident with those predicted by Frost (2003) at T = 1673 K and by the ab initio MD simulation of Li et al. (2006) at T = 2000 K (see Fig. 2). For instance, Li et al. (2006) obtain K_T = 138 ± 6 GPa at T = 2000 K, compared to our value of 137.6 GPa at the same temperature. This remarkable agreement supports the evidence that QHA performs well for Mg₂SiO₄ ringwoodite in the whole P–T range of the mantle transition zone. Conversely, other “internally consistent” thermodynamic assessments give K_T values for ringwoodite which are overestimated (Holland and Powell, 2011) or possibly affected by physical unsoundness (Fabrichnaya et al., 2004).

The mixed P–T derivative of the isothermal bulk modulus has also been constrained in this work. Ab initio B3LYP calculations give ${\left(\frac{{\partial }^{\mathrm{2}}{K}_T}{\partial P\partial T}\right)}_{\mathrm{0}}\cong \mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}$ K⁻¹ at room temperature, which is virtually identical to the assessed value by Dorogokupets et al. (2015) and in qualitative agreement with the experimental results of Meng et al. (1994) within their quite large uncertainties (see Table 1). First-principle MD simulations of Li et al. (2006) provide a higher $K_T^{\prime }$ of 5.2 ± 0.3 at T = 2000 K (against $K_{T,\mathrm{2000}}^{\prime }$ = 4.33 predicted in this work), but also in this case the agreement seems to be reasonable in view of the huge uncertainties which currently affect the definition of thermoelastic properties of deep mantle minerals at simultaneous high-pressure and high-temperature conditions.

3.3 Thermal expansion and thermal expansivity

It is well known that hybrid functionals like B3LYP, which are based on the generalized gradient approximation for the DFT exchange–correlation term, overestimate molar volumes of magnesium silicates by ∼ 1 %–2 %, essentially due to an underbinding trend predicted for Mg–O and Si–O bond lengths (Kohanoff, 2006; Ottonello et al., 2009; Belmonte et al., 2014). The optimized unit cell volume of ringwoodite at the athermal limit (i.e., T = 0 K, P = 0 GPa) is V₀ = 530.9 ų, that is 1 % higher than experimental values obtained by X-ray diffraction at ambient conditions (Sasaki et al., 1982; Katsura et al., 2004). Nevertheless, zero-pressure relative volume thermal expansion (i.e., $V/V_{\mathrm{0}}$) and thermal expansivity (α_V) are accurately reproduced in the framework of QHA up to a limit, which, as a rule of thumb, lies within the Debye temperature and two-thirds of the melting point of the substance. This limit is purely empirical in nature and may change according to the physicochemical properties of the solid phase. In other words, deviations from the observed trend may occur due to the onset of anharmonic effects at temperature conditions not so far from the melting point. In such a case, the crystalline substance can be referred to as a “quasi-harmonic” solid. Ab initio B3LYP results of volume thermal expansion and thermal expansivity are shown in Figs. 3 and 4, respectively.

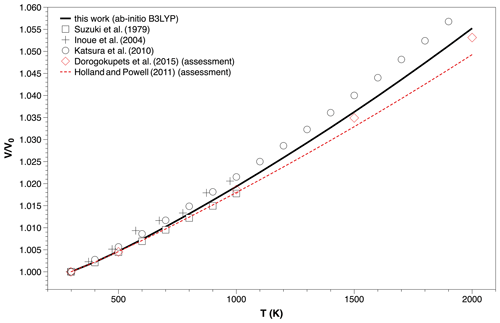
Figure 3 Ab initio B3LYP volume thermal expansion ($V/V_{\mathrm{0}}$) of Mg₂SiO₄ ringwoodite at zero pressure, compared with experimental data (Suzuki et al., 1979; Inoue et al., 2004; Katsura et al., 2010) and thermodynamic assessments (Holland and Powell, 2011; Dorogokupets et al., 2015) at ambient pressure.

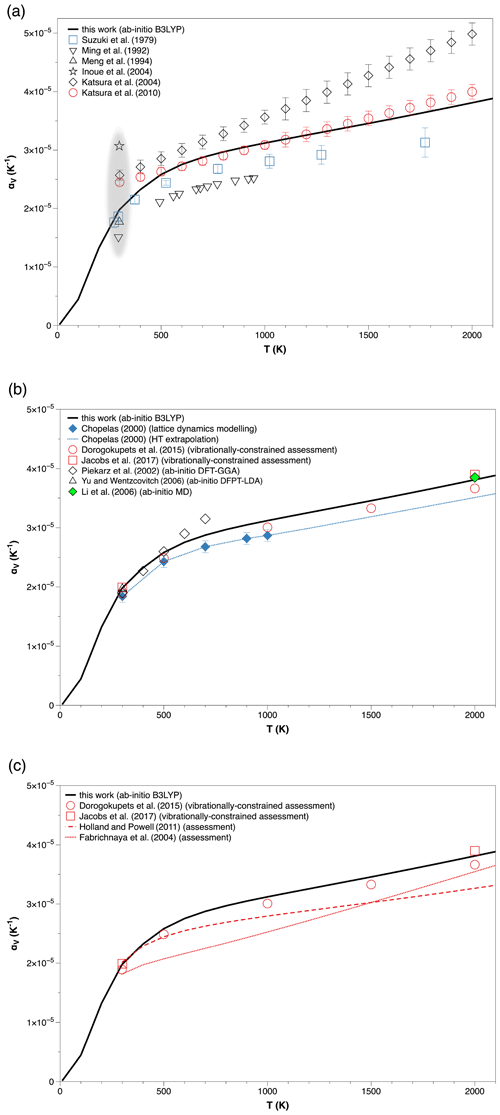
Figure 4 Ab initio B3LYP volume thermal expansivity (α_V) of Mg₂SiO₄ ringwoodite at zero pressure, compared with (a) experimental data (grey shaded area highlights scattering of values at ambient conditions), (b) different theoretical simulations and (c) thermodynamic assessments.

The values of α_V computed at zero pressure and discrete temperatures by the statistical thermodynamic approach described in Sect. 3.2 are fitted by a suitable polynomial function in the temperature range from T_r = 298.15 K to T = 2000 K, as follows:

$$\begin{array}{}\text{(7)}& {\mathit{\alpha }}_V\left(P_{\mathrm{0}},T\right)={\mathit{\alpha }}_{\mathrm{0}}+{\mathit{\alpha }}_{\mathrm{1}}T+{\mathit{\alpha }}_{\mathrm{2}}{T}^{-\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{3}}{T}^{-\mathrm{2}}+{\mathit{\alpha }}_{\mathrm{4}}{T}^{-\mathrm{3}}.\end{array}$$

Fitted numerical coefficients of the polynomial function at P = 0 are α₀ = 1.6033 × 10⁻⁵ K⁻¹, α₁ = 8.839 × 10⁻⁹ K⁻², α₂ = 11.586 × 10⁻³, α₃ = −6.055 K and α₄ = 804.31 K² (see Table 2). Relative volume thermal expansion can thus be obtained by analytical integration of α_V, i.e.,

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{V}{V_{\mathrm{0}}}}\left(P_{\mathrm{0}},T\right)=\exp \underset{T_{\mathrm{r}}}{\overset{T}{\int }}{\mathit{\alpha }}_V\left(P_{\mathrm{0}},T\right)\mathrm{d}T.\end{array}$$

A huge uncertainty exists on the ambient value of volume thermal expansion coefficient of Mg₂SiO₄ ringwoodite (Nestola, 2016), with experimental values ranging from ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = 1.51 × 10⁻⁵ K⁻¹ (Ming et al., 1992) to ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = 3.07 × 10⁻⁵ K⁻¹ (Inoue et al., 2004). ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ can thus vary as much as 100 % according to different experimental investigations. The computed value in this work, i.e., ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = 1.98 × 10⁻⁵ K⁻¹, is not far from the experimental value ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = (1.86 ± 0.09) × 10⁻⁵ K⁻¹ obtained by Suzuki et al. (1979). Both values are quite different from those determined by other experimental works (Meng et al., 1994; Katsura et al., 2004). Again, ambient thermal expansion coefficients calculated by lattice dynamics modeling or other vibrationally constrained assessments are in remarkable agreement with our result (i.e., ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = 1.84 ± 0.10 × 10⁻⁵ K⁻¹ according to Chopelas, 2000; ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = 1.89 × 10⁻⁵ K⁻¹, Dorogokupets et al., 2015; ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = 1.99 × 10⁻⁵ K⁻¹, Jacobs et al., 2017). This result can be interpreted as a clear sign of thermodynamic soundness of thermal expansion data.

Table 2 Ab initio B3LYP thermal expansivity of Mg₂SiO₄ ringwoodite up to mantle transition zone conditions (α_V in K⁻¹). Fitted coefficients of the function ${\mathit{\alpha }}_V(P,T)=({\mathit{\alpha }}_{\mathrm{0}}+{\mathit{\alpha }}_{\mathrm{1}}T+{\mathit{\alpha }}_{\mathrm{2}}{T}^{-\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{3}}{T}^{-\mathrm{2}}+{\mathit{\alpha }}_{\mathrm{4}}{T}^{-\mathrm{3}})\exp (-{\mathit{\alpha }}_{\mathrm{5}}P)$ are valid in the P–T range between 0–25 GPa and 298.15–2000 K.

The calculated trend of volume thermal expansion up to high-temperature conditions provides some insights into the thermodynamic behavior of ringwoodite at deep mantle conditions (Figs. 3 and 4). Ab initio thermal expansivity as calculated in this work is relatively different from the HT extrapolation of experimental data (see Fig. 4a). In particular, B3LYP gives α_V values which are higher than those determined by Suzuki et al. (1979) at T > 1000 K but much lower than the observed trend by Katsura et al. (2004). However, the optimized trend of Katsura et al. (2010) is in excellent agreement with our calculations in the whole temperature range, except for the ambient value (i.e., ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ = 2.45 ± 0.05 × 10⁻⁵ K⁻¹), which seems to be strongly overestimated with respect to our result and to that observed by Suzuki et al. (1979) as well. This leads in turn to a different trend in the relative volume thermal expansion (Fig. 3). The evidence that different DFT and QHA simulations give quite similar values of ${\mathit{\alpha }}_{V_{\mathrm{0}}}$ (see Piekarz et al., 2002; Yu and Wentzcovitch, 2006; Hernández et al., 2015) strengthens the ability of ab initio calculations to identify and select accurate experimental results for thermal expansivity. For instance, the α_V values determined by Ming et al. (1992) are likely affected by severe underestimation (Fig. 4a). On the other hand, the temperature dependence of thermal expansivity may change among different theoretical simulations. Ab initio B3LYP gives ${\left(\frac{\partial {\mathit{\alpha }}_V}{\partial T}\right)}_{P_{\mathrm{0}}}$ similar to those calculated by Chopelas (2000) and Dorogokupets et al. (2015), but sensibly different from that obtained by other ab initio DFT–GGA calculations (Piekarz et al., 2002) (see Fig. 4b). Interestingly, α_V does not display any inflection point in the entire T range investigated in this work, thus confirming that (i) QHA performs exceptionally well for Mg₂SiO₄ ringwoodite up to deep mantle temperatures and (ii) ringwoodite can be considered a “quasi-harmonic” solid in the Earth's mantle transition zone. Further supporting evidence is that the thermal expansivity predicted at T = 2000 K and room pressure by the first-principle molecular dynamics of Li et al. (2006) are almost identical to that predicted by this work, with the former being equal to 3.85 × 10⁻⁵ K⁻¹ and the latter around 3.81 × 10⁻⁵ K⁻¹ (Fig. 4b). This confirms the performance of ab initio B3LYP and QHA calculations since MD simulations, which are able to catch anharmonic effects, give nearly coincident results on thermal expansivity in the high-temperature range. Therefore, intrinsic anharmonic effects do seem to be negligible for Mg₂SiO₄ ringwoodite even at HT (and low-pressure) conditions.

The comparison between ab initio calculations and internally consistent thermodynamic assessments deserves special attention. Figure 4c shows that thermal expansivity assessed via mathematical procedures able to reproduce selected phase equilibria of Mg₂SiO₄ ringwoodite (e.g., Fabrichnaya et al., 2004; Holland and Powell, 2011) turns out to be inaccurate at mantle temperatures. For instance, Holland and Powell (2011) used a thermal pressure Tait EOS, along with some assumptions on thermoelastic properties, to predict thermal expansion of mantle minerals at HP–HT conditions. α_V values obtained for Mg₂SiO₄ ringwoodite are underestimated by 10 %–15 % in the high-temperature range (see Fig. 4c). The same also applies to the relative volume thermal expansion trend depicted in Fig. 3. This is perhaps even more evident if thermal expansion data by Fabrichnaya et al. (2004) are considered in Fig. 4c, which basically means that internally consistent thermodynamic datasets currently developed for deep mantle minerals are not necessarily also physically consistent. In this respect, it does not seem fortuitous that thermodynamic assessments based on Helmholtz free energy and/or constrained by vibrational theory (e.g., Dorogokupets et al., 2015; Jacobs et al., 2017) provide thermal expansion data very close to the ab initio results obtained in this work (Figs. 3 and 4c).

The coupling between thermal expansivity and isothermal bulk modulus provides a further clue on the physical soundness of thermoelastic properties and the robustness of their extrapolation to deep mantle temperatures. This is not a trivial task from an experimental point of view, since αK_T values are difficult to be constrained at those conditions. Kojitani et al. (2016) tried to infer K_T of Mg₂SiO₄ ringwoodite by fitting experimental P–V–T data of Katsura et al. (2004) with a high-temperature third-order Birch–Murnaghan EOS and by assuming α_V of Suzuki et al. (1979) as fixed in the fitting. They obtain ${\left(\frac{\partial K_T}{\partial T}\right)}_P=-\mathrm{0.019}\left(\mathrm{3}\right)$ GPa K⁻¹, which is much less negative than any other theoretical or experimental determinations (see Table 1). This is most likely due to the fact that the two experimental datasets cannot be reconciled by the assessment. Ottonello et al. (2009) obtain a value of ${\left(\frac{\partial K_T}{\partial T}\right)}_P=-\mathrm{0.0104}$ GPa K⁻¹, which is even less negative and leads to an overestimation of K_T values of ringwoodite at HT. In that case, an overestimation may occur because the assessment of thermoelastic properties is not based on the full vDOS but rather on a semiclassical thermodynamic approximation employing the logarithmic volume derivative of the Grüneisen parameter (the so-called q^ht parameter), which is difficult to constrain by lattice dynamics calculations (Anderson, 1995). The average value of the αK_T product calculated for mantle phases over an appropriate temperature range can give useful insights into the accuracy of thermoelastic data (Stixrude and Lithgow-Bertelloni, 2005). If we consider the average value of αK_T of Mg₂SiO₄ ringwoodite over a T range from 300 to 1000 K, namely where the temperature gradient of α_V is steeper, we obtain 45.6 bar K⁻¹ according to our calculations. Vibrationally constrained thermodynamic assessments (e.g., Stixrude and Lithgow-Bertelloni, 2005) give values around 44 bar K⁻¹, in excellent agreement with the ab initio value determined by Eq. (4), while other internally consistent thermodynamic databases could give clearly inaccurate results (e.g., ${\stackrel{\mathrm{‾}}{\mathit{\alpha }{K}_T}}_{\text{300–1000\hspace{0.17em}K}}$ = 37.3 bar K⁻¹ according to Fabrichnaya et al., 2004). As for experimental data, there is a marked difference between the dataset of Katsura et al. (2004) and that of Katsura et al. (2010), with the latter being much closer to ab initio results than the former (i.e., ${\stackrel{\mathrm{‾}}{\mathit{\alpha }{K}_T}}_{\text{300–1000\hspace{0.17em}K}}$ = 52.7 and 48.0 bar K⁻¹, respectively). This confirms the predictive power of state-of-the-art ab initio calculations in constraining the extrapolation of experimental data at deep mantle conditions.

4 Implications: thermal expansivity at mantle transition zone conditions

Thermal expansivity is a key parameter for mantle dynamics. Buoyancy forces that control thermal convection in the Earth's mantle are driven by lateral variations in temperature and density, which are in turn determined by the local volume thermal expansion of the constituent mineral phases (Christensen and Yuen, 1985). Thermal expansivity is commonly assumed as either constant or simply pressure-dependent by most numerical simulations of mantle convection, while simultaneous P–T dependence is only rarely taken into account (Schmeling et al., 2003; Tosi et al., 2013).

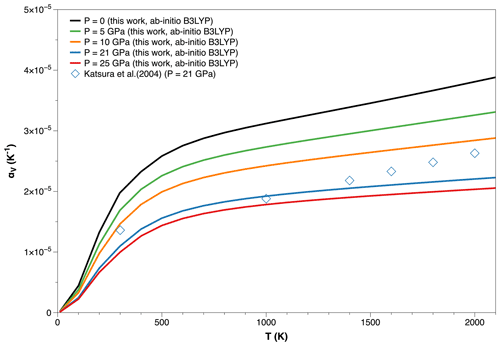
Figure 5 Ab initio volume thermal expansivity (α_V) of Mg₂SiO₄ ringwoodite at different pressures (P = 0, 5, 10, 21 and 25 GPa). Experimental data at P = 21 GPa are from Katsura et al. (2004).

In this work, α_V(P,T) and K_T(P,T) functions of Mg₂SiO₄ ringwoodite are computed in a broad range of P–T conditions compatible with the stability of this phase in the Earth's mantle transition zone (i.e., P = 0–25 GPa, T = 298.15–2000 K). The following six-parameter analytical function is able to reproduce ab initio values in the whole investigated P–T range with a maximum deviation of a few percent:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\mathit{\alpha }}_V(P,T)& =\left({\mathit{\alpha }}_{\mathrm{0}}+{\mathit{\alpha }}_{\mathrm{1}}T+{\mathit{\alpha }}_{\mathrm{2}}{T}^{-\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{3}}{T}^{-\mathrm{2}}+{\mathit{\alpha }}_{\mathrm{4}}{T}^{-\mathrm{3}}\right)\\ & \times \exp (-{\mathit{\alpha }}_{\mathrm{5}}P),\end{array}\end{array}$$

and therefore it has been adopted in this work. The coefficient α₅ in Eq. (9) has been fitted starting from the polynomial function at P = 0 (see Eq. 7), and then applying an exponential pressure dependence (Table 2). A similar parametrization was also implemented by Tosi et al. (2013) in their numerical modeling of mantle convection due to its relatively simple form.

Figure 5 shows ab initio B3LYP thermal expansivity calculated at different pressure conditions (i.e., P = 0, 5, 10, 21 and 25 GPa). α_V(P,T) is strongly pressure-dependent and does not show any inflection point in the whole P–T range investigated in this work, thus supporting again the quasi-harmonic nature of ringwoodite at mantle transition zone conditions. The experimental values obtained by Katsura et al. (2004) at P = 21 GPa are in qualitative agreement with our calculations up to about 1000 K and then deviate at higher temperatures. Even though experimental uncertainties in α_V values are not provided at P = 21 GPa, overestimation of room-temperature α_V seems to also be kept at high pressures.

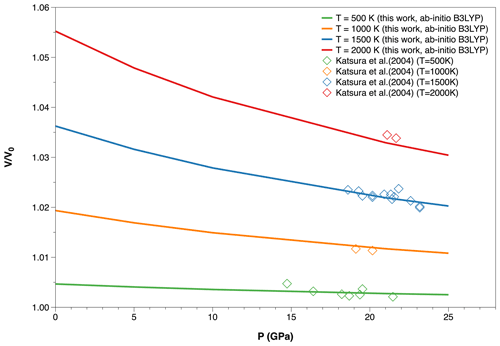
Figure 6 Ab initio volume thermal expansion ($V/V_{\mathrm{0}}$) of Mg₂SiO₄ ringwoodite along different isotherms (T = 500, 1000, 1500 and 2000 K). Experimental data are taken from Katsura et al. (2004).

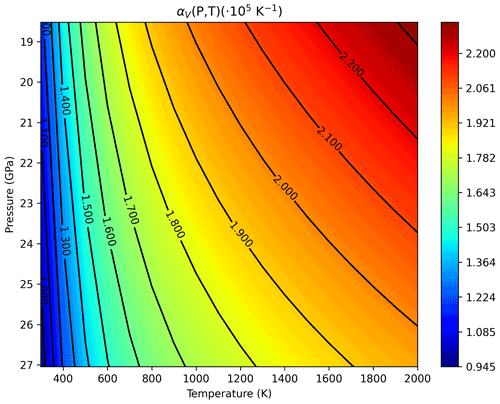
Even more interesting is the analysis of ab initio volume thermal expansion calculated up to mantle transition zone pressures along different isotherms (i.e., T = 500, 1000, 1500 and 2000 K) (Fig. 6). By the computed trends in Fig. 6 it is quite evident that the pressure dependence of volume thermal expansion of ringwoodite becomes more marked with increasing temperature. This means that inaccurate extrapolations of low-pressure data at mantle transition zone conditions could lead to large errors in predicted molar volume and density values at HP–HT, thus affecting phase equilibrium calculations and large-scale numerical modeling of mantle convection at those conditions. Experimental values obtained by in situ X-ray diffraction in a multianvil apparatus by Katsura et al. (2004), although sensibly scattered, turn out to be in good agreement with ab initio results. The combined P–T effects on thermal expansivity of ringwoodite are shown by a contour plot in Fig. 7, which displays calculated α_V(P,T) values within the stability field of the spinel-structured Mg₂SiO₄ polymorph at depths of the lower mantle transition zone (i.e., > 520 km) as inferred by global geophysical models (Dziewonski and Anderson, 1981; Brown and Shankland, 1981). Since contour lines change their slope going from shallow to deep MTZ conditions, the increased pressure dependence of thermal expansivity with temperature is highlighted even more clearly. Ab initio DFT–QHA simulations thus provide a fundamental constraint to interpret deep mantle processes under a mineral physics and thermodynamic perspective.

Figure 7 Contour plot of ab initio volume thermal expansivity α_V(P,T) of Mg₂SiO₄ ringwoodite at mantle transition zone conditions.

5 Conclusions

We showed that modern DFT–QHA calculations with the hybrid functional B3LYP are able to accurately predict volume thermal expansion and thermoelastic properties of Mg₂SiO₄ ringwoodite up to mantle transition zone conditions. Ab initio results of α_V(P,T), $V/V_{\mathrm{0}}(P,T)$ and K_T(P,T) give a physical constraint to the HP–HT extrapolation of thermoelastic properties as determined by laboratory experiments, thus enhancing our understanding of mantle processes (e.g., thermal convection) in planetary interiors. Theoretical analysis of lattice dynamics allowed the interpretation of vibrational spectra at both ambient and high-pressure conditions by suggesting that IR-active and silent modes, along with their mode Grüneisen parameters, play a key role in determining volume thermal expansion of ringwoodite, particularly at high temperatures and pressures. Since literature data on those vibrational modes are still scarce or controversial, the huge uncertainties that currently affect thermal expansivity of this mantle mineral may be readily understood. In this respect, vibrationally constrained thermoelastic properties as computed by ab initio methods revealed that physical unsoundness could be concealed under internally consistent thermodynamic datasets developed for mantle phases. Ab initio thermal expansivity and isothermal bulk modulus calculated in this work in a broad range of P–T conditions (i.e., P = 0–25 GPa, T = 0–2000 K) support the evidence of a quasi-harmonic behavior of ringwoodite in the Earth's mantle transition zone. In fact, high-temperature values of α_V and K_T predicted in this work by DFT–QHA calculations turn out to be nearly coincident with the results of the first-principle molecular dynamics simulation by Li et al. (2006), stressing that intrinsic anharmonic effects are virtually absent at MTZ conditions. Finally, since thermal expansivity of Mg₂SiO₄ ringwoodite is strongly pressure-dependent and its pressure dependence increases with increasing temperature (see Figs. 5–7), extrapolation of low-pressure thermoelastic data to deep mantle conditions should be taken with care to avoid inaccurate or spurious numerical predictions.