the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Influence of water on the physical properties of olivine, wadsleyite, and ringwoodite
Qun-Ke Xia
The incorporation of water in nominally anhydrous minerals plays a crucial role in many geodynamic processes and evolution of the Earth and affects the physical and chemical properties of the main constituents of the Earth's mantle. Technological advances now allow the transport properties of minerals to be precisely measured under extreme conditions of pressure and temperature (P and T) that closely mimic the P–T conditions throughout much of the Earth's interior. This contribution provides an overview of the recent progress in the experimental studies on the influence of water on physical properties (i.e., diffusivity, electrical conductivity, thermal conductivity, sound velocity, and rheology) of olivine, wadsleyite, and ringwoodite together with their applications. In particular, consistency among various experimental data is investigated, discrepancies are evaluated, and confusions are clarified. With such progress in the experimental determination of transport properties of major mantle minerals, we can expect new insights into a broad range of geoscience problems. Many unresolved issues around water inside Earth require an integrated approach and concerted efforts from multiple disciplines.
- Article
(20676 KB) - Full-text XML
- BibTeX
- EndNote
The transport properties of minerals have an important influence on the dynamics and evolution of Earth and other terrestrial planets. Nominally anhydrous minerals (NAMs) in the mantle can store significant concentrations of water as defects in their crystal structures. Water incorporation in NAMs (even a trace amount of water) has long been proposed to have dramatic influences on many physical and chemical properties, such as thermal conductivity (κ) (Chang et al., 2017; B. H. Zhang et al., 2019a), diffusivity (D) (e.g., Kubo et al., 2004; Hier-Majumder et al., 2005; Costa and Chakraborty, 2008; Fei et al., 2013, 2018; Sun et al., 2015, 2018, 2019; B. H. Zhang et al., 2019b), electrical conductivity (σ) (e.g., Karato, 1990; Huang et al., 2005; D. Wang et al., 2006; Yoshino et al., 2006, 2008, 2009; Manthilake et al., 2009; Poe et al., 2010; Yang, 2012; B. H. Zhang et al., 2019c; Liu et al., 2019), sound velocity (VP and VS) (e.g., Jacobsen and Smyth, 2006; J. Wang et al., 2006; Mao et al., 2010, 2011; Buchen et al., 2018; Wang et al., 2019), and rheology (e.g., Mei and Kohlstedt, 2000a, b; Kohlstedt, 2006; Katayama and Karato, 2008a, b; Demouchy et al., 2012; Farla et al., 2015; Kawazoe et al., 2009, 2013, 2016; Faul et al., 2016). It can affect large-scale geodynamics (Ohtani et al., 2004; Karato, 2011), trigger high-conductivity and low-velocity anomalies (Hirschmann, 2010), and change the rheological and thermal structure of the lithosphere (Karato et al., 2001; Hirth and Kohlstedt, 2003; Costa and Chakraborty, 2008; Fei et al., 2013). In general, the species affecting the transport properties of mantle minerals may be H+(proton), (OH)−, or molecular hydrogen (H2) in conjunction with intrinsic point defects in their structure (Moine et al., 2020). We will simply refer to these species as “water” hereafter.
Olivine [α-(Mg,Fe)2SiO4] is one of the most abundant minerals of the Earth's upper mantle (UM), and it transforms to wadsleyite [β-(Mg,Fe)2SiO4] and ringwoodite [γ-(Mg,Fe)2SiO4] in the mantle transition zone (MTZ). Previous studies showed that wadsleyite and ringwoodite can incorporate up to approximately 3 wt. % H2O within their crystal structures (e.g., Inoue et al., 1995; Kohlstedt et al., 1996; Ohtani et al., 2004), whereas the solubility of water in olivine is limited (<0.9 wt. % H2O) over all the pressure and temperature (P–T) conditions of the UM (e.g., Kohlstedt et al., 1996; Mosenfelder et al., 2006; Smyth et al., 2006; Bali et al., 2008; Padrón-Navarta and Hermann, 2017; Fei and Katsura, 2020). A comprehensive dataset of the water content in diverse types of natural samples, including peridotite and granulite xenoliths hosted by alkali basalts, ultrahigh-pressure metamorphic eclogites, and Mesozoic–Cenozoic alkali basalts, has been built not only for eastern China (e.g., Xia et al., 2006, 2013, 2019; Gu et al., 2019), but also for worldwide localities (Demouchy and Bolfan-Casanova, 2016). This dataset provides an integrated picture of the temporal and spatial distribution of water in the lower crust and UM at a continental scale. In addition, the recently discovered ringwoodite inclusion with ∼1.4 wt. % H2O and ice-VII inclusions in diamonds (Pearson et al., 2014; Tschauner et al., 2018) clearly demonstrated a water-rich MTZ, at least locally. Considering water solubility in the crystal structure of wadsleyite and ringwoodite (Inoue et al., 1995; Kohlstedt et al., 1996), the MTZ is expected to contribute greatly to global water circulation (Karato, 2011). In this sense, the water content of the Earth's mantle is a key parameter of the Earth's water budget. Thus, the precise determination of water content in the mantle is essential for understanding various geodynamic processes in the deep Earth, such as mantle convection and water circulation (Karato, 2011).
In the past several decades, although numerous experimental data on water solubility and incorporation mechanism of water in NAMs have been accumulated (e.g., Inoue et al., 1995; Kohlstedt et al., 1996; Demouchy and Mackwell, 2006; Withers et al., 2012; Jollands et al., 2016), determining the real water content and its distribution from such information alone is difficult. Thus, the actual abundance of water in the UM and MTZ is still unknown. Measuring the physical properties (i.e., diffusivity, electrical conductivity, thermal conductivity, sound velocity, and rheology) of mantle minerals as a function of water content and combining multidisciplinary constraints from seismology, magnetotelluric survey, petrology, geochemistry, and theoretical simulation can be used to directly determine the water content and distribution in the Earth's present mantle. Although many studies have investigated the transport properties of NAMs (e.g., Jacobsen and Smyth, 2006; Yoshino, 2010; Yoshino and Katsura, 2013; Gardés et al., 2014, 2015; Karato, 2011, 2019), there are still some controversies and confusion. For example, the effect of water on the electrical conductivity of olivine is often contradictory between different groups (D. Wang et al., 2006; Yoshino et al., 2006; Karato and Dai, 2009; Yoshino and Katsura, 2009, 2012, 2013; Gardés et al., 2015; Dai and Karato, 2015). With respect to the causes of these experimental discrepancies or controversies, one has to fingerprint the type of defect that is involved in each process (from fast electrical conductivity properties to extremely slow rheological processes) (e.g., Berry et al., 2005; Walker et al., 2007; Purevjav et al., 2014, 2016; Caracas and Panero, 2017; Padrón-Navarta and Hermann, 2017; Tollan et al., 2017, 2018; Le Losq et al., 2019). All these processes related to physical properties of NAMs cannot be the consequence of a single defect. Especially, the microscopic substitution mechanisms of water in lattice and type and concentration of point defects needs to be considered carefully.
In the present study, we mainly focus on the influence of water on the physical properties of olivine, wadsleyite, and ringwoodite. Firstly, we critically review the recent advances in diffusivity, electrical conductivity, thermal properties, sound velocity, and rheology; evaluate the reliability of experimental results; and clarify the controversies and discrepancies. Secondly, we present possible links between various transport properties and discuss the geophysical applications. Finally, we provide a summary of the limitations and possibilities of the methodologies and available data and suggest some future directions.
Diffusion is due to thermally activated atomic-scale random motion of particles (atoms, ions, and molecules) in minerals, glasses, melts, and gases (Zhang, 2010). The random motion leads to a net flux when the concentration of a component is not uniform. Diffusion studies in silicate minerals provide important constraints on numerous geodynamics, petrological, and geochemical processes (e.g., Watson and Baxter, 2007; Chakraborty, 2008; Brady and Cherniak, 2010). Several researchers have made a very extensive and detailed review of diffusion coefficients of different elements (such as H, O, Fe–Mg, and other cations) in mantle minerals (e.g., Béjina et al., 2003; Ingrin and Blanchard, 2006; Brady and Cherniak, 2010; Chakraborty, 2010; Zhang, 2017). Herein, we present an overview of the latest diffusion data in olivine, wadsleyite, and ringwoodite after 2010 and mainly emphasize the effect of water on the diffusion coefficient rather than diffusion theory.
If a single mechanism of diffusion is involved, the variation of diffusivity (D) with temperature and pressure obeys the Arrhenius equation for a given species:
where D0, R, H, E, and ΔV are the pre-exponential factor, ideal gas constant, activation enthalpy, activation energy, and activation volume, respectively. If more influencing factors (such as water content, oxygen fugacity, and composition) are simultaneously taken into account, the diffusion coefficient, D, can be rewritten as follows (Dohmen et al., 2007; Zhang, 2017):
where is oxygen fugacity; is oxygen fugacity; X is composition (e.g., iron content); n, r, and p are constants; and α is a parameter related to the activation energy. It is worth noting that the diffusion in crystalline solids is strongly dependent upon point defect (vacancy, interstitial, and substitutional defects) concentrations and temperature. Various atomic mechanisms of diffusion in crystals have been identified and catalogued: vacancy mechanism, interstitial mechanism, divacancy mechanism, interstitialcy mechanism, and interstitial–substitutional exchange mechanism (e.g., Mehrer, 2007; Chakraborty, 2010; de Koker and Stixrude, 2010; Zhang, 2017). In this case, we mainly focus on the experimental data on diffusion in olivine and its high-pressure polymorphs.
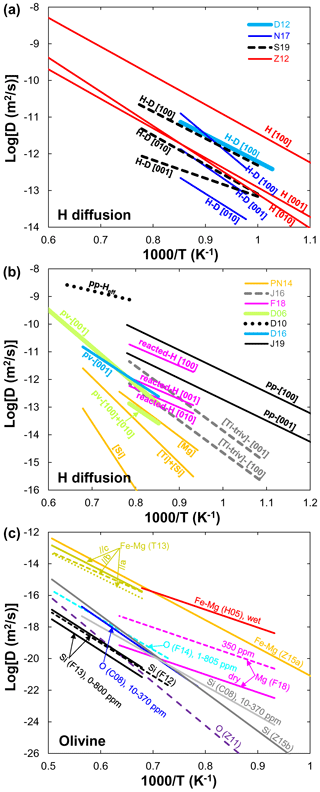
Figure 1(a) Arrhenius plot summarizing experimental results for hydrogen diffusion in olivine. Data sources: Z12 (Zhang, 2012); D10 (Demouchy, 2010); D06 (Demouchy and Mackwell, 2006); D12 (Du Frane and Tyburczy, 2012); N17 (Novella et al., 2017); D16 (Demouchy et al., 2016); J16 (Jollands et al., 2016); S19 (Sun et al., 2019). (b) Arrhenius plot summarizing experimental results for dehydration experiments in olivine. Data sources: D06 (Demouchy and Mackwell, 2006); D10 (Demouchy, 2010); PN14 (Padrón-Navarta et al., 2014); D16 (Demouchy et al., 2016); J16 (Jollands et al., 2016); F18 (Ferriss et al., 2018); J19 (Jollands et al., 2019). Note that pv and pp stand for proton–metal vacancy and proton–polaron exchange mechanism, respectively. (c) Arrhenius plot summarizing experimental results for other elements' (Li, He, Mg, Fe–Mg, O, Si) diffusion in olivine under dry and hydrous conditions. Data sources: C12 (Cherniak and Watson, 2012); DK10 (Dohmen et al., 2010); T13 (Tachibana et al., 2013); H05 (Hier-Majumder et al., 2005); C08 (Costa and Chakraborty, 2008); F12 (Fei et al., 2012); F13 (Fei et al., 2013); F14 (Fei et al., 2014); F18 (Fei et al., 2018); Z11 (Zhang et al., 2011); Z15a (Zhang and Shan, 2015a); Z15b (Zhang and Shan, 2015b).
2.1 Olivine
Over the long history of diffusion studies in olivine, many sets of data have been accumulated. However, not all of these are consistent with each other. A summary of the new advances in diffusion in olivine is provided below.
H. Hydrogen diffusion is one of the fastest transport processes in olivine, but it is quite complicated. Ingrin and Blanchard (2006) and Farver (2010) have provided a detailed review of hydrogen or water diffusion in olivine until the time of publication of each review. Since then, many new data on hydrogen diffusion in olivine have been reported by performing hydrogen–deuterium (H–D) exchange experiments (Fig. 1a) (e.g., Du Frane and Tyburczy, 2012; Novella et al., 2017; Sun et al., 2019) or dehydration experiments (Fig. 1b) (e.g., Demouchy and Mackwell, 2006; Demouchy, 2010; Padrón-Navarta et al., 2014; Demouchy et al., 2016; Jollands et al., 2016, 2019; Ferriss et al., 2018). Du Frane and Tyburczy (2012) measured the hydrogen self-diffusivity by H–D exchange in single crystals of San Carlos olivine between 1023 and 1173 K at 2 GPa parallel to the [100] direction. Using the same experimental method as that of Du Frane and Tyburczy (2012), Novella et al. (2017) determined the hydrogen self-diffusion coefficients in olivine single crystal along the three principal crystal orientations under the upper mantle conditions (2 GPa, 1023–1173 K). Recently, Sun et al. (2019) reported the hydrogen self-diffusivity in olivine at 3–13 GPa and 1000–1300 K as a function of water content. As illustrated in Fig. 1a, the hydrogen diffusion rates and activation enthalpy along the [100] orientation reported by Du Frane and Tyburczy (2012) are consistent with those of Sun et al. (2019). We note that the obtained activation enthalpies of hydrogen diffusion (140±11, 153±21, and 95±19 kJ/mol for [100], [010], and [001], respectively) by Sun et al. (2019) are significantly lower than those determined by Novella et al. (2017) (229±18, 172±19, and 188±8 kJ/mol for [100], [010], and [001], respectively) from a narrow temperature range. This discrepancy could be attributed to the difference in measured temperature range, pressure, and water content. Single-crystal olivine employed in Sun et al. (2019) has a significantly higher water content (150–1648 ppm) than the ones from Novella et al. (2017) (74 ppm). The smaller activation enthalpies determined by Sun et al. (2019) might be due to a lowering of activation energy of proton migration as water content increases. The anisotropy between the [010] and [001] directions reported by Sun et al. (2019) is comparable to that of Zhang (2012) but in contrast to the result from Novella et al. (2017). However, the reason for this difference is unknown, which cannot be explained by difference in the measured temperature/or pressure range for each study.
Dehydration experiment is another effective way to obtain a hydrogen diffusion coefficient in single-crystal or polycrystalline olivine. Padrón-Navarta et al. (2014) and Jollands et al. (2016) studied hydrogen diffusion in Ti-doped forsterite as a function of the type of point-defect mechanism by which the hydroxyl is incorporated. In the case of Ti-bearing forsterite, the defect chemistry is dominated by [Ti] (Ti4+ is in an octahedral site charge-balanced by a substitution of Si4+ by two protons on a neighboring tetrahedral site) and [Si] (four H atoms charge-balance a Si vacancy in a tetrahedral site). Demouchy and Mackwell (2006) and Demouchy et al. (2016) investigated the incorporation and diffusion of hydrogen in San Carlos olivine single crystals by performing hydration/dehydration experiments under hydrothermal conditions at high pressure. Their results showed that hydrogen diffusion in olivine is the fastest along the [001] axis, and hydrogen incorporation is controlled by proton–metal vacancy (PV mechanism) associated defects. Ferriss et al. (2018) carried out sequential dehydration experiments on natural olivine single crystal to determine hydrogen diffusivities at 1 atm. Their experiments revealed that the apparent diffusivities of total H+ vary both over time and for olivine with different defect concentrations. Consequently, hydrogen diffusion rates are slower than proton–polaron redox (in experiments at low temperatures for short times, hydrogen diffuses into olivine by exchange of protons with polarons and electron holes localized on iron atoms occupying octahedrally coordinated metal cation sites) rates but faster than proton–metal vacancy diffusion and with a fast [100] direction (Fig. 1b). Jollands et al. (2019) studied coupled inter-site reaction and hydrogen diffusion in natural olivine. They demonstrated that hydrogen loss from the Si-vacancy defect can be extremely rapid and approaches the fastest known mechanism of proton–polaron diffusion in olivine. Additionally, hydrogen diffusion through grain boundaries in olivine aggregates has been investigated by Demouchy (2010) at 0.3 GPa. She found that the effective hydrogen diffusivity, which includes the grain-boundary effect in olivine aggregates, is the fastest and at least 1 order of magnitude higher than hydrogen in an olivine single crystal. Figure 1b shows a comparison of new data on hydrogen diffusion in olivine from dehydration experiments. It is found that (1) the fastest mechanism for hydrogen diffusion is redox-associated (proton–polaron exchange) through grain boundaries in polycrystalline olivine (Demouchy, 2010), and the slowest diffusion is the tetrahedral site mechanism via silicon vacancy defects [Si] in forsterite single crystal (Padrón-Navarta et al., 2014). (2) Hydrogen diffusion in Ti-doped forsterite is slightly faster than that in pure forsterite. Similarly, hydrogen diffusion is faster in olivine (Ferriss et al., 2018; Jollands et al., 2019) than in forsterite (Padrón-Navarta et al., 2014; Jollands et al., 2016). (3) Hydrogen diffusion in olivine dominated by a proton–polaron mechanism (Demouchy, 2010; Jollands et al., 2019) is faster than the proton–vacancy mechanism (Demouchy and Mackwell, 2006; Padrón-Navarta et al., 2014; Demouchy et al., 2016; Jollands et al., 2016; Ferriss et al., 2018). (4) Despite the underlying cause being unclear, the anisotropy of hydrogen diffusion reported by different groups was significantly inconsistent. For example, the fastest diffusion is along the [001] orientation in Demouchy and Mackwell (2006) and Jollands et al. (2016), but the fastest diffusion is along the [100] orientation in Ferriss et al. (2018) and Jollands et al. (2019). Understanding these issues is necessary for interpreting hydrogen incorporation in olivine and designing future experiments.
Mg and Fe–Mg. Fei et al. (2018) measured Mg lattice diffusion coefficients in iron-free olivine aggregates as a function of pressure (1–13 GPa), temperature (1100–1300 K), and bulk water content (1–350 ppm) using secondary ion mass spectrometry (SIMS) in depth-profiling mode. They demonstrated that the Mg lattice diffusion coefficient was significantly enhanced by dissolved water in olivine (r=1.2 in Eq. 2). For example, at the same pressure, the diffusion coefficient of Mg in hydrous olivine (350 ppm) is at least 2 orders of magnitude faster than that in dry olivine (Fig. 1c). The enhancement of Fe–Mg interdiffusion in olivine by the presence of water has been investigated by Hier-Majumder et al. (2005). They found a large water exponent (r=0.9) but a slightly lower activation energy (220 kJ/mol) compared with that (280–343 kJ/mol) reported in anhydrous olivine (Tachibana et al., 2013; Zhang and Shan, 2015a).
O and Si. Costa and Chakraborty (2008) investigated the effect of water on O diffusion rate in Fe-bearing olivine. They found that, under hydrous conditions, the anisotropy of O diffusion was weak to non-existent. Fei et al. (2014) studied the influence of water content (<1–800 ppm) on O self-diffusion coefficients in forsterite along the b axis at 8 GPa and 1600–1800 K. Surprisingly, their experimental results indicated that water has no significant effect on O self-diffusion rate in forsterite (r≈0.05). Very similar to O diffusion in olivine, Costa and Chakraborty (2008) found that water has little effect on Si diffusion rate in olivine. The diffusion of Si in forsterite single crystal along the b axis reported by Fei et al. (2012, 2013) under anhydrous and hydrous conditions indicated a small exponent (). They concluded that the effect of water on the upper-mantle rheology is very small. As shown in Fig. 1c, the O diffusivity in olivine measured by Costa and Chakraborty (2008) is consistent with that in forsterite reported by Fei et al. (2014) and Si diffusion in olivine (Costa and Chakraborty, 2008; Zhang and Shan, 2015b) but at least 1 order of magnitude higher than O diffusion calculated by Zhang et al. (2011) and Si diffusion in forsterite by Fei et al. (2012, 2013). Analysis of the point defect structure indicated that O diffused by an interstitial mechanism under hydrous conditions, whereas Si diffused by a mechanism involving vacancy complexes (Costa and Chakraborty, 2008; Fei et al., 2012, 2013). It is suggested that, when is high, the defect chemistry could be changed by incorporation of protons in Si vacancies and the hydrated Si vacancies (i.e., H, (2H), (3H), and (4H)) could dominate Si diffusion, possibly leading to a hydrolytic weakening of olivine (Costa and Chakraborty, 2008; Fei et al., 2013).
2.2 Wadsleyite
Diffusion experiments in wadsleyite are much more difficult to perform because crystals large enough to measure diffusion coefficients are difficult to obtain. As a result, diffusion coefficients that are known for these materials come from measurements in coarse polycrystals, while diffusion experiments in wadsleyite single crystals are rare. An additional difficulty associated with diffusion experiments is the in situ control of oxygen fugacity and water fugacity under high P–T conditions.
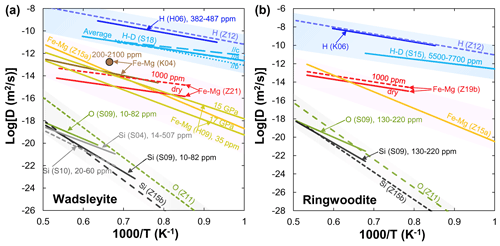
Figure 2Arrhenius plot summarizing experimental results for various elements' (H, Fe–Mg, O, Si) diffusion in wadsleyite (a) and ringwoodite (b). Data sources: H06 (Hae et al., 2006); Z12 (Zhang, 2012); S18 (Sun et al., 2018); K06 (Kudo et al., 2006); K04 (Kubo et al., 2004); H09 (Holzapfel et al., 2009); S04 (Shimojuku et al., 2004); S09 (Shimojuku et al., 2009); S10 (Shimojuku et al., 2010); Z11 (Zhang et al., 2011); Z15a (Zhang and Shan, 2015a); Z15b (Zhang and Shan, 2015b); Z19b (B. H. Zhang et al., 2019b); Z21 (Zhang et al., 2021).
H. Hae et al. (2006) were the first to present hydrogen diffusion in polycrystalline wadsleyite at 15–16 GPa and 1173–1473 K using infrared (IR) spectroscopy. They found that the hydrogen diffusion rate in wadsleyite is essentially the same as the average diffusivity of hydrogen in olivine. The refined diffusion coefficient of hydrogen and activation energy in (Fe,Mg)2SiO4 wadsleyite derived from the cBΩ model (the cBΩ model is a thermodynamic model (Zhang et al., 2010), which suggests the defect Gibbs free energy gact is proportional to the isothermal bulk modulus (B) and the mean volume per atom (Ω) through the relation gact=cactBΩ, where cact is a dimensionless factor) agree well with the experimental data reported by Hae et al. (2006) (Fig. 2a). A much more extensive study of hydrogen self-diffusion in wadsleyite was performed by Sun et al. (2018) from H–D interdiffusion experiments in wadsleyite single-crystal couples. Their results demonstrated that the anisotropy of hydrogen self-diffusion in wadsleyite gradually decreases with increasing temperature.
Fe–Mg. Kubo et al. (2004) first investigated the influence of water on Fe–Mg interdiffusion in wadsleyite at 16–17 GPa and 1503–1803 K under the Ni–NiO (NNO) buffered condition. Their results showed that the Fe–Mg interdiffusion rate in wadsleyite with ∼330 wt. ppm H2O is about 1 order of magnitude faster than that containing 50–90 wt. ppm H2O at 1503 K, suggesting a large water effect on Fe–Mg interdiffusivity. Unfortunately, dehydrated samples in Kubo et al. (2004) during their experiments rendered the relationship between water and Fe–Mg interdiffusion in wadsleyite unreliable. By combining all existing results, Holzapfel et al. (2009) proposed a new expression to constrain the effects of pressure and composition on DFe−Mg and found that the interdiffusivity of Fe–Mg in wadsleyite decreases with increasing pressure. Recently, Zhang et al. (2021) measured Fe–Mg interdiffusion rates in polycrystalline wadsleyite aggregates as a function of water content (up to ∼0.44 wt. % H2O) at 16 GPa and 1373–1773 K by using the diffusion couple method. Their results indicated that water significantly enhanced the rates of Fe–Mg interdiffusion in wadsleyite (r=0.54) (Fig. 2a). In addition, the activation energy (∼113 kJ/mol) obtained by Zhang et al. (2021) was much lower than that (229–289 kJ/mol) determined by Holzapfel et al. (2009) and Zhang and Shan (2015a).
O and Si. Shimojuku et al. (2009) showed that O diffusion is faster than Si diffusion in wadsleyite, and the activation energy (291 kJ/mol) for O diffusion is smaller than that (513 kJ/mol) derived from a thermodynamic cBΩ model by Zhang et al. (2011). After considering the degradation of the depth resolution by the roughness in SIMS measurement and correcting the convolution effect, the Si diffusion rates in Mg2SiO4 wadsleyite under nominally dry conditions (20–60 ppm H2O) obtained by Shimojuku et al. (2010) were comparable to those determined in (Mg0.9Fe0.1)2SiO4 wadsleyite with similar water contents (10–82 ppm H2O) by Shimojuku et al. (2009) but approximately half an order of magnitude smaller than those reported by Shimojuku et al. (2004) (14–507 ppm H2O, Fig. 2a). (In microbeam analysis, the measured concentration profile is always continuous (even the element is discontinuous at the interface of two samples) owing to the spreading of the ion beam and spatial averaging of compositions on both sides of the interface. It is a convolution result of both the finite abrasion of the sample volume and the interface of two samples.) This finding indicates that the effect of water is significantly larger than the convolution effect. Enhancement of the Si diffusivity by incorporating hydrogen possibly leads to water weakening in wadsleyite.
2.3 Ringwoodite
H. The diffusion of hydrogen in synthetic polycrystalline ringwoodite with a grain size of approximately 10 µm was measured by Kudo et al. (2006) in the temperature range from 1173 to 1373 K at 19 GPa. The diffusion rate of hydrogen in ringwoodite is expressed by using the following equation: . Given that the diffusion coefficient in polycrystalline samples is contributed by grain-boundary diffusion and the grain size in real mantle may be greater (∼ millimeter or more), the experimental results of Kudo et al. (2006) are likely to be the maximum value of the diffusion coefficient of hydrogen in the real MTZ. As shown in Fig. 2b for hydrogen diffusion in (Mg,Fe)2SiO4 ringwoodite, the experimental data reported by Kudo et al. (2006) are comparable with that calculated by the cBΩ model (Zhang, 2012). Sun et al. (2015) reported a hydrogen self-diffusion coefficient in Fe-bearing ringwoodite through the interdiffusion of hydrogen and deuterium in a pair of synthesized single crystals with 5500–7700 ppm water at 21 GPa and 1000–1300 K. Note that the results obtained by Sun et al. (2015) are 2 orders of magnitude lower than those reported by Kudo et al. (2006) and Zhang (2012), despite the activation energies being comparable to each other (Fig. 2b).
Fe–Mg. To date, only B. H. Zhang et al. (2019b) have determined the kinetics of Fe–Mg interdiffusion in ringwoodite aggregates as a function of water content (40–6000 ppm H2O) at 20 GPa and 1373–1673 K by using the diffusion couple method. A relatively small water exponent (r=0.25) suggests the non-negligible role of water in enhancing Fe–Mg interdiffusion in ringwoodite. The activation energy (140 kJ/mol) determined by B. H. Zhang et al. (2019b) was much lower than that (345 kJ/mol) reproduced in terms of bulk elastic and expansivity data through a thermodynamic model that interconnects point defect parameters with bulk properties (Zhang and Shan, 2015a).
O and Si. To the best of our knowledge, only Shimojuku et al. (2009) have reported O diffusion rates in ringwoodite to date. The experiments were conducted for (Mg,Fe)2SiO4 ringwoodite at 22 GPa and 1673–1873 K using SIMS measurement. With similar water contents (130–220 ppm H2O), the diffusion rates of O in ringwoodite were slightly higher than those of Si. Meanwhile, the diffusivity and activation energy for Si diffusion in ringwoodite are consistent with those derived from the cBΩ model on the basis of the observed compensation effect for Si diffusion in silicates under anhydrous conditions (Zhang and Shan, 2015b). However, the activation energy for O diffusion in ringwoodite reported by Shimojuku et al. (2009) is inconsistent with that determined by Zhang et al. (2011).
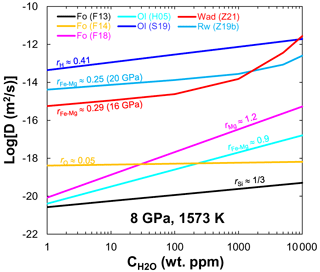
Figure 3 dependences of diffusivity in olivine (8 GPa), wadsleyite (16 GPa) and ringwoodite (20 GPa) at 1573 K. Data sources: F13 (Fei et al., 2013); F14 (Fei et al., 2014); F18 (Fei et al., 2018); H05 (Hier-Majumder et al., 2005); S19 (Sun et al., 2019); Z19b (B. H. Zhang et al., 2019b); Z21 (Zhang et al., 2021).
2.4 Effect of water on diffusivity
On the basis of the foregoing comparisons (Figs. 1 and 2) and discussions, the diffusion rates of different elements in olivine and its high-pressure polymorphs, wadsleyite and ringwoodite, yield the order of (≈DSi). Their water content exponents are in the order of (Fig. 3). This finding implies that water can significantly enhance the DFe−Mg in olivine compared with wadsleyite and ringwoodite, which needs to be verified by further experiments. The magnitude of the enhancement of interdiffusivity in wadsleyite by water is larger than that in ringwoodite () when wt. %. These different characteristics of diffusion response to water may be related to the hydrogen incorporation mechanism in host minerals. Experimental observations (Purevjav et al., 2016; Zhang et al., 2021) and theoretical calculations (Wright and Catlow, 1996; Caracas and Panero, 2017) demonstrated that, for Fe-free hydrous wadsleyite, all hydrogen cations in the crystal should have been fully concentrated into a vacant M3 octahedral sites bonded with oxygen O1. In the case of Fe-bearing hydrous wadsleyite, reduction from ferric to ferrous iron probably drives the formation of Mg vacancies in wadsleyite, which in turn contributes to Fe–Mg interdiffusion. In the case of ringwoodite, the mobility of hydroxyl defects related to an octahedral vacancy is greater than that related to a tetrahedral vacancy (Mrosko et al., 2013). Furthermore, although both tetrahedral and octahedral sites can be simultaneously hydrated in hydrous ringwoodite (Purevjav et al., 2014), Caracas and Panero (2017) showed that the greatest H diffusion rate was yielded by Mg↔2H, followed by Si ↔ Mg + 2H, and the slowest rate by hydrogarnet defect Si ↔ 4H. Thus one would expect [(2H)] to be the main diffusing species during the diffusion process. According to obtained by B. H. Zhang et al. (2019b), Fe–Mg interdiffusion in ringwoodite may be charge-balanced by . The smaller water content exponent obtained here () implies that not all hydrogen is involved in the diffusion process.
Electrical conductivity is very sensitive to temperature and water; therefore, electrical conductivity can be used to constrain and quantify the chemical composition, temperature, and water content and distribution in the Earth's interior (Xu et al., 2000; Yoshino, 2010). In most cases, the T and P dependences of electrical conductivity can be described by the Arrhenius equation:
where σ0 is the pre-exponential factor. The electrical conductivity is generally dominated by one or more conduction mechanisms. For example, the electrical conductivity of hydrous iron-bearing silicate minerals can be expressed by the summation of “dry” (sum of ionic σi and hopping conduction σh) and “wet” (proton conduction σp) mechanisms (Yoshino et al., 2009; Yoshino, 2010; Yoshino and Katsura, 2013):
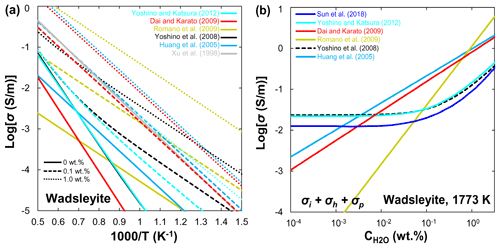
Since the first suggestion by Karato (1990) of the enhancement of electrical conductivity by water in olivine, numerous experimental studies have been carried out on the role of water in electrical conductivity in olivine (e.g., Yoshino et al., 2006, 2009; D. Wang et al., 2006; Poe et al., 2010; Yang, 2012; Dai and Karato, 2014) and its high-pressure polymorphs (e.g., Huang et al., 2005; Yoshino et al., 2008; Romano et al., 2009; Manthilake et al., 2009; Dai and Karato, 2009; Yoshino and Katsura, 2012). Because several review papers have provided a very detailed and comprehensive overview of this topic (Yoshino, 2010; Yoshino and Katsura, 2013; Pommier, 2013; Karato, 2015, 2019), here we will only give a brief introduction and comparison to the influence of water on the electrical conductivity of olivine, wadsleyite, and ringwoodite.
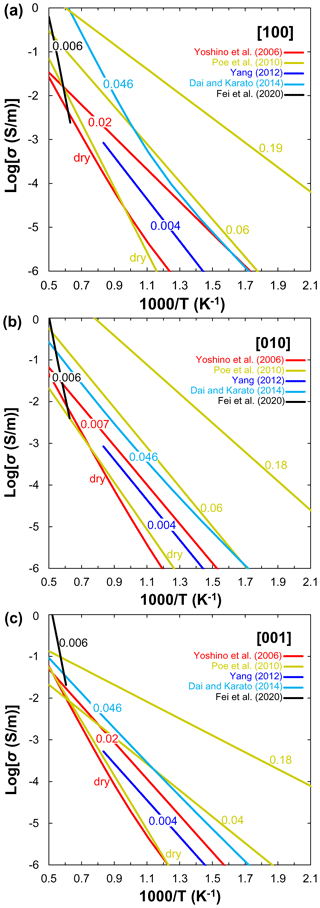
Figure 4Compilation of electrical conductivity data of single-crystal hydrous olivine for (a) [100], (b) [010] and (c) [001] crystallographic directions as a function of reciprocal temperature. The number labels indicate water content in weight percent.
3.1 Olivine
Single crystal. The electrical conductivity anisotropy of hydrous olivine is an important issue for understanding the anisotropic σ beneath the East Pacific Rise (Evans et al., 2005). The effect of water on the electrical conductivity of single-crystal olivine has been reported by several groups (Fig. 4). Yoshino et al. (2006) first measured the electrical conductivity of hydrous single-crystal olivine with 0.01–0.02 wt. % H2O at 3 GPa under low-temperature conditions (<1000 K) to minimize possible dehydration of olivine. Nevertheless, they did not determine how conductivity varies with varying water along any of the three crystallographic directions, but rather assumed that conductivity increased linearly with water content without change in activation energy. The extrapolation of their experimental data to higher temperatures suggests that the electrical conductivity of hydrous olivine at the top of the asthenosphere should be nearly isotropic. Therefore, Yoshino et al. (2006) concluded that the hydration of olivine cannot account for the high-conductivity anisotropy in the UM (Evans et al., 2005). Poe et al. (2010) investigated the electrical conductivity of single-crystal San Carlos olivine as a function of dissolved water content (up to 0.22 wt. % H2O) at 8 GPa. They found that σp is largely anisotropic, the conductivity along [010] is approximately 1 order of magnitude greater than that along other directions when the water content is larger than 0.1 wt. % at high temperature, whereas the electrical anisotropy is negligible when the water content is lower than 0.1 wt. %. Similarly, Yang (2012) reported negligible anisotropy for the proton conduction of a single-crystal olivine with low water content (∼40 ppm) at 1 GPa. By contrast, Dai and Karato (2014) presented new experimental results on the electrical conductivity of hydrous single-crystal olivine at temperatures up to 1373 K and pressure of 4 GPa. They argued that their new results agree well with previous studies at low temperature (<900 K) and significantly deviate at high temperature where the temperature dependence of conductivity increases strongly (Fig. 4). An important point of the investigations of Dai and Karato (2014) is that the electrical conductivity anisotropy (especially along [100]) increases with increasing temperature, and a change in conduction mechanism is observed because the activation energy substantially increases at high temperature. Recently, Fei et al. (2020) measured the ionic conductivity of olivine single crystal as a function of pressure from 2 to 10 GPa, temperature from 1450 to 2180 K, and water content from 20 to 580 wt. ppm. They revealed that olivine ionic conductivity has negative pressure and positive temperature dependences and is significantly enhanced by H2O incorporation. It is clear from Fig. 4 that the anisotropy of proton conduction of olivine reported by different groups disagree with each other. The experimental results from Yang (2012) are consistent with those measured by Yoshino et al. (2006) and Poe et al. (2010). Note that Poe et al. (2010) demonstrated that the conductivity along [010] is the highest in olivine single crystal, whereas the highest conductivity is along the [100] direction in other studies (Yoshino et al., 2006; Dai and Karato, 2014). Dai and Karato (2014) found that the magnitude of electrical conductivity anisotropy increases with an increase in temperature, which is the opposite of early experimental observations (Yoshino et al., 2006; Yang, 2012). In addition, the anisotropic ionic conductivity and activation enthalpies (337–396 kJ/mol) reported by Fei et al. (2020) are significantly higher than those of proton conductivity (Yoshino et al., 2006; Poe et al., 2010; Yang, 2012; Dai and Karato, 2014).
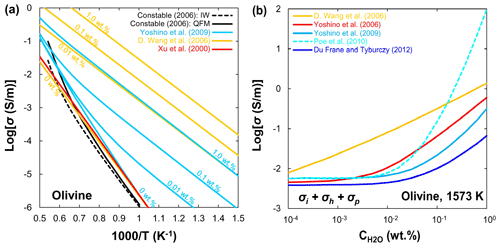
Figure 5Compilation of electrical conductivity data of olivine aggregates as a function of water content. (a) Log conductivity versus reciprocal temperature. (b) Log conductivity versus water content at 1573 K. The number labels indicate water content in weight percent.
Polycrystalline. D. Wang et al. (2006) measured the electrical conductivity of hydrous olivine aggregates at temperature up to 1273 K, which showed high conductivity and strong temperature dependence, and proposed the following relation to fit their experimental data:
where is the water content (in wt. %) and r is the water exponent. However, their results may have been biased because of the significant dehydration of olivine at high temperature, and the contribution of hopping conduction (σh) to bulk conductivity was not considered. Yoshino et al. (2009) identified three conduction mechanisms by measuring the electrical conductivity of olivine aggregates with various amounts of water at a pressure of 10 GPa. They demonstrated the significant effect of water on the electrical conductivity of hydrous olivine and suggested that the behavior of proton conductivity with water content is similar to that of N-type semiconductors through the equation
where α is a constant. As shown in Fig. 5a, the electrical conductivity of anhydrous olivine aggregates is consistent with others (Xu et al., 2000; Constable, 2006; D. Wang et al., 2006; Yoshino et al., 2009). However, at a similar water content, the electrical conductivity determined by D. Wang et al. (2006) is at least 2 orders of magnitude higher than that of Yoshino et al. (2009). Figure 5b shows a compilation of the influence of water content on the bulk conductivity of olivine aggregates at 1573 K. It is found that D. Wang et al. (2006) reported the highest conductivities, while Du Frane and Tyburczy (2012) had the lowest ones that were calculated from H–D interdiffusion in a single crystal. When the water content is low (<0.01 wt. %), the difference in conductivity data among Yoshino's group (Yoshino et al., 2006, 2009), Poe's group (Poe et al., 2010), and Frane and Tyburczy (2012) is small (within 0.2 log unit), while the results vary widely at higher water content. The possible reasons for these discrepancies will be discussed later.
3.2 Wadsleyite
Xu et al. (1998) reported that the electrical conductivity of wadsleyite under MTZ conditions is 2 orders of magnitude higher than that of olivine. Although the results of Xu et al. (1998) were widely accepted as the standard data for hopping conduction in wadsleyite, Huang et al. (2005) attributed the results of Xu et al. (1998) to proton conduction because they found a significant amount of water in Xu et al.'s samples. On the other hand, Huang et al. (2005) and Romano et al. (2009) only reported the proton conduction, whereas other studies (Yoshino et al., 2008; Dai and Karato, 2009; Manthilake et al., 2009; Yoshino and Katsura, 2012) distinguished between small polaron and proton conduction mechanisms of wadsleyite in a wider temperature range. Figure 6a shows a compilation of electrical conductivity data for anhydrous and hydrous wadsleyite at various water contents. The published conductivity data regarding the effect of water on σp in wadsleyite disagree among different groups (Fig. 6), which can be roughly divided into three categories: Karato's group (Huang et al., 2005; Dai and Karato, 2009), Yoshino's group (Yoshino et al., 2008; Manthilake et al., 2009; Yoshino and Katsura, 2012; Sun et al., 2018), and Romano's dataset (Romano et al., 2009). Each set of experimental data is internally consistent in terms of the effect of water on conductivity (σ and r) and activation enthalpy (H). For anhydrous wadsleyite, Yoshino's group (Yoshino et al., 2008; Yoshino and Katsura, 2012) reported higher conductivity values (0.5 log unit) than Karato's group (Dai and Karato, 2009), although these two groups found similar values for H (∼145 kJ/mol) of hopping conduction. As for the hydrous case, the conductivity values measured by Karato's group (Huang et al., 2005; Dai and Karato, 2009) are much higher than those of Yoshino's group (Yoshino et al., 2008; Yoshino and Katsura, 2012) at the same water content (Fig. 3a and b). Romano et al. (2009) obtained the highest absolute conductivity values for hydrous wadsleyite among the published data (Fig. 6a), but they reported the lowest H value (∼64 kJ/mol). Note that the trend of bulk conductivity () with water content at 1773 K is largely different among Karato's group (Huang et al., 2005; Dai and Karato, 2009), Yoshino's group (Yoshino et al., 2008; Yoshino and Katsura, 2012; Sun et al., 2018), and Romano et al. (2009) (Fig. 6b) because each group obtained different values for H and r and used different fitting equations. Consequently, although all of these studies suggest that water can significantly enhance the electrical conductivity, the measured absolute conductivity values and activation enthalpies vary widely between studies.
3.3 Ringwoodite
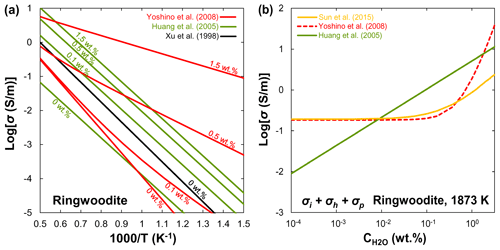
Huang et al. (2005) first measured the electrical conductivity of hydrous ringwoodite, but they did not determine the hopping conduction at high temperatures. Similar to wadsleyite, Yoshino et al. (2008) successfully separated the contributions of hopping and proton conductions in ringwoodite (Fig. 7a). Several important features were revealed by their experiments: (1) the proton conductivity of ringwoodite is approximately 1 order of magnitude higher than that of wadsleyite; (2) the activation energy of proton conduction largely decreases from 95 to 43 kJ/mol with increasing water content from 0.01 wt. % to 1 wt. %; (3) the electrical conductivity increases with increasing water content. For example, the contribution of proton conduction to the bulk conductivity () and calculated conductivity from H–D interdiffusion in single-crystal ringwoodite is negligible at 1873 K and water content below 0.1 wt. % (Sun et al., 2015), but it is much larger than that of Huang et al. (2005) at water content above 0.5 wt. % (Fig. 7b). (4) Small polaron conduction becomes dominant at high temperatures. Overall, the dependence of conductivity on water content measured by Huang et al. (2005) is much weaker than that reported by Yoshino et al. (2008). It is worth noting that, when the water content increases from 0.1 wt. % to 0.5 wt. %, the electrical conductivity increases by only 0.5 log units in Huang et al. (2005); in contrast, it goes up by 0.6–2.5 log units in Yoshino et al. (2008). Indeed, this discrepancy may reflect the different water dependence of conductivity. The water exponent is estimated to be about 0.69 by Huang et al. (2005), while it is equal to 1 in the study of Yoshino et al. (2008).
3.4 Discrepancies and interpretations
On the basis of the above discussions, available experimental data on the magnitude of water's effect on olivine, wadsleyite, and ringwoodite are largely inconsistent as illustrated in Figs. 4–7. These discrepancies between different studies have stimulated several controversies and ongoing debates (e.g., Karato and Dai, 2009; Yoshino and Katsura, 2009, 2012, 2013; Jones, 2014, 2016; Gardés et al., 2015; Dai and Karato, 2015). Importantly, the inconsistencies in the experimental data reported by different researchers have led to large differences in the estimated water content of the UM and MTZ and also created great confusion for the geoscience community. Meanwhile, these controversies and disagreements have the unfortunate and unsatisfactory consequence that those who wish to make use of the experimental results of the effects of water on NAMs must make a decision as to which laboratory's values to choose over the others because they do not know whose experimental data are more reliable.
The possible causes of these existing discrepancies can be simply attributed to three aspects. (1) Experimental technique (low-frequency versus impedance spectroscopy measurements with or without a metal shield in the assembly). Karato and Dai (2009) criticized the use of the low-frequency method by Yoshino's group (Yoshino et al., 2006, 2008) as it tends to produce conductivity tens of a percent smaller than that obtained by impedance spectroscopy. In fact, later studies on hydrous ringwoodite (Yoshino et al., 2008), olivine (Yoshino et al., 2009), and wadsleyite (Yoshino and Katsura, 2012) have proven that the difference in conductivity measured by low-frequency and impedance spectroscopy is very small and that the large data inconsistency between different groups cannot be explained by this technical reason. Another technical difference is that use of the metal guard ring by Karato and colleagues (e.g., Huang et al., 2005; D. Wang et al., 2006; Poe et al., 2010) in their assembly would prevent water purge and lead to the formation of fluid or supercritical liquid by the released free water due to the dehydration of water-rich samples at high temperatures (>900 K) as suggested by Yoshino (2010), Yoshino and Katsura (2012, 2013), and Yang (2012).
(2) Water content determination (unpolarized Fourier-transformation infrared (FTIR) spectroscopy using Paterson calibration versus polarized FTIR by Bell calibration for determining water loss/gain). The determination of sample water content before and after conductivity measurement is a key procedure to judge whether the sample is changed (water loss or gain). Most previous studies between Yoshino's group (e.g., Yoshino et al., 2006, 2008, 2009; Yoshino and Katsura, 2012) and Karato's group (e.g., Huang et al., 2005; D. Wang et al., 2006; Dai and Karato, 2009) used the unpolarized FTIR spectroscopy and the calibration from Paterson (1982) to determine the water content. However, Bell et al. (2003) claimed that the unpolarized FTIR method with the calibration of Paterson (1982) may underestimate the water content in NAMs (especially olivine) by a factor of 3 compared with the application of the Bell et al. (2003) calibration. If this is the case, the conductivity values of NAMs obtained using the unpolarized calibration of Paterson (1982) may also be underestimated by the same factor, except for the study of Poe et al. (2010).
(3) Sample dehydration during conductivity measurement. As for the dehydration of hydrous samples, another very confusing point is that Yoshino's group (Yoshino et al., 2006, 2008, 2009; Yoshino and Katsura, 2012; B. H. Zhang et al., 2012, 2019c; Zhao and Yoshino, 2016) and others (Poe et al., 2010; Yang, 2012) found that water-bearing NAM samples (e.g., olivine, wadsleyite, ringwoodite, orthopyroxene, omphacite, and clinopyroxene) were easily dehydrated during annealing at temperatures higher than 900 K, whereas no sample dehydration occurred in the study of Dai and Karato (2014) even at 1373 K. In fact, the dehydration temperature of a hydrous sample should not vary from laboratory to laboratory.
(4) Formalism to fitting experimental data (Eq. 5 versus Eq. 6). Considering the different dependences of activation enthalpy on water content, Karato's group used Eq. (5) to fit their conductivity data, whereas Yoshino's group used Eq. (6). Obviously, different fitting equations will lead to systematic differences in predicted conductivity data between different laboratories. Consequently, the laboratory-based laws of NAMs' electrical conductivity predict contrasting effects of water, precluding the interpretation of geophysical data in terms of mantle hydration. We found that several researchers (Gardés et al., 2014; Jones, 2014; Karato, 2019) have attempted to develop a unified law to reconcile the large discrepancies in available data on olivine conductivity and test the internal consistency of the database. They argued that the experimental data from different laboratory studies are mostly consistent when the uncertainties and biases in the water contents of the olivine samples are considered. In addition, Karato and Dai (2009) criticized the result from small polaron conduction in wadsleyite and ringwoodite obtained by Yoshino et al. (2008) as not being small polaron conductivity because the samples are not truly dry ones. In fact, preparing truly dry NAM samples under high pressure is very difficult because samples prepared without adding water often contain a certain amount of water (e.g., Yoshino et al., 2008; B. H. Zhang et al., 2019c). From a purely mathematical point of view, the contributions of hopping and proton conductions can be completely separated and predicted by the use of Eq. (4) associated with Eq. (5) or (6). Therefore, the conductivity data from a “truly dry” sample are unnecessary as long as the data of a hydrous sample are reliable (Yoshino and Katsura, 2012).
To sum up, one solution to reconcile or eliminate the abovementioned discrepancies between different laboratories is to use the same water content determination methods and the same formula to fit the experimental data, which will surely confirm which laboratory's experimental data are more reliable. In addition, it is more important to understand the fundamental physical reasons explaining why different experimental methods lead to such differences. We look forward to the early realization of this goal.
The heat transfer properties of major mantle minerals play a crucial role in the Earth's numerous geodynamic processes, such as thermal structure of the lithosphere and mantle convection (Hofmeister, 1999, 2007). Therefore, probing the thermal state of the Earth's interior and its thermal evolution requires detailed knowledge of thermal conductivity (κ) or thermal diffusivity (λ):
where ρ is density and CP is heat capacity at constant pressure. Heat is transmitted within the Earth's crust and mantle mainly by diffusion (in the steady state: conduction) and radiation. As a result, the total thermal conductivity consists of contributions from scattering of quantized lattice vibrations (phonons, termed κp) and radiative attenuation of photons (κr). Generally, in most polycrystalline materials, heat diffusion dominates heat radiation at low temperatures, whereas heat radiation starts to dominate at higher temperatures (>1500 K). At present, direct measurement of radiative heat transfer is still very difficult because of the challenge of experimental technology. Thus, only phonon conduction is presented and discussed here.
In the past decades, substantial collections of mineral thermal properties were compiled by many researchers (e.g., Clauser and Huenges, 1995; Hofmeister, 2007; Clauser, 2011; Hofmeister et al., 2007; Xiong and Zhang, 2019). In this review, we do not present a complete compilation for all available thermal transport property data published to date. Instead, the latest experimental data on the effect of water on the thermophysical properties of olivine, wadsleyite, and ringwoodite are presented.
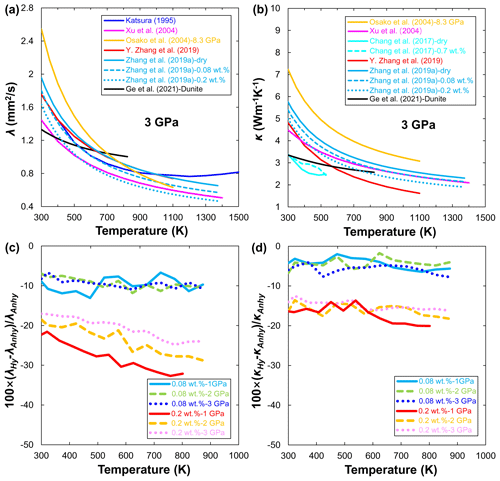
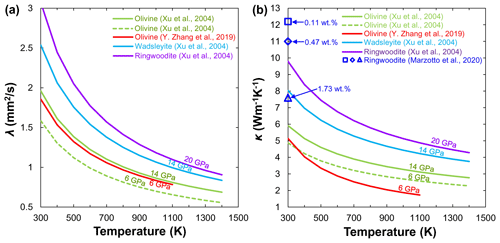
Figure 8Temperature dependence of thermal diffusivity (a) and thermal conductivity (b) for dry (Katsura, 1995; Xu et al., 2004; Osako et al., 2004; Y. Zhang et al., 2019; Ge et al., 2021) and hydrous olivine (Chang et al., 2017; B. H. Zhang et al., 2019a) at 3 GPa. Reduction (%) of the thermal diffusivity (c) and thermal conductivity (d) of hydrous olivine to its anhydrous counterpart as a function of temperature and pressure reported by B. H. Zhang et al. (2019a).
4.1 Olivine
The most prominent methods for measuring thermal diffusivity and thermal conductivity of geomaterials are steady-state (e.g., Ångström method) and transient techniques (e.g., pulse heating method and laser-flash analysis) (Clauser and Huenges, 1995; Hofmeister et al., 2007). The λ and κ of anhydrous olivine have been reported by several researchers (Katsura, 1995; Xu et al., 2004; Osako et al., 2004). Recently, Y. Zhang et al. (2019) applied a pulse heating method to explore the influence of iron on the λ and κ of olivine aggregates. Their results showed that the κ of olivine first decreases and then slightly increases with increasing iron content in olivine. Ge et al. (2021) measured the λ and κ of dunite up to 3 GPa and 823 K. They showed that λ and κ have a very weak temperature dependence (Fig. 8a and b), which is likely due to the presence of some amounts of serpentine in the dunite sample because the λ and κ of serpentine are low and almost independent of temperature (Osako et al., 2010; Ge et al., 2021).
Compared with the available data on anhydrous olivine, only two studies have reported on the effect of water on the thermal properties of olivine so far. Chang et al. (2017) first determined the κ of hydrous single-crystal Fo90 at room temperature and pressures up to 15 GPa by using an ultrafast optical pump–probe technique. They found that the κ of hydrous single-crystal Fo90 has a weaker pressure dependence below 5 GPa. Surprisingly, the values of κ for hydrous olivine are even larger than those of anhydrous olivine under similar P–T conditions (Fig. 8b), which may be due to the large uncertainty of the experimental method itself. By contrast, B. H. Zhang et al. (2019a) systematically investigated the λ and κ of polycrystalline Fo90 as a function of pressure, temperature, and water content (up to 0.2 wt. %). Their experimental results demonstrated that water can significantly reduce the λ and κ of olivine aggregate (Fig. 8a and b). With the increase in water content from 0.08 wt. % to 0.2 wt. %, the absolute values of the λ and κ for olivine samples decrease by 5 %–13 % and 17 %–33 % and by 3 %–8 % and 14 %–21 % (Fig. 8c and d), respectively.
For a given pressure, the overall trends of decreasing the λ and κ with temperature for olivine measured using different experimental methods are roughly consistent as shown in Fig. 8a and b. However, we must emphasize two issues. First, the effects of temperature and pressure on λ and κ were considered separately in most previous studies (e.g., Katsura, 1995; Osako et al., 2004). For example, λ and κ decrease with temperature and are fitted by an empirical form, ; at constant temperature, λ and κ increase with increasing pressure and can be linearly fitted by . Such separated fitting equations further hinder the extrapolation of the available experimental results to the real mantle P–T conditions. Fortunately, Xu et al. (2004) proposed a unified power-law formula to describe the combined influence of temperature and pressure on the λ and κ of olivine:
where λ300 K, 1 bar and κ300 K, 1 bar are the fitting results of λ and κ at room pressure and 300 K, a and b are pressure factors, and n is a fitting parameter. Eqs. (8)–(9) can better fit the λ and κ results obtained from experimental measurements (Xu et al., 2004; Y. Zhang et al., 2019; B. H. Zhang et al., 2019a) and can also conveniently scale laboratory results to real mantle conditions.
Second, besides the effect of pressure and temperature, other factors (Tommasi et al., 2001; Y. Zhang et al., 2019; Ge et al., 2021) such as composition, water, crystal structure, and grain size can also affect the λ and κ of minerals including olivine. For example, even at the same pressure (3 GPa) and using a similar impulse heating technique, the thermal conductivity of anhydrous olivine reported by B. H. Zhang et al. (2019a) is higher than that determined by Y. Zhang et al. (2019) in Fig. 8b. This finding can be mainly attributed to the different grain sizes between B. H. Zhang et al. (2019a) (∼5 µm) and Y. Zhang et al. (2019) (∼1 µm) because a small grain size can enhance the phonon grain-boundary scattering effect. In addition, Xu et al. (2004) used Fo90 aggregates with grain sizes of 30–40 µm, which are much larger than those of samples used by B. H. Zhang et al. (2019a), suggesting the small effect of phonon grain-boundary scattering. However, the absolute values of λ and κ in Xu et al. (2004) are lower than those of anhydrous olivine samples with small grain sizes in B. H. Zhang et al. (2019a) (Fig. 8a and b). This difference may originate from the presence of a small amount of water in Xu et al.'s samples because protonation increases structure disorder of NAMs and adds new vibration modes. As a result, the number of scattering events is more significant in the wet phase, which leads to reduced mean free paths of phonons and decreased λ and κ (B. H. Zhang et al., 2019a).
4.2 Wadsleyite and ringwoodite
Considering the substantial difficulties in performing thermal property measurements under P–T conditions of the MTZ, Xu et al. (2004) first reported the lattice λ and κ of anhydrous (Mg0.9Fe0.1)2SiO4 wadsleyite and ringwoodite at 14 and 20 GPa by using the Ångström method on cylindrical polycrystalline specimens. With increasing pressure, the olivine phase transforms to its high-pressure polymorphs, wadsleyite and ringwoodite, and the corresponding λ and κ increase in the order of (λ or (Fig. 9), which may suggest a discontinuity of κ occurring at 410 and 520 km. Recently, Marzotto et al. (2020) investigated the effect of water on the lattice thermal conductivity of ringwoodite (0.11 wt. %–1.73 wt. % H2O) at pressures up to 25 GPa and room temperature by combing DAC experiments with ultrafast optics. Their results indicated that the incorporation of 1.73 wt. % water substantially reduces the ringwoodite thermal conductivity by more than 40 % at the MTZ pressures. However, Marzotto et al. (2020) did not measure the temperature dependence on the thermal conductivity of hydrous ringwoodite because their experiments were carried out under high pressure and 300 K. Given the importance of wadsleyite and ringwoodite in the MTZ, the effect of water on the λ and κ of wadsleyite and ringwoodite needs to be systematically investigated in the future.
Laboratory measurements of sound wave velocities (compressional (VP) and shear wave (VS) velocity) of minerals at high P–T play a central role in enabling scientists to constrain the constitution, composition, and potential hydration state of the Earth's mantle via a comparison with the velocity profiles derived by seismological observations. The elastic properties of olivine, wadsleyite, and ringwoodite have been studied by using various techniques, including Brillouin spectroscopy (e.g., Sinogeikin et al., 2003), ultrasonic interferometry (e.g., Li, 2003; Higo et al., 2008; Li and Liebermann, 2014), resonant sphere technique (Mayama et al., 2005), and theoretical calculations (e.g., Núñez Valdez et al., 2012; Wang et al., 2019). However, most such measurements have been made at high/or room temperature and ambient pressure (Jackson et al., 2000; Jacobsen et al., 2004) or at high pressure and room temperature (Zha et al., 1996; Li et al., 1996; Li and Liebermann, 2000; Li, 2003; Darling et al., 2004; Jacobsen and Smyth, 2006; J. Wang et al., 2006, 2014; Mao et al., 2010, 2011), and direct measurements of elastic wave velocities under P–T conditions of the MTZ are difficult (Higo et al., 2008; Sinogeikin et al., 2003; Liu et al., 2009; Mao et al., 2012, 2015; Zhang and Bass, 2016).
Recently, simultaneous in situ Brillouin spectroscopy and synchrotron single-crystal X-ray diffraction measurements of the sound velocities and density of single-crystal minerals in an externally or internally heated diamond anvil cell (DAC) were extended to P–T conditions of the MTZ (e.g., Mao et al., 2012, 2015; Zhang and Bass, 2016). The successful application of these techniques to the study of the behavior and physical properties of Earth materials, including unquenchable mantle phases, liquids, and multi-phase aggregates, will greatly improve our interpretation of seismic observations and our understanding of the structure, composition, and dynamics of the Earth's interior.
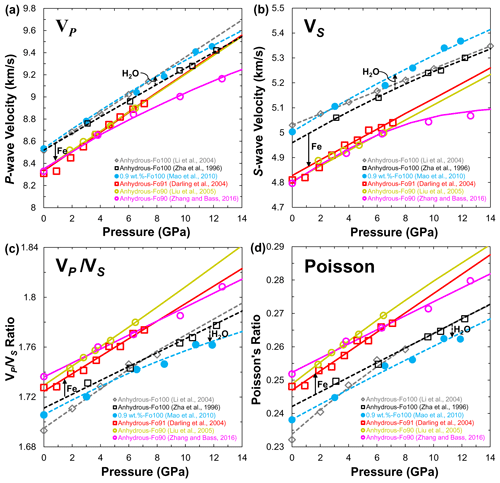
Figure 10(a) Compressional (VP) and (b) shear wave (VS) velocities, (c) ratio and (d) Poisson's ratio of olivine at 300 K as a function of pressure. Data sources: anhydrous olivine (single crystal: Zha et al., 1996; Zhang and Bass, 2016; polycrystal: Li et al., 2004; Darling et al., 2004; Liu et al., 2005); hydrous olivine single crystal (Mao et al., 2010). Closed and open symbols denote the experimental data, solid and dashed lines stand for the calculated results from third-order finite strain theory.
5.1 Olivine
So far, only Mao et al. (2010) have reported measurements of the single-crystal elasticity and velocity of forsterite with 0.9 wt. % H2O to 14 GPa at 300 K by Brillouin scattering. Their results demonstrated that hydration could decrease the magnitude of the velocity contrast at 410 km depth and the ratio of forsterite. Figure 10a and b show the VP and VS of forsterite with 0.9 wt. % H2O compared with previous data obtained under dry conditions at 300 K (Zha et al., 1996; Li et al., 2004; Darling et al., 2004; Liu et al., 2005; Zhang and Bass, 2016), respectively. It is found that the VP of hydrous forsterite (Mao et al., 2010) is almost identical to that of anhydrous forsterite reported by Li et al. (2004) but slightly higher (∼0.8 %) than that measured by Zha et al. (1996). The same trend is also observed in the VS (∼1 %) of hydrous forsterite (Fig. 10b), which suggests that water can even enhance the seismic velocity. Compared to that of the H2O effect, Fe can significantly reduce the VP (∼1.6 %) and VS (∼2.6 %) of anhydrous Fe-bearing olivine (Darling et al., 2004; Liu et al., 2005; Zhang and Bass, 2016) at 1 bar pressure. Note that the VP and VS of anhydrous Fe-bearing olivine measured by Zhang and Bass (2016) showed a marked decrease at pressure more than 7 GPa (Fig. 10a and b). Nevertheless, the low gradients of VP and VS versus pressure on anhydrous olivine reported by Mao et al. (2015) and Zhang and Bass (2016) suggest that linear extrapolations to high pressure/temperature based on experiments performed over a limited pressure/temperature range may overestimate the velocities of olivine at 410 km depth (Zha et al., 1996; Li et al., 1996, 2004; Darling et al., 2004; Liu et al., 2005; Mao et al., 2010).
The ratio is commonly used to identify compositional variations in the Earth's mantle. Figure 10c shows the effect of hydration on the ratio of Fe-free and Fe-bearing olivine. At ambient pressure, the ratio (1.7111) of anhydrous forsterite is almost the same (∼1.7058) as that of the hydrous one. With increasing pressure, the ratio gradually increases. At pressure corresponding to 410 km depth, the of hydrous forsterite with 0.9 wt. % H2O increases to 1.7725 compared with 1.7889 for the anhydrous phase, a difference of 0.92 %. At the same time, the ratios of anhydrous Fe-bearing olivine (Darling et al., 2004; Liu et al., 2005; Zhang and Bass, 2016) are at least 0.79 % higher than those of anhydrous forsterite. This finding suggests that increasing iron content will increase the of forsterite, whereas hydration will decrease the . Similarly, the effects of hydration and iron on Poisson's ratio in Fig. 10d are almost the same as those of the of hydrous and anhydrous olivine.
5.2 Wadsleyite
In addition to Fe, hydration is known to decrease the velocities and elastic properties of olivine polymorphs as a result of bond-weakening defects that accompany hydrogen incorporation as a structural hydroxyl (e.g., Inoue et al., 1995; Kohlstedt et al., 1996; Jacobsen et al., 2004; Jacobsen and Smyth, 2006; J. Wang et al., 2006; Mao et al., 2010). Mao et al. (2011) first measured the single-crystal elasticity of Fe-bearing wadsleyite with 1.93 wt. % H2O using Brillouin scattering up to 12 GPa. Their results were used to evaluate the net effect of Fe and hydrogen on the sound velocities of wadsleyite at pressures relevant to the MTZ. Buchen et al. (2018) conducted simultaneous sound velocity and density measurements on Fe-bearing wadsleyite single crystals with 0.24 wt. % H2O. They found that pressure suppresses the velocity reduction caused by high degrees of hydration in Fe-bearing wadsleyite, ultimately leading to a velocity crossover for VP and VS. Recently, Wang et al. (2019) calculated the full elasticity of hydrous iron-free wadsleyite with 1.63 wt. % H2O under P–T conditions of the 410 km discontinuity on the basis of first-principle calculations. Their calculated results constrained the olivine content of the UM near the 410 km discontinuity and placed constraints on the mantle water content at this depth.
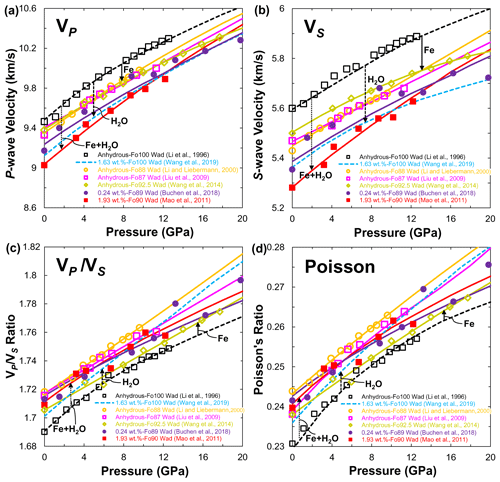
Figure 11(a) Compressional (VP), (b) shear wave (VS) velocities, (c) ratio and (d) Poisson's ratio of wadsleyite at 300 K as a function of pressure. Data sources: anhydrous wadsleyite (single crystal: Wang et al., 2014; polycrystal: Li et al., 1996; Li and Liebermann, 2000; Liu et al., 2009); hydrous wadsleyite single crystal (Mao et al., 2011; Buchen et al., 2018; Wang et al., 2019). Closed and open symbols denote the experimental data, and solid and dashed lines stand for the calculated results from third-order finite strain theory.
With the available experimental data on VP and VS, the effect of iron and hydration on the sound velocities of wadsleyite can be evaluated quantitatively (Fig. 11). Under ambient conditions, compared with the VP (Fig. 11a) and VS (Fig. 11b) of anhydrous pure-Mg wadsleyite reported by Li et al. (1996), the presence of 8 mol %–13 mol % Fe in wadsleyite lowers the VP and VS by 1.4 % and 2.3 %, respectively (Li and Liebermann, 2000; Liu et al., 2009; Wang et al., 2014). When adding 0.24 wt. % and 1.93 wt. % H2O in Fe-bearing wadsleyite (Mao et al., 2011; Buchen et al., 2018), the VP and VS were further lowered by water, leading to total reductions of 3.3 % and 4.7 % in VP and 3.7 % and 5.5 % in VS, respectively. Similarly, adding 1.63 wt. % H2O in Fe-free wadsleyite lowers the VP and VS by 3.7 % and 4.2 %, respectively (Wang et al., 2019), which are almost equivalent to those of Fe-bearing wadsleyite with 0.24 wt. % H2O (Buchen et al., 2018). In combining the results on anhydrous Fe-free and Fe-bearing wadsleyite (Li et al., 1996; Li and Liebermann, 2000; Liu et al., 2009; Wang et al., 2014) with those of slightly hydrous and largely hydrous wadsleyite (Mao et al., 2011; Buchen et al., 2018; Wang et al., 2019), iron and water incorporation lowers the sound velocities of wadsleyite. However, the two effects are difficult to distinguish using sound velocities alone. Figure 11c and d show the ratio and Poisson's ratio of anhydrous Fe-bearing wadsleyite (Li and Liebermann, 2000; Liu et al., 2009; Wang et al., 2014), which are indistinguishable from those of hydrous Fe-bearing wadsleyite (Mao et al., 2011; Buchen et al., 2018) and hydrous pure-Mg wadsleyite (Wang et al., 2019). Among them, the calculated values for the ratio and Poisson's ratio in anhydrous pure-Mg wadsleyite (Li et al., 1996) are the lowest. This observation indicates that an increase in the iron and water contents in wadsleyite will increase the ratio and Poisson's ratio, which is contrary to hydration decreasing the ratio and Poisson's ratio in Fe-free olivine (Fig. 10c and d).
5.3 Ringwoodite
J. Wang et al. (2006) measured the sound velocities and single-crystal elastic moduli of hydrous Mg2SiO4 ringwoodite containing 2.3 wt. % H2O using Brillouin spectroscopy at pressure up to 23.4 GPa and at room temperature. They speculated that the MTZ seismic velocity gradients are not due to “wet” ringwoodite. Jacobsen et al. (2004) and Jacobsen and Smyth (2006) reported the effects of 1 wt. % H2O on the sound velocities and elastic moduli of single-crystal ringwoodite with Fo90 composition up to 9 GPa. Both experiments were performed using a gigahertz ultrasonic interferometer to monitor P- and S-wave travel times under hydrostatic compression in a DAC. Their results indicated that water can significantly reduce the sound velocities and shear moduli of hydrous Fe-bearing ringwoodite; thus, the ratios were elevated by 2.3 % at pressure less than 18 GPa. Mao et al. (2012) investigated the hydration effect on the single-crystal elastic moduli of Fe-bearing ringwoodite with 1.1 wt. % H2O at pressure up to 12 GPa and temperature up to 673 K. They found that the presence of 1.1 wt. % H2O lowers the elastic moduli of Fe-bearing ringwoodite by 5 %–9 %, whereas the sound velocities of hydrous Fe-bearing ringwoodite were modeled from a thermal Birch–Murnaghan equation of state but not directly measured. Their results suggest that the observed seismic velocity anomalies and related depth depression of the 660 km discontinuity could be attributed to thermal variations together with the presence of ∼0.1 wt. % H2O. Recently, Schulze et al. (2018) measured the VP and VS of hydrous (Mg0.89Fe0.11)2SiO4 (with 0.21 wt. %, 1.04 wt. % and 1.71 wt. % H2O) and Mg2SiO4 (with 0.42 wt. % H2O) ringwoodite at pressure up to 22.1 GPa and at room temperature. They showed that the effect of water on the VP and VS decreases with increasing pressure, and the hydration-induced reduction of seismic velocities almost vanishes under conditions of the MTZ.

Figure 12(a) Compressional (VP), (b) shear wave (VS) velocities, (c) ratio and (d) Poisson's ratio of ringwoodite at 300 K as a function of pressure. Data sources: anhydrous ringwoodite (single crystal: Sinogeikin et al., 2003; polycrystal: Li, 2003; Higo et al., 2008); hydrous ringwoodite single crystal (Jacobsen and Smyth, 2006; J. Wang et al., 2006; Schulze et al., 2018). Closed and open symbols denote the experimental data, and solid and dashed lines stand for the calculated results from third-order finite strain theory.
To evaluate the effect of water on the sound velocities of ringwoodite at high pressure, Fig. 12a and b compare the VP and VS of anhydrous and hydrous ringwoodite (Li, 2003; Sinogeikin et al., 2003; Jacobsen and Smyth, 2006; J. Wang et al., 2006; Higo et al., 2008; Schulze et al., 2018) at MTZ pressures and 300 K. If the VP and VS of pure-Mg anhydrous ringwoodite reported by Li (2003) are considered a benchmark, the presence of 9 mol % Fe in ringwoodite (Sinogeikin et al., 2003; Higo et al., 2008) could reduce the VP and VS by 2.2 % and 2.54 % under ambient conditions, respectively. As shown in Fig. 12a, the magnitude of the effect of Fe content on the VP of anhydrous ringwoodite (Sinogeikin et al., 2003; Higo et al., 2008) is comparable to that of the slightly hydrous ringwoodite (Schulze et al., 2018; 0.21 wt. % H2O) but lower than those of the large hydration effect (J. Wang et al., 2006) and a combination of the Fe and H2O effect (Jacobsen and Smyth, 2006; Schulze et al., 2018). Unlike VP, the influence of Fe and H2O on the VS of ringwoodite is great in Fig. 12b. Under ambient conditions, the VS of anhydrous ringwoodite with 9 mol % Fe (Sinogeikin et al., 2003; Higo et al., 2008) or Fe-free ringwoodite with 2.3 wt. % H2O (J. Wang et al., 2006) is about 2.54 % or 4.09 % lower, respectively, than that of the pure-Mg anhydrous ringwoodite reported by Li (2003). However, the VS of hydrous Fe-bearing ringwoodite with 1.0 wt. % H2O reported by Jacobsen and Smyth (2006) is 9.02 % lower than Li's results. Notably, the VP and VS from J. Wang et al. (2006) and Jacobsen and Smyth (2006) indicate obvious crossover with other studies because of the relatively high gradients of VP and VS versus pressure. Schulze et al. (2018) demonstrated that the effect of water on the VP and VS is large at low pressure (<12 GPa), while this effect decreases with increasing pressure and is even negligible under the conditions of the MTZ. They concluded that water might not be detectable by seismic velocity variations in the MTZ.
Figure 12c shows the calculated ratio of anhydrous and hydrous ringwoodite as a function of pressure at room temperature. For Fe-free ringwoodite, water can decrease the ratio of pure-Mg ringwoodite (J. Wang et al., 2006). In contrast, both Fe and H2O content greatly increase the ratio of Fe-bearing ringwoodite (Sinogeikin et al., 2003; Jacobsen and Smyth, 2006; Higo et al., 2008; Schulze et al., 2018). As shown in Fig. 12d, the effects of Fe and H2O on Poisson's ratio of ringwoodite are almost the same as those in the ratio. Water reduces Poisson's ratio of Fe-free ringwoodite, whereas Poisson's ratio of Fe-bearing ringwoodite was enhanced by Fe and H2O. These observations clearly show that the influence of water on the ratio and Poisson's ratio is distinctly different between pure-Mg and Fe-bearing ringwoodite.
The results from theoretical calculations and experimental observations demonstrate that the rheological property of rocks and minerals is frequently described by a power-law creep equation of the form (Mei and Kohlstedt, 2000a, b; Karato and Jung, 2003; Hirth and Kohlstedt, 2003)
where is the axial strain rate; σ is the differential stress; d is the grain size; A is a constant; is the water content (in wt. % H2O); E and ΔV are the activation energy and activation volume for creep, respectively; n is the stress exponent; p is the grain-size exponent; and r is the water exponent. When a deviatoric stress is applied to a polycrystalline sample at low stresses and high temperatures, plastic deformation occurs at a rate that is sensitive to grain size and only weakly dependent on the applied stress. Thus, the deformation mechanism described by Eq. (10) in materials with small grain sizes and/or at low stresses is dominated by diffusion creep () (n=1, p=2–3). By contrast, dislocation creep (, another important mechanism of deformation) is operated for materials with coarse grain size at high stress, in which stress sensitivity is higher and strain rate does not depend on grain size in Eq. (10) (n=3–5, p=0). Especially for olivine-rich rocks with and without melt under anhydrous and hydrous conditions, p≈3 in the diffusion creep region and n≈3.5 in the dislocation creep regime (e.g., Mei and Kohlstedt, 2000a, b; Hirth and Kohlstedt, 2003). In addition, grain-boundary sliding (GBS) accommodated by dislocation motion has been identified as an important deformation mechanism in olivine (Hirth and Kohlstedt, 2003; Hansen et al., 2011). In most cases in the mantle, diffusion creep, dislocation creep, and GBS occur in parallel. Thus, the total strain rate of a sample is a simple sum of strain rates due to each mechanism:
In general, deformation experiments are conducted under conditions close to a transition between these two mechanisms. For each mechanism, the flow law will depend on the water content. The nature of the transition between the “wet” flow law and the “dry” flow law is not very clear because it depends on the details of the microscopic mechanism of deformation, which includes diffusion creep, dislocation creep, and GBS. Therefore, separating the contributions from different mechanisms by simultaneous inversion is important (Hirth and Kohlstedt, 2003).
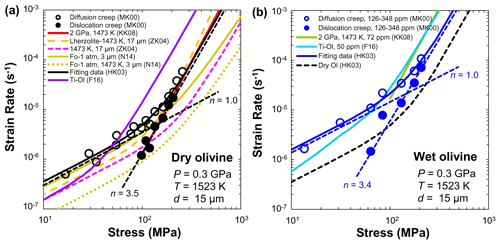
Figure 13Compilation of flow laws (strain rate versus differential stress) for fine-grained olivine aggregates deformed under dry (a) and hydrous (b) conditions. Data sources: MK00 (Mei and Kohlstedt, 2000a, b); HK03 (Hirth and Kohlstedt, 2003); KK08 (Katayama and Karato, 2008a); ZK04 (Zimmerman and Kohlstedt, 2004); N14 (Nishihara et al., 2014); F16 (Faul et al., 2016).
6.1 Olivine
Many efforts have been made to obtain quantitative experimental data on olivine rheology under dry conditions (e.g., Karato et al., 1986; Hirth and Kohlstedt, 1995). Laboratory-based investigations have demonstrated that the viscosity of olivine aggregates depends on temperature, pressure, water content, grain size, and oxygen fugacity (Hirth and Kohlstedt, 2003; Demouchy et al., 2009, 2012, 2013, 2014; Ohuchi et al., 2017). Figure 13a shows a compilation of flow laws for fine-grained olivine aggregates deformed at 0.3 GPa and 1523 K under dry conditions. The strain rate (or reciprocal viscosity) of olivine aggregates (Mei and Kohlstedt, 2000a, b; Hirth and Kohlstedt, 2003; Zimmerman and Kohlstedt, 2004; Katayama and Karato, 2008a, b; Nishihara et al., 2014; Faul et al., 2016) and lherzolite (Zimmerman and Kohlstedt, 2004) increases with increasing stress and temperature. It is worth noting that the stress exponent (n=1 for diffusion creep and n=3.5 for dislocation creep) and grain-size exponent (p=3 for diffusion creep and p=0 for dislocation creep) reported by Mei and Kohlstedt (2000a, b) are in good agreement with other deformation experiments (Karato et al., 1986; Hirth and Kohlstedt, 1995, 2003; Zimmerman and Kohlstedt, 2004; Katayama and Karato, 2008a, b; Tasaka et al., 2015, 2016; Faul et al., 2016; Ohuchi et al., 2017) and theoretical predictions (Coble, 1963).
Compared with deformation of anhydrous olivine, the strain rate of hydrous olivine aggregates greatly increases with increasing water content (Mei and Kohlstedt, 2000a, b; Hirth and Kohlstedt, 2003; Katayama and Karato, 2008a, b; Faul et al., 2016) (Fig. 13b). Nonetheless, the values for the stress exponent and grain-size exponent obtained in hydrous olivine are comparable to those determined under dry conditions. In addition, the water exponent in the diffusion creep regime is 1, but it is 1.2 in the dislocation creep regime. This difference may reflect the importance of various water-derived point defects for the creep behavior of olivine (Mei and Kohlstedt, 2000a, b; Faul et al., 2016). It is worth noting that the creep rate during deformation is limited by the diffusivity of the slowest ionic species diffusing along its fastest path. Intrinsic point defects in olivine include tetrahedral (Si), octahedral (M), and oxygen vacancies and interstitials. Previous studies demonstrated that, under anhydrous conditions, metal vacancies and ferric iron on metal sites are the majority point defects with the dominant charge neutrality condition (Mei and Kohlstedt, 2000a, b; Hirth and Kohlstedt, 2003). Deformation of olivine is rate-controlled by Si as the slowest diffusing ionic species (Hirth and Kohlstedt, 2003; Kohlstedt, 2006). In the presence of water, the concentrations of water-derived ionic point defects may exceed those of and/or and therefore affect defect concentrations, charge neutrality condition, and ionic diffusion. With increasing water fugacity, the charge neutrality condition changes from to . In the case of the latter charge neutrality condition, dislocation climb is rate-limited by diffusion of Si occurring by an interstitial mechanism (Mei and Kohlstedt, 2000a, b). Remarkably, Fei et al. (2012, 2013, 2014) proposed that the effect of water on O and Si self-diffusion in olivine is very limited or even negligible and that water does not significantly affect the creep rate in olivine assuming the diffusion-controlled deformation mechanism in the UM. However, as to the water effect on olivine rheology, Fei et al.'s observations based on diffusion experiments are completely opposite to the results of the deformation experiments (e.g., Mei and Kohlstedt, 2000a, b; Hirth and Kohlstedt, 2003; Katayama and Karato, 2008a, b; Faul et al., 2016).
Except for the creep flow law experiments of olivine discussed above, the fabric transition and slip system of olivine under anhydrous and hydrous conditions have been investigated extensively (e.g., Jung and Karato, 2001; Katayama et al., 2004; Jung et al., 2006; Ohuchi et al., 2012; Ohuchi and Irifune, 2013; Wallis et al., 2019). These experiments revealed that olivine has various types of lattice-preferred orientation and slip system under the different levels of water content and stress. In addition, Girard et al. (2013) and Tielke et al. (2017, 2019) carried out shear deformation experiments to quantify the hydrolytic weakening of olivine single crystals. The brittle behavior of hydrous olivine was investigated by Ohuchi et al. (2018) through pure shear deformation at 1–1.8 GPa and 670–1250 K. Note that all of these experimental findings have important applications for the interpretation of seismic anisotropy, mechanism of shear localization, strength of the mantle lithosphere, and intermediate-depth earthquakes in subduction zones and in the deep UM (e.g., Jung and Karato, 2001; Katayama et al., 2004; Jung et al., 2006; Ohuchi and Irifune, 2013; Ohuchi et al., 2012, 2018; Girard et al., 2013; Tielke et al., 2017, 2019; Wallis et al., 2019).
6.2 Wadsleyite and ringwoodite
Because wadsleyite and ringwoodite are only stable at 410–520 km depth (13–18 GPa) and 520–660 km depth (16–23 GPa) of the MTZ, performing deformation experiments on wadsleyite and ringwoodite is very difficult under the P–T conditions of the MTZ. Generally, a conventional deformation apparatus such as the Griggs or Paterson apparatus can be operated only at low pressures (P<3 GPa or P<0.5 GPa, respectively). Yamazaki and Karato (2001) designed the rotational Drickamer apparatus, in which deformation experiments can be performed to large strain in simple shear geometry. Because anvils are better supported in this design, deformation experiments can be performed even under lower mantle conditions in conjunction with synchrotron X-radiation (Girard et al., 2016). Subsequently, the deformation DIA was developed and has been used up to ∼20 GPa and ∼1700 K (e.g., Wang et al., 2003; Kawazoe et al., 2010).

Figure 14Plots of strain rate versus differential stress for (a) wadsleyite and (b) ringwoodite deformed under dry and wet conditions. Data sources: K13 (Kawazoe et al., 2013); H13 (Hustoft et al., 2013); F15 (Farla et al., 2015); S09 (Shimojuku et al., 2009); X03 (Xu et al., 2003); K16 (Kawazoe et al., 2016).
Several deformation experiments (e.g., Xu et al., 2003; Nishihara et al., 2008; Kawazoe et al., 2010) have been conducted to identify the operating deformation mechanisms and determine the flow law for each mechanism for water-poor polycrystalline wadsleyite and ringwoodite and to constrain the stress exponent n (Fig. 14a). However, due to the very high level of stress and limited experimental data points, the flow law for parameters in Eq. (10) was not well constrained quantitatively by these studies. With the improvement of experimental techniques, more data from a wide range of strain rates, temperature, pressure, grain size, and water content were reported to investigate the rheological behavior of the Earth's deep mantle. For example, Kawazoe et al. (2013) and Farla et al. (2015) demonstrated that water can significantly reduce the strength of wadsleyite under MTZ conditions. The slope of the stress–strain rate data for wadsleyite with 2100 wt. ppm H2O, reported by Hustoft et al. (2013), suggests that dislocation creep is the dominant deformation mechanism under wet conditions (Fig. 14a). Similar to wadsleyite, the dislocation creep strain rates in hydrous ringwoodite (Kawazoe et al., 2016) were markedly enhanced by water incorporation compared with that of anhydrous ringwoodite (Xu et al., 2003). In addition, the inferred strain rates for dislocation creep in wadsleyite and ringwoodite from experimental measurements of Si and O self-diffusion rates in these minerals (Shimojuku et al., 2009) under P–T conditions similar to those in deformation experiments are also plotted in Fig. 14a and b for comparison. The predicted dislocation creep strain rates for ringwoodite by Shimojuku et al. (2009) agree reasonably well with the experimental observations of Kawazoe et al. (2016). However, the results of dislocation creep strain rates between Shimojuku et al. (2009) and others (Hustoft et al., 2013; Farla et al., 2015) are inconsistent in wadsleyite (Fig. 14a), possibly due to the large uncertainties in the selection of the appropriate model parameters as suggested by Hustoft et al. (2013). Recently, Fei et al. (2017) estimated the viscosity of ringwoodite and bridgmanite under the conditions of the MTZ and lower mantle by measuring their dislocation mobilities within their crystal structures.
In this section, we will try to explore the quantitative relations between the different transport processes in silicate minerals. As discussed above, the propagation of elastic wave (compressional and shear wave velocity) and heat transfer (thermal conductivity/thermal diffusivity) are primarily caused by atomic displacements in the vicinity of equilibrium position (e.g., Hofmeister et al., 2007; Karato, 2008). However, three other transport properties, namely electrical conductivity, diffusivity, and rheology, are basically controlled by atomic or ionic transport, in which atomic displacements on spatial and temporal scales are larger than the typical displacements due to atomic vibration about a mean position (e.g., Chakraborty, 1995; Mehrer, 2007; Zhang, 2010; Ni et al., 2015). Here, we do not dig into the underlying physical principles but summarize the quantitative links between them.
7.1 Diffusivity and electrical conductivity
The electrical conductivity in minerals is used in studies of mineral structure and electronic and ionic transport processes. Ionic motion dominates electrical transport in many kinds of silicate glasses. Therefore, studying electrical transport is an important alternative approach to understanding diffusion behavior. If the electrical conduction of a material is dominated by the motion of a single ionic species, the relationship between electrical conductivity (σ) and diffusion coefficient (D) is given by the Nernst–Einstein relation (Karato, 1990; Chakraborty, 1995):
where z is the valence of the conducting species, e is the charge of the electron, c is the concentration of the migrating species, kB is Boltzmann's constant, and HR is the Haven ratio determined by the diffusion mechanism and usually has a value between 0.1 and 1.
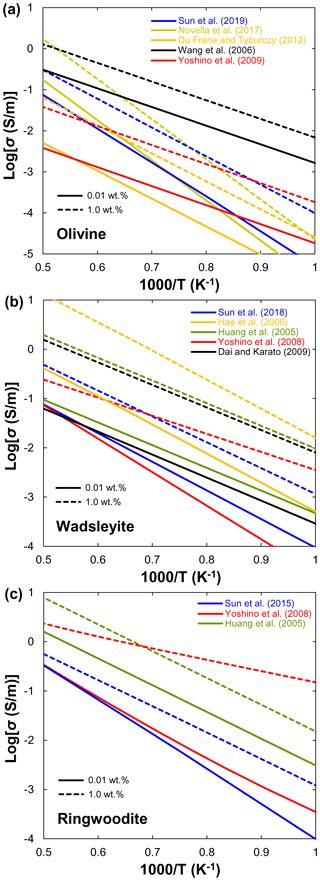
Figure 15Comparison of laboratory conductivity data with the calculated conductivity from hydrogen diffusion results through Eq. (12) as a function of 1 for different water contents in (a) olivine, (b) wadsleyite, and (c) ringwoodite.
Hydrogen diffusion in NAMs may provide a different perspective on how proton conduction affects bulk electrical conductivity with information exclusively on hydrogen mobility. Combined with the Nernst–Einstein relation (Eq. 12) and experimentally determined hydrogen diffusivity in olivine (Du Frane and Tyburczy, 2012; Novella et al., 2017; Sun et al., 2019), wadsleyite (Hae et al., 2006; Sun et al., 2018), and ringwoodite (Sun et al., 2015), these hydrogen diffusion results can be used to constrain the contribution of the total electrical conductivity of corresponding NAMs. As a result, a comparison between the indirect calculated conductivity and direct measured electrical conductivity as a function of water content is shown in Fig. 15a for olivine, Fig. 15b for wadsleyite, and Fig. 15c for ringwoodite, respectively. In this calculation, the isotropic electrical conductivity of polycrystalline olivine and its high-pressure polymorphs was approximately estimated by a geometric mean of the hydrogen diffusivities along each principle axis (Du Frane and Tyburczy, 2012; Novella et al., 2017). Owing to the relatively larger activation energy determined by hydrogen diffusion, the calculated proton conductivities are usually higher than those from laboratory conductivity measurements, except for the studies of Du Frane and Tyburczy (2012) for olivine and Sun et al. (2015) for ringwoodite. This is because electrical conductivity in a material is the sum of conduction of each charge carrier (or defect) type acting in parallel. In general, all defects are present in some amount in every crystal, and each contributes to the total conductivity. In most cases, only one or two types of defects dominate under a given set of thermodynamic conditions. If Eq. (12) is used to calculate the diffusion coefficient from conductivity measurements, one has to separate partial conductivities due to individual ions from total conductivity. By contrast, the electrical conductivity can be estimated from the diffusion coefficient in a similar way if the predominant ionic species (or defect) are the same between diffusion process and electrical conduction. For example, the electrical conductivities of olivine, wadsleyite, and ringwoodite calculated from hydrogen self-diffusion in olivine and its high-pressure polymorphs were applied to constrain the possible water contents in the UM and MTZ (e.g., Karato, 1990; Sun et al., 2015, 2018, 2019).
7.2 Diffusivity and rheology
When a differential stress is applied to a polycrystalline material, a heterogeneous state is created due to heterogeneous mechanical properties. Grain boundaries are weaker than the grains themselves, and hence the mutual sliding of grains along grain boundaries occurs upon the application of stress. Because grain boundaries are a good sink/source for defects (Karato, 2008), the concentration of point defects near grain boundaries will be dependent upon the stress state at grain boundaries. When diffusion along grain boundaries is important, the effective diffusion coefficient should involve the contributions from volume (DV) and grain-boundary (DGB) diffusion:
where δ and d are the thickness of the grain boundary and grain size, respectively.
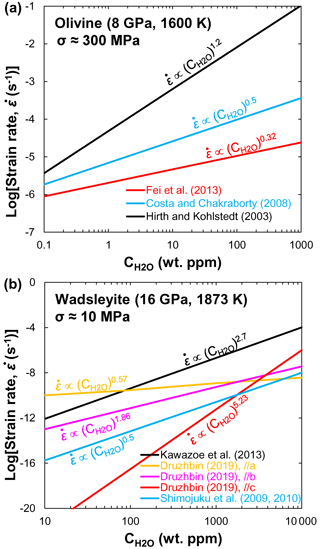
Figure 16Comparison of laboratory strain rate versus with those calculated from Si diffusion data. All data are normalized to 8 GPa, 1600 K, and a stress of 300 MPa for olivine (a) and 16 GPa, 1873 K, and a stress of 10 MPa for wadsleyite (b), respectively. Si self-diffusivities in olivine (Costa and Chakraborty, 2008; Fei et al., 2013) and wadsleyite (Shimojuku et al., 2009, 2010; Druzhbin, 2019) were converted to strain rate using Eqs. (14)–(17) with and parameters reported therein. Note that the water exponent (≈0.5) in the calculation of strain rate (b) by Shimojuku et al. (2009, 2010) is based on the geometric mean of Si self-diffusion in wadsleyite single crystal (Druzhbin, 2019).
The diffusion creep (including Coble creep and Nabarro–Herring creep) and dislocation creep are believed to be driven by the diffusion of the slowest element, that is, Si in silicate minerals, on grain boundaries (for Coble creep) and within grain interiors (for Nabarro–Herring creep and dislocation creep) (Frost and Ashby, 1982; Weertman, 1999). Thus, plastic deformation rates at high temperature in minerals can be calculated from the slowest diffusing species in the major constituent elements. For example, creep due to diffusional mass transport through the bulk of grains (Nabarro–Herring creep) can be expressed as follows (Frost and Ashby, 1982):
where α is a constant (≈13.3), σ is the stress, D is the diffusion coefficient, and Ω is the molar volume. If the diffusion coefficient (D) in Eq. (14) is replaced with an effective diffusion coefficient (Deff) given by Eq. (13), one obtains the following:
If at small grain size and/or at low T, then
This type of creep mechanism in Eq. (16) is referred to as the Coble creep (Coble, 1963). In the case of dislocation creep, dislocations move continuously, responding to applied stress until they cannot glide due to the mutual interaction of the edge portions. Dislocation climb overcomes the obstacle by which the dislocation glide can operate again. Consequently, the plastic strain is accomplished by dislocation glide. In the Weertman model, the strain rate is written as follows (Weertman, 1999):
where G is the shear modulus, b is the Burgers vector, lg is the glide distance, and lc is the climb distance. The ratio of is one of the important parameters for describing the dislocation creep in the Weertman model. In general, the DV and DGB are the slowest diffusion rates of Si, which are known from diffusion experiments measured under P–T conditions similar to that in deformation experiments. Therefore, plastic deformation rates for diffusion creep and dislocation creep at high temperature and high pressure can be calculated from Eqs. (14) to (17) using the Si self-diffusion coefficient in olivine, wadsleyite, and ringwoodite (e.g., Karato, 2008; Shimojuku et al., 2009). As an example, Fig. 16 shows a comparison of strain rate from deformation experiments with the calculated strain rate by the Weertman model (Eq. 17). When all data are normalized to a pressure of 8 GPa, a temperature of 1600 K, and a stress of 300 MPa for olivine (Fig. 16a), it is apparent that the dislocation creep rates reported by deformation experiments (Mei and Kohlstedt, 2000a, b; Hirth and Kohlstedt, 2003) are about 1 to 3 orders of magnitude higher than those calculated from Si diffusion in olivine (Costa and Chakraborty, 2008; Fei et al., 2013) using Eqs. (14)–(17) with . In addition, owing to the difficulties in performing diffusion experiments under the MTZ conditions, few experiments have been reported on the diffusion of silicon in wadsleyite (Shimojuku et al., 2004, 2009, 2010; Druzhbin, 2019) and ringwoodite (Shimojuku et al., 2009). Among them, only Druzhbin (2019) measured the Si diffusion in wadsleyite single crystal as a function of water content. In this calculation, a water exponent (≈0.5) for Si diffusion was obtained by the geometric mean of Druzhbin's results from three principal crystal orientations, which is also comparable to that for Si diffusion in olivine (Costa and Chakraborty, 2008). Consequently, the calculated dislocation creep rates in wadsleyite (Fig. 16b) using a water exponent of 0.5 and parameters of Si diffusion from Shimojuku et al. (2009, 2010) are lower than those determined by plastic deformation experiment (Kawazoe et al., 2013). This discrepancy could be due to the different stress conditions in deformation experiment (Mei and Kohlstedt, 2000a, b; Kawazoe et al., 2013; stress ∼100–540 MPa) and diffusion experiment (e.g., Costa and Chakraborty, 2008; Shimojuku et al., 2009, 2010; Fei et al., 2013; Druzhbin, 2019; stress is negligibly small because of hydrostatic pressure). In fact, the stress range in deformation experiment may exceed estimated stress conditions of the MTZ (∼10 MPa or less) by more than 1 to 2 orders of magnitude. Such high-stress conditions should have produced high dislocation densities, thus resulting in an apparently high water-content dependence of creep rate in olivine (, Hirth and Kohlstedt, 2003) and wadsleyite (, Kawazoe et al., 2013). If this is the case, the high water-content dependence of wadsleyite creep obtained by deformation experiments cannot be applied to the MTZ due to the low stresses and low dislocation density.
8.1 High-conductivity and low-velocity anomalies in the UM
In the UM, some studies have shown that the electrical conductivity in the asthenosphere just below the lithosphere–asthenosphere boundary (LAB) is approximately 10−2 to 10−1 S/m, known as the high conductive layer (HCL, e.g., Evans et al., 2005; Naif et al., 2013). The conductivity largely increases with increasing depth from 50 to 100 km and also becomes strongly anisotropic in this depth range. Initially, the origin of the HCL has been attributed to the presence of hydrous olivine (e.g., Karato, 1990; D. Wang et al., 2006). However, conductivity anisotropy in olivine single crystals appears to have an insufficient effect on electrical conductivity to account for the observed HCL (e.g., Yoshino et al., 2006; Poe et al., 2010; Yang, 2012), which instead may be explained by the presence of partial melt elongated in the direction of plate motion (e.g., Caricchi et al., 2011; Zhang et al., 2014; Pommier et al., 2015; Stern et al., 2015; Zhang and Yoshino, 2020). In addition, water dissolved in olivine is unlikely to produce the conductivity anomalies observed in the UM (Gardés et al., 2014) because the concentration (more than 1000 ppm H2O) of water in minerals required to reach UM conductivities would lead to partial melting of the mantle rocks (Hirschmann, 2010).
Another striking geophysical anomaly identified in the UM is the low-velocity zone (LVZ, e.g., Hirschmann, 2010), which is characterized by low seismic velocities and high attenuation and located in the asthenosphere near the LAB. Under the oceanic plate, the depth range of LVZ appears to coincide with that of the HCL in some regions, with a 20 to 50 km thick layer (e.g., Evans et al., 2005; Naif et al., 2013). As discussed earlier, the LVZ of the UM cannot be explained by the sound velocities of hydrous olivine. Alternatively, the reduced seismic velocity (LVZ) and elevated electrical conductivity (HCL) have been attributed to the presence of partial melting (e.g., Yoshino et al., 2010; Zhang et al., 2014; Chantel et al., 2016; Freitas et al., 2019), although large discrepancies still remain in the laboratory estimations of the amount of melt volume fraction present in the asthenosphere (e.g., Chantel et al., 2016; Freitas et al., 2019; Zhang and Yoshino, 2020).
8.2 Water in the MTZ
Considering the high water storage capacities of wadsleyite and ringwoodite (e.g., Inoue et al., 1995; Kohlstedt et al., 1996), the MTZ has been thought to be a potentially large water reservoir in the Earth's mantle. Contrast of water partition coefficient between wadsleyite and olivine at the UM boundary and between ringwoodite and bridgmanite at the lower mantle boundary would lead to dehydration melting near 410 and 660 discontinuities since excess water from the MTZ cannot be incorporated substantially by minerals with a smaller partition coefficient and lower water solubilities. These partial melts could produce low-velocity and high-conductivity anomalies that can be imaged using seismic or electromagnetic observations (e.g., Bercovici and Karato, 2003; Song et al., 2004; Toffelmier and Tyburczy, 2007; Kawakatsu et al., 2009; Tauzin et al., 2010; Schmerr et al., 2012). Indeed, quantifying the amount of water in the Earth's mantle has been a long-standing challenge in deep Earth research integrating seismology, mineral physics, and geodynamics. On the basis of the above discussion in Sects. 2–6, water can dramatically affect the physical properties of mantle minerals including diffusion, electrical conduction, thermal conduction, sound velocity, and rheology. Therefore, the water content in the MTZ could be estimated according to the various transport properties of olivine, wadsleyite, and ringwoodite and their sensitivity to water.
8.2.1 From electrical conductivity
Electromagnetic studies demonstrated that high-conductivity anomaly is an important feature of the MTZ between depths of 400 and 660 km at many localities (Utada et al., 2003; Tarits et al., 2004; Ichiki et al., 2006; Shimizu et al., 2010), even globally (Kuvshinov and Olsen, 2006; Kelbert et al., 2009). For example, in the region beneath the North Pacific (Utada et al., 2003; Shimizu et al., 2010) and beneath northeastern China (Ichiki et al., 2001), the high-conductivity anomaly observed in the MTZ might be associated with water released from the stagnant slab. Recent electromagnetic studies have shown that the lateral variation in electrical conductivity is largely comparable to the depth variation (e.g., Ichiki et al., 2006; Shimizu et al., 2010), suggesting the strong sensitivity of electrical conductivity to some parameters that change laterally such as temperature and water content.
To better understand the nature of the high-conductivity zone and constrain the water content in the MTZ from the perspective of electrical conductivity, we construct a conductivity–depth profile in the Earth's mantle by extrapolating the experimental conductivity (olivine: Xu et al., 2000; D. Wang et al., 2006; Yoshino et al., 2009; wadsleyite: Huang et al., 2005; Dai and Karato, 2009; Yoshino et al., 2008; Yoshino and Katsura, 2012; ringwoodite: Huang et al., 2005; Yoshino et al., 2008) and hydrogen diffusion data (olivine: Sun et al., 2019; wadsleyite: Sun et al., 2018; ringwoodite: Sun et al., 2015) to the deep Earth in terms of temperature, pressure, and water content. In the present calculation, two sets of conductivity data (Yoshino and coworkers, termed the Yoshino model; Karato and coworkers – the Karato model) and hydrogen diffusion data (diffusion model) were used to calculate the electrical conductivity of the mantle by using Eqs. (1)–(4) and (12). The temperature in the MTZ is based on the average adiabatic mantle geotherm from Katsura et al. (2010). The electrical conductivity of dry olivine aggregates was referenced from Xu et al. (2000).
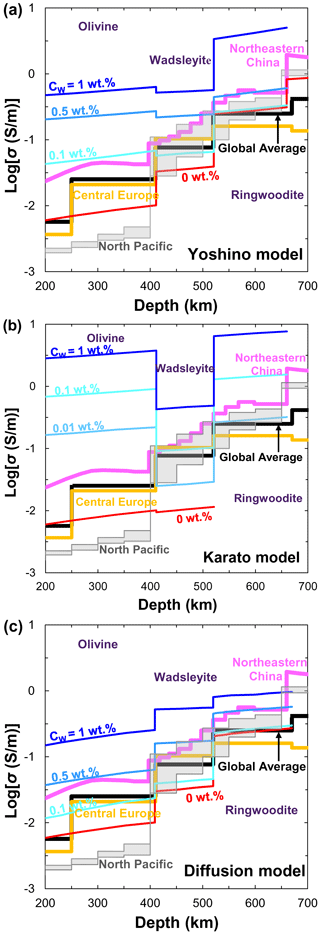
Figure 17Comparison of laboratory-based conductivity–depth profiles of the mantle with olivine composition as a function of water content (wt. %) for the adiabatic mantle geotherm (Katsura et al., 2010) with the geophysically observed electrical conductivity in the mantle. (a) Profiles constructed from data by Yoshino and coworkers (olivine: Yoshino et al., 2009; wadsleyite: Yoshino and Katsura, 2012; ringwoodite: Yoshino et al., 2008). (b) Profiles constructed from data by Karato and coworkers (olivine: D. Wang et al., 2006; wadsleyite: Dai and Karato, 2009; ringwoodite: Huang et al., 2005). (c) Profiles constructed from H self-diffusion data (olivine: Sun et al., 20019; wadsleyite: Sun et al., 2018; ringwoodite: Sun et al., 2015). For dry olivine, data from Xu et al. (2000) are used. Global average (Kelbert et al., 2009); central Europe (Tarits et al., 2004); North Pacific (Utada et al., 2003; Shimizu et al., 2010); northeastern China (Ichiki et al., 2006).
Figure 17 shows a comparison of laboratory-based conductivity–depth profiles of the Earth's mantle for olivine, wadsleyite, and ringwoodite as a function of water content with geophysically observed electrical conductivity in the mantle. The conductivity–depth profiles obtained from the geophysical observations show significant differences from each other. For example, the semi-global reference model beneath the North Pacific Ocean (Utada et al., 2003; Shimizu et al., 2010) indicates that the electrical conductivity sharply jumps at the top of the MTZ (410 km discontinuity) and gradually increases to the top of the lower mantle. Remarkably, the recent global average model by Kelbert et al. (2009) is comparable to that beneath central Europe revealed by Tarits et al. (2004) in the UM and MTZ. However, both models are lower than that beneath northeastern China (Ichiki et al., 2006). By contrast, the laboratory-based conductivity–depth profiles are strongly influenced by the quantitative relationships between mineral conductivity and water content reported by different laboratories. For example, at 410 km discontinuity, the difference between olivine and wadsleyite is negligibly small in the Yoshino model (Fig. 17a), whereas a large drop in electrical conductivity at constant water content can be seen between olivine and wadsleyite according to the Karato model (Fig. 17b). Conversely, the conductivity–depth profiles derived from the diffusion model (Fig. 17c) show a positive conductivity jump at a depth of 410 km. However, when we compare the three laboratory-based models with the global average model by Kelbert et al. (2009) and the model beneath northeastern China (Ichiki et al., 2006), the estimated water content in the UM and MTZ is approximately 0.1 wt. %–0.5 wt. % H2O from the Yoshino and diffusion models, whereas the water content inferred from the Karato model is much less than 0.01 wt.% H2O in the UM and 0.1 wt.% H2O in the lower part of the MTZ. This discrepancy is mainly due to the difference in the dependence of water on the electrical conductivity of olivine, wadsleyite, and ringwoodite investigated experimentally (Yoshino, 2010; Yoshino and Katsura, 2013).
8.2.2 From seismological observations
Seismic wave propagation is sensitive to water incorporation and has thus been proposed as promising geophysical observables to quantify hydration (e.g., Jacobsen and Smyth, 2006; Mao et al., 2011, 2012; Houser, 2016). Seismological methods provide high three-dimensional resolution and offer a variety of observables that have been proposed to be sensitive to hydration, including lateral wave speed variations as depicted by seismic tomography and characteristics of seismic discontinuities (e.g., Houser and Williams, 2010; Schmandt et al., 2014; Houser, 2016; Buchen et al., 2018).

Figure 18Influence of water on the mantle velocity structure. (a) Compressional (VP) and (b) shear wave (VS) velocities of olivine polymorphs in the Earth's mantle along an adiabatic mantle geotherm (Katsura et al., 2010) compared with seismic models (PREM: Dziewonski and Anderson, 1981; AK135: Kennett et al., 1995). Red lines denote the velocity of anhydrous (Mg0.9Fe0.1)2SiO4 olivine polymorphs. Light blue lines represent the velocity of hydrous (Mg0.9Fe0.1)2SiO4 olivine, wadsleyite, and ringwoodite with 0.4 wt. %, 2.0 wt. % and 1.0 wt. % H2O, respectively, based on the data sources (Li et al., 1996, 2003; Sinogeikin et al., 2003; Jacobsen and Smyth, 2006; Higo et al., 2008; Wang et al., 2014; Mao et al., 2010, 2011, 2012, 2015; Buchen et al., 2018). (c) Comparison of water-induced reduction in velocity of (Mg0.9Fe0.1)2SiO4 olivine polymorphs in the Earth's mantle with the low-velocity anomalies in the mantle revealed by seismic observations in the UM (e.g., Song et al., 2004; Kawakatsu et al., 2009; Tauzin et al., 2010; Schmerr, 2012) and MTZ (Sieminski et al., 2003; Kustowski et al., 2008; Houser and Williams, 2010; Schmandt et al., 2014).
In this study, we attempt to constrain the water content and interpret seismic signatures in the potential water-rich region of the UM and MTZ by using the measured sound velocities of olivine, wadsleyite, and ringwoodite at simultaneous high pressure and high temperature by following the method used by Jacobsen and Smyth (2006) and Mao et al. (2012). The water content for hydrous (Mg0.9Fe0.1)2SiO4 olivine, wadsleyite, and ringwoodite is assumed to be 0.4 wt. %, 2.0 wt. % and 1.0 wt. % H2O, respectively, based on previous data (Li et al., 1996; Li, 2003; Sinogeikin et al., 2003; Jacobsen and Smyth, 2006; Higo et al., 2008; Wang et al., 2014; Mao et al., 2010, 2011, 2012, 2015; Buchen et al., 2018). Figure 18 shows the modeled mantle velocity structures for olivine and its high-pressure polymorphs in the Earth's mantle as a function of depth and water content along an adiabatic mantle geotherm (Katsura et al., 2010). As seen in the global seismic models (PREM and AK135 in Fig. 18a, b), the compressional and shear wave velocities exhibit discontinuous increases at certain depths (Dziewonski and Anderson, 1981; Kennett et al., 1995); some distinct features include the low-velocity zone around 80–150 km, jumps at the top of 410 and 660 km depths, and a high-velocity gradient in the MTZ. Importantly, seismic low-velocity zones have been detected above the 410 km discontinuity in various regions (e.g., Song et al., 2004; Tauzin et al., 2010). Clearly, up to ∼3 % and ∼8 % decrease in VP and VS of olivine in the UM (Fig. 18c) are unlikely to be explained by olivine hydration because the sound velocities of olivine are insensitive to water as illustrated in Figs. 10 and 18a, b. In fact, these features were predicted by the “water filter” model (Bercovici and Karato, 2003), in which partial melting atop the 410 km discontinuity would occur with vertical transport of water-rich minerals from the MTZ to the UM. This hypothesis has been verified by recent experimental observations on seismic wave velocity of hydrous peridotites (β→α transition) (Freitas et al., 2017).
In contrast to the 410 and 660 km discontinuities, which are sharp features with reasonably well-defined velocity increases of approximately 5 % in VP and VS arising from the olivine–wadsleyite and ringwoodite–bridgmanite + ferropericlase phase transitions (Dziewonski and Anderson, 1981; Kennett et al., 1995), the 520 km discontinuity is comparatively small, and there is less agreement on the magnitude of the velocity jump. The 520 km discontinuity may not be sharp (e.g., less than 10 km; Benz and Vidale, 1993), but it is perhaps a rather broad (25–50 km) velocity gradient (Revenaugh and Jordan, 1991). As shown in Figs. 11 and 18a, b, the influence of water on the sound velocities of wadsleyite is very limited. Even if wadsleyite contains 2.0 wt. % H2O, the VP and VS under the P–T conditions of the MTZ were reduced by only 0.9 %, and still higher those of the PREM and AK135 models (Fig. 18a, b). This finding suggests that the low-velocity anomalies with 1 %–3 % decrease in VS in the upper part (410–520 km) of the MTZ (e.g., Sieminski et al., 2003; Kustowski et al., 2008) cannot be explained by water alone, which may be caused by partial melting or lateral heterogeneities of composition or temperature in some locations. However, the magnitude of the reduction in seismic wave velocities of ringwoodite by a given amount of water is much greater than previously thought when the combined effect of hydration, temperature, and pressure is taken into consideration. In contrast, Schulze et al. (2018) demonstrated that the influence of hydration on the VP and VS of (Mg0.89Fe0.11)2SiO4 ringwoodite decreases with increasing pressure and vanishes under conditions of the MTZ. This observation suggests that hydrous ringwoodite (Fig. 18c) would be unable to account for the low-velocity anomaly in the lower part (520–660 km) of the MTZ derived from seismological studies (e.g., Sieminski et al., 2003; Kustowski et al., 2008; Houser and Williams, 2010; Schmandt et al., 2014). In other words, it is hard to constrain water content in the UM and MTZ by employing experimental measurements of VP and VS of olivine, wadsleyite, and ringwoodite (Fig. 18).
8.3 Rheology of the UM and MTZ
Diffusion and dislocation creep are considered to be the two main mechanisms of plastic deformation in the Earth's interior. An important question in geodynamics at present is which creep mechanism dominates in the UM and MTZ. If it is diffusion creep, shape-preferred orientation will be produced in olivine, and strain rate proportional to stress will result in Newtonian viscosity. By contrast, if dislocation creep dominates, lattice-preferred orientation will appear, and the strain rate proportional to stress to the power of 3.0–3.5 will lead to non-Newtonian viscosity (Fei et al., 2016). The mechanisms of weakening effects by water (hydrogen) were reviewed by Karato (2008). Given that high-temperature creep is controlled by diffusion-related processes, the enhancement of creep by water is partly due to enhanced diffusion (Costa and Chakraborty, 2008; Kawazoe et al., 2013).
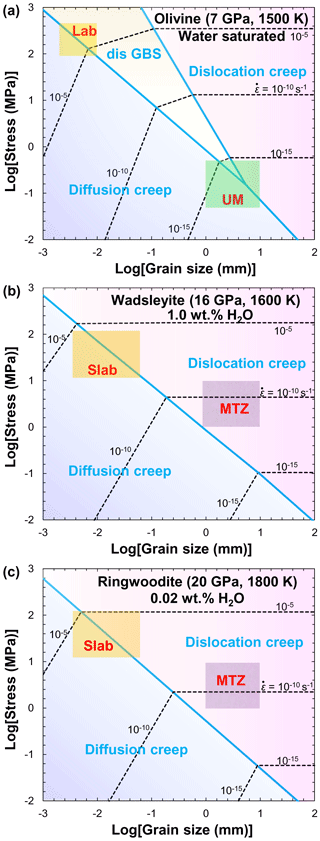
Figure 19Grain-size/stress-deformation mechanism maps for (a) (Mg0.9Fe0.1)2SiO4 olivine (P=7 GPa, T=1500 K, and water-saturated conditions), (b) (Mg0.9Fe0.1)2SiO4 wadsleyite (P=16 GPa, T=1600 K, and wt. % H2O) and (c) (Mg0.9Fe0.1)2SiO4 ringwoodite (P=20 GPa, T=1800 K, and wt. % H2O). The power-law creep constitutive relations in olivine were established by Mei and Kohlstedt (2000a, b) and Hirth and Kohlstedt (2003) and in wadsleyite and ringwoodite calculated from the Si diffusion data (Shimojuku et al., 2009, 2010; Druzhbin, 2019) using Eqs. (14)–(17) with . Note that dis GBS represents dislocation grain-boundary sliding. The thick light blue lines represent boundaries between different creep mechanisms. The orange, green, and dark purple boxes show the possible variations of grain size and stress in the laboratory, UM, MTZ and the subducting slabs, respectively.
Although deformation experiments can provide direct constraints on the details of creep mechanisms, strain rates attained in laboratories are usually on the order of 10−5 s−1, which is 10 orders of magnitude faster than the geological strain rates ( s−1) (see the colored boxes in Fig. 19). This discrepancy in strain rates is unavoidable because deformation experiments must be conducted on a timescale of hours. To enhance the strain rates, grain sizes are reduced to microns, and deviatoric stresses are increased to ∼100 MPa or more; by contrast, the grain size of mantle olivine is typically on the order of millimeters, and deviatoric stresses are expected to be on the order of 1 MPa in most of the mantle (e.g., Karato, 2008). Therefore, considerable extrapolation is involved when using experimentally derived mantle rheology in numerical modeling. However, the extrapolation of experimental data is valid only when extrapolation is within the same deformation mechanism where the same constitutive relationship determined in the laboratory would apply. At the same time, the published results on the plastic deformation of the UM and MTZ minerals should be critically evaluated, and various key parameters (temperature, water content, grain size) in the deep Earth should be estimated in order to assess the mechanism.
When several mechanisms of deformation operate, the use of a deformation mechanism map is a convenient way to understand which mechanism is dominant in a certain parameter space (Karato, 2008). On the basis of Eq. (10) and previous experimental data on olivine rheology (Mei and Kohlstedt, 2000a, b; Karato and Jung, 2003; Hirth and Kohlstedt, 2003; Ohuchi et al., 2017; Gouriet et al., 2019), Fig. 19a shows a deformation mechanism map of olivine on a stress versus grain-size space at a pressure of 7 GPa, a temperature of 1500 K, and water-saturated conditions. This deformation mechanism map for hydrous olivine demonstrates that diffusion creep dominates at lower stresses and smaller grain sizes, and dislocation creep becomes dominant at higher stresses and larger grain sizes. However, Fig. 19a indicates that dislocation GBS is one of the most effective deformation mechanisms at higher pressures and/or lower temperatures (e.g., subducting slabs), as suggested by Ohuchi et al. (2017).
To understand the dominant deformation mechanism in the MTZ, we have constructed the deformation mechanism maps for wadsleyite (Fig. 19b) at a pressure of 16 GPa, a temperature of 1600 K, and a fixed water content of 1.0 wt. % and for ringwoodite (Fig. 19c) at a pressure of 20 GPa, a temperature of 1800 K, and a fixed water content of 0.02 wt. %, respectively. The strain rates for diffusion and dislocation creep were calculated as a function of grain size and stress in terms of Eqs. (14)–(17) and Si self-diffusion data in wadsleyite (Shimojuku et al., 2004, 2009, 2010; Druzhbin, 2019) and ringwoodite (Shimojuku et al., 2009). As discussed in Sect. 7.2, the water exponent in the calculation of strain rate is assumed to be 0.5 for wadsleyite based on the geometric mean of Si self-diffusion in wadsleyite single crystal (Druzhbin, 2019). In this case, it is impossible to calculate the strain rate of ringwoodite as a function of water content, because only Shimojuku et al. (2009) measured Si diffusivities in ringwoodite at a single water content (∼0.02 wt. % H2O). Therefore, the influence of water on the deformation mechanism map for ringwoodite was not considered in this calculation. Our results imply that the dislocation creep mechanism may be dominant in the MTZ (Carrez et al., 2006; Ritterbex et al., 2015). Transitions between diffusion creep and dislocation creep mechanisms may easily occur through slight changes or heterogeneities in grain size and stress at the MTZ (Shimojuku et al., 2004, 2009, 2010; Druzhbin, 2019). In addition, the possible deformation mechanisms for subducting slabs are also illustrated in Fig. 19b, c. The rheological structure of the subducting slab depends strongly on the subduction parameters through temperature that controls the grain size of ringwoodite and the magnitude of forces acting on a slab (Karato et al., 2001). Furthermore, numerical modeling by Karato et al. (2001) shows that, regardless of warm or cold slabs, the subducting slabs lose their strength if the grain-size-sensitive diffusion creep operates because of the grain-size reduction after the olivine–ringwoodite transformation. However, the reliability of the conclusions from the deformation mechanism map depends on the reliability of the data used to construct such a map and also on the estimated values of parameters such as the stress and water-content exponent. Especially, the rheology of the UM, MTZ, and subducting slabs may strongly be affected by water content and chemical environment in the deep Earth. These issues need to be further constrained by deformation experiments with better controlled water fugacity.
Despite its small abundance, water plays an important role in the properties of the Earth's interior, such as mantle convection, chemical differentiation, and seismic signature. In this article, we review the recent advances in the study of the transport properties of olivine, wadsleyite, and ringwoodite under high temperature and high pressure, specifically focusing on the influence of water. We have seen how water is involved in transport processes such as diffusion and deformation, the effect of water being to enhance the kinetics of transport properties (diffusion, electrical conductivity, and rheology) in olivine, wadsleyite, and ringwoodite through the increase in point defect concentrations, especially vacancies. In addition, the dissolution of water in the crystal lattice will weaken chemical bonding and increase structural disorder. Hence, one may expect that seismic wave velocities and thermal conductivity/diffusivity will be reduced by the incorporation of water.
Direct laboratory experimental measurements on the transport properties of NAMs can provide meaningful constraints water content in the mantle. However, these data have shown large discrepancies between research groups, especially for proton conduction in olivine and its high-pressure polymorphs (e.g., D. Wang et al., 2006; Yoshino et al., 2006; Huang et al., 2005; Yoshino et al., 2008; Dai and Karato, 2014; Gardés et al., 2015). As we discussed in Sect. 3, the primary reason for this inconsistency may originate from the different experimental techniques. Another typical example is to estimate the water content in the UM and MTZ by combining geophysical observations and the results of high-pressure experiments (see Figs. 17–18). However, different conclusions are obtained in Sect. 8. In most geophysical studies on the composition (especially for water) of the Earth's interior, the focus is seismological observations such as seismic wave velocities, which are rather insensitive to water content (e.g., Mao et al., 2010, 2011; Buchen et al., 2018) but sensitive to other parameters such as the major element chemistry (e.g., pyrolite versus harzburgite) as shown by Karato (2011). In contrast to seismic wave velocity, electrical conductivity is more sensitive to water content compared with the composition (e.g., Karato, 1990; Yoshino et al., 2010; Yoshino and Katsura, 2013). Meanwhile, the temporal and spatial resolution of magnetotelluric surveys is much worse than that of seismology. Consequently, one cannot obtain robust constraints on water content from geophysical investigations (e.g., seismological observations or magnetotelluric surveys) or laboratory measurements (e.g., electrical conductivity or sound velocity) alone (e.g., Houser, 2016; Wang et al., 2019). This kind of difference between the different methods is not due to the experimental and/or geophysical methods themselves are wrong, but because each method has its own shortcomings or limitations.
The ultimate goal of laboratory measurements on the transport properties of mantle minerals is to explore universal law and construct a quantitative relationship for each transport property as a function of various thermodynamic parameters (T, P, , H2O, etc.). Considering the substantial difficulties of performing experiments under extreme conditions, most experiments were conducted at very limited temperature and pressure conditions. Thus, different equations for the same property (e.g., Eq. 5 versus Eq. 6) were established by different groups, even using the same equation but obtaining different parameter values (see Figs. 13–14). As a result, not surprisingly, the fitting quality and model applicability are frequently unsatisfactory. In many cases, great caution must be exercised with the extrapolation/or interpolation of laboratory-based models to real Earth interior conditions.
There is one point that we must emphasize: the connection between geophysical observations and physical properties of minerals is provided by the thermodynamics of mantle minerals and links between transport properties. As discussed above, enormous progress has been made over the last 2 decades in the ability to measure the physical properties of NAMs under high P–T conditions. Unlike other properties (i.e., diffusivity, electrical conductivity, and rheology), a unified law involving various thermodynamic parameters (T, P, , etc.) has not been established for thermal conductivity and sound velocity yet. The parameterization of these two physical properties in terms of water content and pressure (and temperature) is urgently needed. Further experimental or theoretical studies are required to uncover these unresolved issues to better understand the nature of various geodynamic processes in the mantle.
Importantly, a comprehensive understanding of the composition, structure, and dynamics in the Earth, even a thorough interpretation of magnetotelluric or seismological profiles, needs a systematic multidisciplinary approach, including not only geophysical observations and geochemical analyses, but also laboratory measurements of the physical properties of mantle minerals under high temperature and pressure. Nonetheless, with each method being sensitive to specific parameters and probing different processes, multidisciplinary approaches are becoming more popular within the geoscience community and will cover a wide range of applications in the foreseeable future.
All data derived from this research are presented in the figures and additional requests for raw data should be addressed to Bao-Hua Zhang.
BHZ and QKX designed the research, BHZ compiled and analyzed data, and BHZ and QKX wrote the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Probing the Earth: reviews of OH groups in anhydrous and hydrous minerals”. It is not associated with a conference.
We thank Jannick Ingrin for the invitation to write this review at European Journal of Mineralogy. We appreciate the editorial handling by Patrick Cordier. Constructive comments by associate editor Etienne Balan and two anonymous reviewers helped to improve the manuscript.
This study was financially supported by National Key R&D Program of China (grant no. 2018YFA0702700), Key Research Program of Frontier Sciences of CAS (grant no. ZDBS-LY-DQC015), research funding from School of Earth Sciences, Zhejiang University, and NSF of China (grant nos. 41973056, 41773056).
This paper was edited by Etienne Balan and reviewed by two anonymous referees.
Bali, E., Bolfan-Casanova, N., and Koga, K. T.: Pressure and temperature dependence of H solubility in forsterite: An implication to water activity in the Earth interior, Earth Planet. Sc. Lett., 268, 354–363, https://doi.org/10.1016/j.epsl.2008.01.035, 2008.
Béjina, F., Jaoul, O., and Liebermann, R. C.: Diffusion in minerals at high pressure: a review, Phys. Earth Planet. In., 139, 3–20, https://doi.org/10.1016/S0031-9201(03)00140-7, 2003.
Bell, D. R., Rossman, G. R., Maldener, J., Endisch, D., and Rauch, F.: Hydroxide in olivine: a quantitative determination of the absolute amount and calibration of the IR spectrum, J. Geophys. Res., 108, 2105, https://doi.org/10.1029/2001JB000679, 2003.
Benz, H. M. and Vidale, J. E.: Sharpness of upper-mantle discontinuities determined from high-frequency reflections, Nature, 365, 147–150, https://doi.org/10.1038/365147a0, 1993.
Bercovici, D. and Karato, S. I.: Whole mantle convection and the transition zone water filter, Nature, 425, 39–44, https://doi.org/10.1038/nature01918, 2003.
Berry, A. J., Hermann, J., O'Neill, H. S. C., and Foran, G. J.: Fingerprinting the water site in mantle olivine, Geology, 33, 869–872, https://doi.org/10.1130/G21759.1, 2005.
Brady, J. B. and Cherniak, D. J.: Diffusion in minerals: an overview of published experimental data, Rev. Mineral. Geochem., 72, 899–920, https://doi.org/10.2138/rmg.2010.72.20, 2010.
Buchen, J., Marquardt, H., Speziale, S., Kawazoe, T., Ballaran, T. B., and Kurnosov, A.: High-pressure single-crystal elasticity of wadsleyite and the seismic signature of water in the shallow transition zone, Earth Planet. Sc. Lett., 498, 77–87, https://doi.org/10.1016/j.epsl.2018.06.027, 2018.
Caricchi, L., Gaillard, F., Mecklenburgh, J., and Le Trong, E.: Experimental determination of electrical conductivity during deformation of melt-bearing olivine aggregates: implications for electrical anisotropy in the oceanic low velocity zone, Earth Planet. Sc. Lett., 302, 81–94, https://doi.org/10.1016/j.epsl.2010.11.041, 2011.
Caracas, R. and Panero, W. R.: Hydrogen mobility in transition zone silicates, Prog. Earth Planet. Sci., 4, 9, https://doi.org/10.1186/s40645-017-0119-8, 2017.
Carrez, P., Cordier, P., Mainprice, D., and Tommasi, A.: Slip systems and plastic shear anisotropy in Mg2SiO4 ringwoodite: insights from numerical modelling, Eur. J. Mineral., 18, 149–160, https://doi.org/10.1127/0935-1221/2006/0018-0149, 2006.
Chakraborty, S.: Diffusion in silicate melts, in: Structure, Dynamics and Properties of Silicate Melts, Rev. Mineral. Geochem., 32, 411–503, https://doi.org/10.1515/9781501509384-012, 1995.
Chakraborty, S.: Diffusion in solid silicates – a tool to track timescales of processes comes of age, Annu. Rev. Earth Planet. Sci., 36, 153–190, https://doi.org/10.1146/annurev.earth.36.031207.124125, 2008.
Chakraborty, S.: Diffusion coefficients in olivine, wadsleyite and ringwoodite, Rev. Mineral. Geochem., 72, 603–639, https://doi.org/10.2138/rmg.2010.72.13, 2010.
Chang, Y. Y., Hsieh, W. P., Tan, E., and Chen, J.: Hydration-reduced lattice thermal conductivity of olivine in Earth's upper mantle, P. Natl. Acad. Sci. USA, 114, 4078–4081, https://doi.org/10.1073/pnas.1616216114, 2017.
Chantel, J., Mahtilake, G., Andrault, D., Novella, D., Yu, T., and Wang, Y.: Experimental evidence supports mantle partial melting in the asthenosphere, Sci. Adv., 2, e1600246, https://doi.org/10.1126/sciadv.1600246, 2016.
Cherniak, D. J. and Watson, E. B.: Diffusion of helium in olivine at 1 atm and 2.7 GPa, Geochim. Cosmochim. Ac., 84, 269–279, https://doi.org/10.1016/j.gca.2012.01.042, 2012.
Clauser, C.: Thermal storage and transport properties of rocks, I: Heat capacity and latent heat, Encyclopedia of Solid Earth Geophysics, Springer, the Netherlands, 1423–1431, https://doi.org/10.1007/978-90-481-8702-7_238, 2011.
Clauser, C. and Huenges, E.: Thermal conductivity of rocks and minerals, Rock Phys. Phase Rel., 3, 105–126, https://doi.org/10.1029/RF003p0105, 1995.
Coble, R. L.: A model for boundary diffusion-controlled creep in polycrystalline materials, J. Appl. Phys., 34, 1679–1682, https://doi.org/10.1063/1.1702656, 1963.
Constable, S.: SEO3: a new model of electrical conductivity, Geophys. J. Inter., 166, 435–437, https://doi.org/10.1111/j.1365-246X.2006.03041.x, 2006.
Costa, F. and Chakraborty, S.: The effect of water on Si and O diffusion rates in olivine and implications for transport properties and processes in the upper mantle, Phys. Earth Planet. In., 166, 11–29, https://doi.org/10.1016/j.pepi.2007.10.006, 2008.
Dai, L. and Karato, S. I.: Electrical conductivity of wadsleyite at high pressures and high temperatures, Earth Planet. Sc. Lett., 287, 277–283, https://doi.org/10.1016/j.epsl.2009.08.012, 2009.
Dai, L. and Karato, S. I.: High and highly anisotropic electrical conductivity of the asthenosphere due to hydrogen diffusion in olivine, Earth Planet. Sc. Lett., 408, 79–86, https://doi.org/10.1016/j.epsl.2014.10.003, 2014.
Dai, L. and Karato, S. I.: Reply to comment on “High and highly anisotropic electrical conductivity of the asthenosphere due to hydrogen diffusion in olivine” by Dai and Karato [Earth Planet. Sc. Lett. 408 (2014) 79-86], Earth Planet. Sc. Lett., 427, 300–302, https://doi.org/10.1016/j.epsl.2015.06.042, 2015.
Darling, K. L., Gwanmesia, G. D., Kung, J., Li, B., and Liebermann, R. C.: Ultrasonic measurements of the sound velocities in polycrystalline San Carlos olivine in multi-anvil, high-pressure apparatus, Phys. Earth Planet. In., 143, 19–31, https://doi.org/10.1016/j.pepi.2003.07.018, 2004.
de Koker, N. and Stixrude, L.: Theoretical computation of diffusion in minerals and melts, Rev. Mineral. Geochem., 72, 971–996, https://doi.org/10.2138/rmg.2010.72.22, 2010.
Demouchy, S.: Diffusion of hydrogen in olivine grain boundaries and implications for the survival of water-rich zones in the Earth's mantle, Earth Planet. Sc. Lett., 295, 305–313, https://doi.org/10.1016/j.epsl.2010.04.019, 2010.
Demouchy, S. and Bolfan-Casanova, N.: Distribution and transport of hydrogen in the lithospheric mantle: A review, Lithos, 240–243, 402–425, https://doi.org/10.1016/j.lithos.2015.11.012, 2016.
Demouchy, S. and Mackwell, S. J.: Mechanisms of hydrogen incorporation and diffusion in iron-bearing olivine, Phys. Chem. Mineral., 33, 347–355, https://doi.org/10.1007/s00269-006-0081-2, 2006.
Demouchy, S., Schneider, S. E., Mackwell, S. J., Zimmerman, M. E., and Kohlstedt, D. L.: Experimental deformation of olivine single crystals at lithospheric temperatures, Geophys. Res. Lett., 36, L04304, https://doi.org/10.1029/2008GL036611, 2009.
Demouchy, S., Tommasi, A., Barou, F., Mainprice, D., and Cordier, P.: Deformation of olivine in torsion under hydrous conditions, Phys. Earth Planet. In., 202, 56–70, https://doi.org/10.1016/j.pepi.2012.05.001, 2012.
Demouchy, S., Tommasi, A., Boffa Ballaran, T., and Cordier, P.: Low strength of Earth's uppermost mantle inferred from tri-axial deformation experiments on dry olivine crystals, Phys. Earth Planet. In., 220, 37–49, https://doi.org/10.1016/j.pepi.2013.04.008, 2013.
Demouchy, S., Mussi, A., Barou, F., Tommasi, A., and Cordier, P.: Viscoplasticity of polycrystalline olivine experimentally deformed at high pressure and 900 ∘C, Tectonophysics, 623, 123–135, https://doi.org/10.1016/j.tecto.2014.03.022, 2014.
Demouchy, S., Thoraval, C., Bolfan-Casanova, N., and Manthilake, G.: Diffusivity of hydrogen in iron-bearing olivine at 3 GPa, Phys. Earth Planet. In., 260, 1–13, https://doi.org/10.1016/j.pepi.2016.08.005, 2016.
Dohmen, R., Becker, H. W., and Chakraborty, S.: Fe-Mg diffusion in olivine I: experimental determination between 700 and 1200 ∘C as a function of composition, crystal orientation and oxygen fugacity, Phys. Chem. Mineral., 34, 389–407, https://doi.org/10.1007/s00269-007-0157-7, 2007.
Dohmen, R., Kasemann, S. A., Coogan, L., and Chakraborty, S.: Diffusion of Li in olivine. Part I: experimental observations and a multi species diffusion model, Geochim. Cosmochim. Ac., 74, 274–292, https://doi.org/10.1016/j.gca.2009.10.016, 2010.
Druzhbin, D.: Silicon and oxygen volume diffusion in wadsleyite and implications to mantle transition zone rheology, Doctoral dissertation, Bayreuth, 2019.
Du Frane, W. L. and Tyburczy, J. A.: Deuterium-hydrogen exchange in olivine: implications for point defects and electrical conductivity, Geochem. Geophys. Geosyst., 13, Q03004, https://doi.org/10.1029/2011gc003895, 2012.
Dziewonski, A. M. and Anderson, D. L.: Preliminary reference Earth model, Phys. Earth Planet. In., 25, 297–356, https://doi.org/10.1016/0031-9201(81)90046-7, 1981.
Evans, R. L., Hirth, G., Baba, K., Forsyth, D., Chave, A., and Mackie, R.: Geophysical evidence from the MELT area for compositional controls on oceanic plates, Nature, 437, 249–252, https://doi.org/10.1038/nature04014, 2005.
Farla, R., Amulele, G., Girard, J., Miyajima, N., and Karato, S. I.: High-pressure and high-temperature deformation experiments on polycrystalline wadsleyite using the rotational Drickamer apparatus, Phys. Chem. Mineral., 42, 541–558, https://doi.org/10.1007/s00269-015-0742-0, 2015.
Farver, J. R.: Oxygen and hydrogen diffusion in minerals, Rev. Mineral. Geochem., 72, 447–507, https://doi.org/10.2138/rmg.2010.72.10, 2010.
Faul, U. H., Cline II, C. J., David, E. C., Berry, A. J., and Jackson, I.: Titanium-hydroxyl defect-controlled rheology of the Earth's upper mantle, Earth Planet. Sc. Lett., 452, 227–237, https://doi.org/10.1016/j.epsl.2016.07.016, 2016.
Fei, H. and Katsura, T.: Pressure dependence of proton incorporation and water solubility in olivine, J. Geophys. Res., 125, e2019JB018813, https://doi.org/10.1029/2019JB018813, 2020.
Fei, H., Hegoda, C., Yamazaki, D., Wiedenbeck, M., Yurimoto, H., Shcheka, S., and Katsura, T.: High silicon self-diffusion coefficient in dry forsterite, Earth Planet. Sc. Lett., 345, 95–103, https://doi.org/10.1016/j.epsl.2012.06.044, 2012.
Fei, H., Wiedenbeck, M., Yamazaki, D., and Katsura, T.: Small effect of water on upper-mantle rheology based on silicon self-diffusion coefficients, Nature, 498, 213–215, https://doi.org/10.1038/nature12193, 2013.
Fei, H., Wiedenbeck, M., Yamazaki, D., and Katsura, T.: No effect of water on oxygen self-diffusion rate in forsterite, J. Geophys. Res., 119, 7598–7606, https://doi.org/10.1002/2014JB011141, 2014.
Fei, H., Koizumi, S., Sakamoto, N., Hashiguchi, M., Yurimoto, H., Marquardt, K., Miyajima, N., Yamazaki, D., and Katsura, T.: New constraints on upper mantle creep mechanism inferred from silicon grain-boundary diffusion rates, Earth Planet. Sc. Lett., 433, 350–359, https://doi.org/10.1016/j.epsl.2015.11.014, 2016.
Fei, H., Yamazaki, D., Sakurai, M., Miyajima, N., Ohfuji, H., Katsura, T., and Yamamoto, T.: A nearly water-saturated mantle transition zone inferred from mineral viscosity, Sci. Adv., 3, e1603024, https://doi.org/10.1126/sciadv.1603024, 2017.
Fei, H., Koizumi, S., Sakamoto, N., Hashiguchi, M., Yurimoto, H., Marquardt, K., and Katsura, T.: Mg lattice diffusion in iron-free olivine and implications to conductivity anomaly in the oceanic asthenosphere, Earth Planet. Sc. Lett., 484, 204–212, https://doi.org/10.1016/j.epsl.2017.12.020, 2018.
Fei, H., Druzhbin, D., and Katsura, T.: The effect of water on ionic conductivity in olivine, J. Geophys. Res., 125, e2019JB019313, https://doi.org/10.1029/2019JB019313, 2020.
Ferriss, E., Plank, T., Newcombe, M., Walker, D., and Hauri, E.: Rates of dehydration of olivines from San Carlos and Kilauea Iki, Geochim. Cosmochim. Ac., 242, 165–190, https://doi.org/10.1016/j.gca.2018.08.050, 2018.
Freitas, D., Manthilake, G., Schiavi, F., Chantel, J., Bolfan-Casanova, N., Bouhifd, M. A., and Andrault, D.: Experimental evidence supporting a global melt layer at the base of the Earth's upper mantle, Nat. Commun., 8, 2186, https://doi.org/10.1038/s41467-017-02275-9, 2017.
Freitas, D., Manthilake, G., Chantel, J., Bouhifd, M. A., and Andrault, D.: Simultaneous measurements of electrical conductivity and seismic wave velocity of partially molten geological materials: effect of evolving melt texture, Phys. Chem. Mineral., 46, 535–551, https://doi.org/10.1007/s00269-019-01021-5, 2019.
Frost, H. J. and Ashby, M. F. (Eds.): Deformation Mechanism Maps, Pergamon Press, Oxford, 1982.
Gardés, E., Gaillard, F., and Tarits, P.: Toward a unified hydrous olivine electrical conductivity law, Geochem. Geophys. Geosyst., 15, 4984–5000, https://doi.org/10.1002/2014GC005496, 2014.
Gardés, E., Gaillard, F., and Tarits, P.: Comment to “High and highly anisotropic electrical conductivity of the asthenosphere due to hydrogen diffusion in olivine” by Dai and Karato [Earth Planet. Sc. Lett. 408 (2014) 79–86], Earth Planet. Sc. Lett., 427, 296–299, https://doi.org/10.1016/j.epsl.2015.06.041, 2015.
Ge, J. H., Zhang, B. H., Xiong, Z. L., He, L. F., and Li, H. P.: Thermal properties of harzburgite and dunite at 0.8–3 GPa and 300–823 K and implications for the thermal evolution of Tibet, Geosci. Frontiers, 12, 947–956, https://doi.org/10.1016/j.gsf.2020.01.008, 2021.
Girard, J., Chen, J., Raterron, P., and Holyoke, C. W.: Hydrolytic weakening of olivine at mantle pressure: Evidence of [100](010) slip system softening from single-crystal deformation experiments, Phys. Earth Planet. In., 216, 12–20, https://doi.org/10.1016/j.pepi.2012.10.009, 2013.
Girard, J., Amulele, G., Farla, R., Mohiuddin, A., and Karato, S. I.: Shear deformation of bridgmanite and magnesiowüstite aggregates at lower mantle conditions, Science, 351, 144–147, https://doi.org/10.1126/science.aad3113, 2016.
Gouriet, K., Cordier, P., Garel, F., Thoraval, C., Demouchy, S., Tommasi, A., and Carrez, P.: Dislocation dynamics modelling of the power-law breakdown in olivine single crystals: Toward a unified creep law for the upper mantle, Earth Planet. Sc. Lett., 506, 282–291, https://doi.org/10.1016/j.epsl.2018.10.049, 2019.
Gu, X. Y., Wang, P. Y., Kuritani, T., Hanski, E., Xia, Q. K., Wan, Q. Y.: Low water content in the mantle source of the Hainan plume as a factor inhibiting the formation of a large igneous province, Earth Planet. Sc. Lett., 515, 221–230, https://doi.org/10.1016/j.epsl.2019.03.034, 2019.
Hae, R., Ohtani, E., Kubo, T., Koyama, T., and Utada, H.: Hydrogen diffusivity in wadsleyite and water distribution in the mantle transition zone, Earth Planet. Sc. Lett., 243, 141–148, https://doi.org/10.1016/j.epsl.2005.12.035, 2006.
Hansen, L. N., Zimmerman, M. E., and Kohlstedt, D. L.: Grain boundary sliding in San Carlos olivine: Flow law parameters and crystallographic-preferred orientation, J. Geophys. Res., 116, B08201, https://doi.org/10.1029/2011jb008220, 2011.
Hier-Majumder, S., Anderson, I. M., and Kohlstedt, D. L.: Influence of protons on Fe-Mg interdiffusion in olivine, J. Geophys. Res., 110, 2004JB003292, https://doi.org/10.1029/2004JB003292, 2005.
Higo, Y., Inoue, T., Irifune, T., Funakoshi, K. I., and Li, B.: Elastic wave velocities of (Mg0.91Fe0.09)2SiO4 ringwoodite under P-T conditions of the mantle transition region, Phys. Earth Planet. In., 166, 167–174, https://doi.org/10.1016/j.pepi.2008.01.003, 2008.
Hirschmann, M. M.: Partial melt in the oceanic low velocity zone, Phys. Earth Planet. In., 179, 60–71, https://doi.org/10.1016/j.pepi.2009.12.003, 2010.
Hirth, G. and Kohlstedt, D. L.: Experimental constraints on the dynamics of the partially molten upper mantle: Deformation in the diffusion creep regime, J. Geophys. Res., 100, 1981–2001, https://doi.org/10.1029/94JB02128, 1995.
Hirth, G. and Kohlstedt, D. L.: Rheology of the upper mantle and the mantle wedge: A view from the experimentalists, in: Inside the Subduction Factory, edited by: Eiler, J., Geophys. Monogr. Ser., AGU, Washington, D.C., 138, 83–105, https://doi.org/10.1029/138GM06, 2003.
Hofmeister, A. M.: Mantle values of thermal conductivity and the geotherm from phonon lifetimes, Science, 283, 1699–1706, https://doi.org/10.1126/science.283.5408.1699, 1999.
Hofmeister, A. M.: Pressure dependence of thermal transport properties, P. Natl. Acad. Sci. USA, 104, 9192–9197, https://doi.org/10.1073/pnas.0610734104, 2007.
Hofmeister, A. M., Branlund, J. M., and Pertermann, M.: Properties of rock and minerals-thermal conductivity of the Earth, in: Treatise on Geophysics, edited by: Schubert, G., Elsevier, Amsterdam, 543–577, https://doi.org/10.1016/B978-044452748-6.00048-1, 2007.
Holzapfel, C., Chakraborty, S., Rubie, D. C., and Frost, D. J.: Fe-Mg interdiffusion in wadsleyite: the role of pressure, temperature and composition and the magnitude of jump in diffusion rates at the 410 km discontinuity, Phys. Earth Planet. In., 172, 28–33, https://doi.org/10.1016/j.pepi.2008.09.005, 2009.
Houser, C.: Global seismic data reveal little water in the mantle transition zone, Earth Planet. Sc. Lett., 448, 94–101, https://doi.org/10.1016/j.epsl.2016.04.018, 2016.
Houser, C. and Williams, Q.: Reconciling Pacific 410 and 660 km discontinuity topography, transition zone shear velocity patterns, and mantle phase transitions, Earth Planet. Sc. Lett., 296, 255–266, https://doi.org/10.1016/j.epsl.2010.05.006, 2010.
Huang, X., Xu, Y., and Karato, S. I.: Water content in the transition zone from electrical conductivity of wadsleyite and ringwoodite, Nature, 434, 746–749, https://doi.org/10.1038/nature03426, 2005.
Hustoft, J., Amulele, G., Ando, J. I., Otsuka, K., Du, Z., Jing, Z., and Karato, S. I.: Plastic deformation experiments to high strain on mantle transition zone minerals wadsleyite and ringwoodite in the rotational Drickamer apparatus, Earth Planet. Sc. Lett., 361, 7–15, https://doi.org/10.1016/j.epsl.2012.11.028, 2013.
Ichiki, M., Uyeshima, M., Utada, H., Zhao, G., Tang, J., and Ma, M.: Upper mantle conductivity structure of the back-arc region beneath northeastern China, Geophys. Res. Lett., 28, 3773–3776, https://doi.org/10.1029/2001GL012983, 2001.
Ichiki, M., Baba, K., Obayashi, M., and Utada, H.: Water content and geotherm in the upper mantle above the stagnant slab: interpretation of electrical conductivity and seismic P-wave velocity models, Phys. Earth Planet. In., 155, 1–15, https://doi.org/10.1016/j.pepi.2005.09.010, 2006.
Ingrin, J. and Blanchard, M.: Diffusion of hydrogen in minerals, Rev. Mineral. Geochem., 62, 291–320, https://doi.org/10.2138/rmg.2006.62.13, 2006.
Inoue, T., Yurimoto, H., and Kudoh, Y.: Hydrous modified spinel, Mg1.75SiH0.5O4, a new water reservoir in the mantle transition zone, J. Geophys. Res., 22, 117–120, https://doi.org/10.1029/94GL02965, 1995.
Jackson, J. M., Sinogeikin, S. V., and Bass, J. D.: Sound velocities and elastic properties of γ-Mg2SiO4 to 873 K by Brillouin spectroscopy, Am. Mineral., 85, 296–303, https://doi.org/10.2138/am-2000-2-306, 2000.
Jacobsen, S. D. and Smyth, J. R.: Effect of water on the sound velocities of ringwoodite in the transition zone, in: Earth's Deep Water Cycle, edited by: Jacobsen, S. D. and van der Lee, S., American Geophysical Union, Washington, D.C., 131–145, https://doi.org/10.1029/168GM10, 2006.
Jacobsen, S. D., Smyth, J. R., Spetzler, H., Holl, C. M., and Frost, D. J.: Sound velocities and elastic constants of iron-bearing hydrous ringwoodite, Phys. Earth Planet Inter., 143–144, 47–56, https://doi.org/10.1016/j.pepi.2003.07.019, 2004.
Jollands, M. C., Padrón-Navarta, J. A., Hermann, J., and O'Neill, H. S. C.: Hydrogen diffusion in Ti-doped forsterite and the preservation of metastable point defects, Am. Mineral., 101, 1571–1583, https://doi.org/10.2138/am-2016-55681571, 2016.
Jollands, M. C., Kempf, E., Hermann, J., and Müntener, O.: Coupled inter-site reaction and diffusion: Rapid dehydrogenation of silicon vacancies in natural olivine, Geochim. Cosmochim. Ac., 262, 220–242, https://doi.org/10.1016/j.gca.2019.07.025, 2019.
Jones, A. G.: Reconciling different equations for proton conduction using the Meyer-Neldel compensation rule, Geochem. Geophys. Geosyst., 15, 337–349, https://doi.org/10.1002/2013GC004911, 2014.
Jones, A. G.: Proton conduction and hydrogen diffusion in olivine: an attempt to reconcile laboratory and field observations and implications for the role of grain boundary diffusion in enhancing conductivity, Phys. Chem. Mineral., 43, 237–265, https://doi.org/10.1007/s00269-015-0790-5, 2016.
Jung, H. and Karato, S. I.: Water-induced fabric transitions in olivine, Science, 293, 1460–1463, https://doi.org/10.1126/science.1062235, 2001.
Jung, H., Katayama, I., Jiang, Z., Hiraga, T., and Karato, S. I.: Effect of water and stress on the lattice-preferred orientation of olivine, Tectonophysics, 421, 1–22, https://doi.org/10.1016/j.tecto.2006.02.011, 2006.
Karato, S. I.: The role of hydrogen in the electrical conductivity of the upper mantle, Nature, 347, 272–273, https://doi.org/10.1038/347272a0, 1990.
Karato, S. I. (Ed.): Deformation of earth materials: introduction to the rheology of the solid earth, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511804892, 2008.
Karato, S. I.: Water distribution across the mantle transition zone and its implications for global material circulation, Earth Planet. Sc. Lett., 301, 413–423, https://doi.org/10.1016/j.epsl.2010.11.038, 2011.
Karato, S. I.: Water in the evolution of the Earth and other terrestrial planets, in: Treatise on Geophysics, edited by: Schubert, G., Elsevier, Amsterdam, 105–144, https://doi.org/10.1016/B978-0-444-53802-4.00156-1, 2015.
Karato, S. I.: Some remarks on hydrogen-assisted electrical conductivity in olivine and other minerals, Prog. Earth Planet. Sci., 6, 55, https://doi.org/10.1186/s40645-019-0301-2, 2019.
Karato, S. and Jung, H.: Effects of pressure on high-temperature dislocation creep in olivine polycrystals, Philos. Mag. A., 83, 401–414, https://doi.org/10.1080/0141861021000025829, 2003.
Karato, S. I. and Dai, L.: Comments on “Electrical conductivity of wadsleyite as a function of temperature and water content” by Manthilake et al., Phys. Earth Planet. In., 174, 19–21, https://doi.org/10.1016/j.pepi.2009.01.011, 2009.
Karato, S. I., Paterson, M. S., and Fitz Gerald, J. D.: Rheology of synthetic olivine aggregates: influence of grain-size and water, J. Geophys. Res., 91, 8151–8176, https://doi.org/10.1029/JB091iB08p08151, 1986.
Karato, S. I., Riedel, M. R., and Yuen, D. A.: Rheological structure and deformation of subducted slabs in the mantle transition zone: implications for mantle circulation and deep earthquakes, Phys. Earth Planet. In., 127, 83–108, https://doi.org/10.1016/S0031-9201(01)00223-0, 2001.
Katayama, I. and Karato, S. I.: Effects of water and iron content on the rheological contrast between garnet and olivine, Phys. Earth Planet. In., 166, 57–66, https://doi.org/10.1016/j.pepi.2007.10.004, 2008a.
Katayama, I. and Karato, S. I.: Low-temperature, high-stress deformation of olivine under water-saturated conditions, Phys. Earth Planet. In., 168, 125–133, https://doi.org/10.1016/j.pepi.2008.05.019, 2008b.
Katayama, I., Jung, H., and Karato, S. I.: New type of olivine fabric from deformation experiments at modest water content and low stress, Geology, 32, 1045–1048, https://doi.org/10.1130/G20805.1, 2004.
Katsura, T.: Thermal diffusivity of olivine under upper mantle conditions, Geophys. J. Inter., 122, 63–69, https://doi.org/10.1111/j.1365-246X.1995.tb03536.x, 1995.
Katsura, T., Yoneda, A., Yamazaki, D., Yoshino, T., and Ito, E.: Adiabatic temperature profile in the mantle, Phys. Earth Planet. In., 183, 212–218, https://doi.org/10.1016/j.pepi.2010.07.001, 2010.
Kawakatsu, H., Kumar, P., Takei, Y., Shinohara, M., Kanazawa, T., Araki, E., and Suyehiro, K.: Seismic evidence for sharp lithosphere-asthenosphere boundaries of oceanic plates, Science, 324, 499–502, https://doi.org/10.1126/science.1169499, 2009.
Kawazoe, T., Karato, S. I., Otsuka, K., Jing, Z., and Mookherjee, M.: Shear deformation of dry polycrystalline olivine under deep upper mantle conditions using a rotational Drickamer apparatus (RDA), Phys. Earth Planet. In., 174, 128–137, https://doi.org/10.1016/j.pepi.2008.06.027, 2009.
Kawazoe, T., Karato, S. I., Ando, J., Jing, Z., Otsuka, K., and Hustoft, J. W.: Shear deformation of polycrystalline wadsleyite up to 2100 K at 14–17 GPa using a rotational Drickamer apparatus (RDA), J. Geophys. Res., 115, B08208, https://doi.org/10.1029/2009JB007096, 2010.
Kawazoe, T., Ohuchi, T., Nishihara, Y., Nishiyama, N., Fujino, K., and Irifune, T.: Seismic anisotropy in the mantle transition zone induced by shear deformation of wadsleyite, Phys. Earth Planet. In., 216, 91–98, https://doi.org/10.1016/j.pepi.2012.12.005, 2013.
Kawazoe, T., Nishihara, Y., Ohuchi, T., Miyajima, N., Maruyama, G., Higo, Y., and Irifune, T.: Creep strength of ringwoodite measured at pressure–temperature conditions of the lower part of the mantle transition zone using a deformation–DIA apparatus, Earth Planet. Sc. Lett., 454, 10–19, https://doi.org/10.1016/j.epsl.2016.08.011, 2016.
Kelbert, A., Schultz, A., and Egbert, G.: Global electromagnetic induction constraints on transition-zone water content variations, Nature, 460, 1003–1006, https://doi.org/10.1038/nature08257, 2009.
Kennett, B. L. N., Engdahl, E. R., and Buland, R.: Constraints on seismic velocities in the earth from travel-times, Geophys. J. Inter., 122, 108–124, https://doi.org/10.1111/j.1365-246X.1995.tb03540.x, 1995.
Kohlstedt, D. L.: The role of water in high-temperature rock deformation, Rev. Miner. Geochem., 62, 377–396, https://doi.org/10.2138/rmg.2006.62.16, 2006.
Kohlstedt, D. L., Keppler, H., and Rubie, D. C.: Solubility of water in the α, β and γ phases of (Mg,Fe)2SiO4, Contrib. Mineral. Petrol., 123, 345–357, https://doi.org/10.1007/s004100050161, 1996.
Kubo, T., Shimojuku, A., and Ohtani, E.: Mg-Fe interdiffusion rates in wadsleyite and the diffusivity jump at the 410-km discontinuity, Phys. Chem. Mineral., 31, 456–464, https://doi.org/10.1007/s00269-004-0412-0, 2004.
Kudo, T., Ohtani, E., Hae, R., and Shimojuku, R.: Diffusion of hydrogen in ringwoodite, in: AIP conference proceedings, American Institute of Physics, New York, 148–149, https://doi.org/10.1063/1.2207093, 2006.
Kustowski, B., Ekström, G., and Dziewoński, A. M.: Anisotropic shear wave velocity structure of the Earth's mantle: A global model, J. Geophys. Res., 113, B06306, https://doi.org/10.1029/2007JB005169, 2008.
Kuvshinov, A. and Olsen, N.: A global model of mantle conductivity derived from 5 years of CHAMP, Ørsted, and SAC-C magnetic data, Geophys. Res. Lett., 33, L18301, https://doi.org/10.1029/2006GL027083, 2006.
Le Losq, C., Jollands, M. C., Tollan, P. M. E., Hawkins, R., and O'Neill, H. S. C.: Point defect populations of forsterite revealed by two-stage metastable hydroxylation experiments, Contrib. Mineral. Petrol., 174, 53, https://doi.org/10.1007/s00410-019-1590-6, 2019.
Li, B.: Compressional and shear wave velocities of ringwoodite γ-Mg2SiO4 to 12 GPa, Am. Mineral., 88, 1312–1317, https://doi.org/10.2138/am-2003-8-913, 2003.
Li, B. and Liebermann, R. C.: Sound velocities of wadsleyite β-(Mg0.88Fe0.12)2SiO4 to 10 GPa, Am. Mineral., 85, 292–295, https://doi.org/10.2138/am-2000-2-305, 2000.
Li, B. and Liebermann, R. C.: Study of the Earth's interior using measurements of sound velocities in minerals by ultrasonic interferometry, Phys. Earth Planet. In., 233, 135–153, https://doi.org/10.1016/j.pepi.2014.05.006, 2014.
Li, B., Gwanmesia, G. D., and Liebermann, R. C.: Sound velocities of olivine and beta polymorphs of Mg2SiO4 at Earth's transition zone pressures, Geophys. Res. Lett., 23, 2259–2262, https://doi.org/10.1029/96GL02084, 1996.
Li, B., Kung, J., and Liebermann, R. C.: Modern techniques in measuring elasticity of Earth materials at high pressure and high temperature using ultrasonic interferometry in conjunction with synchrotron X-radiation in multi-anvil apparatus, Phys. Earth Planet. In., 143, 559–574, https://doi.org/10.1016/j.pepi.2003.09.020, 2004.
Liu, H. Y., Zhu, Q., and Yang, X. Z.: Electrical conductivity of OH-bearing omphacite and garnet in eclogite: The quantitative dependence on water content, Contrib. Mineral. Petrol., 174, 57, https://doi.org/10.1007/s00410-019-1593-3, 2019.
Liu, W., Kung, J., and Li, B.: Elasticity of San Carlos olivine to 8 GPa and 1073 K, Geophys. Res. Lett., 32, L16301, https://doi.org/10.1029/2005GL023453, 2005.
Liu, W., Kung, J., Li, B., Nishiyama, N., and Wang, Y.: Elasticity of (Mg0.87Fe0.13)2SiO4 wadsleyite to 12 GPa and 1073 K, Phys. Earth Planet. In., 174, 98–104, https://doi.org/10.1016/j.pepi.2008.10.020, 2009.
Manthilake, G., Matsuzaki, T., Yoshino, T., Yamashita, S., Ito, E., and Katsura, T.: Electrical conductivity of wadsleyite as a function of temperature and water content, Phys. Earth Planet. In., 174, 10–18, https://doi.org/10.1016/j.pepi.2009.01.012, 2009.
Mao, Z., Jacobsen, S. D., Jiang, F., Smyth, J. R., Holl, C. M., Frost, D. J., and Duffy, T. S.: Velocity crossover between hydrous and anhydrous forsterite at high pressures, Earth Planet. Sc. Lett., 293, 250–258, https://doi.org/10.1016/j.epsl.2010.02.025, 2010.
Mao, Z., Jacobsen, S. D., Frost, D. J., McCammon, C. A., Hauri, E. H., and Duffy, T. S.: Effect of hydration on the single-crystal elasticity of Fe-bearing wadsleyite to 12 GPa, Am. Mineral., 96, 1606–1612, https://doi.org/10.2138/am.2011.3807, 2011.
Mao, Z., Lin, J. F., Jacobsen, S. D., Duffy, T. S., Chang, Y. Y., Smyth, J. R., Frost, D. J., Hauri, E. H., and Prakapenka, V. B.: Sound velocities of hydrous ringwoodite to 16 GPa and 673 K, Earth Planet. Sc. Lett., 331, 112–119, https://doi.org/10.1016/j.epsl.2012.03.001, 2012.
Mao, Z., Fan, D., Lin, J. F., Yang, J., Tkachev, S. N., Zhuravlev, K., and Prakapenka, V. B.: Elasticity of single-crystal olivine at high pressures and temperatures, Earth Planet. Sc. Lett., 426, 204–215, https://doi.org/10.1016/j.epsl.2015.06.045, 2015.
Marzotto, E., Hsieh, W. P., Ishii, T., Chao, K. H., Golabek, G. J., Thielmann, M., and Ohtani, E.: Effect of water on lattice thermal conductivity of ringwoodite and its implications for the thermal evolution of descending slabs, Geophys. Res. Lett., 47, e2020GL087607, https://doi.org/10.1029/2020GL087607, 2020.
Mayama, N., Suzuki, I., Saito, T., Ohno, I., Katsura, T., and Yoneda, A.: Temperature dependence of the elastic moduli of ringwoodite, Phys. Earth Planet. Inter., 148, 353–359, https://doi.org/10.1016/j.pepi.2004.09.007, 2005.
Mehrer, H. (Ed.): Diffusion in solids: fundamentals, methods, materials, diffusion-controlled processes, Springer, Berlin, 2007.
Mei, S. and Kohlstedt, D. L.: Influence of water on plastic deformation of olivine aggregates: 1. Diffusion creep regime, J. Geophys. Res., 105, 21457–21469, https://doi.org/10.1029/2000JB900179, 2000a.
Mei, S. and Kohlstedt, D. L.: Influence of water on plastic deformation of olivine aggregates: 2. Dislocation creep regime, J. Geophys. Res., 105, 21471–21481, https://doi.org/10.1029/2000JB900180, 2000b.
Moine, B. N., Bolfan-Casanova, N., Radu, I. B., Ionov, D. A., Costin, G., Korsakov, A. V., Golovin, A. V., Oleinikov, O. B., Deloule, E., and Cottin, J. Y.: Molecular hydrogen in minerals as a clue to interpret ∂D variations in the mantle, Nat. Commun., 11, 3614, https://doi.org/10.1038/s41467-020-17442-8, 2020.
Mosenfelder, J. L., Deligne, N. I., Asimow, P. D. and Rossman, G. R.: Hydrogen incorporation in olivine from 2–12 GPa, Am. Mineral., 91, 285–294, https://doi.org/10.2138/am.2006.1943, 2006.
Mrosko, M., Lenz, S., McCammon, C. A., Taran, M., Wirth, R., and Koch-Müller, M.: Hydrogen incorporation and the oxidation state of iron in ringwoodite: A spectroscopic study, Am. Mineral., 98, 629–636, https://doi.org/10.2138/am.2013.4245, 2013.
Naif, S., Key, K., Constable, S., and Evans, R. L.: Melt-rich channel observed at the lithosphere–asthenosphere boundary, Nature, 495, 356–359, https://doi.org/10.1038/nature11939, 2013.
Ni, H., Hui, H., and Steinle-Neumann, G.: Transport properties of silicate melts, Rev. Geophys., 53, 715–744, https://doi.org/10.1002/2015RG000485, 2015.
Nishihara, Y., Shinmei, T., and Karato, S. I.: Effects of chemical environments on the hydrogen-defects in wadsleyite, Am. Mineral., 93, 831–843, https://doi.org/10.2138/am.2008.2653, 2008.
Nishihara, Y., Ohuchi, T., Kawazoe, T., Spengler, D., Tasaka, M., Kikegawa, T., and Ohtani, E.: Rheology of fine-grained forsterite aggregate at deep upper mantle conditions, J. Geophys. Res., 119, 253–273, https://doi.org/10.1002/2013JB010473, 2014.
Novella, D., Jacobsen, B., Weber, P. K., Tyburczy, J. A., Ryerson, F. J., and Du Frane, W. L.: Hydrogen self-diffusion in single crystal olivine and electrical conductivity of the Earth's mantle, Sci. Rep.-UK, 7, 1–10, https://doi.org/10.1038/s41598-017-05113-6, 2017.
Núñez Valdez, M., Wu, Z., Yu, Y. G., Revenaugh, J., and Wentzcovitch, R. M.: Thermoelastic properties of ringwoodite (FexMg1−x)2SiO4: Its relationship to the 520 km seismic discontinuity, Earth Planet. Sc. Lett., 351–352, 115–122, https://doi.org/10.1016/j.epsl.2012.07.024, 2012.
Ohtani, E., Litasov, D. K., Hosoya, T., Kubo, T., and Kondo, T.: Water transport into the deep mantle and formation of a hydrous transition zone, Phys. Earth Planet. In., 143–144, 255–269, https://doi.org/10.1016/j.pepi.2003.09.015, 2004.
Ohuchi, T. and Irifune, T.: Development of A-type olivine fabric in water-rich deep upper mantle, Earth Planet. Sc. Lett., 362, 20–30, https://doi.org/10.1016/j.epsl.2012.11.029, 2013.
Ohuchi, T., Kawazoe, T., Nishihara, Y., and Irifune, T.: Change of olivine a-axis alignment induced by water: Origin of seismic anisotropy in subduction zones, Earth Planet. Sc. Lett., 317, 111–119, https://doi.org/10.1016/j.epsl.2011.11.022, 2012.
Ohuchi, T., Kawazoe, T., Higo, Y., and Suzuki, A.: Flow behavior and microstructures of hydrous olivine aggregates at upper mantle pressures and temperatures, Contrib. Mineral. Petrol., 172, 65, https://doi.org/10.1007/s00410-017-1375-8, 2017.
Ohuchi, T., Lei, X., Higo, Y., Tange, Y., Sakai, T., and Fujino, K.: Semi-brittle behavior of wet olivine aggregates: the role of aqueous fluid in faulting at upper mantle pressures, Contrib. Mineral. Petrol., 173, 88, https://doi.org/10.1007/s00410-018-1515-9, 2018.
Osako, M., Ito, E., and Yoneda, A.: Simultaneous measurements of thermal conductivity and thermal diffusivity for garnet and olivine under high pressure, Phys. Earth Planet. In., 143–144, 311–320, https://doi.org/10.1016/j.pepi.2003.10.010, 2004.
Osako, M., Yoneda, A., and Ito, E.: Thermal diffusivity, thermal conductivity and heat capacity of serpentine (antigorite) under high pressure, Phys. Earth Planet. In., 183, 229–233, https://doi.org/10.1016/j.pepi.2010.07.005, 2010.
Padrón-Navarta, J. A. and Hermann, J.: A subsolidus olivine water solubility equation for the Earth's upper mantle, J. Geophys. Res., 122, 9862–9880, https://doi.org/10.1002/2017JB014510, 2017.
Padrón-Navarta, J. A., Hermann, J., and O'Neill, H. S. C.: Site-specific hydrogen diffusion rates in forsterite, Earth Planet. Sc. Lett., 392, 100–112, https://doi.org/10.1016/j.epsl.2014.01.055, 2014.
Paterson, M. S.: The determination of hydroxyl by infrared absorption in quartz, silicate glasses and similar materials, Bull. Mineral., 105, 20–29, https://doi.org/10.3406/bulmi.1982.7582, 1982.
Pearson, D. G., Brenker, F. E., Nestola, F., McNeill, J., Nasdala, L., Hutchison, M. T., Matveev, S., Mather, K., Silversmit, G., Schmitz, S., Vekemans, B., and Vincze, L.: Hydrous mantle transition zone indicated by ringwoodite included within diamond, Nature, 507, 221–224, https://doi.org/10.1038/nature13080, 2014.
Poe, B. T., Romano, C., Nestola, F., and Smyth, J. R.: Electrical conductivity anisotropy of dry and hydrous olivine at 8 GPa, Phys. Earth Planet. In., 181, 103–111, https://doi.org/10.1016/j.pepi.2010.05.003, 2010.
Pommier, A.: Interpretation of magnetotelluric results using laboratory measurements, Surv. Geophys., 35, 41–84, https://doi.org/10.1007/s10712-013-9226-2, 2013.
Pommier, A., Leinenweber, K., Kohlstedt, D. L., Qi, C., Garnero, E. J., Mackwell, S. J., and Tyburczy, J. A.: Experimental constraints on the electrical anisotropy of the lithosphere-asthenosphere system, Nature, 522, 202–206, https://doi.org/10.1038/nature14502, 2015.
Purevjav, N., Okuchi, T., Tomioka, N., Abe, J., and Harjo, S.: Hydrogen site analysis of hydrous ringwoodite in mantle transition zone by pulsed neutron diffraction, Geophys. Res. Lett., 41, 6718–6724, https://doi.org/10.1002/2014GL061448, 2014.
Purevjav, N., Okuchi, T., Tomioka, N., Wang, X., and Hoffmann, C.: Quantitative analysis of hydrogen sites and occupancy in deep mantle hydrous wadsleyite using single crystal neutron diffraction, Sci. Rep.-UK, 6, 34988, https://doi.org/10.1038/srep34988, 2016.
Revenaugh, J. and Jordan, T. H.: Mantle layering from ScS reverberations: 2. The transition zone, J. Geophys. Res., 96, 19763–19780, https://doi.org/10.1029/91JB01486, 1991.
Ritterbex, S., Carrez, P. H., Gouriet, K., and Cordier, P.: Modeling dislocation glide in Mg2SiO4 ringwoodite: Towards rheology under transition zone conditions, Phys. Earth Planet. In., 248, 20–29, https://doi.org/10.1016/j.pepi.2015.09.001, 2015.
Romano, C., Poe, B. T., Tyburczy, J., and Nestra, F.: Electrical conductivity of hydrous wadsleyite, Eur. J. Mineral., 21, 615–622, https://doi.org/10.1127/0935-1221/2009/0021-1933, 2009.
Schmandt, B., Jacobsen, S. D., Becker, T. W., Liu, Z., and Dueker, K. G.: Dehydration melting at the top of the lower mantle, Science, 344, 1265–1268, https://doi.org/10.1126/science.1253358, 2014.
Schmerr, N.: The Gutenberg discontinuity: Melt at the lithosphere–asthenosphere boundary, Science, 335, 1480–1483, https://doi.org/10.1126/science.1215433, 2012.
Schulze, K., Marquardt, H., Kawazoe, T., Ballaran, T. B., McCammon, C., Koch-Müller, M., Kurnosov, A., and Marquardt, K.: Seismically invisible water in Earth's transition zone? Earth Planet. Sc. Lett., 498, 9–16, https://doi.org/10.1016/j.epsl.2018.06.021, 2018.
Shimizu, H., Koyama, T., Baba, H., and Utada, H.: Revised 1-D mantle electrical conductivity structure beneath the north Pacific, Geophys. J. Inter., 180, 1030–1048, https://doi.org/10.1111/j.1365-246X.2009.04466.x, 2010.
Shimojuku, A., Kubo, T., Ohtani, E., and Yurimoto, H.: Silicon self-diffusion in wadsleyite: Implications for rheology of the mantle transition zone and subducting plates, Geophys. Res. Lett., 31, L13606, https://doi.org/10.1029/2004GL020002, 2004.
Shimojuku, A., Kubo, T., Ohtani, E., Nakamura, T., Okazaki, R., Chakraborty, S., and Dohmen, R.: Si and O diffusion in (Mg,Fe)2SiO4 wadsleyite and ringwoodite and its implication for rheology of the mantle transition zone, Earth Planet. Sc. Lett., 284, 103–112, https://doi.org/10.1016/j.epsl.2009.04.014, 2009.
Shimojuku, A., Kubo, T., Ohtani, E., Nakamura, T., and Okazaki, R.: Effects of hydrogen and iron on the silicon diffusivity of wadsleyite, Phys. Earth Planet. Inter., 183, 175–182, https://doi.org/10.1016/j.pepi.2010.09.011, 2010.
Sieminski, A., Debayle, E., and Lévêque, J. J.: Seismic evidence for deep low-velocity anomalies in the transition zone beneath West Antarctica, Earth Planet. Sc. Lett., 216, 645–661, https://doi.org/10.1016/S0012-821X(03)00518-1, 2003.
Sinogeikin, S. V., Bass, J. D., and Katsura, T.: Single-crystal elasticity of ringwoodite to high pressures and high temperatures: implications for 520 km seismic discontinuity, Phys. Earth Planet. In., 136, 41–66, https://doi.org/10.1016/S0031-9201(03)00022-0, 2003.
Smyth, J. R., Frost, D. J., Nestola, F., Holl, C. M., and Bromiley, G.: Olivine hydration in the deep upper mantle: Effects of temperature and silica activity, Geophys. Res. Lett., 33, L15301, https://doi.org/10.1029/2006GL026194, 2006.
Song, T. R. A., Helmberger, D. V., and Grand, S. P.: Low-velocity zone atop the 410-km seismic discontinuity in the northwestern United States, Nature, 427, 530–533, https://doi.org/10.1038/nature02231, 2004.
Stern, T. A., Henrys, S. A., Okaya, D., Louie, J. N., Savage, M. K., Lamb, S., Sato, H., Sutherland, R., and Iwasaki, T.: A seismic reflection image for the base of a tectonic plate, Nature, 518, 85–88, https://doi.org/10.1038/nature14146, 2015.
Sun, W., Yoshino, T., Sakamoto, N., and Yurimoto, H.: Hydrogen self-diffusivity in single crystal ringwoodite: implications for water content and distribution in the mantle transition zone, Geophys. Res. Lett., 42, 6582–6589, https://doi.org/10.1002/2015GL064486, 2015.
Sun, W., Yoshino, T., Sakamoto, N., and Yurimoto, H.: Supercritical fluid in the mantle transition zone deduced from H-D interdiffusion of wadsleyite, Earth Planet. Sc. Lett., 484, 309–317, https://doi.org/10.1016/j.epsl.2017.12.032, 2018.
Sun, W., Yoshino, T., Kuroda, M., Sakamoto, N., and Yurimoto, H.: H-D interdiffusion in single-crystal olivine: Implications for electrical conductivity in the upper mantle, J. Geophys. Res., 124, 5696–5707, https://doi.org/10.1029/2019JB017576, 2019.
Tachibana, S., Tamada, S., Kawasaki, H., Ozawa, K., and Nagahara, H.: Interdiffusion of Mg-Fe in olivine at 1400–1600 ∘C and 1 atm total pressure, Phys. Chem. Mineral., 40, 511–519, https://doi.org/10.1007/s00269-013-0588-2, 2013.
Tarits, P., Hautot, S., and Perrier, F.: Water in the mantle: results from electrical conductivity beneath the French Alps, Geophys. Res. Lett., 31, L06612, https://doi.org/10.1029/2003GL019277, 2004.
Tasaka, M., Zimmerman, M. E., and Kohlstedt, D. L.: Creep behavior of Fe-bearing olivine under hydrous conditions, J. Geophys. Res., 120, 6039–6057, https://doi.org/10.1002/2015JB012096, 2015.
Tasaka, M., Zimmerman, M. E., and Kohlstedt, D. L.: Evolution of the rheological and microstructural properties of olivine aggregates during dislocation creep under hydrous conditions, J. Geophys. Res., 121, 92–113, https://doi.org/10.1002/2015jb012134, 2016.
Tauzin, B., Debayle, E., and Wittlinger, G.: Seismic evidence for a global low-velocity layer within the Earth's upper mantle, Nat. Geosci., 3, 718–721, https://doi.org/10.1038/ngeo969, 2010.
Tielke, J. A., Zimmerman, M. E., and Kohlstedt, D. L.: Hydrolytic weakening in olivine single crystals, J. Geophys. Res., 122, 3465–3479, https://doi.org/10.1002/2017JB014004, 2017.
Tielke, J., Mecklenburgh, J., Mariani, E., and Wheeler, J.: The influence of water on the strength of olivine dislocation slip systems, J. Geophys. Res., 124, 6542–6559, https://doi.org/10.1029/2019JB017436, 2019.
Toffelmier, D. A. and Tyburczy, J. A.: Electromagnetic detection of a 410-km deep melt layer in the southwestern United States, Nature, 447, 991–994, https://doi.org/10.1038/nature05922, 2007.
Tollan, P. M. E., Smith, R., O'Neill, H. S. C., and Hermann, J.: The responses of the four main substitution mechanisms of H in olivine to H2O activity at 1050 ∘C and 3 GPa, Prog. Earth Planet. Sci., 4, 14, https://doi.org/10.1186/s40645-017-0128-7, 2017.
Tollan, P. M. E., O'Neill, H. S. C., and Hermann, J.: The role of trace elements in controlling H incorporation in San Carlos olivine, Contrib. Mineral. Petrol., 173, 89, https://doi.org/10.1007/s00410-018-1517-7, 2018.
Tommasi, A., Gibert, B., Seipold, U., and Mainprice, D.: Anisotropy of thermal diffusivity in the upper mantle, Nature, 411, 783–786, https://doi.org/10.1038/35081046, 2001.
Tschauner, O., Huang, S., Greenberg, E., Prakapenka, V. B., Ma, C., Rossman, G. R., Shen, A. H., Zhang, D., Newville, M., Lanzirotti, A., and Tait, K.: Ice-VII inclusions in diamonds: Evidence for aqueous fluid in Earth's deep mantle, Science, 359, 1136–1139, https://doi.org/10.1126/science.aao3030, 2018.
Utada, H., Koyama, T., Shimizu, H., and Chave, A. D.: A semi-global reference model for electrical conductivity in the mid-mantle beneath the north Pacific region, Geophys. Res. Lett., 30, 1194, https://doi.org/10.1029/2002GL016092, 2003.
Walker, A. M., Hermann, J., Berry, A. J., and O'Neill, H. S. C.: Three water sites in upper mantle olivine and the role of titanium in the water weakening mechanism, J. Geophys. Res., 112, B05211, https://doi.org/10.1029/2006JB004620, 2007.
Wallis, D., Hansen, L. N., Tasaka, M., Kumamoto, K. M., Parsons, A. J., Lloyd, G. E., Kohlstedt, D. L., and Wilkinson, A. J.: The impact of water on slip system activity in olivine and the formation of bimodal crystallographic preferred orientations, Earth Planet. Sc. Lett., 508, 51–61, https://doi.org/10.1016/j.epsl.2018.12.007, 2019.
Wang, D., Mookherjee, M., Xu, Y., and Karato, S. I.: The effect of water on the electrical conductivity of olivine, Nature, 443, 977–980, https://doi.org/10.1038/nature05256, 2006.
Wang, J., Sinogeikin, S. V., Inoue, T., and Bass, J. D.: Elastic properties of hydrous ringwoodite at high-pressure conditions, Geophys. Res. Lett., 33, L14308, https://doi.org/10.1029/2006GL026441, 2006.
Wang, J., Bass, J. D., and Kastura, T.: Elastic properties of iron-bearing wadsleyite to 17.7 GPa: Implications for mantle mineral models, Phys. Earth Planet. Inter., 228, 92–96, https://doi.org/10.1016/j.pepi.2014.01.015, 2014.
Wang, W., Walter, M. J., Peng, Y., Redfern, S., and Wu, Z.: Constraining olivine abundance and water content of the mantle at the 410-km discontinuity from the elasticity of olivine and wadsleyite, Earth Planet. Sci. Lett., 519, 1–11, https://doi.org/10.1016/j.epsl.2019.04.018, 2019.
Wang, Y., Durham, W. B., Getting, I. C., and Weidner, D. J.: The deformation-DIA: A new apparatus for high temperature triaxial deformation to pressures up to 15 GPa, Rev. Sci. Instrum., 74, 3002–3011, https://doi.org/10.1063/1.1570948, 2003.
Watson, E. B. and Baxter, E. F.: Diffusion in solid-Earth systems, Earth Planet. Sc. Lett., 253, 307–327, https://doi.org/10.1016/j.epsl.2006.11.015, 2007.
Weertman, J.: Microstructural mechanisms of creep, in: Mechanics and Materials: Fundamentals and Linkages, edited by: Meyers, M. A., Armstrong, R. W., and Kirschner, H., John Wiley and Sons, Boston, 451–488, 1999.
Withers, A. C., Bureau, H., Raepsaet, C. and Hirschmann, M. M.: Calibration of infrared spectroscopy by elastic recoil detection analysis of H in synthetic olivine, Chem. Geol., 334, 92–98, https://doi.org/10.1016/j.chemgeo.2012.10.002, 2012.
Wright, K. and Catlow, C. R. A.: Calculations on the energetics of water dissolution in wadsleyite, Phys. Chem. Mineral., 23, 38–41, https://doi.org/10.1007/BF00202991, 1996.
Xia, Q. K., Yang, X. Z., Deloule, E., Sheng, Y. M., and Hao, Y. T.: Water in the lower crustal granulite xenoliths from Nushan, SE China, J. Geophys. Res., 111, B11202, https://doi.org/10.1029/2006JB004296, 2006.
Xia, Q. K., Liu, J., Liu, S. C., Kovács, I., Feng, M., and Dang, L.: High water content in Mesozoic primitive basalts of the North China Craton and implications for the destruction of cratonic mantle lithosphere, Earth Planet. Sc. Lett., 361, 85–97, https://doi.org/10.1016/j.epsl.2012.11.024, 2013.
Xia, Q. K., Liu, J., Kovács, I., Hao, Y. T., Li, P., Yang, X. Z., Chen, H., and Sheng, Y. M.: Water in the upper mantle and deep crust of eastern China: Concentration, distribution and implications, Natl. Sci. Rev., 6, 125–144, https://doi.org/10.1093/nsr/nwx016, 2019.
Xiong, Z. L. and Zhang, B. H.: Thermal properties of olivine, wadsleyite and ringwoodite – a review, Minerals, 9, 519, https://doi.org/10.3390/min9090519, 2019.
Xu, Y., Poe, B. T., Shankland, T. J., and Rubie, D. C.: Electrical conductivity of olivine, wadsleyite, and ringwoodite under upper-mantle conditions, Science, 280, 1415–1418, https://doi.org/10.1126/science.280.5368.1415, 1998.
Xu, Y., Shankland, T. J., and Poe, B. T.: Laboratory-based electrical conductivity in the Earth's mantle, J. Geophys. Res., 105, 27865–27875, https://doi.org/10.1029/2000JB900299, 2000.
Xu, Y., Weidner, D. J., Chen, J., Vaughan, M. T., Wang, Y., and Uchida, T.: Flow-law for ringwoodite at subduction zone conditions, Phys. Earth Planet. In., 136, 3–9, https://doi.org/10.1016/S0031-9201(03)00026-8, 2003.
Xu, Y., Shankland, T. J., Linhardt, S., Rubie, D. C., Langenhorst, F., and Klasinski, K.: Thermal diffusivity and conductivity of olivine, wadsleyite and ringwoodite to 20 GPa and 1373 K, Phys. Earth Planet. In., 143, 321–336, https://doi.org/10.1016/j.pepi.2004.03.005, 2004.
Yamazaki, D. and Karato, S. I.: Some mineral physics constraints on the rheology and geothermal structure of Earth's lower mantle, Am. Mineral., 86, 385–391, https://doi.org/10.2138/am-2001-0401, 2001.
Yang, X.: Orientation-related electrical conductivity of hydrous olivine, clinopyroxene and plagioclase and implications for the structure of the lower continental crust and uppermost mantle, Earth Planet. Sc. Lett., 317–318, 241–250, https://doi.org/10.1016/j.epsl.2011.11.011, 2012.
Yoshino, T.: Laboratory electrical conductivity measurement of mantle minerals, Surv. Geophys., 31, 163–206, https://doi.org/10.1007/s10712-009-9084-0, 2010.
Yoshino, T. and Katsura, T.: Reply to comments on “Electrical conductivity of wadsleyite as a function of temperature and water content” by Manthilake et al., Phys. Earth Planet. In., 174, 22–23, https://doi.org/10.1016/j.pepi.2009.01.012, 2009.
Yoshino, T. and Katsura, T.: Re-evaluation of electrical conductivity of anhydrous and hydrous wadsleyite, Earth Planet. Sc. Lett., 337–338, 56–67, https://doi.org/10.1016/j.epsl.2012.05.023, 2012.
Yoshino, T. and Katsura, T.: Electrical conductivity of mantle minerals: role of water in conductivity anomalies, Annu. Rev. Earth Planet. Sci., 41, 605–628, https://doi.org/10.1146/annurev-earth-050212-124022, 2013.
Yoshino, T., Matsuzaki, T., Yamashita, S., and Katsura, T.: Hydrous olivine unable to account for conductivity anomaly at the top of the asthenosphere, Nature, 443, 973–976, https://doi.org/10.1038/nature05223, 2006.
Yoshino, T., Manthilake, G., Matsuzaki, T., and Katsura, T.: Dry mantle transition zone inferred from electrical conductivity of wadsleyite and ringwoodite, Nature, 451, 326–329, https://doi.org/10.1038/nature06427, 2008.
Yoshino, T., Matsuzaki, T., Shatskiy, A., and Katsura, T.: The effect of water on the electrical conductivity of olivine aggregates and its implications for the electrical structure of the upper mantle, Earth Planet. Sc. Lett., 288, 291–300, https://doi.org/10.1016/j.epsl.2009.09.032, 2009.
Yoshino, T., Laumonier, M., McIsaac, E., and Katsura, T.: Electrical conductivity of basaltic and carbonatite melt-bearing peridotites at high pressures: implications for melt distribution and melt fraction in the upper mantle, Earth Planet. Sc. Lett., 295, 593–602, https://doi.org/10.1016/j.epsl.2010.04.050, 2010.
Zha, C. S., Duffy, T. S., Downs, R. T., Mao, H. K., and Hemley, R. J.: Sound velocity and elasticity of single-crystal forsterite to 16 GPa, J. Geophys. Res., 101, 17535–17545, https://doi.org/10.1029/96JB01266, 1996.
Zhang, B. H.: Diffusion of hydrogen in (Mg,Fe)2SiO4 and high pressure polymorphs refined by the cBΩ model, J. Asian Earth Sci., 54–55, 9–17, https://doi.org/10.1016/j.jseaes.2012.02.017, 2012.
Zhang, B. H.: An overview of Fe-Mg interdiffusion in mantle minerals, Surv. Geophys., 38, 727–755, https://doi.org/10.1007/s10712-017-9415-5, 2017.
Zhang, B. H. and Shan, S. M.: Thermodynamic calculations of Fe-Mg interdiffusion in (Mg,Fe)2SiO4 polymorphs and perovskite, J. Appl. Phys., 117, 054906, https://doi.org/10.1063/1.4907576, 2015a.
Zhang, B. H. and Shan, S. M.: Application of the cBΩ model to the calculation of diffusion parameters of Si in silicates, Geochem. Geophys. Geosyst., 16, 705–718, https://doi.org/10.1002/2014GC005551, 2015b.
Zhang, B. H. and Yoshino, T.: Temperature-enhanced electrical conductivity anisotropy in partially molten peridotite under shear deformation, Earth Planet. Sc. Lett., 530, 115922, https://doi.org/10.1016/j.epsl.2019.115922, 2020.
Zhang, B. H., Wu, X. P., Xu, J. S., and Zhou, R. L.: Application of the cBΩ model for the calculation of oxygen self-diffusion coefficients in minerals, J. Appl. Phys., 108, 053505, https://doi.org/10.1063/1.3476283, 2010.
Zhang, B. H., Wu, X. P., and Zhou, R. L.: Calculation of oxygen self-diffusion coefficients in Mg2SiO4 polymorphs and MgSiO3 perovskite based on the compensation law, Solid State Ionics, 186, 20–28, https://doi.org/10.1016/j.ssi.2011.01.007, 2011.
Zhang, B. H., Yoshino, T., Wu, X. P., Matsuzaki, T., Shan, S., and Katsura, T.: Electrical conductivity of enstatite as a function of water content: implications for the electrical structure in the upper mantle, Earth Planet. Sc. Lett., 357–358, 11–20, https://doi.org/10.1016/j.epsl.2012.09.020, 2012.
Zhang, B. H., Yoshino, T., Yamazaki, D., Manthilake, G., and Katsura, T.: Electrical conductivity anisotropy in partially molten peridotite under shear deformation, Earth Planet. Sc. Lett., 405, 98–109, https://doi.org/10.1016/j.epsl.2014.08.018, 2014.
Zhang, B. H., Ge, J. H., Xiong, Z. L., and Zhai, S. M.: Effect of water on the thermal properties of olivine with implications for lunar internal temperature, J. Geophys. Res., 124, 3469–3481, https://doi.org/10.1029/2019JE006194, 2019a.
Zhang, B. H., Yoshino, T., and Zhao, C. C.: The effect of water on Fe-Mg interdiffusion rates in ringwoodite and implications for the electrical conductivity in the mantle transition zone, J. Geophys. Res., 124, 2510–2524, https://doi.org/10.1029/2018JB016415, 2019b.
Zhang, B. H., Zhao, C. C., Ge, J. H., and Yoshino, T.: Electrical conductivity of omphacite as a function of water content and implications for high conductivity anomalies in the Dabie-Sulu UHPM belts and Tibet, J. Geophys. Res., 124, 12523–12536, https://doi.org/10.1029/2019JB018826, 2019c.
Zhang, B. H., Zhao, C. C., and Yoshino, T.: Fe-Mg interdiffusion in wadsleyite and implications for water content of the transition zone, Earth Planet. Sc. Lett., 554, 116672, https://doi.org/10.1016/j.epsl.2020.116672, 2021.
Zhang, J. S. and Bass, J. D.: Sound velocities of olivine at high pressures and temperatures and the composition of Earth's upper mantle, Geophys. Res. Lett., 43, 9611–9618, https://doi.org/10.1002/2016GL069949, 2016.
Zhang, Y.: Diffusion in minerals and melts: theoretical background, Rev. Mineral. Geochem., 72, 5–59, https://doi.org/10.2138/rmg.2010.72.2, 2010.
Zhang, Y., Yoshino, T., Yoneda, A., and Osako, M.: Effect of iron content on thermal conductivity of olivine with implications for cooling history of rocky planets, Earth Planet. Sc. Lett., 519, 109–119, https://doi.org/10.1016/j.epsl.2019.04.048, 2019.
Zhao, C. C. and Yoshino, T.: Electrical conductivity of mantle clinopyroxene as a function of water content and its implication on electrical structure of uppermost mantle, Earth Planet. Sc. Lett., 447, 1–9, https://doi.org/10.1016/j.epsl.2016.04.028, 2016.
Zimmerman, M. E. and Kohlstedt, D. L.: Rheological properties of partially molten lherzolite, J. Petrol., 45, 275–298, https://doi.org/10.1093/petrology/egg089, 2004.
- Abstract
- Introduction
- Diffusivity
- Electrical conductivity
- Thermal transport properties
- Sound velocity
- Rheological properties
- Links between transport properties
- Geophysical applications
- Concluding remarks and perspectives
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Diffusivity
- Electrical conductivity
- Thermal transport properties
- Sound velocity
- Rheological properties
- Links between transport properties
- Geophysical applications
- Concluding remarks and perspectives
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References