Defects in olivine

Olivine, a ferromagnesian orthosilicate, is the most abundant mineral in Earth's upper mantle and is stable down to the olivine–wadsleyite phase transition, which defines the 410 km depth mantle transition zone. Olivine also occurs in crustal environments in metamorphic and hydrothermal rocks and is expected to be the major mineral constituent of the Martian and Venusian mantles. The olivine atomic structure is also used in materials science to manufacture lithium batteries. Like any other crystalline solid, including minerals, olivine never occurs with a perfect crystalline structure: defects in various dimensions are ubiquitous, from point, line, and planar defects to three-dimensional (3-D) inclusions. In this contribution, I review the current state of the art of defects in olivine and several implications for key processes occurring in Earth's mantle. Intrinsic and extrinsic point defects are detailed, exemplifying the astonishing diversity of atomic impurities in mantle-derived olivine. Linear defects, one of the key defect types responsible for ductile deformation in crystalline solids, are examined in light of recent progress in 3-D transmission electron microscopy, which has revealed an important diversity of dislocation slip systems. I summarize the principal characteristics of interface defects in olivine: the free surface, grain and interface boundaries, and internal planar defects. As the least-studied defects to date, interface defects represent an important challenge for future studies and are the main application of numerical simulation methods in materials science. I provide an overview of melt, fluid, and mineral inclusions, which are widely studied in volcanology and igneous petrology. Special attention is given to new crystalline defects that act as deformation agents: disclinations (rotational defects) and the potential occurrence of disconnections in olivine, both of which are expected to occur along or near grain boundaries. Finally, I detail outstanding questions and research directions that will further our understanding of the crystalline specificities and paradoxes of olivine and olivine-rich rocks and ultimately their implications for the dynamics of Earth's upper mantle.

1 Introduction

Minerals with perfect crystalline structures do not exist at temperatures above 0 K. Indeed, all minerals contain various types and quantities of defects that can be characterized and studied as a population. These defects can take the forms of misplaced atomic impurities, shifted atomic planes, or foreign minerals or melt pockets captured within the crystalline lattice (e.g., Crawford and Slifkin, 1975; Hirth and Lothe, 1968; Sutton and Balluffi, 1995; Schock, 1985; Schmalzried, 1981; Philibert, 1991). In some cases, defects can lead to important non-stoichiometries, even up to the point of complete structural collapse. Defects are a response from nature to minimize energy under external perturbations such as variations in temperature; pressure; oxidation state; chemical gradients; stress; and thermal, electrical, or magnetic fields. Nevertheless, they are almost invisible entities; as presented by Jean Baptiste Perrin (1926 Nobel laureate in Physics), we must “explain complex visible things by simple invisible things” (in French “expliquer du visible compliqué, par de l'invisible simple”; Perrin, 1913).

This contribution focuses on olivine, which composes 60 %–80 % of Earth's upper mantle. This relatively simple solid-solution silicate mineral is rich in paradoxes, and we do not yet fully understand its complex physical and chemical properties. Olivine is a key mineral in geodynamics because it is the only interconnected mineral phase in the upper mantle, including the lithosphere–asthenosphere boundary where a durable rheological contrast horizontally separates tectonic (lithospheric) plates from the convecting asthenosphere beneath. Olivine is also an important component of Mars' mantle (garnet-bearing wehrlite, 73 % olivine; e.g., McGetchin and Smyth, 1978; Morgan and Anders, 1979; Zuber, 2001), Venus' mantle (Morgan and Anders, 1980), and peculiar meteorites (e.g., pallasites, type-I chondrites; e.g., Scott, 1977; Buseck, 1977; Dodd and Calef, 1971; Jaquet et al., 2021). Nonetheless, the most important olivine reservoir by far is the interstellar medium, where olivine occurs as dust particles. These interstellar olivines originated from the outflows of evolved stars and lost their crystalline structure due to irradiation by solar wind, cosmic rays, and/or supernova shock waves (e.g., Jones, 2007; Carrez et al., 2002; Messenger et al., 2005).

The temperature in Earth's mantle is well above 500 ^∘C and increases with depth. Olivine is stable until the phase transition to its denser polymorph wadsleyite at mantle transition zone conditions (∼ 410 km depth, ∼ 1600 K, 13–14 GPa; Katsura and Ito, 1989; Katsura et al., 2004). The number and types of defects in olivine, as well as interactions between them, change to accommodate these drastic pressure and temperature conditions, in turn modifying the mineral's physical and chemical properties. This feedback loop needs to be qualified and quantified to understand the underlying physics if we are to predict olivine properties at the atom and grain scale and up to the scale of tectonic plates.

Defects in crystals and condensed matter are fundamental subjects in materials science because their manipulation controls material behaviors and properties (e.g., Hull and Bacon, 1989, p. 237; Philibert, 1991). Many texts and reviews are available in the materials science literature, mostly addressing a given type of defect, for example, point defects (e.g., Crawford and Slifkin, 1975; Schock, 1985), dislocations (e.g., Hirth and Lothe, 1968), or grain and interface boundaries (e.g., Sutton and Balluffi, 1995; Han et al., 2018). Other studies focus on physical processes and/or properties involving these defects in Earth minerals, for example ionic diffusion (e.g., Zhang and Cherniak, 2010), plastic deformation (e.g., Poirier, 1976, 1985; Karato and Wenk, 2002), electrical conductivity (e.g., Shankland, 1975; Yoshino et al., 2012), or metasomatic changes in the chemical composition of olivine (e.g., O'Reilly et al., 1997; Foley et al., 2013; O'Reilly and Griffin, 2013; Demouchy and Alard, 2021). These processes and properties notably involve hydrogen, by far the most popular atomic impurity in olivine (e.g., Beran and Zemann, 1969; Beran and Putnis, 1983; Kohlstedt et al., 1996; Mosenfelder et al., 2006; Férot and Bolfan-Casanova, 2012; Demouchy and Bolfan-Casanova, 2016; Blanchard et al., 2017; Demouchy and Alard, 2021).

This contribution is an up-to-date review of the state of the art on atomic to nanometric and millimetric defects in olivine. Their consequences for mantle processes are also briefly discussed to emphasize their importance and relevance. After describing a perfect and ideal olivine, defects will be presented as a function of their spatial dimensions (D). Point (0-D) defects are isolated atoms incorporated into or missing from the crystallographic structure. Linear (1-D) defects are mostly represented by dislocations, lines along which the lattice is sheared. Planar (2-D) defects are surfaces, interfaces, and grain boundaries along which neighboring crystals are joined together. Three-dimensional defects change the crystal lattice over a finite volume and include defect clusters, voids, and mineral or fluid inclusions. Finally, recently observed defects and those expected to occur, although not yet observed in olivine, are discussed: disclinations and disconnections, respectively.

Figure 1 The habit and main crystallographic directions of olivine: (a) theoretical model and (b) automorphic hydrothermal olivine from Sapat, Pakistan.

2 Perfect olivine and natural olivine

Olivine is a solid solution between four end-members, first reported between 1823 and 1929 (Breithaupt, 1823; Lévy, 1824; Gmelin, 1840; Tilley, 1929): forsterite, Mg₂SiO₄ (Fo₁₀₀Fa₀, where Fo and Fa indicate the forsterite and fayalite components, respectively); fayalite, Fe₂SiO₄ (Fo₀Fa₁₀₀); tephroite, Mn₂SiO₄; and larnite, Ca₂SiO₄. The forsterite end-member is colorless, and the presence of Fe in the solid solution gives olivine its namesake olive green color with a slight yellow tint (Fig. 1). This review focuses on the (Mg,Fe)₂SiO₄ composition and considers the Mg end-member as the reference lattice. Due to the immense variety of compositions, olivine is a vast mineral group (e.g., Deer et al., 1997).

Table 1 Cell parameters of olivine end-members and a mantle olivine (representative peridotitic composition, from San Carlos, AZ). Error bars are typically around 0.05 %.

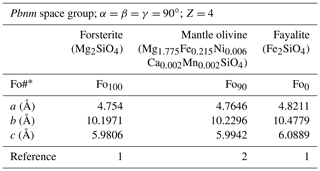
^* Fo# $=\mathrm{100}\times (\mathrm{Mg}/(\mathrm{Fe}+\mathrm{Mg}\left)\right)$; 1: Schwab and Küstner (1977); 2: Abramson et al. (1997).

Olivine crystallizes in the orthorhombic system (space group, Pbnm). The typical crystal habit is illustrated alongside an example of a natural hydrothermal specimen in Fig. 1. The crystallographic parameters of the Mg and Fe end-members and a typical mantle-derived composition are compiled in Table 1. The olivine structure consists of independent SiO₄ tetrahedra linked by two divalent metal (Me) cations (M₁ and M₂) in 6-fold coordination (Fig. 2). Oxygen anions lie in sheets nearly parallel to (100) and are arranged in an approximately hexagonal close-packing structure (Fig. 2a). Each oxygen atom is bonded to one silicon and three octahedrally coordinated Me cations (Fig. 2b). However, because the oxygen atoms are not perfectly close-packed, the coordinated polyhedra around M₁ and M₂ are not identical, and the latter are slightly larger (M₂–O = 2.135 Å) than the former (M₁–O = 2.103 Å). The M₁–O₆ octahedra share edges to form a chain parallel to the [001] axis. These chains are connected by the M₂–O₆ octahedra. Mg and Fe²⁺ are not perfectly distributed between the M₁ and M₂ sites; Fe²⁺ is incorporated into the M₁ site with only slight preference over the M₂ site.

Olivine is abundant in mafic and ultramafic rocks and is thus the dominant mineral constituent of Earth's upper mantle. Its abundance in the upper mantle is on average 67 % but can be as high as 80 % in peridotite and > 90 % in dunite (e.g., Stixrude and Lithgrow-Bertelloni, 2005). Based on analyses of olivine in mantle xenoliths and assuming only iron as atomic impurities, mantle olivines have an average composition close to (Mg_0.9Fe_0.1)₂SiO₄. Furthermore, incorporating the main atomic impurities (minor elements) into the structural formula yields (Mg_1.775Fe_0.215Ni_0.006Mn_0.002Ca_0.002)SiO₄ (e.g., Buening and Buseck, 1973; Frey and Prinz, 1978; Deer et al., 1997).

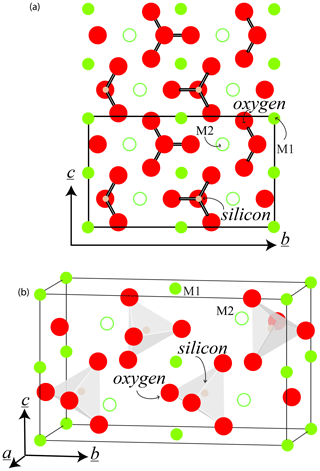
Figure 2 The crystallographic cell of olivine, in the space group Pbnm: (a) in the plane (100) and (b) in three dimensions. The Corey–Pauling–Koltrun color scheme is used for O, Si, and Mg atoms, but the relative radii of the atoms are not preserved to maintain clarity. Empirical atomic radii (±0.12 Å) are O = 0.9 Å, Si = 1.1 Å, and Mg = 1.5 Å (see Slater, 1964).

Olivine is stable at room pressure and temperature, at lower crustal conditions (e.g., in gabbros, ultramafic hydrothermal placers), and in Earth's upper mantle. With increasing temperature and pressure, olivine undergoes a first phase transition into wadsleyite (orthorhombic, Imma at mantle transition zone conditions (1327 ^∘C, 13–14 GPa; Katsura and Ito, 1989; Katsura et al., 2004) and a second transition into ringwoodite (cubic, $Fd\stackrel{\mathrm{‾}}{\mathrm{3}}m$) at greater depths (1400 ^∘C, 17 GPa; Katsura and Ito, 1989; Katsura et al., 2004; see also Pearson et al., 2015, for a unique natural specimen). To date, rare olivines from ultra-deep settings have only been observed in association with retrograde metamorphosed majorite relics (Sautter et al., 1991) or as rare mineral inclusions in diamonds (Kurosawa et al., 1997; Matsyuk et al., 2004; Novella et al., 2015; Taylor et al., 2016; Jean et al., 2016). At lithospheric conditions, i.e., at temperatures below the 1027 ^∘C (1300 K) isotherm, olivine is abundant in peridotite xenoliths transported toward the surface by alkali basalts and kimberlites (e.g., Mercier and Nicolas, 1975; Arai, 1994; Witt-Eickschen and O'Neill, 2005; Bodinier and Godard, 2014), tectonically exhumed in orogenic massifs (e.g., Bodinier and Godard, 2014; Le Roux et al., 2007), or emplaced at slow-spreading mid-ocean ridges (e.g., Godard et al., 2008).

In nature, Fe-bearing magnesian olivine dominates, although other solid solutions are observed: knebelite (Fe,Mn)₂SiO₄ is associated with skarn rocks (Annersten et al., 1984); monticellite (Ca,Mg)₂SiO₄ occurs in carbonatites; and kirschsteinite (Ca,Fe)₂SiO₄ occurs in melilitic or nephelinitic magmas (Deer et al., 1997). Pure Ni₂SiO₄ has never been reported in nature, but (Ni,Mg)₂SiO₄ has been reported in Ni-rich deposits, often co-existing with quartzite, or in serpentinized ultramafic rocks.

Olivine-analogous crystals can be synthesized with complete cationic substitution, e.g., Mg₂GeO₄ (Vaughan and Coe, 1981; Burnley et al., 1991, 2013; Dupas-Bruzek et al., 1998; Shi et al., 2015). Some are useful for studying specific substitutions: e.g., (Mg,Co)₂SiO₄ (Shi et al., 2009, 2010), Ca₂GeO₄ (Tang et al., 2019), or LiFePO₄, the latter of which is used as Li-ion battery material (Islam et al., 2005). To date, the name “olivine” is not approved as a mineral name by the International Mineralogical Association (IMA; https://www.ima-mineralogy.org/Minlist.htm, last access: 28 April 2021), since it is a mineral group name; only the names of naturally occurring end-members are recognized by the IMA, i.e., forsterite, fayalite, tephroite, larnite, etc. (see the IMA list of approved mineral names at http://cnmnc.main.jp/IMA_Master_List_(2020-11).pdf (last access: 28 April 2021).

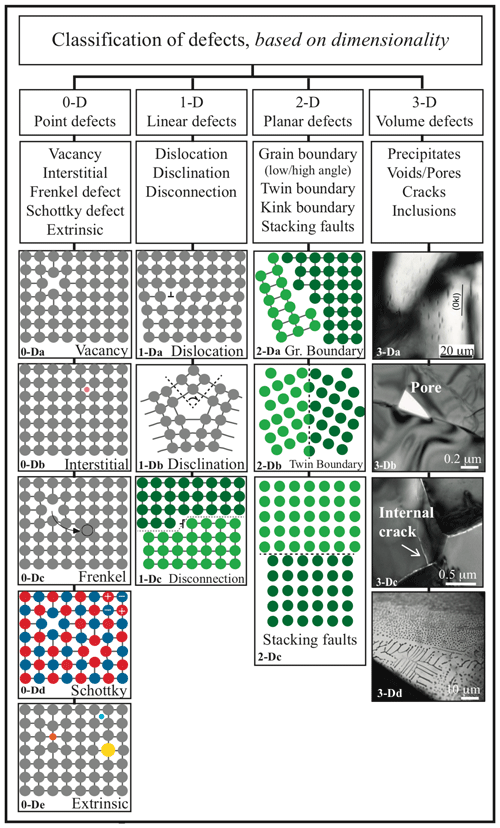
Figure 3 Classification of defects in crystals based on dimensionality. From 3-Da to 3-Dd, examples are provided specifically for olivine: 3-Dc, internal crack and open grain boundaries in nanoforsterite (from Gasc et al., 2019); 3-Da, Ti-rich precipitates in Ti-doped forsterite (from Padrón-Navarta et al., 2014); 3-Db, a pore in He-doped San Carlos olivine (from Burnard et al., 2015); 3-Dc, internal crack in nanoforsterite from Gasc et al. (2019); and 3-Dd, supercritical CO₂ inclusions in San Carlos olivine (unpublished image of sample SC32-1 from Demouchy, 2004).

3 Point defects

A point defect disturbs the mineral lattice at an isolated atomic site and thus is a 0-dimensional defect (0-D). Intrinsic defects, which do not significantly impact stoichiometry or crystallography, are distinguished from extrinsic defects, which are caused by the incorporation of foreign atoms to the lattice and can induce major changes in, e.g., volume and physical and chemical properties as a function of their size and abundance. Intrinsic and extrinsic defects are illustrated schematically in Fig. 3, together with higher-dimensional defects. Note that in materials science, foreign atoms purposely added to the solid are “solutes”, whereas others are “impurities”. In petro-geochemistry, extrinsic point defects are often classified as a function of their concentration in a given mineral, from minor elements (< 1 wt % and > 100 ppm) to trace (< 100 ppm) and ultra-trace (parts-per-billion, ppb, level) elements.

3.1 Intrinsic point defects

Since only three ionic species are present in pure forsterite, the number of intrinsic defects is limited. Using Kröger–Vink notation (Kröger and Vink, 1956; see Appendix A), one distinguishes (1) the vacancies ${{\mathrm{V}}^{\prime \prime }}_{\mathrm{Me}}$, ${{\mathrm{V}}^{\prime \prime \prime \prime }}_{\mathrm{Si}}$, and ${\mathrm{V}}_{\mathrm{O}}^{\mathrm{•}\mathrm{•}}$ from (2) the interstitials ${\mathrm{O}}_{\mathrm{i}}^{\prime \prime }$, ${\mathrm{Mg}}_{\mathrm{i}}^{\mathrm{•}\mathrm{•}}$, and ${\mathrm{Si}}_{\mathrm{i}}^{\mathrm{•}\mathrm{•}\mathrm{•}\mathrm{•}}$. The electroneutral pair $\mathit{\{}{\mathrm{V}}_{\mathrm{Me}}^{\prime \prime }+{\mathrm{Mg}}_{\mathrm{i}}^{\mathrm{•}\mathrm{•}}{\mathit{\}}}^{\times }$ is a Frenkel defect. Anion and cation vacancies that compensate for each other, such as $\mathit{\{}{\mathrm{V}}_{\mathrm{O}}^{\mathrm{•}\mathrm{•}}+{{\mathrm{V}}^{\prime \prime }}_{\mathrm{Me}}{\mathit{\}}}^{\times }$, are a Schottky defect. From the most recent ab initio calculations (Walker et al., 2003, 2006, 2009), the most energetically favorable vacancy within an initially perfect forsterite lattice is ${{\mathrm{V}}^{\prime \prime }}_{{\mathrm{M}}_{\mathrm{1}}}$ (24.48 eV or $\mathrm{3.84}\times {\mathrm{10}}^{-\mathrm{18}}$ J), the next most favorable defects are two oxygen vacancies (${\mathrm{V}}_{{\mathrm{O}}_{\mathrm{3}}}^{\mathrm{•}\mathrm{•}}$, 24.54 eV; ${\mathrm{V}}_{{\mathrm{O}}_{\mathrm{2}}}^{\mathrm{•}\mathrm{•}}$, 25.20 eV), followed by ${{\mathrm{V}}^{\prime \prime }}_{{\mathrm{M}}_{\mathrm{2}}}$ (26.40 eV, $\mathrm{4.16}\times {\mathrm{10}}^{-\mathrm{18}}$) and the last oxygen vacancy (${\mathrm{V}}_{{\mathrm{O}}_{\mathrm{1}}}^{\mathrm{•}\mathrm{•}}$, 27.97 eV). As expected for silicates, silicon vacancies are highly unfavorable (${{\mathrm{V}}^{\prime \prime \prime \prime }}_{\mathrm{Si}}$, 100.81 eV or $\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{17}}$ J). Among these defects, the $\mathit{\{}{{\mathrm{V}}^{\prime \prime }}_{{\mathrm{M}}_{\mathrm{1}}}+{\mathrm{Mg}}_{\mathrm{i}}^{\mathrm{•}\mathrm{•}}{\mathit{\}}}^{\times }$ Frenkel defect is energetically the most favorable configuration, notably for Mg diffusion through a forsterite lattice when a split interstitial is involved (e.g., see Walker et al., 2009, for details). These calculations, as in earlier studies (e.g., Smyth and Stocker, 1975; Brodholt, 1997; Brodholt and Refson, 2000; Richmond and Brodholt, 2000), are for individual defects and not for an increasing number of defects or different types of co-existing defect. These energies are also calculated for atom extraction only, not for the net energetic budget of atom displacement, i.e., extraction, migration, and nearby relocation. This latter calculation is not yet available for complex ionic solids such as forsterite or Fe-bearing olivine.

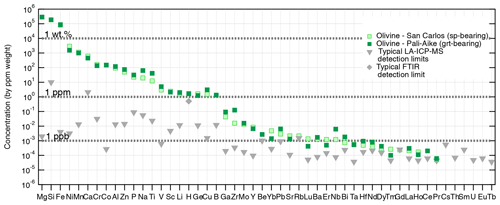
Figure 4 Atomic impurities in San Carlos olivine (spinel-bearing peridotite) ranked by decreasing concentration (ppm), and in a Pali-Aike olivine (garnet-bearing peridotite) for comparison. Typical LA-ICP-MS detection limits are indicated by grey triangles, and the typical unpolarized FTIR detection limit for H by the grey diamond. Analytical details, the original dataset, and further comparison with olivines from other geological settings are available in Demouchy and Alard (2021).

If we take forsterite as the reference lattice, iron is an atomic impurity, even though iron is always present in mantle minerals (Deer et al., 1997, pp. 20–45). In addition, the two oxidation states of iron in olivine must be considered, even if the abundance of ferric iron in olivine is low (< 0.01 wt %; e.g., Duba et al., 1973; Nakamura and Schmalzried, 1983; O'Neill et al., 1993). The presence of iron thus yields additional point defects: ${\mathrm{Fe}}_{\mathrm{Me}}^{\times }$, ${\mathrm{Fe}}_{\mathrm{Me}}^{\mathrm{•}}$, ${{\mathrm{Fe}}^{\prime }}_{\mathrm{Si}}$, ${\mathrm{Fe}}_{\mathrm{i}}^{\mathrm{•}\mathrm{•}}$, and ${\mathrm{Fe}}_{\mathrm{i}}^{\mathrm{•}\mathrm{•}\mathrm{•}}$. Ferrous iron is preferentially incorporated into M₁ vacancies and ferric iron into the M₂ vacancies (e.g., Walker et al., 2009). Furthermore, the presence of ferric iron electrically necessitates formation of vacancies and can produce non-negligible stoichiometric changes at high iron concentrations (i.e., in fayalite; see Nakamura and Schmalzried, 1983). Despite great progress in ab initio calculation capabilities, the incorporation and co-existence of both ferrous and ferric iron in olivine remains difficult to solve, especially considering the extremely diverse range of extrinsic defects (see Sect. 3.2) and variations in temperature, pressure, and oxygen fugacity, among other parameters. One of the primary limitations is the paucity of accurate empirical interatomic potentials used in molecular dynamics calculations and pseudo-potentials and interatomic potentials used in ab initio calculations for silicates (e.g., Mott and Littleton, 1938; Catlow and Mackrodt, 1982; Sanders et al., 1984; Lewis and Catlow, 1985; Eastwood et al., 1980; Vanderbilt, 1990; Kresse and Hafner, 1994).

3.2 Extrinsic point defects

In addition to iron, natural olivines contain a wide range of atomic impurities at various concentration levels (down to ppb). Magmatic and metamorphic olivines contain significantly more atomic impurities than lithospheric mantle olivine (e.g., Bell et al., 2004; De Hoog et al., 2010, 2014; Satsukawa et al., 2017). Nevertheless, compared to pyroxenes, spinel, and garnet, olivine is the most depleted mantle mineral. As in clinopyroxene, the nature and abundance of atomic impurities in olivine (e.g., Ni, Cr, Ti) are commonly used as petrogenetic indicators, specifically targeting deep crustal and mantle processes such as partial melting or metasomatism (e.g., Ringwood, 1955a, b; O'Reilly et al., 1997; De Hoog et al., 2010; Foley et al., 2013; Sanfilippo et al., 2017; Neave et al., 2018). Atomic impurities are also used as proxies for equilibrium temperature (Ca in olivine and co-existing orthopyroxene) and pressure (Al in olivine; e.g., Brey and Kohler, 1990; Witt-Eickschen and O'Neill, 2005; Coogan et al., 2014; D'Souza et al., 2020; Bussweiler et al., 2017). Thanks to recent technical advances, we can now measure a broad array of atomic impurities in olivine, from heavy (e.g., Th, U, at concentrations > 1 ppb) to light (e.g., Li) elements, by laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS; e.g., Tollan et al., 2018; Bussweiler et al., 2019; Batanova et al., 2019; Demouchy and Alard, 2021). Other analytical methods are used to quantify volatile concentrations: H by Fourier transform infrared spectroscopy (FTIR; e.g., Beran and Zemann, 1969; Beran and Putnis, 1983; Rossman, 2006), He and Ar by noble gas mass spectrometry (e.g., Trull et al., 1991; Parman et al., 2005; Tolstikhin et al., 2010; Burnard et al., 2015), and C by secondary ion mass spectrometry (SIMS; e.g., Keppler et al., 2003). Examples of atomic impurity concentrations in olivines from a spinel-bearing peridotite from the well-known San Carlos locality (Arizona) and from a Patagonian garnet-bearing peridotite are provided in Fig. 4 (analytical methods and original data reported in Demouchy and Alard, 2021). The elements are ranked in order of decreasing concentration as in Bussweiler et al. (2019; see their Fig. 2) to show the typical ranges of major, minor, trace, and ultra-trace elements incorporated in mantle olivines. The San Carlos olivine is used as a reference for ranking the elements, and the Patagonian olivine is overlain to highlight slight enrichments or depletions observed in deeper olivines from garnet-bearing peridotites. Elements at concentrations below the typical detection limits (grey symbols; see details in Demouchy and Alard, 2021) are included at the far right.

The incorporation of these atomic impurities in olivine can be predicted following Goldschmidt's rules, which describe the partitioning between the solid phase and co-existing silicate melt at equilibrium (Goldschmidt, 1926, 1937; Ringwood, 1955a, b): (1) if two ions have similar ionic radii and the same electric charge, the smaller will be preferentially concentrated in the mineral; and (2) if two ions have similar ionic radii but different electric charges, the ion with the highest charge will be preferentially concentrated in the mineral. These rules are based on the simple ionic model of minimizing lattice energy (Burns, 1993) and involve an ideal ionic radius in the lattice. However, ions that are theoretically too large or small for a given lattice site radius can still be incorporated, although in smaller quantities. These rules ignore pre-existing intrinsic defects, i.e., defect interactions controlled by electroneutrality, and imply that minerals reached equilibrium with their host melt; thus they are not appropriate for mineral–mineral partitioning in melt-free systems, in which energy minimization occurs after thermodynamics changes to the system (e.g., temperature, pressure, oxygen fugacity). However, this set of rules is a powerful first approximation of mineral–melt trace element partitioning in geochemistry.

The cation coordination number (CCN) is also used to predict the incorporation of atomic impurities. There are again necessary assumptions: (1) cations and anions are treated as rigid spheres, and (2) ionic radii are constant within the lattice. One then calculates the ratio of cation $/$ oxygen radii for each potential extrinsic atom. This approach is very useful for elements similar to Mg in olivine and can be used to predict mineral–mineral partitioning, but it does not account for defect interactions or complex electroneutrality. Ionic radii for silicates are available in Shannon and Prewitt (1969), Shannon (1976), and Whittaker and Muntus (1970). Unfortunately, these empirical radii do not consider specificities of the host mineral lattice and assume that the interatomic distances between oxygens and cations are perfectly constant, which is not the case for olivine (O₁, O₂, and O₃ have different bond lengths to the M₁ and M₂ sites; see Birle et al., 1968). Furthermore, the ratio of radii heavily relies on the ionic radius of O²⁻, which was experimentally determined to be close to 1.40 Å (the value chosen here), although theoretical calculations suggest a lower value of 1.26 Å (Fumi and Tosi, 1964; Whittaker and Muntus, 1970). This lack of accuracy leads to significant discrepancies for the incorporation of large cations in olivine. Ionic radii from Shannon (1976) and Zhang and Xu (1995) are displayed as a function of oxidation state in Fig. 5.

In a first approximation, the population of extrinsic defects depends directly on the initial concentration of intrinsic defects at a given temperature (e.g., mostly following an Arrhenius law; Schmalzried, 1965) and pressure and then on the most energetically favorable simple substitution. To date, these defects are always decrypted as defect pairs (vacancy–cation) or defect reactions (cation–cation) and largely ignore other neighboring defects (vacancy–anion) or the meso-scale electroneutrality of the mineral. In olivine, such defects are of interest in terms of electrical properties, plasticity, and chemical reservoirs in the upper mantle. Simple substitutions and complex associated defects are described below in order of ionic valence.

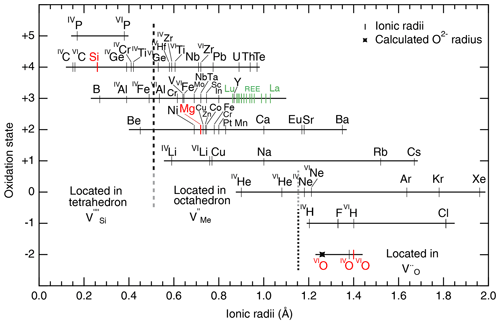
Figure 5 Ionic radii of cations and anions in olivine as a function of oxidation state. Ionic radii are from Shannon (1976), except for noble gases, which are from Zhang and Xu (1995). Note that the high-spin state is reported for the transition metals (as in De Hoog et al., 2010). The calculated ionic radius of O²⁻ from Fumi and Tosi (1964) is also shown for comparison. H could not be included because, to date, the ionic radius of H⁺ in silicates is not known with satisfying accuracy. To guide the eye, Si, Mg, and O are shown in red; the different positions for different coordinations of oxygen are also given, and vertical dashed lines delimit the approximate ranges of ion incorporation into Si, Mg, and O vacancies.

3.2.1 Monovalent cations

The most abundant monovalent cationic impurities in olivine are H⁺, Li⁺, and Na⁺ (Kent and Rossman, 2002; Sykes et al., 1994; Grant and Wood, 2010; Demouchy and Alard, 2021), but Rb⁺ and Cs⁺ are also present as ultra-trace elements (Fig. 4). Whether monovalent cations are incorporated within vacancies or as interstitials remains disputed, especially for hydrogen, which is a mere proton (a full H atom has a radius of only $\mathrm{1.7}\times {\mathrm{10}}^{-\mathrm{5}}$ Å according to Bohr's model). However, theoretical calculations indicate that monovalent cations should be preferentially incorporated into the M₁ site, and divalent and some trivalent elements should be incorporated into the M₂ site (Purton et al., 1997).

The incorporation of K⁺ in olivine is theoretically possible, but its detection remains an analytical challenge as it is quite volatile, and its concentration in olivine is too low for analyses by electron probe microanalysis (EPMA). Furthermore, its mass (³⁹K) is too close to that of argon (⁴⁰Ar) to permit its detection by LA-ICP-MS.

Hydrogen incorporation in olivine has been extensively studied since hydrogen impacts its physical and chemical properties, for example, by enhancing electrical conductivity (Karato, 1989; Yoshino et al., 2006; Poe et al., 2010) and the ionic diffusion of major elements (e.g., Hier-Majumder et al., 2004; Costa and Chakraborty, 2008) and decreasing the strength (e.g., Mackwell et al., 1985; Demouchy et al., 2012; Tielke et al., 2017) and melting temperature (e.g., Kushiro et al., 1968; Gaetani and Grove, 1998) of olivine. Consequently, the distribution of hydrogen in mantle olivine is repeatedly proposed as a key geodynamics parameter (e.g., Regenauer-Lieb and Kohl, 2003; Regenauer-Lieb et al., 2006; Albarède, 2009; Peslier et al., 2010; Masuti et al., 2016). Experimental petrology and mineralogy have been crucial to understanding the primary mechanisms of hydrogen incorporation in mantle olivine as extrinsic point defects (e.g., Kohlstedt et al., 1996; Keppler and Bolfan-Casanova, 2006; Bali et al., 2008; Férot and Bolfan-Casanova, 2012; Gaetani et al., 2014; Padrón-Navarta and Hermann, 2017; Tollan et al., 2018). However, the systematic characterization of the speciation and abundance of hydrogen in mantle olivine from a wide range of geological origins has only begun recently (see reviews by Peslier, 2010, and Demouchy and Bolfan-Casanova, 2016; Demouchy and Alard, 2021). Our understanding of H-bearing point defects has evolved a lot with time from simple equilibrated defects, e.g., $\mathit{\{}\mathrm{2}{\mathrm{OH}}_{\mathrm{O}}^{\mathrm{•}}+{{\mathrm{V}}^{\prime \prime }}_{\mathrm{Me}}{\mathit{\}}}^{\times }$, $\mathit{\{}\mathrm{4}{\mathrm{OH}}_{\mathrm{O}}^{\mathrm{•}}+{{\mathrm{V}}^{\prime \prime \prime \prime }}_{\mathrm{Si}}{\mathit{\}}}^{\times }$, or as interstitial ${\mathrm{H}}_{\mathrm{i}}^{\mathrm{•}}$, to complex, associated defects involving both intrinsic and extrinsic defects, e.g., tetravalent $\mathit{\{}{\mathrm{Ti}}_{\mathrm{Me}}^{\mathrm{•}\mathrm{•}}+\mathrm{2}{{\mathrm{H}}^{\prime \prime }}_{\mathrm{Si}}{\mathit{\}}}^{\times }$ or trivalent $\mathit{\{}{{\mathrm{Al}}^{\prime }}_{\mathrm{Si}}+{\mathrm{OH}}_{\mathrm{O}}^{\mathrm{•}}{\mathit{\}}}^{\times }$ (e.g., Berry et al., 2005; Padrón-Navarta and Hermann, 2017). Complex defects can be extremely diverse, and currently documented examples are summarized in Sect. 3.2.7.

3.2.2 Divalent cations

Ni²⁺, Mn²⁺, Ca²⁺, and Co²⁺ are easily incorporated in the metal site because they have similar ionic radii and identical charges (Fig. 5). Mantle olivines can also contain Zn²⁺, Sr²⁺, Ba²⁺, and Cu²⁺ in low concentrations. Ni is the most abundant atomic impurity in mantle (Fig. 4; e.g., Frey and Prinz, 1978), as well as in magmatic and metamorphic, olivines. Divalent cations are expected to occupy both the M₁ and M₂ sites, with a slight preference for the latter (e.g., Deer et al., 1997), but systematic studies demonstrating the relative occupancies of each minor and trace element are lacking. Doping techniques are commonly used in gemmology to enhance visual quality and can yield marvels such as synthetic cobalt-doped forsterite, which displays a remarkable indigo color and is sold as an imitation of tanzanite.

3.2.3 Trivalent cations

Trivalent cations such as Fe³⁺ and Cr³⁺ (Deer et al., 1997), Al³⁺ and B³⁺ (Sykes et al., 1994), Sc³⁺, and rare Earth elements (REEs – La, Ce, Pr, Nd, Sm, Eu here assumed to be mostly ³⁺, Gd, Tb, Dy, Ho, Er, Tm, Yb, and Lu) are also incorporated into olivine, as reported in natural olivines and experimentally doped forsterite (e.g., Berry et al., 2007; Mallmann et al., 2013; Tollan et al., 2018; Demouchy and Alard, 2021). Cr³⁺ and B³⁺ should preferentially occupy Me vacancies, whereas Al³⁺ can occupy either Me or Si vacancies (e.g., Purton et al., 1997; Grant and Wood, 2010; Blanchard et al., 2017); note that ludwigite (Mg₂FeBO₅) can also form (Takeuchi et al., 1950; Irwin and Peterson, 1999). The oxidation state can influence the coordination of certain elements; e.g., V is incorporated in olivine as V³⁺, not as pentavalent, under normal upper-mantle conditions (e.g., Berry et al., 2007; Mallmann and O'Neill, 2009). Cr³⁺ seems to be the dominant trivalent species in olivine if Fe³⁺ is ignored. To date, the exact amount of Fe³⁺ in olivine remains hard to quantify as it is below the detection limit of Mössbauer spectroscopy (< 100 ppm; e.g., Duba et al., 1973), whereas Cr³⁺ concentrations are 100–200 ppm in mantle olivine and can reach almost 1000 ppm in magmatic olivine (e.g., Foley et al., 2013; Tollan et al., 2018).

3.2.4 Tetravalent cations

Tetravalent impurities such as (1) Ti⁴⁺ and Ge⁴⁺ and (2) Zr⁴⁺, Mo⁴⁺, Hf⁴⁺, and Th⁴⁺ occur in trace and ultra-trace amounts, respectively, in natural olivine (Fig. 4). They can theoretically occupy Si vacancies if a defect reaction does not occur (Fig. 5), but Zr⁴⁺ and Hf⁴⁺ can diffuse as fast as Fe and Mg in olivine at 1200–1500 ^∘C (Jollands et al., 2016). C⁴⁺ has been experimentally incorporated into olivine at very low solubilities (< 1 ppm; Keppler et al., 2003; see also Tingle and Green, 1987); nevertheless, its detection and quantification within the lattice of natural specimens remains very challenging (e.g., Oberheuser et al., 1983). Furthermore, carbon incorporation during the weathering of olivine-rich rocks, such as serpentinization, is a possible mechanism of carbon sequestration (e.g., Olsson et al., 2012; Peuble et al., 2015).

3.2.5 Pentavalent cations

The incorporation of pentavalent impurities such as P⁵⁺ and Ta⁵⁺ is also possible. Phosphorus is the most abundant pentavalent cation in natural olivines and has been successfully used to trace crystalline growth in magmatic olivines (e.g., Shea et al., 2015; Howarth and Gross, 2019). Phosphorus-rich olivine (P concentrations at the percentage-by-mass level) was first noted by Buseck (1977) in pallasites. The incorporation of P is favored due to its small ionic radius compared to, e.g., Al (^IVP = 0.17 Å; ^VIP = 0.38 Å; ^IVAl = 0.38 Å; ^VIAl = 0.535 Å; Fig. 5). In terrestrial olivines, P concentrations are highly variable: magmatic olivines can contain up to 925 ppm P but as little as 80 ppm in potassic lavas or around 200 ppm in komatiitic olivine (e.g., Milman-Barris et al., 2008; Shea et al., 2015; Ersoy et al., 2019). These large variations are attributed not only to rapid growth zoning of olivine in the parent melt (Milman-Barris et al., 2008; Shea et al., 2015) but also to analytical difficulties because P easily interferes with Si. Indeed, the first ionization energy of P (= 10.49 eV) is higher than that of Si (= 8.15 eV). Phosphorus concentrations are also highly variable in mantle olivines, ranging from 11 to 20 ppm in San Carlos olivine to 650 ppm in other mantle olivines (e.g., Brunet and Chazot, 2001; Mallmann and O'Neill, 2009; Mallmann et al., 2009; Baziotis et al., 2017; Demouchy and Alard, 2021). Phosphorus also occurs in higher concentrations in olivine than Ta⁵⁺, which occurs only at the ppb level (Fig. 4). Phosphorus incorporation can be coupled to other extrinsic defects (Al³⁺, Cr³⁺, Li⁺, or Na⁺), though not systematically (e.g., Milman-Barris et al., 2008; Foley et al., 2010). An experimental study on the formation of metastable phosphoran olivine (3 wt %–27 wt % P₂O₅) showed that P⁵⁺ occupies Si vacancies and that charge balance is maintained by metal vacancies (Boesenberg and Hewins, 2010).

3.2.6 Anions and noble gases

Substitutions in olivine are not limited to cationic sites only; anionic impurities are also possible because oxygen vacancies (O₃ or O₂) are theoretically almost as favorable as M₁ vacancies (see Sect. 3.1). The lattice of olivine can incorporate Cl⁻ and F⁻, although the few studies available report low concentrations for these halogens in mantle olivine: 5–6.3 ppm Cl (Beyer et al., 2012) and 100 ppm F in olivine megacrysts (Hervig and Bell, 2005) but only 2–10 ppm F in olivine from spinel-bearing peridotites and 30 ppm F in garnet-bearing peridotites (Beyer et al., 2012). Unusual B-rich olivines also contain high F concentrations (3300–5500 ppm F; Sykes et al., 1994). Partitioning experiments have produced olivine containing 0.17–1.45 ppm Cl and 0.002–2.56 ppm F (Joachim et al., 2015) or higher concentrations when abundant fluid is present (15–400 ppm Cl, 56–900 ppm F; Fabbrizio et al., 2013). Concentrations up to 0.51 wt % F were reported for experimentally F-saturated olivine (Mg₂SiO₄–MgF₂; Grützner et al., 2017), and clinohumite lamellae can occur at higher F concentrations (e.g., Stalder and Ulmer, 2001). Although the incorporation of bromine in olivine was the focus of a preliminary study (Joachim et al., 2016), to date, no publication has reported the successful incorporation of bromine, iodine, or astatine in natural olivine.

Nobles gases are inert at room conditions, but, at the high pressures and temperatures of Earth's interior, distortion of their electron clouds (polarization) allows them to bond with ions in silicates (e.g., Hiyagon and Ozima, 1986), and olivine can incorporate trace amounts of He, Ne, Ar, Kr, and Xe (e.g., Valbracht et al., 1996; Trull et al., 1991; Brooker et al., 2003; Parman et al., 2005; Tolstikhin et al., 2010; Sanloup et al., 2011; Moirera and Kurz, 2013; Burnard et al., 2015; Delon et al., 2018, 2019). Noble gas ionic radii from Zhang and Xu (1995) are included in Fig. 5. Although interstitial sites are a valid hypothetical mechanism of noble gas incorporation, recent studies have shown that He and Ar can also occupy Me vacancies (Delon et al., 2018, 2019) and Xe is more likely to occupy Si vacancies (e.g., Sanloup et al., 2011).

3.2.7 Complex point defects

Although the number of intrinsic defects is limited to three atomic sites and interstitials in the olivine lattice and the concentrations of extrinsic atomic impurities are low, the vast range of atomic impurities leads to innumerable complex defects combining heterovalent ions. Here I summarize only the most recognized complex defects identified in experimental or natural olivines.

The formation of complex defects (or stable coupled substitutions) between monovalent (Mono) and trivalent (Tri) cations might appear straightforward at first, with $\mathit{\{}{{\mathrm{Mono}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{Tri}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$, and are possible for a wide range of compositions, including REEs, which are mostly trivalent (REE³⁺). For example, the association of Li⁺ with Sc³⁺ was calculated to be the most favorable complex defect in olivine (e.g., Purton et al., 1997). Later partitioning experiments at high pressure and temperature (Grant and Wood, 2010) showed that this complex defect is indeed possible but varies as a function of concentration. At low concentrations, $\mathit{\{}{{\mathrm{Li}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{Sc}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$ occurs, but at > 500 ppm Sc, this defect evolves toward $\mathit{\{}{\mathrm{Li}}_{\mathrm{i}}^{\mathrm{•}}+{\mathrm{Sc}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\mathrm{•}\mathrm{•}}$. If alone, Sc³⁺ is simply substituted for Mg and is charge-balanced by the formation of Me vacancies, $\mathit{\{}{{\mathrm{V}}^{\prime \prime }}_{\mathrm{Mg}}+\mathrm{2}{\mathrm{Sc}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$. Grant and Wood (2010) also reported the formation of $\mathit{\{}{{\mathrm{Li}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{Ga}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$, but the formation of stable $\mathit{\{}{{\mathrm{Li}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{Al}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$ or coupling between Na⁺ and Sc³⁺ or Na⁺ and Al³⁺ has not yet been reported.

Hydrogen incorporation has been the focus of specific studies, first on the mechanism of diffusion via the complex defect $\mathit{\{}{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{Fe}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$ (Mackwell and Kohlstedt, 1990; Kohlstedt and Mackwell, 1998), and more recently, LA-ICP-MS measurements have revealed the significant occurrence of $\mathit{\{}{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{Cr}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$, $\mathit{\{}{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{Al}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$, $\mathit{\{}\mathrm{2}{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{V}}_{\mathrm{Mg}}^{\mathrm{•}\mathrm{•}}{\mathit{\}}}^{\times }$, or $\mathit{\{}{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{REE}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$ in mantle olivine (e.g., Tollan et al., 2017, 2018; Demouchy and Alard, 2021). If hydrogen is alone, the Si vacancy is absent, and if the system is water under-saturated, the simple substitution ${\left(\mathrm{2}\mathrm{H}\right)}_{\mathrm{Mg}}^{\times }$ is likely to dominate (Kohlstedt et al., 1996). For boron, $\mathit{\{}{\mathrm{OH}}_{\mathrm{O}}^{\mathrm{•}}+{{\mathrm{B}}^{\prime }}_{\mathrm{Si}}{\mathit{\}}}^{\times }$ is more favorable than $\mathit{\{}{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{B}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$ (Grew et al., 1991; Sykes et al., 1994), but $\mathit{\{}{\mathrm{OH}}_{\mathrm{O}}^{\mathrm{•}}+{{\mathrm{B}}^{\prime }}_{\mathrm{Si}}{\mathit{\}}}^{\times }$, $\mathit{\{}{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{B}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$, and even $\mathit{\{}{{\mathrm{Li}}^{\prime }}_{\mathrm{Mg}}+{\mathrm{B}}_{\mathrm{Mg}}^{\mathrm{•}}{\mathit{\}}}^{\times }$ do not seem to be striking features of mantle-derived olivines (Kent and Rossmann, 2002; Demouchy and Alard, 2021). Neutral complex defects involving only trivalent cations also occur in magmatic olivine, such as ${\left\{{\mathrm{Cr}}_{\mathrm{Mg}}^{\mathrm{•}}{{\mathrm{Al}}^{\prime }}_{\mathrm{Si}}\right\}}^{\times }$ (e.g., Milman-Barris et al., 2008; Shea et al., 2019). As for trivalent cations, the incorporation of Ti with hydrogen has been the subject of specific attention. Alone, Ti cations sit in Si vacancies, but when co-existing with hydrogen, they can form the complex defect ${\left\{{\mathrm{Ti}}_{\mathrm{Mg}}^{\mathrm{•}\mathrm{•}}(\mathrm{2}\mathrm{H}{{)}^{\prime \prime }}_{\mathrm{Si}}\right\}}^{\times }$ by exchange reaction. This type of extrinsic defect, the “titanium-clinohumite-like point defect”, combines the migration of Ti⁴⁺ from a Si vacancy toward a Mg vacancy and two H⁺ ions occupying a Si vacancy, and its existence is supported by experimental studies and ab initio calculations (Berry et al., 2005, 2007a, b; Walker et al., 2007; Padrón-Navarta et al., 2014; Padrón-Navarta and Hermann, 2017; Tollan et al., 2018). This defect is easily detected by FTIR since it displays two intense infrared bands at 3575 and 3525 cm⁻¹ in most mantle olivines (e.g., Berry et al., 2005, 2007; Miller et al., 1987; Demouchy and Alard, 2021; Schmaedicke et al., 2013). It is important to note that such information on hydrogen speciation in olivine cannot be inferred by SIMS. The titanium-clinohumite-like point defect should be noted: ${\left\{{\mathrm{Ti}}_{\mathrm{Mg}}^{\mathrm{•}\mathrm{•}}(\mathrm{2}\mathrm{H}{{)}^{\prime \prime }}_{\mathrm{Si}}\right\}}^{\times }$ in Kröger–Vink notation but sometimes abbreviated as simply [Ti-2H].

Numerous mechanisms of P incorporation in olivine have been proposed, from simple substitutions in Si vacancies (${\mathrm{P}}_{\mathrm{Si}}^{\mathrm{•}}$) to complex defects, but all would require significant Si vacancies to permit the neutral occupancy of two Si sites, e.g., as ${\left\{{{\mathrm{Al}}^{\prime }}_{\mathrm{Si}}{\mathrm{P}}_{\mathrm{Si}}^{\mathrm{•}}\right\}}^{\times }$ (Agrell et al., 1998; Milman-Barris et al., 2008; Boesenberg and Hewins, 2010; Baziotis et al., 2017; Shea et al., 2015, 2019). Theoretically, ${\left\{{{\mathrm{H}}^{\prime }}_{\mathrm{Mg}}{\mathrm{P}}_{\mathrm{Si}}^{\mathrm{•}}\right\}}^{\times }$ should be a favorable complex defect too, but, to date, this incorporation mechanism has not been confirmed.

Atomic impurities in natural olivine comprise almost the entire periodic table; as a result, the list of possible complex associated defects is truly innumerable. Even considering the sum of monovalent, trivalent, and pentavalent impurities, i.e., those introducing the most important electrical imbalance, their distribution in olivine is particularly manifold. Although experimental studies have identified key incorporation mechanisms for simple systems, sometimes by over-doping compared to natural olivine compositions, further progress is still required to fully understand point defects in natural systems, even for simple silicates like olivine.

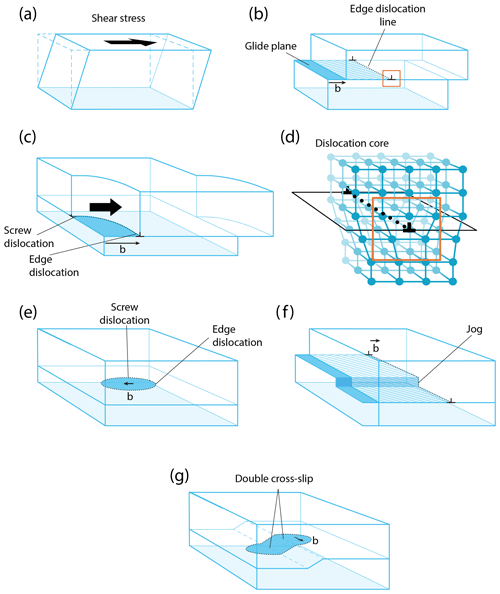
Figure 6 Dislocations in crystalline solids: (a) deformation by shear stress; (b) translation by edge dislocation, showing the glide plane, the dislocation direction, and the Burgers vector b; (c) a screw and edge dislocation; (d) the core of an edge dislocation, corresponding to the orange square in (b); (e) a dislocation loop; (f) dislocation climb by activity on a jog; and (g) dislocation cross slip.

4 Linear defects – dislocations

4.1 Nomenclature and mechanisms of motion

Dislocations are the most widespread one-dimensional defects in crystals. These lines can be considered singularities running through the atomic lattice, along which the crystal order is significantly modified (Fig. 3, 1-Da, and Fig. 6). Their formation, multiplication, annihilation, and mobility control mechanical properties in the ductile (plastic) regime. They also enhance atomic diffusion (diffusion pipe) and can yield the formation of impurity clusters (e.g., Cottrell atmosphere – Cottrell and Bilby, 1949; Snoek effect – Swartz, 1969). Some types of dislocations are primordial during crystal growth (Frank, 1949; Burton et al., 1951), yet growth techniques generally aim to minimize their occurrence (Hoyosa and Takei, 1982). In ionic solids, dislocations can be neutral, but most of time they carry charges (e.g., Hirel et al., 2019), a fundamental property that has received little attention in mineralogy.

The concept of dislocations in solids was introduced by Volterra (1907); their importance in the permanent deformation of metals arose in the 1930s (e.g., Buerger, 1930), and they were applied to creep in Earth minerals and rocks in the 1960s (e.g., Griggs et al., 1960; Raleigh, 1968; Poirier, 1985). Whereas static and mobile dislocations in metals have been observed by transmission electron microscopy (TEM) since the 1950s (e.g., Wilsdorf, 1958), mobile dislocations in very refractory materials such as olivine have only recently been observed (Idrissi et al., 2016).

When stress is applied to a crystal, a dislocation (marked by the two ⊥ symbols in Fig. 6c) can form and glide along specific planes, propagating an elementary shear characterized by the Burgers vector b (Fig. 6a–c). The association of the shear direction (e.g., [100]) and the glide plane (e.g., (010)) is called a slip system, usually noted [uvw](hkl) (in this example, [100](010); this notation is equivalent to (010)[100], and both can be find in the literature). A dislocation is thus determined by two vectors: the line vector u, which varies along the dislocation line, and the Burgers vector b, which is constant. Since a dislocation cannot terminate in a crystal, they often form loops or end on other defects (e.g., other dislocations or in grain boundaries). Two different situations are distinguished. When u and b are perpendicular, a dislocation is called an edge. As shown in Fig. 6, an edge dislocation can move in its glide plane (defined by the line and Burgers vectors) under applied stress and thus can move out of its glide plane if it absorbs or emits point defects (e.g., vacancies) along steps on the line called jogs (Poirier, 1985, p. 56; Fig. 6f). This non-conservative motion occurs only at high temperatures because it requires a meaningful vacancy density and rapid ionic diffusion. The co-existence of climb and glide permits drastic decreases in the mechanical strength of metals, ceramics, and minerals (e.g., Hull and Bacon, 1989; Poirier, 1985; Boioli et al., 2015a, b). When the line vector u and b are collinear, the dislocation is called a screw, which is very important in static growth (e.g., Frank, 1949; Nabarro, 1989). In this case, the slip system is not geometrically constrained, and a screw dislocation can potentially change glide planes as it glides, a process called cross slip. These theoretical concepts are useful for characterizing dislocations, but dislocations change their shape during motion, and the character of a dislocation segment can evolve through time. Note that a dislocation always moves perpendicularly to its line, whatever its character (edge, screw, or mixed). Far from its line, a dislocation is characterized by its long-range elastic field, which is how a dislocation responds to an external stress. Close to the dislocation line, there is a particular atomic arrangement in a region called the dislocation core. This arrangement, which can only be described at the atomic scale, has a strong influence on the mobility of the dislocation and hence on mechanical properties. In a mineral like olivine, with complex crystal chemistry and structure, the core structure is rather complicated, with multiple possible configurations (e.g., as a function of pressure) and even possible transient cores (see Mahendran et al., 2019).

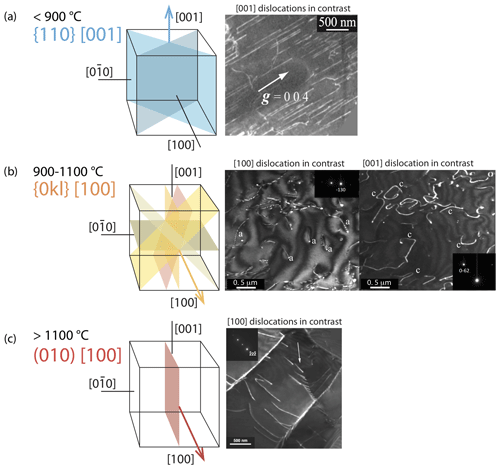
Figure 7 Typical dislocation slip systems in olivine as a function of temperature (redrawn from Carter and Avé Lallemant, 1970): (a) [001] dislocation, typical of low-temperature creep, TEM weak-beam dark-field micrograph from Demouchy et al. (2014); (b) [100] and [001] dislocations co-existing at 1080 ^∘C, TEM weak-beam dark-field micrograph of sample PoEM-8 from Demouchy et al. (2013); and (c) [100] dislocation, sample PI-0546 from Demouchy et al. (2012).

4.2 Dislocations in olivine

The crystallographic lattice of olivine has the peculiarity of having two short axes (a = 4.76 Å; c = 5.66 Å) and one significantly longer axis (b = 10.22 Å). The elastic energy of a dislocation is proportional to the square of the Burgers vector, implying that the shortest lattice repeats, [100] in olivine, usually correspond to the most favorable Burgers vectors. Indeed, [010] dislocations in olivine are almost never observed (Fujino et al., 1993). In mantle-derived olivine, dislocation slip systems were theoretically established and further refined by observations (Carter and Avé Lallemand, 1970; Mussi et al., 2014, 2015). They are illustrated in Fig. 7a–c: [100](010), [100](001), [100]{0kl}, [001](100), [001](010), [001]{110}, [001](140), [001](130), and [001](120). The activity of dislocation slip systems in olivine is strongly dependent on temperature and stress. Based on slip bands formed at the surfaces of experimentally deformed iron-bearing olivine monocrystals, Raleigh (1968) proposed that [001] dislocations glide in the {110} and (100) planes at temperatures below 1000 ^∘C. At 1000 ^∘C, [100] dislocations also occur, and glide in {0kl} planes (Fig. 7d–e). The [001] glide is also strongly active at the lower temperatures and high differential stresses typical of the uppermost mantle (e.g., Raleigh, 1968; Barber et al., 2010; Demouchy et al., 2014; Mussi et al., 2014, 2015). Based on transmission electron microscopy (TEM), Gaboriaud et al. (1981) identified the gliding of both [100] and [001] dislocations in the low-temperature regime (20–900 ^∘C), with a net dominance of [001] screw dislocations. Because the determination of glide planes by standard TEM observations remains very difficult, authors have identified (100) and {110} planes at temperatures above 600 ^∘C via the decoration technique (Kohlstedt et al., 1976). Recent developments with electron channeling contrast imaging in electron microscopy (Miyajima et al., 2018, 2019) and furthermore with TEM electron tomography (Mussi et al., 2014, 2015) have allowed advanced imaging of dislocations, notably the identification of glide planes for the [001] screw dislocation in deformed olivine aggregates. The TEM electron tomography technique also permits a statistic approach; Mussi et al. (2014, 2015) reported the expected (100), (010), and {110} planes but also (140), (130), and (120) glide planes for [001] dislocations, with a net dominance of {110} planes, not (100) or (010). At temperatures typical of the asthenospheric mantle and under low differential stresses, the dominant slip systems in olivine involve [100] glide (i.e., above ca. 1100 ^∘C; Raleigh, 1968; Gueguen, 1979; Ben Ismail and Mainprice, 1999; Couvy et al., 2004; Demouchy et al., 2013). At very high temperatures (1700 ^∘C, too high to be geologically relevant), slip systems identified from experimentally deformed iron-bearing olivine monocrystals using the decoration technique (Kohlstedt et al., 1976) showed the activity of only [100] dislocations in both the (010) and (001) planes. Subsequent TEM analyses of similar iron-free olivine experimentally deformed at temperatures between 1400 and 1650 ^∘C (Gueguen and Darot, 1982) demonstrated the additional activity of [001] dislocations in (100) and (010). Note that in olivine at high temperature (> 1300 ^∘C), the dislocation climb mechanism unlocks edge [100] dislocations, and recent numerical modeling of dislocation dynamics has shown that only a small amount of climb is necessary (< 0.1 % of the strain) to maintain an effective dislocation glide at the macroscale (Boioli et al., 2015a, b). With increasing stress and strain, the accumulation of intragranular dislocations triggers recovery processes, including the formation of arrays (or walls) called subgrain boundaries (see Sect. 5.2.1) that often display a polygonal aspect.

4.3 Olivine paradox

According to the Von Mises (1928) criterion, at least five independent slip systems must be active for plastic flow to occur homogeneously by dislocation glide alone in any crystalline material. This requirement can be simplified to only four slip systems if inhomogeneous flow is allowed (Hutchinson, 1977). Since dislocations in olivine are limited to the [100] and [001] directions with no possibility of shear along [010], only four main slip systems are available: [100](010), [100](001), [001](010), and [001](100). Moreover, as [100](001) and [001](100) systems are not linearly independent, we are left with only two sets of three independent slip systems: (set 1) [100](010), [100](001), and [001](010) or (set 2) [100](010), [001](010), and [001](100). Therefore, polycrystalline olivine does not fulfill the relaxed conditions of Hutchinson (1977), and plastic deformation can only be accommodated if additional degrees of freedom are provided (the “olivine paradox”). Thus, other mechanisms of deformation have been proposed as additional degrees of freedom: (1) climb – although the climb rate in olivine in insufficient to significantly contribute to strain, climb is able to unlock dislocations to overcome obstacles if the density and mobility of jogs is high enough; (2) dislocation-assisted grain boundary sliding as proposed by Hirth and Kohlstedt (1995) (see also Hansen et al., 2011, 2012), which is then grain size dependent; (3) diffusion-accommodated grain boundary sliding (Miyazaki et al., 2013), which is limited to nanoscale grains of olivine (± pyroxenes) and thus is unlikely to be efficient in mantle olivine-rich rocks with grain sizes of 0.1–10 mm and under high lithostatic pressure (> 1 GPa); (4) elastically accommodated grain boundary sliding (Jackson et al., 2013), which also requires very fine grained polycrystalline olivine of constant grain size, in which the grain boundary network is considered equivalent to a very low viscosity layer; however, this contradicts the crystalline sintering observed at high pressure and temperature (Hiraga et al., 2004; Burnard et al., 2015); (5) ionic diffusion operating only at grain boundaries as proposed by Detrez et al. (2015), but they also showed that this mechanism cannot sustain a non-linear rheology in an anisotropic solid such as olivine; (6) disclination-assisted dislocation creep proposed by Cordier et al.  (2014), which involves rotational defects located near grain boundaries (see Sect. 7); or (7) the potential existence of disconnections located at grain boundaries such as the one observed in aluminum metal (see Sect. 7; Rajabzadeh et al., 2014; Sun et al., 2016; Combe et al., 2016, 2019).

5 Interfaces

Interfaces are 2-dimensional (planar) defects, and three types of interfaces are found in polycrystalline materials, including polycrystalline olivine. First, the free surface is the external surface of a crystalline solid in contact with a liquid, vapor, air, or vacuum. Second, the intercrystalline interface delimits the atomic contact between two crystalline solids. When the two solids have the same major element composition and crystalline structure (homophase) but different orientations, such an interface is a grain boundary (e.g., Sutton and Balluffi, 1995); when the solids are different in composition and/or structure (heterophase), it is a two-phase interface. For example, in olivine-rich rocks, an olivine–olivine joint is an olivine grain boundary, whereas an olivine–diopside joint is an olivine–diopside interface. Third, 2-dimensional internal discontinuities in a solid structure are internal-interface defects. These are restricted to stacking faults and antiphase boundaries. All 2-dimensional defects have two characteristics in common: (1) a particular atomic structure that is a function of the crystallographic orientation of the crystal lattices involved and (2) a positive energy, which is usually equal or very close to the surface tension (Sutton and Balluffi, 1995, pp. 350–353).

5.1 Free surfaces

The interaction of the free surface of a mineral in contact with a liquid or vapor is of leading importance in geology, and olivine is no exception. The intrinsic characteristics and properties of interfaces govern many key geological processes, such as grain growth and boundary migration, dissolution kinetics, and absorption kinetics (ionic diffusion). The shape of a free surface is characterized by its structure and energy, which are co-dependent; both the structure and behavior of an interface are determined by the pattern of the atomic plane parallel to the free surface. Note that the interface is not perfectly identical to the atomic plane of reference; minor changes in spacing (bond lengths, free bonds) occur to lower the surface energy. The free surface is then prone to bond interactions and chemical variations. Free bonds at the free surface are preferential ionic absorption sites, leading to the incorporation of impurities (see Sect. 3.2). This may be enhanced by the structure of the free surface (reconstructed or not) based on the presence and abundance of ledges, which can be linked to emerging dislocations. Chemical species that are enriched only at the free surface are surfactants. Interfacial tension is then directly linked to the number (concentration) of free bonds at a given crystalline interface. In metals, which are mostly cubic, interfacial tension is only weakly dependent on the considered interface, whereas in olivine, which has an important structural anisotropy (orthorhombic; $a\approx c<b$), surface tension should vary as a function of crystallographic orientation ($\mathit{\left\{}\mathrm{010}\mathit{\right\}}>\mathit{\left\{}\mathrm{100}\mathit{\right\}}>\mathit{\left\{}\mathrm{001}\mathit{\right\}}$; e.g., Deer et al., 1997; Marquardt et al., 2015). Nevertheless, to date, surface tension anisotropy in olivine has not been systematically quantified.

To date, surfactants such as volatile molecules (CO₂, H₂O, CH₄) are of particular interest for fluid-rich systems on Earth and carbon-rich systems on Mars (e.g., Escamilla-Roa et al., 2018). Atomic-scale numerical modeling is the leading method of investigating these surfactant–mineral reactions (e.g., Watson et al., 1997; Kerisit et al., 2013; Xie et al., 2017). In addition, analyses of noble gas incorporation have important implications for geochronology and Earth's history (³He; e.g., Trull et al., 1991). The most notable contributions (Dukes et al., 1999; Deloule and Robert, 1995) have demonstrated the effective intake of H⁺ and helium (as He⁺) into chondritic olivines via the irradiation of their surfaces by solar wind. As expected, the addition of surfactants impacts the electric charge of the free surface, and achieving electroneutrality minimizes interfacial tension.

The equilibrium shape of a mineral will be the habitus requiring the minimum total interfacial energy in three dimensions. As an anisotropic mineral, the equilibrium shape of olivine is polygonal, with flat facets parallel to the low-energy planes (e.g., Deer et al., 1997; Bruno et al., 2014): {010}, {021}, {110}, {120}, and {101} as illustrated in Fig. 1.

Interfaces in contact with another crystalline solid or a vapor/vacuum are usually sharp, well-defined, planar or stepped surfaces. However, at high pressure and temperature, the atomic density of a near-solidus melt can become high and significantly ordered, like the lattice of the solid. The surface tension of the solid–liquid surface is then less dependent on the crystallographic orientation of the surface plane, yielding a diffuse surface which promotes rapid crystallization and thus enhances the possibility of incorporating atomic impurities (Sutton and Balluffi, 1995; King et al., 2014). This also leads to the competitive formation of euhedral (tablet surfaces), skeletal (hopper cavities or concentrated terranes), and/or dendritic (swallowtail) shapes during dynamic growth as a function of temperature and pressure (see Faure et al., 2003; Welsch et al., 2013; Mourey and Shea, 2019).

The dissolution of olivine interfaces is also expected to be anisotropic (e.g., King et al., 2014), with dissolution rates parallel to [010] being faster than those along [001], which, in turn, are faster than those along [100] at low temperatures (23–90 ^∘C) and room pressure (Awad et al., 2000; King et al., 2014). However, in basaltic liquids at high temperatures (1265–1450 ^∘C), dissolution anisotropy is not as distinct (e.g., Thornber and Huebner, 1985; Chen and Zhang, 2008) and appears to be independent of crystallographic orientation. Furthermore, a recent experimental study at high temperature (1400–1425 ^∘C) and high pressure (1 GPa) reported a specific dissolution mechanism featuring fingered outlines instead of a planar dissolution front (Laumonier et al., 2019), again seemingly independent of crystallographic orientation. As in materials science, the effects of several types of surfactants (HCl, HNO₃, NaOH, NaCl, and organic ligands such as KHP and KOH) in etching olivine surfaces have been tested (e.g., Wogelius and Walther, 1991, 1992; Kobayashi et al., 2001; King et al., 2014). Naturally weathered olivine surfaces are characterized by pairs or arrays of conically etched pits devoid of secondary mineralization. These pits are frequently linked to emergent dislocations or possible nearby fractured and exposed outcrop surfaces (e.g., Velbel, 2009). These features are distinctive of aqueous weathering processes such as serpentinization or iddingsitization (e.g., Boudier et al., 2010).

5.2 Grain boundaries and two-phase interfaces

In metals, ceramics, and rocks, the most important defects are the interfaces between the crystallites–grains. Most of the natural granular rocks on Earth are polymineralic (peridotite, granite), and only a few are almost purely monomineralic (dunite, quartzite, marble). As mentioned above, the interface between the same mineral or crystalline solid is called the grain boundary (e.g., olivine grain boundary) and the interfaces between two different minerals or crystalline solids are called two-phase interfaces (e.g., olivine–enstatite interfaces). It is also important to recall that a grain boundary is a mere interface, not a third component sintering two grains. The percolation of aqueous fluid or silicate melt between two grains or subsequent melt crystallization implies the existence of two free surfaces; therefore, these configurations are not considered grain boundaries or two-solid-phase interfaces.

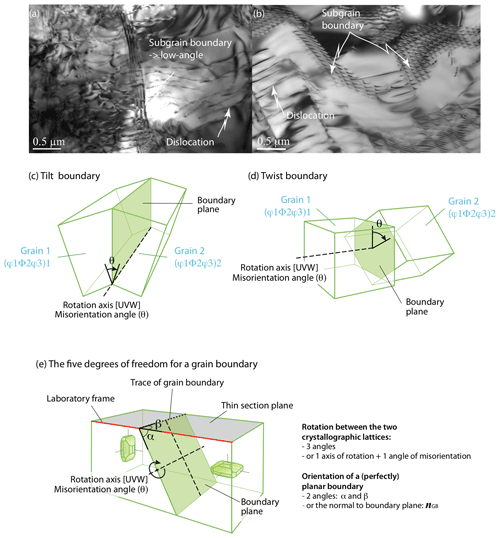
Figure 8 TEM images (courtesy of Patrick Cordier) and sketches of grain boundaries: (a) TEM image showing an almost planar subgrain boundary in nanoforsterite deformed at 0.3 GPa and 1200 ^∘C (sample NF1200-1 from Gasc et al., 2019); (b) subgrain boundary crosscut by the TEM foil plane in a natural San Carlos olivine (He-doped sample PB3 from Burnard et al., 2015); (c) low-angle tilt boundary, with the rotation axis within the grain boundary and rotation angle θ; (d) low-angle twist boundary with the rotation axis perpendicular to the grain boundary and rotation angle θ; and (e) the five macroscopic degrees of freedom required to define a grain boundary, shown for the example of a high-angle tilt boundary with [100] as the axis of rotation.

5.2.1 Grain boundaries

The structure of a grain boundary depends on the crystallographic orientation of the two participant grains. Two types of boundaries are distinguished as a function of the magnitude of the misorientation (θ) between the two lattices: low-angle boundaries (< 15^∘) and high-angle boundaries (> 15^∘). By convention, an angle of 15^∘ is used to separate low- and high-angle boundaries in polycrystalline olivine (Poirier, 1985), but in materials science the cutoff values can range between 5 and 15^∘. A low-angle boundary can simply be described by an array of dislocations, sometimes called a dislocation wall (Fig. 8a, b). At misorientations exceeding 10–15^∘, the dislocation spacing is so small that the dislocation cores overlap and the individual dislocations forming the walls cannot be distinguished by TEM. High-angle boundaries have significantly more complex and disordered structures, including high concentrations of vacancies or unbonded atoms, and are thus easier paths for ionic diffusion. They are also a potential reservoir of atomic impurities, especially for atoms too large to fit within the lattice or with too high a charge to fit a regular atomic site. Furthermore, dislocations are more easily emitted or absorbed at high-angle boundaries (Han et al., 2018). Note that this terminology is equivalent to the distinction between subgrain (low-angle) and grain (high-angle) boundaries. Grain boundaries are preferential sites for the segregation of incompatible elements within a ∼ 1 nm thick interface (Hiraga et al., 2004, and references therein; see also Hayden and Watson, 2008; Burnard et al., 2015). Coincidence boundaries are a specific case of a high-angle boundary in which the geometry matches well the two contacting lattices. Although rare in olivine, they are typical of olivine–serpentine interfaces (e.g., Boudier et al., 2010; Morales et al., 2018). In metals (e.g., faced-centered cubic, fcc), the grain boundary energy increases with increasing misorientation until reaching an energy plateau for high-angle boundaries exceeding 20^∘ (e.g., Shockley and Read, 1949; Read and Shockley, 1952). However, a few crystallographic configurations can lead to low-energy boundary misorientations, called cusps (e.g., Poirier, 1985, p. 67; Tshopp and Mcdowell, 2007). Although such data are not yet available for olivine, it is expected that the incorporation of impurities would lower the grain boundary energy (e.g., Hiraga et al., 2004; Papillon et al., 2009; Marquardt et al., 2015; Faul et al., 2016; Marquardt and Faul, 2018).

We can further describe grain boundaries as a function of the geometry of the misorientation. Tilt, when the lattice is tilted by an edge dislocation array, defining an axis of rotation within the grain boundary plane (Fig. 8c). Twist, when the lattice is rotated by two screw dislocation arrays, defining an axis of rotation perpendicular to the grain boundary plane (Fig. 8d). A mixed boundary, the most common configuration in olivine-rich rocks, comprises both a tilt and a twist component and thus a mixture of edge and screw dislocations. Publications on the nanoscale characterization of bi-crystal olivines with tilt or twist boundaries are markedly rare (e.g., Ricoult and Kohlstedt, 1983; Heinemann et al., 2005), in part because of experimental and sample preparation difficulties. However, as focused ion-beam techniques become increasingly common, we can expect future studies dedicated to olivine grain boundaries; to date, we mostly rely on limited results from atomistic simulations (e.g., de Leeuw et al., 2000).

To define a grain boundary, five macroscopic parameters (or degrees of freedom) are needed (Fig. 8e; e.g., Marquardt et al., 2015): three parameters to specify the orientation of one grain relative to its neighbor (i.e., two angles or the vector of rotation and the angle of misorientation) and two parameters to define the orientation of the boundary plane relative to the other grain (i.e., the vector normal to the boundary plane n_gb or two angles α and β as illustrated in Fig. 8e). As in many ceramics (MgO, Al₂O₃, or TiO₂), low-index planes are the most frequent for olivine grain boundaries (e.g., from Marquardt et al., 2015, {100}, {010}, (051), (031), (053), (15  15  16), (212), or $\left(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{1}}\mathrm{1}\right))$. Based on stereology on 2-D electron backscatter diffraction (EBSD) maps obtained on undeformed or weakly deformed olivine-rich rocks, grain boundaries' character distribution permits the classification of olivine grain boundaries into three groups (Marquardt et al., 2015; Marquardt and Faul, 2018):

• disorientation at 90^∘ relative to the [001] axis, characteristic of all orthorhombic crystals;

• disorientation at ≤10^∘ relative to the [010] axis, typical of subgrain boundaries formed by dislocation glide; and

• disorientation at 60^∘ relative to the [100] axis, the most abundant type of grain boundary in very fine grained natural and synthetic polycrystalline olivine.

Table 2 Summary of the most common types of grain boundaries in natural and synthetic polycrystalline olivines (compilation based on Demouchy et al., 2014; Marquardt et al., 2015; Marquardt and Faul, 2018; Bollinger et al., 2019; Gasc et al., 2019).

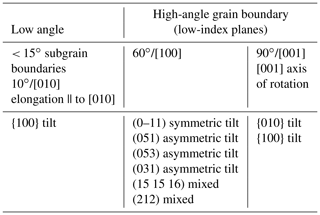
The most abundant types of grain boundaries found in olivine are summarized in Table 2. However, this list applies only to undeformed or very weakly deformed polycrystalline olivine. When strong shape-preferred orientation, crystallographically preferred orientation, and/or foliation are developed in a polycrystal, subgrain boundaries are commonly elongated parallel to [010] (Green and Radcliff, 1972). Basaltic melt segregation was reported to occur via heterogeneous percolation through polycrystalline olivine, with a net avoidance of 60^∘/[010] boundaries (Faul and Fitz Gerald, 1999; Ghanbarzadeh et al., 2015). These results imply that grain boundary energy impacts wetting properties and thus percolation, melt–rock reaction, and extraction. By extrapolation, grain boundary energy should also impact other transport properties such as grain boundary diffusion and migration or electrical conductivity (see also Marquardt and Faul, 2018). For example, the velocity ν of a grain boundary is classically defined as

$$\begin{array}{}\text{(1)}& \mathit{\nu }=-MF,\end{array}$$

with the mobility M defined as

$$\begin{array}{}\text{(2)}& M=M_{\text{o}}\exp (-Q/RT)\end{array}$$

and the driving force F, which can be a difference in stored energy (from defects such as dislocations), the capillary force, or drag from a solute. In Eq. (2), Q is activation energy, R is the gas constant, and T is absolute temperature. When only the capillary force is involved, the grain boundary velocity can be approximated by

$$\begin{array}{}\text{(3)}& \mathit{\nu }\propto -M\mathit{\gamma }\mathit{\kappa },\end{array}$$

with γ being the grain boundary energy and κ the curvature (e.g., Taylor, 1992; Taylor et al., 1992; Sutton and Balluffi, 1995, p. 522). The mechanisms of grain growth in both metals and silicates remain an ever-growing domain of research, and recent and current efforts in materials science are revisiting this simple equation to implement new defects (e.g., disconnections; Han et al., 2018).

To date, only Duyster and Stöckhert (2001) have quantified the interfacial energy of natural high-angle olivine grain boundaries; they reported a value of 1.4±0.4 J m⁻². Furthermore, Karato (1989) experimentally determined the following mobility parameters for very fine grain natural olivine under anhydrous conditions, crustal pressures (0.1–1 GPa), and temperatures of 1200–1400 ^∘C: $M_{\text{o}}=\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{8}}$ m² s⁻¹ and Q=160 kJ mol⁻¹. Experimental data also exist for synthetic forsterite and olivine (e.g., Ohuchi and Nakamura, 2007; Hiraga et al., 2010; Tasaka et al., 2013). Recently, Speciale et al. (2020) reported slower mobility parameters for very fine grained natural olivine: $M_{\text{o}}=\mathrm{1.8}\times {\mathrm{10}}^{\mathrm{3}}$ m² s⁻¹ and $Q=\mathrm{620}\pm \mathrm{145}$ kJ mol⁻¹. The paucity of such data is a strong call for new efforts to constrain olivine interfacial energies under natural conditions.

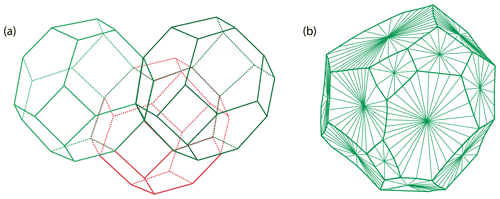
Figure 9 Grain shapes in polycrystalline materials: (a) the theoretical tetrakaidecahedral close-packed configuration with perfectly planar faces and (b) a simulated polyhedron grain with realistic curved faces (redrawn from Lazar et al., 2011).

Figure 10 Natural mantle specimens. (a) Polarized and (b) cross-polarized light microphotographs of a coarse-grained microstructure in a spinel-bearing peridotite from Tariat, central Mongolia (sample Shava SH-11-27 from Demouchy et al., 2019). (c) Natural and (d) cross-polarized light microphotographs of a rare tabular microstructure in a diopside-poor lherzolite with irregularly shaped enstatite from Tok, Siberia (sample 10-16 from Tommasi et al., 2008; images courtesy of Andrea Tommasi): olivines show numerous subgrain boundaries perpendicular to the long axis of the tabular crystals but straight grain boundaries parallel to the rock foliation.

Once the microstructure of a monophase or polycrystalline material has reached its equilibrium, it takes on a polyhedral configuration in three dimensions. The equilibrium of a body-centered cubic (bcc) solid is the close-packed configuration of the tetrakaidecahedra, or the tetrakaidecahedron of Thomson (1894), with flat or lightly curved faces (Fig. 9). Olivine is not cubic but orthorhombic, and its equilibrium microstructure can thus be approximated by such a tetrakaidecahedral close-packed configuration (14 faces) but also by rhombic dodecahedral (12 faces) or octahedral (8 faces) configurations (e.g., Takei and Holtzman, 2009). If not truncated, the equilibrium shape of olivine based on the grain boundary character distribution is a prism with a 9 : 6 : 5 ratio (i.e., {100} : {010} : {001}; see Marquardt et al., 2015, for further details). In igneous petrology, particularly focusing on the microstructures and textures of mantle (olivine-rich) rocks, the equilibrated microstructure is commonly referred to as mosaic equigranular (e.g., Mercier and Nicolas, 1975) and is characterized by equant grains, almost perfectly planar boundaries, triple junctions at ∼ 120^∘, a small grain size (between 0.5 and 1 mm), very rare porphyroclasts (> 1 mm), and homogenously distributed secondary phases (pyroxenes, spinel, and/or garnet). This type of olivine-rich rock typically has a weak crystal-preferred orientation (J index ≈ 2–4; see Bunge, 1982) and a shape factor of ∼ 1.7 (e.g., Demouchy et al., 2019; Tommasi et al., 2020). An example of the mosaic equigranular microstructure is shown in Fig. 10a and b. In some rare cases, olivine grains can develop a strong shape-preferred orientation parallel to the lineation during static recrystallization (induced by melt percolation), as illustrated by the very graphic, tabular microstructure in Fig. 10c and d (Siberian peridotites from Tommasi et al., 2008).

As previously mentioned, the energy of a grain boundary is always positive; thus, a fine-grained polycrystalline aggregate will have a total surface tension energy greater than that of a coarse-grained aggregate. This energy is proportional to the total grain boundary area (if isotropic, it yields $E=\sum _k{\mathit{\sigma }}_k{A}_k$, with E being the total interfacial energy, σ_k the surface tension energy for faces k, and A_k the surface area of face k). If temperature increases, the growth of large grains at the expense of smaller grains is an efficient process to lower the total energy of a polycrystalline solid. Consequently, average grain size provides key information on the microstructure, although it is an incomplete proxy; grain size distributions and shape are as fundamental as average grain size. Recent analytical data types and tools such as EBSD maps and data treatment methods (e.g., ESPRIT DynamicS, OIM, CHANNEL5, ATEX, or MTEX tool box; see Hielscher and Schaeben, 2008; Bachmann et al., 2010; Beausir and Fressengeas, 2013; Fressengeas and Beausir, 2018; Ernould et al., 2020) have greatly eased access to the statistical quantification of these parameters.

5.2.2 Two-phase interfaces

The structural characteristic which differentiates two-phase interfaces from grain boundaries is coherency. It represents the necessity to find the same structural ordering between the two phases, whatever the position along the interface. Semi-coherent interfaces are also possible, for example in the case of organized interfacial dislocation (also called edge-type misfit dislocation; Sutton and Balluffi, 2005, p. 74). This property is largely employed in materials science and thin-film techniques. In mineralogy, a coherent interface commonly involves epitaxial relationships and, to some extent, includes topotaxy (two minerals sharing atomic rows and symmetry characteristics). Topotaxy can be observed between olivine and its high-pressure polymorph wadsleyite, as well as between olivine and clinopyroxenes (e.g., Smyth et al., 2012). Olivine–lizardite relationships are not perfectly coherent and only partially topotactic. In contrast, olivine–antigorite (high-pressure and high-temperature serpentine) interfaces are commonly topotactic with $\left[\mathrm{100}{]}_{\text{atg}}\right|\left|\right[\mathrm{010}{]}_{\text{ol}}$ and $\langle \mathrm{100}{\rangle }_{\text{atg}}\left|\right|\langle \mathrm{100}{\rangle }_{\text{ol}}$. The planes in contact are then $\left(\mathrm{001}{)}_{\text{atg}}\right|\left|\right(\mathrm{100}{)}_{\text{ol}}$ and $\left(\mathrm{001}{)}_{\text{atg}}\right|\left|\right(\mathrm{010}{)}_{\text{ol}}$ (e.g., Boudier et al., 2010).

Noncoherent interfaces are the norm rather than the exception in natural and experimentally synthesized olivine-rich rocks. Furthermore olivine–diopside interfaces were proven to contain more atomic impurities than olivine grain boundaries (Hiraga et al., 2004, and references therein). The partitioning behavior of incompatible elements between the olivine lattice and its boundaries or interfaces was then estimated to be similar to olivine–melt partitioning (e.g., Hiraga and Kohlstedt, 2007; Hiraga et al., 2007). This observation is consistent with materials science studies indicating that, at high temperature, grain boundaries and interfaces behave, in terms of certain aspects or properties, as a glass-like material (e.g., Zhang et al., 2009).

5.3 Intragranular interfaces

In theory, two-dimensional defects occurring within a crystalline lattice are limited to stacking faults and antiphase boundaries. In fcc metals, a stacking fault is usually defined as a defective sequence of atomic planes, which can be extrinsic (the addition of an extra atomic plane) or intrinsic (a missing plane). Extrinsic stacking faults can be created by radiation damage, and intrinsic stacking faults can be created by the condensation of vacancies if located in one specific atomic plane or by a partial dislocation. In minerals, the definition is more general: across a stacking fault, two parts of a crystal are translated by a vector that is not a lattice repeat (2Dc in Fig. 3). Stacking faults in (021) were observed in olivine experimentally deformed at high pressure and high temperature (Couvy et al., 2004). From a purely theoretical point of view, generalized stacking faults (e.g., corresponding to any possible translation vector in a given plane) were successfully modeled for forsterite using first-principles calculations (Durinck et al., 2005).

A third type of intragranular interface is the twin boundary, which is an interface separating two volumes of the same crystal by a symmetrical operation, yielding a particular crystallographic relationship (2-Db in Fig. 3). Twin boundaries can form during mineral growth or plastic deformation (Hull and Bacon, 1989, pp. 14 and 125). They are very rare in olivine and are usually restricted to high-Ca compositions (e.g., Larsen et al., 1942; Azevedo and Nespolo, 2017). The following twin planes have been reported: {011}, {012}, and {031}. Twin boundaries in olivine were initially proposed to explain the curious microstructures of chondritic olivines (Dodd and Calef, 1971).

In natural crustal minerals, one can also find kinks, which can be viewed as the succession of two intragranular boundaries (forming a band), sometimes compensating for each other; however, “kinking” also applies to the bending of an important volume of a mineral lattice (Passchier et al., 2005). The crystallographic misorientation of a kink band is considered to be higher than 15^∘; thus kinks are not another category of sub-grain boundary. As for twin boundaries, kink bands are very rare in olivine but are observed in large grains of peridotitic olivines that were deformed at high temperature (Matysiak and Trepmann, 2012, 2015; Bickert et al., 2021). Kink bands were also observed in experimentally deformed Mg₂GeO₄ olivine (e.g., Burnley et al., 2013), in which they are linked to the shifting of slip systems from [100] to [001] dislocations with increasing pressure.

Antiphase boundaries are defects in atomic ordering over the atomic planes and are usually observed in very ordered crystalline materials. They can also be considered a specific type of stacking fault where one plane of the stacking fault was displaced laterally to produce one antiphase boundary. To date, antiphase boundaries have never been observed in olivine, and only a single study has explored their theoretical existence in olivine-type structures (Tabata et al., 1981). Their main conclusion was that the formation of a cationic antiphase boundary would require the formation and subsequent growth of a metastable nucleus already containing an incoherent cation arrangement. Antiphase boundaries have been reported in ringwoodite, one of the two high-pressure polymorphs of olivine (e.g., Madon and Poirier, 1983), and are repeatedly proposed as a mechanism involved during the olivine–ringwoodite phase transformation (e.g., Green, 1984).

6 Volume defects

Strictly speaking, volume defects are not defects within the olivine atomic structure but important 3-D discontinuities at the nanoscale or larger. Volume defects are very diverse, i.e., from nanovoids or intercrystalline pores to 3-D cracks or mineral, melt, fluid, or mixed inclusions.

6.1 Voids, pores, and cracks

Internal voids (or nanopores) are caused by gases trapped during olivine growth or by vacancy clustering during condensation. Examples of exceptional nanovoids in olivine can be found in Mosenfelder et al. (2011). These cavities can eventually promote nanoscale intracrystalline cracks if a crystal formed under high pressure and was subsequently decompressed. They can be quasi-negative crystalline in shape or simply spherical (3-Db in Fig. 3). These voids or nanopores may represent an additional reservoir for volatile elements (H₂O, H₂, CO₂, He, Ar). Nevertheless, to date, in situ TEM chemical analyses have been unable to identify the gases contained in nanoscale voids or pores within olivine (e.g., Burnard et al., 2015).

Figure 11 Inclusions in olivine: (a, b) optical microphotographs of a spinel inclusion and lily-pad-like cracks in San Carlos olivine; (c, d) optical microphotographs of melt inclusions in magmatic olivines from Piton de la Fournaise (from Bureau et al., 1998; images courtesy of Hélène Bureau); and (e) scanning electron microscope image and (f) TEM image of metal bleb inclusions in dusty olivines (from Leroux et al., 2003; images courtesy of Guy Libourel and Hugues Leroux).

6.2 Mineral inclusions

In magmatic olivines, the main mineral inclusions are Fe–Ti oxides (e.g., ilmenite, a few micrometers to 30 µm in length; e.g., Gurenko et al., 1998), followed in abundance by diopside (5–20 µm). Spinel-group minerals are also found as inclusions, with a notably wide range of compositions; e.g., Gurenko et al. (1998) reported 2.48 wt %–18.69 wt % TiO₂, ${\mathrm{Mg}}_{\mathrm{sp}}\mathit{\#}[\mathrm{Mg}/(\mathrm{Mg}+{\mathrm{Fe}}^{\mathrm{2}+}\left)\right]=$ 0.21–0.58, and ${\mathrm{Cr}}_{\mathrm{sp}}\mathit{\#}[\mathrm{Cr}/(\mathrm{Cr}+\mathrm{Al}\left)\right]=$ 0.17–0.74.

In mantle olivines, chromites are the most common inclusions, often associated with disk-shaped decompression cracks commonly called “lily pads” (Fig. 11a, b). As lamellae, the isotropic cubic spinels have an epitaxial relationship with their {111} faces perpendicular to the [100] axis of olivine (e.g., Roedder, 1965; Leander and Wirth, 2000). Other oxides such as ilmenite or magnetite are also observed in olivine (e.g., Mosenfelder et al., 2006). Olivines from Udachnaya contain a high diversity of mineral inclusions typical of deep-mantle olivines: chromite, garnet, pyroxenes, and sulfides (pyrrhotite, pentlandite, and chalcopyrite; e.g., Lazko and Afanasev, 1974). The concentrations and isotopic compositions of highly siderophile elements in such olivine-hosted sulfides are used as key tracers of the evolution of Earth's mantle (e.g., Alard et al., 2000; see the review by Lorand et al., 2013, and references therein).

The weathering of olivine leads to the crystallization of hydrous minerals such as serpentine, humite minerals, or iddingsite (MgO•Fe₂O₃•3SiO₂•4H₂O). These secondary minerals first occur as mere lamellae before developing into 3-D units. FTIR is a powerful tool for the detection of OH⁻ groups and the identification of the development of these hydrous minerals, even if the olivine remains optically perfectly transparent (Kitamura et al., 1987). Gem-quality hydrothermal olivines from Sapat, Pakistan (Fig. 1b), are embedded in fine-grained serpentine and talc, which penetrate the automorphic crystals as micrometric lamellae (e.g., Gose et al., 2010). This feature is typical of hydrothermal olivine (e.g., Miller et al., 1987).

Furthermore, annealing iron-bearing olivine at 500–900 ^∘C under oxidizing conditions (in air) leads to the formation of sub-nanometric iron-oxide precipitates organized in complex arrays perpendicular to dislocations and observable by TEM (Champness, 1970, her Fig. 5a, needles growing from the dislocation). Similar precipitates are observed in naturally oxidized olivines from a lherzolitic xenolith from Nunivak Island, Alaska (Kohlstedt and Vander Sande, 1975). This peculiar enhancement of dislocation width by inclusions has been used as a tool to increase the discernibility of dislocations by optical microscopy and to build paleopiezometers (e.g., Kohlstedt et al., 1976; Gueguen and Darot, 1980; see Soustelle et al., 2010, for a review and discussion).

6.3 Melt and fluid inclusions

Following Roedder (1984), melt, fluid, and crystal inclusions can be subdivided into primary, pseudo-secondary, and secondary types. Primary inclusions occur either as isolated inclusions or as apparently randomly oriented groups of inclusions that mark crystal-growth zoning in olivine. Pseudo-secondary inclusions occur along healed fractures that do not reach a grain boundary. Finally, secondary inclusions are usually controlled by completely sealed cracks. These three types of inclusion commonly occur in magmatic olivine, indicating complex and heterogeneous entrapment dynamics.

Melt inclusions are common in magmatic olivines (Fig. 11c, d) and range from 5 to 250 µm in size (Gurenko et al., 1998). In general, olivine-hosted melt inclusions are trapped during magmatic crystallization and develop an immobile gas bubble during rapid ascent toward the surface (e.g., Roedder, 1965). These inclusions can evolve until minerals precipitate (mostly clinopyroxene, occasionally with Fe–Ti oxides), leading to the co-existence of multiple phases (glass/gas bubble/daughter crystal). The study of melt inclusions and their statistical compositions is itself an important field in petro-geochemistry since melt inclusions are used as petrogenetic indicators in volcanology, a source of information regarding primitive mantle melts (e.g., Gurenko and Chaussidon, 1995; Gurenko et al., 1998), and as recorders of the compositional evolution and ascent rates of magmas (e.g., Chen et al., 2012). The stability of the volatile compositions of olivine-hosted melt inclusions is repeatedly questioned because partial volatile loss has been demonstrated several times (Portnyagin et al., 2008; Chen et al., 2012; Gaetani et al., 2012; Le Voyer et al., 2014). This is essentially due to the rapid diffusion of water and related species (OH⁻, H⁺) in both olivine and the melt and to possible microcracking. Less drastic cationic losses have also been observed for other elements such as Lu, Tb, and Eu (e.g., Spandler and O'Neill, 2010; Spandler et al., 2007). Thus, olivine-hosted melt inclusions can hardly be considered vaults for light and volatile elements trapped at crustal or mantle depths.

Complex (gas + liquid) fluid inclusions which are almost pure CO₂ are also observed in magmatic (phenocrystic) olivines (Gurenko et al., 1998). Cryothermometry allows compositional estimation if one component dominates the gas + liquid composition (e.g., the triple points of CO₂, CH₄, and N₂ are at −56.6, −182.5, and −210 ^∘C, respectively; e.g., Roedder, 1965, 1984; Gurenko et al., 1998).

One typical feature of mantle-derived olivines is trails of tiny (< 5 µm), liquefied, CO₂-rich (almost pure) inclusions, very often organized in a foil-like distribution and potentially showing a coalescent network (3-Dd in Fig. 3) (see Roedder, 1965). This type of inclusion is not exclusive to olivine; mantle diopside, orthopyroxenes, and plagioclase frequently contain such trails resulting from the healing of microcracks in the presence of an immiscible (dense) supercritical CO₂-rich fluid during their transport by basaltic magmas. These inclusions do not contain much water as mid- or near-infrared FTIR spectra do not show typical H₂O or OH⁻ bands in these sections of olivine grains.

Finally, in primitive meteorites, the olivines composing type-I chondrules frequently contain micrometric metal blebs (Fe₉₈Ni₁Co₁), which are often surrounded by a glass rim. These metal blebs are formed by sub-solidus reduction of iron-rich olivine (Fig. 11e, f). The host olivines are considered to be relic grains that formed after chondrule formation and may provide information on reprocessing events in the protoplanetary disk; they are generally called “dusty olivines” (e.g., Leroux et al., 2003; Einsle et al., 2016).

7 New defects – disclinations and disconnections

Whereas point defects, dislocations, and intergranular defects have been studied for several decades in materials science and mineralogy, two new crystalline defects are attracting new attention in the field of materials science, olivine, and other minerals: disclinations and disconnections. Both are specific types of line defects (1-Db and 1-Dc in Fig. 3).

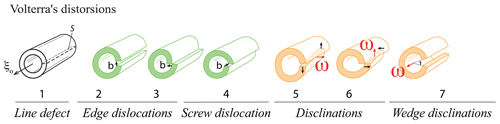
Figure 12 Volterra's distortions (Volterra, 1907). Sketches presenting the different types of deformation induced by (1) a line defect, (2–4) translation defects (dislocations) characterized by the Burgers vector b, and (5–7) rotation defects (disclinations) characterized by the rotation vector f (not shown; only the axis of rotation ω is shown as a black arrow).

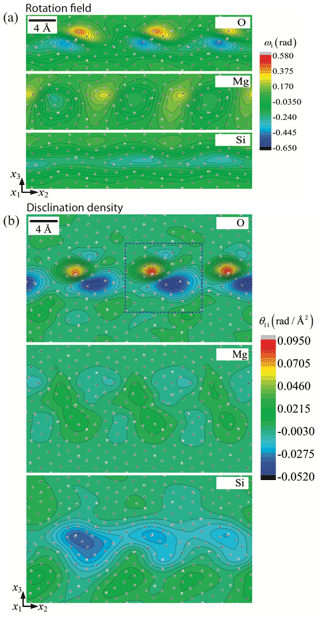
Figure 13 Disclination dipoles along a high-angle (60.8^∘), symmetric, tilt grain boundary in forsterite, obtained by molecular dynamics simulation (reproduced from Sun et al., 2016). (a) The rotation field for ω₁, shown for the three atoms of reference in the forsterite lattice: O (grey), Mg (dark grey), and Si (white). The rotation field can be extracted from high-spatial-resolution and high-angular-resolution EBSD maps, even if the scale of observation is not the same. Smaller EBSD steps provide a higher resolution of the disclinations and their dipoles but greater disclination density; thus special care must be taken when comparing EBSD maps. See Cordier et al. (2014) and Thieme et al. (2018) for in-depth discussion of geometrically necessary dislocation and disclination densities. (b) The disclination density for disclination θ₁₁. The square with a dashed blue outline indicates a disclination dipole. For reference, x₁, x₂, and x₃ are reference axes (see Sun et al., 2016).

7.1 Disclinations

Disclinations were theoretically defined by Volterra (1907) at the same time as dislocations as illustrated in Fig. 12. They are pure rotational defects, and, as with dislocations, one can define different types such as wedge and twist disclinations. The angle and direction of rotation (ω) define the Frank vector f (Frank, 1958). The relative rotational displacement also yields a small, space-dependent Burgers vector associated with the wedge disclination (e.g., Pond et al., 2007). Disclinations have long been considered in liquid crystals and are observed in polymers; biomineralized materials such as seashells; and superconductive materials, metals, and ionic components (e.g., Frank, 1958; Kleman and Friedel, 2008; Hirth et al., 2020; Träuble and Essman, 1968). As with dislocations, disclinations are set into motion by stress, and this motion results in disclination-mediated plasticity (Fressengeas et al., 2011; Beausir and Fressengeas, 2013; Cordier et al., 2014; Sun et al., 2016) which is not accounted for by the well-established dislocation theory (e.g., Hirth and Loth, 1968, p. 4).

Recent advances in EBSD have allowed a high-spatial and/or high-angular resolution of crystallographic misorientation in polycrystalline materials such as metals (e.g., copper; Beausir and Fressegneas, 2013) and rocks (Cordier et al., 2014; Wallis et al., 2016; Thieme et al., 2018). These new data, alongside processing methods identifying variations in misorientation gradients, have revealed disclinations distributed as dipoles along grain boundaries in metals such a copper (Beausir and Fressengeas, 2013; Fressengeas and Beausir, 2018; Ernould et al., 2020) and, more importantly, in experimentally deformed olivine, natural ophiolitic olivine-rich mylonites (Cordier et al., 2014), and numerically modeled forsterite boundaries (Sun et al., 2016, 2018). Examples of a rotation field and disclination density are shown in Fig. 13. Disclination dipoles are ubiquitous along grain boundaries and at triple junctions in fine-grained polycrystalline olivine and are estimated to move together during shear (e.g., Cordier et al., 2014; Sun et al., 2016, 2018). Whereas boundary shear is obvious at the nanoscale, a boundary might appear as the mere translational sliding of one grain relative to another at the macroscale, thus resembling pure grain boundary sliding, which theoretically requires one accommodation mechanism (e.g., cavitation, cracks; see Langdon, 2006, for a review). The lengthy neglect of disclinations as a strain-producing mechanism may be explained by the very high elastic energy they require as individual defects (Friedel, 1967). However, if present as dipoles, the required energy is similar to that of an edge dislocation (a few electronvolts; Romanov and Vladimirov, 1992; Romanov and Kolesnikova, 2009; Sun et al., 2016).

Figure 14 Disconnection along a grain boundary: “a defect inside a defect”. (a) A disconnection is characterized by a dislocation (with Burgers vector b) and a step (height h), or by the Frank vector f (e.g., generalized disclination; see Sun et al., 2018; Hirth et al., 2020). (b) An example of a disconnection along a Cu bi-crystal (grain boundary Σ17(410), redrawn from Combe et al., 2016). Dark and light green and red atoms do not have the same z coordinate.

Unlike for dislocation (Hirsch et al., 1965), there is no established theory of contrast for disclination in transmission electronic microscopy. To date, disclinations are not seen as a discrete and leading new mechanism of plastic deformation but as a companion to dislocations and point defects during deformation, which can help solve the olivine paradox (see Sect. 4.3). It is worth mentioning that, in equilibrated microstructures, all grain boundaries can be described to a first approximation using disclination dipoles. Furthermore, a 3-dimensional close-packed configuration of tetrakaidecahedra (Sect. 5.2.1) is never perfectly space-filling, and thus boundary-plane curvature is expected to occur at triple junctions in mantle rocks.

7.2 Disconnections

A disconnection is a structural step along a planar grain boundary, which exhibits a dislocation character (1-Dc in Fig. 3, Fig. 14). A disconnection forms when a coherent boundary/interface between two crystal lattices terminates. It can be seen as a defect inside a defect, or as a terrace-defect interface (e.g., Han et al., 2018). In this case, the defect is named a coherency disclination or a generalized disclination (Sun et al., 2018; Hirth et al., 2019, 2020). Although the terminology is still debated, a disconnection involves a step of height h and an associated dislocation with Burgers vector b, which belongs to the “displacement shift complete lattice”, or a disclination with Frank vector f (Fig. 14). A topological model is only available for disconnections in albite twins (Hirth et al., 2019), though this research direction is still in its infancy. Disconnections along a labradorite/pericline twin were very recently observed by TEM (Xie et al., 2019); but none have yet been observed in olivine, and the hunt has started. Furthermore, Hirth et al. (2020) proposed that disconnections are key components of twining, during ductile deformation, and recovery mechanisms in minerals such as grain growth (Han et al., 2018).

7.3 Impact on creep of olivine

Creep laws used to predict the high-temperature ductile deformation of olivine are proportional to stress as ∝σⁿ, although they remain entirely empirical (e.g., Hirth and Kohlstedt, 2003; for low-temperature creep, see also Demouchy et al., 2013; Gouriet et al., 2019). The role of grain boundaries, particularly disclinations and/or disconnections, remains hidden within the numerous parameters used to fit experimental data and their accuracy. One can envision that at the low temperatures where transport mechanisms are enhanced by grain boundaries (e.g., Chakraborty, 2008), grain boundaries and their associated defects would have a more important role in ductile deformation than at the high temperatures where dislocation motions in millimetric grains effectively dominate strain accommodation in olivine-rich rocks.

8 Conclusions

Olivine, like any other crystalline solid, contains a range of defects. (1) Point defects are the incorporation sites of minor, trace, and ultra-trace elements, including small volatile elements (H, He) and very large cations (Th), in natural specimens. The mechanisms of elemental incorporation and diffusion are very important to understanding the stability and longevity of chemical reservoirs in the deep Earth, including the water and carbon cycles. Whereas individual incorporation mechanisms and partitioning are fairly well understood, significant advances are needed to understand the interactions among the high diversity of extrinsic point defects. (2) Although the different slip systems in olivine have now been well identified, the role of motion of linear defects, particularly dislocations, at lithospheric temperatures and Earth-like slow strain rates remains a challenge for the understanding and prediction of the partial mechanical coupling at the lithosphere–asthenosphere transition or tectonic boundaries. Future efforts should focus on the localization of ductile deformation, solving the olivine paradox, and implementing the impacts of new defects such as disclinations. (3) Planar defects in olivine are finally receiving the attention they deserve as they could represent a major reservoir for chemical elements and may play a major role in strain accommodation. Statistical quantification of grain boundary planes in synthetic, deformed, and natural olivine-rich rocks remains lacking. (4) Volume defects in olivine are primary tools used to understand the geological evolution of Earth's interior and as a key witness of volcanic activity, and thus they remain an important and extremely active research domain. Moreover, the boundaries between melt/fluid or mineral inclusions and their host olivines remain poorly studied.

Electroneutrality implies that all these defects influence each other, but to date we barely understand their complex interactions. Furthermore, in metals or some simple ionic solids, the addition of atomic impurities commonly yields an increase in mechanical strength at room pressure due to lattice distortion, which then impedes dislocation motions (e.g., Poirier, 1976, pp. 218–221). However, in olivine, the addition of H, Fe, and Ti yields a decrease in strength at high pressure, high temperature, and rapid strain rates typical of laboratory experiments (e.g., Mackwell et al., 1985; Zhao et al., 2009, 2018; Demouchy et al., 2012; Faul et al., 2016; Tielke et al., 2017). The incorporation of charged atomic impurities enhances vacancy concentrations (Nakamura and Schmalzried, 1983; Hier-Majunder et al., 2004), which should enhance jog concentrations and thus dislocation climb and recovery mechanisms (e.g., Poirier, 1985, p. 56; Boioli et al., 2015a, b; Gouriet et al., 2019). Experimentally determined flow laws have reported an almost proportional relationship between strain rate and the concentrations of H, Ti, and Fe (Hirth and Kohlstedt, 2003; Faul et al., 2016; Zhao et al., 2009). Nonetheless, the main challenge remains the extrapolation to geodynamically relevant chemical concentrations and mechanical conditions, which requires the proper understanding of defect interactions from the atomic to the rock (metric) and plate-tectonic scale. Such an understanding is only possible by bridging the different scales and domains of research (mineralogy, sampling natural rocks, physics of condensed matter, materials science, rheological modeling), which remains a genuine challenge for modern geologists.

Appendix A: Kröger–Vink notation

This review uses Kröger–Vink notation to describe point defects (Kröger and Vink, 1956). This notation is used to track atomic species, the site of occupancy, and the electrical balance as ${\mathrm{Atom}}_{\mathrm{site}}^{\mathrm{charge}}$.

• The symbol is the name of the atomic species; a silicon atom is thus written as Si, and a missing atom (equivalent to a vacant site) is written V for vacancy.

• The occupied site is written as the subscript; i.e., Si_Si indicates a silicon atom in a silicon site, Fe_Si is then an iron atom in a silicon site, and V_Si is a vacant silicon site; a silicon atom in an interstitial site is written Si_i.

• The charge for a given site is written as the superscript, and charge equilibrium on a site is indicated as ^×. An excess of one charge on a site is indicated by a single dot as ^• and a deficit of one charge on a site as ^′, and the symbols are repeated to indicate the net charge relative to the theoretical charge for this site, for example, a 2+ charge as ^••. An interstitial always has the same charge as the atom occupying it. As examples, ${\mathrm{Si}}_{\mathrm{i}}^{\mathrm{•}\mathrm{•}\mathrm{•}\mathrm{•}}$ is an interstitial silicon atom, ${{\mathrm{Al}}^{\prime }}_{\mathrm{Si}}$ is an aluminum atom in a silicon site, ${\mathrm{V}}_{\mathrm{O}}^{\mathrm{•}\mathrm{•}}$ is a vacant oxygen site, ${\mathrm{Fe}}_{\mathrm{Mg}}^{\mathrm{•}}$ is a ferric iron (Fe³⁺) in a magnesium site, and ${\mathrm{Fe}}_{\mathrm{Mg}}^{\times }$ is a ferrous iron (Fe²⁺) in a magnesium site.

• Point defect equations must be equilibrated to (1) conservation of atomic site –, i.e., sites are neither created nor destroyed; (2) conservation of atomic species – i.e., there must be the same number of each atomic species before and after the reaction; and (3) maintain electroneutrality.