Breyite inclusions in diamond: experimental evidence for possible dual origin

Inclusions of breyite (previously known as walstromite-structured CaSiO₃) in diamond are usually interpreted as retrogressed CaSiO₃ perovskite trapped in the transition zone or the lower mantle. However, the thermodynamic stability field of breyite does not preclude its crystallization together with diamond under upper-mantle conditions (6–10 GPa). The possibility of breyite forming in subducted sedimentary material through the reaction CaCO₃ + SiO₂ = CaSiO₃ + C + O₂ was experimentally evaluated in the CaO–SiO₂–C–O₂ ± H₂O system at 6–10 GPa, 900–1500 ^∘C and oxygen fugacity 0.5–1.0 log units below the Fe–FeO (IW) buffer. One experimental series was conducted in the anhydrous subsystem and aimed at determining the melting temperature of the aragonite–coesite (or stishovite) assemblage. It was found that melting occurs at a lower temperature (∼1500 ^∘C) than the decarbonation reaction, which indicates that breyite cannot be formed from aragonite and silica under anhydrous conditions and an oxygen fugacity above IW – 1. In the second experimental series, we investigated partial melting of an aragonite–coesite mixture under hydrous conditions at the same pressures and redox conditions. The melting temperature in the presence of water decreased strongly (to 900–1200 ^∘C), and the melt had a hydrous silicate composition. The reduction of melt resulted in graphite crystallization in equilibrium with titanite-structured CaSi₂O₅ and breyite at ∼1000 ^∘C. The maximum pressure of possible breyite formation is limited by the reaction CaSiO₃ + SiO₂ = CaSi₂O₅ at ∼8 GPa. Based on the experimental results, it is concluded that breyite inclusions found in natural diamond may be formed from an aragonite–coesite assemblage or carbonate melt at 6–8 GPa via reduction at high water activity.

1 Introduction

Since the discovery by Joswig et al. (1999), CaSiO₃ inclusions in diamond have been reported by a number of researchers. Monomineralic CaSiO₃ inclusions as well as CaSiO₃ coexisting with larnite, titanite-structured CaSi₂O₅, calcite (aragonite), perovskite, silica polymorphs, orthopyroxene (possibly converted from bridgmanite), clinopyroxene, ringwoodite, ferropericlase, monticellite and cuspidine have been described in diamonds from Kankan, Guinea (Joswig et al., 1999; Stachel et al., 2000; Nasdala et al., 2003); Juína, Brazil (Hayman et al., 2005; Brenker et al., 2007; Walter et al., 2008; Wirth et al., 2009; Bulanova et al., 2010; Pearson et al., 2014; Anzolini et al., 2016; Kaminsky et al., 2016); Machado River, Brazil (Burnham et al., 2016); and the Slave province, Canada (Davies et al., 2004; Tappert et al., 2005). CaSiO₃ was also documented as a daughter mineral of multiphase inclusions in Juína diamond, which presumably formed through the crystallization of carbonatitic melts (Kaminsky et al., 2009). Most of the CaSiO₃ phases were identified as triclinic wollastonite II or walstromite-structured CaSiO₃. The two polymorphs have very similar crystal structures (Joswig et al., 2003), but their relative stability relations are unknown (Dörsam et al., 2009). Therefore, the terms wollastonite II and walstromite-structured CaSiO₃ have often been used synonymously. The name breyite was recently proposed for the latter phase and approved by IMA in 2018 (IMA no. 2018-062; Brenker et al., 2018).

Calcium metasilicate CaSiO₃ occurs in a number of structural modifications, and its phase diagram has been extensively studied. Ringwood and Major (1967) converted wollastonite to a denser phase (breyite) at 3 GPa and ∼900 ^∘C. The wollastonite–breyite boundary was then tightly constrained by experiments (e.g., Essene, 1974; Gasparik et al., 1994; Akaogi et al., 2004). Kanzaki et al. (1991) observed breyite decomposition to larnite (Ca₂SiO₄) and titanite-structured CaSi₂O₅ at 12 GPa and 1500 ^∘C. This reaction was studied in detail by Kubo et al. (1997) and Akaogi et al. (2004). Sueda et al. (2006) experimentally demonstrated that the larnite + CaSi₂O₅ assemblage transforms to CaSiO₃ perovskite at a pressure of ∼14 GPa. Gasparik et al. (1994) determined the melting temperatures of CaSiO₃ polymorphs at pressures of 8–16 GPa. Phase relations of CaSiO₃ are summarized in Fig. 1.

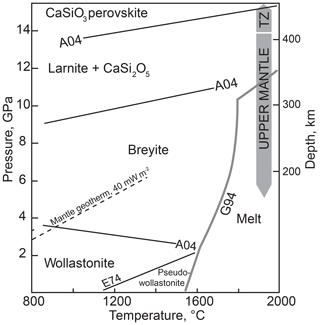
Figure 1 Schematic phase diagram of CaSiO₃ under moderate pressure–temperature conditions. Sources of data: A04, Akaogi et al. (2004); E74, Essene (1974); G94, Gasparik et al. (1994). TZ is the transition zone. The conductive mantle geotherm for a heat flow of 40 mW m⁻² is shown following Hasterok and Chapman (2011). The field of monoclinic wollastonite II (Chatterjee et al., 1984) is omitted.

It is clear from the phase diagram (Fig. 1) that the interpretation of monomineralic breyite inclusions in diamond may be ambiguous. The more common scenario implies the entrapment of CaSiO₃ perovskite in the transition zone or lower mantle and its conversion to breyite upon decompression (e.g., Joswig et al., 1999; Brenker et al., 2007; Harte, 2010; Kaminsky, 2012; Burnham et al., 2016). This interpretation is favored by the ubiquity of CaSiO₃ perovskite in the lower mantle (e.g., Wood, 2000; Irifune and Tsuchiya, 2007), the occurrence of breyite together with ferropericlase ± bridgmanite in a single diamond (Stachel et al., 2000) and coexistence of breyite with ringwoodite in a diamond (Pearson et al., 2014). One problem is the enormous volume change of the CaSiO₃ perovskite to breyite transformation of ∼38 % (Akaogi et al., 2004). Anzolini et al. (2016) estimated a minimum entrapment pressure of breyite in Juína diamond as 5.7 GPa at 1500 K and argued that the inclusion could not have converted from CaSiO₃ perovskite because of the large volume change involved. To accommodate such a volume change, diamond had to have experienced cracking or considerable plastic deformation, features not detected by Anzolini et al. (2016). In contrast, plastic and brittle deformations were observed around breyite inclusions in diamond by Cayzer et al. (2008), Zedgenizov et al. (2015), Burnham et al. (2015, 2016) and Anzolini et al. (2018), which emphasizes the possibility of the dual origin of breyite inclusions in diamond.

The suggestion that a breyite inclusion can form through direct entrapment at 4–10 GPa rather than from a perovskite precursor is consistent with the CaSiO₃ phase diagram (Fig. 1). In this study we explore this possibility by high-pressure experiments in the simple CaO–SiO₂–C–O₂ system with or without H₂O.

2 Problem formulation

In contrast to CaSiO₃ perovskite, breyite is not stable in a peridotitic mantle because of the reaction with low-Ca pyroxene:

$$\begin{array}{}\text{(R1)}& {\mathrm{CaSiO}}_{\mathrm{3}}+{\mathrm{MgSiO}}_{\mathrm{3}}={\mathrm{CaMgSi}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{6}}.\end{array}$$

High-Ca pyroxene is stable up to ∼17–18 GPa (Akaogi et al., 2004), i.e., above the breyite stability field. There are no CaSiO₃ phases in subducted basaltic crust (MORB) up to ∼20 GPa (e.g., Perrillat et al., 2006). Hence, another lithology for breyite crystallization must be looked for. Wollastonite occurs very rarely in high-pressure rocks (Chopin et al., 2008; Galvez et al., 2013a, b) and is absent in subducted sediments (Li and Schoonmaker, 2003). However, the association of calcite and silica is very common in oceanic sediments (Li and Schoonmaker, 2003) and could be a viable source of CaSiO₃ formation via the decarbonation reaction

$$\begin{array}{}\text{(R2)}& {\mathrm{CaCO}}_{\mathrm{3}}+{\mathrm{SiO}}_{\mathrm{2}}={\mathrm{CaSiO}}_{\mathrm{3}}+{\mathrm{CO}}_{\mathrm{2}}.\end{array}$$

Hence, the system CaO–SiO₂–C–O₂ rather than CaSiO₃–C should be considered. Litasov et al. (2017) calculated the position of Reaction (R2) at high pressures under fluid-saturated conditions (Fig. 2). They showed that Reaction (R2) intersects the melting curve of CaCO₃ at pressure close to the graphite–diamond transformation. However, Reaction (R2) becomes metastable even at significantly lower pressures because of the occurrence of the melting reaction

$$\begin{array}{}\text{(R3)}& {\mathrm{CaCO}}_{\mathrm{3}}+{\mathrm{SiO}}_{\mathrm{2}}=\text{melt},\end{array}$$

as indicated by experiments in the CaO–SiO₂–CO₂ system by Wyllie and Huang (1976) and Huang et al. (1980). These studies showed that Reaction (R2) terminates in an invariant point at ∼1.8 GPa and 1320 ^∘C and is metastable at higher pressures. The position of Reaction (R3) in the diamond stability field was not studied experimentally, but it is clear that breyite cannot be produced by decarbonation Reaction (R2) in the presence of a CO₂ fluid or, more precisely, a CO₂–CO fluid whose composition depends on oxygen fugacity (fO₂).

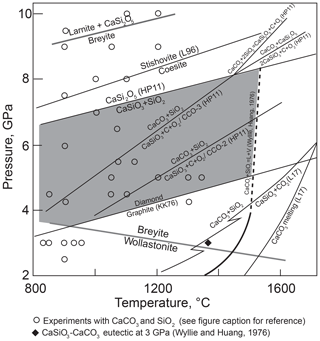
Figure 2 Selected equilibria of the CaO–SiO₂–C–O₂ system relevant for the conditions of breyite crystallization via decarbonation Reaction (R2). Solid gray lines show CaSiO₃ transformation reactions wollastonite to breyite and breyite to larnite + CaSi₂O₅ (Fig. 1). Other lines show experimental and theoretical estimates of equilibria in the system. Sources of data: L96, Liu et al. (1996); HP11, Holland and Powell (2011); L17, Litasov et al. (2017); KK, Kennedy and Kennedy (1976). The reaction CaCO₃ + SiO₂ = CaSiO₃ + CO₂ was calculated by Litasov et al. (2017) for fluid-saturated conditions; kinks on the reaction line are related to the quartz–coesite and wollastonite–breyite transformations. The reaction lines CaCO₃ + SiO₂ = CaSiO₃ + C + O₂ were calculated using thermodynamic data from Holland and Powell (2011) for logfO₂ values CCO – 2 and CCO – 3 in the absence of fluid. Melting of CaCO₃ + SiO₂ was experimentally studied up to 3 GPa (Wyllie and Huang, 1976; Huang et al., 1980) and is extrapolated arbitrarily to higher pressures as a dashed line. Circles show melting experiments in hydrous and anhydrous systems in which coexisting CaCO₃ and SiO₂ were observed (Hammouda, 2003; Yaxley and Brey, 2004; Grassi and Schmidt, 2011a, b; Tsuno and Dasgupta, 2012; Kiseeva et al., 2012, 2013; Poli, 2015; Brey et al., 2015; Mann and Schmidt, 2015; Martin and Hermann, 2018). The shaded field shows the conditions of possible formation of breyite inclusions in diamond.

Decarbonation is possible at lower temperatures, if CO₂ activity is lower than that in the presence of CO₂ fluid or, alternatively, at a fO₂ below the C–CO–CO₂ buffer, via the reaction

$$\begin{array}{}\text{(R4)}& {\mathrm{CaCO}}_{\mathrm{3}}+{\mathrm{SiO}}_{\mathrm{2}}={\mathrm{CaSiO}}_{\mathrm{3}}+\mathrm{C}+{\mathrm{O}}_{\mathrm{2}}.\end{array}$$

Another reaction limiting the possible conditions of breyite crystallization in the diamond stability field is

$$\begin{array}{}\text{(R5)}& {\mathrm{CaSiO}}_{\mathrm{3}}+{\mathrm{SiO}}_{\mathrm{2}}={\mathrm{CaSi}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}.\end{array}$$

Experiments in the CaSiO₃–CaTiO₃ (Kubo et al., 1997) and CaTiSiO₅–CaSi₂O₅ systems (Knoche et al., 1998) at 5.3–16 GPa and 1200 and 1350 ^∘C, respectively, showed that the breyite–coesite assemblage transforms to CaSi₂O₅ in the Ti-free system between 5.3 and 8.7 GPa. Calculations using the thermodynamic data of Holland and Powell (2011) indicate that equilibrium (Reaction R5) lies ∼3.0 GPa above the graphite–diamond boundary (Fig. 2). It is evident that Reaction (R5) limits the pressure range where breyite can form in metasedimentary (silica-saturated) assemblages.

With these considerations in mind, our experimental study had the following goals:

1. to constrain the temperature dependence of melting Reaction (R3) at 6–10 GPa and its position relative to redox Reaction (R4) at low but geologically realistic oxygen fugacities near the iron–wüstite (IW) buffer,

2. to model the formation of CaSiO₃ at low CO₂ activity in the presence of mixed C–O–H fluid, and

3. to obtain experimental constraints for the lower stability limit of Reaction (R5).

3 Experiments

Two types of experiments were conducted. (1) One configuration consisted of three layers (from bottom to top): Fe metal, SiO₂ and CaCO₃. These experiments simulated melting of CaCO₃ (aragonite) + SiO₂ (coesite or stishovite) under anhydrous conditions with simultaneous carbonate reduction at a fO₂ near IW. (2) The second configuration comprised two layers, a mixture of Fe metal and Mg(OH)₂ in the lower part of the sample and a SiO₂–CaCO₃ mixture in the upper part, nonhermetically separated by a Pt disc. These experiments simulated the interaction of CaCO₃ and SiO₂ with a mixed reduced fluid produced by the reaction

$$\begin{array}{}\text{(R6)}& \mathrm{Fe}+\mathrm{Mg}(\mathrm{OH}{)}_{\mathrm{2}}=\mathrm{2}(\mathrm{Fe},\mathrm{Mg})\mathrm{O}+{\mathrm{H}}_{\mathrm{2}}\end{array}$$

and subsequent interaction of H-bearing species with CaCO₃ in the upper zone.

Starting materials for the experiments were prepared from Fe, SiO₂ and Mg(OH)₂ reagents along with natural calcite (Icelandic spar). The initial components were pulverized in an agate mortar to a grain size <20 µm and mixed, when necessary, by grinding under ethanol. Sample powders were packed into Pt capsules with a 1.4 mm inner diameter and ∼2.5 mm long.

The experiments were performed in a Walker-type multianvil apparatus using tungsten carbide cubes with a truncation edge length of 8 mm. The pressure assembly consisted of a 95 % MgO + 5 % Cr₂O₃ octahedron, a zirconia sleeve, a Re foil heater and MgO inserts around the capsule. Any free space was filled with Al₂O₃-based cement of W. Haldenwager Technische Keramic GmbH. Pressure was calibrated against the Mg₂SiO₄ olivine–wadsleyite phase transition at 1200 ^∘C and 13.6 GPa (Morishima et al., 1994), the coesite–stishovite transition at 1650 ^∘C and 10.6 GPa (Zhang et al., 1996), and the CaGeO₃ garnet–perovskite transition at 1200 ^∘C and 5.6 GPa (Ross et al., 1986). The experimental apparatus and pressure calibration were described in detail by Brey et al. (2008). The uncertainty in pressure was estimated as ±0.3 GPa. Temperature was measured with a W₉₅Re₅–W₇₄Re₂₆ thermocouple inserted through an Al₂O₃ ceramic tube at the top end of the capsule. Temperature fluctuations during the experiments were no higher than ±3 ^∘C. The duration of the experiments was 1 to 45 h (Table 1). The experiments were terminated by shutting off the power supply. After the experiment, the capsule was mounted into epoxy, sectioned lengthwise and polished with oil-based diamond pastes. The products were analyzed with a Jeol 8900 Superprobe electron microprobe in wavelength dispersive mode. The microprobe is equipped with five spectrometers along with an energy-dispersive spectroscopy (EDS) system. The following natural and synthetic phases were used as standards: wollastonite for Si and Ca, Al₂O₃ for Al, fayalite for Fe, forsterite for Mg, and albite for Na. The analytical conditions were as follows: 15 kV accelerating voltage, 20 nA beam current, and 20–40 s counting time for peak and background. Minerals were analyzed with a focused beam and quenched melts, with a beam defocused to a 20 µm spot size. Some experiments were analyzed with a Jeol JSM-6490 scanning electron microscope equipped with an INCA analytical system. The accuracy of INCA EDS analysis was inferior to that of the electron microprobe, and these analyses were considered semiquantitative. However, the quality of these analyses was sufficient for identification of experimental phases, most of which were of fixed composition.

Table 1 Conditions and products of experiments.

Mineral abbreviation: Arg, aragonite; Br, breyite; Coe, coesite; Coh, cohenite; Di, diopside; En, enstatite; Fa, fayalite; Fo, forsterite; FPer, ferropericlase; Fs, ferrosilite; Gr, graphite; Ol, Fe–Mg olivine; Opx, Fe–Mg pyroxene; Sti, stishovite

In all anhydrous experiments (type 1), metallic iron coexisted with wüstite (pure FeO), which indicates that the fO₂ was close to the IW buffer reaction:

$$\begin{array}{}\text{(R7)}& \mathrm{2}\mathrm{FeO}=\mathrm{2}\mathrm{Fe}+{\mathrm{O}}_{\mathrm{2}}.\end{array}$$

However, careful inspection of the experimental products revealed that the actual fO₂ could differ from IW. In most cases, the association of metallic iron and wüstite was observed in the central part of the metal zone, whereas its outer part consisted only of pure iron, suggesting that the fO₂ was below IW. Some oxygen fugacity gradient existed evidently between the inner and outer parts of the metal zone. It is reasonable to suggest that the oxygen fugacity in the carbonate zone was controlled by equilibria at the interface between the iron and silica zones. Ferrosilite and fayalite were observed in most experiments of this series between iron metal and silica. Hence, the oxygen fugacity was controlled by the reactions

$$\begin{array}{}\text{(R8)}& \mathrm{2}{\mathrm{Fe}}_{\mathrm{2}}{\mathrm{SiO}}_{\mathrm{4}}=\mathrm{2}\mathrm{Fe}+{\mathrm{Fe}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{6}}+{\mathrm{O}}_{\mathrm{2}}\end{array}$$

or, when fayalite was absent,

$$\begin{array}{}\text{(R9)}& {\mathrm{Fe}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{6}}=\mathrm{2}\mathrm{Fe}+{\mathrm{SiO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}.\end{array}$$

Reactions (R8) and (R9) are sums of equilibrium (Reaction R7) and the following reactions:

$$\begin{array}{}\text{(R10)}& {\displaystyle }& {\displaystyle }\mathrm{2}{\mathrm{Fe}}_{\mathrm{2}}{\mathrm{SiO}}_{\mathrm{4}}=\mathrm{2}\mathrm{FeO}+{\mathrm{Fe}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{6}},\text{(R11)}& {\displaystyle }& {\displaystyle }{\mathrm{Fe}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{6}}=\mathrm{2}\mathrm{FeO}+\mathrm{2}{\mathrm{SiO}}_{\mathrm{2}},\end{array}$$

respectively. Therefore, the logfO₂ relative to the IW buffer can be calculated as

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }\mathrm{IW}=\log f{\mathrm{O}}_{\mathrm{2}}-\log f{\mathrm{O}}_{\mathrm{2}}\left(\mathrm{IW}\right)=\mathrm{\Delta }G\left(\mathrm{10}\right)/\mathrm{2.303}RT\end{array}$$

for the fayalite–ferrosilite–iron assemblage and

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }\mathrm{IW}=\mathrm{\Delta }G\left(\mathrm{11}\right)/\mathrm{2.303}RT\end{array}$$

for the iron–ferrosilite–silica (coesite or stishovite), where ΔG(i) is the Gibbs free energy change of the respective reaction, T is the absolute temperature and R is the universal gas constant. The fO₂ was calculated using the thermodynamic properties of phases from the dataset of Holland and Powell (2011). In most cases, the resulting fO₂ values lie 0.5–1.0 log units below IW (Table 1). To further decrease the fO₂ in one experiment (M753), San Carlos olivine (Mg no. ∼0.9) was added to the starting Fe layer. This produced Fe–Mg olivine and orthopyroxene solid solutions in the Fe zone, which imposed a fO₂ of ∼IW – 1.

Figure 3 Back-scattered electron (BSE) images of the products of anhydrous melting experiment M751 (8 GPa, 1500 ^∘C). (a) Overview of the sample capsule. Black material outside the Pt capsule is epoxy. (b–d) Details of the sample indicated by rectangles in (a). Mineral symbols: Arg, aragonite; Coe, coesite; Fa, fayalite; and Fs, ferrosilite.

In the hydrous experiments (type 2), the buffer assemblage consisted always of metallic Fe free of measurable Pt or any other admixture and ferropericlase with $\mathrm{Mg}/(\mathrm{Mg}+\mathrm{Fe})$ of approximately 0.3–0.4 (Table 1). The composition of ferropericlase was rather uniform in all experiments, with no systematic variations occurring in contact with the capsule. For these experiments, the fO₂ relative to IW was calculated as $\mathrm{\Delta }\mathrm{IW}=\mathrm{2}\ln \left(a_{\mathrm{FeO}}\right)/\mathrm{2.303}RT$, where a_FeO is the activity of FeO in ferropericlase, calculated using the model of O'Neill et al. (2003). The resulting fO₂ values are lower than IW by 0.2–0.3 log units.

4 Experimental results

4.1 Anhydrous aragonite–SiO₂ melting

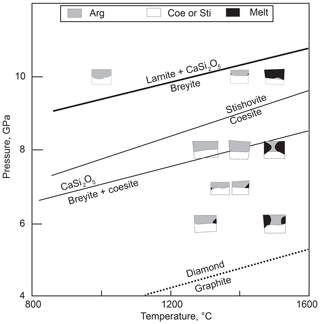
In the subsolidus experiments at temperatures ≤1300 ^∘C, the three layers remained separated with only minor interaction between Fe metal and SiO₂ that produced ferrosilite and fayalite, whereas no interaction was observed between aragonite and SiO₂. At higher temperatures, quenched melt appeared at the contacts between aragonite and SiO₂ (Fig. 3). The first melt portion appears near the walls of capsules, in the zones of highest temperature. The amount of melt increases rapidly between 1400 and 1500 ^∘C (Fig. 4). Minor graphite grains were observed in some experiments in or near the melt pools. Their occasional presence within carbonate crystals suggests that graphite was present during the experiment and is not a quench phase. In the most reduced experiment with olivine in the Fe zone (M753 at 8 GPa, 1300 ^∘C and logfO₂ ∼IW – 1), more extensive graphite formation was observed (Fig. 5). In this experiment, graphite formed a continuous band of small crystals near the coesite–aragonite contact. Despite the considerable amount of graphite, breyite was not observed in this run, indicating that Reaction (R2) remains metastable under such conditions.

4.2 Hydrous experiments

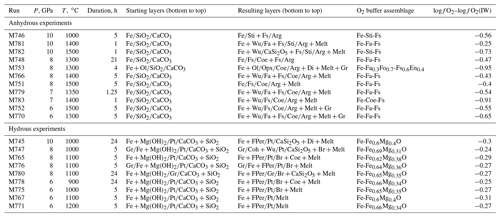
Melt was always present as a major phase in these experiments. The quench texture was very different from that observed in the anhydrous experiments and consisted of a very fine-grained or even glassy matrix and acicular quench coesite or stishovite crystals (Fig. 6). Equilibrium growth of crystals often occurred along the walls or bottom of the capsule. CaSi₂O₅ formed large euhedral crystals up to 30–50 µm across (Fig. 6a, b). Stishovite crystallized as long prismatic crystals, which were easily distinguished from isometric coesite grains. Breyite was observed in minor amounts at 6–8 GPa (Fig. 7) as short-to-long prismatic grains up to 20 µm long (Fig. 6b–d). Diopside occurred in some of the experiments due to Mg contamination from the lower buffer zone. Graphite was present in all experiments both within the melt phase and as inclusions in silicate crystals.

Figure 4 Summary of anhydrous melting experiments. Symbols show schematic relations of run products. Sources of data for mineral reactions are the same as in Figs. 1 and 2.

4.3 Phase compositions

The solid phases mostly have constant compositions and approach ideal stoichiometric element ratios (Table 2). Through contamination with the buffer materials, minor amounts of Mg and Fe were occasionally present in the calcium silicate phases. Aragonite and silica minerals were almost always free of Fe and Mg.

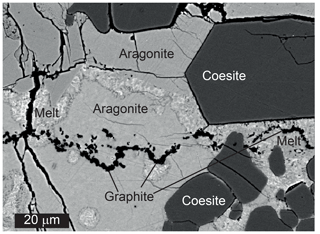
Figure 5 BSE illustrating simultaneous melting and reduction near the aragonite–coesite contact in run M753 at 8 GPa, 1300 ^∘C and $f_{{\mathrm{O}}_{\mathrm{2}}}$ at IW – 1. This run was conducted under more reduced conditions compared with other experiment, which resulted in more extensive graphite formation. Note that, despite significant reduction, breyite was not formed. The melt zone apparently moved upward, probably under the influence of a temperature gradient.

Figure 6 BSE images of hydrous experiments. (a) Run M745 (10 GPa, 1000 ^∘C). Euhedral crystals of CaSi₂O₅ in the lower part of the sample below the zone of pure melt. (b) Run M747 (8 GPa, 1000 ^∘C). Breyite crystallization between the layer of CaSi₂O₅ grains and melt. The black band between breyite and CaSi₂O₅ is a crack filled with epoxy. (c) Run M775 (6 GPa, 1000 ^∘C). Breyite crystals near the wall of the Pt capsule in quenched melt. (d) Run M778 (6 GPa, 900 ^∘C). Coesite grains and long prismatic to acicular breyite crystals at the bottom of the sample.

Table 2 Compositions of experimental phases, wt %.

One standard deviation is given in parentheses.

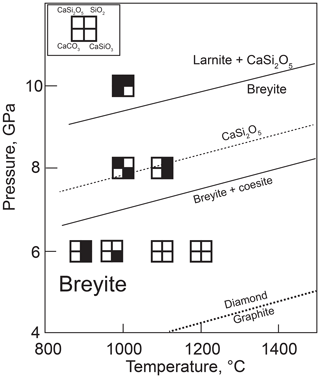
Figure 7 Summary of hydrous melting experiments. Sources of data for mineral reactions are the same as in Figs. 1 and 2. The position of the reaction breyite + coesite = CaSi₂O₅ is shown as calculated from the thermodynamic data of Holland and Powell (2011) (solid line) and from the results of our experiments (dashed line). Note that an additional melt phase is present in all experiments.

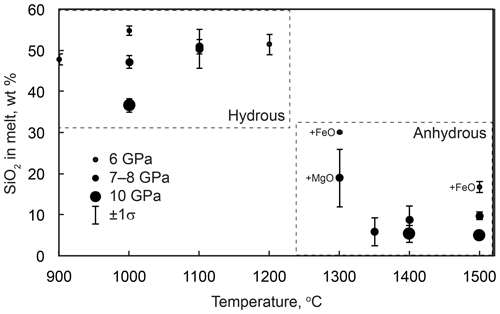
Figure 8 Silica contents in quenched melts from the anhydrous and hydrous experiments. Melts from the anhydrous experiments labeled “+FeO” and “+MgO” were contaminated with FeO and MgO, respectively, from buffer mixtures at a level of several weight percent (Table 2).

The melt composition from the anhydrous melting experiments was rather variable, especially at low temperatures and low melt fractions (Table 2, Fig. 8). This is related to contamination of the CaCO₃–SiO₂ system by Fe from the buffer mixture and, possibly, other chemical components from the starting reagents. The influence of these components was most significant at low melt fractions, as indicated by significant FeO and MgO contents in the melt from some experiments. Melt from run M770 (6 GPa, 1300 ^∘C) contained up to 18 wt % FeO, and its SiO₂ content was also unusually high, ∼30 wt %. At higher temperatures, the amount of impurities decreased and the melt shifted to a Ca carbonate composition with 5–10 wt % SiO₂ (Fig. 8). The melt composition is essentially insensitive to temperature above 1300 ^∘C. The SiO₂ content seems to decrease with increasing pressure, although the available data are insufficient for a quantitative assessment.

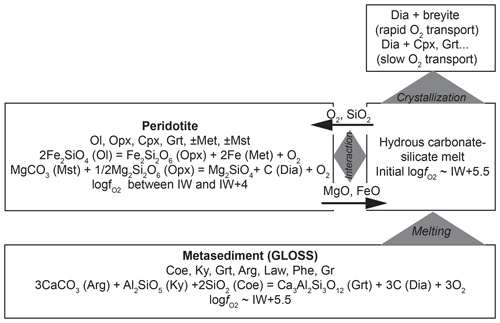
Figure 9 Flow diagram describing a possible scenario for the formation of diamond-hosted breyite inclusions at upper-mantle conditions (6–8 GPa and 1000 ^∘C) through interaction of hydrous carbonated metapelite and reduced peridotite. Mineral assemblages and reactions controlling fO₂ are shown. Black arrows show the fluxes of main components under the influence of chemical potential gradients (e.g., Bulatov et al., 2014).

The compositions of melts from the hydrous experiments are different and can be qualified as hydrous calcium silicate liquids. The content of carbonate species is probably low, which is suggested by the absence of quench carbonates and the abundance of graphite produced by the reduction of starting CaCO₃. The SiO₂ content ranges from ∼35 to 55 wt % and is insensitive to temperature but decreases with increasing pressure (Fig. 8).

5 Discussion and conclusions

5.1 Decarbonation versus melting reactions

The position of melting Reaction (R3) can be only approximately constrained by our experiments. Its eutectic nature is supported by the absence of additional phases over the melting interval and the independence of melt composition on the degree of melting at high temperatures. However, there are obviously departures from the eutectic behavior. The solid assemblage is transformed to melt (until exhaustion of either silica of aragonite) over a considerable temperature interval rather than at a constant temperature (Fig. 4). There are several reasons for such behavior. First, there is a temperature gradient within the capsule. Our estimates (Woodland et al., 2018) indicate that temperature variation within the short capsules used in the experiments could be up to 50 ^∘C. This explains the gradual propagation of the melt zone from capsule walls toward the center of the sample. Secondly, Fe contamination was observed in many experiments, and significant amounts of FeO were dissolved in melts at low melt fraction. This explains the appearance of small amounts of melt very far from the liquidus and the slow increase in the degree of melting at temperatures 100–200 ^∘C below the liquidus. Thirdly, the presence of minor amounts of graphite in some experiments indicates that the melting was at least not always eutectic but peritectic in nature via the reaction

$$\begin{array}{}\text{(R12)}& {\mathrm{CaCO}}_{\mathrm{3}}+{\mathrm{SiO}}_{\mathrm{2}}=\text{melt}+\mathrm{C}+{\mathrm{O}}_{\mathrm{2}}.\end{array}$$

Finally, the presence of minor amounts of H₂O and/or CH₄ cannot be excluded because of impurities in the starting materials and possible hydrogen migration into the capsule during the experiment. Hence, the melt composition was not constant but changed with increasing temperature, causing melting to occur over a finite temperature interval. However, at high melt fractions, the influence of contamination decreases, and the position of disappearance of aragonite should be close to the position of the eutectic reaction.

Our results suggest that Reaction (R3) occurs at temperatures slightly higher than 1500 ^∘C at 6–8 GPa and at ∼1500 ^∘C at 10 GPa. The increase in melt fraction as pressure increases from 6 to 8 GPa at 1500 ^∘C suggests that Reaction (R3) could have a negative slope in the coesite stability field. This is in line with a very weak to negligible pressure effect on the melting temperature of CaCO₃ above 5 GPa (Li et al., 2017). At 10 GPa, stishovite occurs instead of coesite, which results in a larger volume change of the melting reaction and a different (though unconstrained) slope of this melting reaction.

The absence of CaSiO₃ in all experiments of this series implies that Reaction (2) is metastable under CO₂-undersaturated conditions at a fO₂≈ IW – 0.5. This result is at odds with calculations of Reaction (R2) using the thermodynamic properties of phases from Holland and Powell (2011). These calculations indicate that a decrease in fCO₂ and, correspondingly, fO₂ shifts Reaction (R2) to lower temperatures. As depicted in Fig. 2, already at fO₂ values 3 log units below the C–CO–CO₂ (CCO) equilibrium (0.5–3.0 log units above the IW buffer), Reaction (R2) occurs at lower temperatures than CaCO₃–SiO₂ melting over the whole pressure range of breyite stability. Hence, breyite should have been stable rather than aragonite and coesite at least in our highest temperature experiments. The absence of CaSiO₃ in the experimental products could be related to the low melting temperature of the CaSiO₃ + CaCO₃ assemblage. At 3 GPa, the eutectic melting of this assemblage occurs ∼100 ^∘C below the CaCO₃ + SiO₂ eutectic melting point (Huang and Wyllie, 1974). The melting relations of CaSiO₃ + CaCO₃ at 6 GPa were recently studied by Fedoraeva et al. (2019). They determined the aragonite–breyite eutectic temperature to be 1400 ^∘C at 6 GPa, which is lower than the temperature of melting Reactions (R3) and (R12) at this pressure.

The metastability of the aragonite–coesite–breyite assemblage is indirectly supported by the results of other experimental studies. Figure 2 shows the pressure–temperature conditions of melting experiments in various systems in which silica and aragonite (calcite) are present. The silica–calcite–wollastonite assemblage was observed in a single experiment on calcite assimilation in dacitic melt at 0.5 GPa and 1000 ^∘C (Carter and Dasgupta, 2016). In all previous experiments above 3 GPa, the CaCO₃ + SiO₂ assemblage remained stable up to 1400 ^∘C under uncontrolled fO₂. Thus, we conclude that at a fO₂ 0.5–1.0 log units below IW, decarbonation Reaction (R2) is metastable owing to the occurrence of eutectic melting.

5.2 The equilibrium CaSiO₃ + SiO₂ = CaSi₂O₅

Equilibrium (Reaction R5) additionally limits the conditions of possible breyite formation from CaCO₃ and SiO₂. Although it has not been systematically studied experimentally, the position of this equilibrium in pressure–temperature space can be estimated from the thermodynamic data of Holland and Powell (2011). For example, CaSi₂O₅ should become stable at 1100 ^∘C at a pressure of 7.3 GPa. As plotted in Fig. 2, it is apparent that the stability field of breyite is reduced by ∼2 GPa if the metasedimentary assemblage is SiO₂-saturated. However, the results of our hydrous experiments can provide some additional constraints on the actual position of this reaction. Of three experiments performed at 8 GPa and 1100 ^∘C, one produced CaSi₂O₅ (Table 1, Fig. 7). The other two experiments at this temperature produced either breyite + SiO₂ or only breyite. In an additional experiment at 1000 ^∘C, CaSi₂O₅ was found to coexist with breyite but without coesite (Table 1). Thus, the equilibrium (Reaction R5) must lie very close to 8 GPa at 1100 ^∘C, i.e., ∼0.7 GPa higher than its position calculated using the Holland and Powell (2011) data (Fig. 7). This discrepancy is equivalent to a difference in the ΔH of Reaction (R5) of 5.5 kJ, which is approximately equal to the 2σ uncertainty in the ΔH of CaSi₂O₅ as given by Holland and Powell (2011) (2.8 kJ). The uncertainties in ΔH for SiO₂ and CaSiO₃ are much smaller (0.5 kJ). Therefore, it can be concluded that the data of Holland and Powell (2011) are consistent within their 2σ uncertainty with our experimental observations. On the other hand, our results do significantly extend the pressure range of possible breyite crystallization in SiO₂-saturated bulk compositions (Fig. 7).

Under natural conditions, equilibrium (Reaction R5) can be affected by the presence of TiO₂. The titanite-structured CaSi₂O₅ phase from inclusions in diamond is enriched in TiO₂ relative to coexisting breyite. This can be exemplified by the TiO₂ contents of CaSiO₃ (0.02 wt %) and CaSi₂O₅ (0.15 wt  %) inclusions in diamond reported by Joswig et al. (1999). There is no direct experimental evidence on the effect of Ti on Reaction (R5). The experiments of Kubo et al. (1997) on the CaSiO₃–CaTiO₃ system indicate that the pressure of breyite transformation to larnite + CaSi₂O₅ is reduced by ∼0.7 GPa at 1200 ^∘C and a CaTiSiO₅ mole fraction in titanite-structured Ca(Ti,Si)SiO₅ of ∼0.15. If the effect of TiO₂ on Reaction (R5) is of the same order, the presence of ∼0.5 % of CaTiSiO₅ in the titanite-structured phase will have a negligible effect on the breyite stability field.

5.3 Breyite crystallization under hydrous conditions

In the hydrous experiments, the iron–brucite starting mixture served as a source of fluid and an oxygen buffer. Interaction of brucite with iron produced a ferropericlase solid solution along with a reduced H₂O–H₂ fluid. The latter reacted with the adjacent CaCO₃–SiO₂ mixture to form C–O–H fluid species. The high chemical potential of H₂O acted to significantly depress the melting temperature of the CaCO₃–SiO₂ mixture, resulting in complete melting already at 1100 ^∘C and 6 GPa and very high degrees of melting at 1100 ^∘C and 8–10 GPa. No separate fluid phase was observed in these experiments, indicating that all fluid components were dissolved in the melt. The hydrous melt is strongly enriched in SiO₂ compared with the carbonate-dominated melt from the anhydrous experiments (Fig. 8).

The hydrous melt contained abundant suspended graphite crystals. Their nature is uncertain, and some could have formed during quenching. However, most graphite grains probably crystallized in equilibrium with the melt, which is indicated by their nonrandom distribution and very high content in some areas. The identification of equilibrium CaSi₂O₅ and SiO₂ crystals is unambiguous because these phases always occur as euhedral crystals up to 20 µm in size, usually in the lower part of the samples (Fig. 6). In contrast, a quench nature of some breyite crystals might be suspected because of their needle-like morphology (Fig. 6). However, there are several arguments supporting a subliquidus equilibrium origin of most breyite crystals. (1) Their amount is always low and the grains are observed locally near the walls or bottom of a capsule. Here, breyite content might be locally very high (>50 vol %), whereas isolated CaSiO₃ crystals were never found in the free melt volume. (2) There is a continuous transition from acicular to euhedral isometric breyite grains. The latter can hardly be interpreted as a quench phase (Fig. 6). (3) In one sample, a large isometric breyite crystal was observed between the Pt capsule and a continuous coesite layer. In this case, the local melt fraction was obviously too low to produce a large quench crystal.

Thus, our experiments demonstrated that simultaneous crystallization of breyite and diamond is possible as a result of interaction between CaCO₃ and SiO₂ in a metasedimentary source in the presence of reduced H₂O-rich fluid or melt. Although our experiments were made in a strongly simplified system compared with real metasediments, they are directly applicable to interactions in natural environments. Both aragonite and coesite/stishovite are practically pure phases in metasediments under high-pressure, high-temperature conditions (e.g., Brey et al., 2015). Natural breyite contains up to 0.2 wt % FeO and much lower amounts of other components (Joswig et al., 1999; Burnham et al., 2015). Hence, Reactions (R2) and (R4) are not affected by the presence of other components in natural materials. Moreover, melting in natural metasediments occurs at lower temperatures compared with the experimental CaO–SiO₂–CO₂ system because of the fluxing influence of alkalis, which must enhance the metastability of decarbonation Reaction (R2).

The pressure range of breyite inclusion formation is limited by the diamond–graphite transformation at ∼4 GPa and 1100 ^∘C and Reaction (R5) at ∼8 GPa and 1100 ^∘C (Fig. 7). These conditions are slightly above the solidus of hydrous carbonated sediment similar to GLOSS (global subducting sediment) of Plank and Langmuir (1998) coexisting with graphite or diamond (Brey et al., 2015). Hence, hydrous carbonate–silicate melt (or supercritical fluid) can be obtained from subducted sediment, if the temperature of the slab is not high and does not prevent hydrous silicate (lawsonite and phengite) transport to great depths. Such conditions are characteristic of cold subducted slabs (Syracuse et al., 2010).

It is evident from the above discussion that fO₂ is a very important parameter for breyite and diamond crystallization. To quantitatively evaluate a possible scenario for the formation of diamond-hosted breyite inclusions, mineral reactions in sedimentary and peridotitic materials were modeled using the dataset of Holland and Powell (2011). The calculated fO₂ values are expressed in logarithmic units relative to the Fe–FeO buffer (IW).

A proposed scenario of simultaneous breyite and diamond formation at 6–8 GPa and ∼1000 ^∘C is presented diagrammatically in Fig. 9. It involves melt formation in subducted sediments and its subsequent interaction with peridotite. At these depths and temperatures, the mineral assemblage of an hydrous carbonated and C-bearing sediment (GLOSS) includes coesite, kyanite, Ca-rich garnet, aragonite, lawsonite, phengite, graphite and accessory phases (Brey et al., 2015). The fO₂ is controlled by the reaction

$$\begin{array}{}\text{(R13)}& \begin{array}{rl}& \mathrm{3}{\mathrm{CaCO}}_{\mathrm{3}}\left(\text{Arg}\right)+{\mathrm{Al}}_{\mathrm{2}}{\mathrm{SiO}}_{\mathrm{5}}\left(\text{Ky}\right)+\mathrm{2}{\mathrm{SiO}}_{\mathrm{2}}\left(\text{Coe}\right)=\\ & {\mathrm{Ca}}_{\mathrm{3}}{\mathrm{Al}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{12}}\left(\text{Grt}\right)+\mathrm{3}\mathrm{C}\left(\text{Dia}\right)+\mathrm{3}{\mathrm{O}}_{\mathrm{2}}\end{array}\end{array}$$

and is relatively high (logfO₂ ≈ IW +5.5). The mole fraction of grossular in garnet in metasediment at 8 GPa and 1000 ^∘C is 0.3–0.4 (Brey et al., 2015). Accounting for garnet composition using the Berman (1990) model for Ca–Mg–Fe garnet yields even slightly higher logfO₂ values of ∼IW +5.7. Melt produced from such a metasediment will have the same fO₂. It will be saturated with respect to diamond but undersaturated in breyite, because such a redox potential will provide a CO₂ activity that is too high for decarbonation Reaction (R4) to proceed. However, the produced melt can be subsequently reduced through interaction with mantle peridotite, which will eventually result in diamond formation and redox freezing (Rohrbach and Schmidt, 2011). The redox conditions of mantle peridotite can be constrained by the appearance of Fe metal from below and magnesite from above, i.e., the reactions

$$\begin{array}{}\text{(R14)}& {\displaystyle }\mathrm{2}{\mathrm{Fe}}_{\mathrm{2}}{\mathrm{SiO}}_{\mathrm{4}}\left(\text{Ol}\right)={\mathrm{Fe}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{6}}\left(\text{Opx}\right)+\mathrm{2}\mathrm{Fe}\left(\text{Metal}\right)+{\mathrm{O}}_{\mathrm{2}},\text{(R15)}& {\displaystyle }\begin{array}{rl}& {\mathrm{MgCO}}_{\mathrm{3}}\left(\text{Mst}\right)+\mathrm{1}/\mathrm{2}{\mathrm{Mg}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{6}}\left(\text{Opx}\right)=\\ & {\mathrm{Mg}}_{\mathrm{2}}{\mathrm{SiO}}_{\mathrm{4}}\left(\text{Ol}\right)+\mathrm{C}\left(\text{Dia}\right)+{\mathrm{O}}_{\mathrm{2}}.\end{array}\end{array}$$

This yields a wide range of logfO₂ values, from IW to IW +4, which is more reduced than the initial metasediment-derived melt. Note that all the fO₂ values imposed by Reactions (R15)–(R17) are much lower than the CCO buffer at these pressures and temperatures (CCO ≈ IW +8 at 1000–1100 ^∘C and 6 GPa; Jacobsson and Oskarsson, 1994). This implies that a CO₂-rich gas phase is absent, and diamond will remain stable in both metasediment and peridotite. Interaction of metasediment-derived melt with peridotite will result in reduction accompanied by Fe and Mg transfer from peridotite to melt and SiO₂ transfer from melt to peridotite (Bulatov et al., 2014). If the melt is saturated in diamond (melt is derived in a diamond-bearing metasediment), its reduction will immediately result in diamond crystallization. The reduction-induced crystallization of silicate phases will begin later via two possible paths. If transport of O₂ is much faster than that of Fe and Mg, melt reduction and diamond crystallization will eventually result in breyite (or CaSi₂O₅) crystallization and its possible entrapment by growing diamond crystals. Otherwise, in the case of rapid Fe and Mg transport, breyite formation will be suppressed, and clinopyroxene, garnet or merwinite (e.g., Sharygin et al., 2018) will form instead.

The obtained results allow us to speculate about the difference in the origins of breyite inclusions either being trapped at conditions within the breyite stability field or those that formed by retrogression of trapped CaSiO₃ perovskite. Anzolini et al. (2016) emphasized the importance of the very large difference in molar volume between CaSiO₃ perovskite and breyite. They argued that breyite inclusions without any evidence for diamond deformation and/or cracking were probably trapped initially as breyite. Moreover, the large volume change will result in an initial CaSiO₃ perovskite inclusion converting to polymineralic aggregates containing larnite and CaSi₂O₅ (e.g., Joswig et al., 1999) rather than monomineralic breyite. Inspection of the phase diagram in Fig. 2 indicates that CaSiO₃ inclusions coexisting with larnite or stishovite most probably had a perovskite precursor. In contrast, CaSi₂O₅ can be trapped together with breyite at a pressure of ∼8 GPa. Finally, the formation of breyite through reaction of CaCO₃ and SiO₂ implies a metasedimentary precursor, whereas CaSiO₃ perovskite is a phase stable in a peridotitic mantle. Therefore, the two types of breyite inclusions should have specific geochemical and isotopic signatures. It is interesting in this respect that at least some calcium perovskite inclusions in diamond exhibit geochemical signatures of subducted oceanic crust rather than primitive or depleted peridotites (e.g., Walter et al., 2008).