Heat capacity and entropic mixing behaviour of the orthopyroxene solid solution (Mg,Fe)₂Si₂O₆

The heat capacity (C_p) of synthetic members of the orthopyroxene solid solution enstatite (Mg₂Si₂O₆: En)-ferrosilite (Fe₂Si₂O₆: Fs) was measured at between 2 to 300 K using relaxation calorimetry and between 340 to 823 K using differential scanning calorimetry. The samples (nine solid-solution members plus En and Fs) were characterised by optical microscopy and by X-ray powder diffraction methods. The actual compositions of the solid-solution members were checked by comparing the cell volumes determined in this work with corresponding data in the literature which provide a correlation between cell volume and composition.

The C_p's of the endmembers above room temperature can be represented by the following polynomials (J K⁻¹ mol⁻¹): $C_{\mathrm{p}}^{\mathrm{En}}=\mathrm{311.82}\left(\pm \mathrm{6.39}\right)-\mathrm{1824.09}\left(\pm \mathrm{220}\right)\cdot T^{-\mathrm{0.5}}-\mathrm{6.83178}\left(\pm \mathrm{1.18}\right)\times {\mathrm{10}}^{\mathrm{6}}\cdot T^{-\mathrm{2}}+\mathrm{8.81577}\left(\pm \mathrm{1.81}\right)\times {\mathrm{10}}^{\mathrm{8}}\cdot T^{-\mathrm{3}}$ and $C_{\mathrm{p}}^{\mathrm{Fs}}=\mathrm{393.14}\left(\pm \mathrm{6.06}\right)-\mathrm{3941.24}\left(\pm \mathrm{203}\right)\cdot T^{-\mathrm{0.5}}+\mathrm{2.10688}\left(\pm \mathrm{1.06}\right)\times {\mathrm{10}}^{\mathrm{6}}\cdot T^{-\mathrm{2}}-\mathrm{2.97417}(\pm \mathrm{1.62})\times {\mathrm{10}}^{\mathrm{8}}\cdot T^{-\mathrm{3}}.$ Compared to literature and data set values, the polynomial for En yields 1.5 % to 3 % lower heat capacities at high temperatures and should be preferred for phase equilibrium calculations >1000 K.

The standard entropy of En was determined to be $S^{\mathrm{o}}=\mathrm{132.3}\pm \mathrm{1.0}$ J K⁻¹ mol⁻¹ and that of Fs to be $S^{\mathrm{o}}=\mathrm{190.7}\pm \mathrm{1.3}$ J K⁻¹ mol⁻¹ based on the Physical Properties Measurement System (PPMS) measurements.

All solid-solution members and Fs show heat capacity anomalies below ∼50 K. Discrete C_p peaks, related to magnetic ordering, occur at a Néel temperature of T_N=38.4 K in pure Fs, and a double peak occurs at 38 K and at 29 K in the composition En10Fs90. With further dilution of the magnetic Fe²⁺ ion, heat capacity anomalies are present in the form of broad shoulders in the C_p data between approximately 10 and 25 K. At the lowest temperatures, around 2 K, Schottky-type C_p anomalies are visible.

By adopting a Kieffer model for the lattice part of C_p, the excess heat capacities of each compound were derived and decomposed into magnetic and electronic contributions. The calorimetric entropies at 298.15 K (S_cal), when plotted against composition, indicate a linear relationship along the join; i.e. all S_cal values fall on the line defining thermodynamic ideality within error. There are thus no excess entropies of mixing in the En–Fs orthopyroxene solid solution. The same holds true for the volumes.

1 Introduction

Most orthopyroxenes are solid solutions between the endmembers En and Fs. Their thermodynamic and kinetic properties are therefore needed in order to model the P–T–X paths of igneous and metamorphic rocks. The knowledge of the heat capacity behaviour down to very low temperatures allows calculations of thermodynamic variables of state, such as the entropy of mixing. To our knowledge, these kinds of data exist only for the endmembers of the solid solution in the literature. Krupka et al. (1985a, b) measured the low-temperature heat capacities of synthetic En between 5 and 385 K by means of adiabatic calorimetry (AC) and the high-temperature heat capacities between 350 and 1000 K using differential scanning calorimetry. From their cryogenic measurements, the standard entropy S^o of En was determined to be 132.5±0.3 J K⁻¹ mol⁻¹. Also applying AC, Bohlen et al. (1983) measured the heat capacity of Fs at temperatures between 8 and 350 K and derived S^o=189.2 J K⁻¹ mol⁻¹. Cemič and Dachs (2006) used the Physical Properties Measurement System (PPMS) at Salzburg University and a Perkin Elmer DSC 7 at the University of Kiel to measure the heat capacity of Fs in the temperature range between 2 and 820 K. Several other studies dealt with the magnetic, electronic, and optical properties of this endmember (see Zherebetskyy et al., 2010, and references therein). Conducting temperature-dependent X-ray diffraction measurements, the thermal expansion of various natural orthopyroxenes and clinopyroxenes was determined by Hovis et al. (2021). The enthalpy of Mg–Fe ordering was determined calorimetrically by Cemič and Kähler (2000).

The aim of this work is to determine the heat capacities of the endmembers and the intermediate members of the solid solution and to calculate the entropic mixing properties of the system En–Fs.

2 Methods

2.1 Sample synthesis and characterisation

Nine members of the orthopyroxene solid solution (Mg,Fe)₂Si₂O₆ were synthesised at 1.5 GPa and 800 °C using the synthetic endmembers enstatite (Mg₂Si₂O₆ – En) and ferrosilite (Fe₂Si₂O₆ – Fs). The nominal compositions ranged from En90Fs10 to En10Fs90 in steps of 0.1 in the mole fraction X_Fs. The synthesis procedure of Fs has been described in Cemič and Dachs (2006), and that of En has been described in Koch-Müller et al. (1992). Mixtures of the two endmember components were finely ground in an agate mortar and then sealed in a silver capsule together with a small amount (4 µL) of distilled water. The capsule was then inserted into a larger gold capsule containing a mechanical mixture of wüstite and iron. A small amount of water was added, and the capsule was mechanically sealed. The use of the wüstite-iron buffer is intended to keep the oxygen fugacity low in order to prevent a partial oxidation of Fe²⁺ to Fe³⁺ in the pyroxenes.

The synthesis was carried out in a piston cylinder apparatus at 1.5 GPa and 800 °C. The experimental time was varied between 24 and 48 h, depending on the composition. The En-rich samples required a longer duration of the experiment.

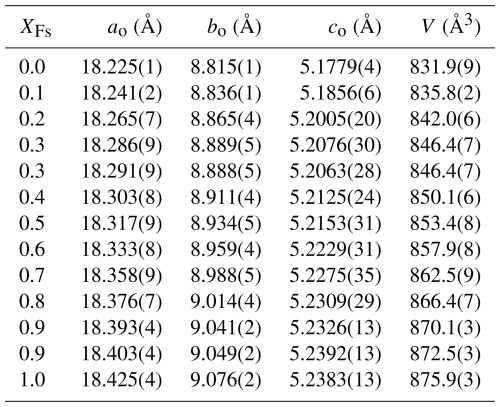
The synthesis products were examined with optical microscopy and powder X-ray diffraction using an automated diffractometer (Siemens D 5000) between 8 and 100 2Θ using Cu–K_α radiation. The step size was 0.016 2Θ, and the measuring time was 11 s per step. The lattice parameters were refined with the Rietveld program Fullprof (Rodriguez-Carvajal, 1990). Gramenopoulou (1981) determined cell volumes of synthetic En–Fs solid-solution members and measured their composition via microprobe analysis, establishing the composition–cell volume relationship V (ų)$=\mathrm{831.9}\left(\mathrm{6}\right)+\mathrm{44.0}{X}_{\mathrm{Fs}}$. Recalculating X_Fs using this relationship and the cell volumes determined in this study, it turns out that measured and nominal compositions agree to within 0.03 mole fractions. Mössbauer spectroscopy performed on the Fs endmember (Cemič and Dachs, 2006) showed that no Fe³⁺ was detected, and we assume that the same applies for the Fe-bearing solid-solution members studied calorimetrically in this work due to identical experimental conditions.

2.2 Calorimetric methods and data evaluation

Low-temperature heat capacities were measured using a commercially available relaxation calorimeter (heat capacity option of the Quantum Design^® Physical Properties Measurement System – PPMS). The data were collected in triplicate at 60 different temperatures between 2 and 300 K, using a logarithmic spacing resulting in a higher data density at a lower temperature. The samples consisted of 18–22 mg of crystallites wrapped in thin Al foil and compressed into a ∼0.5 mm thick pellet; see Geiger and Dachs (2017) or Rosen and Woodfield (2020) for more details on the advantages and disadvantages of this sample preparation technique. The pressed pellet was then attached to the sample platform of the calorimeter with Apiezon N grease to facilitate the required thermal contact. The so-called sample coupling, a parameter provided by the PPMS software, is a measure of the quality of the thermal conductance between platform and sample. It should ideally be close to 100 %; otherwise, C_p's tend to be too low (Dachs and Bertoldi, 2005). Further details on the calorimetric technique and measuring procedures have already been published (Lashley et al., 2003; Dachs and Bertoldi, 2005; Kennedy et al., 2007; Dachs and Benisek, 2011; Rosen and Woodfield, 2020).

In the temperature region between 340 and 820 K, the measurements were made with a Perkin Elmer DSC 7. The experimental technique was similar to that described in Bosenick et al. (1996). The calorimetric molar entropy (S_cal) of each compound at 298.15 K was calculated by numerically solving the integral

$$\begin{array}{}\text{(1)}& S_{\mathrm{cal}}=S^{T=\mathrm{298.15}\mathrm{K}}-S^{T=\mathrm{0}\mathrm{K}}=\underset{\mathrm{0}}{\overset{\mathrm{298.15}}{\int }}{\displaystyle \frac{C_{\mathrm{p}}}{T}}\mathrm{d}T.\end{array}$$

S_cal corresponds to the standard-state (third-law) entropy, S^o, in the case of an ordered endmember (which assumes $S^{T=\mathrm{0}\mathrm{K}}=\mathrm{0}$). Errors in S_cal were estimated according to Dachs and Benisek (2011). The entropy increment of 0–2 K, not covered by measured C_p data, was estimated as described in Sect. 3.2.5.

2.3 Density functional theory (DFT) calculations

Quantum-mechanical calculations were based on the density functional theory (DFT) plane wave pseudo-potential approach implemented in the CASTEP code (Clark et al., 2005; Refson et al., 2006) included in the Materials Studio software from Biovia^®. They were employed to compute the heat capacity at constant volume, C_v, of pure En but not of intermediate compositions or of Fs, where the various magnetic and electronic spin states of Fe²⁺ complicate such calculations. The calculations used the local density approximation (LDA) for the exchange correlation functional (Ceperley and Alder, 1980) and norm-conserving pseudo-potentials to describe the core valence interactions. For the k-point sampling of the investigated unit cells, a Monkhorst–Pack grid (spacing of 0.05 Å⁻¹) was used (Monkhorst and Pack, 1976). The structural relaxation was calculated by applying the BFGS algorithm (Pfrommer et al., 1997), where the convergence threshold for the force on an atom was 0.01 eV Å⁻¹. The lattice dynamical calculations were performed for these relaxed structures within the linear response approximation implemented in CASTEP using the interpolation approach.

3 Results

3.1 Overall heat capacity behaviour and entropy

Measured low- and high-temperature heat capacities of the endmembers En and Fs, as well as of all studied solid-solution members, are shown in Fig. 1 as a function of temperature (all calorimetric data are compiled in Table S1 in the Supplement). The sample coupling was >99 % in the majority of PPMS measurements; only in one case was it around 97 % at low T values.

3.1.1 Endmembers

Enstatite. Fitting the uppermost PPMS data around ambient T and the DSC data of En to a Berman–Brown-type C_p polynomial (Berman and Brown, 1985) yields the following in J K⁻¹ mol⁻¹:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{C}_{\mathrm{p}}& =\mathrm{311.82}\left(\pm \mathrm{6.39}\right)-\mathrm{1824.09}\left(\pm \mathrm{220}\right)\cdot T^{-\mathrm{0.5}}\\ & -\mathrm{6.83178}\left(\pm \mathrm{1.18}\right)\times {\mathrm{10}}^{\mathrm{6}}\cdot T^{-\mathrm{2}}\\ & +\mathrm{8.81577}\left(\pm \mathrm{1.81}\right)\times {\mathrm{10}}^{\mathrm{8}}\cdot T^{-\mathrm{3}}.\end{array}\end{array}$$

Note that this type of polynomial allows extrapolation to temperatures higher than the experimental range. Compared to the low-temperature AC data of Krupka et al. (1985a), PPMS C_p data for En are ∼1 % larger at T<150 K and, at maximum, 1 % smaller above that temperature up to room temperature (Fig. S1a, b). The DSC data measured by Krupka et al. (1985b) are generally larger by 1 %–2 % than the DSC-measured C_p of this study for this phase.

Integrating PPMS-measured $C_{\mathrm{p}}/T$ yields a standard entropy of $S^{\mathrm{o}}=\mathrm{132.3}\pm \mathrm{1.0}$ J mol⁻¹ K⁻¹ for En compared to S^o=132.5 J K⁻¹ mol⁻¹ as derived by Krupka et al. (1985a) from their low-T AC data. Due to the small absolute value of C_p at T<2 K, the entropy increment between 0 and 2 K is very small (<0.00014 J K⁻¹ mol⁻¹) and can be neglected.

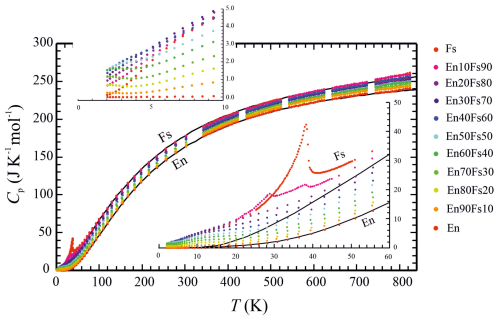
Figure 1 Heat capacities of members of the enstatite (En)–ferrosilite (Fs) binary, as measured in this study. The lower-right inset shows the temperature region of 0 to 60 K, where magnetic heat capacity anomalies dominate, in more detail. The upper-left inset shows the temperature region of 0 to 10 K, where Schottky anomalies occur, in more detail. The two black lines are the lattice (vibrational) heat capacities of En and Fs, from the Kieffer model for C_v, using parameters given in Table 3 and performing the C_v to C_p conversion as described in the text.

Ferrosilite. The encapsulation method for powders as used in this study for the PPMS measurements, i.e. wrapping the synthesised material (around 20 mg) in thin Al foil (weighing ca. 5.5 mg) and then pressing this arrangement into a flat pellet, yields low-TC_p's for Fs that connect smoothly to the DSC data (Fig. S2). Around ambient T, they agree with C_p as determined by Cemič and Dachs (2006), whereas, at lower temperatures, they are up to 2 % larger compared to the older data. The reason for this discrepancy is likely to be the better sample coupling prevailing in the PPMS measurements of this study (>98 %), whereas, in the older measurements, sample couplings were not optimal (88 %–95 %), likely resulting in somewhat too-low heat capacities. Furthermore, DSC Al pans with weights around 55 mg were the containers for the powder samples in these measurements. Due to this approximately 10-times-larger weight compared to the Al foil, as used in this study to encapsulate the powder, the contribution of the container heat capacity to total measured C_p was much larger in the arrangement used by Cemič and Dachs (2006) to measure the heat capacity of synthetic Fs. This constitutes a major shortcoming inherent in the former encapsulation method and was the motivation to develop the “Al foil technique”.

Cemič and Dachs (2006) described a prominent λ-shaped heat capacity anomaly of Fs occurring at 38.7 K and interpreted this transition to be caused by anti-ferromagnetic ordering of the Fe²⁺ spin moments. The remeasured data of this study show the peak of this anomaly at a slightly lower Néel temperature of T_N=38.4 K and a Schottky-like shoulder around 10 K.

From the DSC data combined with the PPMS data around ambient T, we derive the following polynomial for computing Fs's heat capacity above room temperature (J K⁻¹ mol⁻¹):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{C}_{\mathrm{p}}& =\mathrm{393.14}\left(\pm \mathrm{6.06}\right)-\mathrm{3941.24}\left(\pm \mathrm{203}\right)\cdot T^{-\mathrm{0.5}}\\ & +\mathrm{2.10688}\left(\pm \mathrm{1.06}\right)\times {\mathrm{10}}^{\mathrm{6}}\cdot T^{-\mathrm{2}}\\ & -\mathrm{2.97417}(\pm \mathrm{1.62})\times {\mathrm{10}}^{\mathrm{8}}\cdot T^{-\mathrm{3}}.\end{array}\end{array}$$

Around ambient T, this polynomial gives a slightly larger C_p than that published in Cemič and Dachs (2006); above approximately 400 K, both polynomials agree with each other.

Fs's standard entropy is determined to be $S^{\mathrm{o}}=\mathrm{190.7}\pm \mathrm{1.3}$ J K⁻¹ mol⁻¹, 1.5 J K⁻¹ mol⁻¹ larger than that determined by Bohlen et al. (1983) from AC but 4.2 J K⁻¹ mol⁻¹ larger than that given in Cemič and Dachs (2006). Their S^o for Fs constitutes a too-low value for the reasons mentioned above. A small entropy increment $S_{T=\mathrm{2}\mathrm{K}}-S_{T=\mathrm{0}\mathrm{K}}$ still has to be added to the above S^o (see below).

3.1.2 Solid-solution members

Cell volumes along the En–Fs binary, computed from the Rietfeld-derived lattice constants given in Table 1, are plotted in Fig. S3. All volumes fall onto the straight line defining ideal mixing within error, and so there are no excess volumes of mixing in this solid solution.

Table 1 Lattice constants and cell volumes of the synthesised En–Fs solid-solution members, as determined from Rietfeld refinements. For the compositions X_Fs=0.3 and 0.9, two determinations have been made.

The heat capacities of the En–Fs solid-solution members above approximately 50 K show the expected behaviour to fall in a 15–20 C_p-units-wide band, with C_p of En forming the lower limit and C_p of Fs forming the upper limit (Fig. 1). For a constant temperature, it is consistently fulfilled in this band, such that $C_{\mathrm{p}}(X_{\mathrm{Fs}}+\mathrm{0.1})>C_{\mathrm{p}}(X_{\mathrm{Fs}}$); i.e. the heat capacity of a specific solid-solution member is smaller by 1.5–2 J K⁻¹ mol⁻¹ than its next Fe-richer neighbour, with no overlaps or crossings in the data. At lower temperatures, down to the lowest T at which C_p data could be measured (∼2 K), the situation gets more complex. This is the region where magnetic and electronic effects contribute to lattice heat capacity. Noteworthy is the composition En10Fs90. This solid-solution member shows a double magnetic C_p anomaly with one distinctive shoulder at the same temperature as the prominent λ transition in pure Fs (∼38 K) and one, compared to Fs100, considerably smaller peak at ∼29 K (Fig. 1, right inset). In the heat capacity data of the other more Mg-rich compositions, the discrete magnetic C_p peaks observed for Fs and En10Fs90 are obviously flattened out. Magnetic contributions to heat capacity are present here in the form of broad shoulders in the C_p data between approximately 10 and 25 K, decreasing in size with decreasing X_Fs, rather similarly to that observed in olivine solid solutions (Dachs et al., 2007).

At the lowest temperatures, the C_p behaviour of the En–Fs solid-solution members is complicated even more by contributions from Schottky-type C_p anomalies (left inset of Fig. 1). These are seen as plateau-like features (En90Fs10), slight upturns (En80Fs20, En70Fs30, En60Fs40), or shoulders (En50Fs50, En40Fs60, En30Fs70) in C_p from the data portion around the low-temperature end. One would also expect that the heat capacity at 2 K of the Fe-rich compositions should be larger than those of the Mg-rich ones. This is, however, not the case. In fact, C_p of the intermediate compositions is largest at this temperature, around 1.5 J K⁻¹ mol⁻¹, whereas Fe-rich, as well as Mg-rich, solid-solution members show comparable smaller C_p values of <1.0 J K⁻¹ mol⁻¹ around 2 K (Fig. 1, left inset).

Figure 2 is a plot of endmember and solid-solution member calorimetric entropies at 298.15 K (S_cal) as a function of composition (data are given in Table 2). As all the data points fall on the line defining ideal mixing within error, no excess entropies arise from Fe–Mg mixing in the En–Fs binary (note that this type of excess entropy is not to be confused with the excess entropies, S_ex, of an individual solid-solution composition, as tabulated in Table 2, which describes extra contributions to the overall entropy due to magnetic and/or electronic effects (Schottky contribution)). When the entropy increment from 0 to 2 K, not covered by experimental data, is taken into account (see Sect. 3.2.5) and added to S_cal, a small modification of these entropy data occurs, giving S₂₉₈, the total entropy from 0 to 298.15 K.

Table 2 Calorimetric entropies at 298.15 K (S_cal) of members of the En–Fs solid solution, determined from the PPMS-measured low-T heat capacities of this study, compiled in Table S1 (numbers in parentheses are 1 standard deviation and refer to the last digit). Adding the entropy increment 0–2 K, not included in S_cal, yields the total entropy at 298.15 K, S₂₉₈. Additionally given are the vibrational and excess entropies S_vib and S_ex, derived by decomposition of S_cal (errors in S_ex are assumed to be of the same size as for S_cal). S_ex is further decomposed into Schottky-type and magnetic contributions, and the corresponding increments from 0 to 2 K are listed in parentheses (see the text for more details).

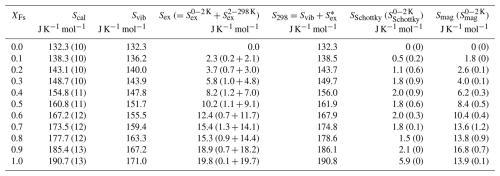
^∗ Note that S₂₉₈ is also equal to the sum $S_{\mathrm{cal}}+S_{\mathrm{ex}}^{\mathrm{0}-\mathrm{2}\mathrm{K}}$ because $S_{\mathrm{vib}}^{\mathrm{0}-\mathrm{2}\mathrm{K}}$ is negligibly small.

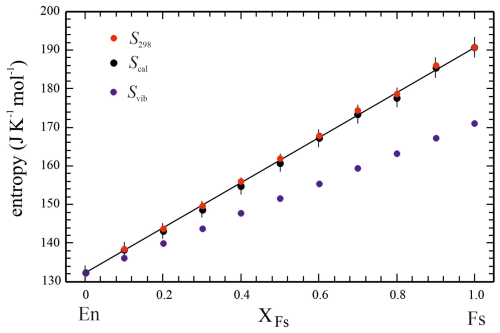
Figure 2 Calorimetric entropies at 298.15 K (S_cal) as a function of composition along the En–Fs solid solution (data from Table 2). Adding estimated entropy increments from 0 to 2 K to S_cal, as described in the text, yields S₂₉₈ for each compound. The vibrational entropies along the solid solution, S_vib, are assumed to be linear combinations of corresponding endmember properties.

3.2 Lattice and excess heat capacity and entropy

The non-lattice or excess heat capacity, defined as C_ex=C_v - C_vib, is obtained by subtracting a model lattice (or vibrational) heat capacity, C_vib, from the experimental heat capacity C_p of a specific composition after converting C_p into C_v, the heat capacity at constant volume. C_ex is relevant for all Fe-bearing En–Fs compositions that have non-lattice contributions to heat capacity, like magnetic (C_mag) or electronic (C_el) ones (Schottky anomalies), in which case, $C_{\mathrm{ex}}=C_{\mathrm{mag}}+C_{\mathrm{el}}$. Designating the difference of C_p−C_v as ΔC, the excess heat capacity can be obtained from the experimental heat capacity $C_{\mathrm{p}}^{\exp }$ using the following relationship:

$$\begin{array}{}\text{(4)}& C_{\mathrm{ex}}=C_{\mathrm{p}}^{\exp }-\left(C_{\mathrm{vib}}+\mathrm{\Delta }C\right)=C_{\mathrm{v}}-C_{\mathrm{vib}}.\end{array}$$

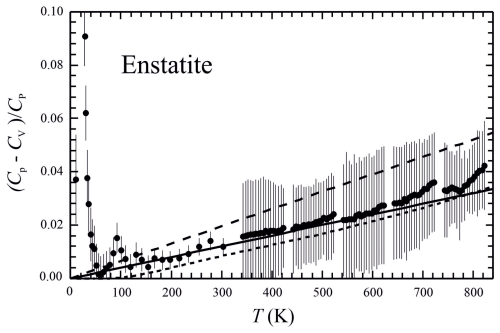
Figure 3 $(C_{\mathrm{p}}-C_{\mathrm{v}})/C_{\mathrm{p}}$ for enstatite as a function of temperature. For C_p, the PPMS- and DSC-measured values of this study were taken, whereas C_v is DFT-computed (error bars are ±2 SDs). Solid line represents Eq. (5) with a slope of m=0.00004. The short-dashed line would result if the C_p−C_v difference were to be calculated from the relation $C_{\mathrm{p}}-C_{\mathrm{v}}=T\cdot V\cdot {\mathit{\alpha }}^{\mathrm{2}}/\mathit{\kappa }$ with computed values for V and α in accordance with those of Hovis et al. (2021), giving a slope of m=0.00005; a steeper slope of m=0.00007 would be required (long-dashed line) to achieve a match of C_v with the DSC data of Krupka et al. (1985b).

3.2.1 Converting C_p into C_v

This conversion could be principally done based on the well-known relationship $C_{\mathrm{p}}-C_{\mathrm{v}}=\mathrm{\Delta }C=T\cdot V\cdot {\mathit{\alpha }}^{\mathrm{2}}/\mathit{\kappa }$. This requires reliable data for the molar volume, V; the thermal expansivity, α; and the isothermal compressibility, κ, for a specific compound. In this study, we adopted the procedure used by Benisek and Dachs (2018) to calculate ΔC. It was shown in this work that the quotient C_p−C_v over C_p for diopside and jadeite behaves linearly with temperatures approaching zero at 0 K so that

$$\begin{array}{}\text{(5)}& (C_{\mathrm{p}}-C_{\mathrm{v}})/C_{\mathrm{p}}=\mathrm{\Delta }C/C_{\mathrm{p}}=m\cdot T,\end{array}$$

where m is the mineral-specific slope of this line. In order to further test this relationship, we applied DFT methods to directly compute C_v of En. Figure 3 is a plot of $(C_{\mathrm{p}}^{\exp }-C_{\mathrm{v}}^{\mathrm{DFT}})/C_{\mathrm{p}}^{\exp }$ for En vs. temperature, showing that a linear relationship is fulfilled well down to T values of around 50 K. We used the solid line indicated in Fig. 3, with a slope of m=0.00004, for computing En's $(C_{\mathrm{p}}-C_{\mathrm{v}})/C_{\mathrm{p}}$. A slightly steeper slope would result if ΔC was computed from $T\cdot V\cdot {\mathit{\alpha }}^{\mathrm{2}}/\mathit{\kappa }$. Solving Eq. (5) for C_p yields the following:

$$\begin{array}{}\text{(6)}& C_{\mathrm{p}}=C_{\mathrm{v}}/(\mathrm{1}-m\cdot T).\end{array}$$

When non-lattice contributions to heat capacity do not play a role, as is the case for En where C_ex=0, experimental C_p can thus be represented by a lattice-dynamic model for C_vib (=C_v) divided by the ($\mathrm{1}-m\cdot T$) term.

3.2.2 Lattice-dynamic model for C_vib of enstatite and ferrosilite

We resort to the model developed by Kieffer (1979, 1980) for lattice vibrations of minerals to compute C_vib of En and Fs. For 10 atoms in the formula of orthopyroxenes and 8 formula units per unit cell, the total number of atoms in the unit cell s=80, and there are 3s=240 possible modes of vibration. The Kieffer model requires cut-off frequencies for the three acoustic branches, as well as lower and upper cut-off frequencies of the optical branches that are treated as one continuum or several continua with cut-offs defined from IR or Raman spectra or computed dispersion relations. Additionally, separate Einstein oscillators, e.g. for representing Si–O stretching modes, can be used. The number n of vibrational modes assigned to each oscillator or optical continuum must then sum up to 3s−3.

For En, we used the parameters given by Kieffer (1980) as a starting point. Based on Eq. (6) and taking m=0.00004, the optical cut-offs and n were varied somewhat to obtain the best agreement with measured C_p over the temperature range of the experimental data. With this relatively simple lattice model for C_vib, the experimental C_p of En could be recalculated with a deviation of less than 1 % in the temperature range 50–800 K (Fig. S4; final parameters are given in Table 3, and a Mathematica program code for computing the Kieffer model is available on request). At the lowest temperatures, where absolute values of C_p get rather small, deviations increase to >10 %.

Table 3 Parameters of the Kieffer model for computing C_v of En and Fs. The values for En are modified from Kieffer (1980), and those for Fs were read from IR powder absorption spectra published by Tarantino et al. (2002). There are, in total, 240 vibrational modes.

The C_vib that we use for Fs as a function of temperature is shown in Fig. 4. The position of this curve is not arbitrary but a consequence of employing the single-parameter phonon dispersion model of Komada and Westrum (1997, as abbreviated KW) for the measured heat capacity data. Analogously to Debye theory, the key feature of the KW model is that a characteristic temperature, θ_KW, is introduced and can be determined by fitting the model to the experimental C_p data (Komada, 1986; Komada and Westrum, 1997; Dachs et al., 2007, 2009). At temperatures above a magnetic phase transition, θ_KW approaches a linear (ideally constant) value that can be used to calculate C_vib. Any marked change in the value of θ_KW reflects the existence of non-lattice heat capacity contributions. In the case of Fs, θ_KW is linear with a rather flat slope above approximately 120 K (Fig. 4, inset), indicating that such contributions can be expected to cease in this temperature range. With m=0.0001 and parameters for the Kieffer model of Fs as given in Table 3, a C_vib matching that computed with the KW model was generated for Fs and was used to compute its C_ex (initial cut-offs were read from its powder absorption spectrum, as published by Tarantino et al., 2002). The deviation of the so-recalculated C_p of Fs based on Eq. (6) from experimental values is <1 % in the temperature range of 140–700 K.

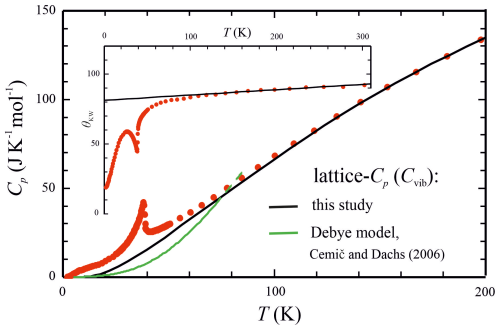
Figure 4 PPMS-measured heat capacity of Fs (red points) compared to model calculations for its lattice C_p. The black curve was computed from the relation $C_{\mathrm{p}}=C_{\mathrm{v}}/(\mathrm{1}-m\cdot T)$ with m=0.0001 (Eq. 6) and adopting the Kieffer model for computing Fs's C_v with the parameters given in Table 3. This approaches experimental C_p at around 120 K and served as the base line to calculate C_ex by subtraction. Cemič and Dachs (2006) used the Debye model for calculating C_v (green curve), which leads to a much larger C_ex. The inset shows θ_KW of the Komada and Westrum (1997) model as a function of temperature.

3.2.3 Excess heat capacities

Whereas the calculation of C_ex is straightforward for the Fs endmember (Eq. 4), we used a linear combination of the vibrational models for C_vib of En and Fs, as described above, to come up with the C_vib of a solid-solution member $(C_{\mathrm{vib}}^{\mathrm{ss}}$) as follows:

$$\begin{array}{}\text{(7)}& C_{\mathrm{vib}}^{\mathrm{ss}}=(\mathrm{1}-X_{\mathrm{Fs}})\cdot C_{\mathrm{vib}}^{\mathrm{En}}+X_{\mathrm{Fs}}\cdot C_{\mathrm{vib}}^{\mathrm{Fs}}.\end{array}$$

This implies that the vibrational properties in the En–Fs solid solution behave as an ideal mixture. With an expression analogous to Eq. (7), the conversion of C_p into C_v was done for each solid-solution member. The resulting excess heat capacities are plotted in Fig. 5 in the temperature range of 0–60 K. They smear out around this T in the Mg-rich compositions, whereas the Fe-rich compounds approach zero C_ex at successively higher T values up to ∼150 K (not shown in Fig. 5). Recalculated C_p above this T, computed from $C_{\mathrm{p}}^{\mathrm{calc}}=C_{\mathrm{vib}}+C_{\mathrm{ex}}+\mathrm{\Delta }C$, deviates by no more than 1 % from the measured C_p of a specific compound up to 820 K.

The features discussed above for the C_p behaviour of the various solid-solution members below 50 K remain, in principle, the same for C_ex. Due to the subtraction of C_vib, which becomes increasingly larger with higher T, shoulders, appearing in Fig. 1 for the C_p behaviour between 10 and 25 K, transform into broad bumps in a plot of C_ex vs. T, with T maxima being shifted to successively lower values and decreasing in size with decreasing X_Fs (Fig. 5). At the lowest temperatures of <5 K, the contribution of C_vib is minor, and the observed plateau-like features and even slight upturns in C_p of Mg-rich to intermediate compositions remain unchanged. Schottky contributions to C_p thus seem to play a greater role in such compositions, with a $\mathrm{Fe}/\mathrm{Mg}$ ratio around 1:1. Unexpectedly, these still have a C_ex of the order of 1.0 to 1.7 J K⁻¹ mol⁻¹ at 2 K.

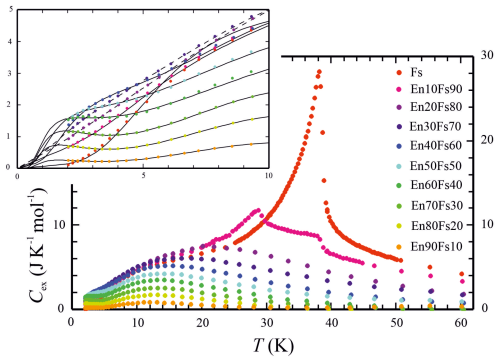
Figure 5 Excess heat capacities C_ex of members of the enstatite (En)–ferrosilite (Fs) binary in the temperature range from 0 to 60 K. C_ex was calculated by subtracting a model lattice heat capacity from measured C_p after converting C_p into C_v. The inset shows the range of 0 to 10 K, where Schottky anomalies play a role, in more detail. Curves in the inset are fits to C_ex and are used for extrapolation of C_ex from 2 K down to 0 K (those for En30Fs70 and En20Fs80 are shown as dashed lines; see the text for more information).

3.2.4 Fitting the excess heat capacities

As mentioned above, we assigned the heat capacity anomalies occurring at the lowest temperatures in the En–Fs solid solution to Schottky anomalies (C_Schottky). We fitted these excess contributions using a simple two-level system (ground state, one exited level) given by the following equation (e.g. Dachs et al., 2007; Rosen and Woodfield, 2020; Jens Biele (DLR Köln, Germany), personal communication, 2024):

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{C}_{\mathrm{Schottky}}& =R\cdot \text{SF}\cdot X_{\mathrm{Fs}}{\left({\displaystyle \frac{\mathit{\theta }}{T}}\right)}^{\mathrm{2}}{\displaystyle \frac{g_{\mathrm{o}}}{g_{\mathrm{1}}}}\\ & \cdot {\displaystyle \frac{\exp (-\mathit{\theta }T)}{{\left[\mathrm{1}+(g_{\mathrm{o}}/g_{\mathrm{1}})\exp (-\mathit{\theta }/T)\right]}^{\mathrm{2}}}},\end{array}\end{array}$$

where R is the gas constant; SF is an empirical scaling factor of order 1; g_o and g₁ are the degeneracies of the ground state and of the first energy state, whereby the ratio $g_{\mathrm{o}}/g_{\mathrm{1}}$ was taken to be similar to that in olivine, namely $\mathrm{1}/\mathrm{2}$ (Aronson et al., 2007); and θ is the energy gap between the two levels of the Schottky anomaly in units of K (not identical with its temperature maximum, which is at lower temperatures of around $\mathit{\theta }/\mathrm{2}$).

For describing C_ex behaviour in the temperature region around the paramagnetic–anti-ferromagnetic sharp λ transition in Fs100 at T_N=38.4 K, Eq. (8) was combined with the following equations (e.g. Gronvold and Sveen, 1974; Dachs et al., 2007, 2009):

$$\begin{array}{}\text{(9a)}& C_{\mathrm{mag}}={\displaystyle \frac{A^{\prime }}{{\mathit{\alpha }}^{\prime }}}\left[{\left({\displaystyle \frac{\mathrm{|}T-T_{\mathrm{N}}\mathrm{|}}{T_{\mathrm{N}}}}\right)}^{-{\mathit{\alpha }}^{\prime }}-\mathrm{1}\right]+B^{\prime }T\text{ for }T<T_{\mathrm{N}},\end{array}$$

and

$$\begin{array}{}\text{(9b)}& C_{\mathrm{mag}}={\displaystyle \frac{A}{\mathit{\alpha }}}\left[{\left({\displaystyle \frac{\mathrm{|}T-T_{\mathrm{N}}\mathrm{|}}{T_{\mathrm{N}}}}\right)}^{-\mathit{\alpha }}-\mathrm{1}\right]+B/T\text{ for }T>T_{\mathrm{N}}.\end{array}$$

The fit for Fs100 is shown in Fig. S5 and fits its C_ex behaviour satisfactorily, with small deviations between 10 and 20 K. The discrete C_p peak at 29 K observed in composition En10Fs90 was fitted in a similar manner.

Because the C_ex–T behaviour of the Fs–En solid-solution members is characterised by broad, asymmetric bumps as Fe²⁺ gets successively diluted by Mg (compositions with X_Fs≤0.8), other empirical functions are required instead of Eqs. (9a) and (9b) for fitting (Fs90En10 is an exception, showing two peak-like features at 29 K and at 38 K; see Fig. 5). In the case of the olivine solid solution, Dachs et al. (2007) used two Gaussian functions for that purpose. In this contribution, we follow this treatment and combine Eq. (8) with three Gaussian functions to model these broad asymmetric C_ex features. The low-temperature side of these features could be fitted relatively well (compositions X_Fs≤0.6), allowing extrapolation from 2 K, the temperature where the experimental data cease, down to 0 K (Fig. 5, inset). The resulting fit parameter θ in Eq. (8) increases with increasing X_Fs, whereas the parameter SF decreases (values are given in the caption of Fig. S6). In Fs70En30 and Fs80En20, the lowermost C_ex data <10 K decrease nearly linearly with falling T, and the fitting of a separate Schottky anomaly, which worked for intermediate and Mg-rich compositions, failed here. The Schottky anomalies in these Fe-rich compositions are obviously superimposed by the increased magnitude of magnetic effects due to the high concentration of Fe²⁺. For these two cases, we assume that the Schottky anomaly follows the trend as indicated by the intermediate to Mg-rich compositions; i.e. we calculated C_Schottky by using extrapolated values for the parameters θ and SF in Eq. (8).

3.2.5 Entropies at 298.15 K

Integrating $C_{\mathrm{ex}}/T$ over the temperature range of 0–2 K, based on the calculated C_ex resulting, as described above, from the fitting procedure of the lowermost C_ex–T data (Fig. 5, inset), yields small entropy increments of the order of 0.1 to 0.7 J K⁻¹ mol⁻¹ for the Mg-rich and Fe-rich compositions, whereas larger values up to 1.2 J K⁻¹ mol⁻¹ are observed for the intermediate compositions (Table 2). The model lattice heat capacities at such low temperatures are so small that they do not affect the total heat capacity significantly and can be neglected.

The entropy increments from 0 to 2 K have to be added to each S_cal value to get the total entropies S²⁹⁸ of all investigated solid-solution members (Table 2). These are thus slightly larger than corresponding S_cal values. This modification is, however, small, and the conclusion of ideal entropic mixing behaviour along the En–Fs solid solution, i.e. zero excess entropies of mixing, remains valid (Fig. 2).

3.2.6 Excess entropies and their decomposition into Schottky-type and magnetic contributions

The derived excess entropies (Table 2) along the En–Fs solid solution are plotted in Fig. 6. Within error, they increase from zero in En in a linear manner to a maximum of 19.8 J K⁻¹ mol⁻¹ in Fs. They were calculated by numerically integrating $C_{\mathrm{ex}}/T$ over the temperature range of positive C_ex and adding the entropy increment from 0 to 2 K.

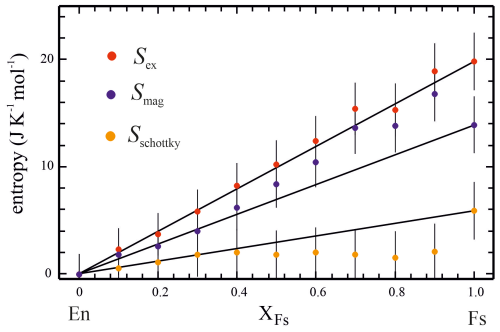
Figure 6 Excess entropy S_ex and its decomposition into Schottky-type and magnetic contributions (S_Schottky and S_mag, respectively) along the En–Fs binary.

The entropy due to Schottky effects, S_Schottky, increases linearly from zero in En to a value of 2.0 J K⁻¹ mol⁻¹ at intermediate compositions and then plateaus at roughly this value. In endmember Fs, it reaches its maximum at a value of 5.9 J K⁻¹ mol⁻¹. This was computed from appropriate integration of $C_{\mathrm{Schottky}}/T$ using the parameters θ and SF in Eq. (8), as given in the caption of Fig. S6.

Because the magnetic entropy, S_mag, was calculated from the relation $S_{\mathrm{mag}}=S_{\mathrm{ex}}-S_{\mathrm{Schottky}}$, it behaves inversely to the latter. Thus, S_mag values larger than that representing ideal mixing result in the Fe-rich portion of the En–Fs binary, where S_Schottky shows a plateau. The largest S_mag value of 16.8 J K⁻¹ mol⁻¹ is observed for the composition En10Fs90, whereas, in endmember Fs, it is 13.9 J K⁻¹ mol⁻¹.

4 Discussion and concluding remarks

4.1 Endmember heat capacities and entropies

For phase equilibrium calculations involving En, it can be concluded that the computation of its heat capacity according to Eq. (1) should be preferred over other representations in the literature (Krupka et al., 1985b; Holland and Powell, 2011) that indicate a larger C_p of the order of 1.5 % at 1000 K increasing to 3 % at 1500 K. This is especially applicable at high temperatures, e.g. for mantle equilibria. The reason for preferring the DSC data of this study compared to those of Krupka et al. (1985b) is shown in Fig. 3. With a value of m=0.00004 in Eq. (5) and using the DFT-computed C_v or, alternatively, the Kieffer model calculated with the parameters given in Table 3, the DSC-measured C_p of En from this study, and even the PPMS data down to approximately 50 K can be represented with a deviation of <1 % (Fig. S4). An almost similar slope of m=0.00005 is obtained if the C_p−C_v difference is calculated independently from the relation $C_{\mathrm{p}}-C_{\mathrm{v}}=T\cdot V\cdot {\mathit{\alpha }}^{\mathrm{2}}/\mathit{\kappa }$ and using values for V and α computed according to Hovis et al. (2021) and following the references cited therein (Fig. 3, short-dashed line). If, alternatively, the DSC data of Krupka et al. (1985b) were preferred, a steeper slope of m=0.00007 would be the required result (Fig. 3, long-dashed line) to achieve a match with those experimental data, in worse agreement with m based on α and V calculated as described in Hovis et al. (2021). This fact supports the validity of the DSC data of this study.

The standard entropy of $S^{\mathrm{o}}=\mathrm{132.3}\pm \mathrm{1.0}$ J K⁻¹ mol⁻¹ for En resulting from the PPMS data of this study agrees within error with that derived from Krupka et al. (1985a) using adiabatic calorimetry (132.5 J K⁻¹ mol⁻¹).

As outlined above, the heat capacity data of Fs above ∼140 K could be well represented, with a deviation of <1 % with the Kieffer model for its C_v (Table 3) and k=0.0001 following Eq. (5) to account for the C_p−C_v difference. At temperatures below 140 K, the Kieffer model parameters were tuned in such a way as to yield similar lattice heat capacities compared to what would result from the KW model (Fig. 4, inset). The so-calibrated Kieffer model served to compute the excess heat capacity of Fs by subtraction (Fig. 5). C_ex shows the prominent λ-shaped anomaly attributed to anti-ferromagnetic ordering peaking at T_N=38.4 K, in good agreement with T_N=38.7 K, as determined by Cemič and Dachs (2006). These authors used the Debye model for computing the lattice heat capacity of Fs, which predicts considerably smaller C_v values (Fig. 5) compared to this study as it considers only the acoustic phonon branches. The Kieffer model for lattice vibrations, on the other hand, includes both acoustic and optical phonon branches, which makes its use preferable because the so-calculated C_v can be expected to closer represent physical reality.

Fs's standard entropy is determined to be $S^{\mathrm{o}}=\mathrm{190.8}\pm \mathrm{1.3}$ J K⁻¹ mol⁻¹ in this study, 1.6 J K⁻¹ mol⁻¹ larger than that determined by Bohlen et al. (1983) from AC and 0.9 J K⁻¹ mol⁻¹ larger than that tabulated in the data base of Holland and Powell (2011). Based on the improved encapsulation technique for powders as used in this study, this S^o should be preferred over the value published by Cemič and Dachs (2006), which is too low for the reasons described above.

The decomposition of Fs's C_ex into magnetic and Schottky contributions is shown in Fig. S5, yielding, after appropriate integration, values of S_mag=13.9 J K⁻¹ mol⁻¹ and S_Schottky=5.9 J K⁻¹ mol⁻¹, summing up to 19.8 J K⁻¹ mol⁻¹ for S_ex, which, in turn, sums up with a vibrational entropy of S_vib=171.0 J K⁻¹ mol⁻¹ to the total entropy S₂₉₈=S^o of Fs (Table 2). The S_mag value obtained by our modelling is only approximately 52 % of the theoretically maximal value of 2Rln5 = 26.8 J K⁻¹ mol⁻¹ for the magnetic entropy. In relation to S^o, 89.6 % of Fs's entropy is of vibrational (or lattice) origin, 7.3 % is of magnetic origin, and 3.1 % of electronic origin (Schottky contribution). In the case of almandine and applying a similar modelling procedure, Dachs et al. (2012) obtained comparable relations. Here, 90.1 % of almandines' total entropy was of lattice origin, 9.5 % was of magnetic origin, and 0.4 % was of Schottky origin. In the case of fayalite, Dachs et al. (2007) estimated the various entropy contributions as follows: 79.5 % lattice, 17.2 % magnetic, and 3.3 % electronic. It is clear that all of these estimations depend critically on the size of C^vib as the outcome of the adopted model for the lattice heat capacity.

4.2 Solid-solution heat capacities and entropies

The measured solid-solution heat capacities (nine compositions, spaced in 0.1 X_Fs intervals) align in a consistent manner at high-enough temperatures (> ca. 140 K), where excess effects (magnetic, electronic) are no longer relevant. The heat capacity of all of these compositions above that temperature could be well represented using a linear combination of endmember lattice models for C_vib of En and Fs according to Eq. (7) and a similar equation used to compute m in Eq. (5) to convert C_v into C_p for the solid-solution members. The so-calculated heat capacities deviate by no more than 1 % from the measured values up to ∼700 K. The excess heat capacities shown in Fig. 5 have then been computed by subtracting these lattice C_p values from the experimental values.

The composition En10Fs90 deserves a special mention. Below ∼30 K, this composition has a larger (excess) heat capacity than the Fs endmember (Figs. 1 and 5), and it shows two magnetic C_p anomalies: a weaker one at the same temperature as T_N of endmember Fs (∼38 K) and a stronger one at a T_N of ∼29 K. The reason for this is unclear, but it might have to do with the fact that Fe²⁺ at the M1 site appears to have a different electronic ground state than Fe²⁺ at the M2 site in orthopyroxene (Shenoy et al., 1969). An almost similar T_N (28 K) was determined by Lin et al. (1993) by applying Mössbauer spectroscopy to a synthetic orthopyroxene with a composition of X_Fs=0.8, whereas an Mg-richer sample (X_Fs=0.51) did not reveal a T_N. Both compositions showing discrete magnetic C_p peaks (pure Fs and En10Fs90) were fitted using Eqs. (8) and (9).

C_ex of all other samples with X_Fs≤0.8 did not show any sharp anomalies but did show broad asymmetric humps down to the lowest temperatures. These cases were fitted combining Eq. (8) with Gaussian functions. The size of these buckles shrinks, and their temperature maximum shifts to successively lower T values with increasing dilution of the magnetically relevant Fe²⁺ by Mg. This is consistent with results from Shenoy et al. (1969). In their study on the magnetic behaviour of the Fe–Mg orthopyroxene system, they observed that samples with X_Fs≤0.4 produced only paramagnetic relaxation spectra and did not show magnetic ordering. From the two magnetic hyperfine fields in orthopyroxene (a smaller one for the M2 site and a stronger one for the M1 site), only the smaller field is present, which was interpreted as meaning that only the M2 site seems to be occupied sufficiently with Fe²⁺ in these magnetically diluted samples.

Schottky-type C_p anomalies are clearly visible in Mg-rich to intermediate compositions as plateaus or even upturns in C_p at the lowest temperatures of less than approximately 5 K (Fig. 5, inset). In pure Fs and En10Fs90, shoulders in the C_p−T behaviour around 10 K on the left flank of the C_p peaks are also attributed to such anomalies. The somewhat surprising observation that, at the lowest temperatures around 2 K, intermediate compositions have the largest C_p values of the order of 1.5 J K⁻¹ mol⁻¹ becomes evident when the Schottky contributions of all solid-solution members are compared (Fig. S6). As a result of the decomposition of C_ex, it is exactly these compositions that have the maxima of their Schottky contributions around 2 K. These maxima shift to higher T values around 10 K with increasing X_Fs so that C_Schottky is smaller for the Fe-rich compositions compared to the intermediate compositions at the lowest T values. The entropy increment S_Schottky from 0 to 2 K is thus largest for these intermediate compositions and constitutes the main contribution to S_ex for low to intermediate X_Fs solid-solution members (Table 2).

The main conclusion of our investigation is that the entropic mixing behaviour along the En–Fs join follows thermodynamic ideality, and all S₂₉₈ (Fig. 2) and S_ex values (Fig. 6) fall on the line connecting endmember entropies within error; i.e. excess entropies of mixing are zero in this solid solution. Deviations from the linear behaviour are observed for the decomposed values of S_mag and S_Schottky in the Fe-rich portion of the binary; i.e. S_mag is larger and S_Schottky is smaller than the linear combinations of endmembers. The composition En10Fs90 even seems to have a larger magnetic entropy than the Fs endmember (16.8 vs. 13.9 J K⁻¹ mol⁻¹). This is shown in Fig. S7, where the entropies S_ex, S_mag, and S_Schottky are compared for Fs and En10Fs90 as a function of temperature. Up to the T_N of Fs at 39 K, S_ex of En10Fs90 is indeed larger than that of the Fe endmember; at that T, there is a crossover, and relations reverse. This observation is not model dependent. Other models for lattice C_p, though yielding other absolute values of C_ex, would preserve this relation. The trends for S_mag and S_Schottky of these two Fe-richest compositions, on the other hand, are clearly model dependent and would apply if Eqs. (8) and (9) described the physics behind the magnetic and electronic excess heat capacities uniquely. The conclusion that En10Fs90 indeed has a larger magnetic entropy than the Fs endmember (Table 2, Fig. 6) depends critically on the magnitude of S_Schottky for this composition as derived from fitting C_ex.

4.3 Are the calorimetric results affected by Fe–Mg ordering?

As shown in the recent study of Benisek et al. (2023) on the vibrational entropy of disordering in omphacite, the entropy of disorder, ΔS_dis, consists of a vibrational and a configurational part. The latter, $\mathrm{\Delta }{\mathrm{S}}_{\mathrm{dis}}^{\mathrm{conf}}$, is routinely computed with some order–disorder model in petrological software applications. Holland and Powell (1996), for instance, derived a value of −13.9 kJ mol⁻¹ for the enthalpy change of the ordering reaction En + Fs = 2 FM from published site preference data showing that Fe²⁺ prefers the M2 site over the M1 site (FM is an ordered ferromagnesion pyroxene with Fe at the M2 site, Mg^M1Fe^M2Si₂O₆). With this ΔH value and applying the symmetric formalism described in this work, a value of $X_{{\mathrm{Fe}}^{M\mathrm{2}}}=\mathrm{0.73}$ would be computed at the synthesis temperature of 800 °C of our samples for the composition En50Fs50 as an example.

With regard to the vibrational part of the entropy of disordering, $\mathrm{\Delta }{S}_{\mathrm{dis}}^{\mathrm{vib}}$, Benisek et al. (2023) found that $\mathrm{\Delta }{S}_{\mathrm{dis}}^{\mathrm{vib}}$ is zero up to high temperatures of around 1000 °C by means of the calorimetric study of several – at different temperatures, disordered – omphacites. This indicates that the vibrational properties in the pyroxene structure are not significantly affected by the combined $\mathrm{Mg}/\mathrm{Al}$ and $\mathrm{Ca}/\mathrm{Na}$ cation ordering. We assume that this also applies for Fe–Mg ordering in the En–Fs solid solution, which involves the partitioning of only two cations, Fe and Mg, over the M sites. Moreover, the Fe–Mg substitution in orthopyroxene behaves thermodynamically ideally with regard to entropy, as shown in this study (Fig. 2). The temperature-dependent redistribution of Fe and Mg due to Fe–Mg ordering is, thus, very unlikely to have a measurable effect on the vibrational entropy of a given orthopyroxene solid-solution compound.