High-pressure behaviour of a CaIrO₃ perovskite-type structure

Structural refinements of single-crystal X-ray diffraction data collected at room temperature both under ambient and under high pressures up to 10 GPa have been used to characterise the octahedral tilting and site distortions of the orthorhombic Pbnm CaIrO₃ perovskite-type phase. The octahedral tilting has been evaluated using both the unit-cell lattice parameters and the displacements of the oxygen and A site from their hypothetical positions in an ideal cubic perovskite structure. The difference between the two types of calculations shows that the assumption of rigid and undistorted octahedra made for determining the tilt angles from the unit-cell parameters is valid only as a first approximation, especially in the case of CaRuO₃, CaRhO₃ and CaIrO₃ perovskites, for which polyhedral distortions are significant. CaIrO₃ perovskite appears to have much larger tilting and distortion than other CaO perovskites, likely causing the structure to be stiffer than expected from the general trend of the bulk moduli defined by other CaO perovskites. Moreover, in contrast to other CaO perovskites for which the Ca polyhedron is more compressible than the octahedral site, the compressibility of the IrO₆ octahedra is very similar to that of the CaO₁₂ polyhedra, giving rise to an octahedral tilting that is independent of pressure at least up to 10 GPa. This behaviour may help reduce the electronic interactions among oxygens of neighbouring octahedra during compression, given the already large tilts present in the CaIrO₃ perovskite structure, and it is likely responsible for the bulk modulus's first pressure derivative being smaller than 4. Larger tilting and distortions are also observed for CaO perovskites that have a Pt-group element occupying the octahedral site. Such perovskites have been found to undergo a phase transformation to an orthorhombic Cmcm post-perovskite phase (CaIrO₃-type structure) at pressures below 25 GPa, suggesting that a large octahedral tilting and polyhedral distortion may be a requisite for stabilising the orthorhombic post-perovskite phase of CaO perovskite-type materials.

1 Introduction

The discovery of a phase transition from orthorhombic Pbnm MgSiO₃ bridgmanite to an orthorhombic post-perovskite Cmcm phase (Murakami et al., 2004; Oganov and Ono, 2004) sparked major interest in the behaviour of CaIrO₃, which is isostructural with post-perovskite under ambient conditions and transforms to a perovskite-type structure at 1–3 GPa and temperatures > 1350 °C (McDaniel and Schneidler, 1972; Hirose and Fujita, 2005; Kojitani et al., 2007a; Stølen and Trønnes, 2007; Trønnes et al., 2006) and therefore can be used as an analogue of the high-pressure MgSiO₃ phases. However, the majority of studies have focused their attention on the behaviour of the Cmcm CaIrO₃ phase, whereas only one study (Cheng et al., 2011) has reported the structural data of the CaIrO₃ perovskite-type phase (CaIrO₃ pv) obtained from synchrotron X-ray powder diffraction. CaIrO₃ pv exhibits an orthorhombic Pbnm symmetry like many other CaO perovskites, which displays different degrees of distortion from the cubic aristotype perovskite structure Pm$\stackrel{\mathrm{‾}}{\mathrm{3}}m$. This distortion is described in terms of octahedral tilting about the pseudo-cubic axes (Glazer, 1972). Several methods have been used in the literature to calculate the tilt angles of the orthorhombic perovskite structure. The simplest way is to make use of unit-cell lattice parameters (i.e. Mitchell, 2002; O'Keeffe et al., 1979; Zhao et al., 1993) under the assumption that the octahedra are rigid and undistorted and that the orthorhombic distortion is therefore due to only octahedral tilting. However, since the octahedral framework in orthorhombic perovskite is neither rigid nor regular, a more accurate description of the octahedral tilting and polyhedral distortion of the orthorhombic perovskite structure is obtained from symmetry-mode analysis with respect to the ideal cubic perovskite structure. Symmetry modes are collective correlated atomic displacements that follow specific symmetry properties (Perez-Mato et al., 2010). The structural distortion in orthorhombic perovskites can be decomposed into contributions from different modes with symmetries given by the irreducible representations (Irreps) of the cubic Pm$\stackrel{\mathrm{‾}}{\mathrm{3}}m$ aristotype structure (Howard and Stokes, 2002, 1998; Perez-Mato et al., 2010). Such decomposition allows the octahedral tilting to be separated from the B- and A-site distortions. Only Irreps at the following k points of the reciprocal space of the cubic perovskite needs to be considered: Γ (0, 0, 0), X (0, 0, $\frac{\mathrm{1}}{\mathrm{2}}$), M ($\frac{\mathrm{1}}{\mathrm{2}}$, $\frac{\mathrm{1}}{\mathrm{2}}$, 0) and R ($\frac{\mathrm{1}}{\mathrm{2}}$, $\frac{\mathrm{1}}{\mathrm{2}}$, $\frac{\mathrm{1}}{\mathrm{2}}$). Using the notation of Miller and Love (1967), Howard and Stokes (1998, 2002) have shown that the two Irreps $R_{\mathrm{4}}^{+}$ and $M_{\mathrm{3}}^{+}$ induce the out-of-phase and in-phase tilt patterns of the perovskite octahedral framework and that they are truly independent of the polyhedral distortion. For Pbnm perovskites, three more Irreps are indicated as secondary symmetry modes, since they do not drive the displacive phase transformation from the cubic to the orthorhombic structure. These modes ($R_{\mathrm{5}}^{+}$, $X_{\mathrm{5}}^{+}$ and $M_{\mathrm{2}}^{+}$) usually have much smaller amplitudes with respect to the $R_{\mathrm{4}}^{+}$ and $M_{\mathrm{3}}^{+}$ primary modes and are responsible for the polyhedral distortion in orthorhombic perovskite. Moreover, whilst the $R_{\mathrm{4}}^{+}$, $M_{\mathrm{3}}^{+}$ and $M_{\mathrm{2}}^{+}$ modes are related only to displacements of the oxygen atoms, the $R_{\mathrm{5}}^{+}$ and $X_{\mathrm{5}}^{+}$ modes are due to displacements of both the oxygen atoms and the Ca atoms occupying the A site. A sketch visualisation of the displacements of the oxygens and A-site cations from their ideal position in the cubic aristotype structure associated with the five symmetry-adapted modes is given in Huang et al. (2021).

For CaB⁴⁺O₃ perovskites, with B representing the cation occupying the octahedral B site, we can expect that octahedral tilting and distortion vary systematically with the size of the B-site cations, since Ca always occupy the cavity (A site) of the three-dimensional octahedral framework. This hypothesis is supported by the fact that the variation in the isothermal bulk modulus (K_T0) of CaB⁴⁺O₃ perovskites with the B cation being Zr, Sn, Ti and Ge falls on a single smooth trend versus the inverse of the molar volume (Ross and Chaplin, 2003), implying that for larger unit-cell volumes (i.e. at lower atom packing densities), the bulk modulus is lower and the perovskites are softer. However, the bulk modulus of CaIrO₃ pv determined both from compression experiments (Boffa Ballaran et al., 2007) and from ab initio calculations (Marbouh et al., 2021) is much higher than that of other CaO perovskites and plots above the trend reported by Ross and Chaplin (2003). Moreover, the first pressure derivative of the bulk modulus, K^′, is smaller than 4, whereas the other CaO perovskites have K^′ values close to 6. In order to shed light on the structural reasons for the anomalous stiffening of CaIrO₃ perovskite with respect to the other CaB⁴⁺O₃ perovskite, we performed a high-pressure diffraction study on a single crystal of CaIrO₃ pv and obtained the variation in the crystal structure of this perovskite up to 10 GPa.

2 Experimental method

2.1 Single-crystal X-ray diffraction under ambient conditions and structural refinements

A single crystal of CaIrO₃ pv with dimensions $\mathrm{69}\times \mathrm{86}\times \mathrm{148}$ µm³ (Ba8x2) was selected from the run product synthesised in a previous study (Trønnes et al., 2006) at 1525 °C and 2.5 GPa in a piston-cylinder apparatus from a starting mixture of high-purity CaCO₃ and IrO₂ decarbonated and sintered at 900–950 °C. A crystal from the same run product was used in the compressibility study performed by Boffa Ballaran et al. (2007). Full-intensity data collection for structural refinements under ambient conditions was performed using the Oxford Diffraction Xcalibur diffractometer equipped with a graphite monochromator; a ceramic X-ray tube with Mo radiation, operated at 50 kV and 40 mA; and a Sapphire 2 CCD detector. Complete and redundant intensity data were collected using ω scans with a width of 0.5° and a default time of 15 s up to 2θ=72.5°. The intensity data were integrated using CrysAlisPro software (Oxford Diffraction, Rigaku), applying Lorentz and polarisation corrections. Given the large linear absorption coefficient of CaIrO₃ pv (μ=60.05 mm⁻¹ for Mo radiation), an analytical absorption correction based on the crystal shape (Clark and Reid, 1995) was also performed together with an empirical correction, taking into account frame and detector area scaling. A total of 568 unique reflections were obtained, of which 526 have I > 2σ(I), with a final discrepancy factor R_int=0.0557. Systematic absences are consistent with the Pbnm space group, which has therefore been used to solve the CaIrO₃ pv structure using the SHELXS programme (Sheldrick, 2015). The Ir and Ca atomic positions were identified using the Patterson algorithm, whereas the oxygen positions in the asymmetric unit were found by analysing the difference electron density map. Structural refinements were performed using the SHELXL programme (Sheldrick, 2015) built in the ShelXle (Hübschle et al., 2011) graphical user interfaces. Neutral scattering factors for Ca, Ir and O were used, and all atoms were refined anisotropically. The crystallographic information file (CIF) is available in the Supplement.

2.2 High-pressure single-crystal X-ray diffraction and structural refinements

Unfortunately, the Ba8x2 crystal was lost while trying to cut it to produce a smaller crystal suited for the high-pressure experiment. Therefore, another crystal (Ba8x4) with dimensions $\mathrm{61}\times \mathrm{34}\times \mathrm{20}$ µm³ was selected. A BX90-type diamond anvil cell (DAC) (Kantor et al., 2012), with diamond culets of 400 µm diameter glued into Boehler–Almax seats with an opening angle of 90°, was prepared with a Re gasket pre-indented to a thickness of ∼ 60 µm from its original thickness of 200 µm. A hole with a diameter of 200 µm was laser-cut into the centre of this indentation to produce the sample chamber. The CaIrO₃ crystal was loaded inside the DAC together with a small ruby sphere as a pressure calibrant (Shen et al., 2020). Neon gas was loaded into the DAC to act as a pressure-transmitting medium, using the gas-loading system installed at the BGI (Kurnosov et al., 2008). The DAC was left to stabilise after each pressure increase for at least 1 d before performing the XRD measurements. The ruby luminescence was measured before and after each XRD measurement by means of a Horiba LABRAM HR Raman micro-spectrometer equipped with an 1800 gr mm⁻¹ grating and a He–Ne laser (λ=632.8 nm) with 20 mW laser power.

Intensity data for all accessible reflections were collected at room temperature and at six different pressure points, including ambient pressure in the DAC without a pressure medium up to 9.7 (1) GPa. Above this pressure, significant broadening of the reflections was observed, and therefore the experiment was interrupted. Data collection at different pressures was performed using ω scans with a step size of 1° in a fixed-φ mode (Finger and King, 1978) up to 63° in 2θ. Every frame was measured for 120 s. The intensity integration was performed using CrysAlisPro software (Oxford Diffraction, Rigaku), applying Lorentz and polarisation corrections. Absorption effects due to the sample and diamonds, as well as shadowing effects due to the gasket, have been taken into account using the Absorb programme (Angel, 2004) implemented in the CrysAlisPro software. Due to the DAC spatial limitation, the resulting number of unique reflections was 241 for the crystal in the DAC under ambient pressure and between 210 and 230 for the collections performed under high pressures. Structural refinements were performed using the SHELX programmes (Sheldrick, 2015) built in the ShelXle (Hübschle et al., 2011) graphical user interface, using the starting parameters obtained in this study under ambient conditions. Neutral scattering factors for Ca, Ir and O were used, and, due to the limited number of unique reflections, all atoms were refined isotropically. Difference Fourier maps show some residual electron density around the Ir atom, given the high electronic number of this atom and the use of an isotropic model. For this reason, uncertainties regarding the oxygen positions are larger than those obtained under ambient conditions but are still sufficiently precise for constraining the high-pressure compression of the CaIrO₃ pv structure. A CIF containing all the high-pressure refinements of crystal Ba8x4 is available in the Supplement.

3 Results and discussion

3.1 Structural features of CaB⁴⁺O₃ perovskites under ambient conditions

The constrained unit-cell lattice parameters of the Ba8x2 sample obtained from a total of 2158 non-unique reflections (Table 1) are within 2σ from those published for another crystal of CaIrO₃ pv taken from the same run product (Boffa Ballaran et al., 2007), obtained using the accurate eight-position centring method (Angel et al., 2000; King and Finger, 1979) with a point detector. The structural data obtained in this study are also in good agreement with those obtained from Rietveld refinements of synchrotron powder diffraction data (Cheng et al., 2011).

The octahedral volumes, V_B, of CaIrO₃ pv and of several CaB⁴⁺O₃ perovskites follow, as expected, a linear trend as a function of the ionic radius (Shannon and Prewitt, 1969) of the cation occupying the octahedral site (Fig. 1), increasing from CaGeO₃ up to the large CaPbO₃ (Table 2). CaIrO₃ and, to a lesser extent, CaRhO₃ deviate slightly from the trend, though. This deviation is also visible in the variation in the V_B values with the molar volume, V_mol (Fig. 2), whereas the volume of the A site, V_A, defined as the volume of the unit cell normalised to the number of formula units minus the volume of the B site ($V_{\mathrm{A}}=V/Z-V_{\mathrm{B}}$), of all the CaB⁴⁺O₃ perovskites, including CaIrO₃, varies linearly as a function of V_mol (Fig. 2).

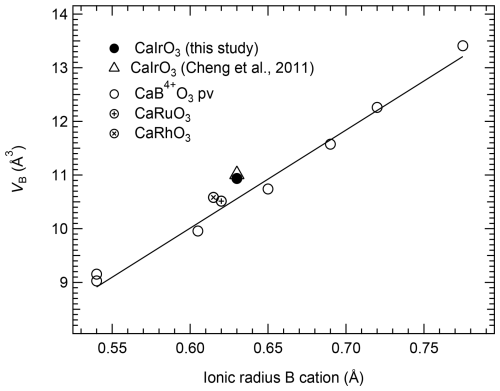
Figure 1 Linear correlation between the octahedral volume, V_B, and the ionic radius of the cation occupying the B site for several CaB⁴⁺O₃ pv (Table 2) and for CaIrO₃ pv investigated in this study and in the study from Cheng et al. (2011). The solid line is a linear weighed fit through the CaB⁴⁺O₃ perovskite data reported in Table 2. The uncertainties are smaller than the symbol size.

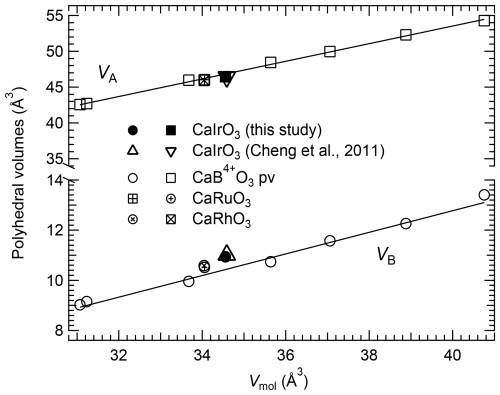
Figure 2 Linear correlation of the octahedral volume, V_B (circles), and the volume of the A site, V_A (squares), with the molar volume, V_mol, of several CaB⁴⁺O₃ pv. The V_B values of CaIrO₃ deviate slightly from the linear trend. Solid lines are linear weighed fits through the CaB⁴⁺O₃ perovskite data reported in Table 2. The uncertainties are smaller than the symbol size.

The octahedral tilting can be expressed in terms of three tilt angles: θ, φ and Φ (O'Keeffe and Hyde, 1977; Zhao et al., 1993), representing the tilt of the octahedra about the pseudo-cubic [110]_pc, [001]_pc and [111]_pc directions of the aristotype Pm$\stackrel{\mathrm{‾}}{\mathrm{3}}m$ perovskite structure. These can be calculated from the a, b and c unit-cell lattice parameters of the Pbnm perovskite structure assuming rigid and non-distorted octahedra according to Zhao et al. (1993):

$$\begin{array}{}\text{(1)}& {\displaystyle }cos\mathit{\theta }=a/b,\text{(2)}& {\displaystyle }cos\mathit{\varphi }=\sqrt{\mathrm{2}}a/c,\end{array}$$

with the Φ tilt being a combination of Eqs. (1) and (2).

$$\begin{array}{}\text{(3)}& \cos \mathrm{\Phi }=\cos \mathit{\theta }\cos \mathit{\varphi }={\displaystyle \frac{\sqrt{\mathrm{2}}{a}^{\mathrm{2}}}{bc}}\end{array}$$

The θ tilt results from the two anti-phase tilts of equal magnitude about the [100]_pc and [010]_pc directions (Glazer, 1972; Megaw, 1973), and it is indicated as the out-of-phase tilt, whereas the φ tilt results from the tilt about the [001]_pc direction and is indicated as the in-phase tilt. The θ and φ tilt angles are plotted as a function of V_mol in Fig. 3. The octahedral tilting increases from CaGeO₃, for which both tilt angles are close to 3°, to CaPbO₃, for which the tilt angles are larger than 10° with θ > φ. CaIrO₃, CaRuO₃ and CaRhO₃ have a much more pronounced octahedral tilting, with the out-of-phase tilt having a larger deviation from the trend defined by the other CaB⁴⁺O₃ perovskites (Fig. 3).

Table 1 Unit-cell lattice parameters and polyhedral volumes of the CaIrO₃ perovskite-type phase measured under ambient conditions and high pressure (Pbnm space group).

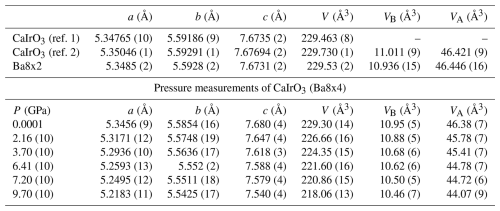
Ref 1: Boffa Ballaran et al. (2007). Ref. 2: Cheng et al. (2011).

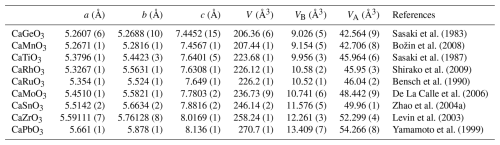
Table 2 Unit-cell lattice parameters and polyhedral volumes of CaB⁴⁺O₃ perovskite-type phases reported in the literature (Pbnm space group).

Since the assumption of rigid octahedra is valid only as a first approximation and, moreover, tilting of the octahedral framework also induces a distortion of the A polyhedron, the atomic positions obtained in this study have been used to calculate the Irreps for the Pbnm CaIrO₃ structure with respect to an ideal cubic perovskite having the same volume using the ISODISTORT programme (Campbell et al., 2006). The same calculations have been performed for the other CaB⁴⁺O₃ perovskites. As expected, the largest amplitudes computed by the programme are those relative to the symmetry-adapted modes $R_{\mathrm{4}}^{+}$ and $M_{\mathrm{3}}^{+}$, which are exclusively responsible for the octahedral tilting. From the amplitude of these two symmetry-adapted modes, it is therefore possible to calculate the out-of-phase and in-phase tilts independently of the polyhedral distortion using the equations reported by Wang and Angel (2011):

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\theta }}_{R_{\mathrm{4}}^{+}}=\arctan \left(\mathrm{2}{d^{\prime }}_{R_{\mathrm{4}}^{+}}\right),\text{(5)}& {\displaystyle }{\mathit{\varphi }}_{M_{\mathrm{3}}^{+}}=\arctan \left(\mathrm{2}{d^{\prime }}_{M_{\mathrm{3}}^{+}}\right),\end{array}$$

where d^′ is derived from the output of ISODISTORT following the procedure outlined by Wang and Angel (2011) (see their example for MgSiO₃ bridgmanite).

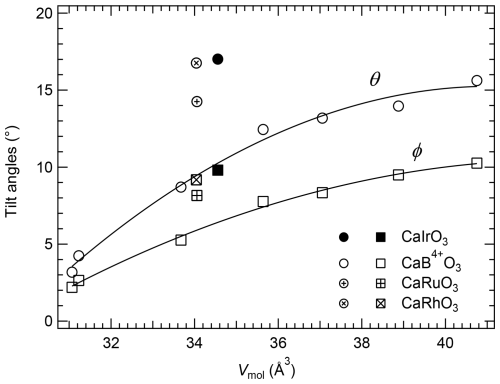
Figure 3 Variation in the out-of-phase, θ (circles), and in-phase, φ (squares), tilts of orthorhombic CaB⁴⁺O₃ pv as a function of their molar volumes. The tilts of CaIrO₃ obtained in this study, as well as those of CaRuO₃ and CaRhO₃, clearly deviate from the trends. The solid curves are polynomial weighed fits through the CaB⁴⁺O₃ perovskite data from Table 2, with CaRhO₃ and CaRuO₃ excluded. The uncertainties are smaller than the symbol size.

The variations with V_mol of ${\mathit{\theta }}_{R_{\mathrm{4}}^{+}}$ and ${\mathit{\varphi }}_{M_{\mathrm{3}}^{+}}$ (Fig. 4) are different from the tilting patterns obtained using the unit-cell lattice parameter values (Fig. 3). Not only is their variation with the molar volume of the CaB⁴⁺O₃ perovskites linear, but the values of the in-phase and out-of-phase tilts are also very similar for all analysed samples. However, similarly to what was observed for the tilts obtained from the unit-cell parameters, the values calculated for CaIrO₃, CaRhO₃ and CaRuO₃ are much larger and deviate from the trend described by the other CaB⁴⁺O₃ perovskites. The difference between the two sets of calculations is due to the fact that the polyhedral distortion in these perovskites is not negligible; nevertheless, even as just a first approximation, the tilt angles obtained from the unit-cell lattice parameters, based on the assumption of rigid and undistorted polyhedra, already highlight the distinctive behaviour of perovskites having a Pt-group element (i.e. Ir, Ru and Rh) occupying the octahedral site.

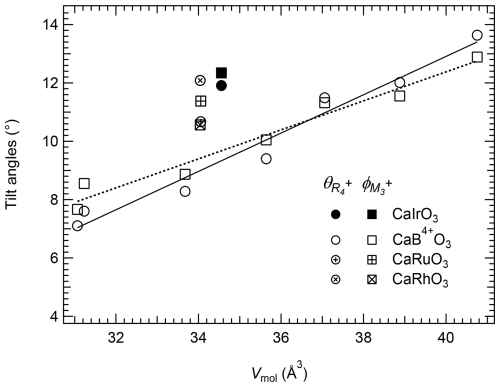
Figure 4 Variation in the out-of-phase, ${\mathit{\theta }}_{R_{\mathrm{4}}^{+}}$, and in-phase, ${\mathrm{\varnothing }}_{M_{\mathrm{3}}^{+}}$, tilts calculated from the symmetry-adapted $R_{\mathrm{4}}^{+}$ and $M_{\mathrm{3}}^{+}$ mode amplitudes for CaB⁴⁺O₃ pv. Note that the values obtained for CaIrO₃, CaRuO₃ and CaRhO₃ clearly deviate from the trends described by the other CaB⁴⁺O₃ pv. The estimated uncertainties are smaller than the symbol size. The solid and dotted lines are linear weighed fits through the ${\mathit{\theta }}_{R_{\mathrm{4}}^{+}}$ and ${\mathrm{\varnothing }}_{M_{\mathrm{3}}^{+}}$ CaB⁴⁺O₃ perovskite data, respectively.

The polyhedral distortion is mainly due to the symmetry-adapted mode $X_{\mathrm{5}}^{+}$ and, in particular, the displacement of the Ca atoms ($X_{\mathrm{5}}^{+}$ A) (Fig. 5), since the amplitudes of the symmetry-adapted modes $R_{\mathrm{5}}^{+}$ and $M_{\mathrm{2}}^{+}$ are practically negligible. The distortion of the A-site polyhedron increases due to the displacement of the Ca atoms toward one side of the cavity, probably in order to have better coordination with at least some of the oxygen atoms, as a consequence of the octahedral frameworks becoming larger with the increasing size of the cation occupying the B site. However, the A sites of CaIrO₃, CaRuO₃ and CaRhO₃ perovskites appear much more distorted than expected from the size of the octahedral cations. The above observations, therefore, suggest that, in the case of the CaO orthorhombic perovskite structures, octahedral tilting and distortion result primarily from the mismatch of the B- and A-cation sizes, whereas, in the case of the Pt-group element perovskites, the B site appears larger than expected, giving rise to a larger orthorhombic distortion. This behaviour may be due to the small difference in electronegativity between the Pt-group elements and the oxygen, causing a weaker and therefore longer-than-expected ionic bond at the octahedral site.

CaIrO₃, CaRuO₃ and CaRhO₃ perovskites transform under high pressure to a post-perovskite phase (orthorhombic Cmcm CaIrO₃-type structure), which is either the stable phase under ambient pressure (CaIrO₃) or the metastable phase that is easily quenchable (Hirose and Fujita, 2005; Kojitani et al., 2007a, b; Shirako et al., 2009). A Cmcm CaIrO₃-type structure has also been found for CaPtO₃ (Inaguma et al., 2008); however, no report of a perovskite structure of this compound is present in the literature.

Akaogi et al. (2010) have reported that there is an inverse correlation between the transition pressure of these perovskites and the tilt angle Φ (Eq. 3). CaSnO₃ pv has a Φ angle similar to that of CaRuO₃ pv, and it has been reported to transform to a post-perovskite structure (Tateno et al., 2010) that can be quenched under room conditions, albeit just as a mixture of perovskite and post-perovskite phases rather than a single phase as for the other three perovskites. The transition, however, occurs above 40 GPa, i.e. at pressures much larger than expected from the Φ tilt trend defined by the Pt-group perovskites (Akaogi et al., 2010), suggesting that not only octahedral tilting but also polyhedral distortion may play a significant role in determining the pressure at which the perovskite-to-post-perovskite phase transformation occurs. The large tilting and polyhedral distortion may also significantly affect the compressibility of these three perovskites, making them stiffer than expected, as observed for CaIrO₃ pv (Boffa Ballaran et al., 2007).

3.2 Compression mechanism of CaB⁴⁺O₃ perovskites

The unit-cell lattice parameters of the Ba8x4 crystal loaded in the DAC under room pressure before loading the pressure-transmitting medium were obtained from a total of 354 non-unique reflections and are in good agreement with those determined for the Ba8x2 crystal (Table 1). The bulk compression behaviour of the Ba8x4 crystal is also in agreement with the equation of state determined by Boffa Ballaran et al. (2007), confirming that CaIrO₃ pv is much stiffer than other CaB⁴⁺O₃ perovskites (Boffa Ballaran et al., 2007; Ross and Chaplin, 2003). The high-pressure structural evolution of non-cubic ABO₃ perovskites under hydrostatic conditions depends on the relative compression of the BO₆ octahedra and AO₁₂ polyhedra (e.g. Zhao et al., 2004b), with consequent change in octahedral tilting. For A²⁺B⁴⁺O₃ perovskites, the BO₆ octahedra are expected to be less compressible than the AO₁₂ polyhedra, and the octahedral tilting is therefore expected to increase with pressure. This is the case for CaSnO₃ (Zhao et al., 2004a) and CaTiO₃ (Zhao et al., 2011), for which it was shown that the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio decreases with increasing pressure. In contrast, the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio obtained in this study for CaIrO₃ pv appears to be independent of pressure (Fig. 6). A weighed linear fit through the data even suggests a slight increase in the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio with pressure, implying that the octahedral site of CaIrO₃ pv has a compressibility similar to or even larger than that of the A site, in contrast to the observed trend for the other two CaB⁴⁺O₃ perovskites.

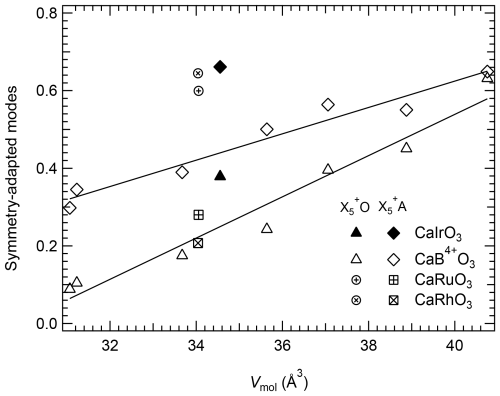
Figure 5 Variation with molar volume in the amplitude of the symmetry-adapted modes $X_{\mathrm{5}}^{+}$ relative to the displacement of the oxygen, $X_{\mathrm{5}}^{+}$O, and Ca atoms, $X_{\mathrm{5}}^{+}$A, from the ideal positions of the aristotype cubic structure for CaB⁴⁺O₃ pv. The values obtained for CaIrO₃, CaRhO₃ and CaRuO₃ deviate from the trends described by the other CaB⁴⁺O₃ pv. Solid lines are linear weighed fits through the CaB⁴⁺O₃ pv data.

Figure 6 Variation with pressure in the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio of CaIrO₃ pv (this study) compared with values for CaSnO₃ (Zhao et al., 2004a) and CaTiO₃ (Zhao et al., 2011). In contrast to what is expected for A²⁺B⁴⁺O₃ perovskites, the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio of CaIrO₃ pv is independent of pressure, at least in the pressure range investigated in this study.

Since the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio can be used to describe the octahedral tilting of orthorhombic perovskites, i.e. the larger the tilt, the larger the deviation of the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio from the ideal value of 5 in the cubic aristotype perovskite, it appears that the orthorhombic distortion of CaIrO₃ due to octahedral tilting remains constant at least up to 10 GPa, in contrast to the other two CaB⁴⁺O₃ perovskites, whose tilting increases with pressure (Zhao et al., 2004a, 2011).

This behaviour is quite surprising since it has been suggested that the perovskite-to-post-perovskite transformation is driven by the repulsion between inter-octahedral anions, which become closer due to the increasing octahedral tilting with pressure. Martin and Parise (2008) analysed the structural data of 70 perovskites under ambient and high-temperature or high-pressure conditions and suggested that a minimum $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio of ∼ 4.03 should be reached in order for the inter-octahedral anion distances to be equal to the intra-octahedral anion distances, hence causing the transition to post-perovskite. These authors show that the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio decreases and octahedral tilting increases with pressure not only for CaSnO₃, but also for other perovskite-structured materials, for example NaMgF₃ and SrCeO₃. This is also valid for the end-member MgSiO₃ bridgmanite and Al-bearing bridgmanite, for which it has been found that the A site is more compressible than the B site (Criniti et al., 2024). Following Martin and Parise (2008), the distances l_[001] between the oxygens in the 8d Wyckoff position along the c axis of the CaB⁴⁺O³ perovskites, normalised with respect to the intra-oxygen distance of the accompanying octahedral site, O–O_oct, are reported as a function of the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio for the CaB⁴⁺O₃ perovskites (Fig. 7). The $l_{\left[\mathrm{001}\right]}/$ O–O_oct distances of CaTiO₃ at 8.11 GPa of CaSnO₃ at 6.73 GPa and CaIrO₃ at 9.7 GPa are also reported in the same figure. All data points closely follow the mathematical model defined by Martin and Parise (2008), likely due to the fact that this inter-anion distance is not sensitive to deformation of the octahedra, as already noted by those authors.

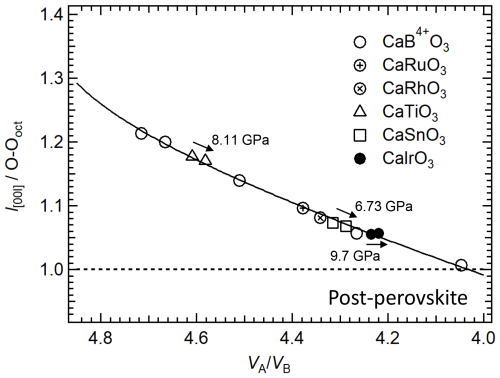
Figure 7 Variation with the $V_{\mathrm{A}}/V_{\mathrm{B}}$ ratio in the inter-oxygen distances l_[001] along the c axis, normalised with respect to the intra-oxygen distance of the accompanying octahedral site, O–O_oct, for the CaB⁴⁺O₃ pv. The high-pressure values for CaIrO₃ pv (this study), CaSnO₃ (Zhao et al., 2004a) and CaTiO₃ (Zhao et al., 2011) are also reported. The solid line is the mathematical model reported by Martin and Parise (2008).

There are, however, two important points to be made: (i) the $l_{\left[\mathrm{001}\right]}/$ O–O_oct values of CaRuO₃ and CaRhO₃ are larger than those of CaSnO₃; therefore if tilting alone was driving the perovskite-to-post-perovskite transition, one would expect a higher transition pressure for CaRuO₃ and CaRhO₃ than for CaSnO₃, contrary to what has been reported, and (ii) in spite of the smaller pressure range investigated for CaTiO₃ and CaSnO₃, the change in $l_{\left[\mathrm{001}\right]}/$ O–O_oct due to increasing pressure is much more accentuated for these two perovskites than for CaIrO₃ (this study), confirming that the octahedral tilting for CaIrO₃ does not change at least up to 10 GPa. This suggests that for CaIrO₃, and likely also for the other Pt-group perovskite-structured materials, octahedral tilts alone are not sufficient to explain the mechanism for the perovskite-to-post-perovskite transition. A major factor driving the phase transformation appears to be the displacement of the Ca atoms, which is already quite large under room conditions for the Pt-group element perovskites (Fig. 5) and increases significantly with pressure for CaIrO₃ relative to the displacement of Ca in the CaSnO₃ structure (Fig. 8).

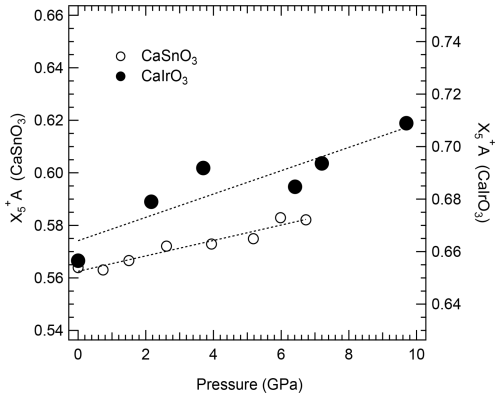
Figure 8 Variation with pressure in the amplitude of the symmetry-adapted modes $X_{\mathrm{5}}^{+}$ relative to the displacement of the Ca atoms, $X_{\mathrm{5}}^{+}$A, from the positions of the aristotype cubic structure for CaSnO₃ (left axis) and CaIrO₃ pv (right axis). The scale of the two axes is identical to better visualise the larger increase in the distortion of CaIrO₃ compared to CaSnO₃. The dotted lines are guides to eye. Uncertainties are smaller than the symbol sizes.

It is very likely that, as the Ca atoms are displaced toward one side of the large A site in CaIrO₃ pv, some of the Ca–O bond distances become shorter, giving rise to a much stiffer A site with respect to that of the CaSnO₃ structure. Because the octahedral tilting in CaIrO₃ is hindered by such polyhedral distortion, we can expect that the structure becomes more unstable under compression, favouring the transformation to the post-perovskite phase at pressures lower than would be expected if octahedral tilting alone were the main cause of the transition.

4 Conclusions

Refinements to single-crystal intensity data collected under both ambient and high-pressure conditions have allowed us to clarify the tilting and distortion of orthorhombic CaIrO₃ pv. Both octahedral tilting (Figs. 3 and 4) and A-site distortion (Fig. 5) of this perovskite are much larger with respect to other CaB⁴⁺O₃ perovskites, causing the CaIrO₃ structure to be much stiffer than expected. The larger tilting and distortion appear to be characteristic of orthorhombic perovskites with a Pt-group element (i.e. Ir, Ru and Rh) occupying the octahedral site. Although there are no compressibility data for CaRuO₃ and CaRhO₃, it can be expected that the bulk modulus will also be larger than the trend shown by several other CaB⁴⁺O₃ perovskites (Ross and Chaplin, 2003) for these two perovskites. Another peculiarity of the CaIrO₃ structure is represented by the fact that the B and A sites have similar compressibility, at least up to 10 GPa, resulting in the octahedral tilt remaining constant instead of increasing with increasing pressure. The similar compression of the two sites may hinder oxygen–oxygen repulsion, which is the main factor responsible for stiffening the perovskite structure with increasing pressure, giving rise to a bulk modulus first pressure derivative, K^′, smaller than 4. Ultimately, we can hypothesise that the relatively large stiffness of CaIrO₃, the similar compressibility of the B and A sites, and the large distortion of the A-site polyhedron play an important role in determining the transformation pressure at which the perovskite structure transforms to the orthorhombic Cmcm post-perovskite and therefore should be a common feature of the Pt-group perovskites for which the same transformation has been reported (Akaogi et al., 2010).