The 8 Å crystal structure and new crystal chemical data of rouxelite from the Monte Arsiccio mine, Apuan Alps, Italy

The crystal structure of rouxelite from the Monte Arsiccio mine, Italy, has been investigated using single-crystal X-ray diffraction (SCXRD) to clarify its crystallography and crystal chemistry. The structure is described in space group C-1, with lattice parameters a= 43.1883(12), b= 8.1037(2), c= 38.1470(10) Å, α= 96.001(2), β= 116.615(2), γ= 95.372(2)°, and V = 11721.7(6) ų. The structure can be considered as being a twofold superstructure (doubled b cell parameter) of the C2$/m$ rouxelite structure previously reported from Buca della Vena mine. The asymmetric unit in the structure of rouxelite contains 53 cation sites and 66 anion sites. The metal sites are composed of 22 Pb positions, 28 Sb positions, one Hg position, and two Cu positions. Among the Pb sites, four are mixed with Tl, Sb, Ag, and As and two are split. Among the Sb sites, three Sb sites are mixed with Pb and As and three are split. The Hg position includes Ag, and two sulfur sites (S65 and S66) are partially occupied. Final refinement, performed as a twin with volume ratios of 0.5489 : 0.4510(14), resulted in an R₁ value of 0.0855 for 55765 unique reflections. The crystal under investigation was an intergrowth with a second domain whose cell parameters correspond to those of launayite. The resulting structural formulae obtained from the SCXRD study for the unit cell is either Cu₈Ag_2.08Hg_3.068Tl₂Pb_83.568As_1.448Sb_111.836S_261.52 (for Z = 1, ch = 2.16) or Cu₈Ag_2.09Hg_3.064Tl₂Pb_83.556As_1.452Sb_111.84S_261.32O_1.52 (for Z = 1, ch = −0.47) (O content could not be reliably determined), making the definition of an ideal formula difficult. Additionally, a substantial volume of new chemical data for rouxelite has been included, covering both the Monte Arsiccio mine and the neighbouring Buca della Vena occurrences, thereby enhancing the previously published data. The crystal chemistry, substitution mechanisms, and modular description of rouxelite as well as the modular relationship to other minerals are also addressed.

1 Introduction

Rouxelite is a very rare Cu-Hg-Pb-Sb sulfosalt, first described by Orlandi et al. (2005) from the Buca della Vena Fe-Ba ore deposit in the Apuan Alps, Tuscany, Italy. It was found in association with bournonite, tetrahedrite, and sphalerite. The published ideal formula is Cu₂HgPb₂₂Sb₂₈S₆₄(O,S)₂, with a Pb $/$ Sb ratio of 0.786. The structure of a twofold subcell was described as monoclinic with the space group C2$/m$ and unit-cell parameters a= 43.113, b=  4.059, c= 37.874, β= 117.35°, V= 5887 ų, and Z= 2. Despite a poor R₁ value of 0.169, the X-ray single-crystal study revealed a novel, interesting, and complex crystal structure with Cu and Hg occupying specific sites. The large discrepancies between empirical (with an electron probe microanalysis (EPMA)-measured O that is too high) formula, structural formula, and ideal formula were not explained. The authors described the structure of rouxelite as a three-component boxwork structure, and they stated that “Very large topologically equivalent columns are recognizable in rouxelite and kobellite, which have about 90 % of their structure motif in common.”

A (Tl-Ag)-bearing rouxelite was later described by Biagioni et al. (2014) from the Ba-Fe ore deposit of the Monte Arsiccio mine, Apuan Alps, Tuscany, Italy. It was found in association with zinkenite and the rare minerals robinsonite and Tl-bearing chovanite. The X-ray powder diffraction pattern of rouxelite material from the Monte Arsiccio mine showed similar unit-cell parameters to those of rouxelite from Buca della Vena. However, X-ray single-crystal studies on Monte Arsiccio rouxelite were not undertaken due to poor-quality diffraction data. The presence of Tl and Ag in the chemistry was emphasized, and the crystal chemistry and substitution mechanisms were analysed in detail (Biagioni et al., 2014).

In connection with our previous analytical work on Monte Arsiccio sulfosalt material, we found rouxelite grains suitable for single-crystal X-ray diffraction (SCXRD), allowing us to perform a successful single-crystal study of this mineral. This study aims to clarify the crystallography and crystal chemistry of rouxelite from the Monte Arsiccio mine. The present paper intends to expand the knowledge and understanding of this very rare and complex mineral in particular and to contribute to the broader field of sulfosalt research in general.

2 Material and experimental methods

2.1 Monte Arsiccio and Buca della Vena material

Two samples (FK055 and FK056) containing rouxelite from Buca della Vena and 14 samples from the Monte Arsiccio mine (4 from one of us (Frank Keutsch) and 10 from German collector Alois Lechner) were analysed using optical microscopy, microprobe analysis, and single-crystal X-ray diffraction methods. Sulfosalt aggregates were carefully extracted from the hand specimens, embedded in epoxy resin, and polished to a final level of 0.25 µm.

An aggregate with sub-parallel intergrown needle-like crystals of rouxelite from the Monte Arsiccio mine (AL) is shown in Fig. 1. The back-scattered electron (BSE) images in Fig. 2a reveal the homogeneous chemical composition of rouxelite grains, extracted from the aggregate shown in Fig. 1, and minimal intergrowths with other minerals. Figure 2b illustrates the complex crystal intergrowth and/or twinning of the single crystals of rouxelite within the same aggregates. Other parts of the sample mentioned above, as well as parts of other samples, show aggregates of mixtures of fine needle-like crystals of zinkenite, rare robinsonite, and a new mineral, i.e. proto-owyheeite (Topa et al., 2024). No oxygen-bearing sulfosalts, such as chovanite, were found in any of the investigated samples.

Figure 1 Photograph of a rouxelite aggregate in a specimen kindly provided by Alois Lechner.

2.2 Electron probe microanalysis

Chemical analyses of rouxelite and associated minerals were carried out using a JEOL Hyperprobe JXA 8530F field-emission-gun electron probe microanalyser (FE-EPMA) at the Central Research Laboratories of the Natural History Museum, Vienna. The analyses employed JEOL and Probe for EPMA software (WDS¹ mode, 25 kV, 20 nA, 1.5 µm beam diameter, and count times of 15 s on peak and 5 s on background positions). The following emission lines and standards were used: AsLα and TlLα (lorándite, TlAsS₂), PbMα (galena), AgLα (Ag metal), SbLα and SKα (stibnite), HgLα (cinnabar), and CuKα (chalcopyrite). Other elements such as Bi and Fe were sought but not detected. Proper empirical correction was made for the interference of the third order of the SbLα line with the analytical AsLα line. Under the analytical conditions described, the detection limits for the measured elements in the rouxelite matrix were as follows (expressed in wt %): S, Cu, and Fe ∼ 0.04; As, Ag, and Sb ∼ 0.06; and Hg, Tl, Pb, and Bi ∼ 0.1. No attempt to measure O content was performed.

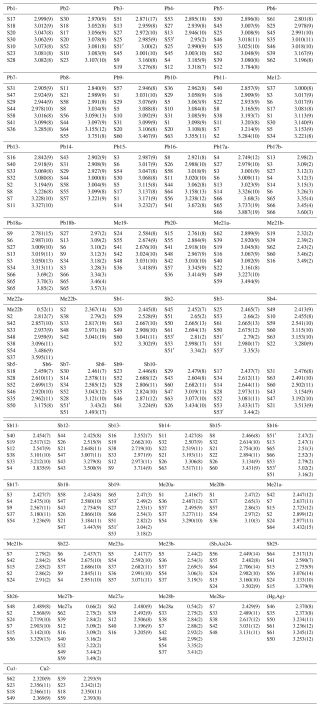
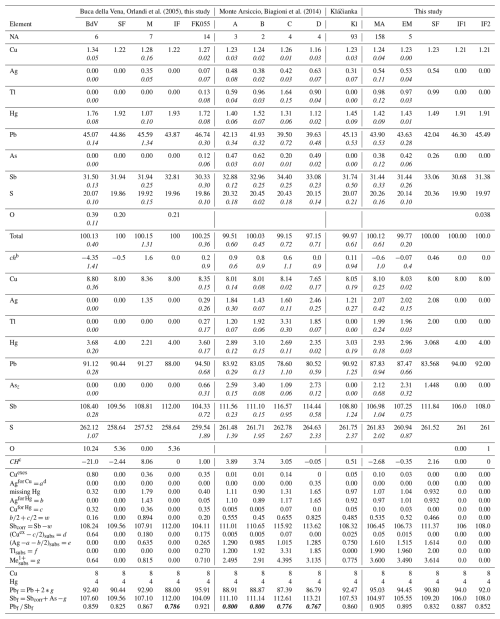
Table 1 New chemical composition data (in wt %) of rouxelite from the Monte Arsiccio mine, including mean values (denoted MV) for all 158 point analyses, for a Cu-low and Cu-high variety, and for the extracted material (EM) for the SCXRD study. Empirical formulae are calculated based on 212 cations (Z= 1). The structure-derived formula (SF) and two newly possible calculated ideal formulae (IF1 and IF2) are also indicated for S261 and S262. Values in italic represent standard deviations.

^a Number of point analyses. ^b ch represents charge balance values calculated as (Σ cation valence – Σ anion valence), and CH normalized charge balance values as ch $/$ (Σ anion valence) using atomic percent values. The two possible ideal formulae for rouxelite from the Monte Arsiccio mine, free of any substitutions, are Cu₈Hg₄Pb₉₄Sb₁₀₆S₂₆₁ and Cu₈Hg₄Pb₉₂Sb₁₀₈S₂₆₂ with ΣMe = 212 and ch = 0 constrains. Note that apfu represents atoms per formula unit.

2.3 Single-crystal X-ray diffraction

Intensity data of a small needle-shaped crystal were collected at room temperature using a STOE StadiVari diffractometer system equipped with an EIGER2 1M CdTe detector. Finely collimated MoKα radiation was employed, utilizing finely sliced ω scans and a detector distance of 70 mm. Data were processed using STOE X-Area software, and intensities were scaled with STOE LANA (Koziskova et al., 2016). More details on the processing of the twinned intensity data are provided below.

3 Chemical data

A large number of point analyses were conducted on several grains of rouxelite extracted from the mentioned samples (NA = 14 for Buca della Vena and 158 for Monte Arsiccio). These new data are presented in Table 1 together with previously published data. In the Buca della Vena material, we detected small amounts of Ag (0.07 wt %), Tl (0.13 wt %), and As (0.12 wt %), in addition to the previously published elements.

For rouxelite from the Monte Arsiccio mine (Table 1), we give four main groups of analyses, represented by their mean values: a global group for all 158 point analyses, a group for a low-Cu variety, a group for a high-Cu variety, and a group for the grain used in the SCXRD study.

Compared to the Buca della Vena material, the Monte Arsiccio material has lower amounts of Cu, Hg, and Pb and higher amounts of Ag, Tl, As, Sb, and S. This indicates a complex mixture of several substitution mechanisms, which will be discussed below in connection with the SCXRD study results.

The empirical formulae for all groups were calculated based on ΣMe = 212 and Z= 1 (from the SCXRD study). The empirical formula for the grain used in the SCXRD study is Cu_8.03Ag_2.02Hg_2.96Tl_1.96Pb_87.47Sb_107.25As_2.31S_260.92.

Accurate measurements of the small amounts of presumable oxygen content could not be obtained due to several basic analytical factors: high absorption of the OKα X-ray analytical line in the high mean atomic number of the rouxelite matrix, the thin carbon film deposited for electrical conductivity of the surface, and the necessity of high accelerating voltage values (25 kV) for the production of the Pb, Tl, and Hg Lα X-ray analytical lines.

Table 2 Single-crystal X-ray diffraction: experimental and refinement details for rouxelite.

4 Crystal structure

4.1 The fragment under investigation

The needle-shaped fragment under investigation, extracted from the aggregate presented in Figs. 1 and 2, was a complex oriented intergrowth of multiple domains. All domains can be derived from a monoclinic C-centred (mC) aristotype structure with cell parameters a ∼ 43.0, b ∼ 4.05 , c ∼ 37.9 Å, and β ∼ 117.6°, corresponding to the structure published by Orlandi et al. (2005). Henceforth, hkl indices will be given with respect to this cell. Figure 3a shows a reconstruction of the h1l plane of reciprocal space. The reflections of the mC aristotype are marked by red circles. Between these reflections are weak reflections corresponding to a twin domain by mirroring at (001) or, equivalently, a twofold rotation about c^*. Two examples are marked with red arrows in Fig. 3a. These reflections, however, were so weak that they were ignored during processing.

As observed by Orlandi et al. (2005) and Biagioni et al. (2014), additional reflections are found at half-integer k values, suggesting a doubling of the b axis, as is commonly observed in many sulfosalt minerals. The k= 1.5 plane shown in Fig. 3b presents a complex diffraction pattern. At least three domains (ignoring the minor twin domain) can be identified. Reflections of two domains (exemplarily marked with green and blue circles In Fig. 3b) are indexed with half-integer h, k, and l values. These correspond to a pair of twin individuals of a twofold superstructure with a modulation wave vector q1 = $\mathrm{1}/\mathrm{2}{\mathit{a}}^{*}$ + $\mathrm{1}/\mathrm{2}{\mathit{b}}^{*}$ + $\mathrm{1}/\mathrm{2}{\mathit{c}}^{*}$. Such a modulation reduces the symmetry from monoclinic to triclinic; therefore, twinning by the monoclinic point symmetry is expected. The reflections of the second twin domain appear at q1^′ = $\mathrm{1}/\mathrm{2}{\mathit{a}}^{*}$ + $\mathrm{1}/\mathrm{2}{\mathit{b}}^{*}$ − $\mathrm{1}/\mathrm{2}{\mathit{c}}^{*}$. The structural discussion below will be based on these two twin domains.

Figure 2 (a) Backscattered-electron image of several homogeneous rouxelite grains. (b) Corresponding plane-polarized optical images, which reveal multiple components and complex twin lamellae.

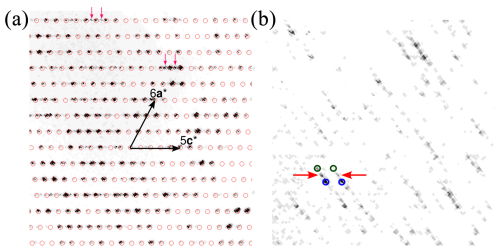
Figure 3 Excerpts of the (a) k= 1 and (b) k= 1.5 planes of reciprocal space of the fragment under investigation. Red arrows indicate weak reflections corresponding to a twin domain by reflection at (001) or, equivalently, a twofold rotation about c^*.

Additionally, even weaker reflections in the half-integer k planes are observed at integral h and l indices (examples marked with red arrows in Fig. 3b), corresponding to a modulation wave vector of q2 = $\mathrm{1}/\mathrm{2}{\mathit{b}}^{*}$. This indicates a fourfold superstructure with a monoclinic primitive (mP) lattice, because the application of 2q to a main reflection (h+k even) results in a systematically absent (h+k odd) reflection. Due to low intensities and the absence of any second-order satellites in the integral k planes, we did not attempt a structural characterization of the fourfold superstructure and ignored these reflections. The cell parameters of this superstructure correspond to the b ∼ 8 Å cell of the sulfosalt launayite, which we will present in an upcoming publication.

In summary, the majority of the fragment consists of an oriented intergrowth of a twin pair of twofold superstructures, the structure discussed herein, and a fourfold superstructure, which is related to the structure of launayite. Additionally, a second orientation was identified where no superstructure reflections were observed due to weak intensities. If this minor part were built analogously, the fragment would be composed of at least six crystalline domains. We did not observe any hints of superstructure reflections for k (neither integral nor half-integral), and we conclude that the b ∼ 8 Å cells described here are the actual cells of rouxelite and the putative launayite analogue.

4.2 Processing of the twin intensities

Concurrent integration using two independent twin domains led to numerical problems during optimization of the orientation matrix, because the non-overlapping reflections (half-integer k) were very weak. Therefore, we decided to integrate using a single triclinic primitive (aP) domain with the reciprocal lattice basis (${\mathit{a}}_i^{*}$, ${\mathit{b}}_i^{*}$, ${\mathit{c}}_i^{*}$)^T = ($-{\mathit{a}}_{\mathrm{1}}^{*}$, $-\mathrm{1}/\mathrm{2}{\mathit{b}}_{\mathrm{1}}^{*}$ − $\mathrm{1}/\mathrm{2}{\mathit{c}}_{\mathrm{1}}^{*}$, $-\mathrm{1}/\mathrm{2}{\mathit{b}}_{\mathrm{1}}^{*}$ + $\mathrm{1}/\mathrm{2}{\mathit{c}}_{\mathrm{1}}^{*}$)^T = ($-{\mathit{a}}_{\mathrm{2}}^{*}$, $\mathrm{1}/\mathrm{2}{\mathit{a}}_{\mathrm{2}}^{*}$ + $\mathrm{1}/\mathrm{2}{\mathit{b}}_{\mathrm{2}}^{*}$ + $\mathrm{1}/\mathrm{2}{\mathit{c}}_{\mathrm{2}}^{*}$, $\mathrm{1}/\mathrm{2}{\mathit{a}}_{\mathrm{2}}^{*}$ + $\mathrm{1}/\mathrm{2}{\mathit{b}}_{\mathrm{2}}^{*}$ $-\mathrm{1}/\mathrm{2}{\mathit{c}}_{\mathrm{2}}^{*}$)^T, corresponding to the real space basis (a_i, b_i, c_i)= (−a₁, −b₁ − c₁, −b₁ + c₁) = (−a₂, a₂ + b₂ + c₂, b₂ − c₂). Here, a subscript “i” indicates the basis vectors used for integration, subscripts “1” and “2” indicate the C-centred bases (see below) of both twin domains, and the superscript T indicates the transpose, since reciprocal bases are given by convention as 3×1 columns. In the (${\mathit{a}}_i^{*}$, ${\mathit{b}}_i^{*}$, ${\mathit{c}}_i^{*}$)^T basis, the reflections of both twin domains are indexed. However, the h+k odd reflections of the original structure, which are absent according to the C centring, are likewise indexed, leading to spurious integrated reflection intensities. These intensity data could be scaled and corrected for the absorption effect. They were then back-transformed into the cells of both twin domains, generating a HKLF5 style reflection file with overlap information.

Instead of the reduced primitive triclinic aP basis (a= 8.1037(2), b= 21.5949(6), c= 33.9287(9) Å, α= 96.359(2), β= 93.308(2), γ= 95.394(2)°, V= 5860.9(3) ų), we chose the C-centred triclinic unit cell (a= 43.1883(12), b= 8.1037(2), c= 38.1470(10) Å, α= 96.001(2), β= 116.615(2), γ= 95.372(2)°, V= 11721.7(6) ų) to be in concordance with the C-centred monoclinic structure published by Orlandi et al. (2005). The relationship of the chosen C-centred basis to the monoclinic basis of the basic structure is (a, b, c) = (a_b − b_b, 2b_b, −b_b + c_b), where a subscript “b” indicates the b ∼ 4 Å basic structure, which clearly shows the doubling of the cell volume. Moreover, this setting allows for better comparison with the related launayite structure (work in progress). The primitive setting is related to the C-centred setting by (a_p, b_p, c_p) = (b, $-\mathrm{1}/\mathrm{2}a$ − $\mathrm{1}/\mathrm{2}b$, $\mathrm{1}/\mathrm{2}a$ + $\mathrm{1}/\mathrm{2}b$ + c), where the subscript “p” stands for primitive.

A reasonable structure solution was obtained in space group C-1 by removing intensities of the second twin domain. All subsequent structure refinements were then performed against the intensities of both domains.

4.3 Structure determination

The structure of rouxelite was solved by the dual-space method implemented in SHELXT (Sheldrick, 2015a), which revealed most of the atom positions, and was subsequently refined using SHELXL (Sheldrick, 2015b). In subsequent cycles of the refinement, remaining atom positions were deduced from difference Fourier syntheses by selecting among the strongest maxima at appropriate distances.

Details on data collection and results of the structure refinement of rouxelite are given in Table 2, and full details are given in the CIF (Crystallographic Information File) deposited in the Supplement (see Supplement S1). The fractional atomic coordinate, occupancies, anisotropic (and isotropic) atomic displacement parameters, charge distribution (CD) values, bond valence sum (BVS), and coordination values are compiled in Table 3. Table 4 gives selected bond lengths.

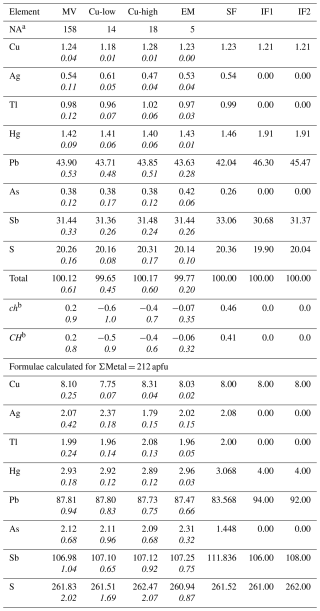
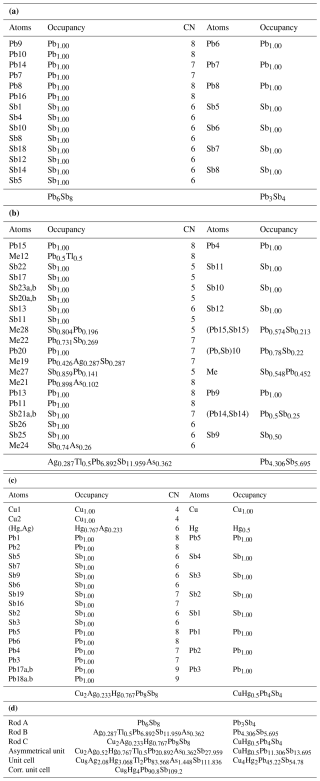
The asymmetric unit (Z= 4) in the structure of rouxelite (Fig. 4) contains 53 cation sites and 66 sites of anions. The metal sites consist of 22 Pb positions, 28 Sb positions, 1 Hg position, and 2 Cu positions.

Table 3 Sites, site occupancies (s.o.), fractional atom coordinates, equivalent displacement parameters (in Ų), coordination numbers (CNs), charge distribution (CD) values and bond valence sum (BVS) values.

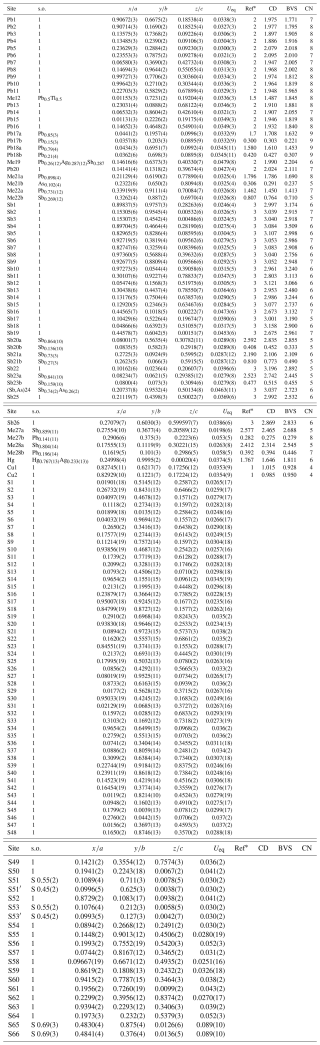
^* Ref is the charge of the site obtained from refinement, whereas CD and BVS represent charge distribution and bond valence sum values, respectively, calculated for the cation sites with the program ECoN21 (Ilinca, 2022).

Four Pb sites are mixed, one with Tl (Me12), one with Ag and Sb (Me19), one with As (Me21) and one with Sb (Me22), and two are split (Me17a, b and Me18a, b). We choose to refine Tl with the site Pb12 and Ag + Sb with the site Me19 on following the site lengths (long for Tl and short for Ag + Sb). The occupancies of Tl (0.5) and Sb (0.287) were imposed to fit the chemistry results and are in agreement with the charge distribution (CD) values calculated with the program ECoN21 (Ilinca, 2021). The Hg site was found to be mixed with Ag (Hg_0.767(13)Ag_0.233(13)) as described by Orlandi et al. (2005). Three Sb sites are mixed, one with As [(Sb,As)24] and two with Pb (Me27 and Me28), whereas another three Sb sites (Sb20, Sb22, and Sb23) are split. Two S sites, S65 and S66, are both partially occupied with 0.69 % (Table 3).

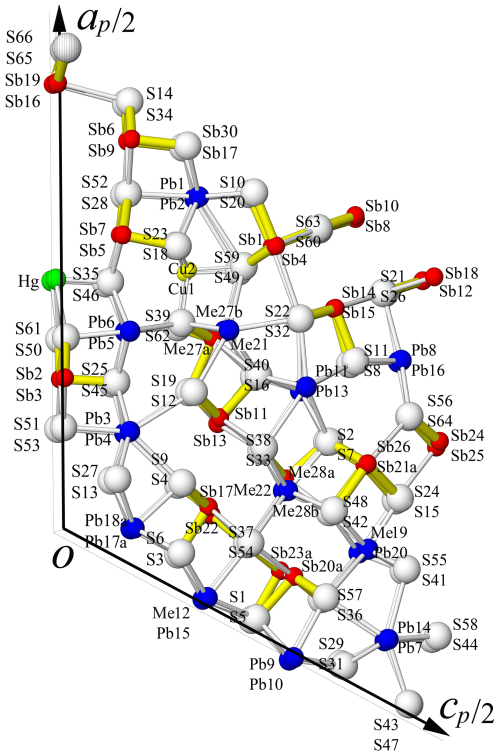
Figure 4 Atom labelling in the asymmetric unit of rouxelite (view along the b axis); white: S sites, dark blue: Pb sites, red: Sb sites, green: Hg site, and yellow Cu sites.

Final refinement as a twin by twofold rotation about [010], corresponding to the lost monoclinic symmetry with volume ratios 0.5489 : 0.4510(14), led to R₁= 0.0855 for 55 765 unique reflections. The Pb content is low and the Sb content is high in the resulting structural formula obtained from the SCXRD study for the unit cell, Cu₈Ag_2.08Hg_3.068Tl₂Pb_83.568As_1.448Sb_111.836S_261.52 compared with the electron microprobe analysis (EMPA) empirical formula Cu_8.03Ag_2.02Hg_2.96Tl_1.96Pb_87.47Sb_107.25As_2.31S_260.92 (both for Z= 1).

Table 4 Selected interatomic distances in the crystal structure of rouxelite.

For the minor As in the Me21b site (occupancy ca. 10 %), the As–S distances were restrained to 2.30(2) Å.

An attempt was made to identify oxygen positions – similar to those identified by Orlandi et al. (2005) – in the vicinity of Sb16, Sb19, S65, and S66. Weak peaks in the electron density maps were observed at reasonable distances from the S atoms (ca. 2.0 and 2.1 Å). When freely refining the occupancies of the S and the putative O atoms, both positions (S65/O65 and S66/O66) refine to a total occupancy of ca. 85 %. The difference electron density peaks could also be an artefact due to ignoring the alternative (q2, mP) launayite-like domain. In fact, as we will show in an upcoming publication, the main structural difference between both structures is precisely this column. Therefore, from the present data it cannot be said whether S65 and S66 are fully occupied (S,O) positions, partially occupied (S,O) positions, or partially occupied S positions.

We therefore present all three options (ΣMe = 212) here and discuss their relation to the corrected empirical formulae in the “Crystal chemistry” section (Sect. 5). Data of all three refinements (CIF) are deposited in the Supplement as S1, S2, and S3 files.

The structural formula for refinement (S1) without O is Cu₈Ag_2.08Hg_3.068Tl₂Pb_83.568As_1.448Sb_111.836S_261.52, with ch = 2.16. The structural formula for O and S occupancies refined independently (S2) is Cu₈Ag_2.092Hg_3.064Tl₂Pb_83.556As_1.452Sb_111.840 (S_261.32O_1.52)_Σ262.84, with ch = −0.47 and 0.059 O wt %. Finally, the structural formula for which the sum of O and S occupancies is fixed to 1 (S3), is Cu₈Ag_2.1Hg_3.056Tl₂Pb_83.548As_1.452Sb_111.844 (S_261.48O_2.52)_Σ264, with ch = −2.81 and 0.098 O wt %.

4.4 Description of the structure

Following the description of the Buca della Vena rouxelite crystal structure by Orlandi et al. (2005), a different approach to its modularity was published by Makovicky and Topa (2009) for that b ∼ 4 Å structure. The present description of the crystal structure of rouxelite from the Monte Arsiccio mine will follow the Makovicky and Topa approach. In a first instance, the structure can be interpreted as a boxwork structure with principal walls, C walls, formed by three cation–anion planes that develop parallel to (001) (referred to hereafter as the C-type module). For every three external Pb atoms, the walls are alternately extended with a Pb polyhedron on each opposite side, creating a succession of “out-of-phase” prominences. The (001) walls are periodically indented around Hg octahedra.

The space between the walls is occupied by two types of rod-like modules A and B. Both module types are delimited by pseudo-tetragonal cation–anion (Q) and pseudo-hexagonal anion–anion (H) boundaries which alternate on adjacent sides of the module. Each H limit is opposed to a Q limit belonging to the neighbouring module and vice versa. Module A is a PbS-like module (referred to hereafter as the A rod), which contains eight Sb pyramids equally divided by a lone electron-pair (LEP) micelle running approximately parallel to ($\stackrel{\mathrm{‾}}{\mathrm{3}}\mathrm{02}$). The A rod is truncated by pairs of pseudo-hexagonal (H) boundaries (two and three sulfur atoms long, respectively). The H ends of the A rod connect to the C walls via Cu tetrahedra, located close to the four-layer prominences. The eight Sb pyramids on each side of the central LEP of the A rod are interspersed with six Pb polyhedra: two “lying” mono-capped trigonal prisms (Pb7 and Pb14) flanked by four “standing” bi-capped trigonal prisms (Pb10, Pb16 and Pb8, Pb9 on the opposite side), which link the A rod to the B-type one, described below.

The S-shaped B-type module is based on the SnS archetype, well-illustrated in the crystal structure of extended (from three to four Pb polyhedra) 8 Å monoclinic boulangerite of Ventruti et al. (2012). The A- and B-type rods alternate along [100] and are periodically translated by the C-centring. Observe that the C-centring translation is $\mathrm{1}/\mathrm{2}a$ + $\mathrm{1}/\mathrm{2}b$ = $\mathrm{1}/\mathrm{2}{a}_b$ + $\mathrm{1}/\mathrm{2}{b}_b$, where the subscript “b” stands for the b ∼ 4 Å basic structure. Thus, for each module there are two kinds (A₁ $/$ A₂ and B₁ $/$ B₂), translated by half an MS₆ octahedron's edge length in the [010] direction, as indicated by different shading in Figs. 5 and 6.

Alternatively, the C wall can be conceptualized as narrow rods elongated parallel to the [010] direction, with four Pb and one Hg octahedra not included (as shown by C₁ and C₂ in Fig. 5), whereby C₁ and C₂ are related by the C-centring translation. This perspective shifts the structural description to an almost fully rod-based interpretation (Makovicky, 1993), which may offer greater efficiency compared to the boxwork approach, particularly when considering the closely related structure of launayite (work in progress). The C₁ and C₂ rods contain four Sb pyramids divided into pairs on each side of a short LEP approximately parallel to (001). The rods relate to the PbS-like “cosalite” structure and connect through a pair of tri-capped trigonal prisms (Pb17 and Pb19; Figs. 5 and 6). However, unlike the previous description of rouxelite by Makovicky and Topa (2009), the Pb5 $/$ Pb6 and the Pb17 $/$ Pb18 pairs of sites in the present structure – corresponding to the Pb1 and Pb3 sites of Orlandi et al. (2005), respectively – are included in the C-type wall and not in the A-type rod.

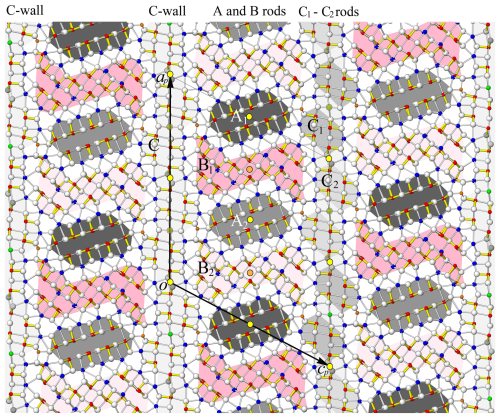
Figure 5 The crystal structure of rouxelite viewed along the b axis (∼ 8.1 Å). Atom colouring is the same as in Fig. 4. Two rods, A (PbS-like) and B (SnS-like), coloured differently (light grey and dark grey, light red and dark red), alternate parallel to the c axis and are flanked by infinite C walls. The light and dark shadings indicate a translation of half an octahedron's edge length in the [010] direction (see Fig. 8). The short, strong Sb (red)–S bonds are indicated in yellow (Sb–S < 2.75 Å). Cation–sulfur bonds longer than 3.6 Å for Pb and 3.3 Å for Sb are not indicated. Yellow discs with black outlines are symmetry centres overlapping at y = 0 and y = 0.5. Orange discs are symmetry centres at y = 0.25 and y = 0.75.

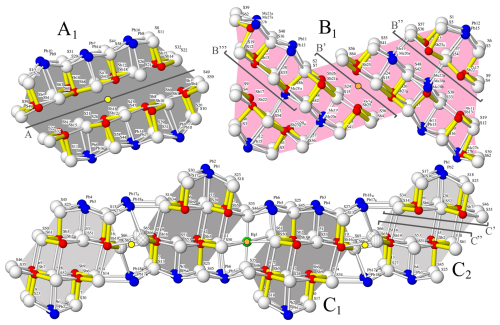
Figure 6 Rod typology of rouxelite. Rods A and C are PbS-like (“cosalite”), whereas B is SnS-like relatable to an extended “boulangerite”. Modules A₁, B₁, and C₁ have symmetry-related equivalents in the structure (see A₂, B₂ and C₂ in Fig. 5). The A, B^′, B^′′, B^′′′, C^′, and C^′′ sections depicted in Fig. 10 are marked on each module type. Outlined yellow and orange discs have the same significance as in Fig. 5.

Since A-, B-, C₁- and C₂-type rods can be derived directly from specific cut-outs of PbS-like (“cosalite”) and SnS-like (extended “boulangerite”) structures (Fig. 7), these rods will tentatively serve as new archetypes for describing related sulfosalt structures.

Two adjacent C₁ (or C₂) rods are mapped by inversion centres (orange discs in Fig. 8) located between the connecting Hg site. The Hg site features octahedral coordination and thus a pair of C₁ (or C₂) rods could be combined to give a single PbS-like rod. Adjacent C₁ and C₂ rods are likewise related by inversion (yellow discs in Fig. 8), but here they are shifted in the [010] direction and connect via S–S interactions. The precise nature of this part of the structure is unknown and requires further investigation. As noted above, the occupancies of these S atoms refine to only ca. 70 %. There are hints of partial substitution by oxygen (blue discs in Fig. 8). However, when freely refining the occupancies, a total occupancy of only 85 % is obtained, indicating anion vacancies. The displacement parameters of the S atoms are distinctly enlarged in the [010] direction, owing to disorder of these positions.

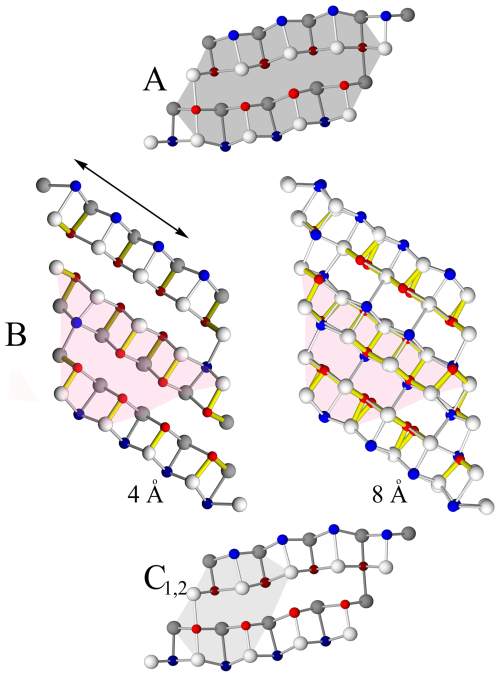
Figure 7 Structural rod types (A, B, C₁, and C₂) as cut-outs from the PbS-like cosalite (A, C) rod and the SnS-like boulangerite (B) rod. Note that cosalite is 4 Å, and boulangerite can present with orthorhombic (with 4 Å) and monoclinic (with 8 Å) variants. The structural rod B is a cut-out from a hypothetical “extended” boulangerite rod (four Pb polyhedra instead of natural three Pb polyhedra). For 4 Å crystal structures anion and cation sites, sitting on different levels (0 and 0.5 or 0.25 and 0.75) along 4 Å axes, are coloured differently.

4.5 The coordination of metal sites

To establish the coordination of various metals in the crystal structure of rouxelite or any other sulfosalt, several criteria can be applied: (1) a global or element-specific coordination radius threshold (4 Å for Pb, 3.05 Å for Sb, etc.); (2) a selection of ligands with non-zero bond weights in CD calculations; and (3) exclusion of neighbouring metals from the coordination sphere, except for metals sharing split positions.

For rouxelite, we have applied these criteria flexibly depending on the specific approach. Generally, the coordinations were determined based on the second norm, derived from CD analyses (Supplement Tables S1 and S2). In general, for Pb positions, this norm produces the same results as a 4 Å coordination radius limit. The coordination number (CN) of Pb varies between 7 and 9, i.e. from mono- to tri-capped trigonal prisms. Higher CNs occur in the C-wall module and coincide with their lateral out-of-phase prominences. However, for Sb, the non-zero bond weight criterion resulted in reduced coordination numbers (CNs spanning from 5 to 7, i.e. tetragonal pyramids, octahedra, and split octahedra). Topological descriptions of the structure took into account the presence of non-bonding interactions across the LEP zones with CNs adapted to such situations (e.g. CN = 5 instead of 6 for Sb).

In the case of opposing bond pair analysis, the coordinations were either reduced to CN = 7 (Pb) or extended to CN = 6 (Sb) (see next section) to allow for the selection of relevant pairs of interatomic distances.

4.6 Site populations and bond pairs

Due to the complexity of the crystal structure, the assigned site populations were tested against element-specific bond-length hyperbolae using the method developed by Trömel (1980) and Berlepsch et al. (2001a, b). This method involves plotting opposing “in-plane” and “out-of-plane” bond lengths present in the coordination octahedra and capped prisms within the structure. The “in-plane” bonds occupy the equatorial planes of octahedra (i.e. the shared bases of the opposing square pyramids) or the bases of capping pyramids, while the “out-of-plane” bonds refer to the opposing bonds that extend toward apical ligands, approximately perpendicular to these “planes”.

In the crystal structure of rouxelite from the Monte Arsiccio mine, all planes referenced by the “in-plane” and “out-of-plane” notions are parallel to the [010] zone axis and share the same orientation as the well-developed LEP micelles. The analysis included the coordination environments of Sb and Pb, considering the first six and seven bond lengths, respectively, in increasing order. For Pb trigonal mono-capped prisms, the selected opposing “out-of-plane” bond pairs – out of the two possible ones – were those exhibiting the maximum S-Me-S bond angles.

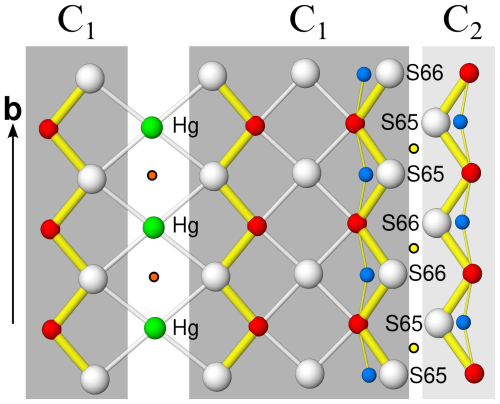
Figure 8 Single atomic sheet showing the C₁-C₁ and C₁-C₂ connections. Yellow discs with black outlines are symmetry centres at y = 0 and y = 0.5. Orange discs are symmetry centres at y = 0.25 and y = 0.75. Putative O positions are shown in blue.

The resulting XY plot is shown in Fig. 9. Generally, the “in-plane” opposing bonds of the Pb-capped prisms plot close to the diagonal of the diagram, suggesting a relatively small difference between the short and long bond lengths. The deviation of points from the Pb hyperbola along the diagonal is presumably due to the specific coordination of Pb, which predominantly falls into the mono- or bi-capped trigonal prism category. The deviating Me19 points correspond to a mixed Pb-Ag-Sb position.

The “in-plane” bond pairs of Sb octahedra tend to deviate from the normal hyperbolic trend, instead describing a linear distribution that is secant to the Sb-specific hyperbola. A similar behaviour was described for dadsonite (Makovicky et al., 2006 – black symbols in Fig. 9) and also observed in the structure of rouxelite from Buca della Vena (Orlandi et al., 2005 – white symbols in Fig. 9). Makovicky et al. (2006) explained this behaviour by invoking the presence of split sites or particular Sb positions located in tightly packed columns. However, due to the large number of Sb polyhedra aligning to a linear distribution in rouxelite, with only a minority of split positions, a different explanation might be required.

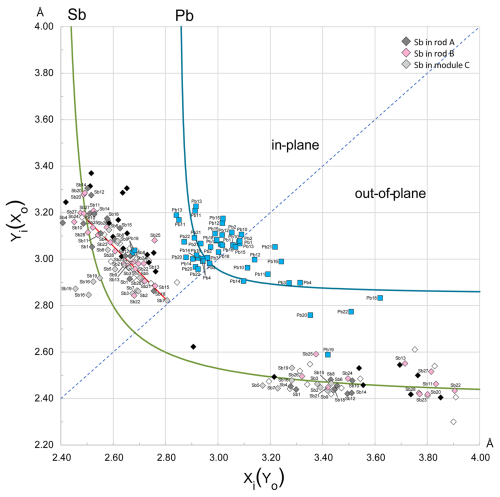
Figure 9 Plot of the opposing bond pairs for the Pb and Sb coordination polyhedra in the crystal structure of rouxelite against element-specific bond-length hyperbolae. For the “in-plane” bonds, the shorter distances (x_i) are plotted along the abscissa, while for the “out-of-plane” pairs the shorter distances (x_o) are plotted along the ordinate. The red segment represents the regression (y = $-\mathrm{1.10696}x+\mathrm{5.8414}$) approximating the linear distribution of Sb “in-plane” bond pairs. The black symbols correspond to the linearly distributed bond pairs for Sb in dadsonite (Makovicky et al., 2006), and the white symbols represent rouxelite from Buca della Vena (Orlandi et al., 2005). The “in-plane” bond pairs of Sb are plotted with different colours according to their host module: A modules are dark grey, B modules are pink, and C modules are light grey (see Fig. 6). Coordination polyhedra of metals in split positions and with minor occupancy were omitted.

The linearity of the distribution primarily suggests a tendency for the opposing “in-plane” bonds to yield quasi-constant sums of distances, 5.5 to 5.8 Å in modules A and B and from 5.3 to 5.7 Å in modules C, thus indicating a highly regular ligand distribution within the square pyramid bases parallel to the b axis (Fig. 10). For such Sb coordination polyhedra, the centroids (Table S2 in Supplement) tend to be very close to the central atoms. Larger deviations of centroids in the square pyramid planes are observable for Sb1, Sb4, Sb10, Sb11, Sb14, Sb16, Sb19, Sb20, and Me27a(Sb), whose opposing bond pairs plot along or close to the Sb hyperbola on both sides. The main variability in the distortion of the coordination octahedra occurs in the longest distances, across the LEP micelles (Fig. 11).

The Armbruster–Hummel diagram (Armbruster and Hummel, 1987) (Fig. 12) is designed to distinguish between Pb and Sb sites by plotting the average distance of the three shortest bonds against the average of the next two shortest bonds. The diagram shows a clear separation between Pb and Sb sites, with the exception of Me19, which represents a mixed Pb-Ag-Sb position.

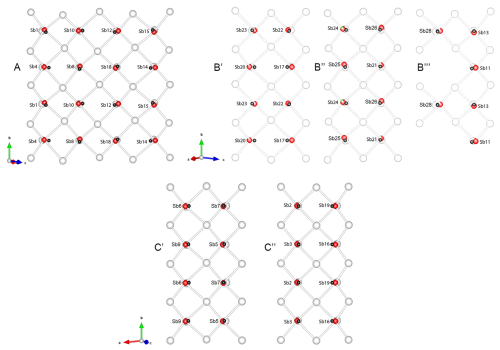
Figure 10 Configurations of square pyramid bases in Sb coordination octahedra forming the pseudo-tetragonal (Q) walls around various modules in rouxelite, as viewed parallel to the [010] axis. A, B^′, B^′′, B^′′′, C^′, and C^′′ symbols indicate the positions of the sections in the structure as shown in Fig. 6. Dark grey spheres are the centroids of the coordination octahedra. Low deviations of the centroids in the planes of the square pyramid bases correspond to Sb coordinations describing a linear distribution of the “in-plane” opposing bonds (see Fig. 9). The sections encompass two periodicities along the b axis.

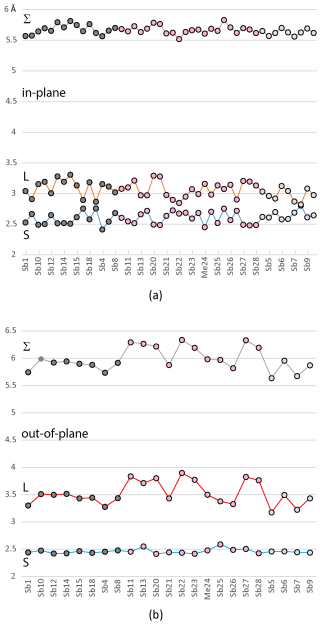
Figure 11 (a) Distribution of the short (S) and long (L) “in-plane” distances for the Sb-dominant coordinations, along with the sum of the opposing bonds (Σ), which shows a very narrow range of variation; (b) similar distribution for the “out-of-plane” bonds, where the major variation occurs in the longer distances across the LEP. Points are grouped according to the host module type: dark grey is module A, pink is module B, and light grey is module C.

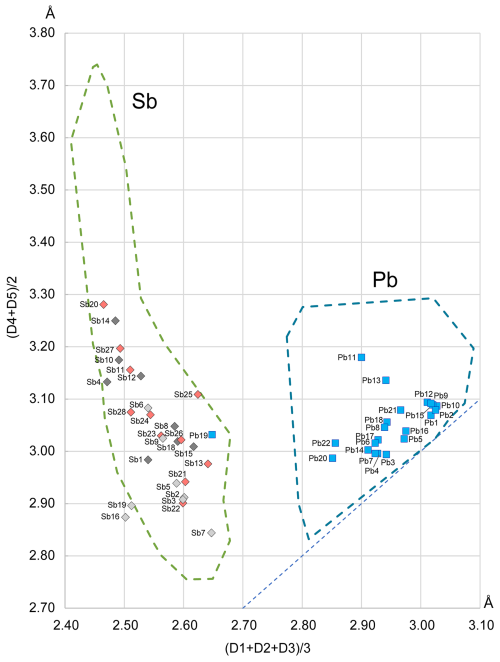
Figure 12 The Armbruster–Hummel (Armbruster and Hummel, 1987) diagram modified to account for the chemical content of rouxelite. The contours of the Sb and Pb fields are compiled using data from over 1700 coordination polyhedra in sulfosalts, a significantly larger dataset than the one used in the original diagram from 1987. The diagonal line represents regular polyhedra where the two mean values are equal. The bond lengths in ascending order are denoted as D1, D2, D3, D4, and D5. The colouring of Sb points reflect their host module (dark grey is module A, pink is module B, and light grey is module C).

5 Crystal chemistry

5.1 Substitutions

For comparison reasons, the new chemical data for Buca della Vena and Monte Arsiccio materials (Table 1) and old chemical data for Buca della Vena (Orlandi et al., 2005) and Monte Arsiccio (Biagioni et al., 2014) are shown together in Table 5, as average chemical compositions of clearly defined groups. Although the unit cell in the C-1 setting contains four asymmetric units, we will describe the chemical composition using the unconventional choice of Z= 1 instead of Z= 4. This approach simplifies comparisons between different empirical and structural formulae by presenting anion and cation contents as more straightforward values. Additionally, with Z= 1, the calculated anion contents are closer to integral values across the various treatments of the O atoms discussed above. The empirical formulae (calculated on the basis of Σmetal = 212 apfu for Z= 1) and all important parameters used to define and quantify the substitution processes and crystal chemistries are also included, as well as the ideal formula of rouxelite from Buca della Vena (Orlandi et al., 2005) and our possible ideal formula of rouxelite from Monte Arsiccio. Crystal-structure-derived formulae and their chemical compositions for both deposits are also presented.

Table 5 Average chemistry (in wt %) and crystal chemistry of published data from Buca della Vena and Magurka (BdV and M by Orlandi et al., 2005), Monte Arsiccio (A to D by Biagioni et al., 2014), Kláčianka (Sejkora et al., 2021), and new data for rouxelite from Buca della Vena (FK055) and Monte Arsiccio (MA, extracted material EM). Empirical formulae are calculated based on 212 cations for all data to allow for comparison. The structure-derived formula (SF) and ideal formula (IF) for rouxelite from Buca della Vena as well as the structure-derived formula (SF) and two possible ideal formulae (IF1 and IF2) for the Monte Arsiccio mine are also given. Values in italic represent standard deviations.

^a Number of point analyses. ^b ch charge balance values calculated as (Σ cation valence – Σ anion valence) using atomic percent values. CH is the charge balance values calculated as (Σ cation valence – Σ anion valence) using apfu values. ^c A possible ideal formula for rouxelite from the Monte Arsiccio mine, free of any substitutions and containing O, is Cu₈Hg₄Pb₉₂Sb₁₀₈S₂₆₁O. ^d a, b, c, w, d, f, and g = $d+e+f$ parameters are explained in the text. The general formula for the Monte Arsiccio material, taking into account all substitution mechanisms, is (Cu + a)₈[Hg + b + c]₄[(Ag $-a-b/\mathrm{2}$)_subs+ (Cu${}^{\mathrm{exes}}-c/\mathrm{2}$) + Tl_subs]_gPb_X−2g (Sb + As)${}_{X+g-w}$S_Z, where coefficients X, Y, and Z for Pb, Sb, and S can be 94, 106, and 261 or 92, 108, and 262, respectively.

The comparison of empirical (EM), Cu_8.03Ag_2.02Hg_2.96Tl_1.96Pb_87.47Sb_107.25As_2.31S_260.92, and structural (SF), Cu₈Ag_2.08Hg_3.068Tl₂Pb_83.568As_1.448 Sb_111.836S_261.52, formulae for a chemically and structurally analysed grain and the results for refined (Hg, Ag), Me12, Me19, Me21, and Me22 sites (Table 3) indicates that Monte Arsiccio's rouxelite clearly presents Ag for Hg, Tl for Pb, and Ag for Pb substitutions, as qualitatively stated by Biagioni et al. (2014).

5.2 Mechanisms of isomorphous substitution

Rouxelite undergoes complex homovalent and heterovalent substitutions such as Sb³⁺ → As³⁺, Cu¹⁺ →Ag¹⁺, main substitution mechanism (MSM) 2Pb²⁺ → Me${}^{\mathrm{3}+}+$ Me¹⁺ (where Me³⁺ is Sb and As and Me¹⁺ is Ag, Cu, and Tl), and 2Hg²⁺ →Sb${}^{\mathrm{3}+}+$ (Cu + Ag)¹⁺. Rouxelite is always Hg deficient, and the missing Hg (under 4 apfu) must be compensated for by a specific Ag and Cu content, with a correction for charge balance for Sb and Ag and Cu. This substitution does not involve Pb.

The process of deriving the ideal formula for rouxelite, while considering the constraints from crystal structure determination, is outlined as follows (see Table 5).

The first step involves Ag compensation (Ag${}_a^{\mathrm{Cu}}$) for a deficit of Cu and Ag compensation (Hg${}_b^{\mathrm{Ag}}$) for a deficit of Hg. The next step involves the total 8 apfu (Z= 1) positions occupied by Cu due to their relatively stable site population. Three scenarios are considered:

• 1.

  Measured Cu content (apfu) is equal to the theoretical 8 apfu; no correction for Cu is needed.

• 2.

  Measured Cu content (apfu) exceeds 8 apfu, requiring the surplus, Cu^exes, to be allocated to

  • 2a.

    compensate for a deficit of Hg (Cu${}_c^{\mathrm{Hg}}$), and/or

  • 2b.

    participate in the MSM (Cu_d).

• 3.

  Measured Cu content (apfu) is deficient and must be compensated for by Ag⁺ (Ag${}_a^{\mathrm{Cu}}$).

The next step ensures that the Hg positions total 4 apfu by compensating any Hg deficiency with either Cu⁺ (Cu${}_c^{\mathrm{Hg}}$) and/or Ag⁺ (Ag${}_b^{\mathrm{Hg}}$) with an extraction of w = (0.5Cu${}_c^{\mathrm{Hg}}+$ 0.5Ag${}_b^{\mathrm{Hg}}$) from Sb, where Sb_corr= Sb  −w, and an extraction of 0.5Cu${}_c^{\mathrm{Hg}}$ from Cu and 0.5Ag${}_b^{\mathrm{Hg}}$ from Ag.

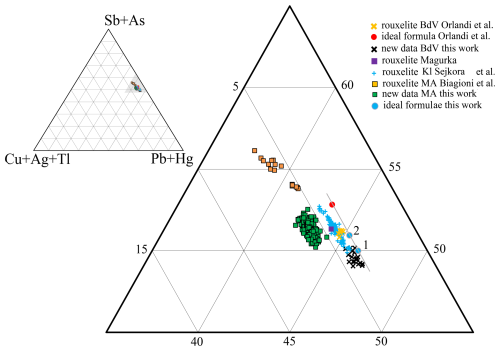
Figure 13 Plots of rouxelite chemistry in the (Cu + Ag + Tl) − (Pb + Hg) − (Sb + As) ternary system. Details are in Table 5. Orlandi's ideal formula Cu₈Hg₄Pb₈₈Sb₁₁₂S₂₅₆(O,S)₈; our formulae for (1) Cu₈Hg₄Pb₉₄Sb₁₀₆S₂₆₁; (2) Cu₈Hg₄Pb₉₂Sb₁₀₈S₂₆₁O. The line indicate a trend of ΣMe₂₁₂S₂₆₄ (red) to ΣMe₂₁₂S₂₆₁O as well as ΣMe₂₁₂S₂₆₁ rouxelite formulae free of any substitution.

Any remaining Cu = (Cu${}^{\mathrm{exes}}-c/\mathrm{2}$)_subst, Ag = (Ag $-a-b/\mathrm{2}$)_subst, and Tl_subs (g = Cu_subst+ Ag_subst + Tl_subst) will enter in the MSM as Me${}_{\mathrm{subst}}^{\mathrm{1}+}$, altering measured Pb to (Pb + 2Me${}_{\mathrm{subst}}^{\mathrm{1}+}$) and corrected Me³⁺ to (Sb_corr+ As-Me${}_{\mathrm{subst}}^{\mathrm{1}+}$). The final correction for all substitution mechanisms is represented by Pb_f and Sb_f values in Table 5.

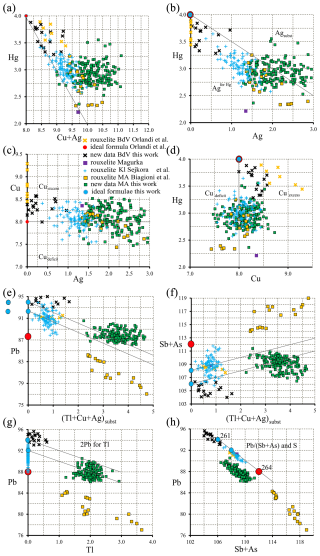
Figure 14 Plots of relevant pairs of element content (expressed as apfu) in rouxelite from Buca della Vena, Monte Arsiccio, and Kláčianka. The lines represent (a) the line in plot Hg vs. Cu + Ag shows that Hg content of Magurka (reference in Orlandi et al., 2005) and a few of our points are slightly under the needed 4 apfu; (b) the line in plot Hg vs. Ag separates the fields of Ag entering into Hg and Ag implied in MSM; (c) the line in plot Cu vs. Ag indicates the fields of deficient Cu filled by Ag and excess Cu going to MSM; (d) the line in plot Hg vs. Cu delimits the fields of deficient Cu and excess Cu; (e, f) the lines in the plot Pb vs. Me${}_{\mathrm{subst}}^{\mathrm{1}+}$ and Sb vs. Me${}_{\mathrm{subst}}^{\mathrm{1}+}$ depict the loss of 2Pb for Me${}_{\mathrm{subst}}^{\mathrm{1}+}$ and the increase of Sb for Me${}_{\mathrm{subst}}^{\mathrm{1}+}$; (g) the line in Pb vs. Tl diagram shows only Tl substitution, and (h) the line in Pb vs. (Sb + As) indicates uncorrected values of Pb $/$ (Sb + As) for all plotted points and the variation of corrected Pb and Sb values of ideal formulae for three values of S apfu.

The three different treatments of O in the refinements (see above) lead to the following corrected structural formulae:

• the corrected structural formula for the refinement without O is Cu₈Hg₄Pb_90.796Sb_109.204S₂₆₁ for S = 261, charge balance = 2.16, and Pb_f $/$ Sb_f= 0.831. The balanced charge valence formula would imply Cu₈Hg₄Pb₉₄Sb₁₀₆S₂₆₁ with Pb_f $/$ Sb_f= 0.887.

• For O and S occupancies refined independently, it is Cu₈Hg₄Pb_90.804Sb_109.200S₂₆₃ for S = 263, ch = −0.47, and Pb_f $/$ Sb_f= 0.832. The balanced charge valence formula would imply Cu₈Hg₄Pb₉₀Sb₁₁₀S₂₆₃ with Pb_f $/$ Sb_f= 0.818.

• The corrected structural formula for sum of O and S occupancies fixed to 1 is Cu₈Hg₄Pb_90.804Sb_109.196S₂₆₄ for S = 264, ch = −2.8, and Pb_f $/$ Sb_f= 0.832. The balanced charge valence formula would imply Cu₈Hg₄Pb₈₈Sb₁₁₂S₂₆₄ with Pb_f $/$ Sb_f= 0.786.

Observe that the Pb_f $/$ Sb_f ratio of the refinement without O shows the best agreement with the chemical analysis (Table 5). We emphasize that no other combinations of Pb_f and Sb_f values for S= 262, 263, or 264 yield an ideal formula that aligns as closely with our empirical and structural formulae.

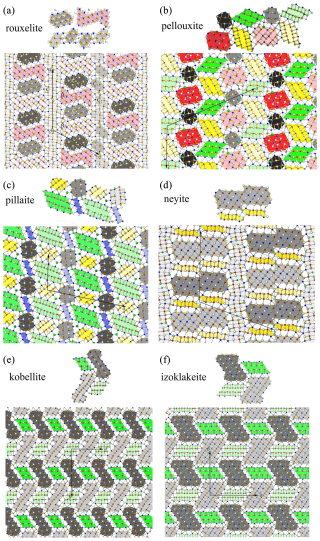
Figure 15 Comparison between the modular description of rouxelite and the modular description of various rod-based and boxwork structures. Dark and light grey coloured rods are of PbS-like archetype (“cosalite”). All others are of the SnS-like archetype (“boulangerite”). The rouxelite rods A, B, C₁, and C₂ do not appear in the crystal structures of (b) pellouxite, (c) pillaite, (d) neyite, (e) kobellite, or (f) izoklakeite.

Therefore, for now we assume no O on the S66 $/$ S67 positions and according to our data the ideal formula of rouxelite from the Monte Arsiccio mine is Cu₈Hg₄Pb₉₄Sb₁₀₆S₂₆₁, with Pb_f $/$ Sb_f= 0.887, which is consistent with the fact that we observed no other O-bearing sulfosalts in the investigated samples. Improved analytics including quantification of O will be necessary to finally settle the issue of the ideal rouxelite formula.

Table 6 Comparative data for rouxelite from the Monte Arsiccio mine (MA) and Buca della Vena (BdV).

^a both for Z= 1, i.e. 212 and 106 metal sites per unit cell, respectively. ^b CH is the charge balance values calculated as (Σ cation valence – Σ anion valence) using apfu values. ^c 1: this work; 2: Orlandi et al. (2005).

Table 7 Independent sites and occupancies by rod type (a: rod A, b: rod B, c: rod C, and d: summary of all) in the crystal structures of rouxelite from the Monte Arsiccio mine (present work) and Buca della Vena (Orlandi et al., 2005). Rod types are represented in Figs. 5 and 6. For both crystal structures, the main substitution mechanisms take place within rod B.

The Pb_f and Sb_f values (95.91 and 104.09) for Buca della Vena material (FK055), measured by us, are not far from the trend expressed by Pb_f and Sb_f values (∼ 95 and ∼ 105) for Monte Arsiccio material, but they differ substantially (∼ 88–89 and ∼ 111–112) from the data published by Biagioni due to lower-corrected Pb, i.e. after accounting for substitution and correction, and higher-corrected Sb values. With both materials being analysed in the same run, we exclude any analytical errors for our analytical data.

These substitutions yield also a general formula, accounting for all types of substitutions, for rouxelite from the Monte Arsiccio mine: (Cu + Ag${}_a^{\mathrm{Cu}}$)₈[Hg + (Ag${}_{b+}^{\mathrm{Hg}}$Cu${}_c^{\mathrm{Hg}}$)]₄[(Ag − Ag${}^{\mathrm{Cu}}-b/\mathrm{2}$)_subst+ (Cu$-c/\mathrm{2}$) + Tl_subst]_g Pb_94−2g)(Sb + As)${}_{\mathrm{106}+g-w}$S₂₆₁ or (Cu + a)₈[Hg + b+c]₄[(Ag $-a-b/\mathrm{2}$)_subst+ (Cu $-c/\mathrm{2}$) + Tl_subst]_gPb_94−2g) (Sb + As)${}_{\mathrm{106}+g-w}$S₂₆₁, with a, b, c, w, d, f, and g being parameters explained above and given in Table 5.

The ternary plot (in atomic percent) in the (Cu + Ag + Tl) − (Pb + Hg) − (Sb + As) system (Fig. 13) for all measured points in Buca della Vena (#20) and Monte Arsiccio (#171) deposits by Orlandi et al. (2005), Biagioni et al. (2014), Kláčianka occurrence by Sejkora et al. (2021), and this work (Table 5) gives a general view of the position of different groups in terms of Me¹⁺, Me²⁺, and Me³⁺. The line indicate the trend for substitution-free formulae with variable S or (S, O) content.

Several binary plots (a to h) employing the same number of points (in apfu) are presented in Fig. 14 and reveal inter-element correlations: (a) the line in plot Hg vs. Cu + Ag shows that Hg content of Magurka (reference in Orlandi et al., 2005) and a few of our points are slightly under the needed 4 apfu, (b) the line in plot Hg vs. Ag separates the fields of Ag entering into Hg and Ag implied in MSM, (c) the line in plot Cu vs. Ag indicates the fields of deficient Cu filled by Ag and excess Cu going to MSM, (d) the line in plot Hg vs. Cu delimits the fields of deficient Cu and excess Cu, (e, f) the lines in the plot Pb vs. Me${}_{\mathrm{subst}}^{\mathrm{1}+}$ and Sb vs. Me${}_{\mathrm{subst}}^{\mathrm{1}+}$ depict the loss of 2Pb for Me${}_{\mathrm{subst}}^{\mathrm{1}+}$ and the increase of Sb for Me${}_{\mathrm{subst}}^{\mathrm{1}+}$, (g) the line in Pb vs. Tl diagram shows only Tl substitution, and (h) the line in Pb vs. (Sb + As) indicates uncorrected values of Pb $/$ (Sb + As) for all plotted points and the variation of corrected Pb and Sb values of ideal formulae for two values of S apfu.

5.3 Comparison with published data

The chemistry of rouxelite from Buca della Vena, Magurka, Monte Arsiccio, and Kláčianka (Sejkora et al., 2021) are compared in Table 5, together with empirical formulae (calculated for ΣMe = 212 for all to enhance the differences among them) and with corrected empirical formulae (i.e. express by Pb_f and Sb_f) for substitution mechanisms presented above. It is evident that corrected empirical formula for Buca della Vena rouxelite does not agree with its structural formula or with the ideal formula proposed by Orlandi et al. 2005 (i.e. Cu₈Hg₄Pb_92.4Sb_106.6(S_262.12O_10.24) _Σ272.36 with ch = −21, Cu₈Hg₄Pb_90.44Sb_109.56(S_258.64O_5.36) _Σ264 with ch = −2.45, or Cu₈Hg₄Pb₈₈Sb₁₁₂(S_258.64O_5.36)_Σ264 with ch = 0, respectively). The Tl-free, Cu-low, Ag-low substituted Kláčianka formula Cu₈Hg₄Pb_92.47Sb_107.53S_261.75 is almost identical with our possible solutions of Cu₈Hg₄Pb₉₂Sb₁₀₈S₂₆₂ or Cu₈Hg₄Pb₉₂Sb₁₀₈S₂₆₁O and clearly departed from corrected empirical formulae of Biagioni et al. (2014) (Table 5).

The unit-cell parameters; space groups; and empirical, structural, and ideal formulae for rouxelite from the Monte Arsiccio mine and Buca della Vena are presented in Table 6 for comparison.

Independent sites and occupancies by rod type in the crystal structures of rouxelite from the Monte Arsiccio mine (present work) and Buca della Vena (Orlandi et al., 2005) are shown in Table 7 and indicate that Tl, Sb, Ag, and As substitutions are present only in the B-type rod of rouxelite.

6 Modularity

The concepts of the modular description of rod-based sulfosalt structures (Makovicky, 1993) and boxwork structures (Makovicky and Topa, 2009) will be further applied to compare the structure of rouxelite with the structure of other sulfosalts. Generally, the PbS-like archetype (“cosalite”) will be represented in different shades of grey, whereas various colours are used for the SnS-like archetype (“boulangerite”). Light and dark shades of the same colour indicate rods with the same topology but translated along the viewing direction. The method of defining the rods in the rouxelite structure (Fig. 7) will be extended to represent other rods in sulfosalt structures. A comparison between the modular descriptions of rouxelite and the modular descriptions of other rod-based and boxwork structures is presented in Fig. 15. Notably, the rouxelite rods A, B, C₁, and C₂ are absent in the crystal structures of pellouxite, pillaite, neyite, kobellite, and izoklakeite and indicate that according to the formalism of Makovicky (1993) rouxelite and the enumerated minerals do not belong to the same family, or in other words rouxelite is modularly not related to the enumerated minerals under the rules outlined by Makovicky.

7 Conclusions

New unit-cell parameters, space group, empirical formulae, and crystal chemistry for rouxelite from the Monte Arsiccio mine have been identified and described, revealing notable differences from previously published data. However, the inability to precisely determine sulfur content through refinement, along with challenges in establishing oxygen content via chemical and refinement methods, complicates direct comparison with the existing literature data. These limitations underscore the need for further studies, particularly to refine sulfur quantification methods and improve the accuracy of oxygen content determination. Such investigations will be essential to fully resolve discrepancies and advance our understanding of rouxelite's crystal chemistry, which might lead to a redefinition of rouxelite. An ideal substitution-free formula for rouxelite is difficult to present, and the possible solutions are expressed by Cu₈Hg₄Pb₉₄Sb₁₀₆S₂₆₁, Cu₈Hg₄Pb₉₂Sb₁₀₈S₂₆₂, or Cu₈Hg₄Pb₉₂Sb₁₀₈S₂₆₁O.

The problems in fully resolving potential S vacancies or substitution by O are at least partially due to the crystal under investigation, being an intergrowth with a second domain whose cell parameters correspond to those of launayite. A comparison of the two structures is in progress and will be published soon. In the future, we hope to acquire high-resolution diffraction data from a non-intergrown crystal that will allow us to resolve the position in detail. Transmission electron microscopy studies might be necessary to investigate the oriented associations of rouxelite and launayite-like phases.

High-precision determination of the oxygen content of rouxelite material from different origins is being performed using EPMA and will be published in due course.