the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Chemical interdiffusion between Na-series tephritic and phonolitic melts with different H2O content, temperature, and oxygen fugacity values
Florian Pohl
Felix Marxer
Stepan Krasheninnikov
Renat Almeev
François Holtz
The diffusive exchange of major elements in Na-series tephrite–phonolite diffusion couples with compositions relevant to the Canary Islands magmatism was determined at 300 MPa and variable H2O concentrations (0.3 wt % to 3.3 wt %), temperatures (1150 to 1300 °C), and fO2 levels (NNO−1.5 to NNO+1.7). Composition-dependent effective binary diffusion coefficients were determined from concentration–distance profiles. Results show a wide range of diffusivities for different cations, consistently following the sequence Na ≫ Al ≫ K ≥ Mg = Fe = Ca > Si > Ti, with a mild diffusivity contrast (0.2–0.8 log units) between tephritic and phonolitic melts. Na is the fastest component, with diffusivities falling ∼1.0 log units above those of Si for any given condition. An anomalously fast Al diffusion is observed, with DAl falling ∼0.4 log units above Si and ∼0.6 log units below Na, suggesting a prevalence of Al–alkali coupling across our range of run conditions. The relationships between log D and H2O content in melt for all cations in an intermediate composition are strongly nonlinear and can be fitted using an exponential function with a convergence in diffusion coefficients for different temperatures with increasing H2O content. Thus, Arrhenius analyses result in a decrease in activation energies from 222–293 kJ mol−1 at 1.7 wt % H2O to 48–112 kJ mol−1 at 3.0 wt % H2O. These results provide new data on chemical interdiffusion in highly alkaline Na-rich melts and suggest that H2O content plays a key role in increasing the chemical efficiency of magma mixing at low temperatures. The obtained dataset is used to test chemical controls of magma mixing in the El Abrigo ignimbrite, Tenerife, where banded pumices involving basanitic–tephritic to phonolitic magmas are common in several compositionally bimodal ignimbrite units.
- Article
(5038 KB) - Full-text XML
-
Supplement
(2855 KB) - BibTeX
- EndNote
The study of the major and trace element composition of the melt phase is an important tool for understanding the evolution of sub-volcanic reservoirs and their pre-eruptive dynamics and timescales. Magma mixing and mingling are common and exert an important influence on the petrological and geochemical evolution of melt and whole-rock compositions, depending on the structure of the magma plumbing system and mixing endmember proportions (Sliwinski et al., 2015; González-García et al., 2022). In crystal-poor systems, the magma hybridization process is mainly controlled by the interaction of melt phases, in which chemical exchange by major and trace cation diffusion plays a key role. Although diffusion is a slow process occurring over small spatial scales, it takes advantage of extensive and complex contact areas between magmas resulting from advection, making it a key process controlling the chemical diversity of hybridizing magmas (Perugini et al., 2010, 2015; De Campos et al., 2011; DeVitre et al., 2019). Chemical variations along diffusion profiles can also provide valuable information on magma interaction and ascent timescales, as recently demonstrated by the application of major element diffusivities to banded pumices and glassy tephra (González-García et al., 2023; Shamloo and Grunder, 2023), giving a complementary insight into results from diffusion modelling on zoned minerals. Moreover, cation diffusion plays an important role in several other magmatic processes such as crystal growth and dissolution (Zhang et al., 1989; Mangler et al., 2023).
Because of this substantial field of application, the study of diffusion in melts at conditions as close as possible to those of natural volcanic systems is of major importance. Indeed, a large dataset of diffusion coefficients and Arrhenius equations has been published in the last decades (Zhang et al., 2010; Zhang and Gan, 2022), covering major elements, trace elements, and volatiles in various conditions. However, some important gaps still exist in the database. Diffusion data in Na-rich alkaline melts typical of ocean island systems are scarce, and consistent information regarding the effect of H2O on cation diffusivity is difficult to find (Baker et al., 2002). The presence of dissolved H2O is known to drastically reduce melt viscosity and consequently increase diffusivities (Dingwell et al., 1996; Romano et al., 2003). Similarly, high Na content and Na K ratios, typical of alkaline ocean island magmas, lead to an additional reduction in melt viscosity compared to K-rich melts in response to the modification of their molecular structure by decreasing the degree of polymerization (Le Losq et al., 2021b). In turn, these chemical variations can influence eruptive styles (Giordano and Dingwell, 2003; Andújar and Scaillet, 2012). To address these issues, we experimentally characterized the diffusive exchange of eight major elements between hydrous tephrite and phonolite melts from the Canary Islands to constrain their diffusive behaviour as a function of H2O content and temperature on the diffusion process. These experiments are relevant to conditions prevailing during magma mixing events recognized in the Las Cañadas edifice, Tenerife (i.e. 1150–1300 °C, 0.3–3.3 wt % H2O, and 300 MPa). The experimental data obtained provide insights into magma mixing events on the island of Tenerife and can potentially be applied to other volcanic systems of analogous composition, such as the Laacher See (Tomlinson et al., 2020) or Mayotte (Berthod et al., 2021).
2.1 Starting materials
Two natural eruption products, which are representative of the Canary Islands volcanism, were selected as experimental starting materials (Table 1). The mafic endmember (PF21) is a tephrite sampled in the Duraznero crater, which was built during the 1949 San Juan eruption on the island of La Palma (Klügel et al., 2000; Fuchs, 2014). Such a tephritic composition is common in the historical volcanism in the Cumbre Vieja volcanic ridge (Klügel et al., 2000, 2005; Pankhurst et al., 2022), and it also resembles tephritic lava flows in the Diego Hernández Formation (DHF) of the Las Cañadas edifice, Tenerife (Bryan et al., 2002), in both major and trace element content. These tephrites represent a widespread step in the differentiation of primitive basanitic magmas in the Canary archipelago and are considered a common endmember for magma mixing events in the DHF (Wolff, 1985; Bryan et al., 2002; Sliwinski et al., 2015; González-García et al., 2022).
Table 1Composition of starting endmembers (both the original starting glass and those from the Fe-poor experiments DC-03 and DC-04) and the TP55 intermediate composition (tephriphonolite) to which most diffusivities are referred throughout this work (see text for details). n is the number of averaged EPMA analyses.
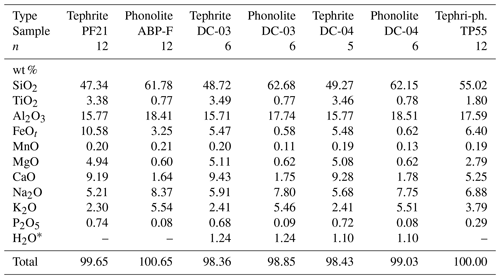
* H2O concentrations in DC-03 and DC-04 were determined by Fourier-transform infrared spectroscopy (FTIR).
The evolved endmember (ABP-F) is a phonolite originating from aphyric white pumices of the El Abrigo ignimbrite (González-García et al., 2022). Phonolites of similar composition are widespread in all ignimbritic units in the DHF (Bryan et al., 2002; Martí et al., 2020), as well as in the Teide–Pico Viejo system (Ablay et al., 1998; Dorado et al., 2021), and are the result of protracted magma differentiation and storage in shallow (<5 km) reservoirs of the Las Cañadas volcano and in the currently active Teide–Pico Viejo system (Andújar et al., 2008, 2010). Phonolites are also present in La Palma, are occasionally involved in magma mixing events, and are represented in historical volcanism on the island (Johansen et al., 2005; Klügel et al., 2022).
These starting materials were crushed and powdered in a ring mill and subsequently melted at 1600 °C for 4 h in a Nabertherm® box furnace at ambient pressure. After quenching in water, the resulting glasses were ground in an agate ball mill and melted again under the same conditions to ensure chemical homogeneity. After three melting and crushing cycles, the resulting glass was crushed again to obtain the final starting material powders for the experimental capsules.
2.2 Experimental setup
Hydrous starting glasses were produced at high pressure and temperature using Au80Pd20 alloy capsules with an inner diameter of 5.0 mm and a length of 35 mm. The capsules were filled with glass powder and, when necessary, appropriate amounts of distilled water, in several steps. Glasses of both endmember compositions were produced as nominally dry (ND; i.e. no added water) and at nominal H2O concentrations of 1.5 wt % and 3 wt %. After loading, capsules were welded shut, and glasses were synthesized at 300 MPa and 1200 °C in two different internally heated pressure vessels (IHPVs; Berndt et al., 2002). Temperatures were controlled with S-type (Pt-Pt90Rh10) thermocouples, and pressure was monitored with calibrated Burster pressure transducers. For all runs, the capsules were quenched isobarically after switching off the power supply of the furnace, resulting in an initial cooling rate of ca. 200 °C min−1. After the synthesis, the glasses recovered from the capsules were cut to obtain cylinders with a length of ca. 3–4 mm, and each cylinder was finely polished on one side.
A first set of starting glasses (experiment set A) was synthesized at fO2 conditions close to the Ni–NiO buffer (NNO, equivalent to 0.6 log units above the quartz–fayalite–magnietite, QFM, buffer) under H2O-saturated conditions in an IHPV equipped with an H2 Shaw membrane for fO2 monitoring (Berndt et al., 2002) using an Ar–H2 pressure medium, with a synthesis duration of 72 h. In the set A synthesis experiments, the H2 partial pressure in the IHPV was adjusted to buffer fO2 close to the NNO equilibrium. Based on the amount of H2 introduced into the vessel, the prevailing oxygen fugacity is estimated to be between NNO−0.1 and NNO+0.8. However, these values only correspond to experimental fO2 if the charges are H2O saturated. In H2O-undersaturated runs, the final fO2 is shifted towards more reducing values by the term 2⋅log(aH2O), where aH2O is the H2O activity in the charge (Botcharnikov et al., 2008). In order to apply this correction, aH2O was approximated by XH2O = H2Omeasured (mol %) H2Osaturation (mol %). H2O saturation values were obtained using the MagmaSat solubility model (Ghiorso and Gualda, 2015). Consequently, experimental oxygen fugacity in the synthesis runs varied between NNO−1.7 and NNO−0.3 (Table S1 in the Supplement).
A second set of glasses (experiment set B) was synthesized at the intrinsic fO2 of the IHPV (Ar-only pressure medium), with fO2 close to NNO+2.3 at H2O-saturated conditions, as verified using CoPd redox sensors (Taylor et al., 1992; Marxer and Ulmer, 2019). As described above, the final experimental fO2 ranged between NNO−0.1 and NNO+1.7 as melts were water-undersaturated. Thus, in both experimental series (set A and B), the most oxidizing conditions were reached in H2O-rich experiments.
Diffusion experiments were run using the diffusion couple method (Baker, 1989, 1991; Nowak and Behrens, 1997), in which the polished sides of phonolitic and tephritic glasses with the same nominal water content are juxtaposed with each other and placed inside an Au80–Pd20 capsule with an inner diameter of 5.1 mm. The denser tephritic glass was placed in the bottom position to avoid gravitational instability during the experiment. The capsules were closed by arc welding and pre-compressed in a cold-seal pressure vessel (CSPV) to check for tightness.
The diffusion experiments were run in the same IHPVs that were used for glass synthesis, at temperatures ranging from 1150 to 1300 °C and a constant pressure of 300 MPa. Table 2 shows a summary of run conditions for all experimental charges. The vessels were pressurized with Ar–H2 (set A) or Ar (set B), and the experiments were run for 2 or 4 h (plus one additional zero-time experiment). The heating ramps from ambient temperature to final dwell temperature were 30 °C min−1 in the set A experiments and 50 °C min−1 in the set B experiments. After each run, a rapid-quench device (Berndt et al., 2002) was activated, allowing the capsule to fall into the cold part of the vessel and cool quickly, with quenching rates up to 50 °C s−1. A total of 13 experiments were run successfully and utilized for the present study (Table 2).
2.3 Analytical procedures
From the starting glasses, 10–20 mg glass chips from both ends of the capsule were used to measure H2O content by pyrolysis and subsequent Karl Fischer titration (KFT; Behrens, 1995; Behrens et al., 1996). The iron oxidation state (Fe3+ ΣFe ratio) was measured by colorimetric wet-chemical analysis (Schuessler et al., 2008). Small glass chips (5–20 mg) from the two ends of the post-synthesis glass cylinders were powdered, dissolved in HF, and analysed by absorption spectrometry in the visual spectrum using a Shimadzu UV 1800 UV–VIS spectrometer. This method allows determination of the Fe3+/ΣFe ratios with high precision (typically within <3 %).
After the diffusion couple experiments, each capsule was cut longitudinally in two halves. A double-polished section was prepared from one half, with a thickness between 100 and 300 µm. The second half was mounted in a 1 in. epoxy resin mount and polished. H2O concentrations were measured by Fourier-transform infrared spectroscopy (FTIR) in the double-polished sections, and an electron probe microanalyser (EPMA) was employed to determine major element concentrations in the epoxy-mounted experimental charges.
In the resulting diffusion couples, H2O concentrations were obtained by FTIR using a Bruker IFS88 spectrometer coupled to an IR-Scope II microscope at the Institute of Earth System Sciences (IESW), Leibniz University Hannover. Absorption coefficients determined for a Na-rich phonolite glass from Teide volcano (Carroll and Blank, 1997) were applied to quantify H2O concentrations, namely and L mol−1 cm−1. No absorption coefficients are published for tephritic glass, but we used the values published for compositionally close shoshonitic glass by Vetere et al. (2011), i.e. and L mol−1 cm−1. To estimate melt density, we used the equations provided by Carroll and Blank (1997) and Vetere et al. (2011). Using these data, water concentrations were estimated using the modified Beer–Lambert law (Stolper, 1982).
Major element oxide concentration profiles (SiO2, TiO2, Al2O3, FeOt, MgO, MnO, CaO, Na2O, K2O, and P2O5) were obtained with a JEOL JXA-iHP200F Hyper Probe electron microprobe equipped with five wavelength-dispersive X-ray spectroscopy (WDS) spectrometers at the IESW, Leibniz University Hannover. Operating conditions were an accelerating voltage of 15 kV, a beam current of 4 nA, and a defocused beam diameter of 12 µm to minimize alkali migration. Accuracy is less than 3 % for concentrations >1 wt % except for CaO and K2O, which have an accuracy of <5 %. For most experiments, two parallel transects were obtained with different lengths and resolutions to capture the widely varying diffusion rates of all major elements (especially Na). In transect 1, intervals between analytical spots were kept as small as possible (typically 15–20 µm). In contrast, the second profile spanned 3 to 4 mm across the interface with separation between analytical spots in the 30–40 µm range. This second profile also allowed us to check for possible disturbances caused by convection in the experiments. Precision and accuracy were determined by measuring VG-568 (rhyolite) and VG-2 (basalt) reference glasses (Jarosewich et al., 1980; Helz et al., 2014).
2.4 Correction for experimental times
Nominal experimental dwells of 2 and 4 h were defined, and actual dwell times were registered for each experiment. However, due to the activation of the diffusion process at a certain temperature before reaching the target experimental temperature, experimental dwell times needed to be corrected by incorporating the effect of heating ramps. Thus, effective experiment durations were calculated by assuming Arrhenian behaviour of diffusivity during heat-up ramps and integrating the diffusivity as a function of T with respect to t during that interval (Zhang and Behrens, 2000). Thus, the effective heating time (teff) can be calculated using the following expression (Koepke and Behrens, 2001):
where DT(t) is diffusivity as a function of temperature, which is itself a function of time, T(t); DTexp is the diffusivity at the experimental dwell temperature (Texp); Ea is the activation energy and R is the ideal gas constant; and h is the duration of the heating ramp. As a first approach, an Ea value of 150 kJ mol−1 was used, which is similar to the final obtained values from the Arrhenius analysis (see Sect. 4.4), resulting in calculated effective heating times on the order of 180 to 500 s. Final effective experiment durations are listed in Table 2. The high cooling rates resulting from rapid quenching allow us to assume instantaneous cooling with no effect on effective run duration.
2.5 Determination of composition-dependent diffusion coefficients
Diffusion in natural multicomponent systems is a complex phenomenon. In such cases, the diffusion of a component not only depends on its own gradient but is also dependent on the gradients of the other components in the system (Chakraborty et al., 1995a, b; Liang, 2010). This dependence can be rigorously described using a multicomponent diffusion matrix, requiring specific experimental strategies. Although multicomponent diffusion matrixes have been obtained for up to seven- and eight-component systems (Guo and Zhang, 2016, 2018), such an approach has never been carried out for systems with large compositional gradients, and thus it is outside of the scope of this work. Instead, we here use the effective binary diffusion (EBD) approach, a simplified procedure in which the diffusivities of each component are treated as binary diffusivities, with all the other components considered to be a single component. Diffusion coefficients (D) obtained via this approach are therefore apparent diffusivities that are not necessarily comparable to those obtained in compositionally different systems.
Due to the variable bulk glass composition along the analysed profiles, a concentration-dependent procedure for determining elemental diffusivities must be used. EBD coefficients were obtained from measured concentration–distance profiles by the modified Boltzmann–Matano methodology of Sauer and Freise (1962; hereafter SF), which does not require knowledge of the Matano interface. In particular, the analytical solution for one-dimensional molar volume independent diffusion from Sauer and Freise (1962) was used:
where c(x) is the normalized concentration of the diffusing component, with c(x)=1 at and c(x)=0 at . A modification of the Python programming language script (Oliphant, 2007) used by González-Garcia et al. (2018) was used to calculate composition-dependent diffusivities from the SF procedure.
The SF method requires that the variation in the molar volume of the melt along the diffusion profile is non-significant. To check this point, we used the Bouhifd et al. (2015) formulation to obtain the molar volume of tephritic and phonolitic melts under our experimental conditions, resulting in a >8 % variation. This value is within the error in the SF method itself and will have an insignificant impact on obtained diffusivities. The error in D was estimated by simple error propagation from uncertainties in involved data, including molar volume variation. Another limitation of the SF method is that D cannot be accurately obtained at the endmember compositions, and for this reason we restrict the calculation of diffusivities in our profiles from 20 % to 80 % of the endmember compositional range.
3.1 Starting glasses and diffusion couples
All synthesis experiments resulted in homogeneous, bubble-free glasses. Phonolitic glasses were crystal-free; however, tephritic glasses showed variable numbers of dendritic quench crystals (<25 µm), likely clinopyroxene, produced during the experiment cool-down phase. In contrast, diffusion couple runs resulted in crystal- and bubble-free glasses, as observed in scanning electron microscope (SEM) backscattered electron (BSE) imaging. This was corroborated by a zero-time experiment performed at 1200 °C and 0.3 wt % H2O, which showed that all quench crystals formed during the synthesis phase of the tephritic glasses effectively dissolved upon heating and before reaching the experimental temperature (Fig. S1 in the Supplement).
H2O content measured by KFT and FTIR in starting materials and diffusion couples agrees well with intended concentrations, except for the nominally dry glasses of experiment set A. In these experiments, the water content measured in starting glasses was 0.8 wt %–1.1 wt %, resulting from a reduction in Fe2O3 in the starting material and H2 influx through the capsule walls. In experiment set B, the same effect resulted in H2O content of 0.3 wt %–0.5 wt %. In the diffusion couples, H2O concentrations, measured by FTIR along a line centred on the interface of the experiments, proved to be constant or close to constant for each experiment. Variations along the line were not higher than 10 %, and hence the average and standard deviation of analysed spots were assumed to be the H2O concentration value for each experiment (Table 2).
Measured molar Fe3+ ΣFe ratios in starting glasses are provided in the Supplement (Table S1). Both set A tephritic and phonolitic glasses show a similar trend, with Fe3+ ΣFe varying from 0.1 to 0.2 with increasing H2O content (see Fig. S3). However, for set B glasses, the observed trends differ for phonolite and tephrite, with Fe3+ ΣFe varying from 0.25 to 0.5 for the tephrite and from 0.45 to 0.65 for the phonolite and again with an increasing trend with increasing H2O owing to the more-oxidizing conditions in H2O-rich melts. This is a result of the fO2 buffering mechanism in the IHPV. Synthesis runs with low H2O content performed under reducing conditions suffered from loss of iron to the Au–Pd alloy capsule (Fig. S4), resulting in a relative loss of ca. 50 % and 80 % of FeO in phonolitic and tephritic glasses, respectively (Table 1). This effect is only significant in the two ND experiments and diminishes progressively with increasing fO2. Experiments run at intrinsic vessel fO2 do not show significant Fe loss (Fig. S4).
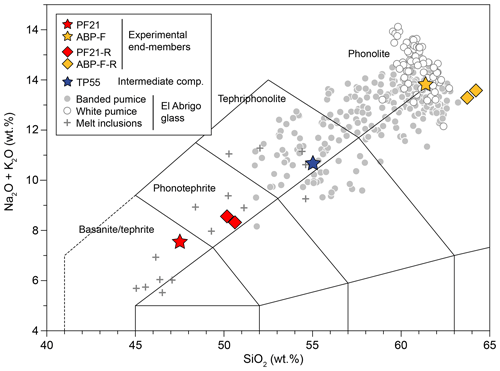
Figure 1Total alkali–silica diagram showing the compositions of initial tephritic (PF21) and phonolitic (ABP-F) endmembers, as well as Fe-poor endmembers from experiments DC-02 and DC-03 (PF21-R and ABP-F-R). The intermediate composition (TP55) for which diffusivities are derived is also shown. Glass compositions from El Abrigo pumices (González-Garcia et al., 2022) are plotted for comparison.

Figure 2(a) Major element oxide concentration–distance profiles measured in experiment DCB-09, with concentrations normalized for endmember concentrations (Cmin=0 and Cmax=1). (b) MnO profile showing prominent uphill diffusion. (c) Full Na2O profile showing the greater extension of the diffusive zone (note the different length scale). Where not shown, error bars are smaller than the symbol.
3.2 Diffusion data
Concentration–distance profiles of 9 of the 10 major oxides measured in the diffusion couple runs resulted in monotonic diffusion profiles with no evidence of uphill diffusion. Figure 2 shows an example of concentration–distance profiles measured with the EPMA, and the complete dataset is included in the Supplement File 2. As expected from compositional contrast, all profiles are asymmetric and extend deeper into the tephritic half of the diffusion couple except for Na, which shows the opposite behaviour. This dataset allows an effective binary diffusion (EBD) approach (Zhang et al., 2010). In contrast to other oxides, the MnO profile shows strong signs of uphill diffusion (Fig. 2b) resulting from multicomponent diffusion effects and thus was left out of the EBD analysis.
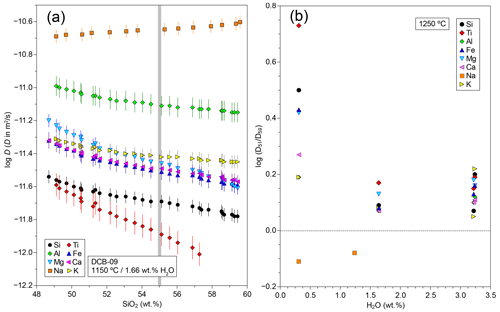
Figure 3Concentration dependence of major element diffusivities in tephrite–basanite couples. (a) Diffusion coefficient vs. SiO2 concentration along run DCB-09, resulting from the SF analysis. The thick vertical line indicates the TP55 composition used as a proxy for diffusion coefficients throughout the text. (b) Variation in the compositional dependence of diffusion coefficients with H2O content at 1250 °C, using the ratio (ratio between diffusivities at 51 wt % and 59 wt % SiO2) as an index.
The application of the SF equation to the diffusion profiles led to continuous variations in D with distance across the profile (Fig. 3) and hence with bulk glass composition. As already noted by observing the shape of the concentration–distance profiles, most components show an inverse correlation between SiO2 content and D, with the only exception being Na, which shows the opposite behaviour. Due to the intrinsically fast diffusivity of Na, its diffusion coefficient could only be determined in the low-temperature and/or low-H2O experiments (seven runs). In the remaining experiments, Na diffusion reached the ends of the experimental charges, and therefore the experiment lost its characteristic of a semi-infinite medium, leading to strongly underestimated Na diffusivity. In the experiments where D was determined for Na, it showed the fastest diffusion among major elements, being consistently ∼1 order of magnitude faster than Si. Surprisingly, Al has the second fastest diffusivity, falling approx. 0.5–0.6 log units below Na and ∼0.4 log units above Si for all experiments. This is an unexpected result, since the network-forming character of Al3+ cations should result in diffusivities close to those of Si and Ti, as observed in most data in the literature (see Sect. 4.5). The Mg–Fe–Ca–K group displays similar diffusivities but always falls between Al and Si. Finally, Ti is the slowest diffusing component, showing values similar to or lower than Si. In comparison to the diffusion couple experiments carried out by González-Garcia et al. (2017) using shoshonite–rhyolite couples, results from tephrite–phonolite couples are highlighted by (1) a lesser prevalence of diffusive coupling to Si, resulting in a wider dispersion of diffusivities, and (2) a lack of uphill diffusion phenomena, with the only exception being Mn.
4.1 Compositional dependence
One of the main factors influencing cation diffusion in silicate melts is the melt chemical composition. Diffusion of divalent, trivalent, and tetravalent cations is usually faster in silica-poor depolymerized melts than in silica-rich polymerized melts, while the reverse is usually true for monovalent cations (e.g. Zhang et al., 2010). As already visible in the asymmetry of composition–distance profiles, there is a clear compositional dependence in our tephrite–phonolite couples, and the SF analysis clearly shows this effect (Fig. 3a). To quantify the degree of compositional dependence of major cation diffusion, we can use the ratio of the diffusion coefficients for 51 wt % SiO2 and 59 wt % SiO2 (). For the 1250 °C experiment series, we find that compositional dependence is higher in the nominally dry experiments, where values are between 1.5 and 5 (equal to a 0.2 to 0.7 log unit difference between the tephritic and phonolitic compositions; Fig. 3b). For H2O content more than 1 wt %, the ratio decreases to 1.1–1.5 (<0.2 log unit difference). Again, the exception is Na, which follows the expected behaviour for monovalent cations and diffuses up to 0.2 log units faster in phonolite than in tephrite.
Due to the rather mild compositional dependence for most elements, we have chosen an intermediate composition equivalent to 55 wt % SiO2 (tephriphonolite) as an index, for which the diffusive behaviour of major components will be described from now on. This melt composition will be hereafter referred to as TP55 (Table 1), and the full dataset of diffusion coefficients is given in Table 2.
Table 2Experiment parameters and diffusivities obtained for the TP55 composition.

All diffusivities correspond to a composition of 55 wt % SiO2 (19.7 mol % Si), referred to as TP55 in the text. D is in m2 s−1. a H2O content is the average of several FTIR measurements in each experiment. b XH2O is calculated as H2O(experiment) H2O(saturation) in mol %. H2O saturation was calculated using the MagmaSat model (Ghiorso and Gualda, 2015).
4.2 Fe diffusion
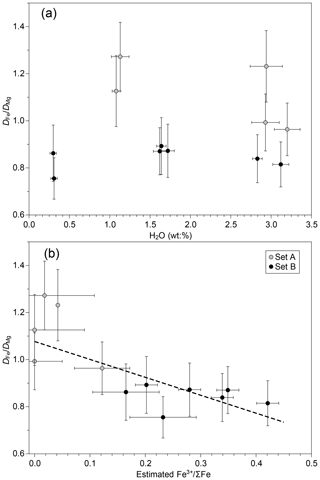
The varying fO2 experimental conditions resulted in variable Fe oxidation states (Fe3+ ΣFe ratio) in experimental sets A and B, as already observed in Fig. S2. The prevailing structural role of Fe2+ as a network modifier and Fe3+ as a weak network former (with some Fe3+ possibly acting as a network modifier; Le Losq et al., 2021a; Moretti and Ottonello, 2022) may result in different diffusivities for both species, although the uncertainty in the behaviour of Fe3+ does not allow us to make a reliable prediction. In any case, due to its higher bond strength, Fe3+ diffusivities are expected to be lower than those of Fe2+ (Zhang et al., 2010). Hence, the measured D of total Fe is expected to be between that of Fe2+ and Fe3+. Our measured diffusion dataset can be used to put some first-order constraints on the differential diffusivity of Fe2+ and Fe3+in the tephrite–phonolite system. Since Fe3+ ΣFe was not determined in the diffusion couples, we used its relationship with estimated fO2 in the synthesis runs (Fig. S3) to obtain a tentative estimate of Fe3+ ΣFe in the diffusion couples (Fig. 4). To avoid the effects of different experimental conditions, Fe diffusivities from each run were normalized to those of Mg from the same experiment. The results suggest that the effect of oxygen fugacity in Fe diffusion is resolved in our experimental dataset (Fig. 4a). values for set B are below 0.9, while in the more-reducing experiments (set A), increases to 0.9–1.3. From these data and the linear fit in Fig. 4b, the difference in diffusivity of Fe3+ and Fe2+ can be estimated. Although the associated errors are large, our results suggest that Fe2+ diffusivity in the tephrite–phonolite system is on the order of 3 to 5 times faster than that of Fe3+ for a given temperature and given H2O content (Fig. 4b). Therefore, our dataset seems to indicate a measurable difference in diffusivity between both Fe species in alkaline silicate melts.
4.3 H2O dependence
Dissolved H2O in melt has already been demonstrated to strongly enhance diffusivities in silicate melts, for both major elements (e.g. Baker, 1991; Baker and Bossányi, 1994; González-García et al., 2017, 2019) and trace elements (Watson, 1981; Baker and Bossányi, 1994; Behrens and Zhang, 2001; Zhang et al., 2010; González-Garcia et al., 2018; Spallanzani et al., 2022). Our experimental dataset confirms this observation, and for the TP55 composition major element diffusion is enhanced by 1.2–1.5 log units (corresponding to a factor of 20–30) when H2O content increases from 0.3 wt % to 3.3 wt % at 1250 °C. At 1200 °C, the enhancement factor amounts to 0.8–1.0 log units for an increase in H2O content from 1.1 to 3.0 wt % H2O (Fig. 5). For the dataset obtained at 1150 °C, with two successful runs at 1.6 wt % and 3 wt % H2O, the enhancement is on the order of 0.5 log units for all elements. Here, runs at different fO2 levels were treated together since oxygen fugacity is not expected to have a major effect on diffusivity, except for Fe (see above).
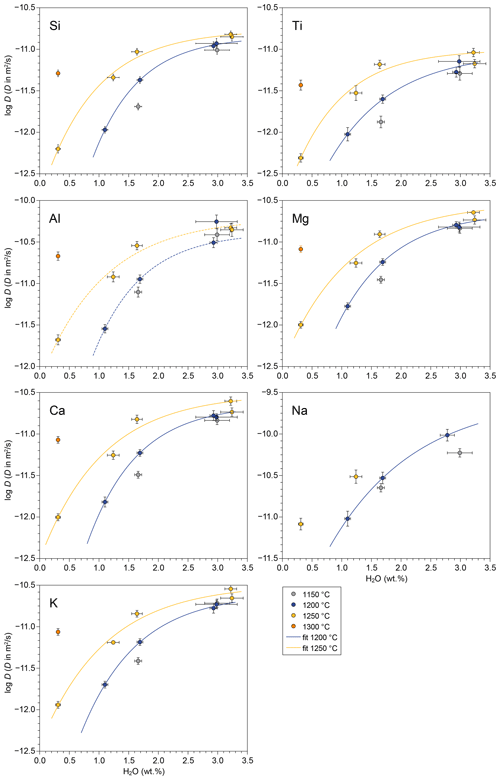
Figure 5Water-dependence of major element effective binary diffusivities for a 55 wt % SiO2 compositional term.
Table 3Parameters a, b, and c obtained from fitting the H2O-dependent diffusivities with an exponential law in the form log , where w is the H2O content in weight percent. RMSE: root-mean-square error.
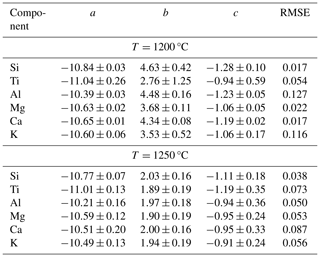
Moreover, the increase in D as a function of H2O in weight percent is clearly nonlinear, and instead it can be modelled by an exponential function in the form , where a, b, and c are fitting parameters, and w is the H2O concentration given in weight percent. Parameter a gives the asymptotic log D value, i.e. the diffusivity at the saturation level. This fitting equation was applied to our diffusion datasets at 1200 and 1250 °C using an instrumentally weighted Levenberg–Marquardt least-squares algorithm in the software QtiPlot v. 1.0.0. Fitting parameters for each component are provided in Table 3. The 1200 °C dataset, spanning 1.1 wt % to 3.0 wt % H2O, can be fitted with a root-mean-square error (RMSE) between 0.02 and 0.13 log D units (with D in m2 s−1). The 1250 °C dataset, spanning 0.3 wt % to 3.2 wt % H2O, yielded an RMSE between 0.04 and 0.09 log D units. Considering H2O content in mole percent instead of weight percent did not change the fitting shape.
Such strongly nonlinear H2O–diffusion relationships are common in the literature (e.g. Baker, 1991; Watson, 1994; Baker et al., 2002; Zhang et al., 2010), but fitting equations are rarely provided. For small variations in H2O content (0.3 wt %–2 wt %), González-García et al. (2017, 2018) found linear relationships for both major and trace elements in shoshonite–rhyolite couples, but the inclusion of diffusivities under dry conditions seemed to make a square-root function more appropriate (González-García et al., 2019). However, different behaviours arise when the effects of water species OH and molecular H2O (H2Om) are considered. FTIR analysis shows that the proportion of OH and H2Om varies with total H2O in melt, with OH being the predominant species at H2O wt % (∼8 mol %). This trend (Fig. S5) is equivalent to those established for other melts (e.g. Lesne et al., 2011). We find that log D follows a similar exponential function with H2Om (in mol %) to that found for total H2O, and a clear relationship with OH cannot be established. However, the best fit comes with the molar ratio [OH] [H2Om], where linear correlations can be observed for all major oxides for H2O >1 wt % (Fig. S6).
It is remarkable to note the convergence of elemental diffusivities towards high H2O content in both datasets, which also includes the data point at 1150 °C and 3 wt % H2O. All experimentally measured diffusivities at such high H2O concentrations are within 0.4 log units, compared to a variation of 0.6–0.8 log units at 1.6 wt % H2O. A consequence of this behaviour is that the diffusivity of the slowest components (in our case, Ti and Si) is more sensitive to the addition of H2O than the fastest ones are, confirming previous observations (e.g. Watson, 1994). The exponential dependence of log D on H2O content is likely controlled by melt viscosity, which follows a similar non-linear evolution with H2O content. Our observation suggests that H2O plays a major role in increasing the efficiency of chemical mixing in interacting melts, virtually equalizing diffusivity variations across a temperature range. Therefore, water-rich magmatic environments, such as those present in the Canary Islands, could be more susceptible to developing efficient mixing between melts than water-poor melts, not only diminishing the viscosity but also reducing the viscosity difference between endmembers. On the contrary, H2O-poor or dry magmas with higher viscosity and slower diffusion kinetics would favour physical mingling over chemical hybridization.
4.4 Arrhenius relations
The temperature dependence of diffusion is well established and is determined by the Arrhenius equation:
where D0 is the pre-exponential factor (m2 s−1), Ea is the activation energy of the diffusion process (J mol−1?), R is the gas constant (J mol−1 K−1), and T is temperature (K). By plotting 1000 T vs. ln D and fitting measured diffusivities with a linear regression, it is therefore possible to calculate D0 and Ea and characterize the T dependence of major element diffusion. The dataset was fitted using the same procedure and software detailed above for obtaining H2O vs. D equations.
From our experimental dataset, Arrhenius equations relating temperature and diffusivity were obtained under specific conditions. The major parameter influencing diffusion in our dataset is H2O content, but its measured value varies up to 0.1 wt %–0.3 wt % for experiments with the same nominal H2O content. Therefore, a correction of diffusion coefficients to a common H2O concentration must be made before plotting the Arrhenius relations. We used the H2O-dependent equations obtained in the previous section (Table 3) to obtain diffusivities at 1200 and 1250 °C for fixed H2O content of 1.66 wt % and 2.99 wt %. These values were determined by the H2O content of the experiments at 1150 °C, where an H2O-dependent equation was not obtained.
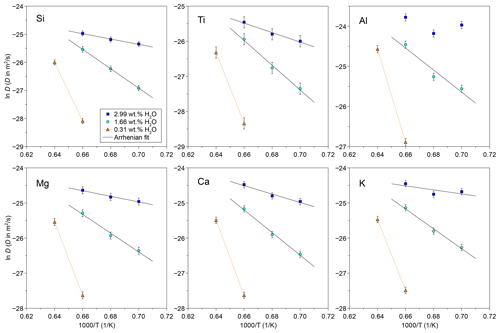
Figure 6Arrhenius relations of TP55 for six major elements at 1.66 wt % and 2.99 wt % H2O. Due to the anomalous behaviour, a linear fit was not obtained for Al at 2.99 wt % H2O. The determined ln D values of the 0.3 wt % series are plotted for reference.
Figure 6 shows Arrhenius fits for Si, Ti, Al, Mg, Ca, and K, and the parameters obtained are summarized in Table 4. Fe is not included due to inconsistencies arising from the different Fe3+ ΣFe ratios in experiments, and Na data are insufficient to obtain Arrhenius parameters of good quality. Results show a coherent picture, indicating a decrease in Ea with increasing H2O content from 220–290 kJ mol−1 at 1.66 wt % H2O to 47–112 kJ mol−1 at 2.99 wt % H2O. Activation energies and ln D0 for both H2O concentrations plot to a single compensation law linear fit (Hart, 1981; Fig. S7). This is in line with previously published data, where H2O content is known to reduce the activation energy of diffusion (Watson, 1981, 1994; Behrens and Zhang, 2001; Spallanzani et al., 2022). Only Al shows anomalous behaviour, where the fitting errors are larger for the 1.66 wt % H2O fit, and the 2.99 wt % H2O dataset does not allow us to obtain a good Arrhenian fit.
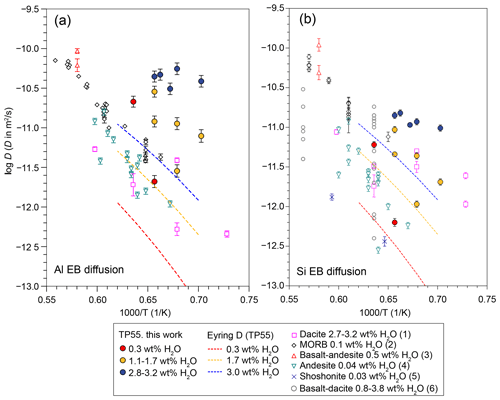
Figure 7(a) Al and (b) Si effective binary (EB) diffusion data obtained in this work compared to bibliographic data. The dashed coloured lines indicate Eyring diffusivity for TP55 at H2O content of 0.3 wt %, 1.7 wt %, and 3.0 wt %, with viscosities calculated using the Giordano et al. (2008) model. Bibliographic data are from (1) Baker and Bossányi (1994), (2) Chen and Zhang (2008, 2009), (3) Lundstrom (2003), (4) Zhang et al. (1989), (5) González-García et al. (2019), and (6) Koyaguchi (1989).
4.5 The case of aluminium
Throughout our complete dataset, Al is the second-fastest-diffusing element after Na, and Al diffusivities are 0.4 log units faster than Si. This behaviour can be considered anomalous, given that the expected network-forming character of Al3+ in the silicate network should result in diffusivities comparable to those of Si4+ and Ti3+. A comparison of our Al diffusivities with published data (Fig. 7) confirms this anomaly. Al diffusion in TP55 melt composition with 2.7 wt % to 3.3 wt % H2O plots between 1 and 2 orders of magnitude above diffusivities measured by Baker and Bossányi (1994) in wet dacite with the same range of H2O content and is comparable to those observed in dry basalts and basanites at 1500 °C (Lundstrom, 2003; Chen and Zhang, 2008, 2009), i.e. 200 to 350 °C hotter than our experimental conditions. This behaviour is not observed in Si, for which diffusivities do not differ strongly from data in the literature for similar water content. The comparison to Eyring diffusivity (i.e. viscosity-related diffusion usually applied to network-forming cations; Glasstone et al., 1941) of TP55 at different levels of H2O content yields similar differences, with Al EBD plotting significantly above Eyring D values for the corresponding melt H2O content (Fig. 7). Although Si data also plot above Eyring D, their deviations are lower and consistent with previous studies (Fanara et al., 2017). The large departure of Al from Eyring diffusivity also contrasts with the comparatively low deviations observed by Fanara et al. (2017) for trivalent cations. The only dataset supporting high Al mobility in silicate melts comes from dynamic-mixing experiments performed with K-series alkaline melts from Campi Flegrei. In such experiments, Perugini et al. (2013, 2015) showed that the relaxation of concentration variance (R, which is highly dependent on diffusivity) of Al is larger than that of most major components, falling between that of Na and K. On the other hand, this behaviour is not observed in chaotic-mixing experiments with subalkaline melts (Morgavi et al., 2013), where Al mobility is similar to those of Si and Ti. Overall, these observations point to a fast Al diffusion mechanism operating in highly alkaline melts, in agreement with our diffusion experiments.
In the silicate melt framework, Al usually plays the role of a network-forming cation (Mysen et al., 1981), and as such its diffusivity is expected to be comparable to that of other network-forming cations in tetrahedral (i.e. 4-fold) coordination (Si, Ti) and to Eyring diffusivity. Departures from this behaviour have been suggested for high-P and peraluminous magmas, suggesting that Al may not be in tetrahedral coordination if the local charge balance is not attained with M+ (Na, K) and M2+ (Ca) cations (Mysen et al., 1981). In molecular dynamics simulations, alkali cations (especially Na+) tend to cluster around Al3+ to compensate for the charge balance (Le Losq et al., 2017), which could lead to increased Al diffusivity, where highly mobile Na cations result in an enhancement effect in Al mobility in the melt. This effect is greatly facilitated in melts with a large Na K ratio, while in K-rich melts the large size of K+ promotes polymerization, which in turn increases viscosities and decreases diffusivities.
A complementary explanation for the observed Al behaviour could potentially reside in multicomponent diffusion effects. Diffusion in complex multicomponent systems is subject to diffusive coupling between oxides, usually resulting in uphill diffusion of one or more components (e.g. Guo and Zhang, 2016, 2018). This is the case for Al in basalt–rhyolite couples or in other systems with similar endmembers (e.g. Koyaguchi, 1989; González-García et al., 2017), but Al uphill diffusion is notably absent in our tephrite–phonolite couples. This behaviour is, however, expected, since the occurrence of uphill diffusion is highly dependent on the arrangement of endmembers in the compositional space, as observed in simple three-component systems (Chakraborty et al., 1995b). Multicomponent diffusion experiments in the system K2O–Al2O3–SiO2 (Chakraborty et al., 1995a, b) suggest again that Al diffusion is coupled to alkalis. The degree of coupling depends on composition (peralkaline vs. peraluminous) and the nature of the gradient of all remaining elements. In our system, an indication of Al–K diffusive coupling comes from their behaviour in the Arrhenius plots (Fig. 6). Al and K show here anomalous behaviour, both deviating from linearity. Diffusivities of Al and K show an increase from 1200 to 1150 °C, especially evident in the 3.0 wt % H2O data. This behaviour could potentially be related to a change in the Al–K diffusive coupling at lower temperatures due to the variation in the intrinsic diffusivity of both elements.
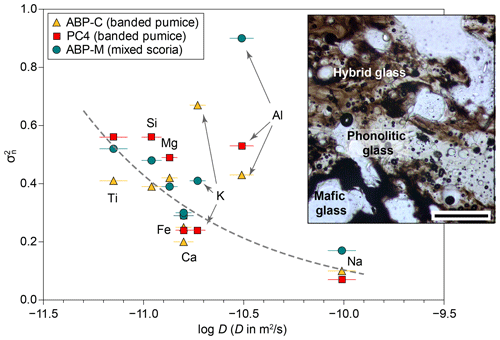
Figure 8Comparison between experimental diffusivities for TP55 composition and normalized concentration variance () for three mixed clasts from the El Abrigo ignimbrite. Plotted diffusivities are from experiment DCB-11 (1200 °C, 2.93 wt % H2O). The inset shows a microphotograph of a mingling and mixing area in El Abrigo banded pumice. The scale bar is 200 µm long.
4.6 Implications for magma mixing in Tenerife
The experimental results obtained in this work can be used to obtain some insights into the petrogenesis of bimodal ignimbrite sheets in the Diego Hernández Formation in Tenerife. In several of these units, the presence of banded pumices suggests the occurrence of magma mixing and mingling shortly before the eruption (González-García et al., 2022). During magma mixing, the combined effects of diffusion and advection progressively reduce the compositional variability in the system and tend to produce a hybrid composition. Perugini et al. (2015) proposed that the concentration variance normalized to that of the starting endmembers () of elemental concentrations in the mixing melts is reduced with time, following an exponential decay function with a decay parameter R that depends, among other parameters, on the diffusion rate of the element considered. In consequence, in systems where magma mixing is the primary process controlling compositional variability, can be used as a measure of the chemical hybridization of the system.
Here we use the compositions of groundmass glass in three crystal-bearing (<30 % crystals) banded pumice clasts from the El Abrigo ignimbrite, Tenerife (González-García et al., 2022), to obtain the values of for Si, Ti, Al, Fe, Mg, Na, and K. Concentration variance was normalized using the compositions of the two endmember melts proposed by González-García et al. (2022), i.e. a phonotephrite represented by the most mafic glass in banded pumices and a high-Zr phonolite from aphyric white pumices. The obtained values were later compared to diffusivities obtained in run DCB-11 (1200 °C, 2.93 wt % H2O). The choice of this experiment for comparison is based on the availability of Na diffusivities and on its high H2O content, close to that expected for the phonolitic melt of the El Abrigo ignimbrite, but analogous results are obtained using any other experiment. However, we should note that experimental temperatures are still 150–200 °C higher than expected for the natural system.
The results (Fig. 8) show a visible correlation between diffusion coefficients and , with slow-diffusing elements showing a lesser homogenization degree than fast-diffusing elements (particularly Na). However, Al and K outliers are present in this trend. The Pearson correlation coefficients for the three products range between 0.21 and 0.45 (in absolute value), but when the Al and K outliers are removed, the correlation improves to 0.84–0.88. These data confirm that the main control of melt chemistry in the banded pumices is the diffusive exchange between endmembers. However, the presence of Al and K outliers is an anomaly in this context and might provide additional insight into the issue of Al diffusivity. Figure 8 shows that the value of Al in the mixed-eruption products does not correlate with the fast Al diffusivity measured in our experiments but instead suggests a slow diffusion mechanism in the natural system. In one of the banded pumices, K follows similar behaviour, with one of the values higher than expected from its measured diffusivity. The experimental results from this work and from Perugini et al. (2013), where high Al mobility was observed, were carried out at temperatures between 1150 and 1300 °C. In contrast, mixing temperatures in the El Abrigo system were significantly lower, likely in the range of 900–1050 °C (González-García et al., 2022) and with the presence of significant proportions of crystals. Experimental studies in simplified Ca- and Na-aluminosilicate glasses have shown that the coordination number of Al3+ is temperature dependent, with lower temperatures favouring 4-fold coordinated Al (IVAl) over 5-fold coordinated Al (VAl; Stebbins et al., 2008; Le Losq et al., 2014). In such aluminosilicate systems, it has been suggested that the formation of VAl results in a reduction in melt viscosity (e.g. Kim et al., 2022) and likely Al-alkali clustering, while the opposite is true for IVAl-dominated melts. We speculate that a variation in the coordination number of Al towards a predominance of IVAl at lower temperatures, like that estimated for the natural system, could potentially result in additional viscosity increase and/or decreased Al-alkali clustering, favouring a comparatively slower Al diffusion compared to at higher temperatures.
Alternatively, the reasons for this behaviour could reside in crystal dissolution and assimilation processes in the natural products. The banded pumices in the El Abrigo deposit are mostly rich in crystals, with two coexisting mineral assemblages in disequilibrium. The partial melting and assimilation of enough quantities of alkali feldspar, as documented in several ignimbrites in the DHF, could potentially result in local Al–K inhomogeneities, which increase their concentration variance relative to a mixing-only scenario. However, our current dataset does not allow us to distinguish between these two possible scenarios, and more experimental data at lower temperatures would be necessary to confirm the occurrence of varying diffusive mechanisms for Al.
Diffusion coefficients of major elements have been obtained from tephrite–phonolite couples with compositions relevant to Canary Islands magmatism. Diffusivities show a wide variation range, with Na and Al being significantly faster (ca. 0.5 and 1 log unit, respectively) than Si. All log D values for an intermediate composition (55 wt % SiO2) have a strongly non-linear relationship with dissolved H2O, which is best captured by an exponential expression. In addition, an apparent convergence of diffusivities is evident towards the water-rich end (3 wt %) of our dataset, which suggests that the addition of H2O could increase magma mixing efficiency by equalizing diffusivities of major elements. Arrhenius equations obtained at 1.66 wt % and 2.99 wt % are also convergent with increasing temperature, and Ea values decrease with H2O content. The anomalous behaviour of Al, which is second in diffusivity only after Na, may be explained by a change in behaviour from network-forming to network-modifying cations by complexation with Na+ and K+ cations. Such behaviour may be a common occurrence in highly alkaline melts. This result suggests the occurrence of a fast diffusion mechanism for Al in our experimental dataset, different from that observed in the literature for sub-alkaline and mildly alkaline melts.
Our results may have important implications for the study of kinetic processes in highly alkaline magmas and particularly for melt hybridization during magma mixing events. The comparison of our experimental results with the chemical distribution in mixed pyroclasts from the El Abrigo ignimbrite confirms that diffusion is the main mechanism controlling the chemical variability in the melt phase. However, the natural Al distribution does not support the fast Al diffusion mechanism observed in the experiment. We suggest that at the low temperatures inferred for the mixing event (900–1050 ° C), Al does not show the fast diffusivities observed in experiments, possibly due to a change in Al coordination and hence a variation in its coupling to Na+ and K+. Alternatively, this could be an effect of the melting and assimilation of a K-feldspar rich mush, which is documented from the El Abrigo eruption.
All data underlying this paper are shown as figures or tables in the paper or are available in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/ejm-36-623-2024-supplement.
DGG had the original idea for the study. DGG, FP, FM, and SK performed the experiments. DGG carried out analyses and data processing. RA supported EPMA analyses. DGG prepared the initial manuscript and figures, and all authors significantly contributed to data interpretation and paper editing.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This article is part of the special issue “Probing the Earth: experiments on and for our planet”. It is a result of the EMPG 2023 conference, Milan, Italy, 12–15 June 2023.
This research was funded by a Humboldt Postdoctoral Fellowship from the Alexander von Humboldt Foundation to Diego González-García. Phillipp Beckmann and Philip Wiegel are acknowledged for assistance during the experimental run performance and EPMA analysis, respectively, and Julian Hübner for assistance with Fe determination in experimental glasses. Felix Marxer, Florian Pohl, François Holtz, and Renat Almeev were supported by the DFG Research Unit 2881 (Diffusion Chronometry). Harald Behrens and Sumit Chakraborty are acknowledged for assistance with data interpretation and comments on an early version of this paper. The original manuscript was significantly improved by thorough reviews from Charles Le Losq and Gianluca Iezzi.
This research has been supported by the Alexander von Humboldt Stiftung (Alexander von Humboldt Postdoctoral Fellowship) and the Deutsche Forschungsgemeinschaft, Research Unit 2881 (Diffusion Chronometry).
The publication of this article was funded by the open-access fund of Leibniz Universität Hannover.
This paper was edited by Simone Tumiati and reviewed by Le Losq Charles and Gianluca Iezzi.
Ablay, G. J., Carroll, M. R., Palmer, M. R., Marti, J., and Sparks, R. S. J.: Basanite–Phonolite Lineages of the Teide–Pico Viejo Volcanic Complex, Tenerife, Canary Islands, J. Petrol., 39, 905–936, 1998.
Andújar, J. and Scaillet, B.: Experimental Constraints on Parameters Controlling the Difference in the Eruptive Dynamics of Phonolitic Magmas: the Case of Tenerife (Canary Islands), J. Petrol., 53, 1777–1806, https://doi.org/10.1093/petrology/egs033, 2012.
Andújar, J., Costa, F., Martí, J., Wolff, J. A., and Carroll, M. R.: Experimental constraints on pre-eruptive conditions of phonolitic magma from the caldera-forming El Abrigo eruption, Tenerife (Canary Islands), Chem. Geol., 257, 173–191, https://doi.org/10.1016/j.chemgeo.2008.08.012, 2008.
Andújar, J., Costa, F., and Martí, J.: Magma storage conditions of the last eruption of Teide volcano (Canary Islands, Spain), B. Volcanol., 72, 381–395, https://doi.org/10.1007/s00445-009-0325-3, 2010.
Baker, D. R.: Tracer versus trace element diffusion: Diffusional decoupling of Sr concentration from Sr isotope composition, Geochim. Cosmochim. Ac., 53, 3015–3023, https://doi.org/10.1016/0016-7037(89)90177-4, 1989.
Baker, D. R.: Interdiffusion of hydrous dacitic and rhyolitic melts and the efficacy of rhyolite contamination of dacitic enclaves, Contrib. Mineral. Petr., 106, 462–473, https://doi.org/10.1007/BF00321988, 1991.
Baker, D. R. and Bossányi, H.: The combined effect of F and H2O on interdiffusion between peraikaline dacitic and rhyolitic melts, Contrib. Mineral. Petr., 117, 203–214, 1994.
Baker, D. R., Conte, A., Freda, C., and Ottolini, L.: The effect of halogens on Zr diffusion and zircon dissolution in hydrous metaluminous granitic melts, Contrib. Mineral. Petr., 142, 666–678, https://doi.org/10.1007/s00410-001-0328-3, 2002.
Behrens, H.: Determination of water solubilities in high-viscosity melts: An experimental study on NaAlSi3O8 and KAlSi3O8 melts, Eur. J. Mineral., 7, 905–320, 1995.
Behrens, H. and Zhang, Y.: Ar diffusion in hydrous silicic melts: implications for volatile diffusion mechanisms and fractionation, Earth Planet. Sc. Lett., 192, 363–376, https://doi.org/10.1016/S0012-821X(01)00458-7, 2001.
Behrens, H., Romano, C., Nowak, M., Holtz, F., and Dingwell, D. B.: Near-infrared spectroscopic determination of water species in glasses of the system MAlSi3O8 (M = Li, Na, K): an interlaboratory study, Chem. Geol., 128, 41–63, https://doi.org/10.1016/0009-2541(95)00162-X, 1996.
Berndt, J., Liebske, C., Holtz, F., Freise, M., Nowak, M., Ziegenbein, D., Hurkuck, W., and Koepke, J.: A combined rapid-quench and H2-membrane setup for internally heated pressure vessels: Description and application for water solubility in basaltic melts, Am. Mineral., 87, 1717–1726, https://doi.org/10.2138/am-2002-11-1222, 2002.
Berthod, C., Médard, E., Di Muro, A., Hassen Ali, T., Gurioli, L., Chauvel, C., Komorowski, J.-C., Bachèlery, P., Peltier, A., Benbakkar, M., Devidal, J.-L., Besson, P., Le Friant, A., Deplus, C., Nowak, S., Thinon, I., Burckel, P., Hidalgo, S., Feuillet, N., Jorry, S., and Fouquet, Y.: Mantle xenolith-bearing phonolites and basanites feed the active volcanic ridge of Mayotte (Comoros archipelago, SW Indian Ocean), Contrib. Mineral. Petr., 176, 75, https://doi.org/10.1007/s00410-021-01833-1, 2021.
Botcharnikov, R. E., Almeev, R. R., Koepke, J., and Holtz, F.: Phase Relations and Liquid Lines of Descent in Hydrous Ferrobasalt–Implications for the Skaergaard Intrusion and Columbia River Flood Basalts, J. Petrol., 49, 1687–1727, https://doi.org/10.1093/petrology/egn043, 2008.
Bouhifd, M. A., Whittington, A. G., and Richet, P.: Densities and volumes of hydrous silicate melts: New measurements and predictions, Chem. Geol., 418, 40–50, https://doi.org/10.1016/j.chemgeo.2015.01.012, 20115.
Bryan, S. E., Martí, J., and Leosson, M.: Petrology and Geochemistry of the Bandas del Sur Formation, Las Cañadas Edifice, Tenerife (Canary Islands), J. Petrol., 43, 1815–1856, https://doi.org/10.1093/petrology/43.10.1815, 2002.
Carroll, M. R. and Blank, J. G.: The solubility of H2O in phonolitic melts, Am. Mineral., 82, 549–556, https://doi.org/10.2138/am-1997-5-615, 1997.
Chakraborty, S., Dingwell, D. B., and Rubie, D. C.: Multicomponent diffusion in ternary silicate melts in the system K2O-Al2O3-SiO2: I. Experimental measurements, Geochim. Cosmochim. Ac., 59, 255–264, https://doi.org/10.1016/0016-7037(94)00283-R, 1995a.
Chakraborty, S., Dingwell, D. B., and Rubie, D. C.: Multicomponent diffusion in ternary silicate melts in the system K2O-Al2O3-SiO2: II. Mechanisms, systematics, and geological applications, Geochim. Cosmochim. Ac., 59, 265–277, 1995b.
Chen, Y. and Zhang, Y.: Olivine dissolution in basaltic melt, Geochim. Cosmochim. Ac., 72, 4756–4777, https://doi.org/10.1016/j.gca.2008.07.014, 2008.
Chen, Y. and Zhang, Y.: Clinopyroxene dissolution in basaltic melt, Geochim. Cosmochim. Ac., 73, 5730–5747, https://doi.org/10.1016/j.gca.2009.06.016, 2009.
De Campos, C. P., Perugini, D., Ertel-Ingrisch, W., Dingwell, D. B., and Poli, G.: Enhancement of magma mixing efficiency by chaotic dynamics: an experimental study, Contrib. Mineral. Petr., 161, 863–881, do:10.1007/s00410-010-0569-0, 2011.
DeVitre, C. L., Gazel, E., Allison, C. M., Soto, G., Madrigal, P., Alvarado, G. E., and Lücke, O. H.: Multi-stage chaotic magma mixing at Turrialba volcano, J. Volcanol. Geoth. Res., 381, 330–346, https://doi.org/10.1016/j.jvolgeores.2019.06.011, 2019.
Dingwell, D. B., Romano, C., and Hess, K.-U.: The effect of water on the viscosity of a haplogranitic melt under P-T-X conditions relevant to silicic volcanism, Contrib. Miner. Petrol., 124, 19–28, https://doi.org/10.1007/s004100050170, 1996.
Dorado, O., Andújar, J., Martí, J., and Geyer, A.: Pre-eruptive conditions at satellite vent eruptions at Teide-Pico Viejo complex (Tenerife, Canary Islands), Lithos, 396–397, 106193, https://doi.org/10.1016/j.lithos.2021.106193, 2021.
Fanara, S., Sengupta, P., Becker, H.-W., Rogalla, D., and Chakraborty, S.: Diffusion across the glass transition in silicate melts: Systematic correlations, new experimental data for Sr and Ba in calcium-aluminosilicate glasses and general mechanisms of ionic transport, J. Non-Cryst. Solids, 455, 6–16, https://doi.org/10.1016/j.jnoncrysol.2016.10.013, 2017.
Fuchs, P.: Petrogenesis of basanite-phonolite series of an oceanic intraplate volcano: combining experimental data and field observations, PhD thesis, Leibniz Universität Hannover, 182 pp., https://doi.org/10.15488/8253, 2014.
Ghiorso, M. S. and Gualda, G. A. R.: An H2O–CO2 mixed fluid saturation model compatible with rhyolite-MELTS, Contrib. Miner. Petrol., 169, 53, https://doi.org/10.1007/s00410-015-1141-8, 2015.
Giordano, D. and Dingwell, D.: Viscosity of hydrous Etna basalt: implications for Plinian-style basaltic eruptions, B. Volcanol., 65, 8–14, https://doi.org/10.1007/s00445-002-0233-2, 2003.
Giordano, D., Russell, J. K., and Dingwell, D. B.: Viscosity of magmatic liquids: A model, Earth Planet. Sc. Lett., 271, 123–134, https://doi.org/10.1016/j.epsl.2008.03.038, 2008.
Glasstone, S., Laider, K. J., and Eyring, H.: The Theory of Rate Processes, McGraw-Hill, New York, ISBN 978-0070233607, 1941.
González-García, D., Behrens, H., Petrelli, M., Vetere, F., Morgavi, D., Zhang, C., and Perugini, D.: Water-enhanced interdiffusion of major elements between natural shoshonite and high-K rhyolite melts, Chem. Geol., 466, 86–101, https://doi.org/10.1016/j.chemgeo.2017.05.023, 2017.
González-Garcia, D., Petrelli, M., Behrens, H., Vetere, F., Fischer, L. A., Morgavi, D., and Perugini, D.: Diffusive exchange of trace elements between alkaline melts: Implications for element fractionation and timescale estimations during magma mixing, Geochim. Cosmochim. Ac., 233, 95–114, https://doi.org/10.1016/j.gca.2018.05.003, 2018.
González-García, D., Vetere, F., Behrens, H., Petrelli, M., Morgavi, D., and Perugini, D.: Interdiffusion of major elements at 1 atmosphere between natural shoshonitic and rhyolitic melts, Am. Mineral., 104, 1444–1454, https://doi.org/10.2138/am-2019-6997, 2019.
González-García, D., Petrelli, M., Perugini, D., Giordano, D., Vasseur, J., Paredes-Mariño, J., Marti, J., and Dingwell, D. B.: Pre-eruptive conditions and dynamics recorded in banded pumices from the El Abrigo caldera-forming eruption (Tenerife, Canary Islands), J. Petrol., 63, egac009, https://doi.org/10.1093/petrology/egac009, 2022.
González-García, D., Boulesteix, T., Klügel, A., and Holtz, F.: Bubble-enhanced basanite–tephrite mixing in the early stages of the Cumbre Vieja 2021 eruption, La Palma, Canary Islands, Sci. Rep., 13, 14839, https://doi.org/10.1038/s41598-023-41595-3, 2023.
Guo, C. and Zhang, Y.: Multicomponent diffusion in silicate melts: SiO2–TiO2–Al2O3–MgO–CaO–Na2O–K2O System, Geochim. Cosmochim. Ac., 195, 126–141, https://doi.org/10.1016/j.gca.2016.09.003, 2016.
Guo, C. and Zhang, Y.: Multicomponent diffusion in basaltic melts at 1350 ° C, Geochim. Cosmochim. Ac., 228, 190–204, https://doi.org/10.1016/j.gca.2018.02.043, 2018.
Hart, S. R.: Diffusion compensation in natural silicates, Geochim. Cosmochim. Ac., 45, 279–291, https://doi.org/10.1016/0016-7037(81)90239-8, 1981.
Helz, R. T., Clague, D. A., Mastin, L. G., and Rose, T. R.: Electron Microprobe analyses of glasses from Kilauea tephra units, Kilauea volcano, Hawaii, USGS, https://doi.org/10.3133/ofr20141090, 2014.
Jarosewich, E., Nelen, J. A., and Norberg, J. A.: Reference Samples for Electron Microprobe Analysis, Geostandard. Newslett., 4, 43–47, https://doi.org/10.1111/j.1751-908X.1980.tb00273.x, 1980.
Johansen, T. S., Hauff, F., Hoernle, K., Klügel, A., and Kokfelt, T. F.: Basanite to phonolite differentiation within 1550–1750 yr: U-Th-Ra isotopic evidence from the A.D. 1585 eruption on La Palma, Canary Islands, Geology, 33, 897, https://doi.org/10.1130/G21663.1, 2005.
Kim, K.-H., Sukenaga, S., Tashiro, M., Kanehashi, K., Yoshida, S., and Shibata, H.: Variation in viscosity of aluminosilicate melts with MgO/CaO molar ratio: Influence of five-fold coordinated aluminum, J. Non-Cryst. Solids, 587, 121600, https://doi.org/10.1016/j.jnoncrysol.2022.121600, 2022.
Klügel, A., Hoernle, K. A., Schmincke, H.-U., and White, J. D. L.: The chemically zoned 1949 eruption on La Palma (Canary Islands): Petrologic evolution and magma supply dynamics of a rift zone eruption, J. Geophys. Res., 105, 5997–6016, https://doi.org/10.1029/1999JB900334, 2000.
Klügel, A., Hansteen, T. H., and Galipp, K.: Magma storage and underplating beneath Cumbre Vieja volcano, La Palma (Canary Islands), Earth Planet. Sc. Lett., 236, 211–226, https://doi.org/10.1016/j.epsl.2005.04.006, 2005.
Klügel, A., Albers, E., and Hansteen, T. H.: Mantle and Crustal Xenoliths in a Tephriphonolite From La Palma (Canary Islands): Implications for Phonolite Formation at Oceanic Island Volcanoes, Front. Earth Sci., 10, 761902, https://doi.org/10.3389/feart.2022.761902, 2022.
Koepke, J. and Behrens, H.: Trace element diffusion in andesitic melts: an application of synchrotron X-ray fluorescence analysis, Geochim. Cosmochim. Ac., 65, 1481–1498, https://doi.org/10.1016/S0016-7037(01)00550-6, 2001.
Koyaguchi, T.: Chemical gradient at diffusive interfaces in magma chambers, Contrib. Miner. Petrol., 103, 143–152, https://doi.org/10.1007/BF00378500, 1989.
Le Losq, C., Neuville, D., Florian, P., Henderson, G., and Massiot, D.: The role of Al3+ on rheology and structural changes in sodium silicate and aluminosilicate glasses and melts, Geochim. Cosmochim. Ac., 126, 495–517, https://doi.org/10.1016/j.gca.2013.11.010, 2014.
Le Losq, C., Neuville, D. R., Chen, W., Florian, P., Massiot, D., Zhou, Z., and Greaves, G. N.: Percolation channels: a universal idea to describe the atomic structure and dynamics of glasses and melts, Sci. Rep., 7, 16490, https://doi.org/10.1038/s41598-017-16741-3, 2017.
Le Losq, C., Cicconi, M. R., and Neuville, D. R.: Iron in Silicate Glasses and Melts, in: Magma Redox Geochemistry, American Geophysical Union (AGU), 233–253, https://doi.org/10.1002/9781119473206.ch12, 2021a.
Le Losq, C., Valentine, A. P., Mysen, B. O., and Neuville, D. R.: Structure and properties of alkali aluminosilicate glasses and melts: Insights from deep learning, Geochim. Cosmochim. Ac., 314, 27–54, https://doi.org/10.1016/j.gca.2021.08.023, 2021b.
Lesne, P., Scaillet, B., Pichavant, M., Iacono-Marziano, G., and Beny, J.-M.: The H2O solubility of alkali basaltic melts: an experimental study, Contrib. Miner. Petrol., 162, 133–151, https://doi.org/10.1007/s00410-010-0588-x, 2011.
Liang, Y.: Multicomponent Diffusion in Molten Silicates: Theory, Experiments, and Geological Applications, Rev. Mineral. Geochem., 72, 409–446, https://doi.org/10.2138/rmg.2010.72.9, 2010.
Lundstrom, C. C.: An experimental investigation of the diffusive infiltration of alkalis into partially molten peridotite: Implications for mantle melting processes, Geochem. Geophy. Geosy., 4, 8614, https://doi.org/10.1029/2001GC000224, 2003.
Mangler, M. F., Humphreys, M. C. S., Geifman, E., Iveson, A. A., Wadsworth, F. B., Brooker, R. A., Lindoo, A., and Hammond, K.: Melt Diffusion-Moderated Crystal Growth and its Effect on Euhedral Crystal Shapes, J. Petrol., 64, egad054, https://doi.org/10.1093/petrology/egad054, 2023.
Martí, J., Zafrilla, S., Andújar, J., Jiménez-Mejías, M., Scaillet, B., Pedrazzi, D., Doronzo, D., and Scaillet, S.: Controls of magma chamber zonation on eruption dynamics and deposits stratigraphy: The case of El Palomar fallout succession (Tenerife, Canary Islands), J. Volcanol. Geoth. Res., 399, 106908, https://doi.org/10.1016/j.jvolgeores.2020.106908, 2020.
Marxer, F. and Ulmer, P.: Crystallisation and zircon saturation of calc-alkaline tonalite from the Adamello Batholith at upper crustal conditions: an experimental study, Contrib. Miner. Petrol., 174, 84, https://doi.org/10.1007/s00410-019-1619-x, 2019.
Moretti, R. and Ottonello, G.: Silicate Melt Thermochemistry and the Redox State of Magmas, Rev. Mineral. Geochem., 87, 339–403, https://doi.org/10.1515/9781501510939-009, 2022.
Morgavi, D., Perugini, D., De Campos, C. P., Ertl-Ingrisch, W., Lavallée, Y., Morgan, L., and Dingwell, D. B.: Interactions between rhyolitic and basaltic melts unraveled by chaotic mixing experiments, Chem. Geol., 346, 199–212, https://doi.org/10.1016/j.chemgeo.2012.10.003, 2013.
Mysen, B. O., Virgo, D., and Kushiro, I.: The structural role of aluminum in silicate melts–a Raman spectroscopic study at 1 atmosphere, Am. Mineral., 66, 678–701, 1981.
Nowak, M. and Behrens, H.: An experimental investigation on diffusion of water in haplogranitic melts, Contrib. Mineral. Petrol., 126, 365–376, https://doi.org/10.1007/s004100050256, 1997.
Oliphant, T. E.: Python for Scientific Computing, Comput. Sci. Eng., 9, 10–20, https://doi.org/10.1109/MCSE.2007.58, 2007.
Pankhurst, M. J., Scarrow, J. H., Barbee, O. A., Hickey, J., Coldwell, B. C., Rollinson, G. K., Rodríguez-Losada, J. A., Lorenzo, A. M., Rodríguez, F., Hernández, W., Fernández, D. C., Hernández, P. A., and Pérez, N. M.: Rapid response petrology for the opening eruptive phase of the 2021 Cumbre Vieja eruption, La Palma, Canary Islands, Volcanica, 5, 1–10, https://doi.org/10.30909/vol.05.01.0110, 2022.
Perugini, D., Poli, G., Petrelli, M., De Campos, C. P., and Dingwell, D. B.: Time-scales of recent Phlegrean Fields eruptions inferred from the application of a “diffusive fractionation” model of trace elements, B. Volcanol., 72, 431–447, https://doi.org/10.1007/s00445-009-0329-z, 2010.
Perugini, D., De Campos, C. P., Dingwell, D. B., and Dorfman, A.: Relaxation of concentration variance: A new tool to measure chemical element mobility during mixing of magmas, Chem. Geol., 335, 8–23, https://doi.org/10.1016/j.chemgeo.2012.10.050, 2013.
Perugini, D., De Campos, C. P., Petrelli, M., and Dingwell, D. B.: Concentration variance decay during magma mixing: a volcanic chronometer, Sci. Rep., 5, 14225, https://doi.org/10.1038/srep14225, 2015.
Romano, C., Giordano, D., Papale, P., Mincione, V., Dingwell, D. B., and Rosi, M.: The dry and hydrous viscosities of alkaline melts from Vesuvius and Phlegrean Fields, Chem. Geol., 202, 23–38, https://doi.org/10.1016/S0009-2541(03)00208-0, 2003.
Sauer, F. and Freise, V.: Diffusion in binären Gemischen mit Volumenänderung, Z. Elektrochem., 66, 353–362, 1962.
Schuessler, J. A., Botcharnikov, R. E., Behrens, H., Misiti, V., and Freda, C.: Oxidation state of iron in hydrous phono-tephritic melts, Am. Mineral., 93, 1493–1504, https://doi.org/10.2138/am.2008.2795, 2008.
Shamloo, H. I. and Grunder, A. L.: Magma mingling and ascent in the minutes to hours before an explosive eruption as recorded by banded pumice, Geology, 51, 957–961, https://doi.org/10.1130/G51318.1, 2023.
Sliwinski, J. T., Bachmann, O., Ellis, B. S., Dávila-Harris, P., Nelson, B. K., and Dufek, J.: Eruption of Shallow Crystal Cumulates during Explosive Phonolitic Eruptions on Tenerife, Canary Islands, J. Petrol., 56, 2173–2194, https://doi.org/10.1093/petrology/egv068, 2015.
Spallanzani, R., Koga, K. T., Cichy, S. B., Wiedenbeck, M., Schmidt, B. C., Oelze, M., and Wilke, M.: Lithium and boron diffusivity and isotopic fractionation in hydrated rhyolitic melts, Contrib. Miner. Petrol., 177, 74, https://doi.org/10.1007/s00410-022-01937-2, 2022.
Stebbins, J. F., Dubinsky, E. V., Kanehashi, K., and Kelsey, K. E.: Temperature effects on non-bridging oxygen and aluminum coordination number in calcium aluminosilicate glasses and melts, Geochim. Cosmochim. Ac., 72, 910–925, https://doi.org/10.1016/j.gca.2007.11.018, 2008.
Stolper, E.: Water in silicate glasses: An infrared spectroscopic study, Contrib. Miner. Petrol., 81, 1–17, https://doi.org/10.1007/BF00371154, 1982.
Taylor, J. R., Wall, V. J., and Pownceby, M. I.: The calibration and application of accurate redox sensors, Am. Mineral., 77, 284–295, 1992.
Tomlinson, E. L., Smith, V. C., and Menzies, M. A.: Chemical zoning and open system processes in the Laacher See magmatic system, Contrib. Miner. Petrol., 175, 19, https://doi.org/10.1007/s00410-020-1657-4, 2020.
Vetere, F., Botcharnikov, R. E., Holtz, F., Behrens, H., and De Rosa, R.: Solubility of H2O and CO2 in shoshonitic melts at 1250 °C and pressures from 50 to 400 MPa: Implications for Campi Flegrei magmatic systems, J. Volcanol. Geoth. Res., 202, 251–261, https://doi.org/10.1016/j.jvolgeores.2011.03.002, 2011.
Watson, E. B.: Diffusion in magmas at depth in the Earth: The effects of pressure and dissolved H2O, Earth Planet. Sc. Lett., 52, 291–301, https://doi.org/10.1016/0012-821X(81)90184-9, 1981.
Watson, E. B.: Diffusion in Volatile-bearing Magmas, Rev. Mineral. Geochem., 30, 371-411, https://doi.org/10.1515/9781501509674-016, 1994.
Wolff, J. A.: Zonation, mixing and eruption of silica-undersaturated alkaline magma: a case study from Tenerife, Canary Islands, Geol. Mag., 122, 623–640, https://doi.org/10.1017/S0016756800032039, 1985.
Zhang, Y. and Behrens, H.: H2O diffusion in rhyolitic melts and glasses, Chem. Geol., 169, 243–262, https://doi.org/10.1016/S0009-2541(99)00231-4, 2000.
Zhang, Y. and Gan, T.: Diffusion in Melts and Magmas, Rev. Mineral. Geochem., 87, 283–337, https://doi.org/10.2138/rmg.2022.87.07, 2022.
Zhang, Y., Walker, D., and Lesher, C. E.: Diffusive crystal dissolution, Contr. Miner. Petrol., 102, 492–513, https://doi.org/10.1007/BF00371090, 1989.
Zhang, Y., Ni, H., and Chen, Y.: Diffusion Data in Silicate Melts, Rev. Mineral. Geochem., 72, 311–408, https://doi.org/10.2138/rmg.2010.72.8, 2010.