Compressibility and thermal expansion of magnesium phosphates

The ambient-temperature compressibility and room-pressure thermal expansion of two Mg₃(PO₄)₂ polymorphs (farringtonite = Mg₃(PO₄)₂-I, with 5- and 6-fold coordinated Mg, and chopinite = “Mg-sarcopside” = ^[6]Mg₃(PO₄)₂-II), three Mg₂PO₄OH polymorphs (althausite, hydroxylwagnerite and ε-Mg₂PO₄OH, all with ^[5]Mg and ^[6]Mg) and phosphoellenbergerite (^[6]Mg) were measured on synthetic powders using a synchrotron-based multi-anvil apparatus to 5.5 GPa and a laboratory high-temperature diffractometer, with whole-pattern fitting procedures. Bulk moduli range from 64.5 GPa for althausite to 88.4 GPa for hydroxylwagnerite, the high-pressure Mg₂PO₄OH polymorph. Chopinite, based on an olivine structure with ordered octahedral vacancies (K₀ = 81.6 GPa), and phosphoellenbergerite, composed of chains of face-sharing octahedra (K₀ = 86.4 GPa), are distinctly more compressible than their homeotypical silicate (127 and 133 GPa, respectively). The compressibility anisotropy is the highest for chopinite and the lowest for phosphoellenbergerite. First-order parameters of quadratic thermal expansions range from v₁ = $\mathrm{2.19}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ for ε-Mg₂PO₄OH to v₁ = $\mathrm{3.58}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ for althausite. Phosphates have higher thermal-expansion coefficients than the homeotypical silicates. Thermal anisotropy is the highest for farringtonite and the lowest for hydroxylwagnerite and chopinite. These results set the stage for a thermodynamic handling of phase-equilibrium data obtained up to 3 GPa and 1000 °C in the MgO–P₂O₅–H₂O and MgO–Al₂O₃–P₂O₅–H₂O systems.

1 Introduction

Magnesium phosphates may be of industrial interest – as binder in refractories and mortars, as rapid-setting cements, in 3D printing, and in the fertiliser industry – but are also of medical interest as a constituent of human urinary stones (e.g. Fang et al., 2022; Haque and Chen, 2019; Song and Li, 2021; Maurice-Estepa et al., 1999). As rock-forming minerals, although less common than other phosphates like apatite or monazite, Mg-phosphates play an important role in late-stage metasomatic processes around alkaline intrusive rocks (as shown by spectacular veins of bobierrite, Mg₃(PO₄)₂ ⋅ 8H₂O, and kovdorskite, Mg₂PO₄OH ⋅ 3H₂O, on the Kola Peninsula, e.g. Liferovich et al., 2000); they are also potential petrological indicators in metamorphic rocks owing to their numerous polymorphic relations.

Indeed, early synthesis work has revealed five polymorphs of Mg₂PO₄OH (labelled α to ε; Raade, 1990) and three polymorphs of Mg₃(PO₄)₂ (I to III, Nord and Kierkegaard, 1968; Berthet et al., 1972; and Jaulmes et al., 1997, respectively). Experimental phase-equilibrium studies (Brunet and Vielzeuf, 1996; Brunet et al., 1998; Leyx et al., 2002; Leyx, 2004) have explored the relations of the Mg₃(PO₄)₂ polymorphs with four of the Mg₂PO₄OH polymorphs and the mineral phosphoellenbergerite, ideally Mg₁₄(PO₄)₆(HPO₄)₂(OH)₆. The Mg₃(PO₄)₂ polymorphs include a low-pressure one (I), the mineral farringtonite found in meteorites, and two high-pressure forms: (II), the Mg analogue of the pegmatite mineral sarcopside, referred to as “Mg-sarcopside” until it was discovered in nature as the mineral chopinite (Grew et al., 2007), and (III), the synthetic high-pressure and high-temperature polymorph (Jaulmes et al., 1997). The phase transitions and the high-temperature behaviour of these three polymorphs were studied using synchrotron radiation and Raman spectroscopy (Hu et al., 2022). The polymorphs of Mg₂PO₄OH include the low-pressure and high-temperature form ε-Mg₂PO₄OH; the intermediate-pressure minerals holtedahlite (γ) and althausite (δ); and hydroxylwagnerite (β), the hydroxyl analogue of wagnerite Mg₂PO₄F. Hydroxylwagnerite and phosphoellenbergerite turned out to be high-pressure phases, actually encountered in ultrahigh-pressure metamorphic rocks (Chopin et al., 2014; Brunet et al., 1998).

The dearth of thermodynamic data even in a simple system like MgO–P₂O₅–H₂O made the extraction of thermodynamic properties (entropy, enthalpy of formation) from the phase-equilibrium data an obvious target, this all the more after calorimetric work on ε-Mg₂PO₄OH (Leyx et al., 2005) and lazulite, MgAl₂(PO₄)₂(OH)₂ (Brunet et al., 2004). Given the broad pressure–temperature (P–T) range of the phase-equilibrium experiments, performed at up to 3 GPa and 1000 °C, knowledge of compressibility and thermal expansion for the relevant phases was a requirement for the thermodynamic analysis of the experimental results. However, volume-property data for magnesium aluminium phosphate minerals are scanty: the few minerals concerned were berlinite, the AlPO₄ analogue of quartz (Troccaz et al., 1967; Sowa et al., 1990); farringtonite, Mg₃(PO₄)₂-I (Schmid-Beurmann et al., 2007); and chopinite, Mg₃(PO₄)₂-II (Hu et al., 2022). On such a narrow and structurally peculiar basis, it proved hazardous to assume average compressibility and thermal-expansion values for magnesium phosphates – or for given structural groups of phosphates, as tentatively done for silicates by Holland and Powell (1985) in their early thermodynamic database. Indeed, although they all are orthophosphates, the relevant Mg-phosphates show a variety of structural types (Table 1): from the relatively open structures of farringtonite and ε-Mg₂PO₄OH with 5- and 6-fold coordinated Mg and packing efficiencies near 19–20 ų per oxygen to more densely packed phases (near 18 ų per oxygen) like althausite and hydroxylwagnerite with again 5- and 6-fold coordinated Mg to compact structures (≤18 ų per oxygen) like chopinite with Mg in edge-sharing octahedra and phosphoellenbergerite with Mg in face-sharing octahedra.

Table 1 Crystallographic properties of synthetic Mg-phosphates.

The unknown behaviour of this structural variety was the incentive for the present study, which reports room-temperature compressibility measurements and room-pressure thermal-expansion data obtained on powders of synthetic farringtonite, chopinite, althausite, hydroxylwagnerite (referred to as OH-wagnerite in the following), ε-Mg₂PO₄OH and phosphoellenbergerite (P-ellenbergerite in the following).

2 Experimental techniques

2.1 Sample synthesis and characterisation

Farringtonite (= Mg₃(PO₄)₂-I), chopinite (= “Mg-sarcopside” = Mg₃(PO₄)₂-II), ε-Mg₂PO₄OH, althausite, OH-wagnerite and P-ellenbergerite were synthesised from stoichiometric mixtures of MgO (Alfa Aesar, 99.95 %, fired at 1300 °C before weighing) added to NH₄H₂PO₄ (Sigma-Aldrich, 99.999 %), reacted with water and heated at 600 °C for 2 h (see Brunet et al., 1998). The mixtures were enclosed, with 10 wt % deionised water for hydroxy-Mg-phosphate synthesis and only water traces for anhydrous Mg-phosphate synthesis, in gold capsules of 3 or 4 mm outer diameter, sealed by arc welding.

Farringtonite and ε-Mg₂PO₄OH were synthesised in externally heated Tuttle-type cold-seal pressure vessels (2 d at 550 MPa, 1000 °C, and 2 months at 60 MPa, 620 °C, respectively); the other higher-pressure phases were synthesised in a piston-cylinder apparatus, using a low-friction $\mathrm{1}/\mathrm{2}$ in. (1.27 cm) diameter NaCl assembly (2 d at 2.2 GPa, 800 °C, for chopinite; at 1.2 GPa, 850 °C, for althausite; at 2.5 GPa, 850 °C, for OH-wagnerite; and at 2 GPa, 750 °C, for P-ellenbergerite).

Synthetic products were characterised by X-ray diffraction (cf. Sect. 2.3, “High-temperature X-ray diffraction”). All the samples were single-phase except the chopinite sample that contained traces of OH-wagnerite in spite of repeated synthesis attempts. Upon heating, the althausite batch used for thermal-expansion measurements also revealed traces of OH-wagnerite which had not been detected before.

2.2 High-pressure X-ray diffraction

In situ high-pressure X-ray diffraction experiments were carried out using a cubic multi-anvil high-pressure apparatus of the Max-80 type, installed at the DORIS III storage ring of HASYLAB (DESY, Hamburg, Germany). Pressure was generated quasi-isostatically by six tungsten-carbide anvils with 6 mm × 6 mm truncation in a cubic arrangement. Details of the apparatus were given by Peun et al. (1995).

The diffraction measurements were performed in energy-dispersive mode using a white synchrotron beam of 100 µm × 100 µm dimension at a fixed 2θ angle, determined for each run under ambient conditions from the diffraction patterns of NaCl obtained at the top, in the middle and at the bottom of the assembly. A radioactive ²⁴¹Am source provided X-ray fluorescence Kα and Kβ lines from Rb, Mo, Ag, Ba and Tb targets for energy calibration of the Ge solid-state detector.

The sample assembly and the experimental technique were similar to that of Grevel et al. (2000a). The cell assembly contained two powdered samples sandwiched by pellets of NaCl or of a NaCl–BN mixture; each sample was mixed with vaseline. Grevel et al. (2000b) have shown that this procedure results in hydrostatic high-pressure conditions. The pressure was measured in the middle and at the ends of the cell using the NaCl or NaCl–BN pellets as calibrants (Decker, 1971). Pressure gradients (due to internal stress) were found to reach 0.1 to 0.2 GPa within the cell and are therefore the major source of pressure uncertainty (Table 2), as compared to those introduced by the refinement of NaCl cell volume (around 10⁻³ GPa) and by the determination of the 2θ angle (10⁻² to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ GPa).

Table 2 Unit-cell parameters of studied Mg-phosphates as a function of pressure at ambient temperature.

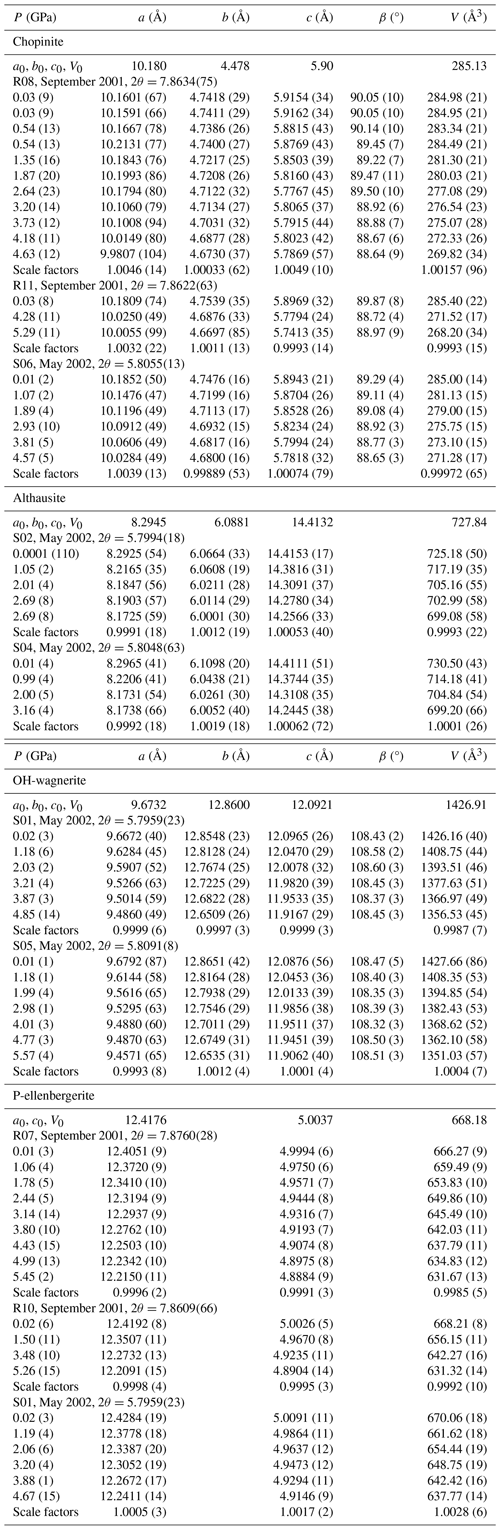
Note: values in brackets are 1σ for cell parameters and refer to the last decimal place. The terms a₀, b₀, c₀ and V₀ denote the mean values for the lattice parameters and unit-cell volume under the lowest pressure of the different measurement runs of each compound. The scale factors resulted from the fit using the Birch–Murnaghan equation of state (EoS) of second order in EosFit7c 7.6.

The externally applied load was increased in most experiments by steps of 10 up to 80 t, which corresponds to sample pressures of 5–5.5 GPa. Diffraction measurements were performed after each loading increment, after a waiting time of at least 10 min which had enabled the sample pressure to reach a steady state. The first, “zero-load” measurement was made after the anvils were brought into contact with the cell, as indicated by an incipient rise of the load value, which was then left to relax. Depending on the extent of this relaxation, the zero-load pressure value measured in situ may depart more or less from the actual room pressure.

Several experimental runs under isothermal conditions at ambient temperature (Table 2) were carried out for each studied mineral (chopinite, althausite, OH-wagnerite and P-ellenbergerite) to check the reproducibility and the consistency of the measurements made over two campaigns (September 2001 and May 2002, R and S run series in Table 2, respectively).

2.3 High-temperature X-ray diffraction

High-temperature diffraction data were collected on a 17 cm vertical Philips PW1050/25 goniometer in angle-dispersive mode, using Ni-filtered CuKα radiation, at the Laboratoire de Cristallochimie du Solide (Université Pierre-et-Marie-Curie, Paris, France), employing a platinum-alloy plate as the heating sample holder. Samples were ground, mixed with a little xylene, spread on the Pt plate to form a thin continuous film and then briefly heated to around 100 °C, at which temperature the xylene evaporates, leaving a thin smooth powder. The heating device and attached thermocouple used during data collection were calibrated in situ by bracketing various structural phase transitions (KNO₃ (α→β), 139 °C; BaCO₃ (γ→β), 811 °C) and melting reactions (KNO₃, 337 °C; KCl, 776 °C; NaCl, 801 °C). Nominal temperatures were corrected using the calibration; the corrected temperatures reported below are believed accurate to within 1 % above 200 °C, within 2 °C below.

The diffraction patterns were recorded over the $\mathrm{20}\mathit{°}<\mathrm{2}\mathit{\theta }<\mathrm{86}\mathit{°}$ range. Four scans were obtained at each temperature and merged, five at room temperature so as to improve the counting statistics for the standard-volume determination. Alloy peaks were not taken into account during the refinement by ignoring some 2θ intervals ([39, 41], [45.5, 47.5], [67, 69.5] and [80.5, 83] at room temperature). The data were collected up to 900 °C for anhydrous phases and up to 400, 500 or 600 °C for hydrous phases, before or until incipient dehydration.

2.4 Whole-pattern refinements

The lattice parameters of the samples were determined by the Rietveld method. Two different programs were run to refine the crystallographic and instrumental parameters: GSAS (Larson and Von Dreele, 1988) for the high-pressure diffraction patterns obtained by energy-dispersive methods (Sect. 2.2) and the DBW program of Young et al. (1995) for the high-temperature diffraction patterns, obtained in angle-dispersive mode (Sect. 2.3).

Available literature data were used as input values for cell parameters (Table 1) and atomic positions; the latter were kept constant throughout the refinement procedure. The refined data set included the cell parameters, the overall scale factor, a profile shape factor, coefficients of the FWHM (full width at half maximum) Caglioti's polynomial and background parameters. Given the number of atoms in the unit cells and the quality of our diffraction patterns, we did not refine the isotropic displacement parameters independently but refined a common B_iso variable for all the oxygen atoms and another variable for the cations. The March–Dollase preferred-orientation factor was also refined for chopinite, ε-Mg₂PO₄OH, and althausite, which showed strong orientation effects. When the samples were multi-phase (i.e. with traces of a parasite compound), the cell parameters, the scale factors, the profile shape factors and the FWHM polynomial coefficients of both phases were refined simultaneously.

For the high-pressure experiments, the NaCl cell parameter was refined from the whole diffraction pattern for each pressure condition and served as the input value to determine pressure from Decker's equation of state (EoS) (Decker, 1971).

For the high-temperature experiments, carried out on a Bragg–Brentano diffractometer, a potential offset of the 2θ zero point had to be considered. We first measured diffraction patterns on the pure compounds and, following Launay et al. (2001), refined the instrumental zero shift simultaneously with the crystal parameters. The results at room temperature were then compared with those obtained under the same conditions with the same compounds mixed with α-Al₂O₃ as internal standard. Refinements indicated that the differences in the lattice parameters were negligible (e.g. P-ellenbergerite with α-Al₂O₃: a=12.426(5) Å, c=5.009(2) Å; P-ellenbergerite without α-Al₂O₃: a=12.426(9), c=5.008(4) Å). Therefore, we chose to go on performing the measurements without internal standard, refining the 2θ-zero shift at room temperature (e.g. P-ellenbergerite: zero shift = −0.185(9)°2θ) and keeping this value of the shift for the high-temperature refinements. The sample displacement (due to holder expansion) was then refined at each temperature step and showed a smooth variation with increasing temperature (e.g. from 0.126 at 101 °C to 0.135 at 405 °C for P-ellenbergerite).

3 Results and discussion

3.1 Compressibility data

The experimental high-pressure data are presented in Figs. 1 to 3. The unit-cell parameters contained in Table 2 were used to determine the room-temperature compressibility of chopinite, althausite, OH-wagnerite and P-ellenbergerite. The strong orientation effects along the (001) perfect cleavage of althausite, combined with the small number of peaks in its diffraction patterns, prevented us from refining the althausite cell parameters for pressures higher than 3.2 GPa.

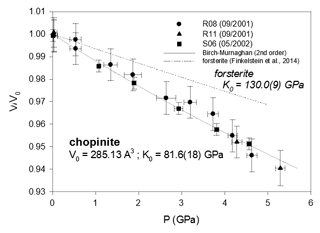
Figure 1 Compressibility data of synthetic chopinite (= Mg₃(PO₄)₂-II = “Mg-sarcopside”), compared to the homeotypical forsterite. Error bars are from Table 2.

Figure 2 Compressibility data of Mg₂PO₄OH polymorphs. Error bars are from Table 2.

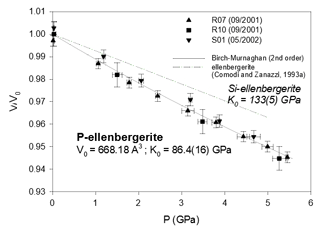
Figure 3 Compressibility data of synthetic phosphoellenbergerite, compared to the homeotypical silicate. Error bars are from Table 2.

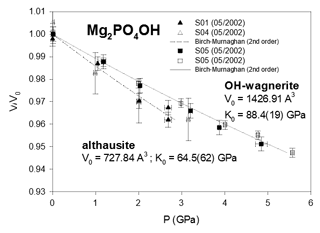
We did not merge the several data sets into a single one for each phase because the measured volumes at room pressure (and temperature) differ by one or more cubic ångströms, e.g. by 4 ų in the case of P-ellenbergerite (Table 2). This indicates that the P–V data of different runs have their own systematic error. This would bias the results if a common V₀ were fitted to a combined data set. Therefore we chose to use EosFit7c (Angel et al., 2014) version 7.6, which allows one to apply individual “scale factors” to the data set of each measurement run in combination with a fixed V₀. The latter was calculated as the mean value of the measured volume data of the individual runs at room pressure and temperature. Such a procedure is equivalent to a fit with individual V₀ values of each data set. The volume data were weighted according to the “effective variance method” (Orear, 1982) proposed by Angel (2000): $w={\mathit{\sigma }}^{-\mathrm{2}}$, where ${\mathit{\sigma }}^{\mathrm{2}}={\mathit{\sigma }}_P^{\mathrm{2}}+{\mathit{\sigma }}_V^{\mathrm{2}}\cdot \left[\right(\partial P/\partial V{)}_T{]}^{\mathrm{2}}$.

A Birch–Murnaghan equation of state truncated at second-order in the energy ($K_{\mathrm{0}}^{\prime }$ set to 4; Angel, 2000) was fitted to the volume data by means of a weighted least-squares regression: $P=\mathrm{3}/\mathrm{2}{K}_{\mathrm{0}}$ [$(V_{\mathrm{0}}/V{)}^{\mathrm{7}/\mathrm{3}}-(V_{\mathrm{0}}/V{)}^{\mathrm{5}/\mathrm{3}}$], where V is the unit-cell volume at high pressure P (in GPa), V₀ the volume at ambient pressure and K₀ the bulk modulus. The data scatter and the need to merge data from different experiments and refine scale factors made it impossible to reliably refine a third-order Birch–Murnaghan EoS. For instance, application of a third-order instead of a second-order EoS to the chopinite data results in a slightly lower w-χ² of 2.67 instead of 2.78 but in an unrealistic negative value for $K^{\prime }=-\mathrm{0.6}\left(\mathrm{2}\right)$. For the other compounds, the w-χ² was increased or unchanged using a third-order EoS (althausite and P-ellenbergerite) and the uncertainty in the bulk modulus K₀ was dramatically increased (althausite, OH-wagnerite and P-ellenbergerite). Therefore we decided to use a second-order Birch–Murnaghan EoS for the fits.

Table 3 Parameters of Berman thermal-expansion and compressibility functions, bulk moduli, and packing efficiencies for studied Mg-phosphates and their silicate equivalents (in italics).

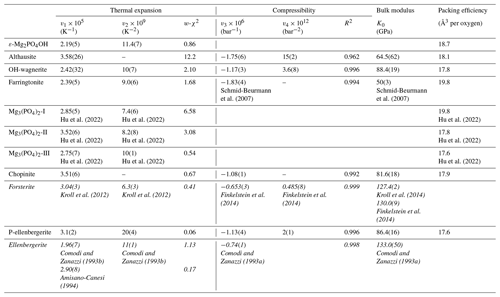
Note: the thermal-expansion parameters v₁ and v₂ and the compressibility parameters v₃ and v₄ of this work and the mentioned literature were calculated using a Berman-type second-order polynomial (Brown et al., 1989; Berman, 1988) $V\left(T\right)=V_{\mathrm{0}}(\mathrm{1}+v_{\mathrm{1}}(T-T_{\mathrm{0}})+v_{\mathrm{2}}(T-T_{\mathrm{0}}{)}^{\mathrm{2}}+v_{\mathrm{3}}(P-P_{\mathrm{0}})+v_{\mathrm{4}}(P-P_{\mathrm{0}}{)}^{\mathrm{2}})$. The v₁ and v₂ values were retrieved from a fit using the function $V\left(T\right)=V_{\mathrm{0}}(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{0}}(T-T_{\mathrm{0}})+\mathrm{1}/\mathrm{2}{\mathit{\alpha }}_{\mathrm{1}}(T-T_{\mathrm{0}}{)}^{\mathrm{2}})$ implemented in EoSFit7c, where v₁=α₀ and $v_{\mathrm{2}}=\mathrm{1}/\mathrm{2}{\mathit{\alpha }}_{\mathrm{1}}$. The v₃ and v₄ values were calculated from a fit of $V\left(T\right)=V_{\mathrm{0}}(\mathrm{1}+v_{\mathrm{3}}(P-P_{\mathrm{0}})+v_{\mathrm{4}}(P-P_{\mathrm{0}}{)}^{\mathrm{2}})$ using OriginPro 7.5. T₀ is the standard temperature (293.15 K), V₀ is the standard volume and P₀=1 bar. For forsterite, the thermal-expansion parameters v₁ and v₂ were derived from the data presented in Kroll et al. (2012, their Fig. 3) with the exception of the data of Bouhifd et al. (1996) >1200 K and the low-temperature data of Kroll et al. (2012). The bulk moduli were taken from the mentioned literature.

From the least-squares fit, the bulk moduli (Table 3) are found to range between 64.5(62) GPa (althausite) and 88.4(19) GPa (OH-wagnerite). They show the gross correlation that can be expected with the oxygen packing efficiency, the more compact structures being less compressible. Compared to other phosphate minerals, magnesium phosphates are less compressible than berlinite (K₀∼41 GPa, calculated from Sowa et al., 1990) but more compressible than hydroxylapatite (K₀=97.5 GPa; Brunet et al., 1999), monazite-(La) or xenotime (K₀=144(2) and 149(2) GPa, respectively; Lacomba-Perales et al., 2010). Besides, whereas the silicates forsterite and ellenbergerite, homeotypical with chopinite and P-ellenbergerite, respectively, are relatively incompressible (K_{0(forsterite)}=127.4 GPa – Kroll et al., 2014; K_{0(ellenbergerite)}=133 GPa – Comodi and Zanazzi, 1993a) and display 3 % average reduction in their molar volume at 5.0 GPa, chopinite and P-ellenbergerite are more compressible with about 5 % volume reduction at 5.0 GPa (K_0(chopinite)=81.6 GPa; K_{0(P-ellenbergerite)}=86.4 GPa). The 25 % octahedral vacancies in chopinite with respect to forsterite (Berthet et al., 1972) may well account for its higher compressibility. Indeed, in the olivine-type phosphate series triphylite–heterosite, LiFe²⁺PO₄ to □Fe³⁺PO₄, the 50 % octahedral vacancies result in a drop of K₀ from 106 to 61 GPa (Dodd, 2007, confirming the first-principle modelling of Maxisch and Ceder, 2006). However, this line of argument alone does not hold for the ellenbergerite series, in which the number of vacancies (in the octahedral single chain) is slightly lower in the softer phosphate (0.2 to 0.3 “atoms” pfu; Brunet et al., 1998; Brunet and Schaller, 1996) than in the stiffer silicate (0.7 to 1.0 “atoms” pfu; Chopin et al., 1986).

For each of the Mg-phosphates studied, the pressure dependence of unit-cell volumes normalised to V_ref=V₀ ⋅ scale factor was also fitted using a Berman-type polynomial (Brown et al., 1989) for specific thermodynamic applications (Table 3). We chose a second-order regression (except for chopinite, first-order, v₄ being not significant): $V\left(P\right)/V_{\mathrm{ref}}=\mathrm{1}+v_{\mathrm{3}}(P-\mathrm{1})+v_{\mathrm{4}}(P-\mathrm{1}{)}^{\mathrm{2}}$; P is expressed in bars, and V_ref is the mean value of the room-pressure volumes V₀ of the different measurement runs multiplied by the refined scale factor derived from the fit using EosFit7 7.6. The v₃ and v₄ Berman coefficients are listed in Table 3.

3.2 Thermal behaviour and expansion data

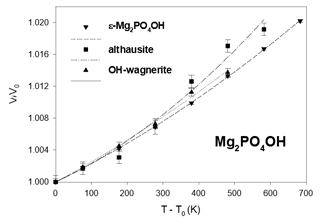
The experimental high-temperature data are presented in Table 4 and Figs. 4 to 6. For the hydrous phases, the measurements were limited by the breakdown of the minerals at high temperature: both althausite and ε-Mg₂PO₄OH began to alter and to form the anhydrous-phase farringtonite at 700 °C. The high-pressure phases OH-wagnerite and P-ellenbergerite showed no evidence of decomposition at 500 and 400 °C, respectively.

Table 4 Unit-cell parameters of studied Mg-phosphates as a function of temperature.

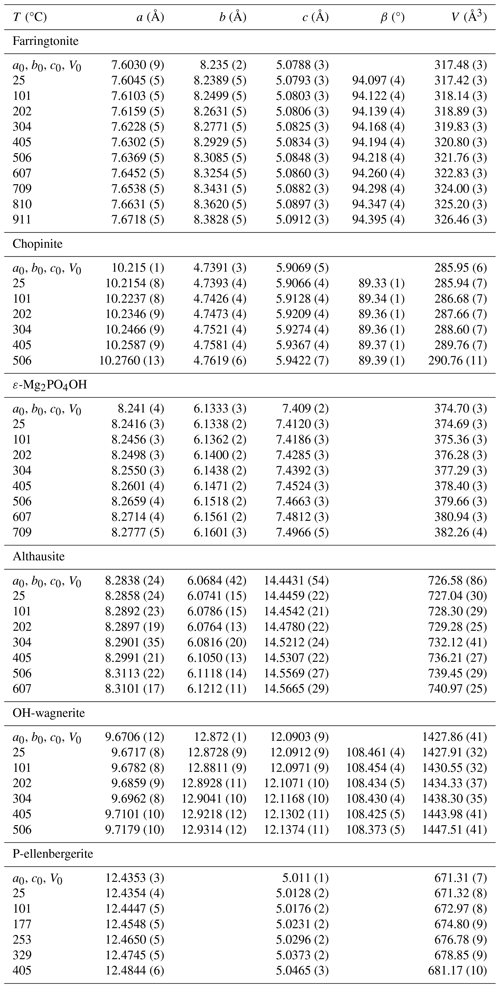
Note: values in brackets are 1σ for cell parameters and refer to the last decimal place. The terms a₀, b₀, c₀ and V₀ are fitted values for the lattice parameters and unit-cell volume resulting from the fit using Berman's (1988) EoS in EoSFit7 7.6.

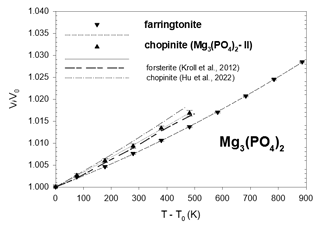
Figure 4 Thermal-expansion data of synthetic farringtonite and of synthetic chopinite compared to the homeotypical forsterite. Error bars are from Table 3.

Figure 5 Thermal-expansion data of Mg₂PO₄OH polymorphs. Error bars are from Table 4.

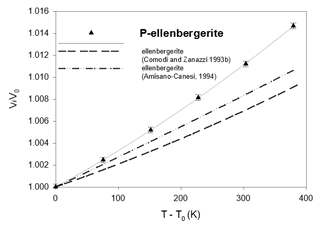
Figure 6 Thermal-expansion data of synthetic phosphoellenbergerite, compared to the homeotypical silicate. Error bars are from Table 4.

The unit-cell volumes all smoothly increase with a parabolic dependence on temperature. The temperature dependence of the unit-cell volume has been fitted to a Berman second-order polynomial (Brown et al., 1989; Berman, 1988) for each Mg-phosphate: $V\left(T\right)=V_{\mathrm{0}}(\mathrm{1}+v_{\mathrm{1}}(T-T_{\mathrm{0}})+v_{\mathrm{2}}(T-T_{\mathrm{0}}{)}^{\mathrm{2}})$, where T₀ is the standard temperature (293.15 K) and V₀ the standard volume. The fits were done using EosFit7c 7.6 with the implemented Berman EoS $V_{\mathrm{0}}(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{0}}(T-T_{\mathrm{0}})+\mathrm{1}/\mathrm{2}{\mathit{\alpha }}_{\mathrm{1}}(T-T_{\mathrm{0}}{)}^{\mathrm{2}})$ using V₀ as well as α₀ and α₁ as fit parameters. Then the coefficients of the second-order Berman polynomial are v₁=α₀ and $v_{\mathrm{2}}=\mathrm{1}/\mathrm{2}{\mathit{\alpha }}_{\mathrm{1}}$. Their values are reported in Table 3, together with those obtained from a fit of Hu et al. (2022) data. As can be realised from Fig. 4, these authors have measured a slightly higher thermal expansion of chopinite = Mg₃(PO₄)₂–II.

Compared to other phosphate minerals, Mg-phosphate thermal expansions are higher than those of monazite ($v_{\mathrm{1}}\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹; e.g. Perrière et al., 2007), berlinite ($v_{\mathrm{1}}=\mathrm{1.9}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹; Troccaz et al., 1967) and hydroxylapatite ($v_{\mathrm{1}}=\mathrm{1.79}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹; Brunet et al., 1999). They are comparable to the expansion of compact silicates like grossular ($v_{\mathrm{1}}=\mathrm{2.38}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹) or pyrope ($v_{\mathrm{1}}=\mathrm{2.15}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹) (calculated from Thiéblot et al., 1998) but exceed those of their silicate structural equivalents: $v_{\mathrm{1}\left(\mathrm{chopinite}\right)}=\mathrm{3.51}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ > $v_{\mathrm{1}\left(\mathrm{forsterite}\right)}=\mathrm{3.04}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ (calculated from Kroll et al., 2012), and $v_{\mathrm{1}\left(\text{P-ellenbergerite}\right)}=\mathrm{3.1}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ > $v_{\mathrm{1}\left(\mathrm{ellenbergerite}\right)}=\mathrm{1.96}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ (calculated from Comodi and Zanazzi, 1993b).

3.3 Anisotropy

The anisotropy of compressibility and thermal expansion of crystals can generally be described by the eigenvectors ${\mathrm{Ev}}_{\mathrm{1},\mathrm{2},\mathrm{3}}$ of the second-rank tensors representing these properties (Nye, 1985). The components of the tensors were determined by temperature- and pressure-dependent X-ray diffraction measurements of the lattice parameters. The corresponding data of the Mg-phosphates and additional minerals are compiled in Tables 5 and 6. In the case of orthorhombic and higher-symmetry compounds (Table 5), the eigenvectors ${\mathrm{Ev}}_{\mathrm{1},\mathrm{2},\mathrm{3}}$ are oriented parallel to the crystallographic axes a, b and c. Therefore, in these cases the anisotropy of the corresponding property can be evaluated by determining the linear expansion α_i and the linear moduli M_i with i = a, b, c along the crystallographic axes. As the linear moduli $M_i=-x_i(\partial P/\partial x_i{)}_T$ with x_i=a, b, c lattice parameter are the inverse of the linear compressibility ${\mathit{\beta }}_i=-\mathrm{1}/x_i(\partial x_i/\partial P{)}_T$, this procedure results directly in diagonalised tensors with α_a=α₁₁, β_a=β₁₁ and so on.

Table 5 Thermal-expansion and compressibility tensor elements of orthorhombic and hexagonal Mg-phosphates and silicates (in italics).

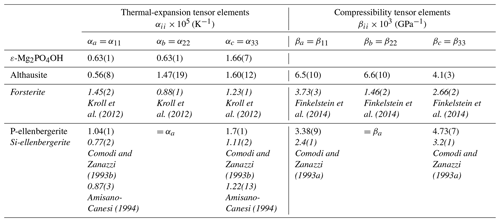
Note: data for forsterite and Si-ellenbergerite were recalculated from the cited literature. In the case of Kroll et al. (2012), data from their Table 1 were used with the exception of the results below 20 °C. Forsterite was in the Pnam setting for consistency with that of chopinite (Table 6).

Table 6 Diagonalised thermal-expansion and compressibility tensor elements of monoclinic Mg-phosphates.

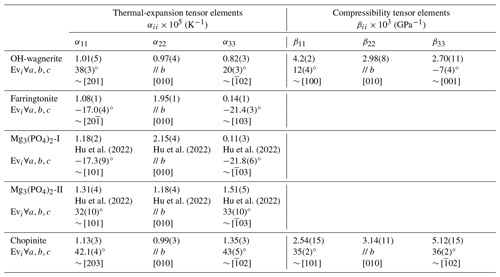
Mg₃(PO₄)₂-II in the P2₁/a setting for consistency with that of chopinite. The thermal expansions of Mg₃(PO₄)₂-I and Mg₃(PO₄)₂-II were recalculated from Hu et al. (2022).

The M_i values were retrieved using EosFit7c 7.6 from the pressure dependence of the lattice parameters and were calculated in the same way as the bulk moduli K₀ of the volume data.

The linear thermal-expansion coefficients α_i were calculated using the implemented Berman EoS of EosFit7c of first-order $V\left(T\right)=V_{\mathrm{0}}(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{0}}(T-T_{\mathrm{0}}\left)\right)$ using V₀ as well as α₀ as fitting parameters.

In the case of the monoclinic compounds farringtonite, chopinite and OH-wagnerite, the orientations of the orthogonal eigenvectors ${\mathrm{Ev}}_{\mathrm{1},\mathrm{2},\mathrm{3}}$ and therefore the axes of the representation quadric (Nye, 1985) differ from those of the crystallographic axes. One eigenvector must lie parallel to the diad axis, which is the b axis in the settings used here. The other two are oriented within the a–c plane. In order to quantify the anisotropy, the values of the properties along the orthogonal eigenvectors were compared. The eigenvalues and eigenvectors of the tensors of expansion and compressibility were calculated using the STRAIN routine in EosFit7c in the range of highest- and lowest-temperature or highest- and lowest-pressure data for each compound (Tables 2 and 4) under the condition that the eigenvectors are unit vectors. In Table 6 the elements of the diagonalised tensors are given together with the orientation of the eigenvectors towards the nearest crystallographic axis (Tables 5 and 6).

In order to compare our results to the recently published lattice parameters of Mg₃(PO₄)₂-I (farringtonite) and Mg₃(PO₄)₂-II (chopinite) by Hu et al. (2022), the monoclinic angle was calculated from their published lattice parameters a, b, c and unit-cell volumes, as the mentioned authors did not give data for the angle β.

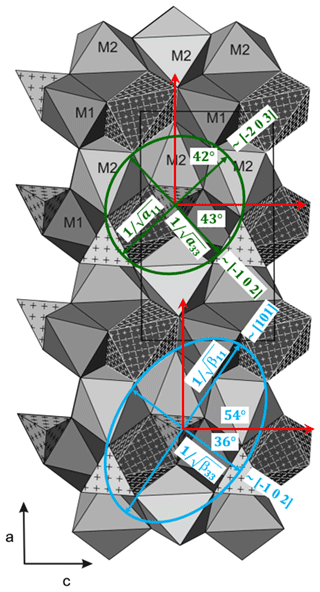
Figure 7 Projection of the chopinite structure along b axis (adapted from Grew et al., 2007). The a and c axes are according to our setting in Table 1. Representation quadric of the tensors of compression (blue) and thermal expansion (green) according to Nye (1985) and Knight (2010).

The compression is slightly anisotropic for the investigated magnesium phosphates, with a maximum compressibility contrast for chopinite (${\mathit{\beta }}_{\mathrm{33}}/{\mathit{\beta }}_{\mathrm{11}}=\mathrm{2.02}$). Figure 7 shows a projection of the olivine-like chopinite structure along the b axis (modified after Grew et al., 2007) together with the representation quadrics of compressibility and the thermal-expansion tensor. The lengths of the axes of the ellipsoids equal the inverse of the square root of the property in that direction (Nye, 1985; Knight, 2010). The directions of both the highest and the lowest compressibility do not match the crystallographic axes. The highest compressibility appears near the [101] direction, whereas the lowest is near [−102]. Compared to forsterite, the tensor is rotated within the (010) plane by 54°. The anisotropy of chopinite in this plane is about ${\mathit{\beta }}_{\mathrm{33}}/{\mathit{\beta }}_{\mathrm{11}}=\mathrm{2.02}$, whereas in forsterite it is (${\mathit{\beta }}_{\mathrm{11}}={\mathit{\beta }}_a)/({\mathit{\beta }}_{\mathrm{33}}={\mathit{\beta }}_c)=\mathrm{1.40}$ (forsterite in the Pnam setting). The vacancies of 50 % of the M1 sites increase the anisotropy of chopinite compared to forsterite. The anisotropy in P-ellenbergerite (${\mathit{\beta }}_c/{\mathit{\beta }}_a=\mathrm{1.40}$) is about the same as in the homeotypical silicate (Mg${}_{\mathrm{1}/\mathrm{3}}$,Ti${}_{\mathrm{1}/\mathrm{3}}$,${\square }_{\mathrm{1}/\mathrm{3}}{)}_{\mathrm{2}}$Mg₆Al₆Si₈O₂₈(OH)₁₀ (${\mathit{\beta }}_c/{\mathit{\beta }}_a=\mathrm{1.33}$) and can be related to the properties of the two main structural elements, the octahedral single and double chains running parallel to c. The dimers of face-sharing octahedra in the double chain have their common face parallel to c, with short Mg–Mg (or Mg–Al) distances across it; they should therefore be least compressible perpendicular to c. This effect combines with the presence of vacancies in the face-sharing octahedra of the single chain on the 6-fold screw axis, which also make this chain easily compressible parallel to c.

Thermal expansion is slightly to moderately anisotropic in the dense phases OH-wagnerite (${\mathit{\alpha }}_{\mathrm{11}}/{\mathit{\alpha }}_{\mathrm{33}}=\mathrm{1.23}$), chopinite (${\mathit{\alpha }}_{\mathrm{33}}/{\mathit{\alpha }}_{\mathrm{22}}=\mathrm{1.36}$) and P-ellenbergerite (${\mathit{\alpha }}_{\mathrm{33}}/{\mathit{\alpha }}_{\mathrm{11}}=\mathrm{1.63}$), but it is more anisotropic in the low-pressure phases ε-Mg₂(PO₄)OH (${\mathit{\alpha }}_{\mathrm{33}}/{\mathit{\alpha }}_{\mathrm{11}}=\mathrm{2.63}$), althausite (${\mathit{\alpha }}_{\mathrm{33}}/{\mathit{\alpha }}_{\mathrm{11}}=\mathrm{2.86}$) and farringtonite (${\mathit{\alpha }}_{\mathrm{22}}/{\mathit{\alpha }}_{\mathrm{33}}=\mathrm{13.9}$). Whereas the near-isotropic behaviour of OH-wagnerite may reflect the three-dimensional nature of its Mg polyhedral framework (Raade and Rømming, 1986b), the high expansion along c in althausite can be related to the existence of a perfect (001) cleavage plane (space group Pnma, hence the preferred-orientation problems). The strong anisotropy of farringtonite thermal expansion is essentially due to the low expansion along c. Along this direction, the Mg(2)O₆ octahedra are connected to each other by two PO₄ tetrahedra and form rather straight (Mg(PO₄)₂O₂) chains, in which the sum of the octahedral and tetrahedral edge lengths controls the c repeat and cannot be much increased by polyhedral tilting.

4 Perspective

This exploratory survey will serve, in the first place, thermodynamic purposes but, together with results on Mg–Al-phosphates (Schmid-Beurmann et al., 2007), allows a few systematic remarks. The room-temperature thermal-expansion coefficients obtained here for Mg-phosphates fall within the range found by Schmid-Beurmann et al. (2007) with MgAlPO₅ and lazulite MgAl₂(PO₄)₂(OH)₂ (${\mathit{\alpha }}_{\mathrm{0}}=\mathrm{0.9}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ to ${\mathit{\alpha }}_{\mathrm{0}}=\mathrm{5.0}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹, respectively), which itself covers most of the range found in the silicate minerals (from ${\mathit{\alpha }}_{\mathrm{0}}=\mathrm{0.15}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ (prehnite) to ${\mathit{\alpha }}_{\mathrm{0}}=\mathrm{3.9}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ (paragonite)). There seems to be a trend towards higher thermal expansions for phosphate minerals as compared to silicates, which we confirm here in the case of isotypic compounds; however, this gross general feature should not obscure the fact that other groups of (synthetic) phosphates do have very low thermal expansion (e.g. Th₄(PO₄)₄P₂O₇; Launay, 2001) or even negative volume expansion for zeolite-type structures (e.g. Amri and Walton, 2009). As to compressibility, that of the Mg-phosphates ranges between $v_{\mathrm{3}}=\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{6}}$ and $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{6}}$ bar⁻¹ and fits within those found for the extreme structural types of berlinite and apatite.

As mentioned before, Mg-containing phosphate minerals have attracted increasing interest in experimental petrology during the last few decades because of their potential as index minerals and the formation of solid solutions with silicates (e.g. Cemič and Schmid-Beurmann, 1995, and Schmid-Beurmann et al., 2000, in addition to the references quoted in the Introduction). However, for a successful application of calculated phase equilibria to geobarometry and/or geothermometry, a resilient basis of thermodynamic data is required. In this sense the current paper can be seen as one more step towards an internally consistent database for phosphate minerals.