the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Crystal chemistry of type paulkerrite and establishment of the paulkerrite group nomenclature
Ian E. Grey
Stephanie Boer
Colin M. MacRae
Nicholas C. Wilson
William G. Mumme
Ferdinando Bosi
A single-crystal structure determination and refinement has been conducted for the type specimen of paulkerrite. The structure analysis showed that the mineral has monoclinic symmetry, space group P2, not orthorhombic, Pbca, as originally reported. The unit-cell parameters are a=10.569(2), b=20.590(4), c=12.413(2) Å, and β=90.33(3)∘. The results from the structure refinement were combined with electron microprobe analyses to establish the empirical structural formula A1[(H2O)0.98K0.02]Σ1.00 A2K1.00 M1(Mg1.02Mn M2(FeTiAl0.24Mg0.02)Σ2.00 M3(Ti Fe (PO4)4.02 X[O1.21F0.47(OH)0.32]Σ2.00(H2O)10 ⋅ 3.95H2O, which leads to the end-member formula (H2O)KMg2Fe2Ti(PO4)4(OF)(H2O)10 ⋅ 4H2O.
A proposal for a paulkerrite group, comprising orthorhombic members benyacarite, mantiennéite, pleysteinite, and hochleitnerite and monoclinic members paulkerrite and rewitzerite, has been approved by the International Mineralogical Association's Commission for New Minerals, Nomenclature and Classification. The general formulae are A2M12M22M3(PO4)4X2(H2O)10 ⋅ 4H2O and A1A2M12M22M3(PO4)4X2(H2O)10 ⋅ 4H2O for orthorhombic and monoclinic species, respectively, where A= K, H2O, □ (= vacancy); M1 = Mn2+, Mg, Fe2+, Zn (rarely Fe3+); M2 and M3 = Fe3+, Al, Ti4+ (and very rarely Mg); X= O, OH, F. In monoclinic species, K and H2O show an ordering at the A1 and A2 sites, whereas O, (OH), and F show a disordering over the two non-equivalent X1 and X2 sites, which were hence merged as X2 in the general formula. In both monoclinic and orthorhombic species, a high degree of mixing of Fe3+, Al, and Ti occurs at the M2 and M3 sites of paulkerrite group members, making it difficult to get unambiguous end-member formulae from the structural determination of the constituents at individual sites. To deal with this problem an approach has been used that involves merging the compositions at the M2 and M3 sites and applying the site-total-charge method. The merged-site approach allows end-member formulae to be obtained directly from the chemical analysis without the need to conduct crystal-structure refinements to obtain the individual site species.
- Article
(2385 KB) - Full-text XML
-
Supplement
(494 KB) - BibTeX
- EndNote
The three secondary Ti-bearing phosphate minerals paulkerrite (Peacor et al., 1984), mantiennéite (Fransolet, 1984), and benyacarite (Demartin et al., 1993, 1997) have similar compositions and powder X-ray diffraction patterns, with reported orthorhombic unit-cell parameters a∼10.5, b∼20.5, and c∼12.4 Å. Demartin et al. (1997) gave the general formula [H2O,K]2TiM12M22(PO4)4(O,F)2 ⋅ 14H2O for the three minerals based on their crystal structure determination for benyacarite (Demartin et al., 1993) in the orthorhombic space group Pbca. They noted that the M1 site is occupied by divalent cations, with dominant Mn2+ in benyacarite and dominant Mg in paulkerrite and mantiennéite, while the M2 site has dominant Fe3+ in benyacarite and paulkerrite and Al in mantiennéite.
Three minerals closely related to benyacarite have received recent approvals from the International Mineralogical Association (IMA) Commission for New Minerals, Nomenclature and Classification (CNMNC). They are pleysteinite (Grey et al., 2023a) and hochleitnerite (Grey et al., 2023b), isostructural with benyacarite, and rewitzerite (Grey et al., 2023c) with a monoclinic (P2 modification of the Pbca benyacarite structure. The six minerals form a group as defined by Mills et al. (2009) with the group name paulkerrite, as the first-described member. The description of paulkerrite however did not include a crystal structure refinement, due to the poor diffracting quality of the crystals (Peacor et al., 1984), raising some doubt about the reported formula. To address this issue, we obtained on loan the type specimen of paulkerrite for crystallographic characterisation and refined the crystal structure using a synchrotron-based single-crystal dataset. The structure analysis showed that type paulkerrite crystals are isostructural with rewitzerite, having monoclinic symmetry, space group P2, a maximum non-isomorphous subgroup of Pbca. The study on rewitzerite established a structural formula for monoclinic paulkerrite-group members of A1A2M12M22M3(PO4)4X2 (H2O)10 ⋅ 4H2O (Grey et al., 2023c), where A1 = prevailing K or H2O, and A2 = prevailing H2O or K.
A common feature of the monoclinic and orthorhombic crystal structures of paulkerrite-group minerals is a high degree of mixing of Ti, Al, and Fe3+ at two non-equivalent but very similar crystallographic sites, M2 and M3. This makes the assignments of dominant constituents at these two sites (and thus the end-member formulae, as defined by Hawthorne, 2002) very sensitive to the location of minor constituents. This problem can be overcome by merging the compositions of the two sites and then obtaining the correct end-member by the site-total-charge method (Bosi et al., 2019a). Application of this procedure resulted in changes to the end-member formulae for some members of the group. A proposal for the establishment of the paulkerrite group with the application of the site-merging procedure for establishment of end-member formulae as defined by Hawthorne (2002), and the resulting revision of some formulae, has been approved by the IMA CNMNC, proposal revised 22-K-bis. We describe here the crystal-chemical characterisation of type paulkerrite and the establishment and nomenclature of the paulkerrite group.
2.1 Description of specimen
The type specimen of paulkerrite is from the 7U7 Ranch, about 40 km west of Hillside, Yavapai County, Arizona. We obtained the type specimen on loan from the Smithsonian Institution, Washington, catalogue number NMNH R7778. Its occurrence, associated minerals and physical properties are described by Peacor et al. (1984). Isolated tabular light-brown crystals of paulkerrite are dispersed with bermanite on fracture surfaces on triplite. Hurlbut (1936), who first reported paulkerrite at the Arizona pegmatite as an unidentified phosphate mineral, gave an analysis of triplite corresponding to MnMg0.65Fe0.35(PO4)F. It is likely that the Mg-bearing triplite is the precursor mineral for paulkerrite, with K, Al, and Ti being provided by decomposed muscovite in the pegmatite surrounding the triplite segregation. Peacor et al. (1984) presented electron microprobe analyses for paulkerrite and noted that the Fe was predominantly Fe3+ based on microchemical tests. They assigned the oxidation state of Mn as Mn2+ based on a better match to the optical properties than for Mn3+. They did note, however, that the triplite matrix mineral is frequently black in colour due to Mn oxidation, and the closely associated mineral bermanite is a mixed Mn valence mineral, Mn2+Mn(PO4)2(OH)2 ⋅ 4H2O.
2.2 Chemical analysis
Tabular crystals of paulkerrite similar to those shown in Figs. 1 to 3 of Peacor et al. (1984) were prepared in a polished epoxy mount for scanning electron microscopy (SEM) and electron microprobe (EMP) analyses. The crystals showed complex chemical zoning due to variations in Mg versus Mn. A back-scattered electron (BSE) image showing the zoning is shown in Fig. 1. In addition, the crystals all displayed a rim, typically 5 to 10 µm wide, enriched in Mn, that has a lighter colour in the BSE image of Fig. 1.

Figure 1Back-scattered electron image of type paulkerrite showing zoning due to Mg Mn substitution and a rim of a Mn-rich paulkerrite-group mineral. Bright sliver of triplite at top of crystal.
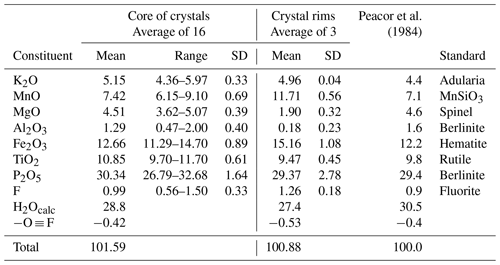
Crystals of type paulkerrite were analysed using wavelength-dispersive spectrometry on a JEOL JXA-8500F Hyperprobe operated at an accelerating voltage of 15 kV and a beam current of 2.2 nA. The beam was defocused to 10 µm (5 µm for rim analyses). Analytical EMP results are given in Table 1 for analyses made in the core regions of crystals (16 analyses) and in the rims (3 analyses). The analyses of Peacor et al. (1984) are included for comparison. There was insufficient material for direct determination of H2O, so it was based upon the crystal structure analysis with 15 H2O per 4 PO4. The water content was used in the matrix correction of the raw EMP data. Bond valence sums (BVSs) calculated from refined bond distances using the parameters of Gagné and Hawthorne (2015) confirmed that the Fe was in the trivalent state only. The mean wt % oxides for the core analyses agree with the analyses reported by Peacor et al. (1984) to within 1–2 SDs. The atomic fractions, scaled to 5M cations and 33 anions, are as follows:
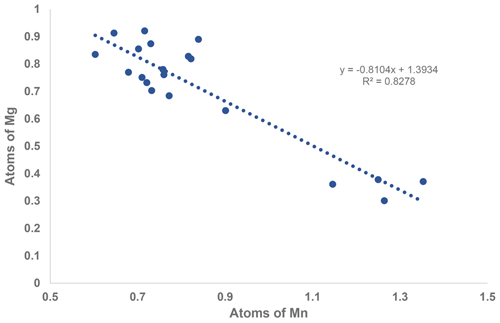
A comparison of the two formulae shows that the major chemical change from the core to the rim is substitution of Mg by Mn. This change is illustrated by the strong negative correlation shown in the scatter plot in Fig. 2. A weaker negative correlation is associated with Fe replacing Al and Ti in the rim, with an increase in the F content.
To express the atomic fractions in the crystal core as a structure-based empirical formula, the least-squares program OccQP (Wright et al., 2000) was used to optimise the site occupations for the M1 to M3 sites, which were then combined with the EMP analyses for K and F: A1[(H2O)0.98K0.02]Σ1.00 A2K1.00
M1(Mg1.02Mn M2(FeTiAl0.24Mg0.02)Σ2.00 M3(TiFe
(PO4)4.02 X[O1.21F0.47(OH)0.32]Σ2.00 (H2O)10 ⋅ 3.95H2O.
Note that the two X sites are non-equivalent (X1 and X2) in the monoclinic symmetry, but as O, (OH), and F are disordered over them, they were merged as X2. By contrast, K and H2O show an ordering at two non-equivalent A1 and A2 sites. The above formula has dominant Mg at M1, Fe3+ at M2, and Ti at M3, consistent with the reported site occupations for paulkerrite (Peacor et al., 1984; Demartin et al., 1997) and giving the end-member formula (H2O)KMg2Fe2Ti(PO4)4(OF)(H2O)10 ⋅ 4H2O.
Single-crystal diffraction data could not be obtained on the thin, Mn-rich rims of the paulkerrite crystals, so the procedure used for the crystal cores could not be used to determine the end-member formula. Instead, the merged-site procedure, described in Sect. 3.2, was applied. In this approach, the larger divalent cations from the EMP analyses are assigned to the M1 site, and the remaining smaller cations are assigned to the (M2 + M3) sites. These are combined with the K and F from EMP analyses to obtain the empirical formula of the rim zones: A1(H2O)1.00 A2K1.00
M1(Mn1.57Mg0.43)Σ2.00 M2+M3(FeTi1.15Al0.03)Σ2.00(PO4)3.93 X(F0.63(OH)0.01
O1.36)Σ2.00(H2O)10 ⋅ 3.74H2O.
The composition at the (M22M3) merged sites is dominated by the atomic arrangement (Fe2Ti), as will be described in Sect. 3.2. The resulting end-member formula corresponding to the crystal rims is (H2O)KMn2Fe2Ti(PO4)4(OF)(H2O)10 ⋅ 4H2O. This is the same as the end-member formula for the crystal cores, except for the replacement of Mg by Mn as the dominant M1 site constituent.
2.3 Crystallography
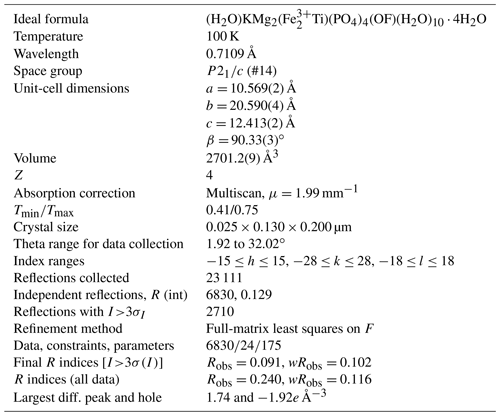
Single-crystal diffraction data were collected on a crystal of type paulkerrite at the Australian Synchrotron MX2 microfocus beamline (Aragao et al., 2018). Intensity data were collected using a Dectris EIGER 16M detector and monochromatic radiation with a wavelength of 0.7109 Å. The crystal was maintained at 100 K in an open-flow nitrogen cryostream during data collection. The diffraction data were collected using a single 21 s sweep of 360∘ rotation around ϕ. The resulting dataset consists of 3600 individual images with an approximate ϕ angle of each image being 0.1∘. The raw intensity dataset was processed using XDS software to produce data files that were analysed using WinGX (Farrugia, 1999) and Jana2006 (Petříček et al., 2014).
A structural model was obtained in monoclinic space group P2 using SHELXT (Sheldrick, 2015) and found to be closely related to the orthorhombic, Pbca structures for benyacarite and pleysteinite. In the monoclinic space group the cation sites in the Pbca structures are each split into pairs of sites, A1 A2, M1a M1b, M2a M2b, and M3a M3b, at positions x, y, z and , , −z. The same atom labelling was used as for the orthorhombic minerals, for ease of comparison. Based on previous structural studies of paulkerrite-group minerals (Demartin et al., 1993; Grey et al., 2023a, b), divalent Mn and Mg were allocated at the M1 sites, Fe, and Ti at the M2 and M3 sites and K and O (for H2O) at the A1 and A2 sites, and the relative amounts of the pairs of site occupants were refined using Jana2006. The site scattering values and the bond distances for the M1 to M3 sites from the refinement were input with chemistry from the EMP analyses to the program OccQP (Wright et al., 2000) to optimise the cation distributions over the different sites. The results showed that the minor Al in paulkerrite preferentially ordered at the M2 sites, and so in the next stage of the refinement the Al content from the EMP analyses was evenly distributed at M2a and M2b sites and its occupancy fixed, while the Fe and Ti contents were refined. The site occupancy refinement for the A1 and A2 sites gave a combined K content of only 0.77 atoms per formula unit (apfu), much lower than the mean EMP value of 1.02 K apfu. With K only at the A1 and A2 sites, the refined occupancies summed to 1.24 K apfu, well above the mean EMP value. We interpreted these results as indicating some vacancies at the A1 and A2 sites. Refinements were made using different fixed amounts of vacancies. The best fit to the EMP analysis for K and the lowest R factors in the crystal-structure refinement were obtained for ∼ 18 % vacancies at the A1 and A2 sites. The final refinement in JANA2006 of atom coordinates, site occupancies, and isotropic displacement parameters converged at Robs=0.091 for 2712 reflections with I>3σI. The high R factor reflects the relatively poor diffracting quality of paulkerrite crystals (Rint=0.13) as noted in the study by Peacor et al. (1984). The high Robs for all data results from the large number of very weak reflections. Further details of the data collection and refinement are given in Table 2. Refined atom coordinates, site occupancies, equivalent isotropic displacement parameters, and BVS are given in Table 3. Polyhedral bond lengths are reported in Table 4.
Table 3Refined site occupancies, atom coordinates and equivalent isotropic displacement parameters (Å2), and bond valence sums (BVS, in valence units) for paulkerrite.
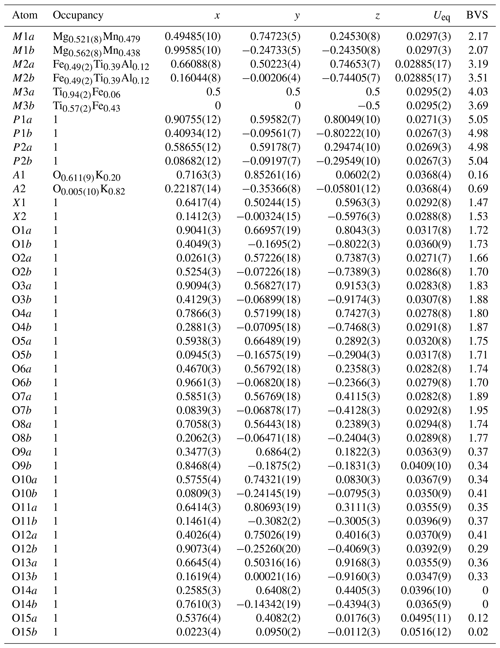
The BVS values are consistent with H2O at the anion sites O9 to O15. As shown in Table 4 this includes H2O coordinated to Mn and Mg at the M1 sites (O9 to O12), H2O coordinated to cations at the M2 sites (O13), and H2O coordinated to K at the A1 and A2 sites (O15). The H2O at the O14 sites is involved in H-bonding only. The BVS values for the constituents at the X sites are consistent with a mix of divalent (O2−) and monovalent (F− and OH−) at these sites. The relatively low BVS values for many of the oxygen anions, O1 to O8, reflect that they are involved as receptors in multiple H-bonds to the H2O molecules. Likely H-bonded pairs with O…O less than 3 Å are given in Table 4. The BVS values for constituents at the M sites reflect the ordering of predominantly divalent cations at M1, trivalent cations at M2, and tetravalent cations at M3 sites, consistent with the site occupancy refinements shown in Table 3. The dominance of Mg at M1 sites, Fe at M2 sites, and Ti at M3 sites shown in Table 3 agrees with the formula for paulkerrite given by Peacor et al. (1984): KTi(Mg,Mn)2(Fe3+,Al,Ti,Mg)2(PO4)4(OH)3 ⋅ 15H2O, which can be rearranged to (H2O)K(Mg,Mn)2(Fe3+,Al,Ti,Mg)2Ti(PO4)4(OH)3 (H2O)10 ⋅ 4H2O to be consistent with more recent formulations (Grey et al., 2023a). Remarkably, the formula of Peacor et al. (1984) was determined without the aid of a crystal structure. The only inconsistency in their formula is the assignment of [(OH)3]3−, whereas the structure determination has the three negative charges provided by two X-site constituents per formula unit [O(F,OH)]3−.
Table 4Polyhedral bond lengths [Å] for paulkerrite.
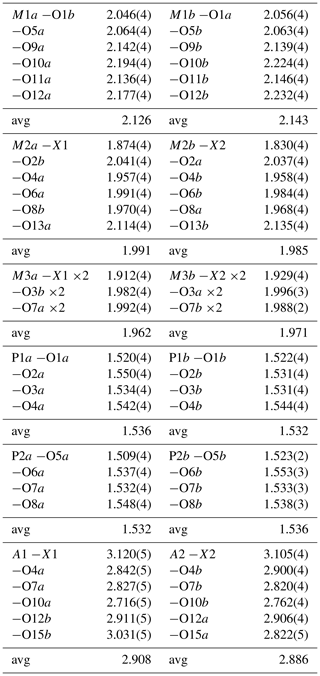
Possible H-bonded O…O pairs. Distances (less than 3 Å) in parentheses.
O1a…O11a (2.82), O1b…O10a (2.92), O1b…O11b (2.77).
O2a…O11b (2.81), O2a…O15b (2.91), O2b…11a (2.84), O2b…15a (2.86).
O3a…O13a (2.91), O3a…O14b (2.85); O3b…O14a (2.81).
O4a…A1 (2.84), O4b…A2 (2.90), O4b…O11b (2.98).
O5a…O13a (2.76).
O6a…O9a (2.82), O6b…O9b (2.84).
O7a…A1 (2.83), O7b…A2 (2.82).
O8a…O14b (2.81); O8b…O14a (2.79).
O10a…A1 (2.72), O10b…A2 (2.76), O12a…A2 (2.91), O12b…A1 (2.91), O15a…A2 (2.82).
The empirical formula in structural form for paulkerrite from the refined site occupancies is as follows:
A1[K0.20(H2O)0.61□0.19]Σ1.00A2(K0.82□0.18)Σ1.00
M1a(Mg0.52Mn0.48)Σ1.00M1b(Mg0.56Mn0.44)Σ1.00
M2a(FeTi0.39Al0.12)Σ1.00M2b(FeTi0.39Al0.12)Σ1.00
M3a(Ti0.47Fe M3b(Ti0.285Fe(PO4)4X1X2 (H2O)10 ⋅ 4H2O, where vacancy, and the oxygen scattering curve was used for X and H2O.
The formula shows dominant H2O at A1 and K at A2, whereas the pairs of M sites each have the same dominant constituent. The same high degree of K and H2O ordering between the pairs of A sites but with the same dominant constituent at each of the pairs of M sites also occurs in monoclinic rewitzerite. On this basis the structural formulae can be simplified by combining the M1a M1b, M2a M2b, M3a M3b, and X1 X2, giving for paulkerrite the following formula: A1[(H2O)0.61K0.20□0.19]Σ1.00 A2(K0.82□0.18)Σ1.00 M1(Mg1.08Mn0.92)Σ2.00 M2(FeTi0.78
Al0.24)Σ2.00 M3(Ti0.75Fe (PO4)4X2(H2O)10
⋅ 4H2O. More generally, the formula A1A2M12M22M3(PO4)4X2(H2O)10 ⋅ 4H2O is given for monoclinic paulkerrite-group members.
2.4 Description of crystal structure
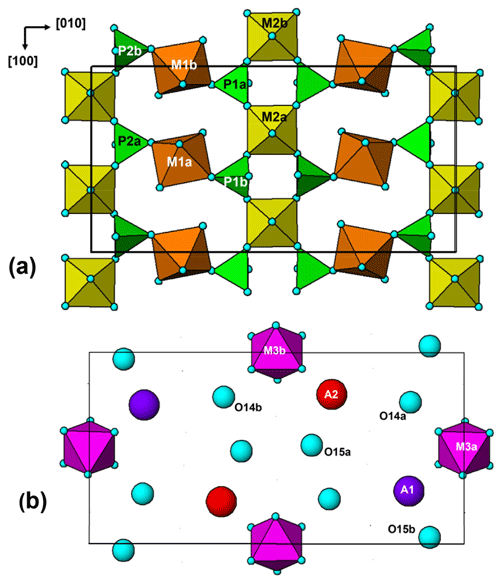
The paulkerrite crystal structure can be described in terms of an alternation of two types of (001) slabs, centred at , and 0, . These are shown in Fig. 3a and b, respectively. The heteropolyhedral layers at and are built from [100] kröhnkite-type chains (Hawthorne, 1985) of four-member rings of corner-connected PO4 tetrahedra and M2O4X(H2O) octahedra. Each PO4 tetrahedron also shares a corner with M1O2(H2O)4 octahedra along [010] to complete the 2D network of polyhedra. The corner-shared linkages form eight-member rings of alternating octahedra and tetrahedra. The (001) slabs at z=0 and comprise isolated M3O4X2 octahedra together with the A-site constituents (K, H2O) and the zeolitic-type H2O groups at sites O14 and O15. The M3O4X2 octahedra share their trans-X vertices with M2O4X(H2O) octahedra in the layers above and below, giving linear trimers that correspond to short segments of the 7 Å chains that are common to many phosphate minerals (Moore, 1970). The M2–M3–M2 trimers are illustrated in Fig. 4. A feature of the trimers is short M2–X distances, with M2a–X1 = 1.87 and M2b–X2 = 1.83 Å, due to displacement of the M2-site atoms from the centres of the octahedra towards the bridging X-site anions with the M3-centred octahedra. This type of displacement is a common feature of chain structures containing Ti (Bamberger et al., 1990). As shown in Fig. 4, the corner-shared connectivity between the kröhnkite-type chains and the M3O4X2 octahedra gives rise to 10-member rings, elongated along [100]. The constituents at A1 and A2 are located in separate rings, centred at 0, y, 0 and , y, , respectively.
It is interesting to note that paulkerrite and rewitzerite have different ordering patterns at the A sites. In paulkerrite dominant H2O occurs at A1 and dominant K at A2, whereas in rewitzerite the ordering is reversed. Potassium at the A sites has a bond to the bridging X-site anion between M2- and M3-centred octahedra, and the reversal of ordering at the A sites appears to be related to the relative amounts of Ti and (Fe, Al)3+ at the M3 sites. For paulkerrite, dominant K at A2 is coordinated to X2, shared with M3b, which has a higher Fe3+ content than M3a (Table 3), and dominant H2O at A1 is coordinated to X1, shared with M3a, having a higher Ti content than M3b. In rewitzerite, where dominant K is at the A1 site, it is the M3a site that has a higher (Al + Fe3+) content (0.63 apfu) than the M3b site (0.58 apfu).
3.1 Approval of the paulkerrite group
Demartin et al. (1997) described paulkerrite (Peacor et al., 1984), mantiennéite (Fransolet, 1984), and benyacarite as members of the paulkerrite group with the general formula [H2O,K]2TiM12M22(PO4)4(O,F)2 ⋅ 14H2O, which can be rearranged to [H2O,K]2M12M22Ti(PO4)4(O,F)2(H2O)10 ⋅ 4H2O. A crystal-structure refinement on the related orthorhombic mineral pleysteinite (Grey et al., 2023a) showed dominant Al at the “Ti” site (corresponding to M3), requiring the more general formula A2M12M22M3(PO4)4X2(H2O)10 ⋅ 4H2O, with K and H2O at A and O, F and OH at X. A further generalisation was required for the monoclinic mineral rewitzerite (Grey et al., 2023c), which has dominant K at one A site and dominant H2O at a second A site in P2, consistent with the general formula A1A2M12M22M3(PO4)4X2(H2O)10 ⋅ 4H2O. The paulkerrite group, with both orthorhombic and monoclinic members, has been approved by the IMA CNMNC, proposal 22-K-bis.
A key feature of the crystal structure of both orthorhombic and monoclinic forms is that M2- and M3-centred octahedra form corner-connected trimers (Fig. 4) corresponding to a short segment of 7 Å chains of octahedra (Moore, 1970), so the octahedra have very similar geometries. For the members for which crystal structures have been refined, there is almost complete mixing of Fe3+ and Ti, or Al and Ti, at the similar M2 and M3 sites. This is illustrated by the empirical formula, in structural form, for the orthorhombic hochleitnerite (Grey et al., 2023b) below: A[(H2O)1.00K1.00]Σ2.00 M1(MnFe M2(TiFeAl0.15)Σ1.96 M3(Ti Fe (PO4)4.00[O1.50F0.23(OH)0.27]Σ2.00(H2O)10 ⋅ 4H2O.
There is an almost equal distribution of Ti and (Fe Al) at both M2 and M3 sites, and different end-member formulae can be obtained depending on which site the minor Al is located. The above formula was obtained by application of the least-squares program OccQP (Wright et al., 2000) to optimise the M1 to M3 site assignments based on the refined site scattering and bond lengths, combined with the chemical analyses. This approach results in the end-member formula (H2O)2Mn2Ti3(PO4)4O2(H2O)10 ⋅ 4H2O with dominant Ti at both the M2 and M3 sites. A serious problem with this formula is that it does not contain K (which would give a charge imbalance) even though the empirical formula has equal amounts of K and H2O at the A site. If the minor Al is constrained to the M3 site rather than the M2 site, the application of the program OccQP gives dominant Fe3+ rather than Ti at the M3 site and leads to the alternative end-member formula [(H2O)K]Mn2Ti2Fe(PO4)4O2(H2O)10 ⋅ 4H2O, which now has K co-dominant at the A site. The end-member formula ambiguity in paulkerrite-group minerals, due to a high degree of mixing of Ti and (Fe3+, Al) at the M2 and M3 sites, can be overcome by merging the compositions of the two sites. The unambiguous end-member can then be obtained using the site-total-charge method (Bosi et al., 2019a, b) applied to the empirical formula with Fe3+, Al, and Ti cations considered as disordered over the M2 and M3 sites. In particular, the site-total-charge method is divided into two steps: one, identifying the dominant end-member charge arrangement from the empirical formula and, two, deriving the dominant end-member formula from this end-member charge arrangement. A list of possible end-member charge arrangements for paulkerrite group minerals with merged M2 and M3 sites is given in Table 5. A particular advantage of this approach is that the end-member formula can be determined disregarding the cation disorder (i.e. from chemical analyses alone) without the need to obtain bond lengths and site scattering for individual sites from a crystal structure refinement. Such an approach will be very useful in the classification of paulkerrite-group-containing specimens in museums and private collections.
3.2 Application of the merged-site procedure
Merging M2 and M3 sites in paulkerrite group minerals, the following atomic arrangements are consistent with an endmember composition: (Al3), (Al2Ti), (Ti2Al), (Ti3), (Fe3), (Fe2Ti), (Ti2Fe).
In accord with the formula A1A2M12(M22M3)
(PO4)4X2(H2O)10 ⋅ 4H2O, the possible end-member charge arrangements are given in Table 5. For visualising the different compositions of merged (M22M3) sites, a ternary diagram should be divided by considering the endmembers Ti3, Ti2Al, Al2Ti, and Al3 along the Ti–Al edge and Ti3, Ti2Fe, Fe2Ti and Fe3 along the Ti–Fe edge, as shown in Fig. 5.
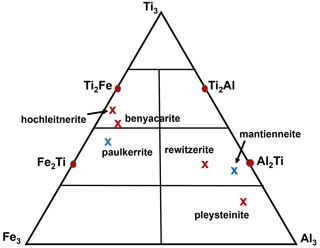
Figure 5Ternary (M22M3) composition diagram showing the location of empirical compositions for paulkerrite group members. Blue crosses correspond to Mg dominant at the M1 site, whereas red crosses have Mn dominant at M1.
Table 6Comparison of end-member formulae previously reported with the new formulae obtained here using the merged (M22M3) site approach.
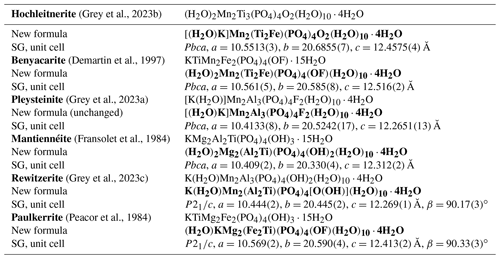
Note added in press: the orthorhombic unit cells for hochleitnerite and pleysteinite were obtained from laboratory diffractometer studies on single crystals (SCs). Recent SC studies using a synchrotron microfocus beam confirm that the unit cells for these minerals have a small monoclinic distortion, as occurs in the minerals rewitzerite and paulkerrite. It is likely that all paulkerrrite-group minerals with 1 atom of K per formula unit are monoclinic.
Crystal structure refinements for five different paulkerrite-group members are consistent in confirming that the M1 site is populated predominantly with the relatively large divalent cations (2 Mn, Mg and Fe). The structural empirical formula is then constructed by assigning 2+ cations (and minor Fe3+ if Mg + Mn <2 apfu, as the size of Fe3+> Ti > Al) to M1 and then assigning remaining Fe plus all Al and Ti to the merged (M22M3) sites. The site-total-charge method (Bosi et al., 2019a) is then applied to determine the dominant merged-site constituents. This is illustrated below for hochleitnerite with the following empirical formula: A[(H2O)1.00K1.00]Σ2.00 M1(MnFe(TiFeAl0.15)Σ2.96 (PO4)4X[O1.50F0.23(OH)0.27]Σ2.00(H2O)10 ⋅ 4H2O.
End-member contributors are the following:
-
(H2O)2Mn2Ti3(PO4)4O2(H2O)10 ⋅ 4H2O, 50 % contribution, limited by the A(H2O) content;
-
[(H2O)K]Mn2(Ti2Fe)(PO4)4O2(H2O)10 ⋅ 4H2O, 75 % contribution, limited by the XO content.
The second formula is the dominant contributor and thus the representative end-member formula for the analysed mineral. This is illustrated graphically in the ternary diagram shown in Fig. 5, where the empirical composition for the merged (M22M3) sites for hochleitnerite is plotted and seen to be located in the compositional field for the end-member (Ti2Fe) rather than that for (Ti3).
Applying the same approach to the other paulkerrite group members gives the end-member formulae reported in Table 6, where they are compared with the original reported formulae. The empirical compositions for the merged (M22M3) sites for the six paulkerrite group members are plotted in Fig. 5.
A positive outcome from the merged sites procedure is that the empirical compositions at (M22M3) now all lie in the correct phase fields for the end-member compositions given in Table 6, when plotted on the ternary composition plot, Fig. 5. This gives confidence to be able to classify new occurrences based on a chemical analysis in conjunction with the ternary plot, without having to obtain a single-crystal refinement. This is an advantage as paulkerrite group minerals often have very poorly diffracting crystals (Peacor et al., 1984; Fransolet et al., 1984).
The Ti-bearing secondary phosphate minerals paulkerrite, mantiennéite, benyacarite, pleysteinite, hochleitnerite, and rewitzerite form a mineral group as defined by Mills et al. (2009). The group has been approved by the IMA CNMNC, revised proposal 22-K-bis. It comprises both orthorhombic members, space group Pbca, and monoclinic members (rewitzerite and paulkerrite), space group P2, with unit-cell parameters given in Table 6. The general formulae for the group members are as follows:
-
A2M12M22M3(PO4)4X2(H2O)10 ⋅ 4H2O for orthorhombic species
-
A1A2M12M22M3(PO4)4X2(H2O)10 ⋅ 4H2O for monoclinic species,
where A= K, H2O, □ (= vacancy); M1 = Mn2+, Mg, Fe2+, Zn, Ca (rarely Fe3+); M2 and M3 = Fe3+, Al, Ti4+ (and very rarely Mg); X= O, OH, F. In monoclinic species, K and H2O show an ordering at the A1 and A2 sites: in paulkerrite H2O prevails at A1 and K at A2, whereas in rewitzerite the ordering is reversed. On the other hand, O, (OH), and F show a disordering over the two non-equivalent X1 and X2 sites, which were hence merged as X2 in the general formula. In both monoclinic and orthorhombic species, the two non-equivalent M2 and M3 sites are structurally very similar, and a high degree of mixing of constituents Fe3+, Al, and Ti occurs at these two sites, introducing considerable ambiguity into the calculation of end-member formulae. To overcome this difficulty, we have used an approach that involves merging the compositions of M2 and M3 and then applying the site-total-charge method. The resulting end-member formulae are reported in Table 6, and the empirical merged-site compositions are plotted in the ternary diagram shown in Fig. 5. The merged-site approach allows end-member formulae to be obtained directly from the chemical analysis without the need to conduct structure refinements to obtain information on the site populations.
Crystallographic data for paulkerrite are available in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/ejm-35-909-2023-supplement.
IEG oversaw the research and wrote the paper. SB collected and processed the single-crystal diffraction data. CMM conducted the EMP analyses. NCW performed the site assignment analysis for paulkerrite. WGM helped with the crystal structure analysis. FB developed the procedure for establishing end-member formulae for the paulkerrite group members.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “New minerals: EJM support”. It is not associated with a conference.
We thank Paul Pohwat (collection manager, minerals) at the Smithsonian Institution for the loan of type specimen of paulkerrite, NMNH R7778. Thanks to Frank Hawthorne for helpful discussions and advice on end-member formulae. The research was undertaken in part using the MX2 beamline at the Australian Synchrotron, part of ANSTO, and made use of the Australian Cancer Research Foundation (ACRF) detector. Thanks to Cameron Davidson for sample preparation for EMP analyses.
This paper was edited by Sergey Krivovichev and reviewed by two anonymous referees.
Aragao, D., Aishima, J., Cherukuvada, H., Clarken, R., Clift, M., Cowieson, N. P., Ericsson, D. J., Gee, C. L., Macedo, S., Mudie, N., Panjikar, S., Price, J. R., Riboldi-Tunnicliffe, A., Rostan, R., Williamson, R., and Caradoc-Davies, T. T.: MX2: a high-flux undulator microfocus beamline serving both the chemical and macromolecular crystallography communities at the Australian Synchrotron, J. Synch. Radiat., 25, 885–891, 2018.
Bamberger, C. E., Begun, G. M., and MacDougall, C. S.: Raman spectroscopy of potassium titanates: Their synthesis, hydrolytic reactions and thermal stability, Appl. Spectrosc., 44, 31–37, 1990.
Bosi, F., Hatert, F., Halenius, U., Pasero, M., Ritsuro, M., and Mills, S. J.: On the application of the IMA-CNMNC dominant-valency rule to complex mineral compositions, Mineral. Mag., 83, 627–632, 2019a.
Bosi, F., Biagioni, C., and Oberti, R.: On the chemical identification and classification of minerals, Minerals, 9, 12 pp., 2019b.
Demartin, F., Pilati, T., Gay, H. D., and Gramaccioli, C. M.: The crystal structure of a mineral related to paulkerrite, Z. Kristallogr., 208, 57–71, 1993.
Demartin, F., Gay, H. D., Gramaccioli, C. M., and Pilati, T.: Benyacarite, a new titanium-bearing phosphate mineral species from Cerro Blanco, Argentina, Can. Mineral., 35, 707–712, 1997.
Farrugia, L. J.: WinGX suite for small-molecule single-crystal crystallography, J. Appl. Crystallogr., 32, 837–838, 1999.
Fransolet, A.-M., Oustriere, P., Fontan, F., and Pillard, F.: La mantiennéite, une novelle espèce minérale du gisement de vivianite d'Anloua, Cameroun, Bull. Mineral., 107, 737–744, 1984.
Gagné, O. C. and Hawthorne, F. C.: Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen, Acta Crystallogr., B71, 562–578, 2015.
Gagné, O. and Hawthorne, F. C.: Chemographic exploration of the milarite-type structure, Can. Mineral., 54, 1229–1247, 2016.
Grey, I. E., Hochleitner, R., Rewitzer, C., Kampf, A. R., MacRae, C. M., Gable, R. W., Mumme, W. G., Keck, E., and Davidson, C.: Pleysteinite, [(H2O)0.5K0.5]2Mn2Al3(PO4)4F2(H2O)10 ⋅ 4H2O, the Al analogue of benyacarite, from the Hagendorf-Süd pegmatite, Oberpfalz, Bavaria, Germany, Eur. J. Mineral., 35, 189–197, https://doi.org/10.5194/ejm-35-189-2023, 2023a.
Grey, I. E., Keck, E., Kampf, A. R., MacRae, C. M., Gable, R. W., Mumme, W. G., Glenn, A. M., and Davidson, C.: Hochleitnerite, [K(H2O)]Mn2(Ti2Fe)(PO4)4O2(H2O)10 ⋅ 4H2O, a new paulkerrite-group mineral, from the Hagendorf-Süd pegmatite, Oberpfalz, Bavaria, Germany, Eur. J. Mineral., 35, 635–643, https://doi.org/10.5194/ejm-35-635-2023, 2023b.
Grey, I. E., Hochleitner, R., Kampf, A. R., Boer, S., MacRae, C. M., Mumme, W. G., and Keck, E.: Rewitzerite, K(H2O)Mn2(Al2Ti)(PO4)4[O(OH)](H2O)10⋅4H2O, a new monoclinic paulkerrite-group mineral, from the Hagendorf-Sud pegmatite, Oberpfalz, Bavaria, Germany, Mineral. Mag., 1–29, https://doi.org/10.1180/mgm.2023.55, 2023c.
Hawthorne, F. C.: Towards a structural classification of minerals: The viMivT2Φn mineral, Am. Mineral., 70, 455–473, 1985.
Hawthorne, F. C.: The use of end-member charge-arrangements in defining new mineral species and heterovalent substitutions in complex minerals, Can. Mineral., 40, 699–710, 2002.
Hurlbut, C. S.: A new phosphate, bermanite, occurring with triplite in Arizona, Am. Mineral., 21, 656–661, 1936.
Mills, S. J., Hatert, F., Nickel, E. H., and Ferraris, G.: The standardisation of mineral group hierarchies: application to recent nomenclature proposals, Eur. J. Mineral., 21, 1073–1080, 2009.
Moore, P. B.: Crystal chemistry of the basic iron phosphates, Am. Mineral. 55, 135–169, 1970.
Peacor, D. R., Dunn, P. J., and Simmons, W. B.: Paulkerrite a new titanium phosphate from Arizona, Mineral. Rec., 15, 303–306, 1984.
Petříček, V., Dušek, M., and Palatinus, L.: Crystallographic Computing System JANA2006: General features, Z. Krisallogr., 229, 345–352, 2014.
Sheldrick, G. M.: Crystal structure refinement with SHELXL, Acta Crystallogr., C71, 3–8, 2015.
Wright, S. E., Foley, J. A., and Hughes, J. M.: Optimisation of site occupancies in minerals using quadratic programming, Am. Mineral., 85, 524–531, 2000.