In situ single-crystal X-ray diffraction of olivine inclusion in diamond from Shandong, China: implications for the depth of diamond formation

We have investigated a suite of natural diamonds from the kimberlite pipe of the Changma Kimberlite Belt, Mengyin County, Shandong Province, China, with the aim of constraining pressures and temperatures of formation. Here we report the non-destructive investigation of an olivine inclusion still entrapped within a lithospheric diamond by single-crystal X-ray diffraction. We were able to refine anisotropically its crystal structure to R₁= 1.42 % using ionized scattering curves; this allows estimation of the composition of the olivine as Mg_1.82Fe_0.18SiO₄. This composition corresponds to a calculated unit-cell volume equal to V= 292.70 ų at room temperature and pressure. We have validated the above-calculated composition and unit-cell volume by releasing the inclusion from the diamond host, resulting in a consistent composition calculated using non-destructive methods of Mg_1.84Fe_0.16SiO₄ and V= 292.80 ± 0.07 ų. Considering that the unit-cell volume of the olivine still inside its diamond host is V= 289.7 ± 0.2 ų, we calculated a residual pressure P_inc= 1.4 ± 0.1 GPa with respect to the released crystal and P_inc= 1.3 ± 0.2 GPa with respect to the volume calculated from the “composition” indirectly retrieved by the structure refinement under ambient conditions. The two values of P_inc overlap within experimental uncertainty. We performed Fourier transform infrared (FTIR) analysis on the diamond host in order to calculate its mantle residence temperature, T_res, which resulted in a value of 1189 ^∘C (for an assumed diamond age of 3 Ga) and 1218 ^∘C (for an age of 1 Ga), with an average T_res equal to 1204 ± 15 ^∘C.

Using the most up-to-date pressure–volume–temperature equations of state for olivine and diamond, the residual pressure P_inc= 1.4 ± 0.1 GPa and average residence temperature of the diamond host T_res= 1204 ^∘C, we retrieved a pressure of entrapment P_trap= 6.3 ± 0.4 GPa. Using the non-destructive approach and relative P_inc = 1.3 GPa, we obtained a perfectly overlapping P_trap= 6.2 GPa, within experimental uncertainty. This entrapment pressure corresponds to depths of about 190 ± 12 km. These results demonstrate that for high-quality crystal structure data measured on inclusions still trapped within diamond hosts, even a non-destructive approach can be used to calculate the depth of formation of diamond–olivine pairs. In terms of geological implications, the results from this work show that Changma diamonds formed under a conductive geotherm lying between 35 and 40 mW m⁻², at a depth of about 190 km. This value lies within the recently reported upper limit of the average depth of formation of worldwide lithospheric diamonds, which is 175 ± 15 km and is in agreement with P–T data obtained in the literature from kimberlite xenoliths.

1 Introduction

Diamonds and their inclusions are among the deepest materials originating from the Earth's interior and their investigation provides a window on the Earth's deep mantle. Lithospheric diamonds represent about 98 %–99 % of all diamonds (Stachel and Harris, 2008; Stachel et al., 2022) and usually form beneath cratonic areas between 120–130 and 200–210 km depth, with an average mode at about 175 ± 15 km (Nimis et al., 2020). The geological importance of lithospheric diamonds is related not only to their depths of formation but also to their ages: these diamonds can be dated up to about 3.5 Gyr ago (Smit et al., 2022), providing information about the evolution of the Earth.

Lithospheric diamonds incorporate different types of mineral inclusions and, based on this, can be further classified as peridotitic (about 63 %), eclogitic (about 35 %) and websteritic (about 2 %) lithospheric diamonds (Stachel and Harris, 2008; Stachel et al., 2022). Olivine, (Mg,Fe)₂SiO₄, is certainly one of the most common inclusions in lithospheric diamonds, representing about 20 % of all inclusions. The knowledge of its composition could provide crucial information about the geological environment in which peridotitic lithospheric diamonds formed (Stachel and Harris, 2008). Unfortunately, at present there are no geobarometers within the literature applicable to single olivine inclusions in diamond and only a single geothermometer based on the Al content in olivine (Bussweiler et al., 2017), which is a reliable geothermometer but rarely applied to olivine inclusions in diamonds (see Korolev et al., 2018; Nimis, 2022; Karaevangelou et al., 2022). An approach that has been reliably applied to single inclusions of olivine in diamond is “elastic geobarometry”, which is mainly based on the significant contrast in the thermoelastic properties between a diamond host and its inclusions; an extensive review of the method and its direct application to olivine inclusions in diamonds is given by Angel et al. (2022). Preliminary work using this approach on olivine inclusions in diamond by Izraeli et al. (1999), Nestola et al. (2011a), Howell et al. (2012) and Angel et al. (2018a) evidences its potential for providing reliable information on the depth of formation of diamond–olivine pairs. In the last 5 years, researchers have also provided several freely available calculation tools to allow application of the elastic geobarometry approach (see, for example, EosFit-7c, Angel et al., 2014; EosFit7 GUI, Gonzalez-Platas et al., 2016; EosFit-Pinc, Angel et al., 2017; stRAinMAN, Angel et al., 2018b; and EntraPT, Mazzucchelli et al., 2021, all available at the following website: http://www.rossangel.com, last access: 26 May 2023) to any host–inclusion system, including for diamond–olivine pairs.

In this work, we conduct a single-crystal X-ray diffraction study on a single inclusion of olivine still trapped within the Changma diamond in order to apply the elastic geobarometry using a non-destructive approach; we have then validated the method by releasing the olivine from its diamond host, remeasuring all data by single-crystal X-ray diffraction and compositions directly by SEM-WDS-EDS. To our knowledge, these are the first reliable data on the pressure of formation for diamonds from Shandong Province, China.

2 Geological backgrounds and samples

In this study, we investigate a suite of natural diamonds selected from the kimberlite pipe of the Changma Kimberlite Belt, Shandong Province, eastern China. The kimberlites are located in the eastern part of the North China Craton (NCC), which is the oldest tectonic block in China, with crustal components dating back as far as 3.8 Ga (Liu et al., 1992; Wu et al., 2008). This craton includes greenstone belts and high-grade metamorphic terrains that underwent metamorphism at 2.5 Ga and were subsequently cratonized at 1.8 Ga as a result of the collision of the eastern and western blocks (Wu et al., 2005; Zhao et al., 2005). After 1.8 Ga, the NCC was buried by a thick succession of Mesoproterozoic to Paleozoic sediments and remained comparatively stable until the Mesozoic. From the Cambrian through the Early Ordovician, thick carbonate sedimentation defined the NCC (Ni and Zhu, 2020). The eastern NCC had significant volcanic activity and granitoid emplacement during the Mesozoic (Wu et al., 2003). In the center and eastern regions of the craton, a significant volume of alkaline basalt with mantle peridotite xenoliths and small lower crustal granulite xenoliths were erupted throughout the Cenozoic (Zheng et al., 2006; Zhang et al., 2008). According to earlier isotope chronology analyses, the Mengyin kimberlites were emplaced between 460 and 480 Ma (Yang et al., 2009; Li et al., 2011).

The Mengyin kimberlites are situated 90 km west of the significant NNE-trending Tan–Lu fault, which divides the early Proterozoic Jiaodong Group in the east from the Archean granite–gneiss of the 2500 Ma Taishan Formation in the west (Wu et al., 2005). From south to north, the Mengyin kimberlites are separated into the Changma, Xiyu and Poli belts (Yin et al., 2005; Yang et al., 2009). According to Zhu et al. (2022), nearly all kimberlites found in Mengyin areas have porphyritic textures with olivine as macrocrysts that have been serpentinized or replaced by carbonates (Fig. 1). The diamonds have a complex habit, with a prevailing octahedral form and with their longest dimension being about 3 mm, and are colorless.

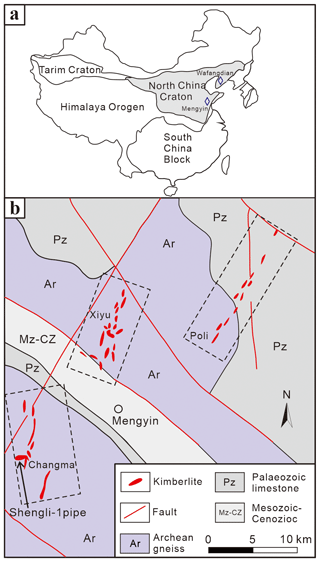
Figure 1 (a) Simplified tectonic map of China, showing the location of the two most important diamond localities in China; (b) simplified geological map of diamond-hosting kimberlites in Mengyin, Shandong (after Zhu et al., 2022).

The studied diamonds were directly collected by one of the co-authors, Huaikun Li, in 1995 from a kimberlite pipe in the Changma belt. In this work, we selected one specific diamond showing a single olivine inclusion to apply elastic geobarometry. The inclusion was located away from the surfaces of the diamond host. Its morphology under optical microscopy was not easy to describe due to the rough surface of the diamond host (Fig. 2). Using electron microscopy, after its release, the inclusion appears prismatic, with the longest axis being about 110 µm (Fig. 3).

Figure 2 Microphotograph of the olivine inclusion studied in this work still trapped within its diamond host. The low quality of the image is mainly due to roughness of the host diamond surface.

Figure 3 Backscattered electron image of the released olivine inclusion from the Mengyin host diamond.

3 Methods

3.1 Single-crystal X-ray diffraction

The olivine inclusion was measured by single-crystal X-ray diffraction before and after its release from the diamond host using a Rigaku Oxford Diffraction SuperNova diffractometer installed at the Department of Geosciences, University of Padua, Italy, equipped with a Dectris Pilatus 200K area detector and with a MoKα X-ray microsource. The instrument was controlled by CrysAlis^Pro software (Rigaku). The sample-to-detector distance was set to 69 mm, and the X-ray beam at the sample position was 120 µm. The working conditions were 50 kV and 0.12 mA. A total of 25 runs for 986 frames were collected with an exposure time of 50 s per frame, for a total of about 14 h of time for the inclusion still trapped inside the diamond host, and 40 s per frame, for a total of about 11 h of time for the inclusion released from the diamond host. Data were collected up to 2θ_max= 64^∘, and data completeness was close to 100 % for both the measurements. The R_int was 2.7 % and 3.4 % for the crystal still trapped in the diamond and released from it, respectively. For the crystal still trapped within the diamond, a special X-ray centering procedure was carried out following the same protocol in Angel et al. (2016); this allowed structural data comparable to normal “in-air” measurements to be obtained. The data were integrated using CrysAlis^Pro (version 42.23a; Rigaku Oxford Diffraction, 2021) and corrected for Lorentz and polarization effects. Structure refinement was performed using the SHELX program in the WinGX package (Farrugia, 2012; Sheldrick, 2015) in the Pbnm space group starting from published atomic coordinates (Nestola et al., 2011a). Crystallographic information files (CIFs) with full refinement details are deposited with this paper. The refinement was carried out using ionic scattering curves taken from the International Tables for X-ray Crystallography (Wilson, 1995), and anisotropic thermal parameters were refined for all atoms following Angel and Nestola (2016). These authors demonstrated, for olivine, that refinements with ionized curves for data collected up to 2θ= 60^∘ provide a Mg# (with Mg# = Mg $/$ (Mg + Fe)) which is the same, within error, as that measured by electron microprobe on the same crystal. The cationic distribution at the two different M2 and M1 crystallographic sites for the olivine inclusion was indirectly retrieved by refining the site occupancy factor of these sites (see Nestola et al., 2011a, b, for a detailed review, and Faccincani et al., 2022).

3.2 Chemical data

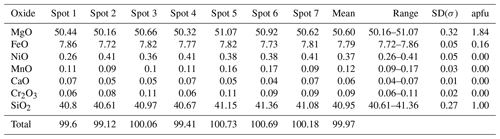
The olivine inclusion was released by mechanical crushing of the host diamond. We crushed the diamond using a steel device, then collected the olivine and positioned it on a thin section, and finally carbon-coated. This procedure did not cause any change in the inclusion in terms of crystal quality according to the X-ray diffraction analysis. The chemical composition of olivine was determined using a Tescan Solaris field-emission SEM at the Department of Geoscience at the University of Padua. This instrument is equipped with the high-resolution Ultim Max 65 Oxford Instruments silicon drift EDS. The operating conditions were 15 keV–3 nA and a 1 µm beam diameter with a working distance of 5 mm. The EDS was standardized using the following natural minerals and artificial oxides: Amelia plagioclase (Si, Al, Na), diopside (Ca), San Carlos olivine (Mg), iron oxide (Fe), manganese and titanium oxide (Mn and Ti), orthoclase (K), chromium oxide (Cr), and nickel oxide (Ni). The current was calibrated using a cobalt reference, and ZAF correction built in the Oxford AZtec software was applied. The compositional data of seven electron microprobe analyses from the released olivine are given in Table 1.

Table 1 Chemical data (in oxide wt %) for the olivine inclusion studied in this work after its release from its diamond host.

3.3 Fourier transform infrared spectroscopy

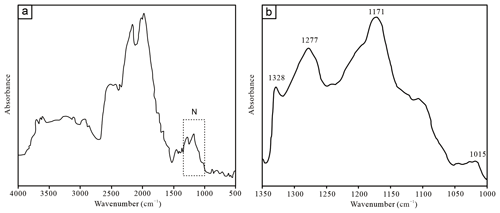
Fourier transform infrared (FTIR) measurements on diamond were acquired at the Department of Industrial Engineering, University of Padua, using a Thermo Scientific Nicolet iS50 spectrometer equipped with a Centaurus FTIR microscope and operated via OMNIC software. The spectra were collected in the 4000–500 cm⁻¹ wavelength range, averaged over 64 scans per measurement, at a spectral resolution of 4 cm⁻¹. Background spectra were collected for 120 s for each analysis after every sample acquisition. The spectrum was subtracted from its corresponding background spectrum. Measurements were performed on diamond grains collected from the crushed diamond material after the olivine inclusion was released. The grains were mounted in wax to allow transmission mode analyses with areas analyzed around 100×100 µm.

The absorbance spectra were processed using DiaMap to obtain the N content and aggregation state (Breeding and Shigley, 2009; Howell et al., 2012). This program fits the individual N absorption band and deconvolutes the spectrum in the 1000-to-1350 cm⁻¹ ranges. Then, the concentrations of nitrogen impurities aggregated in pairs (NA) and of nitrogen impurities aggregated in clusters plus vacancy (NB) were calculated using literature absorption coefficients (Boyd et al., 1994, 1995). Errors in the calculation of nitrogen content (N_tot= NA + NB) and aggregation state are considered ± 10 % (Howell et al., 2012) and depend on the quality of the FTIR spectra. Finally, we used N_tot, NA and the constants from the literature (Taylor et al., 1990; Leahy and Taylor, 1997) (i.e., $E_{\mathrm{a}}/R$ = 81160 K and ln(A) = 12.59, where E_a is the activation energy, R is the gas constant and A is the Arrhenius constant) to calculate the residence temperature, T_res, as a function of time for the olivine diamond. The FTIR approach has been used successfully for inclusion-bearing diamonds to estimate the depth of diamond formation when combined with the X-ray diffraction method (Nestola et al., 2018, 2019). A representative FTIR spectrum for the diamond host and the integrated area over the range 1350–1000 cm⁻¹ are shown in Fig. 4. Absorption within this region is related to the different nitrogen defects and N-aggregation states. The spectra we collected show a weak, sharp band at 1328 cm⁻¹ and a weak, broad band at around 1015 cm⁻¹. Two very broad and intense absorption bands appear at 1277 and 1171 cm⁻¹, respectively. The peak at 1277 cm⁻¹ can be assigned to N impurities aggregated in pairs. N impurities aggregated in clusters of four atoms, and associated structural vacancies are characterized by peaks at 1171 and 1328 cm⁻¹ (Breeding and Shigley, 2009). The peak at 1015 cm⁻¹ is not discussed in the literature; however, it is likely that it could be the secondary B-aggregate absorption and should be proportional to the 1171 cm⁻¹ absorption (Christopher M. Breeding, personal communication, 2023).

Figure 4 (a) Representative FTIR spectrum of the diamond host studied in this work. The absorbance region of N impurities is indicated. (b) Enlargement of the spectrum of diamond in the N impurity region.

4 Results

4.1 Chemical composition and diffraction data of the olivine inclusion

Backscattered electron images of the released crystal show clear evidence for chemical homogeneity over the entire crystal (see Fig. 3). The complete chemical analysis of the released olivine, given in oxide weight percent (wt %) is reported in Table 1. Data quality is demonstrated by an oxide total of 99.97 wt % combined with a calculated cation stoichiometry of 3.003, both within the error of ideal values.

Based on the data in Table 1, the empirical formula of the crystal can be written in terms of Mg, Fe, Si and O alone, as all other elements (as expected for olivine inclusions in diamonds; see Nestola et al., 2011a) are <0.015 atoms per formula unit (apfu) for four oxygens; the formula is as follows: Mg_1.84Fe_0.16SiO₄, with Mg# = 0.92. A composition of Mg# = 0.92 is consistent with most lherzolitic peridotites (see Stachel and Harris, 2008), while Mg# = 0.935 is closer to a harzburgitic peridotite.

Single-crystal X-ray diffraction data for the olivine inclusion still trapped in its diamond host are of very high quality, with a refinement R₁= 1.42 %. The anisotropic refinement and the general quality of the refinement allowed us to retrieve the cationic distribution at the M2 and M1 crystallographic sites indirectly, by refining the site occupancy factor of these sites. Stachel and Harris (2008) analyzed compositional data for more than 800 olivine inclusions released from diamonds and showed that the sum of Ca, Ni, Ti, Mn, Na and Ni is less than 0.01 apfu, which means that the formula of olivine inclusions in diamonds can be expressed solely in terms of the Mg and Fe content of M sites. On this basis, X-ray data imply that the olivine inclusion here has the following formula: Mg_1.82Fe_0.18SiO₄, with Mg# = 0.91.

Using a refinement approach identical to X-ray data collected on the inclusion after its release and after its analysis by SEM, we obtained R₁= 1.44 % and, as expected, the identical cationic distribution obtained for the inclusion while still entrapped in its diamond host. From here, we obtained an identical chemical formula Mg_1.82Fe_0.18SiO₄, with Mg# = 0.91. As such, crystal structure refinements for the trapped and released olivine inclusion result in an identical, inferred Mg# of 91, in close agreement with the value Mg# = 92 obtained by accurate and precise standardized and high-resolution SEM-EDS chemical analyses. The unit-cell volumes of the sample studied in this work are reported in Table 2, whereas all crystallographic information is reported in the CIFs deposited with the paper.

Table 2 Unit-cell volume (and residual pressure, P_inc) of the olivine inclusion still trapped in its diamond hosts (second column), released from it (third column) and calculated (last column) from the crystal structure refinement (see text for more details).

Note the unit-cell volume in column 4 was obtained using the linear regression V (ų)= 307.12–0.1585× % Fo (see the text).

The results from this study show that in the case of high-quality structural data (refinements with very low R₁) collected on olivine inclusions in diamonds, using ionized scattering curves, collecting data at 2θ values not lower than 60^∘ and refining all atoms anisotropically, we can retrieve “compositional” information consistent with that collected using electron beam techniques. This result is especially important for (a) non-destructive investigation of precious stones such as diamonds and (b) investigation of diamonds with multiple olivine inclusions, where in situ X-ray characterization, followed by inclusion extraction, preparation and chemical analysis, is a lengthy and complex process.

4.2 Infrared spectroscopy on the diamond host

FTIR measurements on the host diamond indicate an average N content (N_tot) of 135 ppm and an aggregation of B defect percentage (% IaB) of 74.3 %. These data allow us to classify the diamond as Type IaAB (Chrenko et al., 1977; Breeding and Shigley, 2009). Since geochronological work on Mengyin diamonds was not available, we used ages of 1 Ga and 3 Ga to calculate the T_res at these different ages, respectively. The calculations from this work indicate a mantle residence temperature, T_res, of 1189 ^∘C for the diamond, assuming a mantle residence time of 3 Gyr and of 1218 ^∘C with a shorter assumed mantle residence time of 1 Gyr. Since a short residence at a higher T during the early history of the diamond would not have produced significant effects on the final N-aggregation state (Taylor et al., 1990), the estimated T_res of 1189–1218 ^∘C can be considered a minimum T estimate for diamond formation, with the average T_trap for the residence time between 1 and 3 Gyr being 1204 ^∘C. These crystallization temperatures can be compared with data on Shandong diamonds by Wu et al. (2022), who, through FTIR analyses, provided temperatures in the range 1118–1237 ^∘C, with a mean of 1160 ^∘C, at an assumed diamond formation age of 3 Ga.

5 Elastic geothermobarometry applied to the olivine–diamond pair and their depth of formation

5.1 Choosing the best pressure–volume–temperature equations of state

Application of the elastic geobarometry approach used for single inclusions is dependent on the absence of fractures and a distance of the inclusion from the external faces of the diamond host equal at least to about 3 times the average radius of the inclusion (see Mazzucchelli et al., 2018). Relatively to the fractures, for the inclusion studied in this work, we are not able to completely assure that at the interface between the inclusion and the diamond there are no fractures. However, based on previous data of residual pressures measured on olivine inclusions in diamonds, varying between 0.4 and 0.6 GPa (for instance, Izraeli et al., 1999; Nestola et al., 2011a; Howell et al., 2012), we are quite confident that the diamond–inclusion pair studied in this work, showing a significantly larger P_inc of 1.4 GPa, is not affected by significant fractures; at the same time and for the same reason, it is likely that the inclusion is positioned inside the diamond sufficiently far from the external surfaces of the diamond host not to have released pressure.

The second most important aspect in calculating the depth of formation of the diamond–olivine pair is the choice of pressure–volume–temperature equations of state (PVT-EOSs) for the two phases. For the cubic diamond host, the choice of PVT-EOS is much simpler (Angel et al., 2022) as we can use the published data by Angel et al. (2015), with bulk modulus K₀= 444 GPa, first-pressure derivative K^′ = 4, thermal expansion coefficient α₀= $\mathrm{2.672}\times {\mathrm{10}}^{-\mathrm{6}}$ K⁻¹ and Einstein temperature θ_E= 1500 K, adding the contribution of the shear modulus G₀= 535 GPa. For the olivine inclusion, four published PVT-EOSs can be used (Angel et al., 2018a), termed (1) BM3-MGD.eos, (2) BM4-MGD.eos, (3) BM3-Isothermal.eos and (4) BM4-Isothermal.eos (all these four can be downloaded at http://www.rossangel.com, where EOS data are reported). Both (2) and (4) are useful for data above 15 GPa; since the diamond we have studied definitely formed below 10 GPa, these two PVT-EOSs were not used.

In Fig. 6 in Angel et al. (2018a), for temperatures at 1500 K (the residence T_res of the diamond here studied was calculated between 1189 and 1218 ^∘C and, therefore, is consistent with conditions covered in Fig. 6 in Angel et al., 2018a), the two PVT-EOSs (1) (BM3-MGD.eos) and (3) (BM3-Isothermal.eos) provide a means to assess which is the best fit of experimental data of olivine at high pressure and high temperature: indeed, the experimental data for pressures between 5 and 10 GPa at 1500 K lie exactly at the average between the two PVT-EOSs.

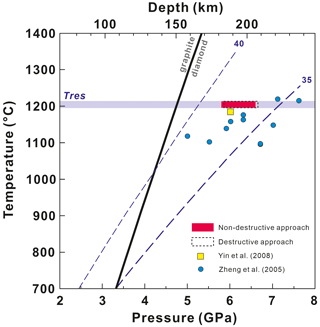
Figure 5 Pressure–temperature diagram showing the calculated pressure of entrapment P_trap for the diamond–olivine pair studied in this work (rectangles represent experimental uncertainties). T_res is the residence T based on the diamond N-aggregation state. Conductive geotherms for 35 and 40 mW m⁻² are quoted from Hasterok and Chapman (2011); the diamond–graphite boundary is quoted from Day (2012).

A further complication in the calculation comes from the possible presence of a fluid rim around olivine inclusions, as shown by Nimis et al. (2016). In Angel et al. (2018a), these authors stated that the presence of such a fluid ensures hydrostatic conditions and, therefore, makes the use of PVT-EOSs valid. A more recent paper published in this European Journal of Mineralogy special issue (Angel et al., 2023) provides detailed analysis of the effect of the presence of such fluid on the entrapment pressure; Angel et al. (2023) state that if we neglect the presence of the fluid rim and use only the PVT-EOSs for olivine, the pressure of entrapment P_trap will be 0.4 GPa too high at 1100 ^∘C. This error decreases with increasing P_trap and is close to zero for P_trap between 6.5 and 7 GPa. We were not able to detect a fluid rim around the olivine inclusion investigated here (this is usually done by micro-Raman spectroscopy) because the roughness of the diamond surface prevented measurement; therefore, we first calculate P_trap and then consider the error that could be accounted for by the presence of fluid.

Summarizing, we can now calculate depth of formation (see next section) using the PVT-EOS of diamond, using an average EOS based on two PVT-EOSs of olivine (1 and 3). All the PVT-EOSs used in this work are provided in the Supplement.

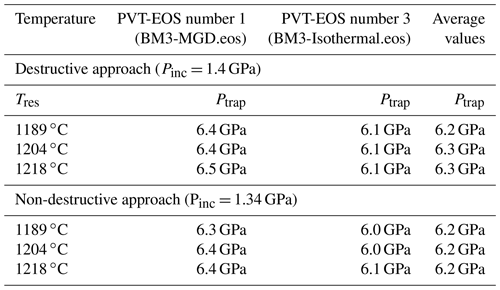
Table 3 Entrapment pressure, P_trap, as a function of the minimum, average and maximum residence temperature, T_res, at P_inc = 1.4 GPa for the destructive approach (olivine inclusion released from its diamond host) and at P_inc= 1.3 GPa for the non-destructive approach (all calculated from the crystal structure refinement). In the last column, the average value between the two EOSs used is reported. The uncertainty in the average value is estimated to be 0.4 GPa.

5.2 Calculation of the depth of formation

The measured unit-cell volume of the olivine inclusion obtained by X-ray diffraction on the released crystal is equal to V= 292.80 ± 0.07 ų, compared to a volume measured when the inclusion was still within the diamond host of V= 289.70 ± 0.2 ų (see Table 2). Even if the volume measured on the inclusion still trapped in the diamond has an uncertainty slightly larger than that of the released one (expected considering that the released one was measured without a surrounding diamond matrix), the two volumes are experimentally comparable, and thus, their difference directly provides a residual pressure P_inc of 1.4 GPa. As stated in Sect. 5.1, this value is calculated using PVT-EOSs (1) and (3); for the P_inc, the two EOSs indeed provide the same value to 3 s.f. (PVT-EOS (1) gives P_inc= 1.382 GPa; PVT-EOS (3) gives P_inc= 1.4 GPa). The calculation of P_inc is performed using the EosFit Calculator software (see http://www.rossangel.com). Propagating experimental uncertainties from the unit-cell volumes, we estimate an uncertainty in P_inc equal to 0.1 GPa; therefore, the final calculation provides P_inc= 1.4 ± 0.1 GPa.

As described in Sect. 4.1, diffraction data allow calculation of the composition of the olivine inclusion, Mg_1.82Fe_0.18SiO₄, with Mg# = 91. For this composition, we calculate a unit-cell volume at room pressure and temperature equal to V= 292.70 ų. As such, this demonstrates how the volume of the olivine inclusions at room pressure and temperature can be determined using a completely non-destructive approach. This volume was calculated using unit-cell volume data for olivines along the forsterite (Fo)–fayalite (Fa) join published by Nestola et al. (2011b) for natural Fo₈₀ (V= 294.17 ų), Fo₇₂ (V= 295.98 ų) and Fo₆₂ (V= 297.28 ų) and by Poe et al. (2010) for Fo₁₀₀ (V= 291.15 ų) and using the volume of the inclusion Fo₉₂ (V= 292.80 ų) measured after its release from the diamond in this work. The linear regression using these volume–composition data (the Fo–Fa join is an ideal solid solution; thus, the volume must change linearly with Fo $/$ Fa variation) is expressed by V (Å${}^{\mathrm{3}})=\mathrm{307.12}-\mathrm{0.1585}\times$ % Fo (R²= 0.9929; the uncertainty estimate from this equation is about 0.3–0.4 Å in the volume). Using the calculated volume of the inclusion from the above linear regression (i.e., V= 292.7 ų), we get P_inc= 1.3 ± 0.2 GPa, which nearly overlaps with the P_inc of 1.4 ± 0.1 GPa obtained using data from the released crystal (which necessitated destruction of the diamond host).

The depth of formation calculated using the residual pressure obtained from volume data on the crystal still trapped, as well as on the same crystal released from the diamond host, can be calculated using EosFit-Pinc (Angel et al., 2017) and using the PVT-EOSs described above for diamond and olivine. The calculation is performed varying the temperature from the minimum T_res= 1189 ^∘C to the maximum T_res= 1218 ^∘C, with the average at 1204 ^∘C. The entrapment pressures at different temperatures using the two PVT-EOSs selected for olivine including the average values are reported in Table 3. Average values are assumed here as the most likely depth of formation, and uncertainty is estimated from minimum and maximum values obtained using the two PVT-EOSs at the minimum and maximum T_res, i.e., 0.4 GPa.

This 0.4 GPa uncertainty also takes into account (a) the effect of any fluid rim around the inclusion, as the uncertainty due to the presence of a fluid film is close to zero from P_trap= 6.5 GPa, which is very close to the average value at 1204 ^∘C, and (b) the uncertainty in the determined residual pressure P_inc.

The same results reported in Table 2 can be reproduced using P_inc= 1.3 ± 0.2 GPa calculated on the inclusion using a non-destructive approach (refining the crystal structure of the inclusion). Indeed, for T_res= 1204 ^∘C and P_inc= 1.3 GPa, we can calculate P_trap= 6.2 GPa, which overlaps to the value of 6.3 GPa reported in Table 3 for the destructive approach and is well within the uncertainty of 0.4 GPa estimated for the entire P_trap calculation.

Importantly, as evident from Table 3, we demonstrate that for high-quality, in situ crystal structure refinement of trapped inclusions, we can retrieve reliable values of depth of formation for diamond–olivine pairs within an uncertainty of 0.4 GPa. This uncertainty would also include the uncertainty that could derive from the possible presence of a fluid rim around the inclusion (Nimis et al., 2016; Angel et al., 2023).

6 Discussions

In this work, we were able to refine the crystal structure of an olivine inclusion still entrapped in its diamond host, with the aim of determining their depth of formation using a fully non-destructive approach. The refinement provided compositional information on olivine, determined as Fo₉₁. The calculated unit-cell volume for this composition was calculated to be V= 292.7 ± 0.4 ų using a linear regression expressing the unit-cell volume of olivine as a function of forsterite–fayalite components. These results, obtained by a truly non-destructive approach, were validated here by releasing the inclusion from its diamond host and measuring its real chemical composition by SEM-EDS analysis and its post-entrapment unit-cell volume by single-crystal X-ray diffraction. In detail, SEM-EDS data imply a composition Fo₉₂ (identical to that inferred by the non-destructive method within the experimental uncertainty) and the unit-cell volume of the real crystal after release is 292.80 ± 0.07 ų, which is totally comparable to the volume determined by the non-destructive method confined to the experimental uncertainty.

The entrapment pressure P_trap calculated using elastic geobarometry and the data measured on the crystal released from its diamond host (i.e., destructive approach) provided an average value of 6.3 ± 0.4 GPa for a residence temperature T_res= 1204 ± 15 ^∘C. P_trap calculated using the data on the inclusion still trapped in its diamond host (i.e., non-destructive approach) provided an average value of 6.2 GPa, identical within error to the value 6.3 GPa (both calculated at the same T_res). In terms of depth of formation, these data imply diamond formation at about 188 ± 12 km.

From a technical point of view, the data we provided definitively show that in the case of a large diamond suite with tens of diamonds to be investigated or in the case of the study of precious diamonds, a non-destructive approach can be adopted to determine their depth of formation. Application of this approach likely results in negligible differences with respect to the calculated depth obtained by a destructive method. However, it should be noted that this is true only when the structural data obtained on the inclusions still trapped in their diamond hosts are of extremely good quality and when specific refinement protocols are used (see Angel and Nestola, 2016).

From a geological point of view, the data we provided report indication of depth of formation by elastic geobarometry for a Chinese diamond using single-crystal X-ray diffraction. The depth of 188 km at a residence time of about 1204 ^∘C indicates that this diamond formed on a conductive geotherm lying between 35 and 40 mW m⁻².

Pressures of formation for Shandong diamonds have been determinedly previously by Yin et al. (2005, 2017) and Yin et al. (2008). Yin et al. (2005, 2017) provided a residual pressure P_inc= 0.65 GPa, determined by micro-Raman spectroscopy on olivine inclusions in diamonds. Yin et al. (2005) used a residence temperature T_res= 1184 ^∘C, given by Chi and Lu (1996) and calculated using phase equilibria for mineral inclusions in diamond. Using the above residual pressure, we can calculate P_trap using the same equations of state used in this work; this calculation gives an average P_trap of 5.08 GPa at 1184 ^∘C. However, we must be aware that the experimental approach used by these authors may not provide a reliable residual pressure for olivine inclusions in diamond for two reasons: (1) the inclusions were not measured before and after their release from the diamond host (and using the same instrument), and thus the actual positions of the Raman bands of olivine at room pressure cannot be determined with precision and accuracy; (2) micro-Raman spectroscopy on solid inclusions in diamonds cannot be simply treated like micro-Raman spectroscopy performed on minerals studied inside a diamond-anvil cell under hydrostatic conditions (Angel et al., 2022). Yin et al. (2017), in order to provide the Raman shift of their olivine inclusions inside the diamond hosts, used data on the Raman shift that olivine shows when compressed hydrostatically within a diamond-anvil cell. This is not a trivial exercise because a “solid olivine” inside a “solid diamond” certainly does not behave identically to a solid olivine inside a hydrostatic fluid, such as that used inside a diamond-anvil cell. As such, residual pressures of olivine inclusions in diamond calculated from Raman spectra must be treated with caution.

Yin et al. (2008) reported values of pressure and temperature of inclusions in diamonds using the well-known Cr-in-diopside geothermobarometer by Nimis and Taylor (2000), and they determined a value for a diamond from Shandong of 6.0 GPa for a temperature of 1194 ^∘C.

A further study indicated that chemical geothermobarometry applied to inclusions in Shandong diamonds is that of Chi and Lu (1996). However, these authors stated that they applied geothermobarometry to inclusions from different diamonds. Chemical geothermobarometry is, strictly speaking, applicable only for demonstrable chemical equilibrium between phases within the same diamond (see Nimis, 2022). If the inclusions in one diamond are not able to freely exchange components or, even worse, the inclusions are not from the same diamonds, then results from geothermobarometry must be considered with extreme caution, as is the case for the data provided by Chi and Lu (1996).

7 Conclusions

Summarizing, we show in Fig. 5, based on the results we obtained in this work, new data of P and T of formation for Shandong diamond together with the data from Yin et al. (2008) with their value of 6 GPa and 1194 ^∘C. Combining the data we collected and those from Yin et al. (2008) (considering their clinopyroxene syngenetic with its diamond host), we can state that, at least for the diamonds studied in these two works, they formed at depths between 180 and 190 km on a geotherm close to 36–37 mW m⁻². This range of depth of diamond formation lies at the upper limit of the depth global mode (e.g., depth of 175 ± 15 km) for the formation of lithospheric diamonds worldwide (Nimis et al., 2020). These results are similar to modern conductive steady-state cratonic geotherms and would indicate, for ancient diamond formation, early cooling of cratonic lithosphere (Stachel et al., 2022). In addition, this geotherm range is in agreement with Griffin et al. (1998) and Zheng et al. (2005), who studied several xenoliths from Shandong kimberlites (i.e., same locality as that of the diamond studied in this work); these authors reported a geotherm between 36 and 40 mW m⁻². The data from kimberlite xenoliths from Zheng et al. (2005) were also added to Fig. 5, showing a general agreement with the data obtained on the diamond studied in this work.