High-pressure and high-temperature structure and equation of state of Na₃Ca₂La(CO₃)₅ burbankite

In this study we report the synthesis of single crystals of burbankite, Na₃Ca₂La(CO₃)₅, at 5 GPa and 1073 K. The structural evolution, bulk modulus and thermal expansion of burbankite were studied and determined by two separate high-pressure (0–7.07(5) GPa) and high-temperature (298–746 K) in situ single-crystal X-ray diffraction experiments. The refined parameters of a second-order Birch–Murnaghan equation of state (EoS) are V₀= 593.22(3) ų and K_T0= 69.8(4) GPa. The thermal expansion coefficients of a Berman-type EoS are α₀= 6.0(2) $\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹, α₁= 5.7(7) $\times {\mathrm{10}}^{-\mathrm{8}}$ K⁻² and V₀= 591.95(8) ų. The thermoelastic parameters determined in this study allow us to estimate the larger density of burbankite in the pressure-temperature range of 5.5–6 GPa and 1173–1273 K, with respect to the density of carbonatitic magmas at the same conditions. For this reason, we suggest that burbankite might fractionate from the magma and play a key role as an upper-mantle reservoir of light trivalent rare earth elements (REE³⁺).

1 Introduction

Carbonatites constitute important ore concentrations of strategic metals, including Nb and rare earth elements (REEs) (Simandl and Paradis, 2018). Carbonates are an important fraction of minerals which concentrate REE elements, and burbankite, (Na,Ca)₃(Sr,Ba,Ce,REE)₃(CO₃)₅, is one of the REE-bearing carbonates in these ore deposits (Wall et al., 2001; Edahbi et al., 2018). Carbonates form as primary crystallizing minerals in magmatic environments, and they may often undergo hydrothermal alteration in successive geologic processes (Zaitsev et al., 2002; Smith et al., 2018).

The burbankite group consists of mineral species which are hexagonal or monoclinic carbonates, characterized by the general formula A₃B₃(CO₃)₅ (Belovitskaya and Pekov, 2004). In the crystal structure of hexagonal members of this group there are two independent cationic sites, A and B, coordinated by 8 and 10 oxygens, respectively, with the formation of AO₈ and BO₁₀ polyhedra. Depending on the considered mineral species, the A site is primarily occupied by Na, Ca and REE³⁺ cations, together with some vacancies, while Sr, Ca, Ba and REE³⁺ cations are in the B site (Belovitskaya and Pekov, 2004). Three carbonate groups are positioned in three different orientations (Belovitskaya and Pekov, 2004). Minerals of this group can occur as hexagonal prismatic crystals, but they can be found more frequently as irregular grains or in their aggregates (Belovitskaya and Pekov, 2004). They are usually transparent; the lustre varies from vitreous to greasy, and in general these minerals do not have any cleavage. They can occur in many different colours (e.g. yellow, green, pale brown, pink), but they are more frequently colourless or white (Belovitskaya and Pekov, 2004).

Burbankite can be found as a primary crystallizing mineral in magmatic systems (e.g. Smith et al., 2018) and as a mineral precipitated from alkaline solutions in lacustrine sediments (Green River Formation in Wyoming; Fitzpatrick and Pabst, 1977) or in caves (Cioclovina cave in Romania; Onac et al., 2009). It is also the most abundant mineral of the group; in fact in one type of “rare earth carbonatites” (e.g. Khibiny, Gornoe Ozero), together with its alteration products, it forms ample accumulations, being potentially the most industrially interesting material for the extraction of REEs, Sr and Ba (Belovitskaya and Pekov, 2004).

Recently, a sodium and calcium carbonate with burbankite structure has been synthesized at high pressure, 6 GPa, and temperature, 1323 K (Rashchenko et al., 2017). The possibility of tuning the chemistry of this material, as a function of pressure and temperature, also suggests the possible existence of a new class of synthetic carbonates with promising non-linear optical properties (Gavryushkin et al., 2014; Rashchenko et al., 2017). Together with alkaline–alkaline earth fluoride carbonates (e.g. Zou et al., 2011), they can lead to an expansion of the interest on carbonates in material science.

Alkaline-rich carbonates are relevant as ore minerals, and they might also play an important role in deep carbonatitic environments as their high-pressure phases may fractionate elements from a carbonatitic melt crystallizing in upper-mantle conditions (Shatzky et al., 2016a, b; Podbordnikov et al., 2019). The experimental determination of Na₂CO₃–K₂CO₃–CaCO₃–MgCO₃ systems at high pressures and temperatures has in fact revealed that above 3 GPa, new classes of Ca-rich alkaline–alkaline earth carbonates are stabilized and are primary liquidus phases, with a possible important role in fractionation of deep carbonatites (Shatzky et al., 2016a, b; Podbordnikov et al., 2019). Burbankite is among these carbonates (Shatzky et al., 2016a, b).

As mentioned above a burbankite-like structure phase was already synthesized at 6 GPa and 1323 K with a composition Na₂Ca₄(CO₃)₅ (Rashchenko et al., 2017). This result reveals the flexibility of this structure in a wide compositional range. Because of the important role of Ca-rich alkaline–alkaline earth carbonates as candidate minerals in upper-mantle carbonatitic systems and the successful synthesis of Na₃Ca₂La(CO₃)₅ at 5 GPa and 1073 K (Merlini et al., 2020), which proves the incorporation of light REE³⁺ (LREE³⁺) in upper-mantle conditions in a burbankite-like structure, we decided to further investigate the crystal chemical evolution and thermoelastic properties of this phase. The paper reports the characterization and the determination of thermoelastic properties of synthetic Na₃Ca₂La(CO₃)₅ at high pressure and temperature.

Figure 1 Burbankite synthetic batch. Dark grey minerals are burbankite crystals, while white spots are a Ca-rich La oxide.

2 Experimental

The synthesis of burbankite single crystals (up to $\mathrm{500}\times \mathrm{200}\times \mathrm{100}$ µm³) was carried out at the experimental petrology laboratory at the Department of Earth Sciences, University of Milan (Italy) (DES-UM), using a multi-anvil module. Carbonate powders were mixed in a stoichiometric proportion of the burbankite chemical composition, Na₃Ca₂La(CO₃)₅. A platinum capsule of 3.5 mm length and 2 mm diameter was used to pack the starting composition and later welded. The multi-anvil experiment was performed with a Cr-doped MgO octahedron of 25 mm edge length combined with tungsten carbide cubes of 32 mm truncation-edge lengths. For the experiment a graphite heater was employed, and temperatures were measured by a Pt-PtRh thermocouple (S type). Temperature is accurate to ± 20 K, with no pressure correction for the e.m.f. (electromotive force) of the thermocouple. Pressure uncertainties were assumed to be ± 3 % according to the accuracy of calibrant reactions (Fumagalli and Poli, 2005). Samples were synthesized at 5 GPa and 1073 K (ramp rate at about 40 K min⁻¹) with a run duration of 24 h. The assemblage of the recovered sample is burbankite and a Ca-rich La oxide (Fig. 1). The two phases were characterized via electron microprobe analyses (EMPAs) at the DES-UM using a Jeol 8200 electron microprobe operating at 15 nA and 15 kV.

The structure of burbankite was obtained by a single-crystal X-ray diffraction measurement at the DES-UM at room temperature using a four-circle κ-geometry Rigaku XtaLAB Synergy diffractometer. The instrument is equipped with a PhotonJet (Mo) X-ray source, operating at 50 kV and 1 mA, with a monochromatized MoKα radiation, and with a hybrid pixel array detector. A single crystal of ca. $\mathrm{100}\times \mathrm{50}\times \mathrm{50}$ µm³ was picked from the experimental charge and glued on a glass fibre, which was attached to a metallic pin and mounted on a goniometer head. During the measurements the detector-to-sample distance was 62 mm and the measurement strategy was programmed with a combination of scans in ω with a 0.5^∘ step and with an exposure time of 1.25 s at each scan step for different 2θ, κ and ϕ positions. Data reductions, including Lorentz–polarization and absorption correction based on the implemented semi-empirical ABSPACK routine, were performed using the software CrysAlis Pro (Rigaku Oxford Diffraction, 2019).

In situ high-pressure (P_H) single-crystal X-ray diffraction measurements have been carried out at the beamline Xpress of the Italian synchrotron Elettra (Basovizza, Italy) up to ca. 7.07 GPa. A synthetic single crystal of burbankite was loaded in a BX90-type diamond-anvil cell (DAC; Kantor et al., 2012). The pressure-transmitting medium used in this experiment was a mixture of methanol : ethanol in 4:1 proportions, which transmits pressure hydrostatically up to the maximum pressure reached in this experiment (Klotz et al., 2009). Ruby fluorescence was used as a pressure standard, and the pressure uncertainty is about 0.05 GPa. The standard P_H single-crystal diffraction setup was used (Lotti et al., 2020), using the MAR3450 imaging plate detector with an X-ray wavelength of 0.49450 Å. The beam size on the sample was approximately 80×80 µm², and the crystal size was ca. $\mathrm{40}\times \mathrm{40}\times \mathrm{20}$ µm³. To extract intensity suitable for structure determination, improvement in data collection protocols has been specifically designed. Automatic alignment of the sample based on its absorption assured the full illumination of the sample during the whole rotation range. The reduced rotation speed during step scans (0.25^∘ s⁻¹) and software synchronization between sample positioning and fast shutter operation resulted in a significant reduction in the R_int of integrated intensities down to 2 %, thus allowing a reliable structural data analysis. The measurement strategy at each pressure step was programmed as ω scans in the range ± 38^∘ with a 1^∘ step scan.

Thermal expansion of burbankite was also characterized by in situ high-temperature (T_H) single-crystal X-ray diffraction measurement at the XRD1 beamline at the Italian synchrotron Elettra (Basovizza, Italy). The wavelength during the experiment was 0.7000 Å, and the detector used was a Pilatus 2M. A single crystal of synthetic burbankite, together with a single crystal of quartz used as standard, was loaded in a quartz-glass capillary, and during the measurement crystals were kept steady with quartz-glass fibres. During the experiment a hot air gas blower was used to increase the T every 30 K in a temperature range from ca. 298 to ca. 746 K, with T uncertainties of ± 1 K. The beam size on the sample is approximately 80×80 µm², and the crystal size, for both the samples, was ca. $\mathrm{60}\times \mathrm{60}\times \mathrm{40}$ µm³.

3 Results

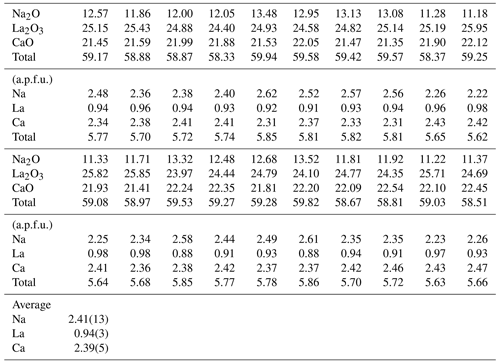
Twenty points were measured on the synthetic batch of the burbankite experiment by EMPA, and the resulting composition is shown in Table 1. The average empirical formula calculated from the 20 analyses and based on 5 oxygens p.f.u. is Na_2.41(14)Ca${}_{\mathrm{0.33}\left(\mathrm{5}\right){\mathit{\square }}_{\mathrm{0.26}}}$Ca_2.06(5)La_0.94(3)(CO₃)₅. Based on the empirical formula calculated on the EMPA data, some vacancies have been evidenced.

Table 1 Major element composition (in wt %) of the synthetic single crystals of burbankite in this study. The chemical formula has been calculated on five oxygens.

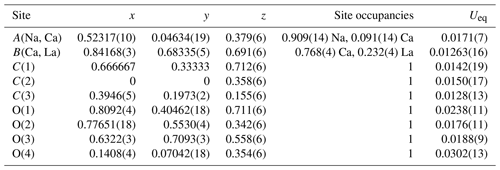
The refined unit-cell constants are a= 10.4238(2) Å, c= 6.2910(2) Å and V= 591.97(2) ų in ambient conditions. The structural solution and refinement were performed in the hexagonal P6₃mc space group using the crystallographic software Jana2006 (Petricek et al., 2014) in agreement with previous studies (Belovitskaya and Pekov, 2004). The burbankite structure is characterized by the presence of two independent cationic sites, A and B, coordinated by 8 and 10 oxygens, respectively, with the formation of AO₈ and BO₁₀ polyhedra and three carbonate sites, which all have different orientations (Fig. 2a). The 8-fold coordination polyhedra form infinite columns disposed at zigzags along the c axis, where neighbouring polyhedra share their faces. The 10-fold coordination polyhedra also form infinite columns made of rings (composed of three 10-fold coordination polyhedra sharing their corners) parallel to the a–c plane, and in the middle of these rings a carbonate lies parallel to the a–b plane, and they share both corners and edges with the 10-fold polyhedra. On the top of each 10-fold polyhedron there is a carbonate group in an oblique direction. These so-formed modules repeat along the c axis but rotated by 180^∘ (Fig. 2b). The site occupancy refinement confirms the presence of Na and Ca in the A site, and of Ca and La in the B site. The principal statistical parameters of the structure refinement are listed in Table 2. Atomic coordinates and site occupancies of structure refinements are given in Table 3. Anisotropic displacement parameters and relevant bond distances are reported in Tables S1 and S2 in the Supplement. The crystallographic information file is also available in the Supplement.

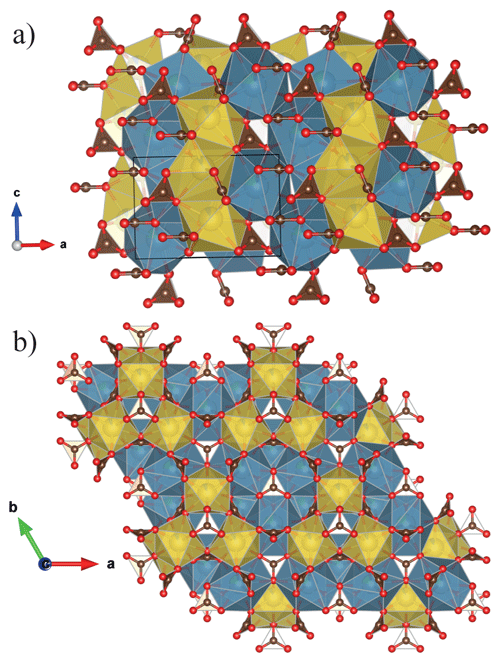
Figure 2 Crystal structure of burbankite (a) projected parallel to [001] the zigzagged AO₈ (yellow) and (b) parallel to (001) where we can observe the 3-fold ring made of BO₁₀ (blue). The representations of the structure are realized using the program VESTA (Momma and Izumi, 2011).

Table 2 Details pertaining to the data collections and structure refinements in ambient conditions of the burbankite studied in this work.

Table 3 Atomic coordinates, site occupancies and equivalent displacement parameters (Ų) in ambient conditions of the burbankite studied in this work.

The evolution of the unit-cell parameters of burbankite at different pressures (P) is reported in Table 4. The volume decreases smoothly with increasing pressure, as shown in Fig. 3, up to the maximum hydrostatic pressure reached in this study of ca. 7 GPa. No phase transition or change in the deformation mechanisms occurs within the P range investigated. The P–V data were fitted using a second-order Birch–Murnaghan equation of state (BM2-EoS; Birch, 1947), since the Eulerian finite strain (fe) vs. normalized stress (Fe) plot (Fe–fe plot, Fig. S1 in the Supplement) of the data can be fitted by a horizontal line (Angel, 2000). The BM2-EoS coefficients were refined simultaneously; data were weighted by their uncertainties in P and V, using the program EoSFit7c (Angel et al., 2014), giving V₀= 593.22(3) ų, K_T0= 69.8(4) GPa and K${}^{\prime }=\mathrm{4}$ fixed (${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}=$ 2.04, and $\mathrm{\Delta }{P}_{\text{max}}=-\mathrm{0.14}$ GPa). The axial compressibility is reported in Fig. S2, and analysis of elastic behaviour indicates large anisotropy, with the a axis less compressible with respect to the c axis.

Table 4 Lattice parameters of burbankite at different pressures, collected using methanol : ethanol (4:1) as the P-transmitting medium (P uncertainty ± 0.05 GPa).

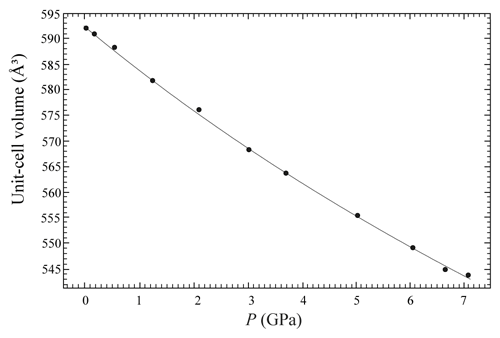
Figure 3 Evolution of the unit-cell volume with pressure of burbankite. The solid line represents the BM2-EoS fit.

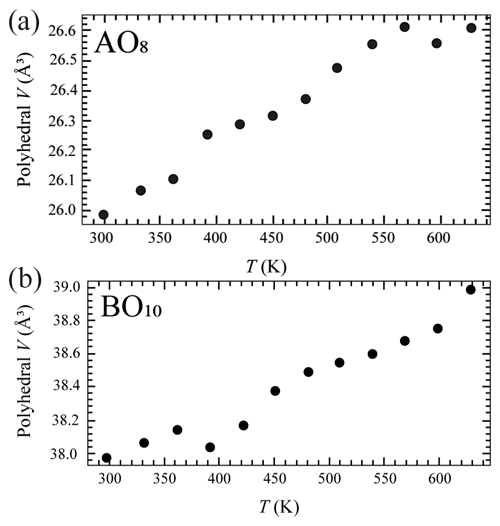
The temperature (T)–volume (V) data collected during the experiment at ambient pressure are reported in Fig. 4 and Table 5. As can be observed from Fig. 4, V increases continuously without evidence of phase transition up to the maximum T reached in this study. The V–T data were fitted using EosFit7c (Angel et al., 2014) using a Berman-type equation of state (EoS) (Berman, 1988). The thermal expansion coefficients obtained are α₀= 6.4(1) $\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹, α₁= 3.3(5) $\times {\mathrm{10}}^{-\mathrm{8}}$ K⁻² and V₀= 591.86(4) (${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}=$ 1). The axial thermal expansion is reported in Fig. S3, and analysis of thermal behaviour of the axes with T indicates large anisotropy, with the a axis less expandable with respect to the c axis.

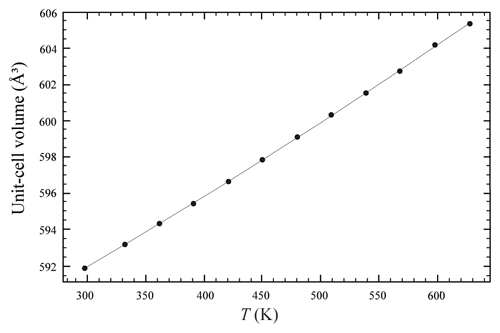
Figure 4 Evolution of the unit-cell volume with temperature of burbankite. Data were fitted with a Berman-type EoS (solid line).

Crystal structure refinements at variable pressures indicate that the 8-fold coordination polyhedra are more compressible than the 10-fold coordinated ones showing an inverse behaviour of the two polyhedra with respect to their volume (Hazen and Finger, 1982). In fact, the smaller polyhedron is slightly more compressible with respect to the bigger one. If we try to fit the volume variation of the two polyhedra with a BM2-EoS, we obtain K_T0= 54(2) GPa for the 8-fold coordinated polyhedra (Table S3 and Fig. 5a), while for the larger one, K_T0= 72(3) GPa (Table S3 and Fig. 5b). Single-crystal structure refinements at variable temperatures reveal a similar thermal expansion for both polyhedra (Fig. 6a and b and Table S4).

Table 5 Lattice parameters of burbankite at different temperatures, collected in a quartz vial (T uncertainty ± 1 K).

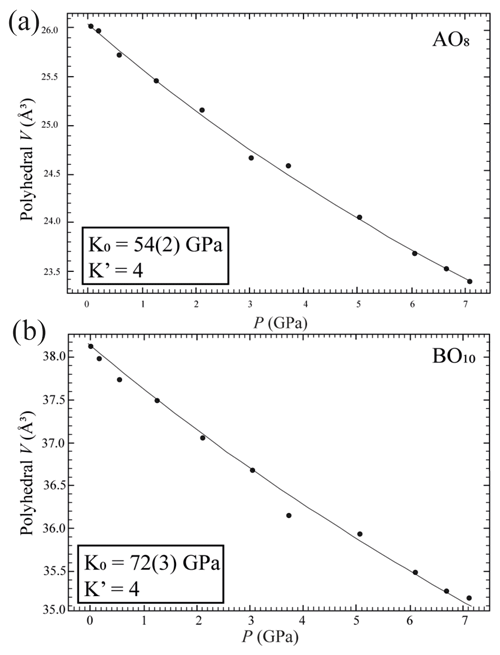
Figure 5 Pressure-induced evolution of AO₈ (a) and BO₁₀ (b) polyhedra in the crystal structure of burbankite. The solid black line represents a BM2-EoS fit to the data.

Figure 6 Temperature-induced evolution of AO₈ (a) and BO₁₀ (b) polyhedra in the crystal structure of burbankite. The fitted thermal expansion using a one-term Holland-and-Powell curve results in 14.5(7) $\times {\mathrm{10}}^{-\mathrm{5}}$ K and 14.5(6) $\times {\mathrm{10}}^{-\mathrm{5}}$ K coefficients, respectively, in the two sites.

4 Discussion and conclusions

The recent discoveries of a new class of Ca-rich alkaline–alkaline earth carbonates, also including Ca₃(Na,K)₂(CO₃)₄ stable above 3 GPa as primary liquidus phases in the system Na₂CO₃–K₂CO₃–CaCO₃ (Shatzky et al., 2016a, b; Podbordnikov et al., 2019), reveal a rich and dynamic environment in carbonatitic systems at high pressure. Closer to the CaCO₃ endmember, burbankite-type Na₂Ca₄(CO₃)₅ was also synthesized (Rashchenko et al., 2017). According to experimental phase diagrams (Shatzky et al., 2016a, b; Podbordnikov et al., 2019), these phases necessarily participate in crystallization and fractionation processes. Our experiments indicate that La burbankite is still stable at 5 GPa, and these candidate minerals are indeed possibly able to fractionate LREE³⁺ and may form a REE reservoir in the upper mantle.

The thermoelastic parameters determined in this study can provide us with a first tool to determine the density of La burbankite in upper-mantle conditions. Indeed, the density of burbankite is ca. 3.2 g cm⁻³ in P and T ranges of 5.5–6 GPa and 1731–1273 K, respectively. Density has been calculated using the equation of state for solids from Holland and Powell (2011). If we compare the density of burbankite with the density of carbonatitic magmas in the same P and T conditions, which are 2.058–3.1 g cm⁻³ (Jones et al., 2013), we can conclude that the burbankite might fractionate from the magma and play a key role as an upper-mantle reservoir of light REE³⁺. Furthermore, if we take into account our synthesis P–T conditions and the stability field of a burbankite-like structure phase (e.g. Podbordnikov et al., 2019), its fractionation might be possible from carbonate-rich fluids metasomatizing the cratonic lithosphere or cold slabs characterized by low geothermal gradients. The possible fractionation of this phase demonstrates that La does not always have an incompatible behaviour as is the case for silicate systems.

It is worth noting that in this example the two independent A and B polyhedra might not obey the inverse relationship, as has already been observed for diopside (Hazen and Finger, 1982). In this study we report a bulk modulus (K_T0= 72 GPa) for the 10-fold coordination polyhedra greater than the bulk modulus for the 8-fold coordination polyhedra (K_T0= 54 GPa) when we would expect the opposite. Burbankite could therefore be another example where the inverse relationship is not rigorously true, and this can be related to the presence of two different types of cation polyhedra other than the rigid carbonate unit (Hazen et al., 2000).