First-principles modeling of the infrared spectrum of Fe- and Al-bearing lizardite

The theoretical vibrational properties of a series of Fe- and Al-bearing lizardite models have been determined at the density functional theory level. Each periodic model displays a single cationic impurity substituted at an octahedral or tetrahedral site of a supercell of lizardite (Mg₃Si₂O₅(OH)₄) containing 162 atoms. The isovalent Fe²⁺ for Mg²⁺ substitution has been considered, as well as the heterovalent substitution of Fe³⁺ or Al³⁺ for Mg²⁺ or Si⁴⁺. Comparison of the theoretical absorption spectra with previously reported experimental spectra of natural and laboratory-grown lizardite samples allows us to propose an interpretation for most of the observed bands. Although the identification of specific bands related to octahedral Fe²⁺ in FTIR spectra is challenging, broad bands at 3584 and 3566 cm⁻¹ reflect the occurrence of octahedral Al³⁺ and Fe³⁺, respectively, in the natural samples. These broad bands likely overlap with potential contribution related to tetrahedral Al³⁺. It is suggested that the modification of the H-bonding pattern related to the incorporation of trivalent ions at tetrahedral sites has an overall broadening effect on the interlayer-OH stretching bands of lizardite.

1 Introduction

The stretching vibrations of OH groups are widely used to probe the local order of hydrous phyllosilicates. Applications range from the determination of the stacking pattern in clay minerals (e.g., Brindley et al., 1986; Prost et al., 1989; Fialips et al., 2001) to the analysis of cationic ordering in solid solutions (e.g. Petit et al., 2004; Baron and Petit, 2016) and to the study of structural phase transitions as a function of pressure (e.g., Johnston et al., 2002; Welch et al., 2012). The small mass of hydrogen leads to frequencies significantly higher than those of other vibrational modes, whereas their relative variations as a function of macroscopic or microscopic perturbations usually do not exceed a few percents. These properties facilitate the identification of the corresponding vibrational spectroscopic signals, most often in the 3000–3700 cm⁻¹ range (e.g., Farmer, 1974; Szalay et al., 2002). In addition, the high frequency and weak dispersion of these “hard modes” result in a localized character (e.g., Salje, 1992), which supports the interpretation of observed spectroscopic changes in terms of modifications of the local atomic-scale environment of OH groups.

The stretching frequencies of OH groups are dominantly controlled by the strength of H bonding and by the nature of the neighboring cations (e.g., Farmer, 1974; Hermansson, 1991; Libowitsky, 1999). In trioctahedral phyllosilicates, specific bands involving the structural OH groups located between the octahedral and tetrahedral sheets of the layers (inner-OH groups) have been unambiguously related to isovalent cationic substitutions in the coordination sphere of the oxygen atom (Petit et al., 2004; Blanchard et al., 2018). The effect of cationic substitutions on interlayer-OH groups, located on the outer side of the octahedral sheets of 1:1 phyllosilicates and pointing in their interlayer spacing, is less clearly established. In this case, the OH stretching modes can involve the coupled motion of the different interlayer-OH groups occurring in the mineral unit cell, leading to a 10 to 20 cm⁻¹ splitting of interlayer-OH modes. The local perturbation of OH vibrations by neighboring cationic substitutions (typically 14 cm⁻¹ for a Fe²⁺ or Ni²⁺ for Mg²⁺ substitution at octahedral sites; Petit et al., 2004) is thus of similar magnitude than the effect of the coupling between the interlayer-OH groups. Furthermore, the potential occurrence of multivalent elements, such as iron, the simultaneous substitution at octahedral and tetrahedral sites by trivalent cations (e.g., Serna et al., 1979), and variations of the cationic ordering and potential intermediate di-tri-octahedral character of extended solid solutions (Bailey, 1988) may affect the interpretation of the vibrational spectra of chemically complex synthetic or natural samples. This is particularly true for the serpentine-group minerals, which can display significant variations of their chemical composition, with a frequent departing from the ideal Mg₃Si₂O₅(OH)₄ formula related to the occurrence of iron and aluminum (e.g., Viti and Mellini, 1997). These elements can play an important role in serpentine-group minerals because the interplay of chemical composition, electrostatic interactions and structural strain has been suggested as a potential control of the layer curvature, driving the growth of the planar lizardite vs. tubular chrysotile variety (e.g., Mellini, 1982; Wicks and O'Hanley, 1988; Viti and Mellini, 1997). The presence of aluminum has also been shown to significantly affect the chemical reactivity of serpentine minerals (Lacinska et al., 2016).

In the present study, we theoretically investigate the effect of Fe and Al substitutions at low concentration on the vibrational and infrared absorption properties of lizardite, the more symmetric planar member of serpentine-group minerals. The theoretical calculation of the IR spectrum of Fe²⁺-, Fe³⁺- and Al³⁺-bearing lizardite supports the assignment of some features of the experimental spectra of serpentine-group minerals to site-specific substitutions and sheds light on the inhomogeneous broadening mechanisms of the other vibrational bands related to cationic substitutions. Although the focus is on the OH stretching modes, the effect of substitutions on the lower-frequency region of the spectra is also discussed.

2 Methods

The theoretical modeling framework is the same as that previously used for investigating the structural and vibrational properties of other phyllosilicates and hydrous minerals (e.g., Balan et al., 2001, 2002). Relevant properties were obtained using density functional theory (DFT) with the generalized gradient approximation (GGA) for the exchange-correlation functional (xc-functional) as proposed by Perdew, Burke, and Ernzerhof (PBE) (Perdew et al., 1996) and a plane-wave/pseudo-potential scheme, as implemented in the PWscf and PHonon codes from the Quantum ESPRESSO package (Giannozzi et al., 2009; http://www.quantum-espresso.org, last access: 23 October 2021). The ionic cores were described by optimized norm-conserving pseudo-potentials from the SG15-ONCV library (Hamman, 2013; Schlipf and Gigy, 2015). The wave functions and the charge density were expanded in plane waves with 80 and 480 Ry cutoffs, respectively, as in previous studies (e.g., Balan et al., 2021b).

Structural properties of Fe- and Al-bearing lizardite were determined using $\mathrm{3}\times \mathrm{3}\times \mathrm{1}$ lizardite supercells (162 atoms) containing one cationic impurity substituting an octahedrally coordinated Mg²⁺ cation or a tetrahedrally coordinated Si⁴⁺ cation. The chemical composition of the corresponding system is (Mg_1−xX_x)₃Si₂O₅(OH)₄ or Mg₃(Si_1−xX_x)₂O₅(OH)₄, where X is the impurity and x=0.037 or 0.055 for a substitution at the octahedral (M) or tetrahedral (T) site, respectively. These systems differ from those investigated by Scholtzová and Smrčok (2005), who considered the structural effect of coupled substitutions by trivalent cations at both M and T sites, which would make it difficult to disentangle each individual effect on vibrational properties. Given the supercell size, the Brillouin zone sampling for electronic integration was restricted to a $\mathrm{1}\times \mathrm{1}\times \mathrm{2}$ k-point grid. The unit-cell parameters of pure lizardite-1T were optimized at zero pressure and then used without further relaxation to produce the Fe- and Al-bearing supercells. Reduced atomic coordinates were relaxed until the residual forces on atoms were less than 10⁻⁴ Ry/a.u. For the models displaying heterovalent substitutions, a compensating homogeneous electrostatic background was spread over the supercell to ensure the macroscopic neutrality of the periodic system. This electrostatic correction avoids the divergence of the system total energy but is not expected to significantly affect the microscopic vibrational properties of ionic systems (e.g., Leslie and Gillan, 1985). Spin-polarized calculations were performed on Fe²⁺- and Fe³⁺-bearing systems, imposing the high-spin state of the isolated paramagnetic ion to the supercell.

Harmonic vibrational (displacements and frequencies of the 486 normal vibrational modes at the Brillouin zone center) and dielectric (Born effective charge tensors and electronic dielectric tensor) properties were calculated from the second-order derivatives of the total energy with respect to atomic displacements and external electric field using the linear response theory (Baroni et al., 2001). The theoretical powder infrared absorption spectra were obtained from the low-frequency dielectric tensor using the approach developed by Balan et al. (2001, 2008). This approach computes the orientational average of the electromagnetic power dissipated in an ellipsoidal particle inserted in an infinite isotropic matrix, which is characterized by a real dielectric constant, assuming that the isolated particle has a size significantly smaller than the IR wavelength. The absorption is equivalent to that of a Maxwell Garnet effective medium in the high-dilution limit (Kendrick and Burnett, 2016). In the calculation of the low-frequency dielectric tensor (Balan et al., 2001), a damping coefficient of 2 cm⁻¹ was arbitrarily used to account for the homogeneous width of absorption bands.

3 Results

3.1 Theoretical properties of pure lizardite

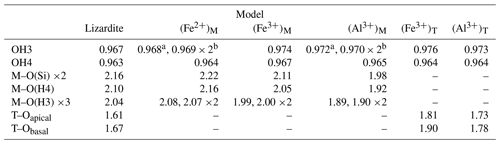
The unit-cell parameters of lizardite-1T (S.G. P31m) ($a=b=$ 5.37 Å, c = 7.36 Å) compare well with previous values obtained at the same theoretical level (e.g., Prencipe et al., 2009; Hossain et al., 2001; Adebayo et al., 2011; Tunega et al., 2012; Ghaderi et al., 2015). As usually observed in DFT modeling performed at the GGA level, they are overestimated with respect to their experimental counterparts (e.g., $a=b=$ 5.3267 Å, c= 7.2539 Å; Gregorkiewitz et al., 1996). Each layer of the structure contains a pseudo-hexagonal silica sheet of corner-shared SiO₄ units linked to a trioctahedral sheet of edge-sharing MgO₂(OH)₄ octahedra. Selected theoretical lengths of cation oxygen bonds (Table 1) are in good agreement with the experimental findings and consistent with previous theoretical calculations (Balan et al., 2002; Prencipe et al., 2009). The Mg–O(Si) distance is the longest Mg–O distance, and the apical Si–O bonds are shorter than the equatorial ones. The interlayer-OH bonds is longer than the inner-OH bond by 0.004 Å. The theoretical magnitude of the ditrigonal distortion ($\mathit{\alpha }=-\mathrm{4.1}$^∘) is slightly overestimated with respect to the experimental value of −2.6^∘ (Gregorkiewitz et al., 1996).

Table 1 Selected theoretical bond lengths (Å) in pure and Fe- and Al-bearing lizardite. The interlayer and inner OH correspond to OH3 and OH4, respectively.

^a OH_m. ^b OH_e.

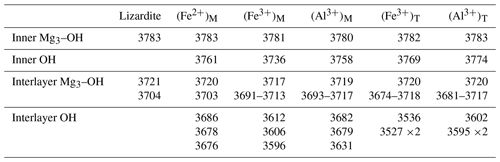
Vibrational properties of lizardite (Table 2) are consistent with those previously determined (Balan et al., 2002; Prencipe et al., 2009). Note however that the theoretical frequencies slightly differ from those of Balan et al. (2002) due to the full relaxation of the unit cell in the present study and use of different pseudo-potentials. The inner-OH stretching mode leads to a weak absorption band at 3783 cm⁻¹ (Fig. 1). The transverse optical (TO) frequency of the in-phase stretching mode (A₁ symmetry) of interlayer-OH groups is calculated at 3721 cm⁻¹ (Table 2) and leads to an absorption band at 3740 cm⁻¹ in the spectrum computed for a (001) platy particle shape (Fig. 1). For a mode polarization along the [001] direction, this higher frequency coincides with the longitudinal optical (LO) frequency of the mode (Balan et al., 2005), indicating a LO–TO splitting of 19 cm⁻¹. This value compares well with those previously determined (21 cm⁻¹, Balan et al., 2002; 14 cm⁻¹, Prencipe et al., 2009). The degenerate out-of-phase stretching mode (E symmetry) of interlayer-OH groups is calculated at 3704 cm⁻¹ (Table 1).

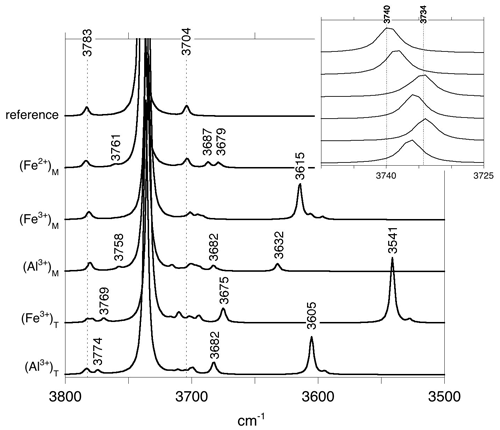
Figure 1 Theoretical absorbance spectra in the OH stretching region of the Fe- and Al-bearing lizardite models. The reference spectrum corresponds to pure lizardite. The spectra have been computed for a platy particle inserted in a KBr medium (ε_KBr=2.25). Due to electrostatic effects, the position of absorption bands can differ from the TO mode frequencies reported in Table 2 (see text). Inset: enlarged view of the main band related to the stretching of interlayer-OH groups in lizardite. The presence of cationic impurities leads to a moderate shift and broadening of this band.

Table 2 Theoretical transverse optical (TO) OH stretching frequencies (cm⁻¹) in pure and Al- and Fe-bearing lizardite. The frequencies reported for Mg₃OH in the substituted models correspond to the main band associated with an in-phase motion of the OH groups and to IR-active modes displaying out-of-phase displacement patterns. Depending on the system, the intensity of the latter can be spread over several modes in the specified frequency range.

At lower frequency (Fig. 2), the stretching modes involving apical or equatorial Si–O bonds correspond to absorption bands at 1062 and 880 cm⁻¹, respectively, with the former being calculated at the LO frequency because of the platy morphology of the particle (Balan et al., 2002). The bands at 643, 607 and 590 cm⁻¹ correspond to the libration of interlayer-OH groups, the libration of inner-OH group and the hindered translation in the [001] direction of interlayer-OH groups, respectively. The bands at 422 and 401 cm⁻¹ correspond to more complex displacement patterns involving the interlayer-OH groups and contributions of Mg and Si cations. Finally, the band at 274 cm⁻¹ involves a collective atomic motion corresponding to an internal shearing of the layers parallel to the (001) plane.

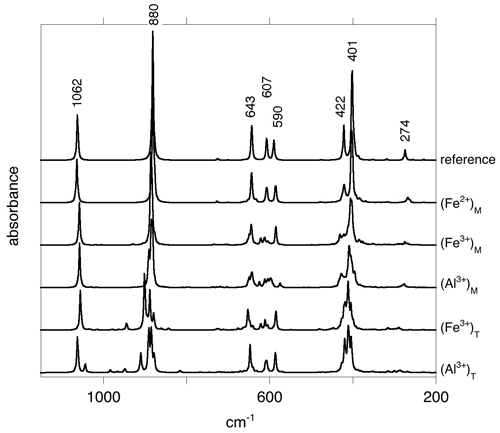
Figure 2 Theoretical absorbance spectra in the mid-infrared region of the Fe- and Al-bearing lizardite models. The reference spectrum corresponds to pure lizardite. The spectra have been computed as in Fig. 1. Note the very small modifications related to the occurrence of Fe²⁺ ions in the octahedral site.

3.2 Theoretical properties of Fe²⁺-bearing lizardite ((Fe²⁺)_M model)

Cationic substitution at the octahedral site reduces the 3m symmetry of the system to a mirror symmetry. The average Fe²⁺ oxygen bond length increases from 2.09 to 2.13 Å due to the slightly larger ionic radius of Fe²⁺ (0.78 Å) compared to that of Mg²⁺ (0.72 Å) (Shannon, 1976). The length of inner-OH (OH4) and interlayer-OH (OH3) groups increases by 0.001 to 0.002 Å with respect to those in pure lizardite (Table 1). The three interlayer-OH groups linked to the substituting cation are not equivalent. The interlayer-OH group located on the mirror plane (noted OH_m) can be distinguished from the two other OH groups (noted OH_e), which are symmetrically equivalent by mirror operation. In the Fe²⁺-bearing system, the OH_m is 0.001 Å shorter than the two OH_e groups.

These local structural changes affect the vibrational properties. The presence of a Fe²⁺ cation in the coordination sphere of the inner-OH group shifts its vibrational frequency from 3783 to 3761 cm⁻¹ (Table 2). The Born effective charge tensor of hydrogen is also affected, and the IR absorption coefficient of the corresponding OH stretching band increases by 33 % with respect to that in pure lizardite. The stretching modes related to the interlayer-OH groups are also shifted at lower frequency with respect to the interlayer stretching modes of pure lizardite (Table 2). Due to the symmetry reduction, the mode at 3686 cm⁻¹ is dominantly related to the shorter OH_m bond, whereas the mode at 3676 cm⁻¹ involves the out-of-phase stretching of the two other OH_e groups. The intermediate mode at 3678 cm⁻¹ combines the in-phase stretching of the OH_e groups with an out-of-phase motion of the OH_m group. Compared with the splitting of interlayer-OH stretching modes of A₁ and E symmetry in pure lizardite (∼ 20 cm⁻¹), the frequency splitting of the OH modes associated with the substitutional defect is reduced to less than 10 cm⁻¹.

The effect of the substituting Fe²⁺ cation on the stretching frequency of the bands related to the other more distant OH groups, which are only linked to Mg cations, does not exceed 1 cm⁻¹ (Fig. 1). The presence of Fe²⁺ has a weak effect on the other vibrational modes of the system (Fig. 2), which is consistent with the limited structural distortion of the octahedral sheet induced by the impurity, also previously reported by Scholtzová and Smrčok (2005). A 3 cm⁻¹ splitting of the band related to the basal Si–O stretching mode leads to a shoulder at 877 cm⁻¹ (not visible on Fig. 2). A more significant change affects the collective mode at 274 cm⁻¹, which is split and downshifted to 264 cm⁻¹. This suggests that the opposite shift reported by Baron and Petit (2016) as a function of Ni concentration in the lizardite-népouite series is predominantly due to the decrease in the system molar volume. This effect is not accounted for by the present modeling approach, which aims at determining the properties of defective systems in the high dilution limit. Weak additional bands related to a modification of the OH libration modes are observed in the 630–670 cm⁻¹ range.

3.3 Theoretical properties of Fe³⁺- and Al³⁺-bearing lizardite

3.3.1 Trivalent cations at octahedral sites ((Fe³⁺)_M and (Al³⁺)_M models)

The occurrence of trivalent Fe³⁺ and Al³⁺ cations at octahedral sites also reduces the system symmetry from 3m to m. The shortening of cation–oxygen bond lengths and contraction of the substituted site are stronger for Al³⁺ than for Fe³⁺, as expected from their respective ionic radii (Fe³⁺: 0.645 Å, Al³⁺: 0.535 Å), which are both significantly smaller than that of the octahedrally coordinated Mg²⁺ ion (0.72 Å) (Shannon, 1976).

The presence of a trivalent cation affects the OH groups belonging to its coordination sphere. The lengthening of the inner-OH (OH4) bonds by 0.003 and 0.002 Å (Table 1) downshifts their stretching frequency by 47 and 25 cm⁻¹ for Fe³⁺ and Al³⁺ cations, respectively. A significant lengthening of interlayer-OH_m and OH_e bonds is also observed (0.007 Å for Fe³⁺, 0.004 Å for Al³⁺). For the Fe³⁺-bearing system, the three interlayer-OH bonds have a similar length despite the lowering of the site symmetry (Table 1). Their coupling leads to three modes respectively computed at 3612 cm⁻¹ for the in-phase motion of the three groups and at 3606 and 3596 cm⁻¹ for their out-of-phase motion (Table 2). A different vibrational pattern is observed for the Al³⁺-bearing system. In this case, the stronger distortion of the octahedral site induces a more significant difference in the length of the interlayer-OH bonds. The longer OH_m bond leads to a mode at 3631 cm⁻¹ (Table 2). The two other modes at 3682 and 3679 cm⁻¹ correspond to the in-phase and out-of-phase motion of the OH_e groups, respectively (Table 2).

Compared to the Fe²⁺-bearing system that mostly show local perturbation of vibrational properties, the presence of octahedrally coordinated trivalent cations has a more significant effect on the vibrational spectrum of lizardite because the perturbation extends toward more distant atoms. The main interlayer-OH stretching band is downshifted by 4 to 6 cm⁻¹, whereas several resonances involving out-of-phase displacement patterns appear in the 3691–3717 cm⁻¹ range (Fig. 1). The apical Si–O stretching band is downshifted by ∼ 9 cm⁻¹, whereas the equatorial stretching modes are split and the main band is upshifted by ∼ 5 cm⁻¹. In the Al³⁺-bearing system, the splitting of the equatorial Si–O modes is stronger than in the Fe³⁺-bearing system, reaching 7 cm⁻¹ (Fig. 2). For both systems, the OH libration and hindered translation modes are significantly affected. The splitting of vibrational modes to a significantly higher number of IR active modes tends to spread the IR absorption over a range of frequencies (Fig. 2), inducing a complex broadening of the signals in the 560–660 cm⁻¹ range.

3.3.2 Trivalent cations at tetrahedral sites ((Fe³⁺)_T and (Al³⁺)_T models)

The substitution of larger Al³⁺ and Fe³⁺ for Si⁴⁺ cations preserves the 3-fold symmetry of the tetrahedral site. It has a significant effect on the cation–oxygen bond lengths, which increase from 1.61 to 1.73 and 1.81 Å for the apical T–O bond and from 1.67 to 1.78 and 1.90 Å for the basal T–O bond for Al³⁺ and Fe³⁺, respectively (Table 1). Due to the relative stiffness of the T–O bonds, the site expansion leads to a rotation of the tetrahedron with a di-trigonal angle locally increasing to ∼ −10^∘ and to ∼ −16^∘ for the Al³⁺- and Fe³⁺-bearing system, respectively (Fig. 3). This increasingly negative value indicates a displacement of the basal oxygen atoms away from the octahedra of the same TO layer (Mellini, 1982). This displacement shortens the H bonds between the basal oxygen atoms of the tetrahedron and the three interlayer-OH groups belonging to the adjacent layer. Similar influence of tetrahedral substitutions on the H-bonding pattern of interlayer-OH groups was previously pointed out by Scholtzová and Smrčok (2005). The length of the three OH bonds pointing to the basal oxygens of the substituted tetrahedron increases to 0.973 and 0.976 Å for the Al³⁺- and Fe³⁺-bearing systems, respectively (Table 1). Due to the 3-fold symmetry, the vibrational pattern involving these three interlayer-OH groups corresponds to an in-phase stretching mode at 3536 and 3602 cm⁻¹ (Table 2) for the Fe³⁺- and Al³⁺-bearing system, respectively, and two degenerate out-of-phase stretching modes leading to weaker bands at a frequency ∼ 10 cm⁻¹ lower. The in-phase stretching mode carries the intensity at 3541 and 3605 cm⁻¹ in the corresponding theoretical absorption spectra (Fig. 1). In comparison, the neighboring inner-OH groups are less affected, with a moderate lengthening inducing a decrease in the OH stretching frequency of 14 and 9 cm⁻¹ for the Fe³⁺- and Al³⁺-bearing systems, respectively.

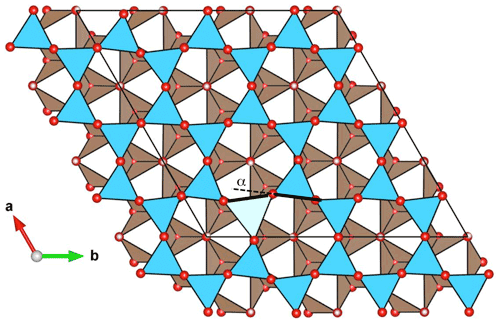
Figure 3 View of the structure of the (Fe³⁺)_T model along the [001] direction. Blue triangle: basal face of silicate tetrahedra; light blue triangle: basal face of the substituted site; red: oxygen atoms; light pink: H atoms; white and brown: faces of the MgO₆ octahedra. The presence of the substituting cation induces a rotation of the tetrahedra moving the basal oxygens away from the octahedral sites, which corresponds to a local increase in the absolute value of the α angle. Structure drawing made with the VESTA software (Momma and Izumi, 2011).

As could be anticipated from the distortion of the tetrahedral sheet, the presence of trivalent cations substituted for Si⁴⁺ cations significantly affects the Si–O stretching modes involving the basal oxygen atoms and the related absorption bands (Fig. 2). The modes below 400 cm⁻¹ are also strongly affected. In comparison, the OH libration and hindered translation are less modified.

4 Discussion: interpretation of experimental lizardite spectra

Theoretical spectra can be compared with previously reported experimental spectra of lizardite (Fig. 4), corresponding to a pure laboratory-grown sample (Mg_100; x=0) (Baron and Petit, 2016); a reference lizardite sample from Monte Fico, Elba (Viti and Mellini, 1997; Fuchs et al., 1998; Balan et al., 2002); and a lizardite sample from New Caledonia (Lz1) previously investigated by Fritsch et al. (2016, 2021). As attested by X-ray diffraction patterns, the crystalline quality is better in the two natural samples than in the synthetic one. The detailed chemical formula proposed for the Monte Fico lizardite is (Mg_2.74Fe${}_{\mathrm{0.10}}^{\mathrm{2}+}$Fe${}_{\mathrm{0.05}}^{\mathrm{3}+}$Al_0.11)_Σ=3.00(Si_1.94Al_0.05Fe${}_{\mathrm{0.01}}^{\mathrm{3}+}{)}_{\mathrm{\Sigma }=\mathrm{2.00}}$O_5.05(OH)_3.95 (Fuchs et al., 1998). Note that this lizardite has been shown to correspond to skeletal crystals with a minor proportion (∼ 10 %) of chrysotile and polygonal serpentine (Capitani et al., 2021). The chemical composition of the Lz1 lizardite corresponds to the formula (Mg_2.76Fe_0.18Ni_0.03Cr_0.02)_Σ=2.99(Si_1.99Al_0.01)O₅(OH)₄. Compared to the Monte Fico lizardite, the Lz1 from New Caledonia is thus richer in iron and almost Al-free. It is noteworthy that a significant fraction of iron in this sample occurs under the trivalent state, as attested by X-ray absorption spectroscopy investigations (Fe${}^{\mathrm{2}+}/$Fe${}^{\mathrm{3}+}=$ 0.15; Farid Juillot, personal communication, 2021). Assuming that all iron ions are located in octahedral sites, this ratio leads to the formula (Mg_2.76Fe${}_{\mathrm{0.02}}^{\mathrm{2}+}$Fe${}_{\mathrm{0.16}}^{\mathrm{3}+}$Ni_0.03Cr_0.02)_Σ=2.99(Si_1.99Al_0.01)O₅(OH)₄. Accordingly, it is expected that the Lz1 lizardite spectrum displays specific features dominantly related to Fe³⁺, whereas the Monte Fico lizardite spectrum should reflect the dominant occurrence of Al³⁺ and octahedral Fe²⁺.

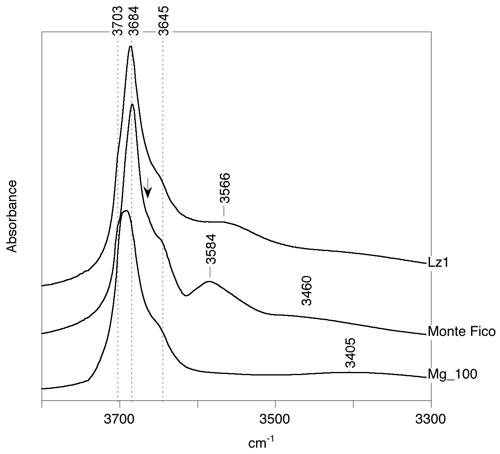
Figure 4 Experimental FTIR spectra of lizardite samples: New Caledonian Lz1 sample from Fritsch et al. (2021), Monte Fico sample from Balan et al. (2002) and laboratory-grown Mg_100 sample from Baron and Petit (2016). The arrow points to the shoulder at ∼ 3664 cm⁻¹ in the spectrum of the Monte Fico sample.

4.1 Vibrational properties of lizardite in the OH stretching range

The experimental FTIR spectra of lizardite display the signals previously interpreted in the light of the theoretical modeling of pure lizardite (Balan et al., 2002; Prencipe et al., 2009). They are ascribed to the inner-OH stretching at 3703 cm⁻¹ and to the in-phase (A₁ symmetry) and out-of-phase (E symmetry) stretching of interlayer-OH groups at 3684 and 3645 cm⁻¹, respectively (Fig. 4). Note that the frequency of the stronger in-phase stretching band of the interlayer-OH groups can display some variability depending on the sample microstructure and experimental geometry. These variations are related to long-range macroscopic electrostatic interactions affecting the vibrational spectra of polar crystals and are commonly observed in the powder spectra of hydrous phyllosilicates (Farmer, 1998, 2000; Balan et al., 2001, 2002, 2005) and layered hydroxides (Balan et al., 2008). In the case of powder spectra recorded on samples with arbitrary particle shapes, the intense band can be observed at a frequency intermediate between the corresponding TO and LO mode frequencies, with a width similar to the LO–TO splitting. For more specific shapes, such as blocky or cubic particles, the spectra can display asymmetric bands with components close to the LO and TO frequencies that can manifest as shoulders or inflection points (Fuchs, 1975). In the case of lizardite, the main band observed in the infrared spectrum of a thin film has been decomposed in two components at 3669 and 3688 cm⁻¹, accounting for its asymmetry (Trittschack et al., 2012). Similarly, a component is observed at ∼ 3664 cm⁻¹ as a shoulder on the low-frequency side of the main band at 3684 cm⁻¹ in the FTIR powder spectrum of the Monte Fico lizardite (Fig. 4). Manifestations of long-range electrostatic effects are also observed in the Raman spectra recorded on oriented single crystals (Farmer, 2000). As discussed by Farmer (2000) for the Raman spectrum of dickite, when the spectrum is recorded on a (001) section in a backscattering geometry, the exchanged wave vector is parallel to the [001] polarization of the in-phase stretching mode of interlayer-OH groups, which enhances the signal at the higher LO frequency. In the case of lizardite, Compagnioni et al. (2021) reports a shift of the main band from 3688.5 cm⁻¹ in the micro-Raman spectrum recorded on an isotropic lizardite section parallel to the (001) plane to ∼ 3678 cm⁻¹ for measurements made on the perpendicular section. In this latter case, the main band appears asymmetric with a component at ∼ 3668–3670 cm⁻¹ (average 3669 cm⁻¹). Accordingly, the LO frequency of the in-phase stretching of interlayer-OH groups should be close to ∼ 3688 cm⁻¹, whereas the component systematically observed at ∼ 3669 cm⁻¹ would correspond to its TO counterpart. The related splitting is consistent with the theoretical LO–TO splitting, which is predicted to be in the 14–21 cm⁻¹ range.

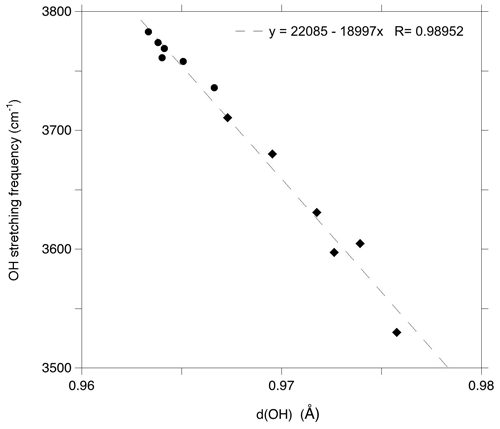
These interpretations enable a comparison of the experimental frequencies with their theoretical counterparts (Fig. 5). The comparison reveals an overestimation of the theoretical stretching frequencies of interlayer-OH groups amounting to 50 cm⁻¹, which is consistent with the observations made on antigorite (∼ 57 cm⁻¹, Balan et al., 2021b). It is also in the range expected from previous investigations on hydrous defects in oxides and silicates (Balan et al., 2020; Balan, 2020). The difference between theoretical and experimental frequencies results from the partial cancellation of two types of errors, one being due to the use of an approximate exchange-correlation functional, which tends to underestimate the vibrational frequencies, and the other to the use of the harmonic approximation, which artificially increases the OH stretching frequencies with respect to their anharmonic values (Balan et al., 2007). The theoretical correlation between bond length and OH frequencies (Tables 1 and 2) for the series of investigated models (Fig. 6) is also consistent with those previously determined at the same theoretical level on a series of hydroxylated defects in diopside and corundum (Balan et al., 2020; Balan, 2020). This relation between the vibrational frequency and a geometrical parameter rules out a contribution of the mass of the surrounding cations to the stretching dynamic of the OH groups, which is decoupled from the motion of other atoms.

Figure 5 Relation between the theoretical frequencies (Fig. 1) and experimentally observed vibrational bands. Open squares: FTIR spectrum of Monte Fico lizardite (Balan et al., 2002); full squares: Raman frequencies of Monte Fico lizardite (Compagnoni et al., 2021). Black circles: signals ascribed to cationic impurities in the vibrational spectra of the Monte Fico and Lz1 lizardite. The average value of theoretical frequencies related to (Fe²⁺)_M (3683 cm⁻¹) almost coincides with the higher-frequency contributions related to Al³⁺ cations (3682 cm⁻¹). The theoretical model overestimates the experimental stretching frequencies of interlayer-OH groups by ∼ 50 cm⁻¹.

Figure 6 Relation between the theoretical stretching frequency (Table 2) and length (Table 1) of OH bonds in the lizardite models. For stretching modes displaying coupled OH contributions, the average values have been considered. Circles: inner-OH groups; diamonds: interlayer-OH groups.

4.2 Vibrational signatures associated with cationic impurities in lizardite

The 21 cm⁻¹ downshift of the inner-OH stretching frequency induced by the presence of Fe²⁺ in its coordination sphere is similar to that determined at the same theoretical level for a Ni²⁺ for Mg²⁺ substitution in talc (23 cm⁻¹, Blanchard et al., 2018). As in talc, the theoretical value however slightly overestimates the experimental observation. Based on the analysis of overtone bands in the near-infrared range (Balan et al., 2021a; Fritsch et al., 2021), the shift between Mg₃–OH and Mg₂Fe–OH in lizardite (16 cm⁻¹) is close to that determined in talc (14 cm⁻¹, Petit et al., 2004). Accordingly, the inner-OH stretching band corresponding to a Mg₂Fe²⁺ environment should occur at ∼ 3687 cm⁻¹, overlapping with the strong band related to the in-phase interlayer-OH stretching band of lizardite.

The signal of interlayer-OH groups in a Mg₂Fe²⁺ environment is theoretically determined at a frequency ∼ 20 cm⁻¹ lower than that of the out-of-phase stretching of interlayer OH in a Mg₃ environment (Fig. 1). However, its contribution is not resolved in the experimental FTIR spectra (Fig. 4) and should mostly contribute to the broadening of the out-of-phase (E symmetry) stretching band identified at 3645 cm⁻¹. Interestingly, the micro-Raman spectrum of lizardite reported by Compagnoni et al. (2021) reveals the occurrence of two components with different polarization properties at ∼ 3653 and ∼ 3642 cm⁻¹. The relative intensity of the component at ∼ 3653 cm⁻¹ is enhanced in the spectrum recorded on an isotropic section parallel to the (001) plane. Based on the comparison with the theoretical frequencies, this component could correspond to the out-of-phase stretching band of pure lizardite, whereas that determined at ∼ 3642 cm⁻¹ could be ascribed to the stretching of interlayer-OH groups in a Mg₂Fe²⁺ environment (Fig. 5). It is noteworthy that the splitting of the bands associated with the substituted site is relatively weak (8 cm⁻¹, Fig. 1), potentially leading to the experimental observation of a single band at the average frequency. However, a contribution of trivalent cations (mostly octahedrally coordinated Al³⁺ in the Monte Fico sample) cannot be excluded as they lead to theoretical absorption signals at similar frequencies (Fig. 1).

Assuming that a difference between experimental and theoretical frequencies close to 50 cm⁻¹ is also valid for the interlayer-OH groups in Al³⁺- and Fe³⁺-bearing models, the bands respectively observed at 3584 and 3568 cm⁻¹ in the Monte Fico and Lz1 samples (Fig. 4) are most likely associated with the occurrence of trivalent cations. Consistently, this type of signal is lacking in the laboratory-grown pure lizardite sample. The shift of the band observed between the Monte Fico and Lz1 samples is also consistent with the respective predominance of octahedrally coordinated Al³⁺ and Fe³⁺ in these samples (Fig. 5).

It is however challenging to discriminate the occurrence of octahedral or tetrahedral Al³⁺. Despite a difference in the associated stretching frequencies amounting to 27 cm⁻¹, both could contribute to the broad signal centered at 3584 cm⁻¹ (half width at half maximum of ∼ 35 cm⁻¹). The contribution related to tetrahedral Fe³⁺ is expected at a frequency 75 cm⁻¹ lower than that associated with octahedral Fe³⁺, corresponding to an expected experimental frequency of ∼ 3490 cm⁻¹. The absence of such a signal suggests that the concentration of tetrahedral Fe³⁺ is too low to be detected in the samples. Additional features can also complicate the identification of bands related to trivalent cations at tetrahedral sites. The expected signal likely overlaps with the broad absorption by water molecules adsorbed at the surface of the particles, which is centered at 3405 cm⁻¹ in the pure and finely divided synthetic lizardite sample (Fig. 4). Moreover, the frequency of the interlayer-OH stretching bands appears to be controlled by the perturbation of the silicate sheet geometry, which affects the H-bonding pattern. Recalling that the present theoretical models correspond to a perfectly ordered cationic distribution because of the periodic boundary conditions, they are expected to only provide a local description of the changes induced by the presence of the impurity. The more random cationic ordering occurring in experimental samples likely induces a distribution of the tetrahedra rotation angles and of the related H-bond lengths, causing a broadening of the OH stretching signal.

To this respect, the occurrence of tetrahedral trivalent cations should efficiently contribute to the broadening of the whole vibrational properties of lizardite, not only affecting the stretching modes of interlayer-OH groups but also the other vibrational modes observed in the mid-IR range. In comparison, low concentration of cations at octahedral sites should have a more local effect and weaker broadening efficiency. It is however noteworthy that higher substitution levels of divalent or trivalent cations can also lead to a significant broadening due to the combined effect of the induced structural strain and increasing variability of cationic configurations, which include the electrostatically favored coupled substitution of trivalent cations at both M and T sites (e.g. Yariv and Heller-Kallai, 1973; Serna et al., 1979; Velde, 1980; Baron and Petit, 2016).