Vibrational anisotropy of δ-(Al,Fe)OOH single crystals as probed by nuclear resonant inelastic X-ray scattering

The formation of high-pressure oxyhydroxide phases spanned by the components AlOOH–FeOOH–MgSiO₂(OH)₂ in experiments suggests their capability to retain hydrogen in Earth's lower mantle. Understanding the vibrational properties of high-pressure phases provides the basis for assessing their thermal properties, which are required to compute phase diagrams and physical properties. Vibrational properties can be highly anisotropic, in particular for materials with crystal structures of low symmetry that contain directed structural groups or components. We used nuclear resonant inelastic X-ray scattering (NRIXS) to probe lattice vibrations that involve motions of ⁵⁷Fe atoms in δ-(Al_0.87Fe_0.13)OOH single crystals. From the recorded single-crystal NRIXS spectra, we calculated projections of the partial phonon density of states along different crystallographic directions. To describe the anisotropy of central vibrational properties, we define and derive tensors for the partial phonon density of states, the Lamb–Mössbauer factor, the mean kinetic energy per vibrational mode, and the mean force constant of ⁵⁷Fe atoms. We further show how the anisotropy of the Lamb–Mössbauer factor can be translated into anisotropic displacement parameters for ⁵⁷Fe atoms and relate our findings on vibrational anisotropy to the crystal structure of δ-(Al,Fe)OOH. As a potential application of single-crystal NRIXS at high pressures, we discuss the evaluation of anisotropic thermal stresses in the context of elastic geobarometry for mineral inclusions. Our results on single crystals of δ-(Al,Fe)OOH demonstrate the sensitivity of NRIXS to vibrational anisotropy and provide an in-depth description of the vibrational behavior of Fe³⁺ cations in a crystal structure that may motivate future applications of NRIXS to study anisotropic vibrational properties of minerals.

1 Introduction

High-pressure experiments have shown that the oxyhydroxide phase δ-AlOOH and the dense hydrous magnesium silicate (DHMS) MgSiO₂(OH)₂, also referred to as δ-phase and phase H, respectively, are stable at pressures and temperatures relevant to Earth's lower mantle (Sano et al., 2008; Nishi et al., 2014; Duan et al., 2018). In experiments on the system MgO–SiO₂–Al₂O₃–H₂O, solid solutions of δ-phase and phase H have been found to coexist with Al-depleted bridgmanite (Ohira et al., 2014; Walter et al., 2015). Similarly, experiments that subjected natural chlorite and antigorite samples to pressures and temperatures of the lower mantle produced complex solid solutions with an FeOOH component in addition to AlOOH and MgSiO₂(OH)₂, again in coexistence with bridgmanite (Nishi et al., 2015). Solid solutions between δ-AlOOH and ϵ-FeOOH have also been synthesized (Nishi et al., 2017; Kawazoe et al., 2017). These experimental observations suggests that high-pressure oxyhydroxide phases may form in Earth's lower mantle when hydrous fluids react with bridgmanite-bearing mineral assemblages.

The vibrational properties of crystalline solids and in particular the energy distribution of lattice vibrations as expressed by the phonon density of states (PDOS) determine central thermodynamic properties, such as heat capacity and vibrational entropy, that are needed to assess phase stabilities and to construct phase diagrams (e.g., Kieffer, 1982). For high-pressure oxyhydroxide phases in the ternary system AlOOH–FeOOH–MgSiO₂(OH)₂, vibrational and thermodynamic properties are needed to evaluate their stability in Earth's lower mantle and to appraise potential geophysical consequences. Vibrational properties of crystals are inherently anisotropic as reflected in the anisotropy of related microscopic and macroscopic properties, such as atomic displacements and thermal expansion. The vibrational anisotropy of crystals can be studied with spectroscopic techniques using visible light, such as Raman and Brillouin scattering and infrared spectroscopy. The wavelengths of light photons, however, restrict their interaction with lattice vibrations to a small subset of the full vibrational spectrum. A more complete picture of lattice vibrations and vibrational anisotropy becomes accessible through inelastic X-ray and neutron scattering techniques.

Nuclear resonant inelastic X-ray scattering (NRIXS) is a synchrotron-based technique that probes the thermal motion of resonant atomic nuclei (Sturhahn and Kohn, 1999; Sturhahn, 2004). An NRIXS spectrum is recorded by fine-tuning the energy of incoming X-rays around the resonance energy of Mössbauer-active atomic nuclei in the sample material. X-rays can be absorbed by atomic nuclei when the X-ray energy matches the nuclear resonance energy. In crystalline solids, vibrational motions of the nuclei modulate the resonance energy and allow for the absorption of X-ray photons with the simultaneous excitation or annihilation of lattice vibrations. The NRIXS spectrum of a crystal therefore contains information about the energies of lattice vibrations. Theoretical and experimental aspects of NRIXS have been explained in detail, for example, by Sturhahn and Kohn (1999) and by Sturhahn (2004). Given the abundance of iron in materials of the solid Earth, most applications of NRIXS in earth sciences made use of the Mössbauer-active iron isotope ⁵⁷Fe to determine vibrational properties (Sturhahn and Jackson, 2007) of materials ranging from Fe-based alloys in the context of Earth's core (e.g., Mao et al., 2001; Lin et al., 2003; Murphy et al., 2011; Morrison et al., 2019) to oxide and silicate minerals of Earth's mantle (e.g., Jackson et al., 2009; Wicks et al., 2010; Zhang et al., 2013; Liu et al., 2017).

The impact of vibrational anisotropy on the sampling of lattice vibrations with NRIXS has been addressed in theory (Kohn et al., 1998; Paulsen et al., 1999; Sturhahn and Kohn, 1999) and with experiments (Chumakov et al., 1997; Paulsen et al., 2001; Rai et al., 2002). For materials of geological relevance, however, systematic analyses of anisotropic NRIXS have not yet been reported. To demonstrate and quantify the effect of vibrational anisotropy on properties derived from NRIXS spectra, we recorded NRIXS spectra on single crystals of δ-(Al,Fe)OOH with the X-ray beam incident along different crystallographic directions. The partial PDOS projected along each probed crystallographic direction was calculated from the NRIXS spectra. We explore the effect of changing the sampled energy range on the Lamb–Mössbauer factor, the mean kinetic energy per resonant atom, and the mean force constant and describe the observed anisotropy of these properties from an experimental perspective by using tensors. The anisotropic vibrational behavior of ⁵⁷Fe atoms is further captured by the anisotropic displacement parameters that we extract from the observed Lamb–Mössbauer factors. Our analyses of NRIXS spectra reveal appreciable vibrational anisotropy of ⁵⁷Fe atoms in δ-(Al,Fe)OOH single crystals at ambient conditions and facilitate future applications of single-crystal NRIXS at high pressures.

2 Methods

2.1 Synthesis and characterization

The synthesis of δ-(Al,Fe)OOH crystals followed a route similar to previous synthesis experiments (Kawazoe et al., 2017). Powders of Al(OH)₃ and ⁵⁷Fe₂O₃ were mixed to obtain a molar ratio of $\mathrm{Al}/(\mathrm{Fe}+\mathrm{Al})=\mathrm{0.8}$ and loaded into an inner Au capsule surrounded by an outer Pt capsule. We used Fe₂O₃ powder enriched with the isotope ⁵⁷Fe (96 % ⁵⁷Fe) to maximize the counting rates of envisaged nuclear resonant scattering experiments. The capsule with the reactants was surrounded by a cylindrical LaCrO₃ heater and inserted into the adjusted cavity of an octahedron of Cr-doped MgO with an edge length of 7 mm. The assembly was placed between eight tungsten carbide anvils with truncated edge lengths of 3 mm (grade TF05, Fuji Die Co., Ltd.) and compressed to a target pressure of 27 GPa using the 15 MN Kawai-type multi-anvil press (IRIS-15) with an Osugi-type guide block system installed at the Bayerisches Geoinstitut, Universität Bayreuth (Ishii et al., 2016, 2019). The sample temperature was increased to approximately 1500 K as estimated from an empirical relationship between temperature and the electrical power applied to the LaCrO₃ heater. The pressure–temperature conditions were held for 5 h. After quenching, the assembly was slowly decompressed to ambient conditions over 15 h. Optically clear, translucent grains with a homogeneous brown color and grain sizes of up to 300 µm were selected from the synthesis product for further analysis and experiments.

A total of 53 electron microprobe spot analyses distributed over eight grains gave an average ratio of $\mathrm{Al}/(\mathrm{Fe}+\mathrm{Al})=\mathrm{0.87}\left(\mathrm{2}\right)$. Three grains with approximate diameters of 50 to 150 µm were mounted on Kapton meshes for single-crystal X-ray diffraction (XRD) and NRIXS measurements. Single-crystal XRD patterns were collected at ambient conditions at the Beckman Institute, California Institute of Technology, on Bruker D8 four-circle diffractometers operated with either Cu Kα or Mo Kα radiation. XRD patterns were consistent with orthorhombic symmetry and indexed according to space group P2₁nm (Suzuki et al., 2000; Sano-Furukawa et al., 2008). Unit cell parameters and crystal orientations were determined from the indexed XRD patterns by least-squares refinements. We specify crystal orientations in terms of the lattice planes (hkl) that were oriented perpendicular to the incident X-ray beam during NRIXS experiments and therefore perpendicular to the X-ray propagation vector s. The X-ray propagation vector s is defined as the unit vector pointing along the X-ray wave vector k, i.e., $\mathit{s}=\mathit{k}/k$. Table 1 summarizes crystallographic information for the three grains used for NRIXS measurements. For each grain, over 90 % of observed reflections could be indexed with a single combination of unit cell and orientation matrix. Any unindexed reflections were weak in intensity and probably arose from volumetrically subordinate crystal domains or minor impurities that can be considered too small to contribute significantly to the detected NRIXS signal.

Table 1 Unit cell parameters of δ-(Al,Fe)OOH single crystals and X-ray propagation vectors for NRIXS experiments.

Note that standard deviations on the last digit are given in parentheses. ^a Number of indexed reflections.

2.2 NRIXS experiments and data analysis

NRIXS spectra were recorded at beamline 3-ID-B of the Advanced Photon Source (APS) at Argonne National Laboratory. Highly monochromatic X-rays were generated by an initial Bragg reflection of the synchrotron radiation on a diamond single crystal followed by a tunable high-resolution monochromator based on four synchronized individual silicon crystals (Toellner, 2000). The resulting energy spectrum of X-rays had a full width of about 1 meV at half of the intensity maximum. Kirkpatrick–Baez mirrors were used to focus the X-ray beam to a half-width of 15×15 µm² at the sample position. The X-ray energy was scanned in 1121 steps from −100 to +180 meV relative to the ⁵⁷Fe resonance energy at 14.4 keV. At each energy step, time-delayed fluorescence photons that are emitted after the resonant absorption of incident X-rays were counted for 2 s by three (crystals X1 and X2) or two (crystal X3) avalanche photodiodes (APDs). The APDs were placed as close as possible to the sample and in a plane perpendicular to the direct X-ray beam. For all measurements, simultaneous forward resonant scattering from an iron foil was recorded by placing the foil in front of a fourth APD located after the sample in the X-ray beam path. All spectra were recorded in air and at ambient conditions.

For each crystal, NRIXS spectra were recorded with the X-ray beam incident along two approximately orthogonal directions. These directions were defined by manually rotating the crystal mount by about 90^∘ and were later associated with normal vectors to the lattice planes (hkl) using single-crystal XRD. The identified normal vectors to the lattice planes (hkl) therefore pointed along the X-ray beam during NRIXS experiments and were hence parallel to the X-ray propagation vector s (Table 1). Based on the angles enclosed by the assigned normal vectors and the deviation from 90^∘, we estimate that crystal orientations with respect to the incident X-ray beam are accurate within ±5^∘.

NRIXS spectra were processed and analyzed using the software PHOENIX (version 3.0.2; Sturhahn, 2000, http://www.nrixs.com, last access: 6 August 2020) that normalizes recorded NRIXS spectra to obtain the phonon excitation probability S(E) and extracts the PDOS g(E) as sampled by the motions of resonant nuclei, i.e., the partial PDOS, using the Fourier-log method (Johnson and Spence, 1974; Sturhahn, 2004). Forward resonant scattering spectra of the sample plus the iron foil were used to describe the instrumental resolution function in the analysis of NRIXS spectra. Among other properties of resonant nuclei, the Lamb–Mössbauer factor f, the mean kinetic energy T per resonant atom (in meV), and the mean force constant D (in N m⁻¹) were determined from the partial PDOS. In the following, we will refer to the partial (projected) PDOS as the (projected) PDOS while keeping in mind the partial or ⁵⁷Fe-selective character. Calculations and least-squares inversions that involved the squared product $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$ (see below) or integrals thereof were performed using commercial data analysis software.

3 Results

3.1 NRIXS spectra

Vibrational modes are sampled by NRIXS according to the squared product $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$ of the X-ray propagation vector $\mathit{s}=\mathit{k}/k$ and the displacement polarization vector e with $\left|\mathit{e}\right|=\mathrm{1}$ (Kohn et al., 1998; Paulsen et al., 1999). Like the X-ray wave vector k, the X-ray propagation vector s is parallel to the incident X-ray beam and to the propagation direction of X-ray photons. The polarization vector e points along the displacement vector u that describes the displacement of resonant nuclei from their equilibrium position by a given vibrational mode. In a crystal, different vibrational modes give rise to different polarization vectors e. As each mode contributes to the NRIXS spectrum according to $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$, changing the X-ray propagation vector s will alter the contributions of individual modes to the NRIXS spectrum. It is important to keep in mind, however, that an NRIXS spectrum records the combined scattering from all resonant isotopes, regardless of their local atomic environment. When incorporated in a crystal structure, resonant isotopes can occupy different sets of symmetry-equivalent crystallographic sites. For crystals, the anisotropy of NRIXS consequently reflects the crystal symmetry rather than the local symmetry of individual crystallographic sites occupied by resonant isotopes and represents an average over all vibrational modes with non-zero components of the polarization vector e along the X-ray propagation vector s.

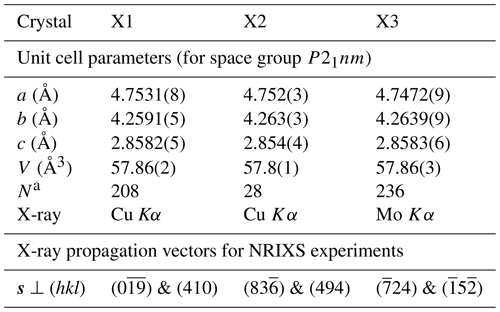
Figure 1 NRIXS spectra of δ-(Al,Fe)OOH single crystals X1 (a), X2 (b), and X3 (c). For each crystal, spectra were recorded with the X-ray beam incident along two different directions s. Vibrational modes that displace resonant ⁵⁷Fe atoms in the direction e are sampled according to the product $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$. For each spectrum, the stereographic projection shows the magnitude of the product $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$ as a function of the polarization vector e. The orientation of stereographic projections is indicated by the crystallographic coordinate system at the bottom. Spectra are vertically offset as indicated for clarity and to demonstrate the high statistical quality of the data.

Figure 1 shows NRIXS spectra recorded for three different crystals of δ-(Al,Fe)OOH with the X-ray propagation vector s pointing along two different crystallographic directions for each crystal (Table 1). For each spectrum, a stereographic projection illustrates how the contribution of vibrational modes to the respective NRIXS spectrum depends on their polarization e as measured by the magnitude of the product $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$ for the selected X-ray propagation vector s. Although the effect of changing the X-ray propagation vector s is difficult to recognize in the raw spectra, the spectra show indications of anisotropy. For example, the peak at energy transfers of about ±20 meV appears most intense for $\mathit{s}⟂\left(\stackrel{\mathrm{‾}}{\mathrm{1}}\mathrm{5}\stackrel{\mathrm{‾}}{\mathrm{2}}\right)$ and least intense for $\mathit{s}⟂\left(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\right)$. In the following, we will examine how the vibrational anisotropy recorded in the NRIXS spectra of Fig. 1 translates into the anisotropy of vibrational properties derived from the NRIXS spectra.

3.2 Vibrational properties

As a result of the polarization-dependent sampling of vibrational modes, an NRIXS spectrum contains information about vibrational anisotropy when recorded on a single crystal with an orientation defined by the X-ray propagation vector. The PDOS extracted from a single-crystal NRIXS spectrum represents a directional image or projection of the PDOS g(E) along the X-ray propagation vector s and is therefore referred to as the projected PDOS g(E,s) (Chumakov et al., 1997; Kohn et al., 1998). Figure 2a shows the projected PDOS extracted from the six NRIXS spectra collected on δ-(Al,Fe)OOH single crystals (Fig. 1). The projections of the PDOS along different X-ray propagation vectors demonstrate how vibrational modes of a given energy contribute to the projected PDOS to different extents depending on their sampling by the X-ray propagation vector. For example, the shape of the dominant peak in the PDOS at energies between 10 and 40 meV and the energy at which this peak reaches a maximum change with the direction of the X-ray propagation vector s. In addition, segments of elevated PDOS at energies between 40 and 50 meV and between 60 and 70 meV are most prominent for $\mathit{s}⟂\left(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\right)$, but essentially absent for s⟂(410), and visible at variable extents for other X-ray propagation vectors. The projected PDOS shown in Fig. 2a therefore clearly reveal the anisotropy of vibrational modes that displace ⁵⁷Fe atoms in single crystals of δ-(Al,Fe)OOH.

The Lamb–Mössbauer factor f measures the probability of recoilless resonant absorption of an X-ray photon by an atomic nucleus (Mössbauer, 1958) and can be derived from NRIXS spectra by identifying the fraction of inelastic scattering events with (1−f) (Sturhahn et al., 1995; Chumakov et al., 1996; Sturhahn and Kohn, 1999). Figure 4a shows Lamb–Mössbauer factors f(s) derived from the six NRIXS spectra of δ-(Al,Fe)OOH single crystals recorded with different X-ray propagation vectors s (Fig. 1). For each spectrum, the interval $\mathrm{\Delta }E=[E^{\ominus },E^{\oplus }]$ of energies that are included in the calculation of Lamb–Mössbauer factors from the NRIXS spectra has been expanded stepwise with $E^{\ominus }=-E^{\oplus }$ for $E^{\oplus }\le \mathrm{100}$ meV and $E^{\ominus }=-\mathrm{100}$ meV for $E^{\oplus }>\mathrm{100}$ meV (Table S1 in the Supplement). This segmental analysis of NRIXS spectra aims at revealing how vibrational modes at different energies contribute to the observed Lamb–Mössbauer factors. Note, however, that the Lamb–Mössbauer factor is strictly defined by evaluating the fraction (1−f) of inelastic scattering events over the entire range of vibrational energies. Here, we refer to results for limited energy ranges as Lamb–Mössbauer factors as well, although they may correspond to apparent magnitudes of Lamb–Mössbauer factors.

For all six NRIXS spectra of δ-(Al,Fe)OOH single crystals, the derived Lamb–Mössbauer factors increase upon expanding the energy interval from $E^{\oplus }=\mathrm{50}$ meV to about 100 meV and remain essentially unchanged for $E^{\oplus }\ge \mathrm{100}$ meV. This indicates that only a small fraction of absorption events interacts with lattice vibrations at energies higher than 100 meV and that the energy range and counting times sampled by the NRIXS spectra capture all relevant vibrational modes. When probed with different X-ray propagation vectors, the Lamb–Mössbauer factor of δ-(Al,Fe)OOH shows substantial anisotropy (Fig. 4a). The X-ray propagation vector $\mathit{s}⟂\left(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\right)$, for instance, samples an effective Lamb–Mössbauer factor of 0.8503(7), while s⟂(410) yields 0.8206(4) although both NRIXS spectra were recorded on the same crystal (X1; see Tables 1 and S1 and Fig. 4).

In analogy to the analysis of Lamb–Mössbauer factors, we calculated mean kinetic energies T(s) and mean force constants D(s) for each of the six NRIXS spectra (Fig. 1) and for a series of energy intervals $\mathrm{\Delta }E=[E^{\ominus },E^{\oplus }]$ with $E^{\ominus }=-E^{\oplus }$ for $E^{\oplus }\le \mathrm{100}$ meV and $E^{\ominus }=-\mathrm{100}$ meV for $E^{\oplus }>\mathrm{100}$ meV. The results are shown in Figs. 5a and 6a and compiled in Tables S2 and S3, respectively. The mean kinetic energies and mean force constants calculated from the NRIXS spectra rise continuously for $E^{\oplus }\le \mathrm{100}$ meV. While the trends for all six X-ray propagation vectors level off at $E^{\oplus }=\mathrm{100}$ meV, mean kinetic energies and mean force constants stagnate for some X-ray propagation vectors, e.g., for $\mathit{s}⟂\left(\mathrm{83}\stackrel{\mathrm{‾}}{\mathrm{6}}\right)$ and $\mathit{s}⟂\left(\stackrel{\mathrm{‾}}{\mathrm{7}}\mathrm{24}\right)$ but seem to slightly rise further at higher energies for other X-ray propagation vectors, e.g., for $\mathit{s}⟂\left(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\right)$ and s⟂(494). The overall pattern of anisotropy of mean kinetic energies and mean force constants probed with different X-ray propagation vectors s resembles the pattern for Lamb–Mössbauer factors (Fig. 4a). The magnitude of the anisotropy, however, increases from the Lamb–Mössbauer factors over the mean kinetic energies to the mean force constants. For $E^{\oplus }>\mathrm{150}$ meV, the relative spread of observed Lamb–Mössbauer factors amounts to

$$\mathrm{2}\times {\displaystyle \frac{f(\mathit{s}⟂(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\left)\right)-f(\mathit{s}⟂(\stackrel{\mathrm{‾}}{\mathrm{1}}\mathrm{5}\stackrel{\mathrm{‾}}{\mathrm{2}}\left)\right)}{f(\mathit{s}⟂(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\left)\right)+f(\mathit{s}⟂(\stackrel{\mathrm{‾}}{\mathrm{1}}\mathrm{5}\stackrel{\mathrm{‾}}{\mathrm{2}}\left)\right)}}=\mathrm{5}\text{ \%},$$

while for the mean force constants we find

$$\mathrm{2}\times {\displaystyle \frac{D(\mathit{s}⟂(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\left)\right)-D(\mathit{s}⟂(\stackrel{\mathrm{‾}}{\mathrm{1}}\mathrm{5}\stackrel{\mathrm{‾}}{\mathrm{2}}\left)\right)}{D(\mathit{s}⟂(\mathrm{0}\stackrel{\mathrm{‾}}{\mathrm{19}}\left)\right)+D(\mathit{s}⟂(\stackrel{\mathrm{‾}}{\mathrm{1}}\mathrm{5}\stackrel{\mathrm{‾}}{\mathrm{2}}\left)\right)}}=\mathrm{45}\text{ \%}.$$

3.3 Tensor analysis

As explained above, the sampling of vibrational modes by NRIXS depends on the relative orientation of the X-ray propagation vector s to the polarization vector e that points in the direction along which resonant atoms are being displaced by a vibrational mode. Displacements of resonant atoms contribute to the observed inelastic scattering according to the squared scalar product $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$. Because of the mathematical properties of this product, a projected vibrational property p(E,s) can be described by a second-rank tensor p_ij(E) that stretches any given polarization vector e(θ,ϕ) onto a vector $\mathit{p}(E,\mathit{\theta },\mathit{\varphi })$ according to

$$\begin{array}{}\text{(1)}& \mathit{p}(E,\mathit{\theta },\mathit{\varphi })=e_i{e}_j{p}_{ij}\left(E\right)\mathit{e}(\mathit{\theta },\mathit{\varphi }),\end{array}$$

with

$$\begin{array}{}\text{(2)}& e_{\mathrm{1}}=\cos \mathit{\varphi }\sin \mathit{\theta },e_{\mathrm{2}}=\sin \mathit{\varphi }\sin \mathit{\theta },e_{\mathrm{3}}=\cos \mathit{\theta }.\end{array}$$

The length $\left|\mathit{p}\right(E,\mathit{\theta },\mathit{\varphi }\left)\right|=e_i{e}_j{p}_{ij}\left(E\right)$ corresponds to the longitudinal effect of the tensor p_ij(E) (Nye, 1985; Haussühl, 2007) and can be identified with the contribution to the projected property at energy E that arises from displacements of resonant nuclei along e(θ,ϕ). By weighting this contribution with the product $|\mathit{s}\cdot \mathit{e}(\mathit{\theta },\mathit{\varphi }){|}^{\mathrm{2}}$ and integrating over all possible polarization vectors e(θ,ϕ), we project the longitudinal effect of the tensor p_ij(E) along the X-ray propagation vector s:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}p(E,\mathit{s})& ={\displaystyle \frac{\mathrm{3}}{\mathrm{4}\mathit{\pi }}}\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{e}_i{e}_j{p}_{ij}\left(E\right){\left|\mathit{s}\cdot \mathit{e}(\mathit{\theta },\mathit{\varphi })\right|}^{\mathrm{2}}\sin \mathit{\theta }\mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }\\ & ={\displaystyle \frac{\mathrm{3}}{\mathrm{5}}}\left[s_{\mathrm{1}}^{\mathrm{2}}\right(p_{\mathrm{11}}\left(E\right)+p_{\mathrm{22}}\left(E\right)/\mathrm{3}+p_{\mathrm{33}}\left(E\right)/\mathrm{3})\\ & +s_{\mathrm{2}}^{\mathrm{2}}\left(p_{\mathrm{11}}\right(E)/\mathrm{3}+p_{\mathrm{22}}(E)+p_{\mathrm{33}}(E)/\mathrm{3})\\ & +s_{\mathrm{3}}^{\mathrm{2}}\left(p_{\mathrm{11}}\right(E)/\mathrm{3}+p_{\mathrm{22}}(E)/\mathrm{3}+p_{\mathrm{33}}(E\left)\right)\\ & +{\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\left(s_{\mathrm{1}}{s}_{\mathrm{2}}{p}_{\mathrm{12}}\right(E)+s_{\mathrm{1}}{s}_{\mathrm{3}}{p}_{\mathrm{13}}(E)+s_{\mathrm{2}}{s}_{\mathrm{3}}{p}_{\mathrm{23}}(E\left)\right)],\end{array}\end{array}$$

where the s_i are the coordinates of the X-ray propagation vector s with respect to the Cartesian basis vectors of the crystal physical reference system. Note that we introduced a factor of 3 to counteract the scaling effect of the term $|\mathit{s}\cdot \mathit{e}(\mathit{\theta },\mathit{\varphi }){|}^{\mathrm{2}}$ when integrated over ϕ and θ. As it is impossible to separate the experimentally observed projection of a vibrational property into the number of contributing modes and the magnitudes of their individual contributions, the tensor p_ij(E) combines all contributions in a single property. A similar description for the anisotropy of the PDOS using a second-rank tensor has been proposed by Sturhahn and Kohn (1999). The factor $|\mathit{s}\cdot \mathit{e}{|}^{\mathrm{2}}$ in Eq. (3) for the projected property can be understood as a selection rule that expresses the polarization-dependent sampling of vibrational modes by NRIXS as opposed to the selectivity of other scattering techniques to the phonon wave vector such as momentum-resolved inelastic X-ray scattering and Brillouin scattering. We will therefore refer to the tensor p_ij(E) as the tensor of the polarized property, i.e., the polarized PDOS g_ij(E), the polarized Lamb–Mössbauer factor f_ij(E), etc.

When a vibrational property has been sampled by NRIXS with a sufficiently large number of different X-ray propagation vectors, the tensor components p_ij(E) can be derived from the collection of observed projections by using Eq. (3) in a least-squares procedure that adjusts the tensor components p_ij(E) for each sampled energy E or energy interval ΔE so as to minimize the squared difference between the experimentally observed projected property and the projection calculated with Eq. (3) for every sampled X-ray propagation vector s. The NRIXS spectra shown in Fig. 1 sample the lattice vibrations of δ-(Al,Fe)OOH single crystals with six different X-ray propagation vectors. The resulting projected properties (Figs. 2a, 4a, 5a, and 6a) should therefore sufficiently constrain the three independent and non-zero tensor components p₁₁(E), p₂₂(E), and p₃₃(E) for orthorhombic symmetry and for each projected property. Consequently, we derived the tensor components p₁₁(E), p₂₂(E), and p₃₃(E) from a least-squares inversion by describing the experimentally observed projections for each of the six X-ray propagation vectors s with expression (3). For the inversions, the off-diagonal tensor components were set to zero, i.e., p_ij(E)=0 for i≠j, while the diagonal tensor components p_ii(E) for $i=\mathrm{1},\mathrm{2},\mathrm{3}$ were treated as adjustable parameters. The Cartesian coordinates s_i of each of the six X-ray propagation vectors s were calculated from the normal vectors to the lattice planes (hkl) as given in Table 1 and fixed during the inversion.

Although this paper focuses on vibrational anisotropy, we note that an isotropic version of a projected vibrational property p(E) can be calculated from the trace of the tensor of the polarized property p_ij(E) as

$$\begin{array}{}\text{(4)}& p\left(E\right)=p_{ij}\left(E\right){\mathit{\delta }}_{ij}/\mathrm{3}.\end{array}$$

In contrast to the projected property, the isotropic property equally represents all modes that displace resonant atoms, regardless of the polarization of the displacement, and therefore contains information on scalar properties that are related to lattice vibrations, such as heat capacity, vibrational entropy, and the Debye velocity. It is further clear from Eq. (4) that the polarized property is equal to the isotropic property, i.e., p_ij(E)=p(E)δ_ij, for crystals of cubic symmetry and for powders of randomly oriented crystallites as well as for glasses.

4 Discussion

4.1 Anisotropy of the PDOS

When the frequencies ω_l(q) and polarization vectors e_l(q) of resonant nuclei are known for every mode l as a function of the phonon wave vector q, the projected PDOS g(E,s) can be calculated as (Chumakov et al., 1997; Kohn et al., 1998)

$$\begin{array}{}\text{(5)}& {\displaystyle }g(E,\mathit{s})& {\displaystyle }={\displaystyle \frac{V}{{\left(\mathrm{2}\mathit{\pi }\right)}^{\mathrm{3}}}}\sum _l\int \mathit{\delta }[E-\mathrm{\hslash }{\mathit{\omega }}_l(\mathit{q}\left)\right]{\left|\mathit{s}\cdot {\mathit{e}}_l\left(\mathit{q}\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{q}\text{(6)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{V}{{\left(\mathrm{2}\mathit{\pi }\right)}^{\mathrm{3}}}}\sum _l\int {\displaystyle \frac{{\left|\mathit{s}\cdot {\mathit{e}}_l\left(\mathit{q}\right)\right|}^{\mathrm{2}}}{\left|{\mathrm{\nabla }}_{\mathit{q}}\mathrm{\hslash }{\mathit{\omega }}_l\left(\mathit{q}\right)\right|}}\mathrm{d}\mathit{q}.\end{array}$$

The Dirac delta function δ[E−ℏω_l(q)] imposes an energy selectivity on the integral (5) over the volume of the first Brillouin zone. Only those modes that vibrate at a frequency ω_l(q) for which E=ℏω_l(q) with the reduced Planck constant $\mathrm{\hslash }=h/\mathrm{2}\mathit{\pi }$ contribute to the projected PDOS g(E,s) at a given energy E. This energy selectivity creates a surface spanned by phonon wave vectors q for which E=ℏω_l(q), and this surface is being integrated over in Eq. (6). Expression (6) emphasizes that the contribution of a vibrational mode to the projected PDOS not only depends on the polarization through the term ${\left|\mathit{s}\cdot {\mathit{e}}_l\left(\mathit{q}\right)\right|}^{\mathrm{2}}$ but also on the mode dispersion through the gradient ∇_qℏω_l(q). Highly dispersive modes with strong gradients ∇_qℏω_l(q) will contribute less to the PDOS than less dispersive modes. As the integral extends over all phonon wave vectors q with E=ℏω_l(q), each mode contributes to the projected PDOS according to its dispersion at a given phonon wave vector q weighted by the squared component of the associated polarization vector e_l(q) along the X-ray propagation vector s. The dispersion relations ω_l(q) and the associated atomic displacements are accessible through density functional perturbation theory (DFPT) (Baroni et al., 2001). Tsuchiya et al. (2008) used DFPT to compute the frequencies of vibrational modes for δ-AlOOH with different configurations of hydrogen sites.

Figure 2 Partial projected PDOS (a) and tensor components of the polarized PDOS (b) for modes that displace ⁵⁷Fe atoms in δ-(Al,Fe)OOH single crystals. The projected PDOS values (a) were extracted from NRIXS spectra recorded with the X-ray beam incident along different directions s and analyzed using a tensor description. The comparison of inversion results with the extracted PDOS (c) indicates that a second-rank tensor captures the anisotropy of the projected PDOS. The tensor components g₁₁, g₂₂, and g₃₃ of the polarized PDOS (b) illustrate how displacements of resonant ⁵⁷Fe atoms along the crystallographic a, b, and c axis, respectively, contribute to the projected PDOS. Extracted PDOS, inversion results, and residuals (a, c) are vertically offset for clarity. Shaded areas indicate uncertainties.

The tensor analysis defined in Sect. 3.3 allows us to adopt an experimental perspective that does not require prior knowledge of the vibrational structure to interpret vibrational anisotropy as sampled by NRIXS. Since expressions (5) and (6) for the projected PDOS can only be evaluated when the relations ω_l(q) and e_l(q) are known for all phonon branches, we will instead describe the projected PDOS using the second-rank tensor g_ij(E) of the polarized PDOS. We derived the tensor components g₁₁, g₂₂, and g₃₃ by inverting the projected PDOS of Fig. 2a as described in Sect. 3.3 and at each sampled energy. Figure 2b shows the derived tensor components g₁₁, g₂₂, and g₃₃ as a function of energy. To assess the quality of the inversion, we calculated the projected PDOS for each experimental X-ray propagation vector with expression (3) by inserting the extracted tensor components g₁₁(E), g₂₂(E), and g₃₃(E) and compare the calculated with the observed projected PDOS in Fig. 2c. Within the propagated uncertainties of the inversion results, the tensor description (3) captures the observed anisotropy of all major peaks and bands of the projected PDOS.

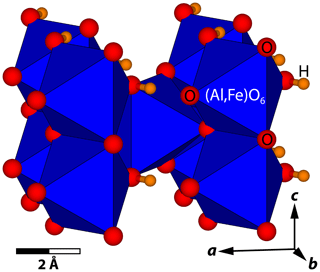
Figure 3 Crystal structure of δ-(Al,Fe)OOH. Atomic positions were taken from Komatsu et al. (2006) and lattice parameters from Table 1 (X1). The positions of oxygen atoms are shown as red spheres, the positions of hydrogen atoms are shown as orange spheres, and (Al,Fe)O₆ octahedra are shown in blue. The crystal structure was drawn with VESTA (version 3.4.6; Momma and Izumi, 2011). Note the edge and corner sharing of (Al,Fe)O₆ octahedra.

For crystals of orthorhombic symmetry, the axes of the crystal physical reference system point along the crystallographic axes as e₁∥a, e₂∥b, and e₃∥c and coincide with the principal axes of any second-rank tensor property. The components g₁₁, g₂₂, and g₃₃ of the polarized PDOS therefore describe the contributions of vibrational modes to the PDOS that displace ⁵⁷Fe nuclei along the a, b, and c axis, respectively. At energies of 15 to 25 meV, for example, we see from Fig. 2b that $g_{\mathrm{22}}>g_{\mathrm{11}}>g_{\mathrm{33}}$. This indicates that displacements of ⁵⁷Fe nuclei along the b axis contribute strongest to the PDOS in this energy range. The situation is reversed at energies between 30 and 80 meV with $g_{\mathrm{33}}>g_{\mathrm{11}}>g_{\mathrm{22}}$, suggesting that vibrations with displacements along the c axis require higher energies than vibrations with displacements along the a or b axis that dominate the PDOS at energies below 30 meV.

The vibrational energies or frequencies of modes that displace ⁵⁷Fe atoms are determined by the bonding environment of Fe atoms on the respective crystallographic site. The crystal structure of δ-(Al,Fe)OOH is shown in Fig. 3 and can be described as a distorted variant of the rutile structure type (Suzuki et al., 2000; Kudoh et al., 2004; Komatsu et al., 2006; Kawazoe et al., 2017). Similar to TiO₆ octahedra in rutile, MO₆ octahedra in δ-(Al,Fe)OOH with M= Al or Fe share edges to form ribbons along the c axis. Neighboring ribbons are offset against each other by one-half of the octahedral edge along c and rotated so that the oxygen atoms of shared edges form the apices of neighboring ribbons. The M–O bonds of these apices point along the diagonal of the a–b plane. As a result, M–M distances are shortest along the c axis and give rise to stronger repulsion between metal cations. Consequently, we would expect that displacements of Fe atoms along the c axis and towards the nearest M³⁺ cation require higher forces than displacements within the a–b plane and that Fe atoms vibrate at higher frequencies along the c axis than within the a–b plane. The variation of the components of the polarized PDOS with energy as derived from NRIXS spectra of δ-(Al,Fe)OOH single crystals reflects this anisotropic bonding environment of Fe atoms in δ-(Al,Fe)OOH.

When interpreting the polarized PDOS, it is important to keep in mind that the magnitude of any component g_ij combines both the number and dispersion of modes with an appropriate polarization. Peaks in the components g₁₁ and g₂₂ of the polarized PDOS at energies between 20 and 25 meV can therefore indicate that ⁵⁷Fe atoms are preferentially displaced within the a–b plane at these energies, that the corresponding modes are less dispersive than modes that displace ⁵⁷Fe atoms along the c axis, or a combination of both. DFPT calculations on δ-AlOOH suggest that the PDOS arises entirely from acoustic modes at energies below 19 meV (∼150 cm⁻¹) (Tsuchiya et al., 2008). At such low energies, the total number of modes is therefore equal to 3. The energies of optic modes overlap with those of acoustic modes at higher energies and dominate the PDOS of δ-AlOOH at energies above 38 meV (∼300 cm⁻¹) (Tsuchiya et al., 2008). Note that we found g₃₃ to drop to 0 between 20 and 23 meV. This points to an energy gap between acoustic and optic modes that displace ⁵⁷Fe atoms along the c axis.

4.2 Anisotropy of the Lamb–Mössbauer factor

Since inelastic scattering arises from momentum transfer to the atomic nucleus, i.e., from recoil, that results in the excitation or annihilation of lattice vibrations, the Lamb–Mössbauer factor is directly related to the PDOS (Singwi and Sjölander, 1960; Chumakov et al., 1996; Kohn and Chumakov, 2000):

$$\begin{array}{}\text{(7)}& f\left(\mathit{s}\right)=\exp \left(-E_{\text{R}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{g(E,\mathit{s})}{E}}{\displaystyle \frac{\mathrm{1}+e^{-\mathit{\beta }E}}{\mathrm{1}-e^{-\mathit{\beta }E}}}\mathrm{d}E\right),\end{array}$$

where E_R is the recoil energy of the resonant nucleus, and β is the inverse product of the Boltzmann constant and absolute temperature. In an NRIXS experiment on a single crystal, the PDOS is projected along the X-ray propagation vector s, and the observed Lamb–Mössbauer factor will consequently reflect any existing anisotropy of the projected PDOS g(E,s). Anisotropy of the Lamb–Mössbauer factor has previously been observed for ⁵⁷Fe in FeBO₃ crystals (Chumakov et al., 1997; Kohn et al., 1998) and in Fe-bearing molecular crystals (Paulsen et al., 1999).

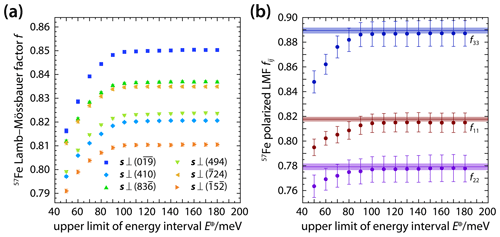
Figure 4 Lamb–Mössbauer factors of ⁵⁷Fe atoms in δ-(Al,Fe)OOH single crystals. Lamb–Mössbauer factors (a) were derived from NRIXS spectra recorded with the X-ray beam incident along different directions s and by stepwise increasing the analyzed energy interval. The anisotropy of the Lamb–Mössbauer factor (LMF) can be described using a second-rank tensor with the components f₁₁, f₂₂, and f₃₃ (b) that can be obtained by inverting (solid circles) the observed Lamb–Mössbauer factors (shown in a) or by integrating (horizontal lines) the components of the polarized PDOS (Fig. 2b). Shaded areas indicate uncertainties.

In addition to showing how the anisotropy of the projected PDOS is transmitted to the observed Lamb–Mössbauer factor, expression (7) implies that the contribution of vibrational modes to the Lamb–Mössbauer factor depends on their energy as well as on temperature (see also Eq. 8 for the mean kinetic energy and Eq. 9 for the mean force constant). The relevant energy range of vibrational modes that have the strongest influence in constraining the Lamb–Mössbauer factor, or another vibrational property at a given temperature, is difficult to precisely assess a priori when the PDOS has not been determined for the material of interest. Whether a recorded NRIXS spectrum covers the complete relevant energy range, however, can be verified by incrementally increasing the energy range that is included in the analysis of the NRIXS spectrum and in the calculation of derived properties, such as the Lamb–Mössbauer factor. As long as an expansion of the analyzed energy range gives rise to a significant change of the derived vibrational property, new contributions of vibrational modes are being added, provided that the background count rates have been assessed correctly. Any significant change of the derived vibrational property that arises from expanding the analyzed energy range could indicate that vibrational modes in the added energy increment contribute significantly to the derived property and that the complete relevant energy range has not yet been included in the analysis. Conversely, the invariance of a derived property upon expansion of the analyzed energy range indicates that contributions of vibrational modes are insignificant over the added energy increment, because the PDOS is very low within the added energy increment, the energy- and temperature-dependent weighting of vibrational modes suppresses their contribution, and/or the upper limit of the analyzed energy range has exceeded the vibrational energies of the material. A segmental analysis of NRIXS spectra can therefore be used to assess whether the sampled energy range has been chosen to include all relevant contributions of vibrational modes to a derived vibrational property. If the magnitude of a derived vibrational property stagnates upon expanding the analyzed energy range towards the complete sampled range, one can be optimistic that the sampled energy range covers all relevant vibrational modes.

For a given X-ray propagation vector s, the Lamb–Mössbauer factor f(s) is related to the projected PDOS g(E,s) via Eq. (7). The observed anisotropy of the Lamb–Mössbauer factor can therefore be described in an analogous way to the anisotropy of the projected PDOS by defining a second-rank tensor f_ij of the polarized Lamb–Mössbauer factor as defined in Sect. 3.3. For each analyzed energy interval ΔE, the components f_ij can be determined from the observed Lamb–Mössbauer factors of Fig. 4a by least-squares inversion. Figure 4b shows the inversion results in terms of the non-zero components f₁₁, f₂₂, and f₃₃, which are also listed in Table S1. Alternatively, the tensor components f_ij can be obtained by inserting the components g_ij(E) of the polarized PDOS into relation (7) and evaluating the integral. The tensor components f_ij as derived from the tensor of the polarized PDOS g_ij(E) are shown in Fig. 4b as horizontal lines. As the energy interval ΔE is extended, each component approaches the value calculated from the polarized PDOS. For $E^{\oplus }\ge \mathrm{100}$ meV, the components derived from both approaches, i.e., from the segmental analysis of NRIXS spectra and by integrating individual components of the polarized PDOS, become indistinguishable within their uncertainties. As a general result, we find that for δ-(Al,Fe)OOH single crystals $f_{\mathrm{33}}>f_{\mathrm{11}}>f_{\mathrm{22}}$ and that individual components of the polarized Lamb–Mössbauer factor differ by up to 13 %.

The observed anisotropy of the Lamb–Mössbauer factor results from the uneven excitation of vibrational degrees of freedom at ambient temperature. At low energies, the PDOS is dominated by modes polarized along the a and b axes (Fig. 2b). These low-energy modes are preferentially excited at room temperature. At a temperature of 300 K, for example, the factor that describes the thermal effect on the Lamb–Mössbauer factor in the integral (7) decreases from 5.2 for an energy of 10 meV to 1.9 at 30 meV and to 1 at 100 meV. As a result, ⁵⁷Fe atoms vibrate preferentially within the a–b plane at room temperature. Inelastic scattering events are therefore more probable for X-ray propagation vectors with small components along the c axis. The probability for recoilless absorption events, in turn, is largest for X-ray propagation vectors with large components along the c axis. In accordance with the sequence $g_{\mathrm{22}}>g_{\mathrm{11}}>g_{\mathrm{33}}$ at lowest energies (Fig. 2b), the components of the polarized Lamb–Mössbauer factor (Fig. 4b) suggest that displacements of ⁵⁷Fe atoms along the b axis are most likely to contribute to inelastic scattering at room temperature.

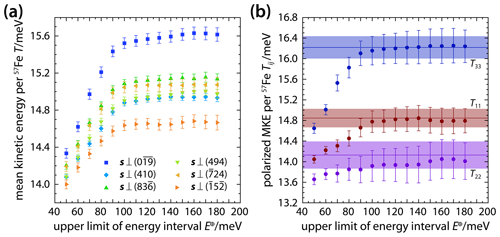
Figure 5 Mean kinetic energies per vibrational mode and per ⁵⁷Fe atom in δ-(Al,Fe)OOH single crystals. Mean kinetic energies (a) were derived from NRIXS spectra recorded with the X-ray beam incident along different directions s and by stepwise increasing the analyzed energy interval. The anisotropy of the mean kinetic energy (MKE) can be described using a second-rank tensor with the components T₁₁, T₂₂, and T₃₃ (b) that can be obtained by inverting (solid circles) the observed mean kinetic energies (shown in a) or by integrating (horizontal lines) the components of the polarized PDOS (Fig. 2b). Shaded areas indicate uncertainties.

4.3 Anisotropy of the mean kinetic energy

While the PDOS describes the distribution of vibrational modes over their energies, we observed from the analysis of the anisotropy of the Lamb–Mössbauer factor in Sect. 4.2 that for a given temperature not all vibrational modes are excited to the same extent. The amount of energy that a crystal accommodates in the form of lattice vibrations can be expressed as the mean kinetic energy per vibrational mode. An NRIXS spectrum contains information about the mean kinetic energy T per vibrational mode and per resonant atom. More precisely, the mean kinetic energy T per vibrational mode and per resonant atom can be calculated from the second-order moment of the phonon excitation probability S(E) (Lipkin, 1999; Sturhahn, 2004) and is related to the projected PDOS as follows (Kohn and Chumakov, 2000):

$$\begin{array}{}\text{(8)}& T\left(\mathit{s}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}g(E,\mathit{s})E\left[{\displaystyle \frac{\mathrm{1}}{e^{\mathit{\beta }E}-\mathrm{1}}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\right]\mathrm{d}E.\end{array}$$

When the PDOS is projected along the X-ray propagation vector s, the mean kinetic energy T(s) measures the energy stored in vibrational modes that displace resonant atoms in directions e with a component along the X-ray propagation vector s. As a result, the anisotropy of the projected PDOS g(E,s) is transferred to the mean kinetic energy T(s), and the relation between the X-ray propagation vector s and the mean kinetic energy T(s) per vibrational mode and per resonant atom can be expressed using the second-rank tensor T_ij of the polarized mean kinetic energy.

With the connection between the mean kinetic energy and the PDOS in mind as expressed in relation (8), it becomes clear that the steep rise in mean kinetic energies up to about 100 meV (Fig. 5a) reflects the overall shape of the PDOS. The majority of vibrational modes have energies below 100 meV (Fig. 2b), and modes of this energy range are predominantly excited at room temperature. Additional but weak contributions to the mean kinetic energy at higher energies arise from modes with energies in excess of 100 meV. The detection of these high-energy contributions demonstrates the gain in information offered by a segmental analysis of NRIXS spectra and emphasizes the advantages of recording NRIXS spectra over energy ranges that extend beyond the energy range of apparently non-zero PDOS.

Absolute mean kinetic energies differ substantially for different X-ray propagation vectors, highlighting the anisotropic accommodation of vibrational energy by the crystal structure of δ-(Al,Fe)OOH. Figure 5b illustrates the anisotropy of the mean kinetic energy T(s) in terms of the tensor components T₁₁, T₂₂, and T₃₃ that have been derived by inverting the data of Fig. 5a (Table S2) and by inserting the components g_ij(E) of the polarized PDOS into relation (8). Both approaches give consistent results for $E^{\oplus }\ge \mathrm{100}$ meV. For the component T₂₂, however, the closest match between the results of segmentally analyzing NRIXS spectra and of integrating the component g₂₂(E) of the polarized PDOS is obtained at $E^{\oplus }=\mathrm{160}$ meV. This observation might indicate that modes with displacements along the b axis contribute to the mean kinetic energy up to this energy.

From the overall relation $T_{\mathrm{33}}>T_{\mathrm{11}}>T_{\mathrm{22}}$, we conclude that vibrational modes that displace ⁵⁷Fe atoms along the c axis store more kinetic energy per mode and per ⁵⁷Fe atom than modes that displace ⁵⁷Fe atoms within the a–b plane. Similarly, vibrational displacements of ⁵⁷Fe atoms along the a axis accommodate more kinetic energy than displacements along the b axis. We saw from the analysis of the polarized PDOS (Fig. 2b) that $g_{\mathrm{33}}>g_{\mathrm{11}}>g_{\mathrm{22}}$ at energies above 30 meV; i.e., most modes at energies above 30 meV displace ⁵⁷Fe atoms along the c axis, and more modes displace ⁵⁷Fe atoms along the a axis than along the b axis. Although the situation changes at energies below 30 meV (Fig. 2b), it is the product of mode density, energy, and population that is integrated to the mean kinetic energy in expression (8). At room temperature, the observed anisotropy of the mean kinetic energy therefore seems to be dominated by the anisotropy of the PDOS in the energy range from 30 to 100 meV.

4.4 Anisotropy of the mean force constant

The third-order moment of the phonon excitation probability S(E) is related to the force constant that describes the site potential of resonant atoms for small displacements from their equilibrium positions (Lipkin, 1999; Sturhahn, 2004). The NRIXS experiment samples displacements of resonant atoms that arise from combinations of vibrational modes. In principle, each vibrational mode is characterized by an individual force constant that depends on the displacement pattern of all atoms in the crystal structure. Since an NRIXS spectrum only contains information about the displacements of resonant atoms and the associated energies, it provides access to the mean force constant, averaged over the displacement patterns and energies of all vibrational modes that displace resonant atoms. The mean force constant D(s) can be calculated from the projected PDOS as (Kohn and Chumakov, 2000)

$$\begin{array}{}\text{(9)}& D\left(\mathit{s}\right)={\displaystyle \frac{M}{{\mathrm{\hslash }}^{\mathrm{2}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}g(E,\mathit{s})E^{\mathrm{2}}\mathrm{d}E,\end{array}$$

with the mass M of resonant nuclei.

As with the Lamb–Mössbauer factor and the mean kinetic energy, we expect the mean force constant to inherit the anisotropy of the projected PDOS and define the second-rank tensor D_ij of the polarized mean force constant according to the definition in Sect. 3.3. Inverting the observed mean force constants shown in Fig. 6a at each energy interval for the tensor components D_ij yields the components D₁₁, D₂₂, and D₃₃ as shown in Fig. 6b and listed in Table S3. For a given energy interval, the sequence of observed mean force constants for different X-ray propagation vectors resembles the sequence observed for Lamb–Mössbauer factors and mean kinetic energies and consequently yields the same overall anisotropy with $D_{\mathrm{33}}>D_{\mathrm{11}}>D_{\mathrm{22}}$.

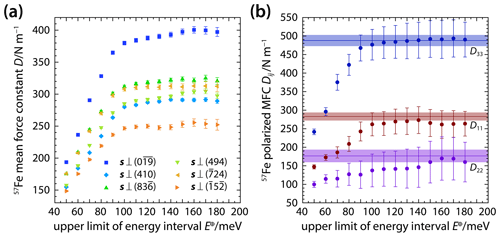
Figure 6 Mean force constants for ⁵⁷Fe atoms in δ-(Al,Fe)OOH single crystals. Mean force constants (a) were derived from NRIXS spectra recorded with the X-ray beam incident along different directions s and by stepwise increasing the analyzed energy interval. The anisotropy of the mean force constant (MFC) can be described using a second-rank tensor with the components D₁₁, D₂₂, and D₃₃ (b) that can be obtained by inverting (solid circles) the observed mean force constants (shown in a) or by integrating (horizontal lines) the components of the polarized PDOS (Fig. 2b). Shaded areas indicate uncertainties.

The mean force constant is proportional to the bonding forces that act to retain ⁵⁷Fe atoms on their equilibrium positions in the crystal structure. The polarized version of the mean force constant allows resolving the directional variation of these bonding forces. Based on the crystal structure of δ-(Al,Fe)OOH (Fig. 3) and the analysis of the polarized PDOS in Sect. 4.1, we concluded that bonding forces are strongest along the c axis. The sequence of tensor components $D_{\mathrm{33}}>D_{\mathrm{11}}>D_{\mathrm{22}}$ underscores this conclusion as the mean force constant is highest for displacements along the c axis. Whereas the polarized PDOS provides a detailed picture of the relation between the energy and polarization of modes, the polarized mean force constant averages bonding forces over the entire energy interval ΔE.

The probability for a vibrational mode to interact with the resonant absorption of an X-ray photon by a ⁵⁷Fe nucleus, i.e., to be excited or annihilated by an inelastic scattering process, decreases with increasing mode energy as does the population of vibrational states at a given temperature (Sturhahn, 2004). At room temperature, both effects can suppress the detection of modes with energies in excess of about 100 meV because the resulting inelastic scattering is often too weak to rise above the level of spurious intensity caused by electronic noise. We see from expression (9), however, that the PDOS at a given energy contributes to the mean force constant as the product of the PDOS and the energy squared. The mean force constant is therefore particularly sensitive to high-energy modes. An additional gain of contributions to the mean force constant at energies above 140 meV might be resolved for the component D₂₂ in Fig. 6b.

For energy intervals with $E^{\oplus }\ge \mathrm{120}$ meV, the components D₁₁ and D₃₃ converge with their values obtained by inserting the components g₁₁(E) and g₃₃(E), respectively, of the polarized PDOS into expression (9). For the component D₂₂, however, the results of the segmental analysis and the integration of the component g₂₂(E) of the polarized PDOS become most consistent for $E^{\oplus }=\mathrm{160}$ meV. The energy range from 140 to 170 meV corresponds to the range of frequencies (1100 to 1400 cm⁻¹) that have been predicted for O−H⋯O bending vibrations in δ-AlOOH using DFPT (Tsuchiya et al., 2008) and observed using Raman and infrared spectroscopies (Ohtani et al., 2001; Kagi et al., 2010). While modes at these energies are not readily discernible in the projected or polarized PDOS of Fig. 2, modes at energies E≥100 meV may contribute to the value of the mean force constant of δ-(Al,Fe)OOH owing to the sensitivity of the mean force constant to high-energy modes as indicated by Eq. (9). The displacements of ⁵⁷Fe atoms by these potential high-energy modes appear to be concentrated within the a–b plane as indicated by the rise of the component D₂₂ and the weak anti-correlation between the components D₂₂ and D₁₁ in the relevant energy range (Fig. 6b).

5 Applications

5.1 Anisotropy of atomic displacements

The preceding sections have shown how the vibrational anisotropy of ⁵⁷Fe atoms in the crystal structure of δ-(Al,Fe)OOH gives rise to anisotropic properties that span observational, energetic, and dynamical properties, from the fraction of inelastic scattering events as captured by the Lamb–Mössbauer factor over the kinetic or thermal energy to the force constants of the local site potential. Ultimately, the vibrational anisotropy of ⁵⁷Fe atoms should also be reflected on the structural level in terms of the displacements u of ⁵⁷Fe atoms from their equilibrium positions. X-ray and neutron diffraction experiments can constrain the magnitude and anisotropy of atomic displacements by deriving anisotropic displacement parameters U_ij that describe the mean-square displacement 〈u²〉 as a second-rank tensor (Willis and Pryor, 1975; Dove, 1993). Single-crystal NRIXS experiments provide access to the anisotropic displacement parameters U_ij through the anisotropic Lamb–Mössbauer factor f(k):

$$\begin{array}{}\text{(10)}& \begin{array}{rl}-\ln f\left(\mathit{k}\right)& =\langle {\left|\mathit{k}\cdot \mathit{u}\right|}^{\mathrm{2}}\rangle \\ & =k^{\mathrm{2}}\langle {\left|\mathit{s}\cdot \mathit{u}\right|}^{\mathrm{2}}\rangle \\ & =k^{\mathrm{2}}[\langle u_{\mathrm{1}}^{\mathrm{2}}\rangle s_{\mathrm{1}}^{\mathrm{2}}+\langle u_{\mathrm{2}}^{\mathrm{2}}\rangle s_{\mathrm{2}}^{\mathrm{2}}+\langle u_{\mathrm{3}}^{\mathrm{2}}\rangle s_{\mathrm{3}}^{\mathrm{2}}+\mathrm{2}(\langle u_{\mathrm{1}}{u}_{\mathrm{2}}\rangle s_{\mathrm{1}}{s}_{\mathrm{2}}\\ & +\langle u_{\mathrm{1}}{u}_{\mathrm{3}}\rangle s_{\mathrm{1}}{s}_{\mathrm{3}}+\langle u_{\mathrm{2}}{u}_{\mathrm{3}}\rangle s_{\mathrm{2}}{s}_{\mathrm{3}}\left)\right]\\ & =k^{\mathrm{2}}[U_{\mathrm{11}}{s}_{\mathrm{1}}^{\mathrm{2}}+U_{\mathrm{22}}{s}_{\mathrm{2}}^{\mathrm{2}}+U_{\mathrm{33}}{s}_{\mathrm{3}}^{\mathrm{2}}+\mathrm{2}(U_{\mathrm{12}}{s}_{\mathrm{1}}{s}_{\mathrm{2}}\\ & +U_{\mathrm{13}}{s}_{\mathrm{1}}{s}_{\mathrm{3}}+U_{\mathrm{23}}{s}_{\mathrm{2}}{s}_{\mathrm{3}}\left)\right],\end{array}\end{array}$$

with the wave vector k=ks and $k=\mathrm{2}\mathit{\pi }/\mathit{\lambda }$ for X-ray photons of the nuclear resonance energy (λ=0.8619 Å for ⁵⁷Fe). For diffraction experiments, the Debye–Waller factor replaces the Lamb–Mössbauer factor while the anisotropic displacement parameters U_ij are defined in an analogous way by replacing the X-ray wave vector with the diffraction vector (Willis and Pryor, 1975; Dove, 1993).

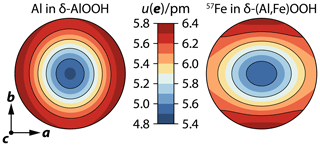
Figure 7 Root of the mean-square displacement $u\left(\mathit{e}\right)=\sqrt{e_i{e}_j{U}_{ij}}$ (RMSD) as a function of the displacement direction e for Al atoms in δ-AlOOH (left) and ⁵⁷Fe atoms in δ-(Al,Fe)OOH (right). Note the different scales for the RMSD for Al and ⁵⁷Fe atoms. The orientation of stereographic projections is indicated by the crystallographic coordinate system at the bottom left.

Komatsu et al. (2006)

Table 2 Anisotropic displacement parameters for Al and ⁵⁷Fe atoms in δ-(Al,Fe)OOH single crystals.

Note that standard deviations on the last digit are given in parentheses. Values in italics were fixed during analyses.

By using relation (10) in a least-squares inversion with the six experimental wave vectors s (Table 1) and the respective Lamb–Mössbauer factors for $E^{\oplus }\ge \mathrm{150}$ meV (Table S1) as observational input, we derived anisotropic displacement parameters U_ij for ⁵⁷Fe atoms in δ-(Al,Fe)OOH single crystals. As with previous tensor analyses in this study, off-diagonal components were set to zero, i.e., U_ij=0 for i≠j, since NRIXS samples the crystal symmetry rather than the local site symmetry. The results are given in Table 2 together with anisotropic displacement parameters for Al atoms in δ-AlOOH that have been derived from single-crystal synchrotron X-ray diffraction experiments (Komatsu et al., 2006).

Figure 7 shows color-coded stereographic projections of the root of the mean-square displacement (RMSD) $u\left(\mathit{e}\right)=\sqrt{e_i{e}_j{U}_{ij}}$ as a function of the displacement direction or polarization e for ⁵⁷Fe atoms in δ-(Al,Fe)OOH and Al atoms in δ-AlOOH. With largest displacements in the a–b plane and smallest displacements along the c axis, the anisotropic displacement patterns of both atomic species appear qualitatively similar. Likewise, the difference between the largest and smallest displacements, in terms of the RMSD, spans about 1 pm in both cases. The magnitudes of the RMSD, however, are systematically smaller for aluminum by about 0.6 pm. For Al atoms in δ-AlOOH, the RMSD is largest for displacements along the a axis, while we found largest RMSD along the b axis and a higher degree of anisotropy of the RMSD within the a–b plane for ⁵⁷Fe atoms in δ-(Al,Fe)OOH.

The overall pattern of the RMSD can be explained with the atomic structure of δ-(Al,Fe)OOH (Fig. 3). As MO₆ octahedra share edges to form ribbons along the c axis, the repulsion between metal cations M is strongest in this direction and impedes displacements towards neighboring cations. Displacements within the a–b plane, in contrast, do not lead to close approaches between metal cations because MO₆ octahedra are linked via shared anions at their corners that counteract M–M repulsion and allow for larger displacements. Differences between the anisotropic displacement patterns of ⁵⁷Fe and Al atoms may arise from differences in chemical bonding and ionic size. When compared to Al³⁺, the electronic configuration of Fe³⁺ comprises an additional shell of 3s and 3p electrons as well as five electrons in 3d orbitals. While the additional shell of core electrons results in a larger effective ionic size of Fe³⁺, electrons in d orbitals interact with the coordinating oxygen anions and may impart a directional character to chemical bonding as indicated by the strong anisotropy of the mean force constant (Fig. 6). Larger magnitudes of the RMSD of ⁵⁷Fe atoms might therefore reflect larger bond lengths to the coordinating oxygen anions, while the anisotropy of the RMSD might point to more directed chemical bonds with additional contributions of covalent bonding from d electrons. It is important, however, to keep in mind that the anisotropic displacement parameters for ⁵⁷Fe and Al atoms have been derived from different experimental techniques. While X-ray diffraction samples the electron density distribution, NRIXS directly probes the displacements of resonant atomic nuclei. Single-crystal NRIXS experiments might therefore offer a valuable complement to diffraction experiments for investigating the anisotropic displacements of atoms from their equilibrium positions in crystal structures.

5.2 Anisotropic thermal stresses

As a macroscopic expression of vibrational anisotropy, crystals develop anisotropic thermal stresses upon heating. When the crystal is free to expand, as in the case of isobaric heating, anisotropic thermal stresses are balanced by anisotropic thermal expansion, and the overall stress state will remain hydrostatic. When a crystal is confined to a specific volume or shape, however, anisotropic thermal stresses may give rise to deviatoric stresses in addition to a change in pressure. A mineral inclusion entrapped in a host crystal, for example, is forced into a shape that maintains mechanical equilibrium with the host crystal. Host–inclusion pairs that involve materials with anisotropic compressibility and thermal expansivity can be expected to develop deviatoric stresses within and around the inclusion upon changes in temperature or in the external stress state as they may result from the release of the host crystal to ambient conditions (Mazzucchelli et al., 2019; Nestola, 2020).

The pressure and temperature at which an inclusion was trapped by the host crystal can be reconstructed using elastic geobarometry (Rosenfeld and Chase, 1961; Howell et al., 2012; Angel et al., 2014b). Reconstructing the entrapment conditions of host–inclusion pairs when either material has a crystal symmetry lower than cubic requires modeling the anisotropic (cold) elastic and thermal stresses that arise from disparate relaxation of the host and inclusion phases (Mazzucchelli et al., 2019; Nestola, 2020). While the compressibility tensor κ_ij determines the stresses from elastic relaxation, anisotropic thermal stresses τ_ij can be described by the anisotropic generalization of the Grüneisen parameter in the form of a second-rank tensor γ_ij (Thomsen, 1970; Davies, 1974; Stixrude and Lithgow-Bertelloni, 2005):

$$\begin{array}{}\text{(11)}& {\mathit{\tau }}_{ij}=-{\mathit{\gamma }}_{ij}{\displaystyle \frac{{\mathrm{\Delta }}_{\text{TH}}U}{V}},\end{array}$$

with the change Δ_THU in internal energy that results from an (isochoric) change in temperature. According to the definition of the Grüneisen tensor as the derivative of vibrational frequency ω with respect to strain η_ij, ${\mathit{\gamma }}_{ij}=-\partial \ln \mathit{\omega }/\partial {\mathit{\eta }}_{ij}$ (Thomsen, 1970; Davies, 1974; Stixrude and Lithgow-Bertelloni, 2005), the components γ_ij can be derived from experiments or computations that trace the changes in vibrational frequencies with compression. Since the vibrational frequencies are considered to be scalar properties, any crystal with compressional anisotropy will develop different strains along different directions upon compression and will hence be characterized by an anisotropic Grüneisen tensor.

Single-crystal NRIXS experiments and the analysis of vibrational anisotropy outlined in Sect. 3.3 potentially open an alternative way to constrain anisotropic thermal stresses. Murphy et al. (2011) showed how the vibrational Grüneisen parameter can be derived from the changes in the PDOS along a series of compression steps by proposing a volume-dependent scaling relation for the PDOS. When the anisotropic compression behavior of the material is known, a similar analysis can be used to analyze the changes in the PDOS that result from strain along different crystallographic directions and hence to constrain the Grüneisen tensor γ_ij. As an alternative, the scaling approach of Murphy et al. (2011) can be applied to the tensor components of the polarized PDOS. In this case, however, the Grüneisen parameter would describe the compression-induced changes in the PDOS of a hypothetical material with vibrational properties that are fully captured by the respective component g_ii(E) of the polarized PDOS, i.e., of a hypothetical cubic crystal for which g(E)=g_ii(E). This idea is analogous to the concept of linearized equations of state that describe the variation of the length a of a vector a, for example, a vector along one of the unit cell edges, with pressure and temperature by treating the cubed length a³ like the unit cell volume of a hypothetical cubic crystal V_a=a³ (Angel et al., 2014a; Buchen et al., 2017). The thermal stress along any direction of such a hypothetical cubic crystal would be given by

$$\begin{array}{}\text{(12)}& {\mathit{\tau }}_{\mathit{a}}=-{\mathit{\gamma }}_{\mathit{a}}{\displaystyle \frac{{\mathrm{\Delta }}_{\text{TH}}{U}_{\mathit{a}}}{V_{\mathit{a}}}}\end{array}$$

and the thermal expansivity by

$$\begin{array}{}\text{(13)}& {\mathit{\alpha }}_{\mathit{a}}={\displaystyle \frac{{\mathit{\gamma }}_{\mathit{a}}{C}_{V\mathit{a}}}{K_{\mathit{a}}{V}_{\mathit{a}}}}.\end{array}$$

The change Δ_THU_a in internal energy and the isochoric heat capacity C_Va can be estimated by approximating the vibrational structure of the hypothetical cubic crystal with the polarized PDOS $g_{\mathit{a}}\left(E\right)=a_i{a}_j{g}_{ij}\left(E\right)/a^{\mathrm{2}}$ for displacements along the vector a with coordinates a_i defined with respect to the axes of the crystal physical reference system. The bulk modulus K_a of the hypothetical cubic crystal can be calculated from the linear modulus k_a for the direction a as $\mathrm{3}{K}_{\mathit{a}}=k_{\mathit{a}}=a_i{a}_j{k}_{ij}/a^{\mathrm{2}}$ with the components k_ij of the tensor of linear moduli or the incompressibility tensor. Although the thermal stress along a given direction should ideally be identical when calculated based on definitions (11) and (12), it is important to note that the Grüneisen parameter γ_a is not directly related to the components of the tensor γ_ij since both refer to different vibrational structures. Differences between both approaches may arise from the partial character of the PDOS when derived from NRIXS spectra, in particular when the Grüneisen tensor γ_ij has been determined from data obtained by techniques other than NRIXS.

Accurate modeling of thermal stresses is required to reconstruct the entrapment conditions of inclusions, for example, in super-deep diamonds that provide the most direct evidence for the mineral content of the lower mantle (Harte, 2010; Kaminsky, 2012; Nestola, 2017; Nestola et al., 2018). Although high-pressure oxyhydroxide phases have not yet been reported as inclusions in diamonds, other hydrous high-pressure phases have been identified in diamonds that formed at depths of the mantle transition zone (Wirth et al., 2007; Pearson et al., 2014). Diamond inclusions suggested to have formed even deeper in the mantle further point to the presence of hydrous fluids at depths of the uppermost lower mantle (Palot et al., 2016; Tschauner et al., 2018). The inferred genetic relationship between deep diamond formation and hydrous fluids or melts (Harte, 2010) permits the hypothesis that high-pressure oxyhydroxide phases might eventually be discovered as inclusions in diamonds as well. High-pressure NRIXS experiments on single crystals of high-pressure oxyhydroxide phases and minerals found as inclusions may help to constrain their anisotropic thermal properties and to reconstruct their entrapment conditions. In addition to NRIXS experiments on crystals compressed in diamond anvil cells, it might be possible to collect NRIXS spectra directly on a crystal entrapped as an inclusion in a natural diamond as long as the concentration of Mössbauer-active isotopes, i.e., ⁵⁷Fe, in the inclusion is high enough.

6 Conclusions

We recorded NRIXS spectra with high statistical quality on single crystals of the high-pressure oxyhydroxide phase δ-(Al,Fe)OOH at ambient conditions to investigate the effect of vibrational anisotropy of ⁵⁷Fe atoms on the projected PDOS and related properties. The projected PDOS of δ-(Al,Fe)OOH single crystals shows substantial sensitivity to the projection direction as defined by the X-ray propagation vector. To describe the anisotropy of the projected PDOS, we defined a second-rank tensor that captures the pattern of motion of ⁵⁷Fe atoms in terms of the polarization of atomic displacements as a function of energy. We derived the non-zero components of this tensor for δ-(Al,Fe)OOH single crystals from the experimentally observed projected PDOS.

The bonding environment of ⁵⁷Fe atoms in the crystal structure of δ-(Al,Fe)OOH gives rise to highly anisotropic vibrational properties as expressed in the Lamb–Mössbauer factor, the mean kinetic energy per vibrational mode, and the mean force constant, all of which can be analyzed using second-rank tensors in analogy to the projected PDOS. The observed anisotropy of these properties can be explained by exploring their relation to the projected PDOS and to the crystal structure of δ-(Al,Fe)OOH. We further translated the anisotropy of the Lamb–Mössbauer factor into anisotropic displacement parameters for ⁵⁷Fe atoms in δ-(Al,Fe)OOH and compared the results with reported anisotropic displacement parameters for Al atoms in δ-AlOOH.

Our results on δ-(Al,Fe)OOH single crystals highlight the sensitivity of NRIXS to vibrational anisotropy. The proposed tensor formulation provides an appropriate framework to analyze and describe the anisotropy of NRIXS-related properties from an experimental perspective. Describing the anisotropy of Lamb–Mössbauer factors, for example, may prove helpful in analyzing Mössbauer spectra that were collected on single crystals and with polarized X-rays generated by synchrotrons (Solomatova et al., 2019). Although our measurements were conducted at ambient conditions, we note that NRIXS experiments are fully compatible with high-pressure devices such as diamond anvil cells that are capable of transferring the experimental protocol of single-crystal NRIXS to study the impact of pressure on vibrational anisotropy. As an example, we proposed a conceivable way to constrain anisotropic thermal stresses from high-pressure single-crystal NRIXS data with potential applications in elastic geobarometry for mineral inclusions. High-pressure single-crystal NRIXS experiments might be particularly suited to detect changes in the vibrational properties that arise from phonon softening or spin transitions of iron cations in mineral phases at high pressures, such as changes in hydrogen bonding and the spin transition of Fe³⁺ cations in δ-(Al,Fe)OOH (Ohira et al., 2019, 2021).

Understanding the vibrational behavior of iron in minerals is of general interest for mineralogical research given the high geochemical abundance of iron in Earth's crust, mantle, and core. Our analysis of single-crystal NRIXS spectra provides an in-depth description of the vibrational behavior of Fe³⁺ cations in a mineral structure of unprecedented detail, spanning structural, energetic, and dynamical properties. The vibrational properties of individual atomic species affect key processes in minerals such as chemical diffusion and reactions, isotope fractionation, and thermal conduction. Anisotropy in the vibrational behavior will therefore impart anisotropy to these processes with consequences, for example, for observed rates of diffusion or isotope exchange. As a transition metal, iron can be challenging to treat with density functional theory (DFT) computations that have evolved as a valuable tool in addressing a wide range of mineralogical problems. Detailed descriptions of the vibrational behavior of iron in crystal structures as derived from single-crystal NRIXS experiments could help assess the validity of different DFT approaches. In view of the potential to advance our understanding of the vibrational behavior of iron and other elements with Mössbauer-active isotopes in crystal structures, our results on ⁵⁷Fe in δ-(Al,Fe)OOH may stimulate the application of single-crystal NRIXS experiments to study the vibrational anisotropy of minerals and other crystalline solids.