Quantification of major and trace elements in fluid inclusions and gas bubbles by laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) with no internal standard: a new method

Recent advances in laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) open new perspectives for quantification of trace metals and metalloids in mineral-hosted fluid inclusions and glass-hosted gas bubbles. This work is devoted to a new method applied to quantify element concentrations (at parts-per-million and weight percent levels) in natural and synthetic fluid inclusions and gas bubbles by using only an external calibrator in cases where internal standardization is unavailable. For example, this method can be applied to calculate element (metal and metalloid) concentrations in carbonic (C–O–H) fluid inclusions and bubbles. The method is devoted to measuring incompatible (with the host mineral and glass) trace elements originally dissolved into the trapped fluid. The method requires precise estimation of the fluid density, the inclusion/bubble volume or average radius, and measurement of the laser ablation crater radius by independent microanalytical techniques as well as accurate data on the concentration of major/minor elements compatible with the host mineral (or host glass). This method, applicable for analyses of hydrous carbonic fluid inclusions and gas bubbles hosted in silicate minerals and glasses, relies on the absence of a matrix effect between fluid, host mineral and daughter phases (silicate, oxide or sulfide) and the external calibrator (e.g., reference silicate glasses) during the LA-ICP-MS analysis, an assumption validated by the use of femtosecond lasers.

1 Introduction

Development of new methods for a “standardless” quantification of fluid composition is of utmost importance in geochemical research, particularly nowadays, given the continuous evolution of analytical facilities and the difficulties in providing reliable internal calibration. For example, Rickers et al. (2004) and Cauzid et al. (2006) have proposed a method for standardless quantification of major and trace element contents in fluid and melt inclusions based on synchrotron radiation-induced X-ray fluorescence. However, in situ techniques such as those provided by laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) are much more readily available to geologists. Leach and Hieftje (2001) developed a method for standardless analysis of synthetic alloys by single-shot LA-ICP-MS, but this turned out to be only semiquantitative. To our knowledge, to this day there is no method allowing the standardless analysis of the fluid phase contained in fluid inclusions nor in gas bubbles commonly found as inclusions in glass.

The traditional method used by the majority of researchers to quantify LA-ICP-MS analyses requires internal standardization (an internal calibrator) in order to produce an absolute measure of the elements contained in a fluid inclusion. Most commonly, fluid or melt inclusions contain either a saline fluid (commonly NaCl) or a silicate component, respectively. In the latter case, the inclusion can be heated and quenched to a homogenous silicate glass which is measurable by an electron microprobe (e.g., Borisova et al., 2006, 2008, 2012; Vikentiev et al., 2012), although this is a long and complex process. In both cases, independent measures of the concentration of Na or other major elements (Al, Si, Cl) are used for internal standardization to quantify the concentrations of the trace elements (< 1000 ppm) (e.g., Longerich et al., 1996; Schafer et al., 1999; Halter et al., 2002; Heinrich et al., 2003; Borisova et al., 2006, 2012; Pettke et al., 2012; Seo et al., 2011; Vikentiev et al., 2012). However, the trace element contents in other, less common but nonetheless important types of inclusions such as those containing pure gaseous C–O–H species as well as in gas bubbles in glasses and glass-inclusion-hosted bubbles (e.g., Kamenetsky et al., 2002; Lowenstern, 2015; Schiavi et al., 2020) have never been quantified for trace elements because of the infeasibility of internal standardization. As an example, Kamenetsky and Kamenetsky (2010) described Cu- and Ag-bearing CO₂-rich bubbles in basaltic glasses from the Macquarie Island ophiolite but could not evaluate their trace element concentrations.

Recently, several attempts were made to estimate trace element contents in NaCl-poor inclusions (or in gas bubbles) using LA-ICP-MS data by estimating a value for the internal calibrator. Hanley and Gladney (2011) described quartz-hosted, Ni-, Cu-, Pd-, Bi-, Te- and Fe-bearing CO₂-rich inclusions from the Roby zone, Lac des Iles Complex (Ontario, Canada), as containing only minor bulk NaCl (0.1 wt %–1 wt % NaCl_equiv). They suggested the Na contents in the inclusions and used these values as an internal calibrator to quantify the trace metals in the inclusions. Scambelluri et al. (2004) tried quantifying the trace element concentrations in NaCl-poor carbonic fluid inclusions by using a best-guess value of 2 wt % NaCl_equiv as the maximum fluid salinity. Spandler et al. (2007) attempted the same task by relaying on mass balance considerations. Ferrando et al. (2009) assumed a Si concentration and used it as an internal calibrator for inclusions from ultrahigh-pressure rocks of the Brossasco-Isasca Unit of the Southern Dora-Maira Massif without any further correction for the host mineral contribution to the bulk fluid inclusion signals. All of these attempts to apply guessed concentrations to fluid composition quantification only produced results plagued by likely high uncertainties (sometimes undiscussed and non-evaluated) and no means to assess them. To further increase the need for standardless quantification, it is now established that high concentrations of metals can be transported by pure carbonic fluids (e.g., CO- or CO₂-bearing; Simakin et al., 2016, 2021). The high concentration of metals has been detected but not quantified in the produced CO-rich synthetic fluid inclusions and bubbles. Therefore, in order to quantify the trace element concentrations in natural and synthetic low-NaCl carbonic fluid inclusions and gas bubbles, where either no or only minor concentrations of internal standards for the LA-ICP-MS method are available, we have developed the method discussed below.

2 Method

2.1 Quantification of element concentrations in fluid inclusions and gas bubbles

The method that we propose builds on the consideration of element pairs: (i) a first element, termed X, which must be strongly compatible in the mineral hosting the fluid inclusion or gas bubble; a second element, termed Y, which is enriched in the fluid or vapor and must be strongly incompatible in the host mineral (host glass). The concentration of X must be known, while that of Y is unknown. All other elements investigated must belong either to the host-compatible X group or to the host-incompatible Y group, which represents the unknown elements contained in the fluid inclusion or gas bubble. (ii) The method assumes chemical homogeneity of the measured inclusion and of the host mineral in the investigated zone. (iii) An additional requirement is that, during LA-ICP-MS analysis, there are no or only small matrix effects interfering between the investigated fluid–mineral (or fluid–glass) pair and the external calibrator (e.g., reference silicate glass), both of which must be analyzed for the same isotopes under the same analytical conditions. That means that the isotopic sensitivities should be similar between the different matrices (fluid, silicate, oxide or sulfide, and silicate calibrator) with no matrix effect. These conditions can be obtained using femtosecond lasers for the ablation (Fernandez et al., 2007; Velasquez et al., 2012, 2018; Poitrasson and d'Abzac, 2017; and references therein) as they have been shown to overcome matrix effects, which occur regularly with nanosecond lasers. Indeed, the interaction between the laser-induced plasma and the end of the laser pulse no longer exists in the femtosecond laser ablation regime (Poitrasson and d'Abzac, 2017). As a result, the specific femtosecond laser–matter interaction has led to greatly reduced chemical fractionation effects, allowing application of matrix-independent calibration for both elemental and isotopic analysis. The next benefit of femtosecond laser ablation is the independence of the laser–matter interaction from the optical properties of the target. This makes it capable of fully controlled and efficient ablation of optically transparent materials like quartz and calcite (Poitrasson and d'Abzac, 2017). Nevertheless, the 193 nm ultraviolet nanosecond excimer laser has been demonstrated to produce small matrix effects between fluids, silicates, oxides and possibly sulfides (Horn et al., 2001; Heinrich et al., 2003), and as such it is an excellent alternative to femtosecond lasers.

The method implies that laser ablation sensitivities for elements X and Y in a reference material (i.e., external silicate glass calibrator such as the NIST standard reference material (SRM) series) are known, which can be expressed as

$$\begin{array}{}\text{(1)}& S^{X/Y}={\displaystyle \frac{S^X}{S^Y}}={\displaystyle \frac{{\sum }_{\text{I}}X}{{\sum }_{\text{I}}Y}}{\displaystyle \frac{C^Y}{C^X}},\end{array}$$

where $S^{X/Y}$ is a sensitivity factor; S^X and S^Y represent chosen isotope sensitivities (in counts per second per ppm, cps ppm⁻¹); ∑_IX and ∑_IY are integrated (background-subtracted) LA-ICP-MS pattern intensities (cps) for a chosen isotope; and C^X and C^Y are the concentrations (ppm) of element X and Y, respectively.

Considering an ablated host mineral (glass) zone where the fluid phase (gas bubble or fluid inclusion) is localized, the ratios of element concentrations are calculated according to the equation

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{C_{\text{ablation}}^Y}{C_{\text{ablation}}^X}}={\displaystyle \frac{S^X}{S^Y}}{\displaystyle \frac{{\sum }_{\text{I}}Y}{{\sum }_{\text{I}}X}}=S^{X/Y}{\displaystyle \frac{{\sum }_{\text{I}}Y}{{\sum }_{\text{I}}X}}=S^{X/Y}{k}^{Y/X},\end{array}$$

where $C_{\text{ablation}}^X$ and $C_{\text{ablation}}^Y$ are the concentrations of elements X and Y in parts per million in the ablated zone, respectively. The coefficient $k^{Y/X}=\frac{{\sum }_{\text{I}}Y}{{\sum }_{\text{I}}X}$ relates the background-subtracted integrated intensities ∑_IX and ∑_IY (cps) for the selected isotopes in the ablated zone of the host mineral–fluid (glass–fluid) inclusion system.

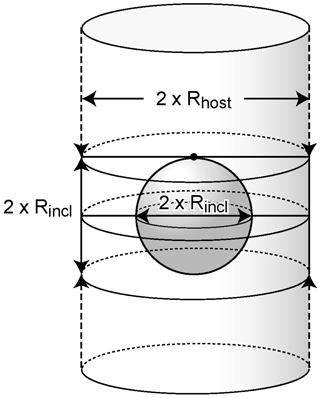
Figure 1 Simplified ablation geometry of a fluid inclusion (gas bubble) with radius R_incl (µm) within the ablated host mineral (glass) idealized as a cylinder of radius R_host.

The following assumptions must hold true:

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }{M}_{\text{ablation}}^X=M_{\text{host}}^X,\text{(4)}& {\displaystyle }& {\displaystyle }{M}_{\text{ablation}}^Y=M_{\text{incl}}^Y,\end{array}$$

where $M_{\text{ablation}}^X$ and $M_{\text{ablation}}^Y$ are the masses (g) of elements X and Y in the ablated zone, and $M_{\text{host}}^X$ and $M_{\text{incl}}^Y$ are the masses of elements X and Y contained, respectively, in the ablated host mineral and in the ablated inclusion (Fig. 1). If we set M_ablation equal to the total mass (g) of the ablated zone, i.e., the host mineral plus the inclusion, we can write

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }{C}_{\text{ablation}}^Y={\displaystyle \frac{M_{\text{ablation}}^Y}{M_{\text{ablation}}}}={\displaystyle \frac{M_{\text{incl}}^Y}{M_{\text{ablation}}}},\text{(6)}& {\displaystyle }& {\displaystyle }{C}_{\text{ablation}}^X={\displaystyle \frac{M_{\text{ablation}}^X}{M_{\text{ablation}}}}={\displaystyle \frac{M_{\text{host}}^X}{M_{\text{ablation}}}},\end{array}$$

which, combined, result in

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{C_{\text{ablation}}^Y}{C_{\text{ablation}}^X}}={\displaystyle \frac{M_{\text{incl}}^Y}{M_{\text{host}}^X}}.\end{array}$$

Recalling Eqs. (2) and (7) we can write

$$\begin{array}{}\text{(8a)}& {\displaystyle \frac{C_{\text{ablation}}^Y}{C_{\text{ablation}}^X}}=S^{X/Y}{k}^{Y/X}={\displaystyle \frac{M_{\text{incl}}^Y}{M_{\text{host}}^X}},\end{array}$$

and therefore

$$\begin{array}{}\text{(8b)}& M_{\text{incl}}^Y=M_{\text{host}}^X{S}^{X/Y}{k}^{Y/X}.\end{array}$$

Let us now consider the following two equations, which relate mass and densities:

$$\begin{array}{}\text{(9a)}& M_{\text{incl}}={\mathit{\rho }}_{\text{incl}}\times v_{\text{incl}}\end{array}$$

and

$$\begin{array}{}\text{(9b)}& M_{\text{host}}={\mathit{\rho }}_{\text{host}}\times v_{\text{host}},\end{array}$$

where ρ_incl, ρ_host (g cm⁻³) and v_incl, v_host (cm³) are the densities and volumes of the inclusion and the host, respectively. If we define $C_{\text{incl}}^Y$ as the concentration (ppm) of element Y in the inclusion, we can write

$$\begin{array}{}\text{(10a)}& C_{\text{incl}}^Y={\displaystyle \frac{M_{\text{incl}}^Y}{M_{\text{incl}}}}={\displaystyle \frac{M_{\text{incl}}^Y}{p_{\text{incl}}{v}_{\text{incl}}}}.\end{array}$$

It follows that

$$\begin{array}{}\text{(10b)}& C_{\text{incl}}^Y={\displaystyle \frac{M_{\text{incl}}^Y}{p_{\text{incl}}{v}_{\text{incl}}}},\end{array}$$

and

$$\begin{array}{}\text{(11a)}& C_{\text{host}}^X={\displaystyle \frac{M_{\text{host}}^X}{p_{\text{host}}{v}_{\text{host}}}},\end{array}$$

with $C_{\text{host}}^X$ representing the concentration of element X in the host mineral or host glass. Finally, if we write

$$\begin{array}{}\text{(11b)}& M_{\text{host}}^X=C_{\text{host}}^X{\mathit{\rho }}_{\text{host}}{v}_{\text{host}}\end{array}$$

and, substituting Eq. (8b) into Eq. (10b), find

$$\begin{array}{}\text{(12)}& C_{\text{incl}}^Y={\displaystyle \frac{M_{\text{host}}^X{S}^{X/Y}{k}^{Y/X}}{p_{\text{incl}}{v}_{\text{incl}}}},\end{array}$$

we can insert Eq. (11b) into Eq. (12) to obtain the final equation:

$$\begin{array}{}\text{(13)}& C_{\text{incl}}^Y={\displaystyle \frac{C_{\text{host}}^X{p}_{\text{host}}{v}_{\text{host}}{S}^{X/Y}{k}^{Y/X}}{p_{\text{incl}}{v}_{\text{incl}}}},\end{array}$$

which gives the concentration, in parts per million, of the unknown element Y in the fluid inclusion or gas bubble as a function of the concentration, in parts per million, of a compatible element (X) measured independently in the host mineral (glass), the densities (g cm⁻³) and volumes of the ablated inclusion and host (µm³), a sensitivity factor, and the integrated laser ablation intensities (cps) for Y in the inclusion (bubble) and for the known element X in the host.

Table 1 Quantification of a Au–Ag-rich, quartz-hosted fluid inclusion, applying the traditional protocol as well as the new method.

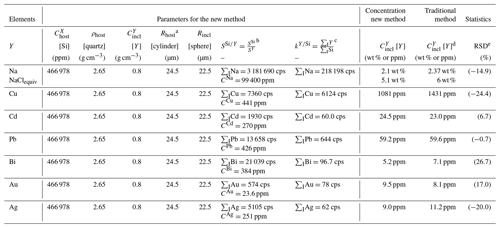
^a The volume of the host (v_host) is a function of both R_host and R_incl. The R_host crater radius is measured on the surface of the host mineral or glass after the LA-ICP-MS session; we measured this value using a scanning electron microscope (SEM).
^b The reference major element (SiO₂= 69.7 wt %, Na₂O = 13.4 wt %) and trace metal concentrations in the NIST SRM 610 glass are recommended values from the GeoReM database (Jochum et al., 2011). The background-subtracted intensity is an average value calculated for five bracketing measurements of NIST SRM 610 glass during the same ablation session (measured at the same ablation conditions). $S^{\text{Si}/Y}$ is the ratio of sensitivities in the external calibrator (NIST SRM 610 glass), where $S^{\text{Si}}=\frac{{\sum }_{\text{I}}\text{Si}}{C^{\text{Si}}}$ cps ppm⁻¹, ${\sum }_{\text{I}}\text{Si}=$ 163 542 cps, and C^Si= 324 400 ppm.
^c The ratio of the integrated isotopic intensities (cps) for [X] or [Si], where ${\sum }_{\text{I}}\text{Si}=$ 206 000 cps.
^d Inclusion U294 from rhyolite of the Uzel'ginskoe magmatic–hydrothermal Cu–Zn sulfide ore field, Urals, Russia, analyzed using the “traditional method” by Vikentiev et al. (2012). The inclusion radius has been measured by high-resolution optical microscopy, whereas bulk salinities and density of the inclusion have been determined by the classical microthermometric method. During the LA-ICP-MS runs, the ablated material was carried in a flow of helium gas, which was mixed with argon in a transporting tube connected to a quadrupole ICP-MS (Agilent 7500ce, Agilent Technologies). Ablation was via a Ti:sapphire laser (Pulsar 10, Amplitude Technologies) operating at 800 nm, which produced 55 fs pulses with a maximum energy of 12 mJ.
^e [RPD] – the relative percent difference for the concentrations calculated based on the new method (this work) compared to the values obtained by the “traditional method” (based on NaCl_equiv contents measured by microthermometry) by Vikentiev et al. (2012).

2.2 Testing the new method based on a known quartz-hosted, metal-rich fluid inclusion

To validate the new method, we have used a fluid inclusion that had been previously characterized by the traditional LA-ICP-MS method, using a femtosecond laser, by Vikentiev et al. (2012) (inclusion U294; Table 1) and have set out to quantify its trace (Cu, Ag, Cd, Au, Pb, Bi) and major (Na) element concentrations using our procedure. This is a large fluid inclusion measuring 45 µm in diameter, which contains a saline aqueous fluid. It is characterized by a homogenization temperature T_h equal to 245 ^∘C and a density p_incl of 0.8 g cm⁻³. Its composition was originally obtained using the Na concentration derived independently by microthermometry as an internal standard (6 wt % NaCl_equiv). For the purpose of our test, Si was chosen as the highly compatible element in the quartz host, with an estimated concentration ($C_{\text{host}}^{\mathrm{SiO}\mathrm{2}})$ of 99.9 wt % (equal to $C_{\text{host}}^{\mathrm{Si}}$ of 466 978 ppm; Table 1). The inclusion radius (R_incl) was measured at 22.5 µm. The average ablation crater radius (R_host) was 24.5 µm, measured using a JEOL JSM-6360 LV scanning electron microscope (GET, Toulouse, France). In summary, calculations were conducted with an average (R_host) radius of 24.5 µm. Considering simplified geometries of a sphere and a cylinder, respectively, for the ablated inclusion and the host quartz (Fig. 1), the volumes of the inclusion and the host quartz are $v_{\text{incl}}=\mathrm{4}/\mathrm{3}\left[\mathit{\pi }{R}_{\text{incl}}^{\mathrm{3}}\right]$ and $v_{\text{host}}=\mathrm{4}/\mathrm{3}\mathit{\pi }\left[\right(\mathrm{1.5}{R}_{\text{incl}})R_{\text{host}}^{\mathrm{2}}-R_{\text{incl}}^{\mathrm{3}}]$, where R_incl and R_host are the radiuses of the inclusion and the ablated zone of the host mineral, respectively. Alternatively, the inclusion volume and radius may be measured by X-ray micro-tomography (Creon et al., 2018). We know that the femtosecond laser has no matrix effect between the external calibrator and the measured host mineral–fluid inclusion system (e.g., Velasquez et al., 2012; Poitrasson and d'Abzac, 2017; and references therein). Therefore, if we apply Eq. (13) using radii for volumes, we have

$$\begin{array}{}\text{(14)}& C_{\text{incl}}^Y=\left[C_{\text{host}}^X\right]\left[{\displaystyle \frac{p_{\text{host}}}{p_{\text{incl}}}}\right]\left[{\displaystyle \frac{\mathrm{1.5}{R}_{\text{host}}^{\mathrm{2}}}{R_{\text{incl}}^{\mathrm{2}}}}-\mathrm{1}\right]\left[S^{X/Y}{k}^{Y/X}\right].\end{array}$$

In the equation, $S^{X/Y}$ is $\frac{S^{\text{Si}}}{S^{\text{Au}}}$, where S^Si and S^Au are chosen isotopic sensitivities (cps ppm⁻¹) calculated for an external calibrator (NIST SRM 610; Table 1) for Si (as element X) and Au (as element Y). In Eq. (14), $k^{\mathrm{Au}/\mathrm{Si}}=\frac{{\sum }_{\text{I}}\text{Au}}{{\sum }_{\text{I}}\text{Si}}$, where ∑_IAu and ∑_ISi are the integrated (background-subtracted) LA-ICP-MS intensities (cps) for the elements Y (Au) and X (Si), respectively, where ∑_IAu was integrated in the fluid inclusion burst zone, while the integration for ∑_ISi was shifted to the signal of quartz only (Fig. 2a). We performed several comparisons of critical major and trace element concentrations (e.g., Na, Au, etc.) calculated according to Eq. (14) with those obtained by the traditional method (Table 1, Supplement 1). The comparison suggests that the optimal period for integrating the Y signal of the LA-ICP-MS pattern is 2.5 s, corresponding to the signal related to the fluid ablation. Given a host quartz ablation rate of 0.42 µm per pulse, or 2.1 µm s⁻¹ with a repetition rate of 5 Hz (d'Abzac, 2010; Courtieu et al., 2011), the integrated period of ∼ 2.5 s corresponds to the integration of a ∼ 5 µm quartz ablation pattern. Indeed, the integration period for element Y should correspond to the peak(s) of the ablation pattern related to the introduction of the NaCl-bearing fluid from the ablated inclusion to the ICP-MS system. The calculated concentrations (based on Eqs. 13 and 14) are from 0.7 % to 24 % (exceptionally, 27 % for Bi) of the relative percentage difference (RPD) between major and trace element contents, obtained by the traditional method of LA-ICP-MS quantification. The values obtained for the major element Na and its corresponding NaCl_equiv concentration (5.1 wt %; Table 1) are within the 15 % RPD limit agreement with those estimated based on microthermometry (6 wt % NaCl_equiv).

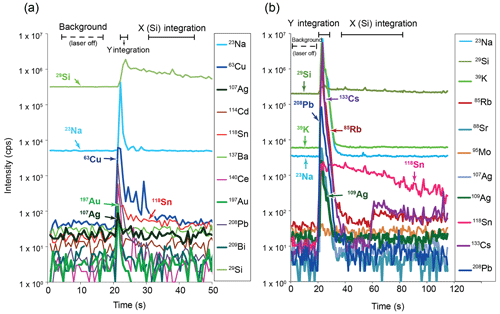
Figure 2 (a) Femtosecond LA-ICP-MS pattern of the ablation of a fluid inclusion hosted in natural quartz (Au–Ag-rich inclusion U294, courtesy of Ilya Vikentiev). Quantification by the traditional method gives $C_{\text{incl}}^{\text{Au}}=\mathrm{8.1}$ ppm and $C_{\text{incl}}^{\text{Ag}}=\mathrm{11.2}$ ppm (Vikentiev et al., 2012). Ablation was performed with a near-infrared femtosecond laser using a repetition rate of 5 Hz and an energy of ∼ 1 mJ per pulse; the ablation rate was 0.42 µm per pulse or 2.1 µm s⁻¹. Measurement of the Y element is done by integrating the spectra obtained during bursting of the fluid inclusion, represented here by the 2.5 s peak interval marked by a “Y integration” line (Y elements considered here are Na, Cu, Ag, Cd, Au, Pb, Bi). The flat pattern right after the inclusion peak is taken to represent ablation of the host mineral (here quartz) for 30 s, so the integration for the X element (here Si) is shifted to this interval (“X (Si) integration”) line. (b) Femtosecond LA-ICP-MS pattern of the ablation of a fluid inclusion hosted in natural quartz (pegmatite inclusion 019-E1, courtesy of Rainer Thomas). For example, quantification by the traditional method gives $C_{\text{incl}}^{\text{Cs}}=$ 22 700 ppm (Borisova et al., 2012). Ablation was performed with a near-infrared femtosecond laser using a repetition rate of 5 Hz and an energy of ∼ 1 mJ per pulse; the ablation rate was 0.42 µm per pulse or 2.1 µm s⁻¹. Measurement of the Y element is done by integrating the spectra obtained during bursting of the fluid inclusion, represented here by the 6.1 s peak interval marked by a “Y integration” line (Y elements considered here are Na, K, Rb, Sr, Mo, Sn, Ag, Cs, Pb). The flat pattern right after the inclusion peak is taken to represent ablation of the host mineral (here quartz) for 30 s, so the integration for the X element (here Si) is shifted to this interval (“X (Si) integration”) line.

Additionally, we have quantified a second fluid inclusion (019-E1, Borisova et al., 2012). This is a metal-rich, pegmatitic-quartz-hosted fluid inclusion measuring 50 µm in average diameter, which contains crystalline salts and a saline aqueous fluid. It is characterized by a homogenization temperature T_h equal to ∼ 600 ^∘C and a density p_incl of 1.2 g cm⁻³. Its composition was originally obtained using the Na concentration derived independently by microthermometry as an internal standard (34.4 wt % NaCl_equiv; Fig. 2b, Table 2, Supplement 2). We performed several comparisons of major and trace element concentrations (e.g., Na, K, Rb, Sr, Mo, Sn, Ag, Cs, Pb) calculated according to Eq. (14) with those obtained by the traditional method (Table 2). The comparison suggests that the optimal period for integrating the Y signal of the LA-ICP-MS pattern is 6.1 s, corresponding to the signal related to the fluid inclusion ablation. The fluid is evacuated more rapidly from an inclusion just after its opening compared to the ablated host; the LA-ICP-MS signals of the fluid and the host are decoupled (there is a small shift in the signal). Indeed, the integration period for element Y should correspond to the strongest peak(s) of the ablation pattern related to the introduction of the NaCl-bearing fluid from the ablated inclusion to the ICP-MS system. The calculated concentrations (based on Eqs. 13 and 14) are from 2.2 % to 14.5 % of the relative percentage difference (RPD) between major and trace element contents, obtained by the traditional method of LA-ICP-MS quantification. The values obtained for the major element Na and its corresponding NaCl_equiv concentrations (30.9 wt %; Table 1) are within the 10 % RPD limit, which is in good agreement with those estimated based on microthermometry (34.4 wt % NaCl_equiv).

Table 2 Quantification of a NaCl-rich quartz-hosted fluid inclusion, applying the traditional protocol as well as new method.

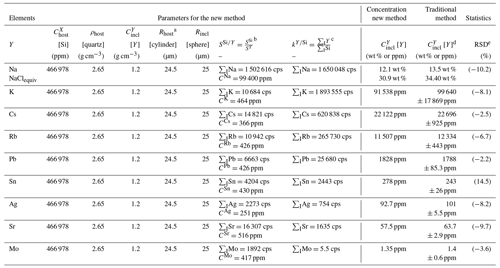
^a The volume of the host (v_host) is a function of both R_host and R_incl. The R_host crater radius may be measured on the surface of the host mineral or glass after the LA-ICP-MS session; we measured two values (maximal and minimal) of R_host in quartz using the SEM, but in this case, we used an average of the two.
^b The reference major element (SiO₂= 69.7 wt %, Na₂O = 13.4 wt %) and trace metal concentrations in the NIST SRM 610 glass are recommended values from the GeoReM database (Jochum et al., 2011). The background-subtracted intensity is an average value calculated for five bracketing measurements of NIST SRM 610 glass during the same ablation session (measured at the same ablation conditions). $S^{\text{Si}/Y}$ is the ratio of sensitivities in the external calibrator (NIST SRM 610 glass), where $S^{\text{Si}}=\frac{{\sum }_{\text{I}}\text{Si}}{C^{\text{Si}}}$ cps ppm⁻¹, ${\sum }_{\text{I}}\text{Si}=\mathrm{50}\mathrm{316}$ cps, and C^Si= 324 400 ppm.
^c The ratio of the integrated isotopic intensities (cps) for [X] or [Si], where ${\sum }_{\text{I}}\text{Si}=$ 63 315 cps.
^d Inclusion 019-E1 from the Ehrenfriedersdorf pegmatite (Erzgebirge, Germany), analyzed using the “traditional method” by Borisova et al. (2012). The inclusion radius has been measured by high-resolution optical microscopy, whereas bulk salinities and density of the inclusion have been determined by the classical microthermometric method. During the LA-ICP-MS runs, the ablated material was carried in a flow of helium gas, which was mixed with argon in a transporting tube connected to a quadrupole ICP-MS (Agilent 7500ce, Agilent Technologies). Ablation was via a Ti:sapphire laser (Pulsar 10, Amplitude Technologies) operating at 800 nm, which produced 55 fs pulses with a maximum energy of 12 mJ.
^e [RPD] – the relative percent difference for the concentrations calculated based on the new method (this work) compared to the values quantified by the “traditional method” (based on NaCl_equiv contents measured by microthermometry) by Borisova et al. (2012).

The application of Eqs. (13) and (14) for the calculations of major and trace element concentrations in the CO₂- and CO-rich inclusions requires determination of the C–O–H fluid density. This may be performed based on micro-Raman spectroscopy (e.g., Borisova et al., 2014) or theoretically if the proportions of the gas components are well determined or known (e.g., Kokh et al., 2016, and references therein).

2.3 An additional test for the quantification method

The correctness of the integrated period of the laser ablation pattern (∑_IY) may be verified by considering two instead of one known (major, minor or trace) element concentrations in the host mineral or glass ($C_{\text{host}}^X$ and $C_{\text{host}}^W$). Therefore, the test requires measuring the intensities of four isotopes (X, Y, W, Z) during the ablation. Elements X and W, compatible with the host quartz or silicate glass (quenched silicate melt), may be non-volatile elements like Ti, Al, Mg and Cr (or moderately volatile Si), which are easily quantifiable by microanalytical techniques (e.g., electron probe microanalysis (EPMA), LA-ICP-MS method). Two equations for $C_{\text{host}}^X$ and $C_{\text{host}}^W$ are thus combined to form the following equation:

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{C_{\text{incl}}^Y}{C_{\text{incl}}^Z}}={\displaystyle \frac{C_{\text{host}}^X{S}^{X/Y}{k}^{Y/X}}{C_{\text{host}}^W{S}^{W/Z}{k}^{Z/W}}},\end{array}$$

where, respectively, $C_{\text{incl}}^Y$ and $C_{\text{incl}}^Z$ are the calculated concentrations of incompatible elements Y and Z (ppm) in the fluid inclusion (gas bubble) based on Eq. (13); $C_{\text{host}}^X$ and $C_{\text{host}}^W$ are the known concentrations of compatible elements X and W (ppm) in the host mineral; $S^{X/Y}=\frac{S^X}{S^Y}$ and $S^{W/Z}=\frac{S^W}{S^Z}$ are ratios of sensitivities (cps ppm⁻¹) in an external calibrator (reference silicate glass) measured at the same conditions as those applied for the fluid analysis; and $k^{Y/X}$ and $k^{Z/W}$ are coefficients relating ratios of the integrated intensities after background subtraction (cps). The $k^{Y/X}$ is equal to $\frac{{\sum }_{\text{I}}Y}{{\sum }_{\text{I}}X}$, and $k^{Z/W}$ is equal to $\frac{{\sum }_{\text{I}}Z}{{\sum }_{\text{I}}W}$ for the selected isotopes in the ablated zone of the host mineral–fluid inclusion (host glass–bubble) system. Thus, the concentration ratios for two incompatible elements $C_{\text{incl}}^Y$ and $C_{\text{incl}}^Z$ as well as the integration period Δt, which determines the values of the isotopic intensities ∑I(Δt) (∑_IX, ∑_IY, ∑_IZ, ∑_IW for the selected isotopes of elements X, Y, Z, W; cps), may be precisely evaluated based on the known concentrations of two (major or minor) elements ($C_{\text{host}}^X$ and $C_{\text{host}}^W$) which are compatible with the host mineral (host glass). This test may be applied to and is highly recommended for the glass-hosted fluid bubbles.

3 Conclusions

We have developed a new method for standardless quantification of element concentrations (at parts-per-million to weight percent levels) in natural and synthetic fluid inclusions and gas bubbles by femtosecond LA-ICP-MS analysis using only an external calibrator. As an example, the new method may be applied to estimate the major and trace element (metal and metalloid) concentrations in hydrous carbonic (C–O–H such as CO- or CO₂-rich etc.) fluid inclusions and bubbles, with uncertainties mostly better than 25 % (the uncertainties for Bi reach 27 %). The new method requires precise quantification of the fluid density, the inclusion or bubble volume or average radius, and measurement of the laser ablation crater radius by independent microanalytical techniques. By means of independently obtained concentration data for two elements in the host mineral (glass), it is possible to verify the quantification of the fluid composition. Because femtosecond lasers greatly reduce matrix effects compared to classical nanosecond lasers, ICP-MS coupled to femtosecond lasers offers new perspectives for standardless quantification of fluid inclusions, gas bubbles and potentially C–H-rich (organic) matrices. This method may be tested with modern ultraviolet nanosecond (e.g., excimer type) lasers, which have been demonstrated to have moderate matrix effects between aqueous fluids, oxides, (possibly sulfides) and silicates. This method is provided as a user-friendly Excel spreadsheet, available as Table S1 in the Supplement.