the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Thermodynamic properties, crystal structure and phase relations of pushcharovskite [Cu(AsO3OH)(H2O) ⋅ 0.5H2O], geminite [Cu(AsO3OH)(H2O)] and liroconite [Cu2Al(AsO4)(OH)4 ⋅ 4H2O]
Alexandra M. Plumhoff
Jakub Plášil
Edgar Dachs
Artur Benisek
Jiří Sejkora
Martin Števko
Mike S. Rumsey
Juraj Majzlan
The phases pushcharovskite, geminite and liroconite were synthesized or acquired and characterized by powder X-ray diffraction, infrared spectroscopy, electron microprobe analysis, thermogravimetric analysis and optical emission spectrometry, as needed. Their thermodynamic properties were determined by a combination of acid-solution calorimetry and relaxation calorimetry, resulting in Gibbs free energies of formation (ΔfGo, all values in kilojoules per mole) of (pushcharovskite, Cu(AsO3OH)(H2O)⋅0.5H2O) and (geminite, Cu(AsO3OH)(H2O)). For the natural liroconite (Cu2Al[(AsO4)0.83(PO4)0.17](OH)4⋅4H2O), kJ mol−1. The estimated ΔfGo for the endmember Cu2Al(AsO4)(OH)4⋅4H2O is −2931.6 kJ mol−1. The crystal structure of liroconite was refined (R1=1.96 % for 962 reflections with I>3σ(I)) by single-crystal X-ray diffraction and the positions of H atoms, not known previously, were determined. Liroconite is a rare mineral, except for several localities, notably Wheal Gorland in England. Thermodynamic modelling showed that liroconite will be preferred over olivenite if the Al(III) concentration in the fluid reaches levels needed for saturation with X-ray amorphous Al(OH)3. We assume that such fluids are responsible for the liroconite formation during contemporaneous oxidation of primary Cu–As ores and pervasive kaolinization of the host peraluminous granites. pH had to be kept in mildly acidic (5–6), and the activities of dissolved silica were too low to form dioptase. The main stage with abundant liroconite formation was preceded by an acidic episode with scorodite and pharmacosiderite and followed by a late neutral to mildly basic episode with copper carbonates. Geminite and pushcharovskite, on the other hand, are minerals typical for very acidic solutions. At the studied site in Jáchymov (Czech Republic), extremely acidic water precipitates arsenolite; sulfate is removed by formation of gypsum. Geminite associates with other acidic minerals, such as slavkovite, yvonite and minerals of the lindackerite group. Pushcharovskite is metastable with respect to geminite and probably converts quickly to geminite under field conditions.
- Article
(7511 KB) - Full-text XML
-
Supplement
(100 KB) - BibTeX
- EndNote
Variability in the chemical composition and crystal chemical properties of secondary copper minerals lends them for the understanding of the formation and evolution of oxidation zones of ore deposits (Magalhães et al., 1988, 1986; Williams, 1990). Among others, copper arsenates are also common and widely distributed minerals in such oxidation zones (e.g. Števko et al., 2017; Southwood et al., 2020) where they form through weathering of sulfidic minerals. Copper arsenates are capable of taking up and releasing not only copper and arsenic but also other elements such as lead, zinc and selenium (e.g. Ingwersen, 1990). Release of such elements can lead to deterioration of the natural environment. Thermodynamic and crystallographic data, combined into internally consistent thermodynamic databases, can help to predict and explain the occurrence and assemblages of copper arsenates and associated minerals.
Geminite was reported as a new species by Sarp and Perroud (1990) on material from Cap Garonne (Var, France) as Cu(AsO3OH)(H2O). Pushcharovskite was described later by Sarp and Sanz-Gysler (1997) on material from the same site with the same ideal chemical composition and space group P–1. They concluded that pushcharovskite is a polymorph of geminite and structurally related to yvonite (Cu(AsO3OH)(H2O)⋅H2O).
The crystal structure of pushcharovskite was determined by Pushcharovsky et al. (2000) on a sample from the type locality using a synchrotron radiation source. Revision of the chemical data (electron microprobe) after the structure solution and refinement allowed the conclusion that the ideal formula is Cu(AsO3OH)(H2O)⋅0.5H2O. Hence, pushcharovskite and geminite are not polymorphs but a series of hydrates of Cu(AsO3OH)(H2O).
Liroconite was named by Wilhelm Karl von Haidinger in 1825 (Mohs and Haidinger, 1825), and before this it was known as octahedral arsenate of copper (de Bournon, 1801). One of the first descriptions of the crystal structure of liroconite was in 1962 as Cu2Al[((As1P)O4)(OH)4]⋅4H2O by Giuseppetti et al. (1962).
In this work, we report the thermodynamic properties of the copper arsenates pushcharovskite (ideally Cu(AsO3OH)(H2O)⋅0.5H2O), geminite (Cu(AsO3OH)(H2O)) and liroconite (Cu2Al(AsO4)(OH)4⋅4H2O). Pushcharovskite and geminite were synthesized in our laboratory and characterized by X-ray powder diffraction, Fourier-transform infrared spectroscopy, thermogravimetric analyses and inductively coupled optical emission spectroscopy. The natural samples of geminite and liroconite were characterized by X-ray powder diffraction and an electron microprobe. Enthalpies of formation were measured by acid-solution calorimetry. Additionally, the standard entropy of pushcharovskite was measured by relaxation calorimetry and combined with the enthalpy of formation to calculate its Gibbs free energy of formation. The standard entropies of geminite and liroconite were estimated. Using the thermodynamic data, we then assign specific conditions of formation to these and associated minerals.
Pushcharovskite was synthesized by a modified wet chemical procedure after Majzlan et al. (2015), Guillemin (1956) and Toman (1978). All solutions were prepared with deionized water. The first starting solution for this synthesis was 100 mL of 0.1 M As2O5, which was heated to approximately 60 ∘C so that the arsenic oxide powder dissolved completely. The solution was allowed to cool down and later brought to the desired temperature (20, 30, 40, 50 or 80 ∘C) for the synthesis. The second starting solution was 100 mL of 0.1 M Cu(OH)2 heated separately to the desired temperature (20, 30, 40, 50 or 80 ∘C), noting that Cu(OH)2 does not completely dissolve. After reaching the desired temperature, the arsenical solution was poured in to the cupric suspension under constant stirring. The glass beaker with the final mixture was covered with aluminium foil and left in an oven for 60 min. The resulting suspension was filtered hot and washed several times with deionized water. This synthesis is sensitive to temperature; its sensitivity to the cover is also peculiar. If the suspension is left uncovered and under constant stirring, olivenite (Cu2(AsO4)(OH)) will form.
Geminite was synthesized by reacting 0.92 g As2O5 powder with 0.35 g powder of malachite (Cu2CO3(OH)2) in 10 mL of deionized water. First, the arsenic oxide powder was mixed with the deionized water and dissolved (see above). After the arsenical solution cooled down to room temperature, the malachite powder was added into the beaker. The mixture was stirred shortly and then left standing for 20 h at room temperature. The final product was filtered and washed with deionized water and dried at room temperature (synthesis after Guillemin, 1956).
The malachite used for the geminite synthesis was synthesized after Tanaka and Yamane (1992). The starting solutions of 100 mL of 0.1 M Cu(NO3)2 and 100 mL of 0.15 M Na2CO3 were filled into borosilicate glass bottles and heated separately in a water bath to 35 ∘C with a thermostat. After temperature stabilization (∼ 24 h), both solutions were mixed into one flask and left in the water bath for another 24 h. The final product was filtered and washed with deionized water and dried at room temperature.
The natural sample of geminite (private collection) is from Jáchymov, Czech Republic. The specimen originates from the Geschieber vein at the Daniel adit level in the Svornost mine. Geminite is associated with minor arsenolite (As2O3) and lavendulan (NaCaCu5(AsO4)4Cl⋅5H2O) on the specimen, growing on milky-white quartz without any apparent hypogene sulfidic mineral. Additional specimens studied also originate from Jáchymov, from the Giftkies adit (Unruhe area) situated at the north-eastern part of the ore district. The Jáchymov ore district is located on the southern slope of the Erzgebirge, approximately 20 km north of Karlovy Vary, and belongs to the NW–SE-striking Gera-Jáchymov fault zone (Viehweg, 1995), and most of the ore minerals were deposited during the Variscan mineralization from mesothermal fluids (Ondruš et al., 1997). The ore district is limited by several major fault zones and the Giftkies adit is located in the north-eastern corner of this fault-bound area.
The natural liroconite sample grows on aggregates of older strashimirite and is from the type locality Wheal Gorland at St. Day, Cornwall, UK, from the collection of the National Museum in Prague (cat. no. P1N 26.818). The mine Wheal Gorland is part of the Camborne-Redruth mining district which is situated in Cornwall, the south-western part of Great Britain, approximately 90 km west of Plymouth. The Variscan granitic pluton in Cornwall is peraluminous, and the small granite bodies that host the mineralization, Carn Brea and Carn Marth, are more aluminous than the average Cornubian granite (Charoy, 1986). Several types of ore mineralizations were emplaced in these granitic rocks in Variscan and late Variscan times (Chesley et al., 1993). The last stage of significant mineralogical changes is the pervasive kaolinization, placed in the Cretaceous–Tertiary period (Sheppard, 1977). The kaolin deposits are thought to be trough- or funnel-shaped and may reach depths of 200 m. The copper mine Wheal Gorland is located on the east contact zone of the Carn Marth granite, working within both the intrusion and the altered country rock, known as “killas”. The oxidation zone of this arseniferous copper mine reaches 180 m depth and was the subject of extensive mineral collecting in the late 18th and early 19th centuries.
Powder X-ray diffraction (PXRD) patterns of all samples were collected with a Bruker D8 ADVANCE DaVinci diffractometer (Institute of Geosciences, Friedrich-Schiller University of Jena, Germany) employing CuKα radiation (λ=1.54058 Å). The patterns were collected at room temperature between 5 and 90∘ 2θ, with a step size of 0.02∘ 2θ and a time per step of 1.0 s. Lattice parameters were refined with the software TOPAS (Bruker, 2009; Coelho, 2018).
Single-crystal X-ray diffraction data were acquired with a Rigaku SuperNova single-crystal diffractometer (Institute of Physics, ASCR, v.v.i., Prague, Czech Republic) equipped with an Atlas S2 detector and using the mirror-monochromatized MoKα radiation (λ=0.71073 Å) from a microfocus X-ray tube, providing a high-flux brilliant beam. Corrections for background, Lorentz effect and polarization were applied to the data during reduction in the CrysAlis package (Rigaku, 2019). The correction for absorption was carried out using Gaussian correction combined with empirical scaling in the JANA2006 software (Petříček et al., 2014). Single-crystal XRD data were collected for a tabular 0.080 mm × 0.065 mm × 0.045 mm large single crystal of liroconite from Cornwall (also used for calorimetric study). The structure has been solved independently of previous structure investigations (Burns et al., 1991) using a charge-flipping algorithm of the program SHELXT (Sheldrick, 2015) and subsequently treated by the least-squares refinement in JANA2006 (Petříček et al., 2014). Another single-crystal XRD dataset was collected for a fragment of geminite crystal from Jáchymov, of a prismatic shape and approximate dimensions of 0.060 mm × 0.013 mm × 0.009 mm.
The chemical composition was determined by wavelength dispersive analyses using a Cameca SX100 electron microprobe (Laboratory of Electron Microscopy and Microanalysis of Masaryk University and the Czech Geological Survey in Brno, Czech Republic) with an acceleration voltage of 15 kV, a sample current of 5 nA and a beam diameter of 10 µm. The following lines and standards were used: Kα: albite (Na), almandine (Fe), Co (Co), gahnite (Zn), lammerite (Cu), Mg2SiO4 (Mg), Ni2SiO4 (Ni), sanidine (Al, K, Si), ScVO4 (V), spessartine (Mn), SrSO4 (S), topaz (F), fluorapatite (P, Ca), vanadinite (Cl); Lα: lammerite (As); Lβ: Sb (Sb); Mα: vanadinite (Pb); Mβ: Bi (Bi). Peak counting times (CTs) were 20 s for main elements and 60 s for minor elements; the CT for each background was one-half of the peak time. The raw intensities were converted to the concentrations automatically using PAP (Pouchou and Pichoir, 1985) matrix-correction software.
The Cu and As concentration in the fine-grained pushcharovskite sample was analysed with a simultaneous radial inductively coupled optical emission spectrometer (ICP-OES) 725ES (Agilent, University of Jena, Germany) with a charge-coupled device (CCD) detector and an ASX-520 autosampler (Teledyne CETAC). The sample (∼ 10 mg) was diluted in 10 mL of 20 % HNO3.
Fourier-transform infrared (FT-IR) transmission spectra were recorded using a Nicolet iS10 spectrometer (University of Jena, Germany). The samples (1–2 mg) were mixed with KBr (FTIR spectroscopy grade, Merck), gently ground and pressed to pellets. The pellets were measured at wavenumbers from 4000 to 400 cm−1 with 64 scans per spectrum at a resolution of 4 cm−1. The spectra were baseline-corrected and normalized to maximum intensity.
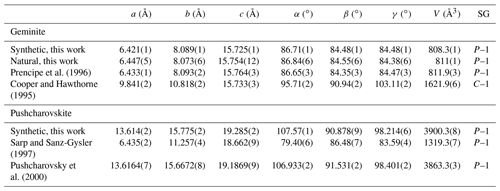
Table 1Unit cell parameters for geminite and pushcharovskite from this work, compared to values from studies on natural material.
The thermogravimetric analysis (TGA) was performed on a Setaram TG 92 (University of Jena, Germany), flushed with argon gas and a heating rate of 10 K min−1. Samples ground to fine powder were filled in corundum ceramic cups (15–30 mg) and subjected to the TG analysis.
The acid-solution calorimeter (University of Jena, Germany) is a commercial IMC-4400 isothermal microcalorimeter (Calorimetry Sciences Corporation), modified for the purposes of acid-solution calorimetry (Majzlan, 2017). The liquid water bath of the calorimeter is held at a constant temperature of 298.15 K with fluctuations smaller than 0.0005 K. The solvent was 25 g of 5 N HCl and is contained in a polyetheretherketone (PEEK) cup with a total volume of 60 mL. The PEEK cup is then closed with a PEEK screw lid and inserted into the calorimeter, where it stabilizes for about 8 h. During the stabilization and the experiment, the solvent is stirred by a SiO2 glass stirrer by a motor positioned about 40 cm from the active zone of the instrument. The samples were pressed into a pellet and weighed on a microbalance with a precision of 0.002 mg. The pellets are then dropped through an SiO2 glass tube into the solvent, and the heat produced or consumed during the dissolution was measured. The heat flow between the reaction cup and the constant temperature reservoir was then integrated to calculate the caloric effect. A typical experiment lasts 40–60 min and the end of the experiments is judged from the return of the baseline to the pre-experiment position. The pellet mass of each measured phase was calculated according to the stoichiometry of the thermochemical cycle.
Heat capacity was measured with a commercially designed relaxation calorimeter (Physical Properties Measurement System by Quantum Design) at Salzburg University, Austria. With due care, accuracy can be within 1 % for 5 to 300 K and 5 % for 0.7 to 5 K (Kennedy et al., 2007). The powdered sample was wrapped in a thin Al foil and compressed to produce a 0.5 mm thick pellet, which was then placed onto the sample platform of the calorimeter for the measurement. Measurements were conducted in the temperature interval from 2 to 300 K. The heat capacity between 260 and 280 K was measured by differential scanning calorimetry (DSC) using a PerkinElmer Diamond DSC. Details of the method are described in Benisek et al. (2012).
The programs Geochemist's Workbench® (Bethke, 2011; Bethke et al., 2019) and PHREEQC (Parkhurst and Appelo, 1999) with the Lawrence Livermore National Laboratory (LLNL) thermodynamic database were used for some of the thermodynamic calculations performed in this work. The database was extended with the data for geminite, pushcharovskite, liroconite (this work), olivenite (Majzlan et al., 2015), euchroite (Majzlan et al., 2017), cornubite and clinoclase (Magalhães et al., 1988).
All of the studied samples consist of a single phase, except for the natural geminite, which contains a minor arsenolite impurity. The full-profile fit of the PXRD data of geminite indicates 1.1 mass % of arsenolite in the mixture. The quality of the geminite crystal prevented us from the collection of a dataset with reasonable intensity statistics. Therefore, we report here only the unit cell parameters (Table 1). The lattice parameters of pushcharovskite (refined after Pushcharovsky et al., 2000) are shown in Table 1. The potassium atom, which is in the structure of the natural sample of Pushcharovsky et al. (2000), was deleted for the refinement to account for the lack of potassium in this sample of pushcharovskite.
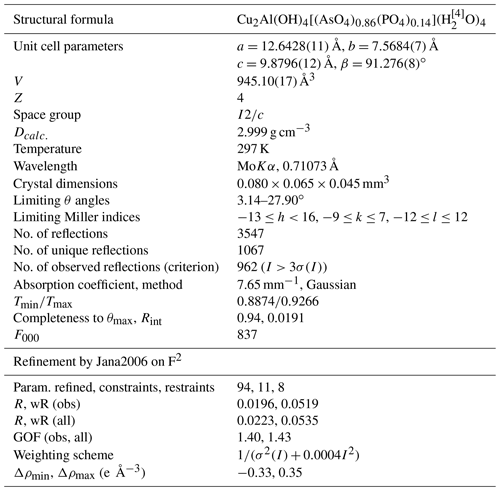
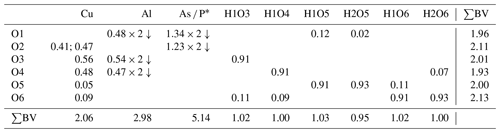
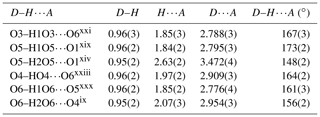
The structure solution of liroconite revealed nearly all atomic positions except for hydrogen atoms; those were localized from the difference Fourier maps and refined keeping soft constraints of 0.98(4) Å on the O–H distances as well as H–O–H angles, 105(1)∘ within the H2O molecules and with the Uiso of each H set to 1.2 times that of the donor O atom. The final refinement including 94 parameters, 8 restraints and 11 constraints smoothly converged to R=0.0196 and wR = 0.0519 for 962 unique observed reflections, having I>3σ(I), with goodness of fit (GOF) = 1.40. Crystallographic details, data collection and refinement parameters are given in Table 2. Atom coordinates and displacement parameters are listed in Table 3. The bond-valence analysis (after Brown, 2002), based on refined interatomic distances (Table 4), is provided in Table 5 using the bond-valence parameters given by Gagné and Hawthorne (2015) and Brown (2002). The crystallographic information file (CIF) and the structure factor list were deposited in the Supplement.
Table 3Atom coordinates and equivalent and anisotropic displacement parameters for liroconite.
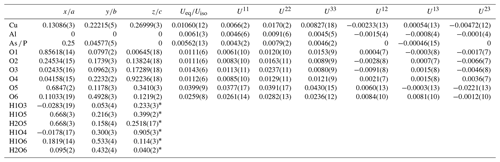
* Atoms refined with isotropic displacement parameter se to 1.2×Ueq of the parent O atoms. Occupancy of the As ∕ P site refined to 0.856(3) ∕ 0.144(3).
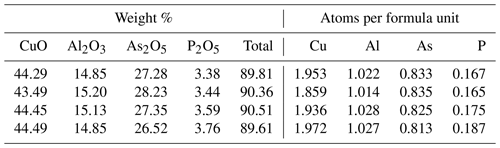
The results of the electron microprobe analyses of liroconite are shown in Table 6. The concentrations of Mn, Ca, Pb, Co, Ni, Zn, Fe, Mg, Na, K, Sb, V, S, Si and Cl were below the detection limits. Totals much below 100 % (Table 6) are caused by the presence of H2O in the structure of liroconite, but they do not correspond to the expected H2O content of ∼ 25 wt. %. Desiccation patterns, seen as numerous cracks in the liroconite crystals, confirm that the sample lost much H2O (at least 4 H2O per formula unit) under the vacuum inside the instrument. The weight percent of each oxide is CuO 44.18±0.41, Al2O3 15.01±0.16, As2O5 27.35±0.61 and P2O5 3.54±0.15. Based on (As + P) = 1 apfu (atoms per formula unit), the average empirical formula for the studied liroconite is Cu1.93Al1.02[(AsO4)0.83(PO4)0.17](OH)4⋅4H2O. As deficiencies on the Cu and Al positions in the structure are unlikely, we consider the values of 1.93 and 1.02, respectively, for these two positions with an analytical uncertainty. The slight difference in the formula between the crystallographic refinement, Cu2Al(OH)4[(AsO4)0.86(PO4)0.14](H2O)4, and the electron microprobe analysis is within analytical uncertainty. For the calorimetry work, we adopt the formula of Cu2Al[(AsO4)0.83(PO4)0.17](OH)4⋅4H2O with the corresponding molecular mass of 425.6088 g mol−1.
The As and Cu contents of pushcharovskite are 28.96±0.15 wt. % As and 31.70±0.39 wt. % Cu. This leads to Cu0.96(As1.04O3OH)(H2O)⋅0.5H2O. The deviations of the stoichiometric coefficients of Cu and As from 1 are within analytical uncertainties. For calorimetry, we adopt the ideal formula Cu(AsO3OH)(H2O)⋅0.5H2O with the corresponding molecular mass 230.4945 g mol−1.
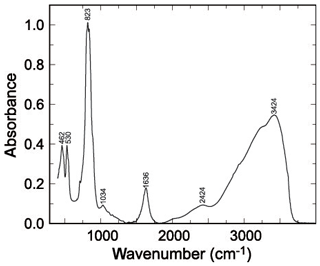
Figure 1FTIR spectrum of pushcharovskite. Bands are marked with their positions in reciprocal centimetres.
The infrared spectra of pushcharovskite and the wavenumbers of the bands are displayed in Fig. 1. This spectrum is comparable to the one shown in Chukanov (2014). Some of the weak bands described by Chukanov (2014) are not seen in our spectra, but the strong bands are comparable. Bands observed in the range of 400 to 560 cm−1 are assigned to bending vibrations of the AsO4 groups, and those in the range of 750 to 950 cm−1 are assigned to AsO4 stretching vibrations (Frost et al., 2002; Martens et al., 2003). The bands around 1632 and 3426 cm−1 are attributed to the O–H stretching and bending modes of water. Furthermore, the bands around 3315 and 3572 cm−1 correspond to the hydroxyl ions (Frost et al., 2002; Martens et al., 2003).
Pushcharovskite was also investigated by thermogravimetric analysis (Fig. 2). Molecular H2O is released at temperatures less than 127 ∘C and the sample seems to be completely dehydrated at 530 ∘C. One of the experiments was stopped at 900 ∘C (point 1 in Fig. 2), and the powder XRD showed that the sample contained a mixture of Cu2As2O7 and Cu3(AsO4)2. After heating to 1600 ∘C (point 2 in Fig. 2), the sample consisted of metallic copper, some arsenic, and minor arsenic copper (As2Cu) and cuprite (Cu2O). The measured mass loss is 17.34±1.41 wt. %. If all expected water (total 2H2O) is released, the mass loss should be around 15.6 % (after stoichiometric calculations). This difference between the measured and the calculated mass loss could be due to water adsorption of H2O onto the fine-grained sample.
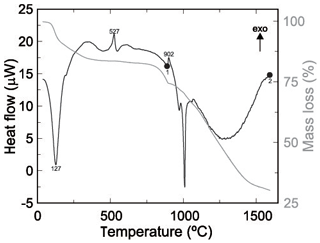
Figure 2Thermogravimetric analysis of pushcharovskite. The extrema in the heat flow are labelled with the corresponding temperature (∘C). Two separate runs were stopped at temperatures, marked by circles on the heat flow curve, and the products were investigated with PXRD. Details are in the text.
4.1 Crystal structure and hydrogen-bonding network in liroconite
The crystal structure of liroconite revealed by the current work corresponds to the structural model proposed by Kolesova and Fesenko (1968) and Burns et al. (1991); nevertheless it contains one substantial difference (see below). Moreover, here, we additionally present the positions of the H atoms, which were not localized by the previous structural studies.
Table 4Selected interatomic distances (Å) and polyhedral-distortion measures in the structure of liroconite.
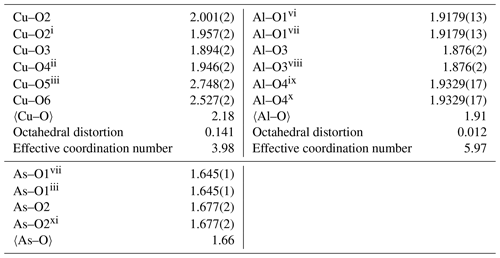
Symmetry codes: (i) , , ; (ii) x, , ; (iii) , −y, z; (iv) −x, , ; (v) x, , ; (vi) x−1, y, z; (vii) , −y, −z; (viii) −x, −y, −z; (ix) x, y, z−1; (x) −x, −y, ; (xi) , y, −z.
Unlike previous studies (I2∕a), we present our model in the space group I2∕c (non-standard setting of the C2∕m). Our choice was driven by the minute difference in reflection statistics that were present. While our space group choice was violated by five reflections (having ), the space group I2/a was contradicted by nine reflections (including 4 h0l reflections with h= odd) of the approximately same I∕σ(I). The refinement led to satisfactory results (Table 2); therefore we decided to retain this space group choice.
The structure of liroconite is a heteropolyhedral framework that consists of infinite octahedral–tetrahedral (Al2(AsO4)2(OH)4) chains running parallel to (100) decorated by edge-sharing (Cu2O2(OH)4(H2O)4) dimers that are cross-linking these chains. The Al3+ cations are in a regular octahedral coordination. The Cu2+ cations are six-fold coordinated in a strongly distorted manner (Table 4).
Types and the distinct roles of the H2O in structures of hydrated oxysalts were described and reviewed in detail and can be found elsewhere (Hawthorne, 1992, 2012; Hawthorne and Schindler, 2008; Hawthorne and Sokolova, 2012; Schindler and Hawthorne, 2008). Generally, there are several types of H2O moieties in crystal structures, and each of them plays a slightly distinct role in structure bonding. Particular types of H2O can be distinguished based on the coordination number of O atoms in these H2O groups. In the structures of oxysalts, there are transformer, non-transformer and inverse-transformer H2O groups with [3]-, [4]- and [5]-fold coordinated O atoms, respectively. Their role is generally to transfer the bond valence from cations (Lewis acids) to anions (Lewis bases), keeping the structure together, as the strengths of these components are equal or similarly matching, following the valence-matching principle of the bond-valence theory (Hawthorne, 2012; Brown, 2002, 2009).
The structure of liroconite contains two symmetrically independent H2O molecules and two symmetrically independent OH groups. Those two H2O molecules (with O5 and O6 atoms) are linked to the Cu site, forming elongated vertices of the Cu(H2O)2O2(OH)2 octahedron, which is strongly distorted (Table 4) due to the Jahn–Teller effect on Cu2+, which leads to the (4 + 2) configuration (Burns and Hawthorne, 1995). Both H2O molecules extend linkage between Cu dimers and infinite M–T chains. The typology of the H2O groups in the structure of liroconite is particularly interesting, since the H2O groups linked to the Cu site are in fact not transformer groups with [3]-coordinated O central atoms but inverse-transformer H2O groups, since each H2O accepts one additional H bond (and thus it is [4]-coordinated) from the OH groups (Fig. 3). The geometry of hydrogen bonds in the crystal structure of liroconite is summarized in Table 7. The structural formula of liroconite is , where Z=4 and Dcalc.=2.9992 g cm−3.
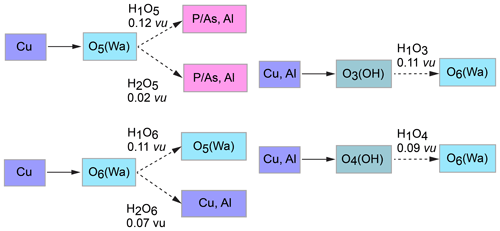
Figure 3Hydrogen bonding in the structure of liroconite: Cu ∕ Al – octahedrally coordinated cations; Wa – H2O molecule; OH – hydroxyl group; → H bond; bond strengths are given in valence units (vu).
4.2 Enthalpies of formation
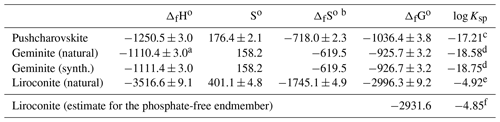
The enthalpies of formation were determined by acid solution calorimetry. Heat consumed or released by the system was measured by dissolving pellets of each sample in 5 N HCl. Reference compounds are needed to construct the thermodynamic cycle from which the enthalpies of formation will be determined. The enthalpies of formation of the reference compounds must be known accurately, so we used KCl, HCl⋅9.96H2O, KH2AsO4 and CuO as the references; HCl⋅9.96H2O is the composition of the calorimetric solvent, 5 N HCl. The choice of these reference compounds was explained, discussed and justified by Majzlan (2017). No problems were encountered with the dissolution of the studied or reference phases. Application of the appropriate thermochemical cycles (Table 8) gave the enthalpies of formation summarized in Table 9.
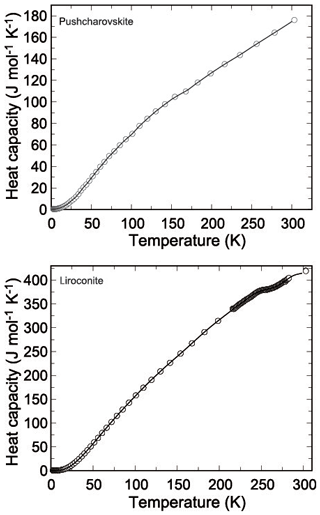
Figure 4Low-temperature heat capacity of pushcharovskite and liroconite. Circles show the measured data, and the curves are the polynomials used for fitting.
4.3 Low-temperature heat capacity and entropies
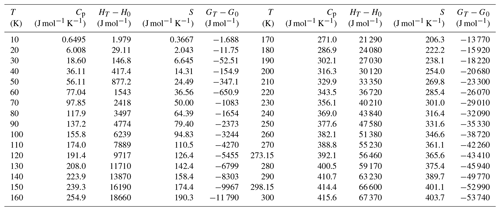
Heat capacity of pushcharovskite and liroconite was measured by relaxation calorimetry from 2 to 300 K (Fig. 4a, b). Data below 12 K, including an extrapolation to 0 K, were fitted with extended Debye polynomials. Data above 12 K were fitted with series of orthogonal polynomials. These fits were used to calculate the value of enthalpy and entropy increments at regular intervals by integrating Cp∕T (Tables 10, 11).
There are no anomalies in the Cp data for pushcharovskite. For liroconite, there is a flat anomaly at around T=250 K (Fig. 4b). This anomaly was confirmed by a detailed measurement with closely spaced temperature intervals. The nature and cause for this anomaly, however, are not clear.
The entropy of geminite was calculated (Table 9) based on the simple Kopp rule stating that the entropy of a phase is simply the sum of entropies of its components. The components and their entropy are CuO (So= 42.6 J mol−1 K−1) (all Robie and Hemingway, 1995), As2O5 (105.44) (Nordstrom and Archer, 2003) and H2O (ice, 41.94) (Majzlan et al., 2003). The entropy of pushcharovskite, calculated by the same algorithm, would be 179.2 J mol−1 K−1, fairly close to the experimental datum of 176.4±2.1 J mol−1 K−1.
Table 9Thermodynamic properties of the studied phases.
The formation reactions are defined in Table 10, reactions ΔH18, ΔH19 and ΔH20. All enthalpy and Gibbs free-energy values are in kilojoules per mole, and all entropy values are in
joules per mole per kelvin.
a Corrected for the arsenolite impurity.
b Calculated from the entropies of elements in their standard state
(from Robie and Hemingway, 1995).
c–f Solubility products were calculated with these auxiliary data (kJ mol−1): (Robie and Hemingway, 1995), (Nordstrom et
al., 2014), (Grenthe et al., 1992), (Robie and Hemingway, 1995), (Robie and Hemingway,
1995).
These equilibrium constants refer to the following reactions:
c ,
d ,
e ,
f .
4.4 Gibbs free energies of formation and solubility products
Combining the entropies and enthalpies of formation, using the relationship of the thermodynamic functions , results in the Gibbs free energies of formation for pushcharovskite, geminite and liroconite (Table 9). Table 9 includes solubility products from these values.
The solubility products, just like the enthalpies of formation, are influenced by the choice of the auxiliary data. The calculation of solubility products requires the Gibbs free energies of formation of aqueous ions in their standard state. Herein lies the problem with the decision as to which values should be used. This issue becomes alarming in some cases, for example, for liroconite in this study. Using the values from Robie and Hemingway (1995) and the value for from Nordstrom et al. (2014), the solubility product for liroconite (natural sample with phosphate in its structure) is −5.57. Using the critical selection from Grenthe et al. (1992), the same variable changes to −4.92. The reason for the difference is the massive change in the Gibbs free energy of formation of the phosphate () ion. Here, to preserve consistency with our previous studies on copper phosphates and arsenates (Majzlan et al., 2015, 2017), we adopt the same values as before (listed in footnote for Table 9). The users of thermodynamic databases who are performing geochemical calculations should be aware of such differences and their implications for their results.

Figure 5(a) Liroconite growing on greenish scorodite. (b) Ceruleite (spherical aggregates) with liroconite crystals. (c) Liroconite overgrown by azurite crystals. (d) Pseudomorphs of cornwallite after liroconite. (e) Clinoclase growing on liroconite. (f) Liroconite crystals with chalcophyllite (greenish tabular crystals). All samples from Wheal Gorland, England.
4.5 Thermodynamics of the endmember liroconite
For geochemical modelling, it is desirable to possess the thermodynamic properties of the endmember liroconite, Cu2Al(AsO4)(OH)4⋅4H2O. The estimate is based on the same reasoning as in the case of euchroite (Majzlan et al., 2017). The copper phosphates appear to be less soluble than the copper arsenates and the difference in the solubility product for the olivenite–libethenite pair is 0.44 log units. Assuming the same difference between liroconite and its phosphate analogue, the solubility product for the endmember liroconite would be .
Table 10Molar thermodynamic functions for pushcharovskite, Cu(AsO3OH)(H2O)⋅0.5H2O, molecular mass 230.4945 g mol−1.
5.1 Liroconite: associated minerals and thermodynamic models
The oxidation zone at the Wheal Gorland mine in Cornwall is known for the occurrence of a number of copper arsenates (clinoclase, chalcophyllite, chenevixite, ceruleite, cornwallite, liroconite, olivenite), copper carbonates (azurite, malachite) and ferric arsenates (pharmacosiderite, scorodite). There are rich accumulations of cuprite and native copper, and the gangue is mainly quartz and fluorite.
The most common supergene minerals directly associated with liroconite are other copper arsenates, especially olivenite, strashimirite and clinoclase. The temporal relationship of liroconite and all its associated phases is complex, with examples seen of liroconite both before and after the other copper arsenates (Fig. 5), including pseudomorphs of copper arsenates after liroconite (Fig. 5d). For instance, liroconite grows on clinoclase or vice versa (Fig. 5e). Overall trends can be observed, but one must allow for the appreciation that local conditions of formation moved in, out and returned to areas of pH-pε that were suitable for liroconite growth, as seen on a few rare examples where a second generation of liroconite can be observed, ultimately indicating simplistic crystallization pathways possible in two directions. Many specimens showing a quartz-remnant sulfide vein assemblage where liroconite is present are characterized by an initial, presumed amorphous gel-like phase which has not been extensively studied, which may be followed by pharmacosiderite, which is never seen post liroconite. The main liroconite crystallization phase can additionally be preceded by malachite, parnauite, olivenite, strashimirite or clinoclase. Parnauite tends to be much more common pre-liroconite than the other phases, yet some examples post-liroconite are observed. Strashimirite and clinoclase are very intimately associated with liroconite and must have very similar conditions of formation, possibly co-genetic, although it is noteworthy that they tend to be slightly more prevalent in well-crystallized examples post-liroconite. Olivenite, the most frequently associated mineral, is also more common post liroconite, but it has a clear role to play and is quite rich in some specimens pre-liroconite. Direct association of liroconite with cornwallite, and the other darker-green microcrystalline arsenates cornubite and cornwallite, is less common, but always post-liroconite. Malachite is slightly more dominant post-liroconite. Despite the fact that both liroconite and chalcophyllite were rather common minerals at Wheal Gorland, dominating the interest in the copper arsenates from here in the 18th and 19th centuries, surprisingly there are only a few specimens where liroconite is directly associated with chalcophyllite. In this case liroconite is younger and grows on chalcophyllite (Fig. 5f). There are also examples of liroconite growing on older crusts of ceruleite or being overgrown by ceruleite (Fig. 5b). Azurite is observed in association with liroconite at Gorland where it is generally post-liroconite (Fig. 5c), but at Ting Tang mine where azurite is especially common it may be older as well as younger than liroconite. Scorodite was only very rarely encountered in direct association with liroconite and is always older than liroconite (Fig. 5a).
Among the minerals associated with liroconite, accurate thermodynamic data are available for olivenite, azurite and scorodite in particular. There are no data for some of the rarer minerals (e.g. parnauite, strashimirite) and they will not be considered further. Consider the dissolution reaction of liroconite,
with . Combining with the dissolution reaction for olivenite (see Majzlan et al., 2015) gives a reaction that relates liroconite and olivenite,
with . The reaction quotient for this reaction is pH − log a(Al3+).
In the acidic region, where Al3+ is the predominant Al(III) species, the concentrations of Al3+ necessary for the crystallization of liroconite must be formidable. At pH = 3, for example, the equilibrium . The formation of liroconite under acidic conditions is essentially impossible. Using the equilibrium among the Al(III) species,
with , the reaction can be rewritten as
with and . Hence, under circumneutral conditions, for equilibrium between the two crystalline phases, both abundant at Wheal Gorland. This activity should be compared to activities expected when the aluminium solubility is controlled by common minerals. For gibbsite,
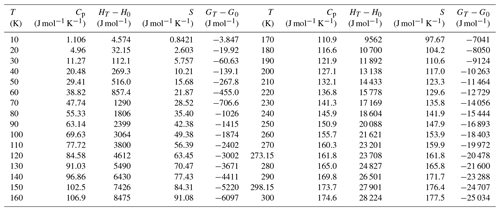
with and . This means that in the presence of gibbsite, the aluminium concentration should be much lower than that necessary for the crystallization of liroconite. Gibbsite may not directly precipitate from supersaturated aqueous solutions but X-ray amorphous Al oxides precipitate rapidly and may transform with time to gibbsite or a similar phase. These simple calculations hint that the formation of liroconite requires somewhat unusual conditions and explain its rarity. Figure 6 shows that the aluminium concentrations, necessary for the crystallization of liroconite, are consistently several orders of magnitude higher than the aluminium solubility controlled by well crystallized gibbsite or even kaolinite. The Al(III) concentrations, needed to stabilize liroconite, are very close to the Al(III) concentration needed to reach saturation with respect to X-ray amorphous Al(OH)3. Herein lie the clues to the formation of liroconite and also to its rarity.
Figure 6Solubilities of some common Al−Fe minerals, compared to the Al(III) concentrations needed to stabilize liroconite. All curves are calculated by PHREEQC (Parkhurst and Appelo, 1999). The curve for olivenite–liroconite was calculated by forcing a fluid to be in equilibrium with both phases simultaneously.
The granitic rocks in Cornwall are well known for their pervasive and deep kaolinization (e.g. Scott et al., 1996; Sheppard, 1977). An important observation is that kaolinization is especially intensive in the vicinity of the hydrothermal veins in the St Austell granite (Psyrillos et al., 1998), but this spatial association implies no genetic link. The much older veins and fracture zones provided channels for the weathering fluids. Sheppard (1977) wrote that “… the post-magmatic vein systems were critical in `preparing the ground' for subsequent deep-weathering processes and generation of kaolinite”. In a geochemical model of kaolinization (Psyrillos et al., 1998), feldspars were converted to assemblages of kaolinite, pyrophyllite or zeolite. The initial Al molality of the weathering fluids was set to 10−10 at pH = 5, much lower than that needed for the formation of liroconite. In this model, pyrophyllite was used as a representative mineral for the smectites which were also detected in the weathered rocks. We must also point out that Wheal Gorland is not located in the St Austell granite but in another outcropping granitic body in Cornwall that is even more rich in aluminium than the St Austell body (Charoy, 1986).
In the presence of a sufficient amount of dissolved silica, aluminium will be bound in minerals whose solubility is higher than that of gibbsite (Del Nero and Fritz, 1990), for example kaolinite or montmorillonite. Yet, for the formation of liroconite, even higher Al(III) concentrations than those controlled by kaolinite are needed (Fig. 6). Aqueous Al(III) concentrations, if controlled by montmorillonite, are higher than those for kaolinite, but still not sufficient for liroconite. According to Sheppard (1977) and Psyrillos et al. (1998), kaolinite formed in an environment rich in Al(III) and SiO2(aq) at low temperatures (20 ∘C) and mildly acidic pH. Our calculations predict that the formation of kaolinite must have been preceded by the release of Al(III) and SiO2(aq) from the rock-forming feldspars and precipitation of X-ray amorphous Al(OH)3 as a precursor to kaolinite and gibbsite at Wheal Gorland. Only in this way could the Al(III) concentration have been sustained at levels high enough for precipitation of a large amount of liroconite.
An integral part of the model of Psyrillos et al. (1998) is the release of a large amount of SiO2(aq). The dissolved silica must have been carried away because kaolinite veins contain neither quartz nor chalcedony. The modelled activities of SiO2(aq) reached fairly high values, in some cases up to . The authors assert that the precipitation of quartz was kinetically hindered, even though supersaturation was reached (for quartz, saturation is reached at , for amorphous silica at ). Under these conditions, two logical questions are whether the occurrence of copper silicates can be expected and why they are not reported from Wheal Gorland.
For dioptase, the dissolution reaction is
with , using the thermodynamic data for dioptase from Kiseleva et al. (1993). For this reaction,
Fixing log a(Cu2+) at 10−4, saturation would be reached at pH = 6 at but at pH = 5 only at (note that . Assuming that this copper activity is correct and the maximum activity of SiO2(aq) was that proposed by the models of Psyrillos et al. (1998), the formation of the main mass of liroconite at Wheal Gorland would have to be restricted to a narrow range of conditions between pH ≈ 5 (near the predominance field of and precipitation of X-ray amorphous Al(OH)3) and pH ≈ 6 (above which dioptase could precipitate). The conclusions regarding the formation conditions of dioptase conform to the results of Ingwersen (1990), who analysed the assemblages dioptase + azurite + malachite in Tsumeb (Namibia). He deduced that the environment conducive for the precipitation of dioptase is that with higher pH (8–9) and high copper and silica activity, typical for the silicified dolomitic rocks in Tsumeb. Such conditions were obviously not met at Wheal Gorland.
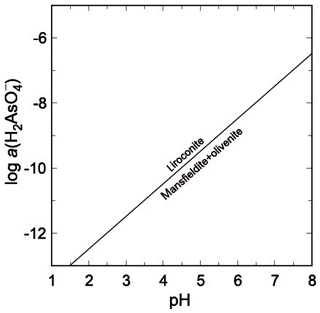
Another possible assemblage that does not occur in Wheal Gorland would be that of olivenite + mansfieldite. Its relationship to liroconite is expressed by
with log K7=14.48 and .
Liroconite is restricted to environments with higher pH and lower As(V) molalities (Fig. 7). At pH = 6, the , lower than expected for an oxidation zone with arsenates. This relationship suggests that pH may have been higher than 6, which is, however, not fully compatible with the formation conditions for kaolinite and possible precipitation for dioptase.
In summary, we propose that the main stages of the evolution of the oxidation zone in Wheal Gorland were contemporaneous with the pervasive kaolinization. The initial stages of weathering were probably marked by low pH, typical for initial sulfide weathering (so-called aggressive acid mine drainage), as witnessed by the older scorodite and pharmacosiderite. Fluctuations in the weathering and kaolinization intensity resulted in multiple liroconite generations, associated with olivenite and other copper arsenates. They may have formed at mildly acidic to circumneutral conditions. Fluids were able to leach and remove SiO2(aq) efficiently so that the amorphous Al(OH)3 controlled the Al(III) solubility at high concentrations before the conversion of most Al and Si to kaolinite. This supposition is partially supported by the reports of gibbsite occurrence at Wheal Gorland (http://mindat.org, last access: November 2019), although the details are not known to us. On the other hand, pH and the Cu and SiO2(aq) activities were kept below the threshold necessary for dioptase formation. The exhaustion of the acidity-generation capacity of the sulfides and cessation of kaolinization processes led to the terminal weathering stages, in near-neutral to mildly basic conditions with elevated p(CO2,g), with the resulting younger azurite. The meaning of the observation that the Cu–Al phases liroconite and chalcophyllite rarely occur together remains unclear. No information can be extracted from the other associated minerals as their formation conditions are unknown.
The evolution of an oxidation zone from strongly acidic to circumneutral or mildly basic values is a common phenomenon. Such evolution has been deduced for, among others, the copper-rich oxidation zones in Farbište (Slovakia) (Števko et al., 2011) or Bamba Kilenda (Congo) (Arne, 2014). The pH shift from early to mature stages has also been observed in general for oxidation zones generated by pyrite weathering (e.g. Jambor, 1994; Leverett et al., 2005; Velasco et al., 2013). It is interesting that kaolinite is mentioned repeatedly as a mineral associated with the weathering processes at sites worldwide (Leverett et al., 2005; Arne, 2014), but iron oxides may also be abundant. In that case, aluminium solubility could have been controlled by the AlOOH or Al2O3 component in the iron oxides. In addition, copper arsenates are particularly sensitive to the presence of other metal cations (e.g. Pb2+) and are then replaced by Pb–Cu arsenates, such as in Tsumeb (Ingwersen, 1990). Hence, elevated concentrations of other metals (Fe3+, Pb2+, etc.) may hinder the crystallization of liroconite. In the case of Fe3+, iron oxides control the Al solubility at very low concentrations. For Pb2+, mixed Cu–Pb arsenates are preferred over Cu arsenates (see Ingwersen, 1990). The formation of liroconite requires circumneutral fluids in an Al-rich environment that is poor in Fe, Pb or other interfering metals.

Figure 8(a) Geminite crystals on the milky-white quartz. Geschieber vein, Daniel level, Svornost mine, Jáchymov. (b) Geminite crystals partially overgrown by bluish lavendulan. Matrix is represented by quartz. Geschieber vein, Daniel level, Svornost mine, Jáchymov. (c) Geminite aggregate partially overgrown by bluish yvonite. White fine-grained phase is arsenolite. Giftkies adit, Jáchymov. (d) Geminite crystal in a cavity of strongly altered native arsenic. Octahedral colourless crystals belong to arsenolite. Geister vein, sixth Geister level, Rovnost mine, Jáchymov. Photograph (a) by Stephan Wolfsried and (b–d) by Pavel Škácha.
5.2 Geminite: associated minerals and thermodynamic models
Despite the relatively large number of specimens, geminite belongs to less common arsenate minerals in Jáchymov, yet it has been reported in several distinctive weathering associations on different ore veins. Crystals used in the current study (Fig. 8a) were extracted from a specimen originating from the Geschieber vein at the Daniel adit level of the Svornost mine. The matrix is milky-white quartz without any sulfides. The supergene association is dominated by geminite, in prismatic crystals of greenish colour, with minor arsenolite and a sparse lavendulan. Lavendulan partly overgrows older geminite (Fig. 8b). The sources of Cu and As are probably tennantite, bornite and chalcocite, which occur in the vein nearby. Specimens with geminite were found on the floor of the adit and we conclude that Cu–As-bearing aqueous solutions were descending (dripping, flowing) down onto the floor from the parts of the vein and ore stope above. Similar mineral association has been encountered in the old mining workings of the Giftkies adit (Unruhe area, Jáchymov). Specimens containing geminite somewhat resemble those from the Svornost mine, but they contain fragments of surrounding mica schists and thinner white quartz veins. At Svornost, despite geminite being more common, it is only directly associated with arsenolite. On a few specimens from Giftkies, geminite is associated with additional yvonite (Fig. 8c). The remainder of this association comprises lavendulan, slavkovite and cyanotrichite. In just one specimen, geminite forms directly upon/within weathered aggregates of tennantite. It is assumed that tennantite is the source of Cu and As. The third type of geminite occurrences in Jáchymov is its association with minor arsenolite on strongly weathered/corroded native arsenic (Fig. 8d). Such specimens originate from the Geister vein in the Rovnost mine in the western parts of the Jáchymov deposit. While the source of As is the native arsenic, Cu was probably derived from fine-grained tennantite that has been found in trace amounts within the massive arsenic.
In summary, geminite is a product of weathering of quartz–arsenic veins with minor amounts of other primary minerals. Carbonates are either not present or accessory. The most common minerals associated with geminite are arsenolite, gypsum, lavendulan and those of the lindackerite group.
The most faithful companion of geminite is arsenolite, with the dissolution reaction
with . At low pH, the solubility should therefore be remarkable and . Rough calculations, using the composition of sample J-2 in Majzlan et al. (2014) show that in this solution is +0.05. These calculations are only very approximate because the solution, with its high ionic strength (0.43 m), is well out of the range of applicability of the Debye–Hückel equation implemented in PHREEQC. Yet, they suggest that the solution is slightly supersaturated with respect to arsenolite, in good agreement with the field observations. We should also note that since the publication of Majzlan et al. (2014), we were able to measure Eh in the field and input this value (pε=9.63) into the PHREEQC calculations.
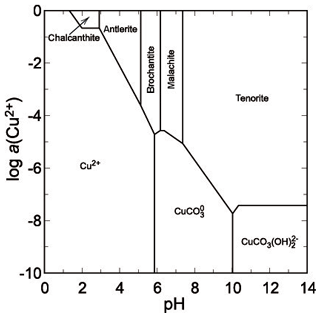
The second mineral that is close to saturation is gypsum, with a saturation index (SI) of −1.3 (slightly undersaturated). In the extremely acidic droplets with pH ∼ 0, the concentration of sulfate reaches 30–50 g L−1 (Majzlan et al., 2014), but it should be noted that the arsenate concentrations were about 10 times higher. A phase diagram for copper sulfates (Fig. 9) shows that under such conditions, all these phases are soluble. Upon slight pH increase, chalcanthite could precipitate but the solutions possess sufficient Ca to precipitate gypsum instead. Hence, even when pH should increase, the copper could not be scavenged and removed by sulfates. At higher pH and even moderate to low activity of Cu(II), devilline would be expected (Fig. 10) but does not occur in our samples from Jáchymov. The pH of these solutions was therefore maintained at very low values throughout the crystallization.
The droplets found directly on weathering arsenic (Majzlan et al., 2014) certainly represent an extreme case of As enrichment and an environment conducive to the precipitation of arsenolite. Initially, most of the arsenic is found as As(III); X-ray absorption spectroscopy determined 87 % As(III) (Majzlan et al., 2014) while thermodynamic predictions (PHREEQC) gave 64 %. The pentavalent arsenic is removed by minerals such as kaatialaite or the copper arsenates described here. Geminite is undersaturated (SI −5.2) in the acidic droplets but approaches saturation as more As is oxidized or the solutions leach additional Cu from the primary ores. The dissolution reaction of geminite under acidic conditions is
with log K9=2.15 and pH.
Figure 11pε-pH diagram of the system for T=298.15 K, , , olivenite is suppressed from the calculations.
Although there are no thermodynamic data available for yvonite, slavkovite or lindackerite-group minerals, their chemical compositions attest that they are an integral part of the acidic assemblage with geminite. All of them contain protonated–acidic arsenate group in their formulae AsO3OH (or HAsO4), for slavkovite Cu13(AsO4)6(AsO3OH)4⋅23H2O (Sejkora et al., 2010a), for yvonite Cu(AsO3OH)⋅2H2O (Sarp and Černý, 1998), and for the lindackerite group ACu4(AsO4)2(AsO3OH)2⋅9H2O, where A= Cu, Zn, Co, Ca, Ni, Mg, with lindackerite (Vogl, 1853), ondrušite (Sejkora et al., 2011), hloušekite (Plášil et al., 2014) and veselovskýite (Sejkora et al., 2010b) having their type locality in Jáchymov (see Škácha et al., 2019, for more information). From its type locality in the Salsigne mine (France, Sarp and Černý, 1998), yvonite was described in association with geminite, lindackerite and pushcharovskite. All these minerals should be expected to crystallize from strongly acidic solutions, just like geminite. In agreement with the observations, the phase diagram shows a small field for geminite at very low pH and high Cu and As(V) molalities (Fig. 11).
Because carbonates are absent or extremely scarce, it has to be assumed that Ca in Jáchymov originated from acidic attack on rock-forming feldspars. This assumption is supported by the frequent presence of lavendulan for which Na is an essential component of its structure. In addition, Škácha et al. (2019) reported that many lavendulan specimens from Jáchymov contain an appreciable amount of K, hinting also at the dissolution of K-feldspars.
5.3 Pushcharovskite: associated minerals and thermodynamic models
So far only two localities of pushcharovskite are known. The first is the type locality Cap Garonne, Var, France, where it is associated with geminite, lindackerite, yvonite and mahnertite in quartz gangue (Sarp and Sanz-Gysler, 1997). Pushcharovskite is also found in Salsigne in Aude, France, where it is associated with geminite, lindackerite and yvonite (Pushcharovsky et al., 2000).
Pushcharovskite is a higher hydrate of geminite, with the appropriate simple chemical reaction
with 3.8 kJ mol−1 showing that geminite is the stable phase even under standard conditions, that is, water vapour as an ideal gas with fugacity of 1 bar. In order to stabilize pushcharovskite, the pressure of water vapour and the relative air humidity would have to reach huge values which are not even worth discussion. The situation somewhat resembles the relationship between olivenite and euchroite,
with kJ mol−1, and calculated relative air humidities for equilibrium at near-surface conditions of 400 % (Majzlan et al., 2017). Hence, pushcharovskite can be seen as a metastable precursor to geminite, which is itself metastable with respect to olivenite but probably forms faster under acidic conditions. Because of its marked metastability, pushcharovskite should only be a transient phase that rapidly dehydrates to geminite. That would also explain its extreme rarity in nature.
The underlying research data are available at https://doi.org/10.22032/dbt.41075 (Plumhoff and Majzlan, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/ejm-32-285-2020-supplement.
AMP conducted the research and investigation process, specifically performing the experiments and data collection for powder-X-ray diffraction, ICP-OES, FT-IR and acid-solution calorimetry. JP provided the natural sample of geminite and collected and described the single-crystal X-ray data. Additionally, he wrote parts about mineral associations of geminite. JS provided the natural sample of liroconite and collected and processed the electron microprobe analyses. ED and AB collected and processed the data of the relaxation and differential scanning calorimetry. MS and MSR wrote parts about the mineral associations where they have special knowledge. JM was responsible for the conceptualization, funding acquisition and the supervision. AMP prepared the initial draft and following manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We thank Taras L. Panikorovskii and the one anonymous reviewer for their constructive reviews.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. MA 3927/26-1) and the Czech Science Foundation (grant no. 17-09161S).
This paper was edited by Giuseppe Cruciani and reviewed by Taras Panikorovskii and one anonymous referee.
Arne, L.: Nature and formation processes of the supergene Pb-Zn-Cu-V mineralisation of Bamba Kilenda, Bas-Congo province, DR Congo, PhD Dissertation, University Gent, 121 pp., 2014.
Benisek, A., Kroll, H., and Dachs, E.: The heat capacity of fayalite at high temperatures, Am. Mineral., 97, 657–660, https://doi.org/10.2138/am.2012.3924, 2012.
Bethke, C.: Geochemical and biogeochemical reaction modeling, 2nd edn., Cambridge University Press, Cambridge, New York, xix, 543 pp., 2011.
Bethke, C., Farrell, B., and Yeakel, S.: GWB Reaction Modeling Guide, 12th edn., Champaign, Illinois, 2019.
Brown, I. D.: Recent developments in the methods and applications of the bond valence model, Chem. Rev., 109, 6858–6919, https://doi.org/10.1021/cr900053k, 2009.
Brown, I. D.: The Chemical Bond in Inorganic Chemistry: The Bond Valence Model, Oxford University Press, UK, 2002.
Bruker: TOPAS, Bruker AXS, Karlsruhe, Germany, 2009.
Burns, P. C. and Hawthorne, F. C.: Coordination-geometry structural pathways in Cu2+ oxysalt minerals, Can. Mineral., 33, 889–905, 1995.
Burns, P. C., Eby, R. K., and Hawthorne, F. C.: Refinement of the structure of liroconite, a heteropolyhedral framework oxysalt mineral, Acta Crystallogr. C, 47, 916–919, https://doi.org/10.1107/S0108270190010939, 1991.
Charoy, B.: The Genesis of the Cornubian Batholith (South-West England): The example of the Carnmenellis Pluton, J. Petrol., 27, 571–604, https://doi.org/10.1093/petrology/27.3.571, 1986.
Chesley, J. T., Halliday, A. N., Snee, L. W., Mezger, K., Shepherd, T. J., and Scrivener, R. C.: Thermochronology of the Cornubian batholith in southwest England: Implications for pluton emplacement and protracted hydrothermal mineralization, Geochim. Cosmochim. Ac., 57, 1817–1835, https://doi.org/10.1016/0016-7037(93)90115-D, 1993.
Chukanov, N. V.: Infrared spectra of mineral species: Extended library, Springer Geochemistry/Mineralogy, Springer Netherlands, 2014.
Coelho, A. A.: TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C, J. Appl. Crystallogr., 51, 210–218, https://doi.org/10.1107/S1600576718000183, 2018.
Cooper, M. A. and Hawthorne, F. C.: The crystal structure of geminite, Cu2+(AsO3OH)(H2O), a heteropolyhedral sheet structure, Can. Mineral., 1111–1118, 1995.
de Bournon, C.: Description of the Arseniates of Copper, and of Iron, from the County of Cornwall, Proc. R. Soc. Lon. Ser.-A, 91, 169–192, 1801.
Del Nero, M. and Fritz, B.: Thermodynamic modelling of the influence of water activity on the gibbsite-kaolinite-quartz system in lateritic weathering conditions, Chem. Geol., 84, 45–48, https://doi.org/10.1016/0009-2541(90)90160-9, 1990.
Frost, R. L., Martens, W. N., and Williams, P. A.: Raman spectroscopy of the phase-related basic copper arsenate minerals olivenite, cornwallite, cornubite and clinoclase, J. Raman Spectrosc., 33, 475–484, https://doi.org/10.1002/jrs.880, 2002.
Gagné, O. C. and Hawthorne, F. C.: Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen, Acta Crystallogr. B, 71, 562–578, https://doi.org/10.1107/S2052520615016297, 2015.
Giuseppetti, G., Coda, A., Mazzi, F., and Tadini, C.: La struttura cristallina della liroconite Cu2Al[(As1P)O4(OH)4]⋅4H2O, Period. Mineral, 31, 19–42, 1962.
Grenthe, I., Fuger, J., Konings, R. J. M., Lemire, R. J., Muller, A. B., Nguyen-Trung, C., and Wanner, H.: Chemical thermodynamics of uranium, 1, North-Holland Amsterdam, 1992.
Grevel, K.-D. and Majzlan, J.: Internally consistent thermodynamic data for metal divalent sulphate hydrates, Chem. Geol., 286, 301–306, https://doi.org/10.1016/j.chemgeo.2011.05.016, 2011.
Guillemin, C.: Mineralogy of the arsenates, phosphates, and vanadates of copper. I. Arsenates of copper, Bull. Soc. fr. minéral. cristallogr., 79, 7–95, 1956.
Hawthorne, F. C.: A bond-topological approach to theoretical mineralogy: Crystal structure, chemical composition and chemical reactions, Phys. Chem. Miner., 39, 841–874, https://doi.org/10.1007/s00269-012-0538-4, 2012.
Hawthorne, F. C.: The role of OH and H2O in oxide and oxysalt minerals, Z. Kristallogr. Cryst. Mater., 201, 183–206, https://doi.org/10.1524/zkri.1992.201.14.183, 1992.
Hawthorne, F. C. and Sokolova, E.: The role of H2O in controlling bond topology: I. The [6]Mg(SO4)(H2O)n (n=0–11) structures, Z. Kristallogr. Cryst. Mater., 227, 594–603, https://doi.org/10.1524/zkri.2012.1473, 2012.
Hawthorne, F. C. and Schindler, M.: Understanding the weakly bonded constituents in oxysalt minerals, Z. Kristallogr. Cryst. Mater., 223, 41–68, https://doi.org/10.1524/zkri.2008.0003, 2008.
Ingwersen, G.: Die sekundären Mineralbildungen der Pb-Zn-Cu-Lagerstätte Tsumeb, Namibia (Physikalisch-chemische Modelle), PhD Dissertation, 234 pp., 1990.
Jambor, J. R.: Mineralogy of sulfide-rich tailings and their oxidation products, in: Environmental Geochemistry of Sulfide Mine-Wastes, 22nd edn., edited by: Jambor, J. R. and Blowes, D. W., Mineralogical Association of Canada Short Course, 59–102, 1994.
Kennedy, C. A., Stancescu, M., Marriott, R. A., and White, M. A.: Recommendations for accurate heat capacity measurements using a Quantum Design physical property measurement system, Cryogenics, 47, 107–112, https://doi.org/10.1016/j.cryogenics.2006.10.001, 2007.
Kiseleva, I. A., Ogorodova, L. P., Melchakova, L. V., and Bisengalieva, M. R.: Thermodynamic properties of copper silicate: dioptase: Cu6Si6O18⋅6H2O, J. Chem. Thermodyn., 25, 621–630, https://doi.org/10.1006/jcht.1993.1057, 1993.
Kolesova, R. V. and Fesenko, E. G.: Determination of the crystal structure of liroconite, Cu2Al(AsO4)(OH)4(H2O)4, Kristallografiya, 13, 396–402, 1968.
Leverett, P., McKinnon A. R., and Williams, P. A.: Supergene geochemistry of the Endeavor ore body, Cobar, NSW, and relationships to other deposits in the Cobar basin, Regolith, 191–194, 2005.
Magalhães, M. C. F., De Jesus, J. D. P., and Williams, P. A.: The chemistry of formation of some secondary arsenate minerals of Cu(II), Zn(II) and Pb(II), Mineral. Mag., 52, 679–690, 1988.
Magalhães, M. C. F., Pedrosa de Jesus, J. D., and Williams, P. A.: Stability constants and formation of Cu(II) and Zn(II) phosphate minerals in the oxidized zone of base metal orebodies, Mineral. Mag., 50, 33–39, 1986.
Majzlan, J.: Solution calorimetry on minerals related to acid mine drainage – methodology, checks, and balances, Acta Geol. Slovaca, 9, 171–183, 2017.
Majzlan, J.: Thermodynamic stabilization of hydrous ferric oxide by adsorption of phosphate and arsenate, Environ. Sci. Technol., 45, 4726–4732, https://doi.org/10.1021/es1040249, 2011.
Majzlan, J., Števko, M., Dachs, E., Benisek, A., Plášil, J., and Sejkora, J.: Thermodynamics, stability, crystal structure, and phase relations among euchroite, Cu2(AsO4)(OH)⋅3H2O, and related minerals, Eur. J. Mineral., 29, 5–16, https://doi.org/10.1127/ejm/2017/0029-2584, 2017.
Majzlan, J., Zittlau, A. H., Grevel, K.-D., Schliesser, J., Woodfield, B. F., Dachs, E., Števko, M., Chovan, M., Plášil, J., Sejkora, J., and Milovská, S.: Thermodynamic Properties and Phase Equilibria of the Secondary Copper Minerals Libethenite, Olivenite, Pseudomalachite, Kröhnkite, Cyanochroite, and Devilline, Can. Mineral., 53, 937–960, https://doi.org/10.3749/canmin.1400066, 2015.
Majzlan, J., Plášil, J., Škoda, R., Gescher, J., Kögler, F., Rusznyak, A., Küsel, K., Neu, T. R., Mangold, S., and Rothe, J.: Arsenic-rich acid mine water with extreme arsenic concentration: mineralogy, geochemistry, microbiology, and environmental implications, Environ. Sci. Technol., 48, 13685–13693, https://doi.org/10.1021/es5024916, 2014.
Majzlan, J., Grevel, K.-D., and Navrotsky, A.: Thermodynamics of Fe oxides: Part II. Enthalpies of formation and relative stability of goethite (α-FeOOH), lepidocrocite (γ-FeOOH), and maghemite (γ-Fe2O3), Am. Mineral., 88, 855–859, https://doi.org/10.2138/am-2003-5-614, 2003.
Martens, W. N., Frost, R. L., Kloprogge, J. T., and Williams, P. A.: The basic copper arsenate minerals olivenite, cornubite, cornwallite, and clinoclase: An infrared emission and Raman spectroscopic study, Am. Mineral., 88, 501–508, https://doi.org/10.2138/am-2003-0404, 2003.
Mohs, F. and Haidinger, W.: Treatise on Mineralogy: Or The Natural History of the Mineral Kingdom, Band 1, Archibald Constable, Edinburgh, 1825.
Nordstrom, D. K. and Archer, D. G.: Arsenic Thermodynamic Data and Environmental Geochemistry, in: Arsenic in Ground Water: Geochemistry and Occurrence, edited by: Welch, A. H. and Stollenwerk, K. G., Kluwer Academic Publishers, Boston, MA, 1–25, 2003.
Nordstrom, D. K., Majzlan, J., and Königsberger, E.: Thermodynamic Properties for Arsenic Minerals and Aqueous Species, Rev. Mineral. Geochem., 79, 217–255, https://doi.org/10.2138/rmg.2014.79.4, 2014.
Ondruš, P., Veselovský, F., Hloušek, J., Skála, R., Vavřín, I., Frýda, J., Cejka, J., and Gabašová, A.: Secondary minerals of the Jachymov (Joachimsthal) ore district, J. Geosci., 42, 3–76, 1997.
Parker, V. B.: Thermal properties of uni-univalent electrolytes, 2, NBS Ntl. Stand. Ref. Data Series, 66 pp., 1965.
Parkhurst, D. L. and Appelo, C. A. J.: User's guide to PHREEQC (Version 2): A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations, Wat.-res. inv. report, 99, 312 pp., 1999.
Petříček, V., Dušek, M., and Palatinus, L.: Crystallographic Computing System JANA2006: General features, Z. Kristallogr. Cryst. Mater., 345–352, https://doi.org/10.1515/zkri-2014-1737, 2014.
Plášil, J., Sejkora, J., Škoda, R., Novák, M., Kasatkin, A. V., Škácha, P., Veselovský, F., Fejfarová, K., and Ondruš, P.: Hloušekite, (Ni,Co)Cu4(AsO4)2(AsO3OH)2(H2O)9, a new member of the lindackerite supergroup from Jáchymov, Czech Republic, Mineral. Mag., 78, 1341–1353, https://doi.org/10.1180/minmag.2014.078.5.16, 2014.
Plumhoff, A. and Majzlan, J.: External Appendix to Publication: “Thermodynamic properties, crystal structure and phase relations of pushcharovskite, geminite and liroconite”, Jena, Digitalen Bibliothek Thüringen (DBT), https://doi.org/10.22032/dbt.41075, 2020.
Pouchou, J. and Pichoir, F.: “PAP” (phi-rho-z) procedure for improved quantitative microanalysis, in: Microbeam Analysis, edited by: Armstrong, J. T., San Francisco Press, San Francisco, 104–106, 1985.
Prencipe, M., Pushcharovsky, D. Y., Sarp, H., and Ferraris, G.: Comparative crystal chemistry of geminite Cu[AsO3OH]H2O and related minerals, Mosc. U. Geol. B., 51, 51–58, 1996.
Psyrillos, A., Manning, D. A. C., and Burley, S. D.: Geochemical constraints on kaolinization in the St Austell Granite, Cornwall, England, J. Geol. Soc., 155, 829–840, https://doi.org/10.1144/gsjgs.155.5.0829, 1998.
Pushcharovsky, D. Y., Teat, S. J., Zaitsev, V. N., Zubkova, N. V., and Sarp, H.: Crystal structure of pushcharovskite, Eur. J. Mineral., 12, 95–104, https://doi.org/10.1127/0935-1221/2000/0012-0095, 2000.
Rigaku: CrysAlis CCD and CrysAlis RED, Rigaku-Oxford Diffraction Ltd, Yarton, Oxfordshire, UK, 2019.
Robie, R. A. and Hemingway, B. S.: Thermodynamic properties of minerals and related substances at 298.15 K and 1 bar (105 Pascals) and at higher temperatures, 2131, U.S. Geological Survey Bulletin, 461 pp., 1995.
Sarp, H. and Černý, R.: Description and crystal structure of yvonite, Cu(AsO3OH)2H2O, Am. Mineral., 83, 383–389, https://doi.org/10.2138/am-1998-3-423, 1998.
Sarp, H. and Sanz-Gysler, J.: La Pushcharovskite, , un nouveau minéral de la mine de Cap Garonne, Var (France), Arch. Sci., 50, 177–186, 1997.
Sarp, H. and Perroud, P.: La Geminite Cu2As2O7⋅3H2O, un Nouveau Minéral de la Mine de Cap Garonne, Var, France, Schweiz. mineral. petro. Mitt., 70, 309–314, 1990.
Schindler, M. and Hawthorne, F. C.: The stereochemistry and chemical composition of interstitial complexes in uranyl-oxysalt minerals, Can. Mineral., 46, 467–501, https://doi.org/10.3749/canmin.46.2.467, 2008.
Scott, P. W., Hart, F. W., and Smith, D.: The quantitative mineralogy of ceramic grade kaolin from the St. Austell Granite and its relationship to chemistry and physical properties, Proc. Ussher Soc., 9, 91–96, 1996.
Sejkora, J., Plášil, J., Ondruš, P., Veselovský, F., Císařová, I., and Hloušek, J.: Slavkovite, Cu13(AsO4)6(AsO3OH)4⋅23H2O, a new mineral species from Horní Slavkov and Jáchymov: description and crystal-structure determination, Can. Mineral., 48, 1157–1170, https://doi.org/10.3749/canmin.48.5.1157, 2010a.
Sejkora, J., Plášil, J., Veselovský, F., Císařová, I., and Hloušek, J.: Ondrušite, CaCu4(AsO4)2(AsO3OH)2⋅10H2O, a new mineral species from Jáchymov ore district, Czech Republic: Description and crystal-structure determination, Can. Mineral., 49, 885–897, https://doi.org/10.3749/canmin.49.3.885, 2011.
Sejkora, J., Ondruš, P., and Novák, M.: Veselovskýite, triclinic , a Zn-dominant analogue of lindackerite, N. Jb. Miner. Abh., 187, 83–90, https://doi.org/10.1127/0077-7757/2010/0165, 2010b.
Sheldrick, G. M.: SHELXT – integrated space-group and crystal-structure determination, Acta Crystallogr. A, 71, 3–8, https://doi.org/10.1107/S2053273314026370, 2015.
Sheppard, S. M. F.: The Cornubian batholith, SW England: D∕H and 18O∕16O studies of kaolinite and other alteration minerals, J. Geol. Soc., 133, 573–591, https://doi.org/10.1144/gsjgs.133.6.0573, 1977.
Škácha, P., Plášil, J., and Horák, V.: Jáchymov – a mineralogical pearl of Krušné Hory Mts., Academia, 682 pp., 2019.
Southwood, M., Števko, M., and Carr, P.: Tsumeb: Zincolivenite and the adamite-olivenite series, Rock. Min., 6, in press, 2020.
Števko, M., Sejkora, J., and Bačík, P.: Mineralogy and origin of supergene mineralization at the Farbište ore occurrence near Poniky, central Slovakia, J. Geosci., 273–298, https://doi.org/10.3190/jgeosci.098, 2011.
Števko, M., Sejkora, J., and Súl'ovec, Š.: Contribution to the chemical composition of libethenite from the type locality: Podlipa copper deposit, L'ubietová (Slovak Republic), Bull. Mineral. Petrolog., 25, 252–259, 2017.
Tanaka, H. and Yamane, M.: Preparation and thermal analysis of synthetic malachite CuCO3⋅Cu(OH)2, J. Therm. Anal., 38, 627–633, https://doi.org/10.1007/BF01979390, 1992.
Toman, K.: Ordering in olivenite–adamite solid solutions, Acta Crystallogr. B, 34, 715–721, https://doi.org/10.1107/S0567740878003933, 1978.
Velasco, F., Herrero, J. M., Suárez, S., Yusta, I., Alvaro, A., and Tornos, F.: Supergene features and evolution of gossans capping massive sulphide deposits in the Iberian Pyrite Belt, Ore Geol. Rev., 53, 181–203, https://doi.org/10.1016/j.oregeorev.2013.01.008, 2013.
Viehweg, M.: Regionale Verteilung der Uranlagerstätten Sachsens und Thüringens, Z. Geol. Wiss., 23, 547–552, 1995.
Vogl, J. F.: Über das Vorkommen einer dem Voltzin ähnlichen Schwefelzink-Verbindung in Joachimsthal, Z. mont. Ver. Erzg., 1, 5, 1853.
Wagman, D. D., Evans, W. H., Parker, V. B., Halow, I., and Bailey, S. M.: Selected values of chemical thermodynamic properties, Tables for the first thirty-four elements in the standard order of arrangement, 270-3, NBS Technical Note, 264 pp., 1991.
Williams, P. A.: Oxide Zone Geochemistry, Ellis Horwood Ltd., Chichester, 286 pp., 1990.