Determination of the H₂O content in minerals, especially zeolites, from their refractive indices based on mean electronic polarizabilities of cations

It is shown here that the H₂O content of hydrous minerals can be determined from their mean refractive indices with high accuracy. This is especially important when only small single crystals are available. Such small crystals are generally not suitable for thermal analyses or for other reliable methods of measuring the amount of H₂O. In order to determine the contribution of the H₂O molecules to the optical properties, the total electronic polarizability is calculated from the anhydrous part of the chemical composition using the additivity rule for individual electronic polarizabilities of cations and anions. This anhydrous contribution is then compared with the total observed electronic polarizability calculated from the mean refractive index of the hydrous compound using the Anderson–Eggleton relationship. The difference between the two values represents the contribution of H₂O. The amount can be derived by solving the equation ${\mathit{\alpha }}_{\mathrm{calc}}=\sum _i{n}_i{\mathit{\alpha }}_{i\mathrm{cat}}+\sum _j\left({\mathit{\alpha }}_j^o\times {\mathrm{10}}^{-\left[\frac{N_j}{V_{\mathrm{m}}^{\mathrm{1.2}}}\times {\left(n_j+n_W\right)}^{\mathrm{1.2}}\right]}\right)+n_w\times {\mathit{\alpha }}_W$ for the number n_w of H₂O molecules per formula unit (pfu), with the electronic polarizabilities α_cat for cations, the values N and α^o describing the anion polarizabilities, the number n of cations and anions, and the molar volume V_m, using a value of α_W=1.62 ų for the electronic polarizability of H₂O. The equation is solved numerically, yielding the number n_w of H₂O molecules per formula unit. The results are compared with the observed H₂O content evaluating 157 zeolite-type compounds and 770 non-zeolitic hydrous compounds, showing good agreement. This agreement is expressed by a factor relating the calculated to the observed numbers being close to 1 for the majority of compounds. Zeolites with occluded anionic or neutral species (SO₃, SO₄, CO₂, or CO₃) show unusually high deviations between the calculated and observed amount of H₂O, indicating that the polarizabilities of these species should be treated differently in zeolites and zeolite-type compounds.

1 Introduction

The water content of hydrous minerals and synthetic compounds is usually determined by thermogravimetric methods recording the weight loss upon dehydration at an increasing temperature. If the chemical composition of the anhydrous part of the compound is known, its formula weight can be calculated along with the number of H₂O molecules representing the weight loss. Whereas the cation content can be derived from microchemical analyses, e.g., by electron microprobe analyses (EMPA) or analytical transmission electron microscopy (ATEM), on species with a size of a few microns, thermoanalytical methods for the determination of the water content require an amount of a sample in the range of a few milligrams. The same applies to carbon hydrogen and nitrogen (CHN) analyzers which usually need a few milligrams for accurate analyses. Alternatively, the H₂O content could be derived from the measured density if the specimen is big enough for the experimental determination of the density. The determination of the water content becomes less accurate if lower amounts or even just one single crystal with a size of about 100 µm and a mass of a few micrograms or less exists.

It is well known that the optical properties vary with the amount of H₂O in a crystalline compound. We mention two examples: Hey and Bannister (1932a) studied the effect of dehydration on the optical properties of natrolite, and Medenbach et al. (1980) investigated the variation in the refractive index of synthetic Mg-cordierite with H₂O content, finding a linear relationship between the mean refractive index and the weight fraction of H₂O. All studies we know so far are empirical descriptions of the dependence of the refractive indices on the H₂O content derived by calibration curves for a special system of compounds. Here, we describe a theoretical approach for determining the H₂O content from mean refractive indices of compounds with known chemical composition of the anhydrous part. We show that the number of H₂O molecules per formula unit (pfu) can be determined with high accuracy from the mean refractive indices of hydrous crystals.

A special focus is on the zeolite group of minerals, representing a large and popular group of hydrous minerals. Zeolites represent one of the most important classes of materials, used as catalysts in oil refineries for the production of gasoline and as ion exchangers as an additive, e.g., in household detergents for the softening of water. Following the definition of the subcommittee on zeolites of the International Mineralogical Association (Coombs et al., 1998), “A zeolite mineral is a crystalline substance with a structure characterized by a framework of linked tetrahedra, each consisting of four O atoms surrounding a cation. This framework contains open cavities in the form of channels and cages. These are usually occupied by H₂O molecules and extra-framework cations that are commonly exchangeable”.

Table 1 Entries of zeolite-type compounds used for the comparison of observed and calculated H₂O content.

^a Chemical composition normalized according to the formula unit as listed in Coombs et al. (1998). ^b Mean refractive index $<n>$. ^c Molar volume V_m per formula unit. ^d Observed total electronic polarizability calculated
from mean refractive index using Eq. (1). ^e Observed number of H₂O molecules per formula unit as given in the respective literature. ^f Number of H₂O molecules per formula calculated as explained in the text, using the
program POLARIO (Fischer et al., 2018). ^g Factor relating the calculated to the observed H₂O content. ^h lp is lattice parameters, and RI is refractive index. ⁱ Chabazite with composition
Na_0.08K_0.42Ca_0.84Mg_0.29Sr_0.03Ba_0.09Al_3.17Fe_0.08Si_8.81O₂₄⋅10.84H₂O was omitted because of Fe₂O₃ impurities (Passaglia, 1970).

2 Theoretical background

Our approach is based on the fact that the total electronic polarizability of a mineral or synthetic compound can be calculated from the sum of the individual contributions of the electronic polarizabilities α_cat of cations and α_an of the anions, following the procedure described by Shannon and Fischer (2016). Thus, the total polarizability of the anhydrous compound can be calculated from the chemical composition which then can be compared with the total polarizability derived from the observed mean refractive indices of the hydrous compound. The difference represents the contribution of the H₂O molecules. To obtain the H₂O content, refractive indices are measured, e.g., by immersion methods with a spindle stage on a petrographic microscope. Anisotropic indices are averaged according to $(n_x+n_y+n_z)/\mathrm{3}$ or $(\mathrm{2}{n}_o+n_e)/\mathrm{3}$, yielding the mean refractive index $<n>$.

The total observed polarizability of the hydrous compound is then calculated from the mean refractive index $<n>$ using the Anderson–Eggleton relationship (Anderson, 1975; Eggleton, 1991; see Shannon and Fischer, 2016, for an explanation):

$$\begin{array}{}\text{(1)}& {\mathit{\alpha }}_{\mathrm{obs}}={\displaystyle \frac{\left(n^{\mathrm{2}}-\mathrm{1}\right)V_{\mathrm{m}}}{\mathrm{4}\mathit{\pi }+\left(\frac{\mathrm{4}\mathit{\pi }}{\mathrm{3}}-\mathrm{2.26}\right)\left(n^{\mathrm{2}}-\mathrm{1}\right)}},\end{array}$$

with the molar volume V_m of one formula unit.

The total electronic polarizability of the anhydrous compound can be calculated from the sum of the individual ion contributions (Shannon and Fischer, 2016) according to

$$\begin{array}{}\text{(2)}& {\mathit{\alpha }}_{\mathrm{calc}}=\sum _{i=\mathrm{1}}^{N_{\mathrm{cat}}}{m}_i\times {\mathit{\alpha }}_{i\mathrm{cat}}+\sum _{i=\mathrm{1}}^{N_{\mathrm{an}}}{n}_i\times {\mathit{\alpha }}_{\mathrm{ian}},\end{array}$$

with

$$\begin{array}{}\text{(3)}& {\mathit{\alpha }}_{\mathrm{an}}={\mathit{\alpha }}_{-}^o\times {\mathrm{10}}^{-N_o/V_{\mathrm{an}}^{\mathrm{1.2}}},\end{array}$$

where α_cat is taken from Table 4 and ${\mathit{\alpha }}_{-}^o$ and N_o from Table 5 in Shannon and Fischer (2016), and the anion volume V_an is calculated from the molar volume V_m divided by the number of anions and H₂O molecules.

The difference between observed and calculated polarizabilities $\mathrm{\Delta }=({\mathit{\alpha }}_{\mathrm{obs}}-{\mathit{\alpha }}_{\mathrm{calc}})$ is due to the contribution of H₂O. However, Δ cannot be simply divided by the electronic polarizability 1.62 ų of H₂O because it is treated like an anion and not like a cation (Shannon and Fischer, 2016). Therefore, the number n_w of H₂O molecules has an influence on the calculation of the anion volume V_an in Eq. (3), so it is needed to calculate the contribution of the anions even for the anhydrous part of the compound.

If we combine Eqs. (2) and (3) and separate the contribution of H₂O from the other anions, we get

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathit{\alpha }}_{\mathrm{calc}}=& \sum _i{n}_i{\mathit{\alpha }}_{i\mathrm{cat}}+\sum _j\left({\mathit{\alpha }}_j^o\times {\mathrm{10}}^{-\left[\frac{N_j}{V}\times {\left(n_j+n_W\right)}^{\mathrm{1.2}}\right]}\right)\\ & +n_w\times {\mathit{\alpha }}_W,\end{array}\end{array}$$

with $V=V_{\mathrm{m}}^{\mathrm{1.2}}$, the number n_w of H₂O molecules per formula unit, and the electronic polarizability α_W=1.62 ų of H₂O.

Replacing α_calc in Eq. (4) by α_obs from Eq. (1) and solving for n_w yields the number of H₂O molecules per formula unit.

The solution is done numerically using the program POLARIO (Fischer et al., 2018).

3 Dataset

We tested the approach on hydrous minerals with known chemical composition, water content, and refractive indices, taken from Table S1 in Shannon et al. (2017) and additional entries compiled here. The group of zeolite minerals is treated separately because it represents one of the most important classes of hydrous minerals and because we used mean electronic polarizability for the calculation of their total polarizabilities in contrast to the non-zeolitic minerals, where the total polarizabilities are calculated from electronic polarizabilities of cations with specific coordination numbers (CNs). Whereas the cation coordination is known for most of the non-zeolitic minerals, it is not clearly determined for most of the zeolite species where the chemical composition and the refractive indices have been determined but not the crystal structure. Therefore, Table 1 lists the results on 149 zeolites obtained with mean electronic polarizabilities, and Table S1 in the Supplement lists the results on 770 non-zeolitic minerals and synthetic compounds based on electronic polarizabilities taken from Table 4 in Shannon and Fischer (2016) for specific coordination numbers of cations. For the zeolites, the mean electronic polarizabilities of a cation in a certain oxidation state is calculated as the average of all cations of the same kind with different coordination numbers weighted by the number of entries used to determine the polarizability (see Table 4 in Shannon and Fischer, 2016). The mean values are listed in Table 2. They are internally stored in POLARIO (Fischer et al., 2018) used to calculate the water content of zeolites in Table 1. Zeolite entries are selected if they belong to one of the 237 types listed in the Database of Zeolite Structures of the International Zeolite Association (Baerlocher and McCusker, 2019). Thus, it also contains minerals like cancrinite which are not considered to be zeolite minerals but topologically have a zeolite-type framework. Only those entries are included in Table 1 where the optical data, the chemical composition, and the unit-cell parameters are available for the same specimen. There are a few exceptions where it was clear that the data from different publications can be assigned to the same crystal. We were aiming for a dataset large enough to have a representative selection and not necessarily for completeness.

All entries in Table 1 conform to the criteria listed above. However, the entries at the end of Table 1 (no. 145 to 149) show unusual deviations between observed and calculated H₂O content which are assumed to be due to uncertainties in the chemical composition. Zeolites and zeolite-type compounds having occluded anionic or neutral species also show high deviations and are listed separately in Table 3. Details are discussed below. Not considered in this compilation of hydrous minerals are compounds containing elements where the electronic polarizabilities have not been determined in Shannon and Fischer (2016). These are, for example, cations with lone-pair electrons (Tl⁺, Sn²⁺, Pb²⁺, As³⁺, Sb³⁺, Bi³⁺, S⁴⁺, Se⁴⁺, Te⁴⁺, Cl⁵⁺, Br⁵⁺, and I⁵⁺) which do not fit the simple scheme of additivity. Also excluded from the compilation are compounds with sterically strained structures (Gagné et al., 2018) and some compounds with corner-shared or edge-shared octahedral networks (see Shannon and Fischer, 2016; Shannon et al., 2017) showing systematic deviations between observed and calculated polarizabilities.

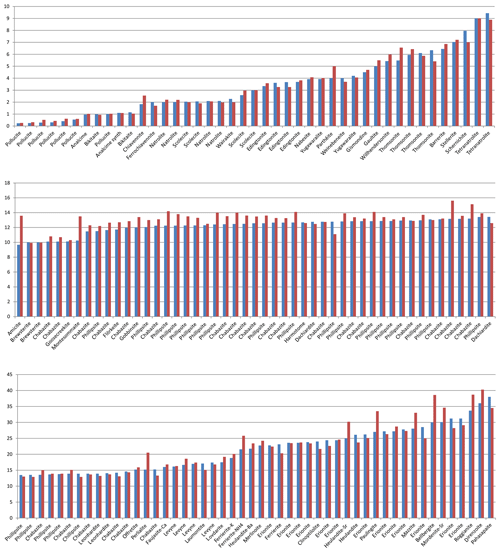
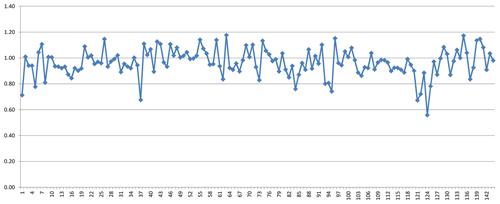
Figure 1 Histogram of observed (blue) and calculated (red) water content. Entries 145 to 149 are omitted (see text for explanation). The two entries with H₂O content >50 (8 – boggsite; 69 – gottardiite) are not shown.

Figure 2 Plot of factors relating calculated to observed amount of H₂O in zeolite-type minerals. The sequence from left to right follows the sequence of entries in Table 1. Entries 145 to 149 are omitted (see text for explanation).

4 Example

The approach used here is demonstrated in the example of synthetic analcime (entry 2 in Table 1) having the chemical composition Na_0.9Al_0.9Si_2.1O₆ ⋅1.1H₂O, with data from sample 1 in Table 1 of Černý (1974). The following steps are taken to determine the water content from the refractive indices.

1. The observed total electronic polarizability α_obs is calculated using Eq. (1) with V_m=160.71 ų (unit-cell volume from Table 1 in Černý, 1974, V=2571.35 ų, divided by the number of formula units, Z=16) and isotropic n=1.486, yielding α_obs=13.034 ų.

2. The calculated total electronic polarizability α_calc of the anhydrous part of the chemical composition is calculated using the additivity rule with the individual electronic polarizabilities of ions from Shannon and Fischer (2016). Because the coordination number (CN) of Na is not determined in analcime (Černý, 1974), a mean value for Na with different CNs is used calculated according to α(Na) $=(\mathrm{17}\cdot \mathrm{0.760}+\mathrm{27}\cdot \mathrm{0.650}+\mathrm{207}\cdot \mathrm{0.560}+\mathrm{97}\cdot \mathrm{0.490}+\mathrm{197}\cdot \mathrm{0.430}+\mathrm{49}\cdot \mathrm{0.380}+\mathrm{25}\cdot \mathrm{0.340}+\mathrm{5}\cdot \mathrm{0.300}+\mathrm{9}\cdot \mathrm{0.270})/\mathrm{633}=\mathrm{0.489}$ ų, with values taken from Table 4 in Shannon and Fischer (2016). For the framework atoms Al and Si, the respective values for CN =4 are used. Electronic polarizabilities and the mean values are internally stored in the program POLARIO (Fischer et al., 2018), which is used for all calculations. Thus, α_calc(anhydrous) $=\mathrm{0.9}\cdot \mathit{\alpha }$(Na) $+\mathrm{0.9}\cdot \mathit{\alpha }$(Al) $+\mathrm{2.1}\cdot \mathit{\alpha }$(Si) $+\mathrm{6}\cdot \mathit{\alpha }$(O) $=\mathrm{0.9}\cdot \mathrm{0.489}+\mathrm{0.9}\cdot \mathrm{0.533}+\mathrm{2.1}\cdot \mathrm{0.284}+\mathrm{6}\cdot \mathrm{1.688}=\mathrm{11.439}$ ų, where α(O) is calculated using Eq. (3), with ${\mathit{\alpha }}_{-}^o=\mathrm{1.79}$ ų and N=1.776 ų taken from Table 5 in Shannon and Fischer (2016) and $V_{\mathrm{an}}=V_{\mathrm{m}}/\mathrm{6}=\mathrm{26.79}$ ų.

3. The difference ${\mathit{\alpha }}_{\mathrm{obs}}-{\mathit{\alpha }}_{\mathrm{calc}}=\mathrm{1.595}$ ų represents the contribution of H₂O to the total electronic polarizability. The individual electronic polarizability of H₂O taken from Table 5 in Shannon and Fischer (2016) is α( H₂O) =1.62 ų. However, the simple determination of the number of H₂O molecules n_w pfu according to $n_w=\mathrm{1.595}/\mathrm{1.62}=\mathrm{0.98}$ is not correct because n_w adds to the anion volume (V_an=V(O) +V(H₂O) $=V_{\mathrm{m}}/(n_{\mathrm{O}}+n_w)$ and thus contributes to the polarizability of the anhydrous part as well as that expressed in Eq. (4). Only the solution of Eq. (4) solved for n_w yields the correct value. This is done numerically in POLARIO, yielding 1.09 H₂O molecules pfu, which compares well with the observed 1.100 molecules determined in Černý (1974).

   Alternatively, the H₂O content could be calculated using the Gladstone–Dale approach after Mandarino (1976), where the refractive index n is calculated from $n=K_c\cdot D+\mathrm{1}$ with $K_c=\sum _i\frac{k_i{p}_i}{\mathrm{100}}$ and where k_i values are Gladstone–Dale constants, p_i values are weight percentages, and D is the density (see also Shannon and Fischer, 2016). For the example of analcime, the resulting number of H₂O molecules would be 0.89 H₂O per formula unit using Gladstone–Dale constants from Mandarino (1981) and Eggleton (1991). A detailed comparison between our polarizability approach and the Gladstone–Dale concept will be published in a follow-up paper.

5 Comparison between observed and calculated H₂O content in hydrous minerals

As mentioned above, the group of zeolite minerals was studied separately using mean electronic polarizabilities for the calculations. Figure 1 shows the water content calculated with Eq. (4) compared with the water content derived from analytical determinations as published in the respective references listed in Table 1. The factors relating the calculated to the observed values are shown in Fig. 2. It clearly demonstrates that the calculated values show a reasonable fit with the observed amount of H₂O, with factors f=n_w(obs)∕n_w(calc) being close to 1. Outliers in Figs. 1 and 2 are mainly explained by uncertainties in the determination of chemical compositions and/or refractive indices.

Table 2 Electronic polarizabilities α of cations from Table 4 in Shannon and Fischer (2016) averaged over different coordination numbers, including NH₄ and five H_xO_y species.

In paulingite (145), something must be wrong in the chemical composition. The authors state the following: “The Al∕Si ratio of 0.15 given by the analysis conflicts with the cation composition … which requires an Al∕Si ratio of 0.47. Either the analysis is internally inconsistent, or else anions must be present outside the tectosilicate framework” (Kamb and Oke, 1960). The composition given in Table 1 is scaled to 42 framework cations and fixed to 84 O atoms corresponding to a factor of 3.5 relative to the original composition given in Kamb and Oke (1960), whereas 89.95 O atoms would be needed for charge compensation, which, however, does not represent a TO₂ framework. Alternatively, in the second line 145 in Table 1 the non-oxygen content is scaled down to achieve charge balance. Then the factor relating calculated and observed H₂O content changes from 1.83 to 1.62, which is lower but still rather high. In later work, Lengauer et al. (1997) investigated paulingite (94) with a different composition with 27 H₂O molecules derived from thermogravimetric analysis (TGA) and 33.5 H₂O calculated from the refractive index, yielding a factor of 0.81. The misfits for pollucite (146–148) might be due to errors in the chemical composition and/or the determination of the H₂O content. According to Beger (1969) the sum of Cs + H₂O should be equal to 1, whereas it is 0.34, for example, in pollucite (148). In tschörtnerite (149), “A quantitative determination of H₂O∕OH was not possible because of the small amount of material available” (Effenberger et al., 1998). A number of 14 molecules pfu was calculated by difference from electron microprobe analyses (EMPAs), and 20 H₂O were determined from the crystal-structure analysis. A loss of H₂O is assumed due to the high-vacuum measuring conditions in the EMPA: “A part of the total amount of H₂O is given as OH in order to achieve charge balance” (Effenberger et al., 1998). In total, this yields high uncertainties concerning the real H₂O content in tschörtnerite. The authors assume an H₂O content ≥20, which is much closer to the amount of 27.4 molecules calculated by us.

There are nine compounds listed in Table 3 containing anionic and/or neutral species (SO₃, SO₄, CO₂, or CO₃) occluded in the zeolite cavities. All these compounds show unusually high deviations between the observed and calculated amount of H₂O. It is apparent that these species in zeolites must be treated separately in our concept, with individual electronic polarizabilities deviating from other sulfates, sulfites, and carbonates. For liottite (156 in Table 3; Merlino and Orlandi, 1977b) the number of H₂O molecules was even calculated to be negative because the total polarizability of the anhydrous part of the compound was already higher than the corresponding observed value. However, it was shown in subsequent work by Ballirano et al. (1996) that it does not contain H₂O, which might confirm our findings in addition to the problem with the anionic species.

Table 3 Entries of zeolite-type compounds with occluded anionic species. Numbering continues to the sequence in Table 1.

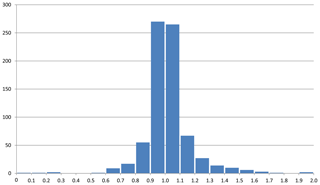
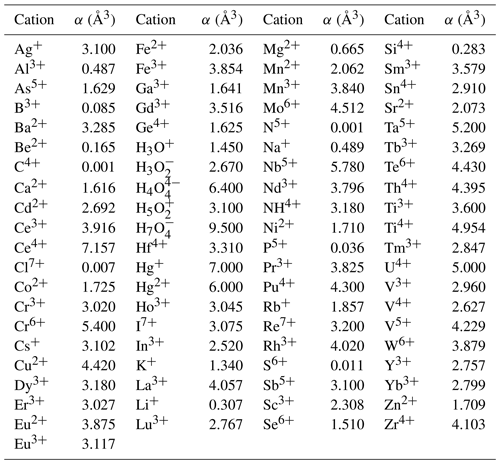
The mean value of the factor relating the calculated amount of H₂O to the observed one is more or less meaningless because high and low factors, each representing large errors, level each other out. More significant is the distribution of factors as shown in Fig. 3, where the bars in the histogram represent the frequency of occurrence of factors within a range of factors indicated on the horizontal axis. The mode is between 0.9 and 1.0, with 64 % of the factors between 0.9 and 1.1 and 86 % between 0.8 and 1.2.

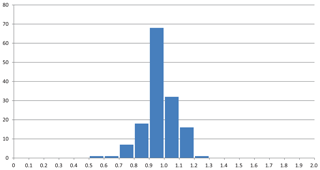
Figure 3 Frequency of occurrence of the factors for the zeolite entries 1–144 listed in Table 1 and shown in Fig. 2. (a) Factors calculated from polarizability analysis using different electronic polarizabilities for cations with different coordination numbers (from Table 4 in Shannon and Fischer, 2016). (b) Factors calculated from polarizability analysis using mean electronic polarizabilities from Table 2.

The situation is similar for the non-zeolitic minerals listed in Table S1, with 770 entries. The factors relating the calculated number of H₂O molecules to the observed ones are plotted in Fig. 4, which shows a few outliers caused by inaccuracies in the chemical compositions, difficulties in the measurement of the refractive indices, or the observed H₂O content just estimated or calculated and not determined by thermal analyses. Lotharmeyerite (entry 675) shows the largest deviation from 1 in Fig. 4a and b because of uncertainties in the observed OH (partially disordered) and H₂O content (Yang et al., 2012). Because the majority of the entries show a reasonable fit with factors close to 1, we do not discuss here specific reasons for deviations. It should be noted that these factors are calculated irrespective of the precision of the number of molecules listed in the original publications. The number of H₂O molecules for the first 30 entries in Table S1, for example, is given in integral numbers by the authors but calculated with all decimal places. If the calculated values are rounded to integers, they correspond exactly to the observed numbers except chukhrovite (27), where 12 H₂O molecules are measured and 11.28 are calculated.

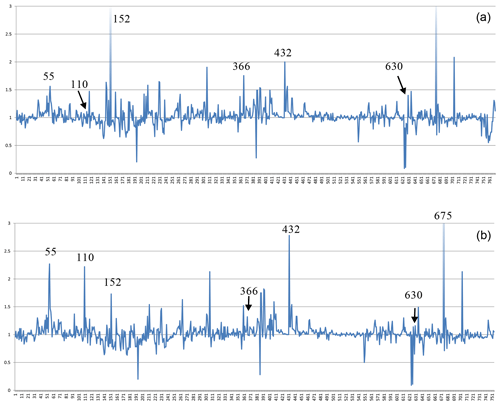
Figure 4 Plot of factors relating calculated to observed amount of H₂O in non-zeolitic minerals. The sequence from left to right follows the sequence of entries in Table S1.

Thus, there are various sources of possible deviations. This might include rounded numbers, especially for low H₂O content, where a number of 1 H₂O molecule could be anything between 0.5 and 1.5 and therefore might already represent an error of 50 %. Other sources of errors are uncertainties in the chemical compositions, especially when they are based on energy-dispersive X-ray spectroscopy (EDX) analyses, estimated and not experimentally determined H₂O content, insufficient quality of crystals for accurate measurements of the refractive indices, and also errors in our empirically determined electronic polarizabilities of cations and anions (Shannon and Fischer, 2016), which are derived in least-squares procedures. The cumulation of such errors will be reflected by factors significantly deviating from 1. Despite these influences, the data shown in Figs. 1 to 5 clearly show that there is on average a very good fit between the observed and calculated amount of H₂O. In general the best results are achieved using the individual electronic polarizabilities of cations with specific coordination numbers (Table 4 in Shannon and Fischer, 2016). However, mean polarizabilities (Table 2) yield results that are sufficiently accurate if the CN of cations has not been determined. This is shown in Fig. 4, comparing the two approaches yielding essentially similar results with a few outliers. Entries 55 (priceite), 110 (calcioancylite-Nd), and 432 (bassanite), for example, have factors much higher for mean polarizabilities, but entries 152 (milarite), 366 (Li₂SO₄ ⋅ H₂O), and 630 (martyite), for example, have factors closer to 1 as compared with the corresponding values from the individual polarizabilities. Generally we recommend verifying questionable results derived from mean polarizability with corresponding calculations using the CN-dependent polarizabilities.

Figure 5 Frequency of occurrence of the factors for the non-zeolite entries listed in Table S1 and shown in Fig. 4. The three outliers with factors >2 are omitted.

6 Conclusions

The evaluation of 927 hydrous minerals and inorganic compounds showed that their H₂O content can be calculated from their mean refractive indices if the anhydrous part of the chemical composition is known. Thus, single crystals with dimensions <100 µm, usually used in X-ray diffraction analyses, can be used to determine the number of H₂O molecules per formula unit if higher amounts of the sample are not available for thermal analyses. Based on the excellent overall agreement between the observed and calculated H₂O contents of 157 zeolites and 770 other hydrates and the unusual deviations of paulingite, pollucite, tschörtnerite, liottite, and lotharmeyerite, we suggest that when strong disagreements occur, the refractive index, composition, and/or crystal structure should be more carefully investigated.