Cation disordering in ankerite as a function of Fe content

Order–disorder transitions in minerals are of significance for technological applications and for the development of models that aid the understanding of the dynamics and composition of the Earth's interior. The present study investigates the effect of Fe content in ankerite, Ca(Fe_xMg_1−x)(CO₃)₂ (0 $\le x\ge \mathrm{0.7}$, $R\overline{\mathrm{3}}$ space group), on the distribution of cations in its crystal structure as a function of temperature. This investigation was conducted using ex situ experiments in a piston cylinder apparatus performed at 2–3 GPa and variable-temperature conditions (450–1000 °C). Crystal structure refinements, using single-crystal X-ray diffraction data, indicate that the temperature of the order–disorder phase transition in ankerite, when the space group changes from $R\overline{\mathrm{3}}$ to $R\overline{\mathrm{3}}c$, is significantly influenced by the amount of Fe in the mineral's crystal structure, being full disordering conditions attained at 1000 and 800 °C in ankerites with x=0.3 and x=0.7, respectively. Prior to undergoing the order–disorder phase transition, it is shown that Fe exhibits a greater aptitude than Mg to exchange in the place of Ca (and vice versa). Mg, conversely, has a tendency to be bound at the M2 site or to exchange in smaller quantities than Fe. Furthermore, the significance of Fe as a parameter influencing the chemo-physical behavior of ankerite, as well as the temperature and character of the disordering process, is highlighted. This has the potential to significantly impact the mineral physics of ankerite under non-ambient conditions, particularly with regard to compressibility, phase stability, thermal and electric conductivity, and its role in the Earth's mantle geophysical modeling.

1 Introduction

The study of the order–disorder phenomena in minerals has been a matter of considerable effort during the last few decades in many research fields (e.g., Zucchini et al., 2024, 2017, 2014, 2012a, b; Ke et al., 2024; Jing et al., 2023; Kreller and Uberuaga, 2021), and it has been demonstrated to strongly influence mass transport and conductivity in complex oxides (e.g., spinel, pyrochlore, perovskite) (e.g., Kreller and Uberuaga, 2021; Vu et al., 2021; Goto et al., 2021; Kennedy and Ismunandar, 1999), with important implications for the design of new functional materials for technological applications, such as photovoltaic panels, solid-state batteries (Vu et al., 2021; Sau et al., 2023), and materials used for environmental protection (e.g., Ce-based materials, Goto et al., 2021). The order–disorder transitions in minerals are important not only for technological applications, but also for modeling and understanding the dynamics and composition of the Earth's interior and other celestial bodies, as they are factors influencing phase stability under non-ambient conditions (e.g., Panero, 2008; Zucchini et al., 2024; Bassett and Skalwold, 2021; Fastelli et al., 2025).

Different types of disordering can be encountered in minerals (Hazen and Navrotsky, 1996), that is, (1) positional disorder, namely the atomic positions are affected by some positional disorder as a result of thermal agitation; (2) rotational disorder, which is the rotation of some molecules in the crystal structure as a consequence of variations in external parameters (e.g., P, T, composition); (3) distortional disorder, meaning distortion in more than one equivalent way from high-symmetry structures; and (4) substitutional disorder, that is, the random distribution of atoms over two or more sites, which takes place in a mineral's crystal structure as a consequence of change in temperature (T) or chemical composition (Redfern, 2000).

The effect of pressure (P) on the order–disorder, particularly the positional disorder, is evident in the evolution of hydrous layered structures, their stability, and their phase transition. When a layered system is subjected to external pressure, the interlayer distance decreases considerably more than the intralayer distance. In such conditions, the OH groups interact more strongly, which is believed to lead to a reversible disorder in the H sublattice. Raugei et al. (1999) introduced the concept of pressure-induced H frustration in Mg(OH)₂ and Ca(OH)₂. Hermann and Mookherjee (2016) demonstrated how the pressure phase transition, induced by hydrogen disordering, can affect the stability of brucite and, in turn, the storage of water in the deep mantle.

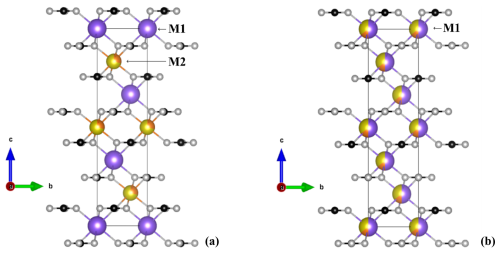
Figure 1 Crystal structures of ordered (a) and disordered (b) ankerites with chemical formula Ca(Mg_0.3Fe_0.7)(CO₃)₂, used in the present work. The name of each cationic site is shown in the figure. Colors: purple is Ca, yellow is Fe, orange is Mg, black is C, and white is O.

Pressure also has an important effect on substitutional disorder (hereafter cation disorder), and high-pressure conditions usually favor cation ordering in different minerals, such as Mg–Fe in orthopyroxenes, spinels, garnets, perovskite-like compounds, and some rhombohedral carbonates (Hazen and Navrotsky, 1996, and references therein). In contrast, inspiring work on CaFe(CO₃)₂ has shown that its disordered form is stabilized under high-pressure conditions (Davidson et al., 1993; Chai and Navrotsky, 1996), which is interesting considering that the diffusion of ions, distributed from the ordered to the disordered configurations, would affect the behavior of carbonates recycled by subduction into the Earth's mantle in terms of stability, elasticity (Zucchini et al., 2014, 2017, 2024), and conductivity (Horai and Simmons, 1969; Jing et al., 2023). Cation disorder is relevant to the mineral physics of carbonates (Zucchini et al., 2014, 2017, 2024; Merlini et al., 2016), strongly influencing their stability, polymorphic transformations, and compressibility to the point of possibly even affecting their elastic behavior under non-ambient conditions (Zucchini et al., 2024). In particular, Fe-bearing carbonates are of considerable interest as Fe-bearing phases in the Earth's interior (Cerantola et al., 2017). Among them, FeCO₃ has an $R\overline{\mathrm{3}}c$ space group, and Fe is the only cation in octahedral coordination that can be replaced by Mg²⁺ with a completely solid solution in the MgCO₃–FeCO₃ system. This is not the case for the CaCO₃–MgCO₃–FeCO₃ series, where Fe²⁺ only partially substitutes Mg²⁺, giving rise to ankerite – Ca(Fe_xMg_1−x)(CO₃)₂ – where $\mathrm{0}\le x\ge \mathrm{0.7}$ ($R\overline{\mathrm{3}}$ space group). A few studies have dealt with explaining the reason for such behavior, and the most accredited theories invoke, on the one hand, the excessive distortion of the cation octahedra resulting from Fe²⁺ substitution (Rosenberg and Foit, 1979) and, on the other hand, the lower enthalpy of disordering in pure ankerite – CaFe(CO₃)₂ – with respect to dolomite – CaMg(CO₃)₂ – which may explain the non-existence in the nature of ordered CaFe(CO₃)₂ in the CaMg(CO₃)₂–FeCa(CO₃)₂ join (Chai and Navrotsky, 1996; Navrotsky et al., 1999).

The structure of ankerite is made of alternating Ca²⁺ and (Mg,Fe)²⁺ layers in octahedral coordination (M1 and M2 sites, respectively, Fig. 1) that are intercalated by planar and parallel CO${}_{\mathrm{3}}^{\mathrm{2}-}$ groups (Fig. 1). As the temperature increases, the onset of cation disorder occurs, as in dolomite (Reeder and Wenk, 1983); i.e., cations start to randomly distribute among cationic sites up to a critical temperature (T_c), which is a function of Fe content (Franzolin et al., 2012). At T_c, the disordering process is completed, and the ankerite space group changes from $R\overline{\mathrm{3}}$ (dolomite-like structure, Fig. 1a) to $R\overline{\mathrm{3}}c$ (calcite-like structure, Fig. 1b).

An accurate understanding of the disordering process that occurs in ankerite as a function of P–T and Fe content might be an important component in the modeling of inner-Earth composition and dynamics, likely contributing to the potential carbonate capacity in the subducting slabs. The present work is devoted to studying the disordering process in two natural ankerite samples characterized by different Fe content. Experimental treatments at different temperatures and pressures of 2 to 3 GPa performed in a piston cylinder apparatus allowed for the retrieval of differently ordered samples, whose crystal structure was characterized by means of single-crystal X-ray diffraction. Results coming from the present work allowed for the characterization of the crystal chemistry of the order–disorder phase transition and the description of the ankerite structure in terms of the unit cell dimensions, distortion parameters, and crystal structure geometry of the differently ordered samples.

2 Materials and methods

2.1 The ankerite samples

Several ankerite samples were analyzed, kindly provided by the Natural History Museum of Copenhagen. Among them, two samples were chosen based on their different Fe content and excellent crystallinity: sample Ank7, with chemical formula Ca(Mg_0.3Fe_0.7)(CO₃)₂, and sample Ank3, with chemical formula Ca(Mg_0.6Fe_0.3Mn_0.1)(CO₃)₂. Chemical composition was determined by means of Jeol JXA8200 electron-probe microanalysis (EPMA) at the high-pressure laboratory of the National Institute of Geophysics and Volcanology (INGV, Rome). Analyses were performed on carbon-coated samples under high-vacuum conditions, using an accelerating voltage of 15 kV, an electron beam current of 7.5 nA, and a beam diameter of 2–3 µm. Elemental counting times were 10 s on the peak and 5 s on the background. Corrections for inter-elemental effects were made using a ZAF (Z: atomic number, A: absorption, F: fluorescence) procedure. Calibration was performed using a range of standards from Micro-Analysis Consultants (MAC): albite (Si–PET, Al–TAP, Na–TAP), forsterite (Mg–TAP), augite (Fe–LIF), apatite (Ca–PET, P–PET), orthoclase (K–PET), rutile (Ti–LIF), rhodonite (Mn–LIF), and JEOL Cr metal (Cr–LIF). MAC (serial number 11763) dolomite and chromite were used as quality monitor standards. Accuracy and precision were better than 5 %, except for low elemental abundances, for which they were typically better than 10 %.

A total of five to six points were analyzed in the studied samples, and results are given in Table S1 in the Supplement.

2.2 Thermal treatment

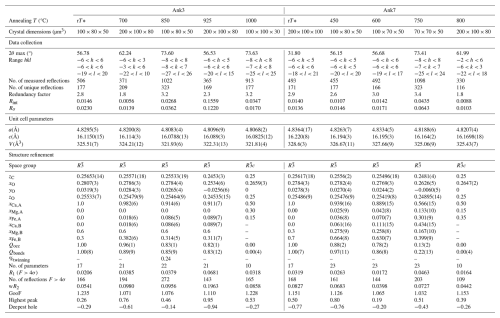
Experimental treatments at 3 GPa were carried out in a piston cylinder at the Bayerisches Geoinstitut (Bayreuth, Germany) in the framework of the DFG Core Facility for High-Pressure Research funding program, whereas two experiments performed at 2 GPa (Ank3-3 and Ank7-4) were carried out at the high-pressure–high-temperature laboratory at the Dipartimento di Scienze della Terra at the University of Pisa (Pisa, Italy). Different annealing temperatures were chosen, based on the simulations given in Franzolin et al. (2012) for the temperature composition of the long-range-order parameter. The experimental pressure of 2–3 GPa was used in all eight experiments in order to avoid decarbonation. Thermal treatment conditions are listed in Table 1.

Table 1 Thermal treatment conditions.

A standard 13 mm talc–pyrex–graphite–MgO assembly and Pt capsules (3 mm OD) were used for the experiments performed at Bayerisches Geoinstitut; for the experiments performed at the University of Pisa, NaCl was used instead of talc for the assembly and Au instead of Pt for the capsule. Capsules were filled with approximately 120 mg of optically clear crystals of Ank3 and Ank7, gently crushed into small rhombohedra with an agate mortar in order to fill the capsule without excessive pore space and recover good-quality single crystals after the heat treatment. Capsules were sealed at both ends using an arc welder to avoid contamination of the crystal with the assembly materials. The assembly was cold pressurized to 90 % of the final pressure, and the remaining 10 % pressure was applied after heating (“hot-piston-in” technique). Temperature was measured using a Pt–Pt90Rh10 thermocouple, having a precision of 5 °C.

2.3 Single-crystal X-ray diffraction

Single-crystal X-ray diffraction analyses were performed on both Ank3 and Ank7 prior to annealing to verify the good crystallinity of the samples, as well as on optically clear single crystals separated from the piston-cylinder-run products. The instrument used was an Oxford diffraction Xcalibur diffractometer with a CCD detector and MoKα radiation (λ=0.7107 Å), located at the Department of Physics and Geology of the University of Perugia (Italy). The detector distance to the sample was 66 mm with a pixel size of 60.6 µm. Measurements were carried out in an ω scan mode, and the scan width and exposure time were set depending on the crystal size. Data reduction was performed using the CrysAlisPro package (version 1.171.43.137a, Rigaku Oxford Diffraction, 2024), and an empirical absorption correction was applied using the SCALE3 ABSPACK algorithm. Structure refinements were carried out by means of ShelXle software (Hübschle et al., 2011). Neutral atomic scattering factors were used, and anisotropic displacement parameters were refined together with atomic positions and cation occupancies. In order to refine cation disorder in the analyzed samples, we refined cation occupancy at the (0, 0, 0) and (0, 0, $\mathrm{1}/\mathrm{2}$) special positions that are occupied exclusively by Ca at the former and by (Mg, Fe, Mn) at the latter, in the fully ordered state. In disordered structures, the two sites are occupied by a mixture of Ca, Mg, Fe, and Mn, provided that the full occupancy of each cationic site is respected. As the close scattering factors of Fe and Mn and based on the observation that Mn accounts for only 0.1 a.p.f.u. in the Ank3 crystal structure, Mn was combined with Fe for structure refinements. This approach is in agreement with Reeder and Dollase (1989). In order to set up the necessary constraints during cation occupancy refinement, the SUMP command in SHELX-97 (Sheldrick, 1997) was used. Constraints on atomic position and thermal parameters, which were imposed to be the same for each cationic species occupying the same atomic site, were also used. Moreover, realizing that the refinement of more than two atomic species in one site would probably be rather unstable, we added a further constraint on chemical composition, following the suggestions in Sheldrick (1997), in accordance with the EPMA data presented here.

Refinements were performed in the $R\overline{\mathrm{3}}$ space group in all the samples, except those at the highest annealing temperatures (Ank3-4 and Ank7-4). Cation site occupancy at (0, 0, 0) and (0, 0, $\mathrm{1}/\mathrm{2}$) was refined together with atomic positions and anisotropic thermal parameters. The careful analysis of the distribution of X-ray diffraction intensities in Ank3-4 and Ank7-4 showed additional systematic absences that are characteristic of the $R\overline{\mathrm{3}}c$ space group. Moreover, structure refinements initially performed in the $R\overline{\mathrm{3}}$ space group in these samples showed, on the one hand, site-scattering values and cation-to-oxygen distances that became very close for the two cation sites and, on the other hand, the z position of both C and O and y position of O that approach special positions, as in calcite-like structures ($R\overline{\mathrm{3}}c$ space group). These observations led us to the conclusion that in Ank3-4 and Ank7-4, cations were distributed statistically at both (0, 0, 0) and (0, 0, $\mathrm{1}/\mathrm{2}$) sites, and, therefore, structure refinements of Ank3-4 and Ank7-4 were carried out in the $R\overline{\mathrm{3}}c$ space group.

The quantification of the degree of order in the annealed samples was performed following two different approaches. On the one hand, the long-range-order parameter Q_occ (Eq. 1) was used, which is based on Ca, Mg, and Fe(Mn) occupancies in the M1 and M2 cationic sites (see Fig. 1 for the location of the M1 and M2 sites), following the theory that describes disorder in omphacites (e.g., Carpenter et al., 1990; Boffa Ballaran et al., 1998) and in other carbonate minerals (e.g., Bromiley et al., 2007). On the other hand, the order parameter Q_bonds was derived from the mean bond lengths (Eq. 2; Carpenter et al., 1990).

$$\begin{array}{}\text{(1)}& {\displaystyle }{Q}_{\mathrm{occ}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\times \left({\displaystyle \frac{X_{\mathrm{Ca}}^{\mathrm{M}\mathrm{1}}-X_{\mathrm{Ca}}^{\mathrm{M}\mathrm{2}}}{X_{\mathrm{Ca},\mathrm{TOT}}}}+{\displaystyle \frac{(X_{\mathrm{Mg}}^{\mathrm{M}\mathrm{2}}+X_{\mathrm{Fe}}^{\mathrm{M}\mathrm{2}})-(X_{\mathrm{Mg}}^{\mathrm{M}\mathrm{1}}+X_{\mathrm{Fe}}^{\mathrm{M}\mathrm{1}})}{X_{\mathrm{Mg},\mathrm{TOT}}+X_{\mathrm{Fe},\mathrm{TOT}}}}\right)\text{(2)}& {\displaystyle }{Q}_{\mathrm{bonds}}=C\times \left|{\displaystyle \frac{\langle \text{M1}-\text{O}\rangle -\langle \text{M2}-\text{O}\rangle }{\frac{\mathrm{1}}{\mathrm{2}}\left(\langle \text{M1}-\text{O}\rangle +\langle \text{M2}+\text{O}\rangle \right)}}\right|\end{array}$$

In Eq. (2) the C parameter has a constant value (Carpenter et al., 1990) and is calculated from the structure refinements of the ordered Ank3 and Ank7. Both Q_occ and Q_bonds have values from 1 to 0 for a fully ordered and a fully disordered configuration, respectively.

Details of crystal size dimension, data collection, data extraction, structure refinements, and order degrees are given in Table 2. The geometrical parameters of coordination polyhedra and their distortion features were analyzed by means of VESTA (Momma and Izumi, 2011) and CrystalPalace software (Angel et al., 2025), and results for selected parameters are listed in Table 3. The complete list of geometrical parameters in terms of bond distances and angles is given in the CIF files in the Supplement.

Table 2 Details of data collection and reduction.

* rT means room temperature.

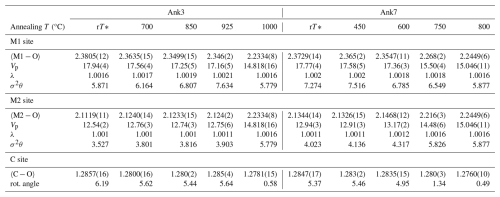
Table 3 Bond lengths (in Å) and polyhedral volume (V_p in ų) are listed together with selected distortion parameters: polyhedral angle variance (σ²θ), quadratic elongation (λ) (Robinson et al., 1971), and rotation angle of CO₃ (rot. angle; see the text for details). When errors are not given, precision is in accordance with data figures.

3 Results

3.1 Cation disordering

Data extraction and refinement (Table 2) gave satisfactory results with the assumption of a mono-crystal model for almost all of the studied samples. Only the Ank3-2 sample was found to be affected by twinning, introduced in the structure refinement according to$\left\{\mathrm{11}\overline{\mathrm{2}}\mathrm{0}\right\}$ twin law, as already observed for dolomite (Zucchini et al., 2012a). The refined site scattering for the (0, 0, 0) and (0, 0, $\mathrm{1}/\mathrm{2}$) atomic positions was typical of a fully ordered cation distribution in natural Ank3 (20.0 and 17.6 electrons for the M1 and M2 sites, respectively) and Ank7 (20.0 and 21.8 electrons for the M1 and M2 sites, respectively). Given the higher atomic number of Fe with respect to both Ca and Mg, M2 in Ank7 has a higher site scattering than M1 in the fully ordered configuration; the opposite occurs in Ank3. The onset of cation disorder was already registered at the lowest annealing temperature, and both Q_occ and Q_bonds decrease as annealing T increases, as listed in Table 2. Full disorder was attained at T_c=1000 °C in Ank3 and at T_c=800 °C in Ank7; that is, the higher the Fe content, the lower the disordering temperature, in agreement with Franzolin et al. (2012).

The comparison between the two parameters Q_occ and Q_bonds is given in Fig. 2, and good agreement between their values is observed, thus confirming the reliability of results of cation occupancy refinements (Table 2).

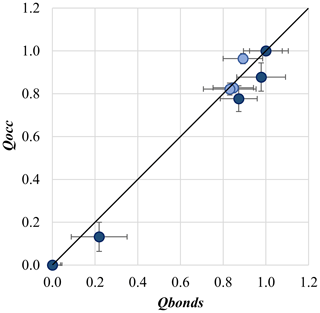
Figure 2 Comparison between the order parameter calculated through refined site occupancy (Q_occ) and that calculated by using bond lengths (Q_bonds).

The refined cationic occupancies at both the M1 site and the M2 site showed that, as the annealing T is increased, Ca is mainly replaced by Fe compared to Mg. In particular, while at Ank7 both Fe and Mg replace Ca, with the former contributing more than the latter, at Ank3 the scattering values imply that Mg most likely remains at M2 or exchanges to a very low content; therefore, refinements in Ank3 were carried out by fixing Mg at the M2 site and refining only the Ca and Fe occupancies.

With further T increases, in Ank3 disorder remains quite low, being Q_bonds=0.83 in Ank3 at 925 °C. Full disorder was attained at 1000 °C, and the only cationic site in the $R\overline{\mathrm{3}}c$ space group has occupancy related to stoichiometry. In Ank7, an intermediate step before reaching the fully disordered state is observed at 750 °C, where the refined occupancy of Ca in M1 strongly decreases, while Fe and Mg increases, reaching Q_bonds=0.22, as also confirmed by the site scattering of M1 that increases from 20.02 at 600 °C to 20.74 at 750 °C and the site scattering of M2 that decreases from 21.78 at 600 °C to 21.06 (Fig. 3b and c), very closely approaching the site-scattering value of a fully disordered Ank7 (20.90 by stoichiometry). Full disorder was attained at 800 °C in Ank7, with M1 site scattering averaged by stoichiometry.

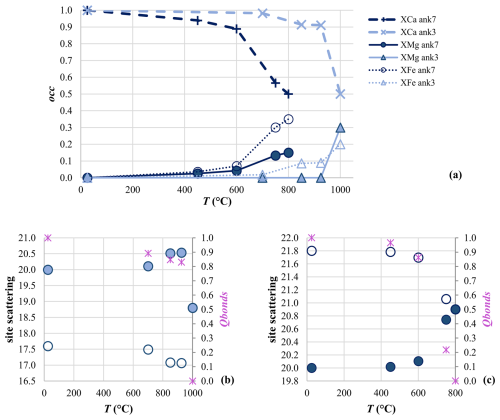
Figure 3 Cation site occupancy (occ) as a function of T for the M1 site (a). Site scattering for M1 (filled symbols) and M2 (empty symbols) in Ank3 (b) and Ank7 (c), given together with the order parameters Q (pink asterisks), as a function of the annealing T.

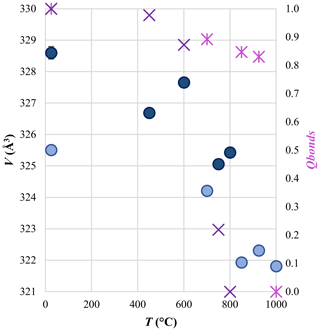
Unit cell parameters derived from SC-XRD data (Table 2) showed an increase in unit cell dimensions with increasing Fe content due to the larger size of Fe with respect to Mg, with a stronger effect on the c axis than on the a axis, in agreement with literature data (e.g., Reeder and Dollase, 1989). At the same time, a decrease in unit cell volume as disorder increases was also observed (Fig. 4), with a volume difference between the fully disordered and the fully ordered state of approximately −1.0(1) %, in agreement with Chai and Navrotsky (1996). However, in contrast to the findings of Chai and Navrotsky (1996), an increase in both the a and the c axes as disorder proceeds is observed in this study (Table 2).

Figure 4 Unit cell volume (left ordinate) of Ank3 (light blue circles) and Ank7 (dark blue circles). Q_bonds parameters (right ordinate) of Ank3 (pink asterisks) and Ank7 (violet crosses). Both are as a function of T.

3.2 Polyhedral geometry

In Table 3 the list of selected geometrical parameters for the M1, M2, and C sites are given.

In the ordered Ank3 and Ank7, the M1 site (filled by Ca) has higher dimensions than M2 (occupied by Mg and Fe), with a difference in polyhedral volume (V_p) of approximately 5 ų. As shown in Fig. 5, volumes of the M1 site in both Ank3 and Ank7 are consistent with data for calcite, whereas M2 has volumes close to Fe magnesite in Ank3 and siderite in Ank7, in agreement with the higher Fe content in the latter. As a general tendency, with the progress of cation disorder, M1 contracts and M2 expands, consistent with the higher dimension of Ca with respect to Mg and Fe and in agreement with the behavior of dolomite (Fig. 5). While the M1 dimensions of Ank3 and Ank7 are comparable, and this is confirmed as disorder increases, the M2 polyhedron in Ank7 is larger than that of Ank3 of ∼0.5 ų in the ordered samples, given the higher amount of Fe in the former with respect to the latter. As the degree of disorder increases, the difference in V_p increases slightly, reaching approximately 1 ų at Q_bonds∼0.8. The decrease (increase) in M1 (M2) polyhedral volume becomes pronounced in Ank7 annealed at 750 °C (Q_bonds=0.22), whereas no intermediate points are observed for Ank3 before reaching complete disorder, as expected based on previous considerations.

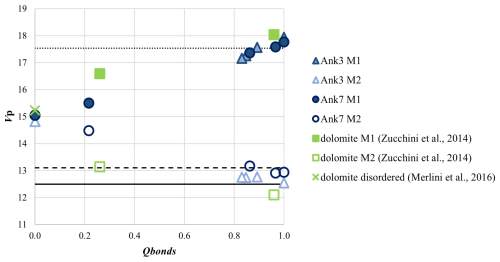
Figure 5 Polyhedral volume (V_p) for the M1 and M2 sites in Ank3 and Ank7 as a function of disordering. Symbols and colors are given in the legend. For comparison, data for ordered and disordered dolomite (green symbols, Zucchini et al., 2014; Merlini et al., 2016) are given together with Fe magnesite (solid line, Merlini et al., 2016), siderite (dashed line, Graf, 1961), and calcite (dotted line, Ishizawa et al., 2013). Errors are within symbols.

Figure 6 Comparison between calculated (〈M1−O〉 calc and 〈M2−O〉 calc) and refined (〈M1−O〉 ref and 〈M2−O〉 ref) cation-to-oxygen bond distances for the M1 site (a) and M2 site (b). Dark and light blue refers to Ank3 and Ak7, respectively. The 1:1 line between refined and calculated bond distances is given.

The refined polyhedral geometry was also the basis for a supplementary check on site occupancy refinement. The cation-to-oxygen bond distances were calculated from the refined cation occupancy, based on Ca–O, Mg–O, and Fe–O distances in pure calcite (Ishizawa et al., 2013), magnesite (Ross, 1997), and siderite (Graf, 1961). The cation-to-oxygen bond distances were then calculated based on refined cation occupancies. As shown in Fig. 6, good agreement is observed between refined cation-to-oxygen bond distances and those calculated by cation occupancy.

In Table 3, the distortion parameters σ²θ (polyhedral angle variance) and λ (quadratic elongation) are listed for M1 and M2 in the different disordering configurations. The evolution of σ²θ and λ is analogous in the differently ordered samples, and, in Fig. 7, we report the trend shown by σ²θ vs. Q_bonds. Distortion is slightly higher in Ank7 with respect to Ank3, and M2 always shows higher distortion than M1 in the $R\overline{\mathrm{3}}$ structures. Under ordered conditions, distortion parameters for M1 and M2 are consistent with values for calcite and Fe magnesite, respectively, in agreement with the ordered cationic distribution. At the onset of disorder, in the M2 site a clear trend is observed, with an increase in polyhedral distortion in both Ank3 and Ank7 due to the larger size of Ca replacing Mg and Fe, which has the effect of a marked increase in polyhedral distortion. The M1 site shows a less evident trend of polyhedral distortion with respect to M2, probably given the smaller dimensions of Mg and Fe compared to Ca, which can be accommodated by making slight modifications to the M1 distortion.

When the full disorder is reached and the space group varies from $R\overline{\mathrm{3}}$ to $R\overline{\mathrm{3}}c$, the polyhedral volume of the only M1 site and its distortion become similar in the two samples, with V_p=14.82(2) ų and σ²θ=5.78 in Ank3 and V_p=15.05(1) ų and σ²θ=5.88 in Ank7.

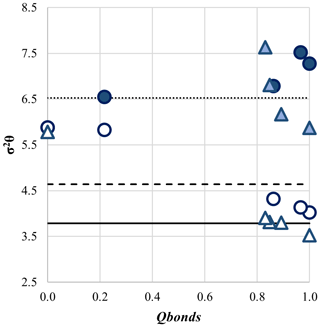
Figure 7 Polyhedral angle variance (σ²θ) as a function of the order parameter (Q_bonds) for Ank3 and Ank7. Legend is in accordance with Fig. 5.

Interesting results were obtained for the carbonate group, and the focus was directed towards two parameters related to disordering. Firstly, the z coordinate of the C atom gradually approaches the special position of 0.25, which is characteristic of $R\overline{\mathrm{3}}c$ carbonates. Secondly, attention was given to the rotation of CO${}_{\mathrm{3}}^{\mathrm{2}-}$ (Tables 2 and 3, respectively) about the three-fold axes in $R\overline{\mathrm{3}}$ carbonates with respect to the $R\overline{\mathrm{3}}c$ structures, which arises as a consequence of the difference in bond lengths between M1 and M2 in the former. Rotation angle was calculated as the difference between the angle O–C–Ca (Fig. 8) in calcite (120.84° from Graf, 1961) and in the analyzed samples.

The behavior of the fully ordered Ank3 and Ank7 is comparable; that is, the rotation angle is 6.19 and 5.37° (Fig. 9), respectively, while z_C=0.2562(2) and 0.2565(1), respectively, close to data for ordered dolomite. As disorder approaches, the rotation angle of the CO${}_{\mathrm{3}}^{\mathrm{2}-}$ group decreases and approaches values for disordered dolomite (Fig. 9). The same behavior is shown for z_C, which lies in general positions in the $R\overline{\mathrm{3}}$ crystal structures and approaches the special position 0.25 ($R\overline{\mathrm{3}}c$ structures) as disorder increases, in agreement with dolomite.

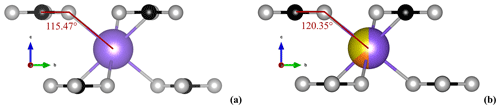
Figure 8 Zoomed-in portion of the M1 site in the ordered Ank7 (rT) (a) and in the fully disordered Ank7 (T_c=800 °C) (b) crystal structures, where the O–C–Ca angle, used for comparison with data in calcite (Graf, 1961), is shown. For colors, refer to Fig. 1.

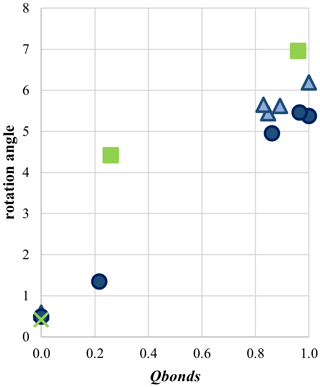
Figure 9 Rotation angle (in °), calculated as the difference between the angle O–C–Ca (shown in Fig. 8) in calcite (120.84° from Graf (1961) and in the analyzed samples. Data for ordered and partially disordered dolomite (green squares, Zucchini et al., 2012a, 2014) and disordered dolomite (green cross, Merlini et al., 2016) are shown. Light and dark blue refers to Ank3 and Ank7, respectively.

4 Discussion

Results of structure refinement in the differently ordered ankerite samples confirm the decrease in T_c with the increase in the Fe content in ankerite, as proposed by Franzolin et al. (2012). Results show that the site scattering of M1 and M2 is strongly influenced by the Fe content. In both Ank3 and Ank7, during the disordering process, Ca in M1 is mainly replaced by Fe (Fig. 3a), already at the lowest annealing temperatures. This behavior is enhanced in Ank3, where the refinement of cation occupancy in the M1 and M2 sites converged with Mg constrained in the M2 site. Thus, no Mg replacement occurred in Ank3 up to the highest annealing T before full disordering. Alternatively, it may have occurred but at such a low level that it was undetectable using the cation occupancy refinement approach. The persistence of Mg in the M2 site in Ank3 and the low-Mg exchange in Ank7 at the lowest annealing temperatures are not surprising, as Mg is the smallest cation among Ca, Mg, and Fe (and Mn), and it tends to occupy the small M2 site more favorably. Furthermore, it is important to consider that the mean Fe–O bond distance in pure siderite is approximately 2.14 Å (Graf, 1961) and that of MgO in pure magnesite is around 2.10 Å (Effenberger et al., 1981). In contrast, the cation-to-oxygen bond distance in the ordered Ank3 and Ank7 structures is 2.112(1) and 2.129(1) Å, respectively. This suggests that, under thermal agitation caused by the increase in temperature, Fe exhibits a preference for the M1 site, which is larger than M2 and provides more favorable accommodation for it.

In both Ank3 and Ank7, the disordering process was effective, and we were able to retrieve fully disordered samples at 800 °C for Ank7 and 1000 °C for Ank3. The variation in Q with the annealing T (Eq. 2) can be expressed following Carpenter et al. (1990):

$$\begin{array}{}\text{(3)}& Q={\left(\mathrm{1}-{\displaystyle \frac{T}{T_{\mathrm{C}}}}\right)}^{\mathit{\beta }},\text{ for }T<T_{\mathrm{c}},\end{array}$$

where β describes the order of the phase transition and has values of 0.5 for a second-order phase transition and 0.25 for a tricritical phase transition (Carpenter et al., 1990).

In order to decipher the order of the transitions in the two studied samples, we examine the trend between $Q_{\mathrm{bonds}}^{\mathrm{2}}$ (β=0.5) and $Q_{\mathrm{bonds}}^{\mathrm{4}}$ (β=0.25) as a function of the annealing T, following Bromiley et al. (2007), and results are given in Fig. 10.

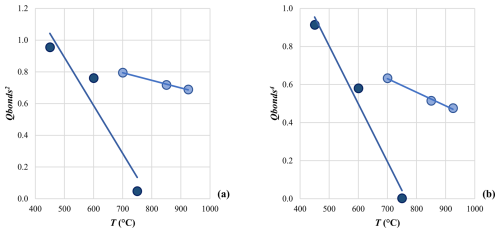
Figure 10 Behavior of $Q_{\mathrm{bonds}}^{\mathrm{2}}$ (a) and $Q_{\mathrm{bonds}}^{\mathrm{4}}$ (b) as a function of the annealing T. In both graphs, lines are the linear fits between the two variables for Ank3 (light symbols) and Ank7 (dark symbols).

For Ank3, both β=0.5 and β=0.25 seem to show a good fit, with the coefficient of determination (R²) of the linear fit equal to 0.994 and 0.992, respectively. However, we have to point out that the Q range used to calculate the linear relationship is quite small, being Q_bonds in the range of 0.96–0.82 for Ank3 (excluding the fully ordered samples as we do not have data at the highest temperature before disordering). In contrast, data for Ank7 do not demonstrate a linear tendency, whether in the $Q_{\mathrm{bonds}}^{\mathrm{4}}$ vs. T or $Q_{\mathrm{bonds}}^{\mathrm{2}}$ vs. T relationships. The least squares method was employed to obtain an accurate estimate of β, and the result was β=0.16(1). Given that β is lower than 0.25, we can speculate that the order–disorder phase transition in Ank7 is characterized by a first-order character. This would imply that abrupt changes in the Ank7 physical properties occur during the order–disorder phase transition, such as its elastic behavior (Carpenter and Salje, 1998).

Comparing the present data with the model proposed by Franzolin et al. (2012), the disordering temperatures of Ank3 and Ank7 (present work), as well as those of dolomite in Zucchini et al. (2012a), are somewhat higher than expected and also higher compared to the fully disordered conditions attained at 750 °C in the ankerite sample recently analyzed by Zucchini et al. (2024). This can be explained by some reordering processes that can occur during quenching in different portions of the annealed samples. Moreover, the comparison of SC-XRD data (present work) with XRPD data from Franzolin et al. (2012) could lead to biases, such as (1) a general tendency for powder refinement procedures to underestimate the order parameter and for the single-crystal refinement of twinned crystals to overestimate it and (2) a tendency for the smaller grain size of powdered samples used in XRPD to favor the onset of disordering (Zucchini et al., 2012a).

Recent findings on the elastic behavior of ankerite under non-ambient conditions (Zucchini et al., 2024) have indicated that the order–disorder phase transition in ankerite is most likely to occur in the mantle wedge at 150–250 km depth, exerting a significant influence on the mineral's elastic behavior. In fact, the calculated bulk sound velocities for disordered ankerite shows the lowest values among other phases (Zucchini et al. 2024), suggesting that it may play a role in determining low-velocity anomalies and large delay times observed in the mantle wedge (e.g., Chantel et al., 2012). The present data allowed us to speculate that Fe content exerts a significant influence on the nature of the order–disorder phase transition in ankerite, with important implications for the physical properties of ankerite under non-ambient conditions. This finding carries significant consequences for the mineral physics of ankerite, particularly concerning the relationship between elastic constants and heat capacity, both of which exhibit explicit sensitivity to these phase transitions (Sondergeld et al., 2005).

5 Conclusions

The study reported here shows that cation disorder occurs over the mineral's octahedral sites and that the degree of disorder increases with both temperature and Fe content. Full-disordering conditions are attained at 1000 °C in Ca(Mg_0.6Fe_0.3Mn_0.1)(CO₃)₂ and 800 °C in Ca(Mg_0.3Fe_0.7)(CO₃)₂, as confirmed by diffracted intensities, refined site scattering of cationic sites, and geometrical features of the refined crystal structure (atomic positions, distortion parameters, polyhedral dimensions). Concurrently, the refined cationic occupancy of the M1 and M2 sites in the differently ordered ankerite samples demonstrated that Fe exchanges at lower T than Mg, with the latter preferentially located at the M2 site.

Fe content in ankerite exerts a significant influence on the character of the order–disorder phase transition. Data reported here indicated that the order–disorder phase transition, studied through ex situ experiments, has a first-order character in the ankerite with the highest Fe content [Ca(Mg_0.3Fe_0.7)(CO₃)₂], whereas either second-order or tricritical behavior was observed for Ca(Mg_0.6Fe_0.3Mn_0.1)(CO₃)₂. These differences may have implications for the physical properties of ankerite with different Fe content at the order–disorder transition and, in turn, may influence its behavior within the inner Earth.

In light of the present findings, it is evident that further experimentation on ankerite is required in order to conduct a comprehensive analysis of the impact of Fe content on both the variation in phase transition character and the mineral physics of ankerite, in terms of elasticity, compressibility, phase stability, and thermal conductivity.