The thermal expansion of monticellite and olivine

The thermal expansion of two natural monticellite (CaMgSiO₄) samples was measured by X-ray powder diffraction between 298 and 1250 K. Axial expansion in monticellite is anisotropic with α(c) > α(b) ≥α(a), with the volume expansion nearly equivalent to that of synthetic forsterite as measured in the same laboratory, although forsterite axes expand as α(b) > α(c) > α(a). Kroll physical and Fei empirical models have been used to describe the volume and axial thermal expansion of both minerals. High-temperature structural data for these minerals show that the Ca-occupied M2 polyhedron in monticellite expands less than the Mg-occupied site in forsterite, resulting in comparatively lower expansion along the b crystallographic axis. But greater expansion of the M1 polyhedron in monticellite accounts for greater expansion along its c axis and, in turn, the nearly equivalent volume expansion relative to that of forsterite.

1 Introduction

Thermal expansion is a key thermodynamic property of any mineral or mineral assemblage and is indeed a basic property associated with mechanical behaviour of the assemblage wherever it is found. Thermal strain is a critical parameter in structural geology and engineering; moreover, knowledge of volume changes in materials as functions of temperature (T) and pressure (P) is required in order to predict high $T/P$ equilibria in natural, synthetic and industrial systems (e.g. Holland and Powell, 2011).

The thermal expansion coefficient (α) of a material is defined as (∂V/$\partial T)/V$. To obtain the latter it is necessary to describe the functional relation between volume and temperature. In minerals, thermal expansion has commonly been approximated as constant due to the lack of data of a suitable quality, yet theoretical and experimental considerations show more complex behaviour. Moreover, thermal expansion is related to vibrational behaviour and therefore heat capacity, which does not change linearly with temperature. Generally, therefore, the relationship of mineral volume to temperature requires careful nonlinear modelling of V−T data.

Several proposed physical and empirical models describing V−T behaviour are summarised in Angel et al. (2014). Experimentally, the measurement and expression of thermal expansion with temperature are challenging because deviations from linearity are relatively small at high T but considerably more significant below room T. Models, therefore, require high-quality V−T data.

Although thermal expansion data for minerals have been tabulated since 1990 (Fei, 1995), the need for higher-quality data has prompted further investigation in the most common mineral families, including plagioclase (Tribaudino et al., 2011; Hovis et al., 2010), alkali feldspar (Hovis et al., 2008), garnet (Angel et al., 2022), olivine (Suzuki, 1975; Kroll et al., 2012), pyroxene (Knight and Price, 2008; Hovis et al., 2021), amphibole (Tribaudino et al., 2008, 2022) and tourmaline (Hovis et al., 2023), for which physical models have been used to fit high-temperature volume data.

Natural olivine is a solid solution of forsterite (Fo; Mg₂SiO₄) and fayalite (Fa; Fe₂SiO₄), with minor Ca and Mn. As a key phase in the upper mantle, it has been studied extensively. In their paper on olivine thermal expansion, Kroll et al. (2012) provide a helpful synthesis of previous literature. They also model the thermal expansion of forsterite–fayalite solid solutions, merging the results from as many as 16 different investigations on natural and synthetic samples. The Kumar physical equation was used to model the volume of forsterite–fayalite olivine with temperature at any composition. Previous results are discussed using a number of physical models, and a careful analysis is done for the thermodynamic implications of each model.

In contrast to the detailed investigation of olivine, the thermal behaviour of Ca–Mg and Ca–Fe phases with an equivalent structure to olivine, namely monticellite (CaMgSiO₄) and kirschsteinite (CaFeSiO₄), has been scarcely studied. In natural settings, monticellite is found in siliceous and magnesian limestones as well as high-temperature metamorphic rocks or metasomatised skarns. It also occurs in industrial environments, such as steel-making slags, commonly as a main constituent of the slag (e.g. Ferreira Neto et al., 2016), and in bottom and fly ash from municipal solid-waste incinerators (MSWIs; Ferraro et al., 2023). The thermal expansion of monticellite is therefore of interest not only in modelling metamorphic parageneses, but also from a socioeconomic perspective. In fact, monticellite-bearing industrial waste is secondary raw materials in cement and ceramics, where thermal expansion is a critical feature related to the cracking of the product after recycling.

To our knowledge, the only high-temperature investigation on monticellite is that of Lager and Meagher (1978), who reported single-crystal high-temperature structures of monticellite and two additional olivine-group minerals (glaucochroite CaMnSiO₄ and Ni-olivine Ni₂SiO₄) at three temperatures in addition to room T. Thermal expansion was modelled linearly; differences in the volume thermal expansion among olivines of different compositions were not considered, although a different pattern of axial expansion in Ca vs. Mg–Fe olivines was noted. Expansion along the b axis was determined to be related to that of the M2 polyhedron.

Here, we report unit-cell parameters measured between 298 and 1250 K on two monticellite samples. These results are part of the high-temperature measurements performed over multiple years at Cambridge University and Lafayette College, nearly all of which have been published (Hovis et al., 1999, 2003, 2006, 2008, 2010, 2021, 2023; Tribaudino et al., 2022). The present results were made at Lafayette College using the same setup for both monticellite and synthetic forsterite, as reported in more recent papers (e.g. Hovis et al., 2021, 2023).

2 Experimental

Two natural monticellite specimens, one each from the US National Museum of Natural History (NMNH) and the American Museum of Natural History (AMNH), from the localities of Magnet Cove, Hot Spring County, Arkansas (NMNH C2796), and Crestmore, Riverside County, California (AMNH 27907), respectively, were investigated by X-ray powder diffraction. The compositions of these samples are

Ca_0.997Mg_0.869Fe_0.107Mn_0.036Si_0.992O₄ (Schaller, 1935)
(Σ= 2.005) and Ca_1.017Mg_0.916Fe${}_{\mathrm{0.070}}^{+\mathrm{2}}$Mn${}_{\mathrm{0.006}}^{+\mathrm{2}}$Zn_0.001Si_0.995O₄ (Σ= 2.010), respectively (RRuff, courtesy of AMNH). The chemical compositions were not re-measured. Room-temperature unit cells of the samples are very similar, with a slightly larger volume (0.5 Å³) for the Magnet Cove specimen (Table 1), likely due to its higher Fe and Mn content. X-ray powder diffraction measurements were conducted on these samples from room T to ∼1250 K at mostly 50 K intervals on a Panalytical Empyrean X-ray powder diffraction system equipped with an Anton Paar HTK 1200N heating stage. NIST (NBS) 640a silicon powder was mixed with each sample to serve as an internal standard. Actual sample temperatures were checked through independent experiments on several compounds that display second-order phase transitions, as described in detail by Hovis et al. (2021).

Table 1 Unit-cell parameters for monticellite and forsterite.

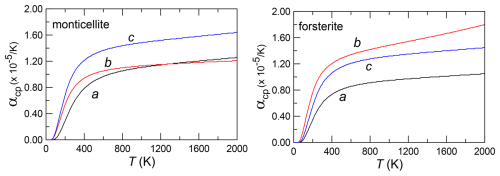
For comparison with monticellite, we also made high-T X-ray powder diffraction (XRD) measurements on end-member forsterite utilising a sample synthesised by Donald Lindsley and provided to us by Melinda Darby Dyar. High-T unit-cell volume results for this sample (Fig. 1) are in excellent agreement with the previous forsterite (Fo₁₀₀) data of Kroll et al. (2012).

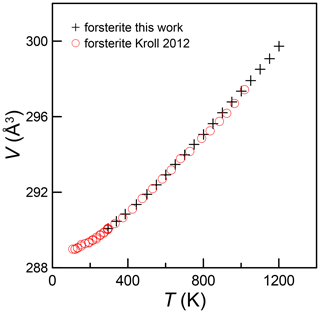
Figure 1 Unit-cell volumes of pure forsterite with temperature from the present investigation compared with results from Kroll et al. (2012). As in the following figures, the error is smaller than the size of the symbol.

X-ray measurements were made at temperatures (T) ranging from room T (taken as 22 °C) to ∼ 928 °C on a Panalytical Empyrean XRD system equipped with an Anton Paar HTK 1200N heating stage. The actual sample temperature was checked periodically by conducting separate experiments on four different compounds (KNO₃, KClO₄, K₂SO₄, BaCO₃), which collectively undergo reversible phase transformations at temperatures covering the range ∼ 130 to ∼ 815 °C. Each of these samples was X-rayed at small T increments across their phase transformation, then cooled in small T increments across the same transition, heated again and so on, while inspecting the X-ray pattern at each temperature. Generally, it was found over time that the observed temperatures of our experiments were 16 to 28 °C above the set temperature displayed on the controller console. Appropriate adjustments were made during data reduction to correct for this difference.

Each mineral was X-rayed from room T to a set T of 900 °C at (mostly) 50 °C intervals. X-ray scans were conducted from 15 to 80° 2θ over a 30 min period at each T, except for some Fe-bearing specimens for which run times of 50 or 60 min were employed. All measurements utilised Ni-filtered Cu Kα radiation. Isometric silicon (NIST SRM 640a) with a stated room-T unit-cell dimension of 5.430825 Å was used as an internal standard in all experiments. Silicon peak positions were adjusted for temperature utilising the Si thermal expansion data of Parrish (1953).

Generally, unit-cell dimensions were calculated utilising the X-ray software of Holland and Redfern (1997). For both monticellite and forsterite samples, the data for 23 to 30 well-defined XRD maxima occurring between 20 and 77° 2θ were utilised to compute unit-cell dimensions; many of the diffraction maxima used for unit-cell calculations were common to all refinements within each mineral. To avoid the automated indexing of low-intensity X-ray peaks related to potential phase impurities, the hkl identities of all peaks were assigned manually, for which the American Mineralogist Crystal Structure Database (Downs and Hall-Wallace, 2003) was invaluable. Because of manual indexing rather than the automated indexing now available on XRD systems, we consider the stated standard deviations of the computed unit-cell dimensions to be realistic. The wavelength of Cu Kα₁ radiation for all calculations was taken to be 1.540598 Å.

In the appendix of this paper we also report data for fayalite and several natural olivine samples having intermediate Fe : Mg ratios. These provide comparative data relative to literature values. Note, however, that stated compositions for some of the natural NMNH samples are estimates based on d₁₃₀ values, not on direct chemical determinations. Furthermore, no buffer was added to avoid Fe oxidation. Unlike monticellite and forsterite, then, oxidation of these Fe-bearing samples was typically evidenced by brownish to reddish discolouration of unloaded samples at the conclusion of an XRD experiment. This, of course, indicates changing composition of Fe-bearing samples once oxidation is initiated during rising T. Room- and high-temperature unit-cell data for monticellite and forsterite are given in Table 1, whereas data for other samples can be found in the appendix.

3 Results and discussion

3.1 Thermal expansion of monticellite and forsterite

In Fig. 2, we show the relative axial and volume expansion of the forsterite and monticellite samples alongside the Lager and Meagher (1978) monticellite. Volume expansion of forsterite and both monticellites is superimposed. Expansion along the a axis for monticellite and forsterite shows a similar trend up to 900 K, but monticellite shows greater expansion above this temperature. Along the b axis, forsterite expands more than monticellite, whereas monticellite expands more than forsterite along c.

Figure 2 Axial and volume expansion in monticellite (present work; Lager and Meagher, 1978) and forsterite (present work).

In a review on comparative crystal chemistry of orthosilicate minerals, Smyth et al. (2000) report “Linear volume thermal expansion coefficients at one atmosphere range from a low of about 3.0 × 10⁻⁵ K⁻¹ for monticellite and glaucochroite (Lager and Meagher, 1978) to about $\mathrm{4.4}\times {\mathrm{10}}^{-\mathrm{5}}$ K⁻¹ for forsterite (Takéuchi et al., 1984)”, that is, a much higher thermal expansion for forsterite than monticellite. The apparent conflict with present data, however, is invalid, as these authors interpret the variation in V with T as linear, which is improper over large T ranges such as 23 to 1600 °C for forsterite and 25 to 795 °C for monticellite. Indeed, Hovis et al. (2021) and numerous other studies show clearly that linear fits ignore the existence of nonlinear V−T relations, although comparisons over relatively short T ranges can indeed be useful. Moreover, comparison of thermal expansion coefficients over T ranges where V−T relations are nearly linear should be done over equivalent temperature ranges. In fact, comparison of present monticellite data with the forsterite data of Takéuchi et al. (1984) via a linear fit over nearly the same temperature range (298–1223 K) produces nearly identical thermal expansion coefficients, 3.58(30) for forsterite versus 3.53(4) and 3.56(5) × 10⁻⁵ K⁻¹ for the two monticellite samples.

Because monticellite is a magnesium refractory with a melting point (1771 K, Cui et al., 2023) well beyond our experimental range, note that we have taken particular care in modelling volume and thermal expansion at the highest temperatures using both physical and empirical models.

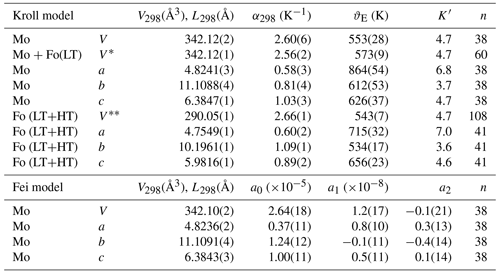
It should be noted that Kroll et al. (2012) used the Kumar physical model in their work, which gives results that are almost equivalent to the models in Holland and Powell (2011) and Tribaudino et al. (2011). These formulations were implemented in the EosFit package under the name of “Kroll model” (Angel et al., 2014). In that model, a scaled Einstein-like formulation for lattice energy is proposed, and relations of volume with temperature are explicitly written as

$$\begin{array}{}\text{(1)}& \begin{array}{rl}V& =V_{\mathrm{298}}\mathit{\{}\mathrm{1}-{\mathit{\alpha }}_{\mathrm{298}}{K}^{\prime }{\mathit{\vartheta }}_{\mathrm{E}}(e^{{\mathit{\vartheta }}_E/\mathrm{298}}-\mathrm{1}{)}^{\mathrm{2}}/\left[\right({\mathit{\vartheta }}_{\mathrm{E}}/\mathrm{298}{)}^{\mathrm{2}}{e}^{{\mathit{\vartheta }}_{\mathrm{E}}/\mathrm{298}}\left)\right]\\ & [\mathrm{1}/(e^{{\mathit{\vartheta }}_{\mathrm{E}}/T}-\mathrm{1})-\mathrm{1}/(e^{{\mathit{\vartheta }}_{\mathrm{E}}/\mathrm{298}}-\mathrm{1}\left)\right]{\mathit{\}}}^{-\mathrm{1}/K^{\prime }}.\end{array}\end{array}$$

This model requires four parameters: (1) unit-cell volume, (2) thermal expansion at the reference temperature (generally 298 K), (3) the first derivative of the bulk modulus (K) and (4) the Einstein temperature (ϑ_E). The latter two parameters describe the deviation from linear behaviour; any uncertainty in temperature and/or volume affects their value. These cannot be refined together, as they are highly correlated. High-pressure in situ investigation can determine the bulk modulus and its derivatives, but for monticellite only a single-crystal high-pressure investigation exists (Sharp et al., 1987), in which the first derivative of the bulk modulus with pressure was not refined. As a result, we have assumed K^′ to be the same as that reported for forsterite in Kroll et al. (2012), namely $K^{\prime }=$ 4.7. This value is similar to $K^{\prime }=$ 5.1 determined experimentally in forsterite by Nestola et al. (2011). Slight differences from this value did not worsen the fit but did change the Einstein temperature, with reference volume and thermal expansion remaining almost unchanged.

To improve statistics, the two monticellite data sets were modelled together after rescaling for the difference in volume. Moreover, in view of the apparent similarity between forsterite and monticellite expansion, we fit the monticellite data with and without the data below room temperature for forsterite (Kroll et al., 2012). The thermal expansion of forsterite was modelled by merging the data on synthetic forsterite from this work with those of Kroll et al. (2012) and Kajiyoshi and Suzuki (1996).

A refinement of volume with temperature was also done using the Fei empirical model. This model has the advantage of only requiring the experimental V−T data, without the need for extra information from other physical quantities. Results show that thermal expansion is related to temperature as

$$\begin{array}{}\text{(2)}& \mathit{\alpha }=a_{\mathrm{0}}+a_{\mathrm{1}}T+a_{\mathrm{2}}{T}^{-\mathrm{2}}\end{array}$$

and to volume as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{V}_{\mathrm{0}}& =V_{\mathrm{0}}\exp \left[a_{\mathrm{0}}\right(T-T_{\mathrm{ref}})+(T^{\mathrm{2}}-T_{\mathrm{ref}}^{\mathrm{2}})a_{\mathrm{1}}/\mathrm{2}\\ & -a_{\mathrm{2}}(\mathrm{1}/T-\mathrm{1}/T_{\mathrm{ref}})],\end{array}\end{array}$$

where V₀ is the volume at the reference temperature, and a₀, a₁ and a₂ are refinable parameters; the reference temperature was taken to be 298 K.

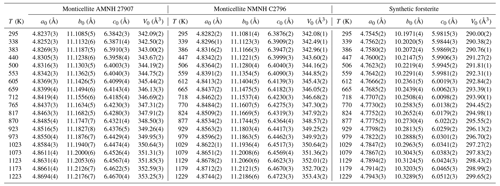
The volume thermal expansion with T is reported in Fig. 3. Here, thermal expansion coefficients of monticellite with or without low-temperature forsterite are indistinguishable. Monticellite thermal expansion is very close to that of forsterite up to the highest temperature. In addition, the Fei model shows reasonable agreement with physical models, which was not observed for forsterite by Kroll et al. (2012).

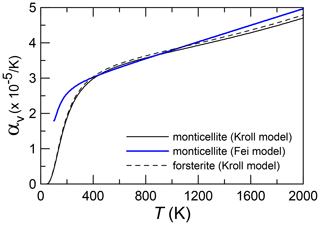
Figure 3 Variation in the volume expansion coefficient with temperature in forsterite and monticellite modelled with the Kroll model, as in Angel et al. (2014), and in monticellite modelled according to the Fei empirical model. The fit was done by merging the two monticellite data sets. Independent fitting of each monticellite would not lead to representable differences from the above.

The parameters for each fit are reported in Table 2.

Table 2 Parameters for the Kroll and Fei models of thermal expansion. Mo – monticellite, Fo(LT) – data between 100 and 298 K from forsterite (Kroll et al., 2012) fitted together with those of the two monticellite specimens, Fo(LT+HT) – forsterite refined (volume – data from this work, Kroll et al. (2012), and Kajiyoshi and Suzuki (1996); a, b and c parameters; this work and Fo(LT) from Kroll et al. (2012)), n – number of data.

3.2 Axial thermal expansion

Axial linear thermal expansion parameters have also been modelled in monticellite through physical and empirical approaches. For volume, the two monticellite data sets have been merged, after rescaling. The first derivative for the axial bulk modulus was retrieved from Kroll et al. (2016), on CoMg olivine, in the absence of reliable estimations on monticellite, whereas the Einstein temperature was refined. Data for CoMg olivine were preferred because its axial expansion is closer than other olivines to that of monticellite.

The axial expansion along c is higher at all temperatures (Fig 4). Below 1200 K, b expansion is higher than that along a. At higher temperatures, due to the higher Einstein temperature, expansion along a keeps pace with that along b. Parameters for the physical and Fei empirical models are reported in Table 2.

Figure 4 Axial expansion with temperature in monticellite and forsterite.

In forsterite, expansion along b and c is similar (Fig. 4) but lower along a, at all temperatures. In fayalite, however, the presence of Fe decreases expansion along b, an effect similar to that observed in the replacement of Mg by Ca (Kroll et al., 2014).

The relatively greater expansion along the b axis in forsterite versus the c axis in monticellite results in similar volume thermal expansion for the two minerals. The contrasting behaviour along the two axes that results from Ca-for-Mg exchange is likely related to the contrast in polyhedral expansion for these minerals.

The structure of olivine (Fig. 5) is based on a chain of distorted octahedra along the c axis, centred by the M1 cation, which lies in the special position 0, 0 and 0. The M1 octahedra share an edge with the adjacent octahedra and with the Si-centred tetrahedron. The M1 polyhedral chains are linked by larger and more distorted octahedra in the M2 polyhedron, whereas the SiO₄ tetrahedra are located between the M1 and M2 polyhedra. In monticellite, the M2 site is fully occupied by Ca, whereas Fe, Mg and Mn occupy M1. In ferromagnesian olivine, the two sites are occupied by Fe and Mg with no site preference by either cation. Forsterite, of course, has both cation sites fully occupied by Mg.

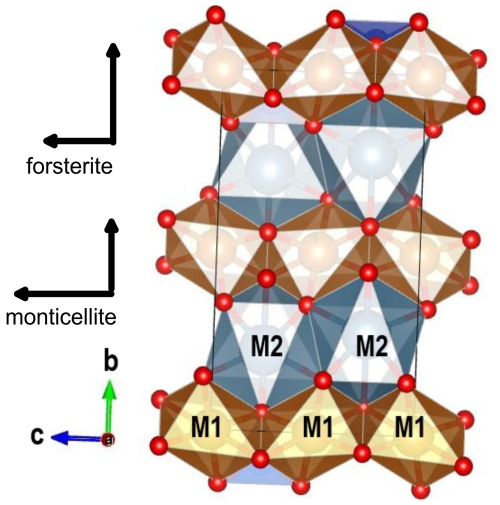
Figure 5 Crystal structure of monticellite at 298 K (Lager and Meagher, 1978). The relative size of thermal expansion in forsterite and monticellite is shown.

Owing to the small amounts of Fe and Mn in the investigated monticellite specimens, forsterite and monticellite differ only in the exchange of Ca for Mg in M2. The length of the c unit cell edge is mainly determined by the size of the M1 polyhedra. Along the b axis, octahedral chains are interposed by M2 polyhedra, which do not form a chain, and provide links between the M1 chains. Consequently, expansion along c relates to that of the M1 polyhedral chain, whereas that along b is determined by the M2 cation. In monticellite, the M2 cation is Ca, which makes the site larger and the bond distances greater than in forsterite. Detailed analysis of thermal polyhedral expansion is hindered by the lack of high-quality structural data on forsterite and monticellite at high temperature. The available structures on monticellite (Lager and Meagher, 1978) and forsterite (Hazen, 1976; Takéuchi et al., 1984) still provide interesting possibilities. The thermal expansion of M1 average polyhedral distances is significantly greater in monticellite (3.71(14) × 10⁻⁵ K⁻¹) than in forsterite, which was assessed to be 3.12(28) × 10⁻⁵ K⁻¹ by Takéuchi et al. (1984) and 3.04(74) × 10⁻⁵ K⁻¹ by Hazen (1976). However, thermal expansion of the average M2 bond lengths is higher in forsterite (3.52(28) × 10⁻⁵ K⁻¹ and 3.96(44) × 10⁻⁵ K⁻¹) than in monticellite (3.15(21) × 10⁻⁵ K⁻¹) (Lager and Meagher, 1978). The overall effect of lower expansion of the M2 polyhedron and greater expansion of M1, therefore, in large part offsets the comparative volume expansion of the two minerals.

4 Concluding summary

In the present investigation, we measured volume and axial thermal expansion of both monticellite and forsterite. Contrary to previous observations, volume expansion was found to be nearly equivalent in the two minerals.

In monticellite, relative magnitudes of expansion along the various unit-cell axes are α(c) > α(b) ≥α(a), but forsterite axes expand relatively as α(b) > α(c) > α(a) (Kroll et al., 2014). The pattern in monticellite thermal expansion is similar to that observed in fayalite but with a axial expansion seemingly overtaking that along b at lower temperatures relative to monticellite. The crossover occurs at 450 K in fayalite vs. 1250 K in monticellite (Lager and Meagher, 1978). It is also similar to Co olivine, where the a-axis expansion approaches but does not overtake that along b, even at the highest temperatures (Kroll et al., 2019). In Ni olivine, axial expansion follows the α(c) > α(b) > α(a) pattern, with expansion along c closer to that along b (Kroll et al., 2019). Axial expansion of forsterite is instead similar to that of Mn olivine (Kroll et al., 2019). Patterns of axial expansion intermediate to those of forsterite and fayalite/monticellite have been found in Fe–Mg (FeMgSiO₄) and Co–Mg (CoMgSiO₄) olivine (Rinaldi et al., 2005; Kroll et al., 2014, 2016), with α(c) ≅α(b) > α(a). Although the explanation of different axial expansion patterns in isostructural olivines is not clear, present results show that the pattern of higher expansion along c is not simply related to the presence of some feature in transition metals, which are almost absent in the present monticellite samples.

The present results also confirm that axial thermal expansion and compression show different patterns. In monticellite, as in olivine, compression is greater along b but less along c and a (Sharp et al., 1987). It is interesting that monticellite, fayalite, and Co and Ni olivine do not follow an inverse relation between pressure-induced axial compression and temperature-induced thermal expansion.

Finally, the present work provides a basis for further investigation of thermal behaviour in natural and industrial monticellite-bearing assemblages.

Appendix A: Additional data on the thermal expansion of olivine

During the course of the investigation at Lafayette College, several natural olivine samples of intermediate composition along the forsterite–fayalite join were examined. We take this opportunity to provide these results to interested communities (Supplement Table S1), recognising the current significant database. The present results will provide useful comparative data to the results of previous work. Compositions of the examined samples are reported in Table S1. Again, some Fo contents are estimated using the d₁₃₀ interplanar spacing (Yoder and Sahama, 1957). We also reiterate that upon removal of Fe-bearing samples at the conclusion of each high-T experiment, samples showed a reddish or reddish-brown colour indicative of oxidation. Analyses of the data reflect such effects, typically for data collected above 850 K. Deterioration occurring at even lower T can be seen for samples with relatively high Fe contents. Figure A1 shows linear thermal expansion coefficients based on data between room temperature and 800 K. The linear equation, relating thermal expansion with composition, is

$$\begin{array}{}\text{(A1)}& {\mathit{\alpha }}_V=\mathrm{3.45}\left(\mathrm{3}\right)-\mathrm{0.0044}\left(\mathrm{5}\right)x_{\mathrm{Fa}}.\end{array}$$

Such T limitation was done to avoid iron oxidation effects and Fe–Mg order–disorder in the M2 and M1 sites, which would be kinetically inhibited at relatively low T. These results, together with those from Redfern et al. (2000) and Kroll et al. (2012), confirm that the substitution of Fe reduces thermal expansion, at least at these lowest temperatures (Fig. A1).

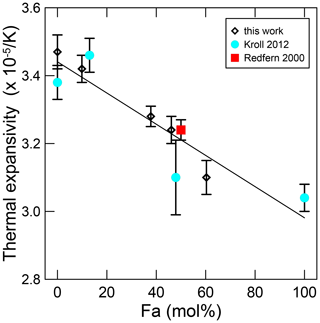
Figure A1 Thermal expansion between 298 and 800 K for members of the forsterite–fayalite olivine system.

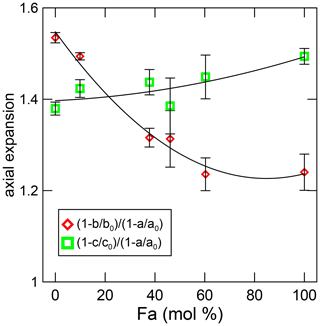
Figure A2 Axial expansion along the b and c axes with respect to that along the a axis. In this work, the average of the data from T > 450 K.

Compared with high pressure, thermal expansion decreases continuously with forsterite, whereas in olivine, with a composition between Fo₉₂Fa₈ and Fo₆₂Fa₃₈, the bulk modulus does not change in either volume or axial compressibility (Nestola et al., 2011). The unit-cell ratio at room pressure is $a/a_{\mathrm{0}}:b/b_{\mathrm{0}}:c/c_{\mathrm{0}}=$ $\mathrm{1.00}:\mathrm{2.15}:\mathrm{1.26}$ for all compositions at high pressure, whereas present data show that it changes from $\mathrm{1}:\mathrm{1.53}\left(\mathrm{2}\right):\mathrm{1.37}\left(\mathrm{3}\right)$ in forsterite to $\mathrm{1}:\mathrm{1.24}\left(\mathrm{8}\right):\mathrm{1.49}\left(\mathrm{3}\right)$ in fayalite (Fig. A2). Note that expansion along the c axis changes considerably in the same range where axial compressibility does not change.

Appendix B: Mineralogical research at non-ambient conditions in Italy: a dedication to Paola Bonazzi

In situ high-temperature research on materials was initiated in Italy in the late 1980s. Prior to this era the crystal structures of most common minerals had already been investigated, and only a few newly found mineral species or difficult-to-solve structures were left to be described. Even under these circumstances, however, certain types of worthwhile research on mineral families had not yet taken place. For example, how does chemical composition affect crystal structure within mineral families? With this subject in mind, we dedicate this paper to Paola Bonazzi, who made truly important crystallographic contributions in helping to answer this question for both the sulfide and the epidote mineral groups.

Additionally, in the 1980s there was the related matter of how minerals, even common ones, change their structures with increasing temperature and/or pressure. This new dimension of mineral sciences was aided considerably by the work Comparative Crystal Chemistry: Temperature, Pressure, Composition and the Variation of Crystal Structure (New York: Wiley) by Hazen and Finger (1982), which summarised the results of a decade of investigation in this new field of in situ high-pressure and high-temperature structural investigation. The mineralogical and materials communities quickly gained acquaintance with new laboratory facilities to perform high-temperature investigations and for the group in Perugia, led by Pierfrancesco Zanazzi, also high-pressure investigations.

Initially, the goal was to determine the crystal structures that exist under elevated $T/P$ conditions. These provided important crystallographic information as to the response of mineral structures to non-ambient conditions. A forward-looking topic promoted by the group in Cambridge was that of phase transitions in minerals and the link between thermodynamic behaviour and ferroelastic or co-elastic strain induced by the transition. Yet, strain had to be measured via accurate and precise data, which was inconsistent with studies where the determination of crystal structure was the key aim of the investigation. This helped lead to improvements in temperature (and pressure) calibration, as well as in the precision of measurements, which in turn led to greater detail and the discovery of subtle features such as strain coupling and order parameter saturation.

Next came the “discovery” of synchrotron radiation along with neutron diffraction facilities equipped with high-quality high pressure (HP) and high-temperature (HT) capabilities run by well-trained experimentalists. The availability of higher-quality data from non-conventional sources and various laboratories (including especially Bayerisches Geoinstitut) opened another field of investigation, namely that of basic thermodynamic properties, such as Grüneisen parameters and both Debye and Einstein temperatures, which could be linked by the thermal expansion measured experimentally via X-ray diffraction. To this end, unit-cell data below room temperature (down to 0 K), commonly affected by magnetic transitions, were of interest. New studies do continue, and the quality of such results is ever improving. Presently, the aim is not with respect to the mineral itself, but rather applications to petrology and the materials sciences.

It is with these thoughts in mind that we conclude this paper by honouring Paola Bonazzi for her work performed under non-ambient temperature conditions (as in the present monticellite investigation), alongside Chelazzi et al. (2011), where crystal structure at high temperature was determined on the Ca₂Sb₂O₇ weberite-type compound, and Bindi and Bonazzi (2003), where the wave vector of an incommensurate structure was measured at low temperature.