the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Depth profile analyses by femtosecond laser ablation (multicollector) inductively coupled plasma mass spectrometry for resolving chemical and isotopic gradients in minerals
Martin Oeser
Ingo Horn
Ralf Dohmen
Stefan Weyer
Femtosecond laser ablation (fs-LA) coupled to a multicollector inductively coupled plasma mass spectrometry (MC-ICP-MS) instrument has been proven to be a powerful means to analyze isotope ratios of “non-traditional” stable isotope systems with high spatial resolution, precision, and accuracy. The technique has been successfully applied, e.g., to investigate diffusion-generated isotopic zoning of the elements Li, Mg, and Fe in magmatic crystals. Here, we present a novel sampling technique employing a fs-LA system that is equipped with a computer numerical control (CNC) laser stage, using the open-source software LinuxCNC. Combining this laser set up with ICP-MS or MC-ICP-MS allows us to perform depth profile analyses of major and trace elements, respectively, as well as metal stable isotope variations of Fe and Mg in olivine crystals and in experimental diffusion couples.
Samples are ablated in circular patterns with profile diameters of 100–200 µm using a laser spot size of 25–30 µm. Depending on the scan speed and the repetition rate of the laser, each ablated sample layer is between 300 nm and 3.0 µm thick. The integrated signal of one ablated layer represents one data point of the depth profile. We have tested this technique by analyzing 5–50 µm deep depth profiles (consisting of 15–25 individual layers) of homogeneous and chemically zoned olivine crystal cuboids. The minor and trace element analyses of the zoned cuboids, conducted by fs-LA-ICP-MS, were compared with “horizontal” profiles analyzed in polished sections of the cuboids with electron probe microanalysis (EPMA). Furthermore, we analyzed Fe–Mg isotopic depth profiles of the same cuboids with fs-LA-MC-ICP-MS, of which the chemically zoned ones also showed isotopic zoning at identical scales. Isotopic depth profiles were also conducted on an unzoned olivine cuboid that was coated with a 26Mg- and 56Fe-enriched olivine thin film (of ∼ 800 nm) in order to investigate top-to-bottom contamination during depth profiling.
Our results indicate that (i) concentration data acquired by fs-LA depth profiling match well with EPMA data, (ii) precise and accurate Fe and Mg isotopic data can be obtained (i.e., precision and accuracy are ≤ 0.12 ‰ and ≤ 0.15 ‰ for both δ26Mg and δ56Fe, respectively), and (iii) potential top-to-bottom contamination during depth profiling of isotope ratios can be avoided. The technique presented herein is particularly suitable for the investigation of minerals or glasses with chemical and/or isotopic gradients (e.g., diffusion zoning) vertical to planar surfaces. It can also be applied in materials sciences in order to analyze thin films, coatings, or surface contaminations on solids.
- Article
(6956 KB) - Full-text XML
-
Supplement
(4377 KB) - BibTeX
- EndNote
Depth profile analyses using laser-based sampling techniques have repeatedly been performed during the last 2 decades to investigate the elemental compositions of a variety of materials on a micrometer to sub-micrometer scale (Plotnikov et al., 2001; Pisonero and Günther, 2008; Limbeck et al., 2017), in many cases focusing on the characterization of coatings on steel or other high-tech industrial materials. In particular, the coupling of laser ablation (LA) systems with inductively coupled plasma mass spectrometry (ICP-MS) has been shown to be a versatile depth profiling tool to resolve small-scale chemical, as well as isotopic variations (Sarah et al., 2007; Krachler et al., 2019; and references therein). Conventionally, such LA-ICP-MS depth profile analyses have been conducted by ablating a single spot on the sample for a certain duration with a low ablation frequency (1–5 Hz) at low laser fluence (< 2 J cm−2 ), thus slowly drilling into the sample and continuously recording a rather unstable signal with the ICP-MS instrument (Pisonero and Günther, 2008). This approach yields ablation rates of a few tens to hundreds of nanometers per pulse and vertical spatial resolutions on the order of 0.3–9 µm. The vertical spatial resolution is influenced by the laser beam shape (Gaussian vs. flat-top), surface roughness of the sample and the LA crater, ablation behavior of the sampled material, and mixing of sample material from different layers during ablation and transportation (Pisonero et al., 2007).
Apart from applications in the field of materials science, it has been demonstrated that – in the realm of Earth sciences – LA depth profile analyses are also suitable to investigate Hf isotope variations, U–Pb ages, and trace element zoning in zircon (Woodhead et al., 2004; Steely et al., 2014; Marsh and Stockli, 2015; Zirakparvar, 2015; Nakazato et al., 2022). Despite the widespread use of LA multicollector ICP-MS (LA-MC-ICP-MS) systems for spatially resolved measurements of radiogenic and stable isotopic compositions of geomaterials – for an overview of recent advances see, e.g., Degryse and Vanhaecke (2016), Woodhead et al. (2016), and Balaram et al. (2022) – studies of laser-based depth profile analyses of metal stable isotopes have, to our knowledge, not yet been conducted, except for Li isotope diffusion profiles in experimental Li phosphate glasses (Welsch et al., 2017). Femtosecond laser ablation systems coupled to a MC-ICP-MS instrument should be particularly suitable for such depth analyses, as it has been demonstrated that femtosecond laser ablation (fs-LA) is capable of sampling a variety of minerals stoichiometrically (d'Abzac et al., 2013, 2014; Zheng et al., 2017). Furthermore, stable isotope measurements by fs-LA-MC-ICP-MS can be performed with high precision and high accuracy and without the need of sample–standard matrix matching (Horn et al., 2006; Fernández et al., 2007; Steinhoefel et al., 2009; Oeser et al., 2014; Lazarov and Horn, 2015; Zheng et al., 2018; Steinmann et al., 2019; Kaufmann et al., 2021; Xu et al., 2021, 2022a; Lin et al., 2019, 2022), although significant differences in, e.g., Fe isotopic compositions exist between fs-LA-produced particles with different sizes (d'Abzac et al., 2013, 2014; Zheng et al., 2017). Still, in order to obtain highly precise stable isotope ratios, the detection of a sufficiently large number of ions in a certain amount time is required. This can be achieved by maintaining a high signal intensity measured on the detector and/or by increasing the total integration time for an analysis. Furthermore, high-precision isotope ratio analyses by MC-ICP-MS have additionally aimed at acquiring a statistically significant number of individual isotope ratio measurements for a single analysis (typically > 20 integrations; Schoenberg and von Blanckenburg, 2005; Dauphas et al., 2009). These constraints require both a sufficiently high and stable signal to be recorded for several seconds (i.e., at least 4 s given a minimum integration time of ∼ 0.2 s for an individual ratio measurement). However, because of larger signal instabilities of previously used sampling approaches of “single shot” LA-MC-ICP-MS depth profile analysis (Cottle et al., 2009; Krachler et al., 2019), long integration times for single shot analyses is challenging to attain. Here, we present a novel laser-based approach in which sample material is ablated in circular patterns for > 50 s, employing a computerized numerical control (CNC) of the laser ablation stage in the x and y direction, building on the approach briefly presented in Welsch et al. (2017).
High vertical and/or horizontal spatial resolution of chemical and/or isotopic data is frequently required to resolve small-scale variations in these data in minerals. One prime example of such variations is the coupled chemical and isotopic zoning in crystals from igneous rocks (Jeffcoate et al., 2007; Sio et al., 2013; Oeser et al., 2015; Richter et al., 2016; Collinet et al., 2017; Oeser et al., 2018). Likewise, experimental studies investigating chemical diffusion and the diffusion-driven isotope fractionation in minerals rely on high-precision analytical methods with high spatial resolution, such as (MC-)SIMS (secondary ion mass spectrometry) or LA-(MC-)ICP-MS (Dohmen et al., 2010; Richter et al., 2014; Jollands et al., 2016a; Richter et al., 2017; Sio et al., 2018). However, respective diffusion-driven zoning patterns are frequently short with length scales < 50 µm, limiting the applicability of laser-based sampling techniques given a typical laser spot size of 20–30 µm. On the other hand, in situ MC-SIMS analyses of stable isotope ratios can provide a horizontal spatial resolution on the order of ∼ 5–10 µm (Fiege et al., 2014; Kita et al., 2003; Richter et al., 2016; Villeneuve et al., 2019), but these analyses appear to suffer from sample composition and instrument-dependent matrix effects (Bell et al., 2009; Sio et al., 2013; Su et al., 2015). In order to meet the need for an in situ method capable of resolving short (< 50 µm) chemical and isotopic diffusion profiles, this study presents a fs-LA depth profiling technique which allows for high-precision analyses of chemical and isotopic compositions of minerals and glasses, achieving a vertical spatial resolution of 1–2 µm. The sample material targeted in this study is San Carlos olivine crystal cuboids which are chemically and isotopically zoned in Fe and Mg. However, the presented technique can, in theory, also be applied to other matrices (e.g., oxides, glasses, metals). The ability to perform high-precision in situ analyses of stable isotope ratios and trace element contents on a micrometer scale in solids is also highly relevant for diffusion studies in materials science. For example, diffusion and diffusion mechanisms of cations in, e.g., spinel and rutile are frequently investigated (Kolli and Van der Ven, 2021; Xiao et al., 2018; Dohmen et al., 2019), as spinel (e.g., as LiMn2O4) represents an important electrode material for Li-ion batteries (Bhattacharya and Van der Ven, 2010; Huang et al., 2021; Liu et al., 2022), while rutile is used in a large variety of applications due to its potential to be employed as a semiconductor (Hanaor and Sorrell, 2011). Previous studies have demonstrated that diffusion-generated metal isotope fractionation can characterize diffusion mechanisms in solids (Richter et al., 2014; Dohmen et al., 2010; Richter et al., 2017; Van Orman and Krawczynski, 2015). For spinel, it has been shown that, e.g., Fe–Mg interdiffusion changes from a vacancy diffusion mechanism to an interstitial mechanism with decreasing oxygen fugacity at constant temperature (Vogt et al., 2015). The two different diffusion mechanisms should then be associated with different isotope fractionation factors which can be quantified by measuring the diffusion-generated Fe–Mg isotopic variations. High-precision in situ techniques with high horizontal or vertical spatial resolution – as developed in the present study – are thus a prerequisite for such investigations.
2.1 Samples
The samples analyzed in this study belong to a collection of centimeter-sized, gem-quality olivine single crystals from San Carlos, Arizona (USA). The same collection has previously been used in several studies which investigated diffusion processes in olivine (Dohmen et al., 2002, 2007, 2010). The olivine single crystals used in this study were oriented by X-ray Laue diffraction and cut into cuboids ( mm) perpendicular to the [100], [010], or [001] axis (space group: Pbnm) using a diamond saw. Representative images of the San Carlos olivine crystal cuboids are shown in Figs. S1 and S2 in the Supplement. The surfaces perpendicular to [010] were polished. A centimeter-sized “reference” San Carlos olivine single crystal was embedded in epoxy and polished to expose its core.
The powder source employed for the diffusion experiments was prepared from crushed and ground San Carlos olivine crystals and was enriched in Fe (added as pure Fe metal, Johnson Matthey Puratronic), Li (added as pure Li4SiO4), and Si (added as pure SiO2), resulting in a nominal composition of Fo60. Additionally, the powder was enriched in 25Mg (using a 25MgO spike) and in 57Fe (using a 57Fe2O3 spike). Notably, as the crushed and ground San Carlos olivine crystal material is “diluted” by adding a fayalite component (Fe + SiO2; see above), the powder is depleted in several minor and trace elements (e.g., Ni, Mn, V, Cr) relative to the San Carlos olivine crystal (SC-OLc) cuboids, triggering a diffusive flux of these elements from the cuboids into the powder during the diffusion experiments (see below). The powder was homogenized in a mortar, annealed at 1200 ∘C for 24 h in an Al2O3 crucible in a gas-mixing furnace with CO and CO2 flux controlling fO2 at the quartz–magnetite–fayalite buffer (QFM), and again homogenized in a mortar.
In addition to the powder source diffusion couples (see Sect. 2.2), we prepared a thin film coating on a SC-OLc cuboid by pulsed laser deposition using a setup at the Ruhr University Bochum (Dohmen et al., 2002). Here, the synthesized olivine powder was used as the target material for the ablation with an excimer laser (Lambda LPX 305i) in a vacuum chamber, generating a thin film of ∼ 800 nm thickness with a composition of about Fo60 in contact with a homogeneous SC-OLc cuboid. During the pulsed laser deposition the thin film became strongly fractionated regarding its Fe and Mg isotope compositions, with δ56Fethin-film≈3.9 ‰ (relative to IRMM-14) and δ26Mgthin-film≈16.5 ‰ (relative to DSM-3). The δ57Fe and δ25Mg values of the thin film are even higher, with δ57Fethin-film≈140 ‰ and δ25Mgthin-film≈31 ‰ (see also Table S1 in the Supplement), due to the fact that the target material for the ablation, the synthesized olivine powder, had previously been enriched in 25Mg and 57Fe. The method of thin film coating is commonly used for diffusion experiments. However, notably, this diffusion couple was not annealed in an experimental run but was rather used for testing whether the LA depth profiling technique suffers from potential top-to-bottom contamination (see Sect. 4.5).
2.2 Powder source experiments
For the powder source diffusion experiments, three SC-OLc cuboids were buried in the synthesized olivine powder in an Al2O3 crucible and annealed in a gas-mixing furnace at atmospheric pressure. The applied conditions of the different experimental runs are summarized in Table 1. After the diffusion experiments, two of the three SC-OLc cuboids per experimental run were embedded in epoxy and polished to expose their cores for lateral analyses of the chemical diffusion profiles by electron probe microanalysis (EPMA). The third SC-OLc cuboid was used for depth profile analyses by fs-LA-(MC-)ICP-MS.
3.1 Electron probe microanalysis
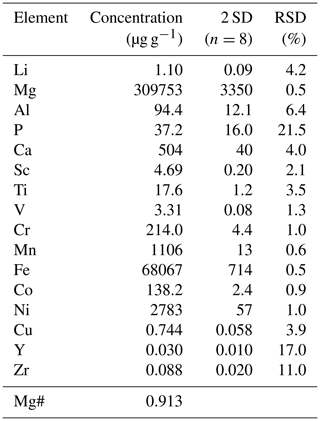
The chemical composition of the crystals embedded in epoxy was analyzed employing a JEOL JXA-iHP200F field emission electron microprobe. The applied microprobe settings are as follows: probe current 15 nA, acceleration voltage 15 kV, and beam diameter 1 µm. The calibration reference materials (CRMs) employed in this study include the MongOL olivine standard (Batanova et al., 2019; for Si and Mg), as well as augite (for Ca), NiO (for Ni), and Fe2O3 (for Fe). Counting times were 10 s on peak and 5 s on background on each side of the peak. The accuracy and reproducibility of the measurements were checked by repeated measurements of MongOL (Batanova et al., 2019) and San Carlos (Jarosewich et al., 1980) olivine standards (Table S2 in the Supplement).
On the large “reference” San Carlos olivine crystal, two line analyses – with 50–60 individual measurements on each line – were conducted in order to (i) investigate the “bulk” chemical composition and (ii) test the chemical homogeneity of the crystal. One line was run in the core domain of the crystal and the second line from the rim of the crystal towards the core.
3.2 Femtosecond laser ablation system
The femtosecond laser ablation (fs-LA) system employed in this study was identical to the one used in, e.g., Oeser et al. (2014), Schuth et al. (2017), and Kaufmann et al. (2021), a Spectra-Physics “Solstice”. It consists of a 100 fs Ti–sapphire seed laser operating at a fundamental wavelength of 775 nm and a Nd : YLF pump laser pumping at a repetition rate of 500 Hz. The pulse width of the amplifier output is ∼ 100 fs. The frequency of the output beam (infrared) is quadrupled by three barium beta borate crystals, converting it to a UV beam with a final wavelength of 194 nm. The pulse energy of this final UV beam is ∼ 0.01 mJ. Given a laser spot size of 30 µm in diameter on the sample, this results in a fluence of ∼ 1.4 J cm−2.
3.3 Computer numerical control (CNC) of the LA stage
The laser beam was focused through a modified New Wave UP 193 stage/visualization system onto the sample which was mounted in a self-built ablation cell with a volume of ∼ 30 cm3 and a washout time of ∼ 20 s. The laser spot size used in this study was 25–30 µm in diameter. The movement of the x and y axes of the stage, and thus of the sample under the laser beam, was controlled using the open-source software LinuxCNC operating in real time. This software is typically used to control production equipment, such as milling machines, 3D printers, and lathes, applying machine language (so-called G-codes). The flexibility of the G-codes allowed us to ablate sample material in circular patterns with diameters of 100–200 µm (“profile diameter”). By a stepwise decrease in the ring diameter by 1.75 µm for 100 µm diameter profiles or by 3.5 µm for 200 µm diameter profiles and, thus, overlapping the ablation trail several times, it is possible to homogenously remove sample material layer by layer, in our case drilling into the sample parallel to the diffusion direction (Fig. 1). Depending on the scan speed and the repetition rate of the laser (typically between 20 and 60 Hz), each ablated sample layer was between 300 nm and 3.0 µm thick. After ablation of one layer the laser shutter was closed for 5 s to allow for a washout of the ablation cell. An adjustment of the z position after ablation of one layer was not necessary because the focal point of the laser beam was set to be ∼ 130 µm below the initial sample surface in order to avoid the ionization of helium above the sample, which would significantly alter the pulse duration (cf. Lazarov and Horn, 2015; Steinmann et al., 2019). Compared to this offset (∼ 130 µm), the ablation rate for each layer (i.e., the layer thickness) is very small, typically 1–2 µm. Thus, the change in ablation efficiency during progressive deepening of the laser pit is negligible (see Sect. 4.2 for further details). The integrated signal of one ablated layer represented one data point of the depth profile. The total depth of the profile could be controlled by the number of ablated layers (typically 15–25 layers) and also depended on the thickness of each layer, which in turn was controlled by the applied laser settings (repetition rate, scan speed, and spot size).

Figure 1Reflected light image (a), 3D view (b), and cross section (c) of a ∼ 26 µm deep laser pit in a San Carlos olivine cuboid, generated by the fs-LA depth profiling technique described herein and consisting of 20 individual layers. As long as the laser partly ablates material from these tilted walls while running in circular patterns towards the center of the pit, the analyzed sample material is a mixture of material from various depths (and was thus discarded from data evaluation). Images were acquired with a KEYENCE VK-X 3D laser microscope (see below). The schematic in (d) illustrates the stepwise movement of the laser beam (after having run one particular circle) towards the center of the pattern. The colored digits correspond to the number of beam overlaps for one particular position (color-coded). As soon as the beam movement has covered the size of the laser spot (e.g., 25 µm), the number (n) of beam overlaps remains constant, in this case n = 12. When this point is reached, the ablation of sample material in the crater is homogeneous, resulting in the observed flat bottom of the crater.
The advantage of ablating sample material in circular patterns (achieved using G-codes in LinuxCNC), as compared to, e.g., rectangular patterns in raster mode (Nakazato et al., 2022), is that analyzing mixtures of sample material from various depths can simply be avoided by discarding the outermost circles, where the laser spot touches the tilted pit walls, from data acquisition (see Sect. 3.6 for details). During the ablation of sample material in raster mode, the laser beam would hit the tilted pit walls of the rectangular pattern repeatedly, leading to a “contamination” of the currently analyzed layer, as shown by Nakazato et al. (2022). In their study, Nakazato et al. (2022) avoided this by producing a “moat” around the targeted sampling area so that material in the sloped edge of the ablation pit was removed prior to ablation of sample material for data acquisition. This approach requires a highly precise spatial matching of moat and sampling area, and the drilling of a moat is needed before every sampling of a layer. In contrast, in our approach ablation of sample material from the tilted walls of the laser pit (and thus from various depths) only occurs at the beginning of each layer analysis. The signal acquired in this short time interval can thus be easily excluded from data evaluation to obtain a “contamination-free” layer analysis (see Sect. 3.6).
3.4 The fs-LA-sector field-ICP-MS analysis
Major, minor, and trace element concentrations were analyzed employing a fast-scanning sector field ICP-MS instrument (SF-ICP-MS; Thermo Scientific Element XR) that was connected to the fs-LA system at the Institute of Mineralogy, Leibniz University Hannover. A mixture of helium and argon was used as the carrier gas to transport the sample aerosol from the ablation cell to the ICP-MS instrument. All elements were measured in low-mass-resolution mode.
For the chemical characterization of the reference SC-OLc, as well as for all analyses of the reference glasses (see below), sample ablation was performed in raster mode where each raster had a size of ∼ 90×80 µm, applying a laser spot size of 30 µm in diameter, a laser scan speed of 25 µm s−1, and laser repetition rate of 31–36 Hz. Each analysis started with a 35 s background acquisition, followed by an ablation interval of 50–60 s.
For the acquisition of a chemical depth profile, the time for one analysis was increased to ∼ 30 min, covering 30 s of background signal at the beginning, the ablation signal of 20–25 sample layers, and 30 s of background signal at the end.
The external calibration of the acquired data was performed using the USGS reference glasses BCR-2G and BIR-1G (see also Tables S3a and b), and Si (as determined by EPMA) was used for internal standardization. Data reduction was realized in iolite (Paton et al., 2011). The synthetic andesite reference glasses ARM-1 and ARM-3 (Wu et al., 2019) were repeatedly analyzed as unknowns in order to test the accuracy and reproducibility of the obtained major, minor, and trace element data (Table S3a).
3.5 The fs-LA-multicollector-ICP-MS analysis
When Fe or Mg isotope ratios were analyzed, the ablated sample particles were transported in a He gas stream from the ablation cell to a Neptune Plus MC-ICP-MS instrument (Thermo Scientific) employed in this study. Prior to entering the torch, the sample aerosol was mixed with an Ar flow carrying aspirated Milli-Q H2O (for Mg isotope analyses) or Ni standard solution NIST SRM 986 (used for mass bias correction during Fe isotope analyses), as described in Oeser et al. (2014). The detector setups and detailed mass bias and mass interference correction strategies used for Fe and Mg isotope analyses are specified in Oeser et al. (2014).
For the isotopic characterization of the reference SC-OLc, sample ablation was performed in raster mode where each raster had a size of ∼ 110×90 µm, applying a laser spot size of 30 µm in diameter, a laser scan speed of 20 µm s−1, and laser repetition rate of ∼ 16 Hz for Mg isotopes (analyzed in medium mass resolution) or 71 Hz for Fe isotopes (analyzed in high mass resolution). These repetition rates were chosen in order to match the measured signal intensities of samples and CRMs. The ablation of silicate reference glasses, serving as bracketing CRMs (see below), was also performed in raster mode with a raster size of ∼ 150×150 µm, using a laser spot size of 30 µm in diameter and a laser scan speed of 20 µm s−1. The laser repetition rate applied on the reference glasses was adjusted in order to match the acquired signals during sample analysis within ± 15 %. For all measurements in raster mode, each analysis started with a ∼ 32 s background acquisition (30 cycles with a cycle integration time of 1.05 s), followed by an ablation interval of 120–130 s. An entire depth profile analysis on a (zoned) SC-OLc cuboid consisted of one block of up to 1900 cycles with a cycle integration time of 1.05 s, which equals ∼ 33 min of total analysis time. This covers ∼ 32 s of background analysis at the beginning and the analysis of 15–25 layers, including 5 s laser-off time for sample washout between the layers.
3.6 Data evaluation for depth profiling
The processing of the acquired in situ data was conducted using a modified version of the LamTool Excel macro (for isotope ratio analysis), originally developed by Košler et al. (2008), or by using iolite (for concentration depth profiles, see above; Paton et al., 2011). Depending on the scan speed of the laser (typically between 50 and 170 µm s−1) and the profile diameter, the signal time during the ablation of one layer of sample material ranged from 60 to 120 s. However, 30 % of this signal time at the beginning of each ablation had to be excluded from the data evaluation because in this time interval some sample material is ablated from the wall of the laser pit and, thus, represents a mixture of sample material from various depths (Fig. 1). Hence, the average isotope ratio (or average chemical composition) of one layer was calculated from ∼ 30–85 individual isotope ratio measurements (or concentration measurements) (Fig. 2). The average isotope ratio was then used to calculate a δ value of one sample layer relative to a bracketing CRM, using the following equation for Mg isotopes:
where x is either mass 25 or 26. The CRM employed during in situ Mg isotope analyses was the MPI-DING silicate reference glass GOR132-G (Jochum et al., 2006; Oeser et al., 2014). For Fe isotope data, we applied a similar approach, as follows:
where y is either mass 56 or 57. We employed the USGS silicate reference glasses BHVO-2G or BCR-2G as bracketing CRMs. Those δ values (relative to a CRM) were subsequently converted to δ values relative to IRMM-14 (for Fe isotopes) or relative to DSM-3 (for Mg isotopes), as described in Oeser et al. (2014) using the following values: BHVO-2G – δ56Fe = 0.099 ± 0.042 ‰, δ57Fe = 0.152 ± 0.049 ‰; BCR-2G – δ56Fe = 0.085 ± 0.037 ‰, δ57Fe = 0.127 ± 0.059 ‰; GOR132-G – δ25Mg = −0.089 ± 0.030 ‰, δ26Mg = −0.174 ± 0.039 ‰ (see also Tables S4 and S5). The internal precision (2σ) of the δ value of one sample layer was calculated by propagating the errors (SE) of the bracketing standards (n≈120 cycles) and of the analyzed sample layer (n = 30–80 cycles), as follows:
where R is either 56Fe 54Fe, 57Fe 54Fe, 25Mg 24Mg, or 26Mg 24Mg.
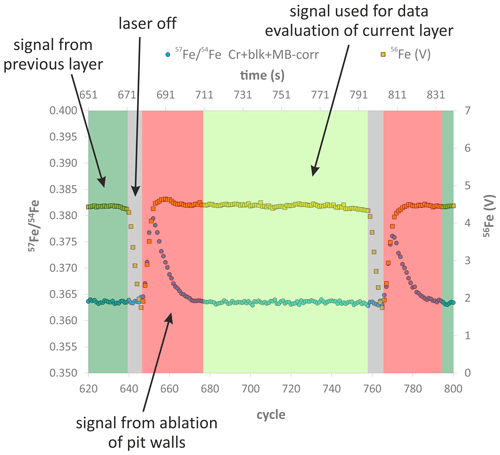
Figure 2Evolution of the 56Fe signal (in volts) and the interference-, blank-, and mass-bias-corrected 57Fe 54Fe with time (one cycle = 1.05 s), during a LA depth profile analysis of a chemically and isotopically zoned SC-OL crystal cuboid. The high 57Fe 54Fe in the red time interval results from ablation of sample material from the tilted pit walls (see Fig. 1), so material from the upper parts of the profile (which have much higher 57Fe 54Fe) is mixed with material from the currently sampled layer. Furthermore, during this red time interval some material from the previous layer is still washed out of the tube connecting the ablation cell to the MC-ICP-MS instrument, as indicated by the decrease in the 56Fe signal during the laser-off time interval that, however, does not reach 0 V before the next ablation interval starts. Consequently, the signal acquired in the red time interval was excluded from data evaluation.
3.7 3D laser microscopy
The depth of the laser-generated depth profile pits was determined by employing a KEYENCE VK-X 3D laser microscope at the Institute of Soil Science, Leibniz University Hannover, working with a laser intensity of 10 %, a brightness of ∼ 1450 (on a scale between 0 and 16 380), and a step size in the z direction of 0.05–0.10 µm. Using a lens with 20× magnification resulted in an image size of ∼ 720 × 540 µm (1024 × 768 pixels) in the x–y plane. Further details of the method can be found in Müehl et al. (2011) and Saulick et al. (2018).
4.1 Chemical and isotopic composition of reference San Carlos olivine crystal
The large reference San Carlos olivine crystal analyzed in this study represents a Mg-rich olivine (Mg# = 0.91) with low Ti and Ca contents (∼ 18 and ∼ 500 µg g−1, respectively), clearly indicating a mantle origin (Foley et al., 2013). The results of two line analyses conducted by EPMA (Fig. 3), as well as the limited variability in minor and trace element concentrations, obtained by fs-LA-ICP-MS analyses in raster mode (Table 2), demonstrate that the crystal is chemically homogeneous on a millimeter scale. It should be noted, however, that San Carlos olivine can show significant minor and trace element variability, both between individual grains and within a single grain (Bussweiler et al., 2019; Lambart et al., 2022). The variability in δ56Fe and δ26Mg values, gathered by fs-LA-MC-ICP-MS in raster mode, is rather limited (Fig. 4). The δ56Fe values range from −0.03 ‰ to −0.25 ‰, with an overall mean of −0.13 ± 0.15 ‰ (2 SD, n=16). Iron isotope compositions measured in the core domain show a tendency towards slightly heavier values (δ56Fecore= −0.07 ± 0.09 ‰ 2 SD, n=8) than those measured near the rims (δ56Fe0.18 ± 0.10 ‰ 2 SD, n=8). However, given the long-term analytical uncertainty of fs-LA-MC-ICP-MS analyses (0.12 ‰ in δ56Fe; see also Table S4; Steinhoefel et al., 2009; Oeser et al., 2014), values of both crystal regions agree within analytical uncertainty. The δ26Mg values range from −0.18 ‰ to −0.52 ‰, with an overall mean of −0.32 ± 0.20 ‰ (2 SD, n=18). The relatively large 2 SD uncertainty mainly results from the variability in δ26Mg values measured near the rim of the crystal. The core domain of the crystal appears to be more homogenous, with an average δ26Mgcore = −0.29 ± 0.14 ‰ (2 SD, n=7). However, a systematic difference in the Mg isotopic compositions of the core and rim of the crystal has not been observed (Fig. 4).
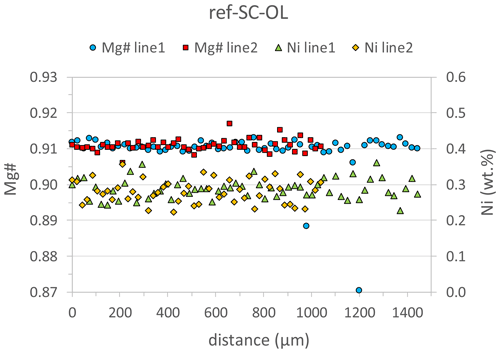
Figure 3Results of two line analyses by EPMA, indicating that the large reference San Carlos olivine crystal is chemically homogeneous in terms of Mg# and Ni contents on a millimeter scale. Line1 was run in the core domain of the crystal and line2 from the rim towards the core. The two outliers in Mg# for line1 represent analyses with low totals (< 94 %, Table S2), indicating that the electron beam hit a crack (or another imperfection) in the crystal.
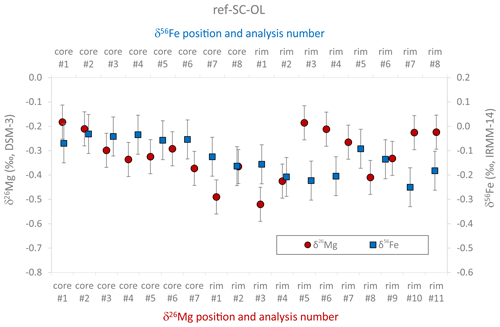
Figure 4Summary of Mg and Fe isotopic data acquired in situ in raster mode on the large reference San Carlos olivine crystal, indicating that the core domain of the crystal is fairly homogeneous, while some variations in isotopic compositions are observed near the rims of the crystal (> 2 mm away from the core domain). Error bars are the internal 2σ precision as calculated using Eq. (3).
4.2 Horizontal and vertical spatial resolution
As mentioned above, the diameter of the ablated circular patterns of a depth profile is 100–200 µm, which, in turn, represents the horizontal spatial resolution of the LA depth profiling technique. The depth of the analyzed profiles varies between 5 and 50 µm depending on the applied repetition rate of the laser, the scan speed of the laser (which depends on the profile diameter if the analysis time for one layer is supposed to be ∼ 70 s), the laser spot size, and the number of ablated layers for an individual depth profile. For example, using a laser repetition rate of 56 Hz, a scan speed of 93 µm s−1, and profile diameter of 100 µm and ablating 11 layers resulted in a profile depth of 30 µm (Fig. 5). Thus, the vertical spatial resolution (i.e., the thickness of one ablated layer) for this particular profile is 2.7 µm. A better vertical spatial resolution (< 1 µm per layer) can be obtained by using a larger profile diameter (i.e., 200 µm), a lower laser repetition rate, and a higher scan speed (Fig. 5).
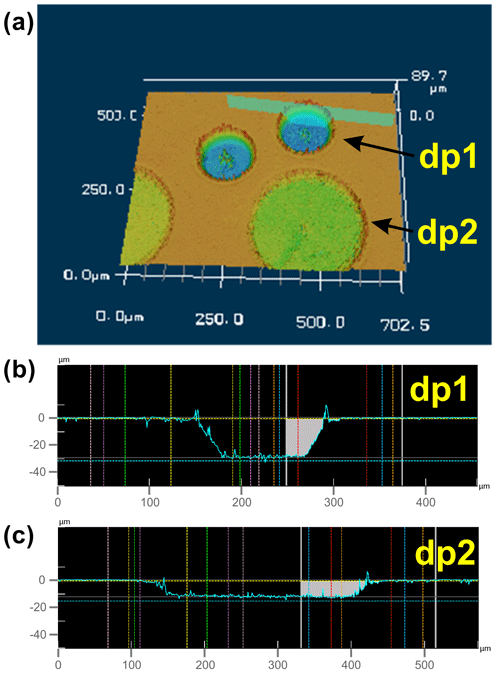
Figure 5The 3D view (a) and cross sections (b, c) of laser pits in a San Carlos olivine cuboid, generated by the fs-LA depth profiling technique ablating 11 individual layers with a diameter of ∼ 100 µm for depth profile 1 (dp1), resulting in a total depth of 30 µm (b), and 10 layers with a diameter of ∼ 200 µm for depth profile 2 (dp2), resulting in a total depth of ∼ 7.5 µm (c). Further LA parameters are as follows: for dp1, 56 Hz repetition rate, 93 µm s−1 scan speed, and ∼ 25 µm laser spot size; for dp2, 50 Hz repetition rate, 140 µm s−1 scan speed, and ∼ 30 µm laser spot size.
The vertical spatial resolution of our technique is determined by dividing the total depth of the profile by the number of ablated layers, assuming that the ablation rate during the acquisition of a depth profile remains constant despite an increasing depth of the profile pit. This was tested by the following experiments. (1) We “drilled” three individual depth profiles into pure Sn metal, always using a laser repetition rate of 10 Hz. For profile-A 10 layers, for profile-B 25 layers, and for profile-C 50 layers were ablated. The total depths of these profiles are shown in Fig. 6a. The linear relationship between profile depth and number of ablated layers indicates that all ablated layers have the same individual thickness (∼ 0.5 µm per layer), i.e., the ablation rate remains constant despite an increasing profile depth. A second test was conducted to check if the ablation rate increases linearly with an increasing laser repetition rate during progressive deepening of the profile pit. For this, three individual profiles were analyzed in epoxy resin, keeping the number of ablated layers constant. A laser repetition rate of 20 Hz for profile-D, 50 Hz for profile-E, and 100 Hz for profile-F was used. The linear relationship between profile depth and applied laser repetition rate (Fig. 6b) demonstrates that up to a profile depth of ∼ 180 µm, the laser repetition rate (within the investigated range of 20–100 Hz) remains linearly correlated with the laser ablation rate during progressive deepening of the profile pit.
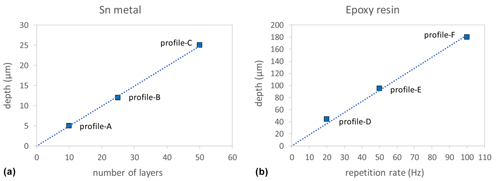
Figure 6Measured depths of LA depth profiles analyzed in Sn metal (a), where the laser repetition rate was kept constant (at 10 Hz), but the number of ablated layers was varied, and in epoxy resin (b), where the number of ablated layers was kept constant (10 layers), but the laser repetition rate varied (see main text for details). Dotted lines are linear regression lines through the origin.
4.3 Chemical LA depth profile and “horizontal” EPMA data
In order to check the accuracy of the concentration data acquired by fs-LA-ICP-MS depth profiling, we have compared the depth profiles of several chemically zoned (regarding Mg#) SC-OLc cuboids with “horizontal” profiles, analyzed conventionally with EPMA. For this comparison, we used chemically zoned SC-OLc cuboids from powder source diffusion experiments of which those dedicated for EPMA were embedded in epoxy and polished to expose their cores. Both profile types (LA depth and horizontal EPMA) were measured along all three crystallographic axes to study various profile length scales. The results of this comparison are shown in Fig. 7. Both techniques exhibit a clear Fe–Mg chemical zoning in the analyzed SC-OLc cuboids with diffusion length scales between 4 and ∼ 30 µm, depending on the experimental conditions and the crystallographic orientation of the measured profile. Importantly, the concentration data (Mg#) acquired by fs-LA depth profiling match well with EPMA data for crystals from the same experiment along the same axes, in terms of both absolute Mg# values and zoning width. Furthermore, the vertical spatial resolution of the fs-LA depth profile technique (with a laser spot size of ∼ 30 µm) is comparable to the horizontal spatial resolution of the EPMA (with a beam diameter of 1 µm).
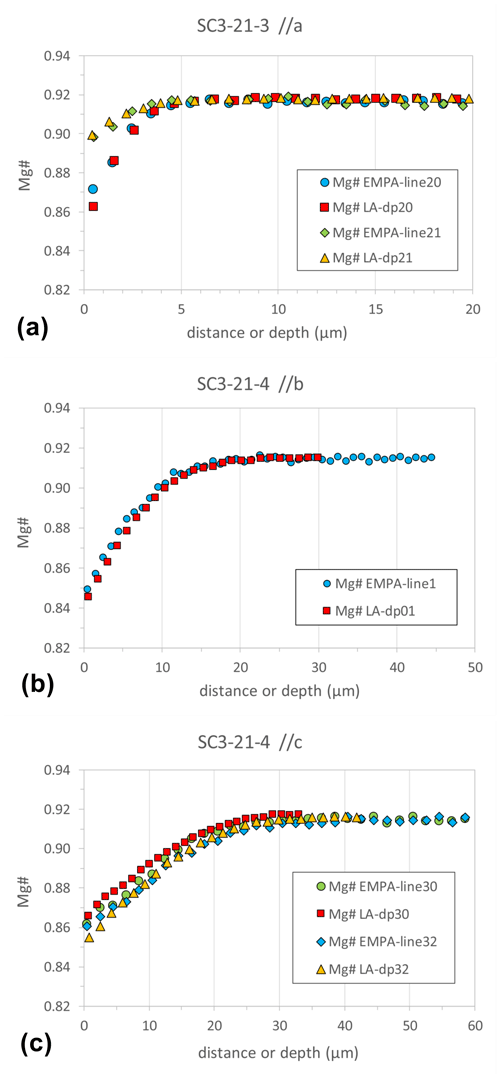
Figure 7Chemical (Mg#) diffusion profiles along the three crystallographic axes (a, b, c) acquired by LA depth profiling in comparison with “horizontal” profile data from EPMA in SC-OL crystal cuboids.
Additionally, as mentioned above, the compositional contrast between powder source and SC-OLc cuboids in terms of minor and trace elements triggers a diffusive flux of these elements out of (Ni, Mn, Cr, V) or into (Li) the SC-OLc cuboids. As shown in Fig. 8, the LA depth profiling technique coupled with SF-ICP-MS is capable of resolving the generated diffusion profiles of such elements in the crystal cuboids. This offers the opportunity to investigate the diffusivities of minor and trace elements in olivine (and other silicate minerals), for which large variations in experimentally determined diffusion coefficients have been discussed repeatedly (Ito and Ganguly, 2006; Cherniak and Dimanov, 2010; Spandler and O'Neill, 2010; Jollands et al., 2016b; Zhukova et al., 2017; Jollands et al., 2018), even if the diffusion length scale of the element of interest is on the order of only 5–10 µm (see, e.g., Ni and Cr in Fig. 8b). The exponential decrease in V, Ni, Cr, and Mn concentrations towards the rim of the crystal cuboid (depth = 0 µm) is consistent with the diffusion of these elements out of the crystal into the surrounding powder. Likewise, the increase in the Li concentration towards the rim of the crystal is consistent with the diffusive flux of Li from the Li-enriched powder into the crystal.
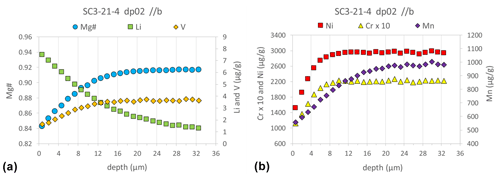
Figure 8Major (Mg#), minor (Ni, Mn, Cr), and trace element (Li and V) diffusion profiles analyzed by fs-LA depth profiling combined with SF-ICP-MS on a SC-OLc cuboid that was annealed in a powder source diffusion experiment for 139 h at 1199 ∘C. The 2 SE uncertainty for each data point is smaller than the symbol size (see also Table S10).
4.4 Assessment of isotope fractionation with depth
A potential drawback of laser ablation analyses which produce deep laser ablation pits is the (artificial) fractionation of elements and isotopes with increasing pit depth (Horn et al., 2000; Jackson and Günther, 2003; Kosler et al., 2005; Fryer et al., 1995). Laser-induced elemental fractionation has been observed to become significant if the depth : diameter ratio of the ablation crater is > 6 (Mank and Mason, 1999). A study by Woodhead et al. (2004) on Hf isotopic compositions in zircon indicated that precise and accurate Hf isotope analyses by nanosecond LA (ns-LA) depth profiling are feasible for ablation pits with aspect ratios (depth : width) of up to 2:1. To our knowledge, such clear quantification does not exist for potential depth-related Mg and Fe isotope fractionations; however, Oeser et al. (2018) have demonstrated that the deepening of a laser ablation trench (with a final depth of ∼ 40 µm) generated by line scans does not produce any significant Fe isotope fractionation, i.e., < 0.1 ‰ difference in 56Fe 54Fe measured at the beginning of the analysis as compared to the end of the analysis.
We have analyzed one Fe isotope and one Mg isotope depth profile, consisting of 20 ablated layers each, into a homogeneous SC-OLc cuboid in order to investigate a potential depth-related isotope fractionation during the sampling process. Results of these analyses are shown in Fig. 9. The δ56Fe values of individual layers scatter around a value of −0.11 ‰ (relative to IRMM-14) with 2 SD of 0.12 ‰. This variability is comparable to the long-term analytical uncertainty of in situ Fe isotope analyses of silicates in our fs-LA-MC-ICP-MS lab. Importantly, the mean δ56Fe value of the uppermost seven layers (−0.11 ± 0.13 ‰) is almost identical to the mean δ56Fe value of the lowermost seven layers (−0.10 ± 0.13 ‰), showing that depth-related isotope fractionation during the depth profile analyses is absent. The δ26Mg values of individual layers show slightly higher scatter around a value of −0.42 (relative to DSM-3) with 2 SD of 0.20 ‰. However, similar to Fe, the average Mg isotopic composition of the uppermost seven layers (−0.42 ± 0.17 ‰ ) is indistinguishable from that of the lowermost seven layers (−0.35 ± 0.16 ‰). The higher scatter of the δ26Mg values may result from slight drifts in the instrumental mass bias of the MC-ICP-MS during the > 25 min long analysis of the depth profile. During in situ Fe isotope analyses, such mass bias drifts are mostly corrected by using the measured Ni isotope ratios of the simultaneously aspirated Ni reference solution as an external mass bias monitor (Oeser et al., 2014). However, for in situ Mg isotope analyses, the instrumental mass bias can only be corrected by conventional sample–standard bracketing, which does not account for short-term mass bias fluctuations (Chen et al., 2017; Zhu et al., 2018; Xu et al., 2022b), i.e., during the determination of the depth profile.
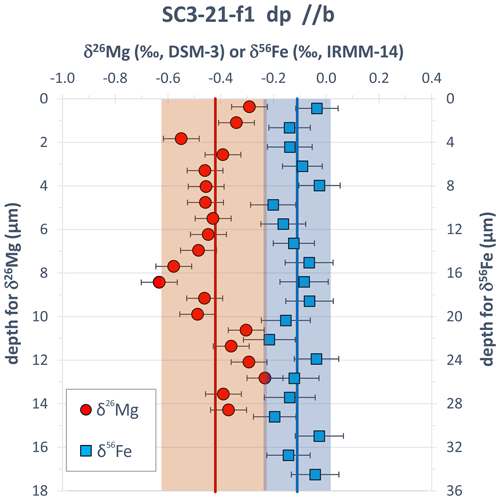
Figure 9Fe and Mg isotope depth profile data for a SC-OLc cuboid which was not annealed in a diffusion experiment, showing no obvious depth-related (artificial) fractionation trend of Mg and Fe isotopes during fs-LA depth profile analyses. Error bars are the internal 2σ precision as calculated using Eq. (3). The red and the blue vertical lines represent the mean δ26Mg and δ56Fe values, respectively, of the two profiles, with the shaded areas showing the 2 SD variation. The smaller depth of the δ26Mg profile mainly results from the lower laser repetition rate applied in this depth profiling test (see also Sect. 3.5).
Additional evidence for the absence of any resolvable isotope fractionation during progressive deepening of the profile pit comes from the investigation of experimentally generated Fe–Mg isotopic (and chemical) diffusion profiles in SC-OLc cuboids. Figure 10 shows an example of Fe–Mg chemical and isotopic diffusion profiles acquired by fs-LA depth profiling in a SC-OLc cuboid which was annealed in a powder source diffusion experiment (as described above) for 93 h at 1250 ∘C. The chemical zoning of Mg# is ∼ 34 µm wide and strongly coupled with Fe–Mg isotopic zoning. The inversely correlated fractionation of the Fe and Mg isotopes is a consequence of the Fe–Mg interdiffusion process (Fe diffuses into and Mg out of the olivine), and it has previously been observed repeatedly in olivine crystals from natural volcanic rocks (Teng et al., 2011; Sio et al., 2013; Oeser et al., 2015; Collinet et al., 2017; Oeser et al., 2018). The unzoned interior of the crystal (at depth > 34 µm) shows broadly constant Fe and Mg isotopic compositions which are within the δ56Fe and δ26Mg range observed for the large reference SC-OLc. Any depth-related (artificial) isotope fractionation would lead to a deviation of the measured δ56Fe and δ26Mg values from this expected range, which was not observed.

Figure 10Fe–Mg chemical and isotopic diffusion profiles acquired by fs-LA depth profiling in SC-OL crystal cuboid. The blue and red areas show the range in δ56Fe and δ26Mg, respectively, expected for the unzoned interior of the crystal (depth > 34 µm) from analyses of the large reference SC-OLc. Error bars are the internal 2σ precision as calculated using Eq. (3). The lines are modeled Fe–Mg chemical and isotopic zoning patterns, assuming Fe–Mg interdiffusion between the SC-OL crystal cuboid and the powder source with a fixed rim composition (at depth = 0 µm) of Mg# = 0.767. The diffusion-driven isotope fractionation was modeled by applying the empirical formula of Richter et al. (1999): , with βMg= 0.18 and βFe= 0.17 and where e and f are two isotopes of a certain element (e.g., 54Fe and 56Fe). Further details of such a diffusion model, simulating diffusion-driven isotope fractionation based on Fe–Mg interdiffusion in olivine, are given in Oeser et al. (2015).
4.5 Depth profiles in thin film–olivine couple
In order to test whether the fs-LA depth profiling technique suffers from potential top-to-bottom contamination during an individual depth profile analysis, we have measured Fe and Mg isotope depth profiles in a thin film–San Carlos olivine couple. The topmost layer of such a profile predominantly consists of thin film material and shows very high δ56Fe, δ57Fe, δ25Mg, and δ26Mg values (Fig. 11). The latter was produced during the production of the thin film by pulsed laser deposition, most likely by fractionation of the gas atoms in the plasma in the vacuum chamber after ablation and subsequential condensation on the polished olivine crystal. Furthermore, as the target material for the ablation was previously spiked with 25Mg and 57Fe, the enrichment of these two isotopes is particularly strong in the thin film. Any contamination from this isotopically heavy layer into the depth profile pit measured in the SC-OL crystals would induce a shift in the Fe and Mg isotope compositions towards heavy values. Such a shift was barely observed, and δ56Fe, δ57Fe, δ25Mg, and δ26Mg values analyzed during depth profiling into the SC-OLc cuboid – after having drilled through the thin film – are close to the range expected for the unzoned interior of the crystal (Fig. 11). Some of the analyzed Fe isotopic compositions show a tendency towards slightly heavier (∼ 0.1 ‰) δ56Fe values. This shift is, however, smaller than the long-term analytical uncertainty for in situ δ56Fe values obtained in our fs-LA-MC-ICP-MS lab (Steinhoefel et al., 2009; Oeser et al., 2014; Collinet et al., 2017). Regarding the δ57Fe profile, the shift towards heavier values is slightly more evident, especially for the first layer analyzed in the crystal, likely resulting from the fact that the enrichment of 57Fe in the thin film is extremely high (δ57Fethin-film≈140 ‰), thus pointing to a small contamination for the analyses of the topmost layers in the crystal. Still, by using the ratio of the δ57Fe shift in the first two layers from the average δ57Fe of the reference SC-OLc (ref-SC-OLc; Δ57Fe ≈ 0.5 ‰) and the δ57Fe of the thin film, this contamination can be estimated to be < 0.5 %, which can be regarded as negligible. Concerning Mg, the isotopic difference between the thin film and SC-OLc is also very large (> 15 ‰), and the first two to three layers analyzed in the crystal show slightly heavier δ26Mg and δ25Mg values than the following eight layers, potentially hinting at a small contribution from the very heavy thin film above. Just as for Fe, this potential contamination can be estimated to be < 0.5 % if using the ratio of the Mg isotopic shift in the first three layers from the average δ25Mg of the ref-SC-OLc (Δ25Mg ≈ 0.1 ‰) and the δ25Mg of the thin film (≈ 31 ‰).
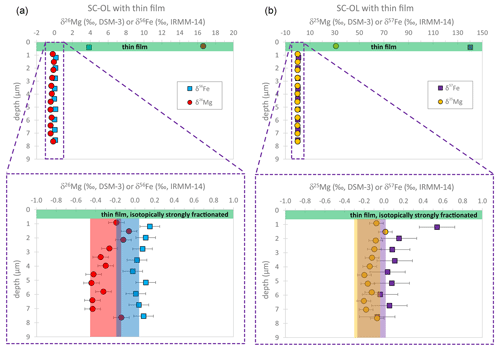
Figure 11The fs-LA depth profile data of δ56Fe and δ26Mg (a), as well as δ57Fe and δ25Mg (b), for the thin film–SC-OL couple. After drilling through the isotopically fractionated thin film, the measured Fe–Mg isotopic compositions are close to the range expected for the interior of the unzoned crystal (blue, red, purple, and yellow areas).
With the here-presented technique of fs-LA depth profiling combined with SF- and MC-ICP-MS, high-precision chemical and isotopic analyses can be performed with high vertical spatial resolution. This technique is particularly advantageous for the analyses of thin micrometer-scale chemically or isotopically distinct zones parallel to planar surfaces of crystals, glasses, or other materials and may be useful to analyze, e.g., crystal coatings or short chemical and isotopic diffusion profiles in crystals (or glasses). Compared to conventional in situ analyses by fs-LA-(MC-)ICP-MS using single-spot or line-scan modes, the significantly higher data point density that can be achieved along the chemical/isotopic gradient results in a ∼ 10 times higher spatial resolution. Additionally and more importantly, each data point can be measured with high precision due to the relatively long counting time (> 30 s) for each ablated layer and the stable signal recorded with the MC-ICP-MS instrument (Fig. 2). Hence, the method is suitable for stable isotope analyses of metals, and internal precisions (2σ) between 0.06 ‰ and 0.12 ‰ can be achieved for, e.g., δ26Mg and δ56Fe.
Femtosecond LA depth profile analyses of chemical compositions in olivine crystals can be performed with a vertical spatial resolution that is similar to the horizontal spatial resolution of electron probe microanalyses, i.e., on the order of 1–2 µm (Fig. 7). The crucial advantage of the fs-LA depth profiling technique, when coupled with an ICP-MS instrument, is the relatively large amount of analyte material available per analyzed sample layer combined with the much better sensitivity of the ICP-MS instrument, enabling the analysis of trace elements, such as Li, at high precision and low limits of detection (Tables S3b and S10). This allows the investigation of diffusivities of various trace elements in olivine (and likely also other minerals) if the experimental setup is suitable to generate chemical gradients of such elements in the crystal (Fig. 8).
The high vertical spatial resolution combined with the high precision for both chemical and isotopic composition is not only relevant for studies in the realm of Earth Sciences (Kelly et al., 2014; Marsh and Stockli, 2015; Nakazato et al., 2022), but it can also be applied in materials science studies where chemical and/or isotopic heterogeneities in solids are of high interest, as the physical properties of some high-tech materials or coatings/thin films strongly depend on the contents of some minor and trace elements (Dobson et al., 2000; Bleiner et al., 2003; Balcaen et al., 2005; Lee and Lim, 2015). Our depth profile analyses in the thin film–olivine couple indicate that top-to-bottom contamination during depth profiling (as presented herein) are minor, opening the opportunity to reliably perform quantitative characterizations of micrometer-thick coatings on steel or silicon wafers (Lee and Lim, 2015). Furthermore, resolving the variation in stable isotopic compositions on a micrometer scale is extremely useful to investigate diffusion mechanisms in solids, as the latter strongly affects the correlation coefficient (f) of diffusion and, thus, also the magnitude of diffusion-driven isotope fractionation (Van Orman and Krawczynski, 2015).
A prerequisite for the applicability of the presented method, however, is a sufficiently large lateral expansion (> 100 µm) of the chemically and isotopically distinct zones that are supposed to be analyzed. Furthermore, the sample needs to have a well-defined and planar crystal (or glass or metal) interface that can be mounted in the ablation cell perpendicularly to the laser beam in order to enable drilling with the laser into the sample parallel to the direction of diffusion. As such, the method may be particularly suitable for the experimental investigation of chemical diffusion, as shown in the example above, with diffusion zoning of 5–40 µm. Given these pre-requisites, it may be challenging to apply the technique on natural crystals (e.g., in volcanic rocks) that may have experienced diffusive processes. In order to analyze diffusion profiles in naturally zoned crystals by fs-LA depth profiling, the crystals must be separated from the matrix and have a flat crystal face that was in contact with a melt or an adjacent crystal and that can be mounted into the laser ablation cell perpendicularly to the laser beam. Finally, the precision and accuracy of fs-LA depth profile analyses have not been investigated for diffusion profiles with length scales > 50 µm, and analytical uncertainties may increase significantly for profile depths > 60 µm due to incomplete mobilization of sample material from the deep laser pit which would result in lower and more unstable signals recorded by the MC-ICP-MS instrument or due to elemental and/or isotopic fractionation with a higher aspect ratio of the laser pit (Woodhead et al., 2004). However, chemical and isotopic diffusion profiles with length scales > 50 µm can be analyzed satisfactorily by LA-(MC-)ICP-MS using horizontal line scans parallel to the diffusion direction (Jollands et al., 2016a; Oeser et al., 2018; Jollands et al., 2018). Thus, the LA depth profiling technique presented in this study is able to probe a depth range (5–50 µm) that is larger than the range typically accessed by SIMS depth profiling (Breeding et al., 2004; Genareau et al., 2007; Kelly et al., 2014) but, on the other hand, can provide a higher (vertical) spatial resolution than horizontal laser line scans. Most importantly, the combination of fs-LA depth profiling and MC-ICP-MS is capable of investigating variations in stable isotopic compositions on a micrometer scale and at a precision suitable to resolve diffusion-driven isotope fractionation in minerals and glasses or other small-scale isotopic anomalies in solids.
The data sets underlying this research are available in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/ejm-35-813-2023-supplement.
MO performed the in situ analyses; compiled, analyzed, and visualized the data; and wrote the initial manuscript. RD and SW designed the concept of the research, ensured funding, and reviewed and modified the manuscript. RD conducted diffusion experiments and provided samples and materials for the latter. IH set up the CNC of the laser stage, ran initial depth profiling tests, and reviewed and edited the manuscript. All authors contributed to the discussion and interpretation of the results, as well as to the revision of the peer-reviewed manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Renat Almeev and Philip Wiegel for their support during electron probe microanalyses. Julius Eschenauer is thanked for his help with the sample preparations and diffusion experiments. Thoughtful and constructive reviews by Yannick Bussweiler and Thomas Pettke, as well as efficient editorial handling by Klaus Mezger, are gratefully acknowledged. This study benefited from constructive discussions within the team of the German Research Foundation (DFG)-funded research unit FOR 2881 “Diffusion chronometry of magmatic systems”.
This research has been supported by the Deutsche Forschungsgemeinschaft within the research unit FOR 2881 (grant no. WE 2850/19-1).
The publication of this article was funded by the open-access fund of Leibniz Universität Hannover.
This paper was edited by Klaus Mezger and reviewed by Thomas Pettke and Yannick Bussweiler.
Balaram, V., Rahaman, W., and Roy, P.: Recent advances in MC-ICP-MS applications in Earth and environmental sciences: Challenges and solutions, Geosyst. Geoenviron., 1, 100019, https://doi.org/10.1016/j.geogeo.2021.100019, 2022.
Balcaen, L. I. L., Lenaerts, J., Moens, L., and Vanhaecke, F.: Application of laser ablation inductively coupled plasma (dynamic reaction cell) mass spectrometry for depth profiling analysis of high-tech industrial materials, J. Anal. At. Spectrom., 20, 417–423, https://doi.org/10.1039/b412287a, 2005.
Batanova, V. G., Thompson, J. M., Danyushevsky, L. V., Portnyagin, M. V., Garbe-Schönberg, D., Hauri, E., Kimura, J. I., Chang, Q., Senda, R., Goemann, K., Chauvel, C., Campillo, S., Ionov, D. A., and Sobolev, A. V.: New Olivine Reference Material for In Situ Microanalysis, Geostand. Geoanal. Res., 43, 453–473, https://doi.org/10.1111/ggr.12266, 2019.
Bell, D., Hervig, R., Buseck, P., and Aulbach, S.: Lithium isotope analysis of olivine by SIMS: Calibration of a matrix effect and application to magmatic phenocrysts, Chem. Geol., 258, 5–16, https://doi.org/10.1016/j.chemgeo.2008.10.008, 2009.
Bhattacharya, J. and Van der Ven, A.: Phase stability and nondilute Li diffusion in spinel Li1 + xTi2O4, Phys. Rev. B, 81, 27–30, https://doi.org/10.1103/PhysRevB.81.104304, 2010.
Bleiner, D., Lienemann, P., Ulrich, A., Vonmont, H., and Wichser, A.: Spatially resolved quantitative profiling of compositionally graded perovskite layers using laser ablation-inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 18, 1146–1153, https://doi.org/10.1039/b301907a, 2003.
Breeding, C. M., Ague, J. J., Grove, M., and Rupke, A. L.: Isotopic and chemical alteration of zircon by metamorphic fluids: U-Pb age depth-profiling of zircon crystals from Barrow's garnet zone, northeast Scotland, Am. Mineral., 89, 1067–1077, https://doi.org/10.2138/am-2004-0719, 2004.
Bussweiler, Y., Giuliani, A., Greig, A., Kjarsgaard, B. A., Petts, D., Jackson, S. E., Barrett, N., Luo, Y., and Pearson, D. G.: Trace element analysis of high-Mg olivine by LA-ICP-MS – Characterization of natural olivine standards for matrix-matched calibration and application to mantle peridotites, Chem. Geol., 524, 136–157, https://doi.org/10.1016/j.chemgeo.2019.06.019, 2019.
Chen, K.-Y., Yuan, H.-L., Liang, P., Bao, Z.-A., and Chen, L.: Improved nickel-corrected isotopic analysis of iron using high-resolution multi-collector inductively coupled plasma mass spectrometry, Int. J. Mass Spectrom., 421, 196–203, https://doi.org/10.1016/j.ijms.2017.07.002, 2017.
Cherniak, D. J. and Dimanov, A.: Diffusion in Pyroxene, Mica and Amphibole, Rev. Mineral. Geochemistry, 72, 641–690, https://doi.org/10.2138/rmg.2010.72.14, 2010.
Collinet, M., Charlier, B., Namur, O., Oeser, M., Médard, E., and Weyer, S.: Crystallization history of enriched shergottites from Fe and Mg isotope fractionation in olivine megacrysts, Geochim. Cosmochim. Ac., 207, 277–297, https://doi.org/10.1016/j.gca.2017.03.029, 2017.
Cottle, J. M., Horstwood, M. S. A., and Parrish, R. R.: A new approach to single shot laser ablation analysis and its application to in situ Pb/U geochronology, J. Anal. At. Spectrom., 24, 1355–1363, https://doi.org/10.1039/b821899d, 2009.
d'Abzac, F.-X., Beard, B. L., Czaja, A. D., and Konishi, H.: Iron Isotope Composition of Particles Produced by UV-Femtosecond Laser Ablation of Natural Oxides, Sulfides, and Carbonates, Anal. Chem., 85, 11885–11892, 2013.
d'Abzac, F. X., Czaja, A. D., Beard, B. L., Schauer, J. J., and Johnson, C. M.: Iron distribution in size-resolved aerosols generated by UV-femtosecond laser ablation: Influence of cell geometry and implications for in situ isotopic determination by LA-MC-ICP-MS, Geostand. Geoanal. Res., 38, 293–309, https://doi.org/10.1111/j.1751-908X.2014.00281.x, 2014.
Dauphas, N., Pourmand, A., and Teng, F.-Z.: Routine isotopic analysis of iron by HR-MC-ICPMS: How precise and how accurate?, Chem. Geol., 267, 175–184, https://doi.org/10.1016/j.chemgeo.2008.12.011, 2009.
Degryse, P. and Vanhaecke, F.: Status and prospects for quasi-non-destructive analysis of ancient artefacts via LA-ICP-MS, Elements, 12, 341–346, https://doi.org/10.2113/gselements.12.5.341, 2016.
Dobson, K. D., Visoly-Fisher, I., Hodes, G., and Cahen, D.: Stability of CdTe/CdS thin-film solar cells, Sol. Energy Mater. Sol. Cells, 62, 295–325, https://doi.org/10.1016/S0927-0248(00)00014-3, 2000.
Dohmen, R., Becker, H.-W., Meissner, E., Etzel, T., and Chakraborty, S.: Production of silicate thin films using pulsed laser deposition (PLD) and applications to studies in mineral kinetics, Eur. J. Mineral., 14, 1155–1168, 2002.
Dohmen, R., Becker, H.-W., and Chakraborty, S.: Fe–Mg diffusion in olivine I: experimental determination between 700 and 1,200 ∘C as a function of composition, crystal orientation and oxygen fugacity, Phys. Chem. Miner., 34, 389–407, https://doi.org/10.1007/s00269-007-0157-7, 2007.
Dohmen, R., Kasemann, S. A., Coogan, L., and Chakraborty, S.: Diffusion of Li in olivine, Part I: Experimental observations and a multi species diffusion model, Geochim. Cosmochim. Ac., 74, 274–292, https://doi.org/10.1016/j.gca.2009.10.016, 2010.
Dohmen, R., Marschall, H. R., Ludwig, T., and Polednia, J.: Diffusion of Zr, Hf, Nb and Ta in rutile: effects of temperature, oxygen fugacity, and doping level, and relation to rutile point defect chemistry, Phys. Chem. Miner., 46, 311–332, https://doi.org/10.1007/s00269-018-1005-7, 2019.
Fernández, B., Claverie, F., Pécheyran, C., and Donard, O. F. X.: Direct analysis of solid samples by fs-LA-ICP-MS, TrAC Trends Anal. Chem., 26, 951–966, https://doi.org/10.1016/j.trac.2007.08.008, 2007.
Fiege, A., Holtz, F., Shimizu, N., Mandeville, C. W., Behrens, H., and Knipping, J. L.: Sulfur isotope fractionation between fluid and andesitic melt: An experimental study, Geochim. Cosmochim. Ac., 142, 501–521, https://doi.org/10.1016/j.gca.2014.07.015, 2014.
Foley, S. F., Prelevic, D., Rehfeldt, T., and Jacob, D. E.: Minor and trace elements in olivines as probes into early igneous and mantle melting processes, Earth Planet. Sc. Lett., 363, 181–191, https://doi.org/10.1016/j.epsl.2012.11.025, 2013.
Fryer, B. J., Jackson, S. E., and Longerich, H. P.: The design, operation and role of the laser-ablation microprobe coupled with an inductively coupled plasma-mass spectrometer (LAM- ICP-MS) in the Earth sciences, Can. Mineral., 33, 303–312, 1995.
Genareau, K., Hervig, R., and Clarke, A.: Geochemical variations in late-stage growth of volcanic phenocrysts revealed by SIMS depth-profiling, Am. Mineral., 92, 1374–1382, https://doi.org/10.2138/am.2007.2468, 2007.
Hanaor, D. A. H. and Sorrell, C. C.: Review of the anatase to rutile phase transformation, J. Mater. Sci., 46, 855–874, https://doi.org/10.1007/s10853-010-5113-0, 2011.
Horn, I., Rudnick, R. L., and McDonough, W. F.: Precise elemental and isotope ratio determination by simultaneous solution nebulization and laser ablation-ICP-MS: Application to U-Pb geochronology, Chem. Geol., 164, 281–301, https://doi.org/10.1016/S0009-2541(99)00168-0, 2000.
Horn, I., Von Blanckenburg, F., Schoenberg, R., Steinhoefel, G., and Markl, G.: In situ iron isotope ratio determination using UV-femtosecond laser ablation with application to hydrothermal ore formation processes, Geochim. Cosmochim. Ac., 70, 3677–3688, https://doi.org/10.1016/j.gca.2006.05.002, 2006.
Huang, Y., Dong, Y., Li, S., Lee, J., Wang, C., Zhu, Z., Xue, W., Li, Y., and Li, J.: Lithium Manganese Spinel Cathodes for Lithium-Ion Batteries, Adv. Energy Mater., 11, 1–21, https://doi.org/10.1002/aenm.202000997, 2021.
Ito, M. and Ganguly, J.: Diffusion kinetics of Cr in olivine and 53Mn–53Cr thermochronology of early solar system objects, Geochim. Cosmochim. Ac., 70, 799–809, https://doi.org/10.1016/j.gca.2005.09.020, 2006.
Jackson, S. E. and Günther, D.: The nature and sources of laser induced isotopic fractionation in laser ablation-multicollector-inductively coupled plasma-mass spectrometry, J. Anal. At. Spectrom., 18, 205–212, https://doi.org/10.1039/b209620j, 2003.
Jarosewich, E., Nelen, J. A., and Norberg, J. A.: Reference Samples for Electron Microprobe Analysis, Geostand. Newsl., 4, 43–47, 1980.
Jeffcoate, A., Elliott, T., Kasemann, S., Ionov, D., Cooper, K., and Brooker, R.: Li isotope fractionation in peridotites and mafic melts, Geochim. Cosmochim. Ac., 71, 202–218, https://doi.org/10.1016/j.gca.2006.06.1611, 2007.
Jochum, K. P., Stoll, B., Herwig, K., Willbold, M., Hofmann, A. W., Amini, M., Aarburg, S., Abouchami, W., Hellebrand, E., Mocek, B., Raczek, I., Stracke, A., Alard, O., Bouman, C., Becker, S., Dücking, M., Brätz, H., Klemd, R., de Bruin, D., Canil, D., Cornell, D., de Hoog, C.-J., Dalpé, C., Danyushevsky, L., Eisenhauer, A., Gao, Y., Snow, J. E., Groschopf, N., Günther, D., Latkoczy, C., Guillong, M., Hauri, E. H., Höfer, H. E., Lahaye, Y., Horz, K., Jacob, D. E., Kasemann, S. a., Kent, A. J. R., Ludwig, T., Zack, T., Mason, P. R. D., Meixner, A., Rosner, M., Misawa, K., Nash, B. P., Pfänder, J., Premo, W. R., Sun, W. D., Tiepolo, M., Vannucci, R., Vennemann, T., Wayne, D., and Woodhead, J. D.: MPI-DING reference glasses for in situ microanalysis: New reference values for element concentrations and isotope ratios, Geochem. Geophy. Geosy. 7, Q02008, https://doi.org/10.1029/2005GC001060, 2006.
Jollands, M. C., Burnham, A. D., O'Neill, H. S. C., Hermann, J., and Qian, Q.: Beryllium diffusion in olivine: A new tool to investigate timescales of magmatic processes, Earth Planet. Sc. Lett., 450, 71–82, https://doi.org/10.1016/j.epsl.2016.06.028, 2016a.
Jollands, M. C., Hermann, J., St. O'Neill, H. C., Spandler, C., Padrón-Navarta, J. A., O'Neill, H. S. C., Spandler, C., and Padrón-Navarta, J. A.: Diffusion of Ti and some Divalent Cations in Olivine as a Function of Temperature, Oxygen Fugacity, Chemical Potentials and Crystal Orientation, J. Petrol., 57, 1983–2010, https://doi.org/10.1093/petrology/egw067, 2016b.
Jollands, M. C., O'Neill, H. S. C., Van Orman, J., Berry, A. J., Hermann, J., Newville, M., and Lanzirotti, A.: Substitution and diffusion of Cr2+ and Cr3+ in synthetic forsterite and natural olivine at 1200–1500 ∘C and 1 bar, Geochim. Cosmochim. Ac., 220, 407–428, https://doi.org/10.1016/J.GCA.2017.09.030, 2018.
Kaufmann, A. B., Lazarov, M., Kiefer, S., Majzlan, J., and Weyer, S.: In situ determination of antimony isotope ratios in Sb minerals by femtosecond LA-MC-ICP-MS, J. Anal. At. Spectrom., 36, 1554–1567, https://doi.org/10.1039/d1ja00089f, 2021.
Kelly, C. J., Mcfarlane, C. R. M., Schneider, D. A., and Jackson, S. E.: Dating micrometre-thin rims using a LA-ICP-MS depth profiling technique on zircon from an archaean metasediment: Comparison with the SIMS depth profiling method, Geostand. Geoanal. Res., 38, 389–407, https://doi.org/10.1111/j.1751-908X.2014.00314.x, 2014.
Kita, N. T., Mostefaoui, S., Liu, Y. Z., Togashi, S., and Morishita, Y.: Application of high precision SIMS analyses to the early solar system chronology, Appl. Surf. Sci., 203/204, 806–809, https://doi.org/10.1016/S0169-4332(02)00829-2, 2003.
Kolli, S. K. and Van der Ven, A.: Elucidating the Factors That Cause Cation Diffusion Shutdown in Spinel-Based Electrodes, Chem. Mater., 33, 6421–6432, https://doi.org/10.1021/acs.chemmater.1c01668, 2021.
Kosler, J., Pedersen, R. B., Kruber, C., and Sylvester, P. J.: Analysis of Fe isotopes in sulfides and iron meteorites by laser ablation high-mass resolution multi-collector ICP mass spectrometry, J. Anal. At. Spectrom., 20, 192–199, 2005.
Košler, J., Forst, L., and Sláma, J.: LamDate and LamTool: Spreadsheet-based data reduction for laser ablation ICP-MS, Laser Ablation ICP-MS Earth Sci. Curr. Pract. Outst. Issues Mineral. Assoc. Canada, Short Course Ser., 40, 315–317, 2008.
Krachler, M., Bulgheroni, A., Martinez Ferri, A. I., Ma, Y., Miard, A., and Garcia, P.: Single shot laser ablation MC-ICP-MS for depth profile analysis of U isotopes in UO2 single crystals, J. Anal. At. Spectrom., 34, 1965–1974, https://doi.org/10.1039/c9ja00212j, 2019.
Lambart, S., Hamilton, S., and Lang, O. I.: Compositional variability of San Carlos olivine, Chem. Geol., 605, 120968, https://doi.org/10.1016/j.chemgeo.2022.120968, 2022.
Lazarov, M. and Horn, I.: Matrix and energy effects during in-situ determination of Cu isotope ratios by ultraviolet-femtosecond laser ablation multicollector inductively coupled plasma mass spectrometry, Spectrochim. Acta B, 111, 64–73, https://doi.org/10.1016/j.sab.2015.06.013, 2015.
Lee, J. S. and Lim, H. B.: Laser ablation of titanium nitride coated on silicon wafer substrate for depth profiling using ICP-MS, Appl. Surf. Sci., 327, 483–489, https://doi.org/10.1016/j.apsusc.2014.11.123, 2015.
Limbeck, A., Bonta, M., and Nischkauer, W.: Improvements in the direct analysis of advanced materials using ICP-based measurement techniques, J. Anal. At. Spectrom., 32, 212–232, https://doi.org/10.1039/c6ja00335d, 2017.
Lin, J., Liu, Y., Hu, Z., Chen, W., Zhang, C., Zhao, K., and Jin, X.: Accurate analysis of Li isotopes in tourmalines by LA-MC-ICP-MS under “wet” conditions with non-matrix-matched calibration, J. Anal. At. Spectrom., 34, 1145–1153, https://doi.org/10.1039/c9ja00013e, 2019.
Lin, J., Liu, Y., Yang, A., Chen, W., Zhu, L., and Hu, Z.: Non-matrix-matched calibration of Mg isotopic ratios in silicate samples by fs-LA-MC-ICP-MS with low mass resolution under wet plasma conditions, J. Anal. At. Spectrom., 37, 592–602, https://doi.org/10.1039/d1ja00396h, 2022.
Liu, Z., Qin, L., Cao, X., Zhou, J., Pan, A., Fang, G., Wang, S., and Liang, S.: Ion migration and defect effect of electrode materials in multivalent-ion batteries, Prog. Mater. Sci., 125, 100911, https://doi.org/10.1016/j.pmatsci.2021.100911, 2022.
Mank, A. J. G. and Mason, P. R. D.: A critical assessment of laser ablation ICP-MS as an analytical tool for depth analysis in silica-based glass samples, J. Anal. At. Spectrom., 14, 1143–1153, https://doi.org/10.1039/a903304a, 1999.
Marsh, J. H. and Stockli, D. F.: Zircon U-Pb and trace element zoning characteristics in an anatectic granulite domain: Insights from LASS-ICP-MS depth profiling, Lithos, 239, 170–185, https://doi.org/10.1016/j.lithos.2015.10.017, 2015.
Müehl, G. J. H., Rüehlmann, J., Goebel, M. O., and Bachmann, J.: Application of confocal laser scanning microscopy (CLSM) to visualize the effect of porous media wettability on unsaturated pore water configuration, J. Soils Sediments, 12, 75–85, https://doi.org/10.1007/S11368-011-0395-7, 2011.
Nakazato, M., Asanuma, H., Niki, S., Iwano, H., and Hirata, T.: Depth-Profiling Determinations of Rare Earth Element Abundances and U-Pb Ages from Zircon Crystals Using Sensitivity-Enhanced Inductively Coupled Plasma-Time of Flight-Mass Spectrometry, Geostand. Geoanal. Res., 46, 603–620, https://doi.org/10.1111/ggr.12446, 2022.
Oeser, M., Weyer, S., Horn, I., and Schuth, S.: High-Precision Fe and Mg Isotope Ratios of Silicate Reference Glasses Determined In Situ by Femtosecond LA-MC-ICP-MS and by Solution Nebulisation MC-ICP-MS, Geostand. Geoanal. Res., 38, 311–328, https://doi.org/10.1111/j.1751-908X.2014.00288.x, 2014.
Oeser, M., Dohmen, R., Horn, I., Schuth, S., and Weyer, S.: Processes and time scales of magmatic evolution as revealed by Fe–Mg chemical and isotopic zoning in natural olivines, Geochim. Cosmochim. Ac., 154, 130–150, https://doi.org/10.1016/j.gca.2015.01.025, 2015.
Oeser, M., Ruprecht, P., and Weyer, S.: Combined Fe-Mg chemical and isotopic zoning in olivine constraining magma mixing-to-eruption timescales for the continental arc volcano Irazú (Costa Rica) and Cr diffusion in olivine, Am. Mineral., 103, 582–599, https://doi.org/10.2138/am-2018-6258, 2018.
Paton, C., Hellstrom, J., Paul, B., Woodhead, J., and Hergt, J.: Iolite: Freeware for the visualisation and processing of mass spectrometric data, J. Anal. At. Spectrom., 26, 2508–2518, https://doi.org/10.1039/c1ja10172b, 2011.
Pisonero, J. and Günther, D.: Femtosecond Laser Ablation Inductively Coupled Plasma Mass Spectrometry: Fundamentals And Capabilities For Depth Profiling Analysis, Mass Spectrom. Rev., 27, 609–623, https://doi.org/10.1002/mas.20180, 2008.
Pisonero, J., Koch, J., Wälle, M., Hartung, W., Spencer, N. D., and Günther, D.: Capabilities of Femtosecond Laser Ablation Inductively Coupled Plasma Mass Spectrometry for Depth Profiling of Thin Metal Coatings, Anal. Chem., 79, 2325–2333, https://doi.org/10.1021/ac062027s, 2007.
Plotnikov, A., Vogt, C., Hoffmann, V., Täschner, C., and Wetzig, K.: Application of laser ablation inductively coupled plasma quadrupole mass spectrometry (LA-ICP-QMS) for depth profile analysis, J. Anal. At. Spectrom., 16, 1290–1295, https://doi.org/10.1039/b105441b, 2001.
Richter, F., Watson, B., Chaussidon, M., Mendybaev, R., and Ruscitto, D.: Lithium isotope fractionation by diffusion in minerals, Part 1: Pyroxenes, Geochim. Cosmochim. Ac., 126, 352–370, https://doi.org/10.1016/j.gca.2013.11.008, 2014.
Richter, F., Chaussidon, M., Mendybaev, R., and Kite, E.: Reassessing the cooling rate and geologic setting of Martian meteorites MIL 03346 and NWA 817, Geochim. Cosmochim. Ac., 182, 1–23, https://doi.org/10.1016/j.gca.2016.02.020, 2016.
Richter, F., Chaussidon, M., Bruce Watson, E., Mendybaev, R., and Homolova, V.: Lithium isotope fractionation by diffusion in minerals, Part 2: Olivine, Geochim. Cosmochim. Ac., 219, 124–142, https://doi.org/10.1016/j.gca.2017.09.001, 2017.
Richter, F. M., Liang, Y., and Davis, A. M.: Isotope fractionation by diffusion in molten oxides, Geochim. Cosmochim. Ac., 63, 2853–2861, 1999.
Sarah, G., Gratuze, B., and Barrandon, J.-N.: Application of laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) for the investigation of ancient silver coins, J. Anal. At. Spectrom., 22, 1163–1167, https://doi.org/10.1039/b704879c, 2007.
Saulick, Y., Lourenço, S. D. N., Baudet, B. A., Woche, S. K., and Bachmann, J.: Physical properties controlling water repellency in synthesized granular solids, Eur. J. Soil Sci., 69, 698–709, https://doi.org/10.1111/EJSS.12555, 2018.
Schoenberg, R. and von Blanckenburg, F.: An assessment of the accuracy of stable Fe isotope ratio measurements on samples with organic and inorganic matrices by high-resolution multicollector ICP-MS, Int. J. Mass Spectrom., 242, 257–272, https://doi.org/10.1016/j.ijms.2004.11.025, 2005.
Schuth, S., Horn, I., Brüske, A., Wolff, P. E., and Weyer, S.: First vanadium isotope analyses of V-rich minerals by femtosecond laser ablation and solution-nebulization MC-ICP-MS, Ore Geol. Rev., 81, 1271–1286, https://doi.org/10.1016/J.OREGEOREV.2016.09.028, 2017.
Sio, C. K., Roskosz, M., Dauphas, N., Bennett, N. R., Mock, T., and Shahar, A.: The isotope effect for Mg-Fe interdiffusion in olivine and its dependence on crystal orientation, composition and temperature, Geochim. Cosmochim. Ac., 239, 463–480, https://doi.org/10.1016/j.gca.2018.06.024, 2018.
Sio, C. K. I., Dauphas, N., Teng, F.-Z., Chaussidon, M., Helz, R. T., and Roskosz, M.: Discerning crystal growth from diffusion profiles in zoned olivine by in situ Mg–Fe isotopic analyses, Geochim. Cosmochim. Ac., 123, 302–321, https://doi.org/10.1016/j.gca.2013.06.008, 2013.
Spandler, C. and O'Neill, H. S. C.: Diffusion and partition coefficients of minor and trace elements in San Carlos olivine at 1,300 ∘C with some geochemical implications, Contrib. Mineral. Petrol., 159, 791–818, https://doi.org/10.1007/s00410-009-0456-8, 2010.
Steely, A. N., Hourigan, J. K., and Juel, E.: Discrete multi-pulse laser ablation depth profiling with a single-collector ICP-MS: Sub-micron U-Pb geochronology of zircon and the effect of radiation damage on depth-dependent fractionation, Chem. Geol., 372, 92–108, https://doi.org/10.1016/j.chemgeo.2014.02.021, 2014.
Steinhoefel, G., Horn, I., and von Blanckenburg, F.: Matrix-independent Fe isotope ratio determination in silicates using UV femtosecond laser ablation, Chem. Geol., 268, 67–73, https://doi.org/10.1016/j.chemgeo.2009.07.010, 2009.
Steinmann, L. K., Oeser, M., Horn, I., Seitz, H.-M., and Weyer, S.: In situ high-precision lithium isotope analyses at low concentration levels with femtosecond-LA-MC-ICP-MS, J. Anal. At. Spectrom., 34, 1447–1458, https://doi.org/10.1039/C9JA00088G, 2019.
Su, B.-X., Gu, X.-Y., Deloule, E., Zhang, H.-F., Li, Q.-L., Li, X.-H., Vigier, N., Tang, Y.-J., Tang, G.-Q., Liu, Y., Pang, K.-N., Brewer, A., Mao, Q., and Ma, Y.-G.: Potential Orthopyroxene, Clinopyroxene and Olivine Reference Materials for In Situ Lithium Isotope Determination, Geostand. Geoanal. Res., 39, 357–369, https://doi.org/10.1111/j.1751-908X.2014.00313.x, 2015.
Teng, F.-Z., Dauphas, N., Helz, R. T., Gao, S., and Huang, S.: Diffusion-driven magnesium and iron isotope fractionation in Hawaiian olivine, Earth Planet. Sc. Lett., 308, 317–324, https://doi.org/10.1016/j.epsl.2011.06.003, 2011.
Van Orman, J. A. and Krawczynski, M. J.: Theoretical constraints on the isotope effect for diffusion in minerals, Geochim. Cosmochim. Ac., 164, 365–381, https://doi.org/10.1016/j.gca.2015.04.051, 2015.
Villeneuve, J., Chaussidon, M., Marrocchi, Y., Deng, Z., and Watson, E. B.: High-precision in situ silicon isotopic analyses by multi-collector secondary ion mass spectrometry in olivine and low-calcium pyroxene, Rapid Commun. Mass Spectrom., 33, 1589–1597, https://doi.org/10.1002/rcm.8508, 2019.
Vogt, K., Dohmen, R., and Chakraborty, S.: Fe-Mg diffusion in spinel: New experimental data and a point defect model, Am. Mineral., 100, 2112–2122, https://doi.org/10.2138/am-2015-5109, 2015.
Welsch, A. M., Behrens, H., Murawski, D., and Horn, I.: Lithium Mobility in Borate and Phosphate Glass Networks, Z. Phys. Chem., 231, 1303–1321, https://doi.org/10.1515/zpch-2016-0927, 2017.
Woodhead, J., Hergt, J., Shelley, M., Eggins, S., and Kemp, R.: Zircon Hf-isotope analysis with an excimer laser, depth profiling, ablation of complex geometries, and concomitant age estimation, Chem. Geol., 209, 121–135, https://doi.org/10.1016/j.chemgeo.2004.04.026, 2004.
Woodhead, J. D., Horstwood, M. S. A., and Cottle, J. M.: Advances in isotope ratio determination by LA-ICP-MS, Elements, 12, 317–322, https://doi.org/10.2113/gselements.12.5.317, 2016.
Wu, S., Wörner, G., Jochum, K. P., Stoll, B., Simon, K., and Kronz, A.: The Preparation and Preliminary Characterisation of Three Synthetic Andesite Reference Glass Materials (ARM-1, ARM-2, ARM-3) for In Situ Microanalysis, Geostand. Geoanal. Res., 43, 567–584, https://doi.org/10.1111/ggr.12301, 2019.
Xiao, W., Xin, C., Li, S., Jie, J., Gu, Y., Zheng, J., and Pan, F.: Insight into fast Li diffusion in Li-excess spinel lithium manganese oxide, J. Mater. Chem. A, 6, 9893–9898, https://doi.org/10.1039/c8ta01428k, 2018.
Xu, L., Zhang, W., Luo, T., Yang, J. H., and Hu, Z.: In situ Fe isotopic analyses of fourteen reference materials using a synthetic Cr standard for mass bias and isobaric interference corrections by femtosecond LA-MC-ICP-MS, J. Anal. At. Spectrom., 36, 747–757, https://doi.org/10.1039/d0ja00465k, 2021.
Xu, L., Yang, J.-H., Wang, H., Xie, L.-W., Yang, Y.-H., Huang, C., and Wu, S.-T.: Analytical feasibility of a new reference material (IRMM-524A Fe metal) for the in situ Fe isotopic analysis of pyrite and ilmenite without matrix effects by femtosecond LA-MC-ICP-MS, J. Anal. At. Spectrom., 37, 1835–1845, https://doi.org/10.1039/d2ja00151a, 2022a.
Xu, L., Yang, J. H., Xie, L. W., Wang, H., Yang, Y. H., Huang, C., and Wu, S. T.: Evaluation of plasma condition, concentration effect, position effect, and nickel-doping method on non-matrix-matched Fe isotopic analysis by femtosecond laser ablation multi-collector inductively coupled plasma mass spectrometry, Spectrochim. Acta B, 189, 106374, https://doi.org/10.1016/J.SAB.2022.106374, 2022b.
Zheng, X.-Y., Beard, B. L., Lee, S., Reddy, T. R., Xu, H., and Johnson, C. M.: Contrasting particle size distributions and Fe isotope fractionations during nanosecond and femtosecond laser ablation of Fe minerals: Implications for LA-MC-ICP-MS analysis of stable isotopes, Chem. Geol., 450, 235–247, https://doi.org/10.1016/j.chemgeo.2016.12.038, 2017.
Zheng, X.-Y., Beard, B. L., and Johnson, C. M.: Assessment of matrix effects associated with Fe isotope analysis using 266 nm femtosecond and 193 nm nanosecond laser ablation multi-collector inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 33, 68–83, https://doi.org/10.1039/C7JA00272F, 2018.
Zhu, C., Lu, W., He, Y., Ke, S., Wu, H., and Zhang, L.: Iron isotopic analyses of geological reference materials on MC-ICP-MS with instrumental mass bias corrected by three independent methods, Acta Geochim., 37, 691–700, https://doi.org/10.1007/s11631-018-0284-5, 2018.
Zhukova, I., O'Neill, H., and Campbell, I. H.: A subsidiary fast-diffusing substitution mechanism of Al in forsterite investigated using diffusion experiments under controlled thermodynamic conditions, Contrib. Mineral. Petrol., 172, 1–12, https://doi.org/10.1007/s00410-017-1365-x, 2017.
Zirakparvar, N. A.: Cathodoluminescence guided zircon Hf isotope depth profiling: Mobilization of the Lu-Hf system during (U)HP rock exhumation in the Woodlark Rift, Papua New Guinea, Lithos, 220–223, 81–96, https://doi.org/10.1016/j.lithos.2015.01.026, 2015.
- Abstract
- Introduction
- Samples and experimental setup
- Analytical methods
- Results and discussion
- Advantages and limitations of the technique and some conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Samples and experimental setup
- Analytical methods
- Results and discussion
- Advantages and limitations of the technique and some conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement