the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Pseudo-cubic trigonal pyrite from the Madan Pb–Zn ore field (Rhodope Massif, Bulgaria): morphology and twinning
Yves Moëlo
A new occurrence of pyrite crystals with rhombohedral habit, up to several centimeters in length, is described from the Madan Pb–Zn ore field (Rhodope Massif, south Bulgaria), where it constitutes a late pyrite generation. As observed in the past in other deposits, the ideal rhombohedron is derived from the pyritohedron by suppression of half of its faces (six “polar faces”) around a ternary axis. In studied crystals, together with six main “equatorial faces”, additional minor faces correspond to cube faces as well as polar faces. Such a dissymmetry indicates that the crystallographic point group of these crystals is , a subgroup of the eigensymmetry of a rhombohedron taken as geometric face form. Twinning by metric merohedry confirms such a symmetry decrease and permits the definition of this type of pyrite as a dimorph of cubic pyrite, i.e., pseudo-cubic trigonal pyrite (pyrite-R). Twin operations belong to the set of symmetry operations absent in point group relative to pyrite symmetry : reflection about the {100} plane or two-fold rotation about the direction. Four twin types have been distinguished (name, chromatic point group): three contact twins (reflection, m′; rotation, 2′; trapezoidal, (m(2)m(2)2(2))(4)), as well as one penetration twin (crossed, . Composition planes always correspond to {100}, but there are two types of twin interfaces. More complex twinned samples may develop erratically during crystal growth. Other twin variations as well as genetic aspects of such a type of pyrite are discussed.
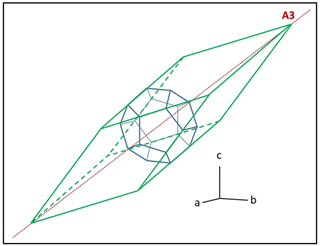
Pyrite is the most common sulfide in the Earth crust, together with pyrrhotite, predominant in magmatic rocks. Its crystal habits generally reflect its cubic symmetry: cube, octahedron and “pyritohedron” (pentagonal dodecahedron). Rarely, asymmetrical forms are observed. In the fundamental Atlas der Kristallformen of Goldschmidt (1920) (see also Dana's System of Mineralogy – Palache et al., 1944), crystals with tetragonal or rhombohedral (pseudo-)symmetries are described. The rhombohedral habit (“pyrhombohedron”) directly derives from the pyritohedron by the suppression of half of its faces (Fig. 1), as firstly described by Jeremejew (1887). Very recently, Žorž et al. (2022) have described pyrite with tetrahedral habit from the Lavrion Pb–Zn ore district (Greece).
The present study deals with the morphological study of a new occurrence of pyrite with rhombohedral habit, from the Madan Pb–Zn ore field (Rhodope Massif, south Bulgaria). Such a morphology permits us to assign this peculiar pyrite to a pseudo-cubic trigonal derivative (pyrite-R) of cubic pyrite, with symmetry point group . A significant part of collected samples corresponds to twinned crystals according to several twin laws, which confirms such a symmetry decrease.
Goldschmidt (1920, and references herein) cites four old studies (the first in 1858) describing pyrite crystals whose habitus indicates a rhombohedral-type asymmetry. These pyrites come from Germany (two occurrences: Freiberg and Gommern), Russia (Ural), and Japan (Tohira). Figure 403, Table 126, of Goldschmidt (1920) is a reproduction of that initially given by Jeremejew (1887) for a pyrite crystal from south Ural (Russia). One century later, another occurrence of rhombohedral crystals was described by Honma et al. (1987) in the Aikawa ore deposit of the skarn type (Chichibu mine, Saitama prefecture, NE of Tokyo). X-ray powder diffraction as well as electron microprobe data agree quite well with ideal pyrite. Etching by KMnO4 of polished sections revealed framboidal and cellular-like textures, which would indicate, according to these authors, the formation of this pyrite variety from neutral conditions at a low temperature.
Oganov (1996) described an occurrence of rhombohedral pyrite from Mount Kinzhal (northern Caucasus, Russia). Goniometric measurements indicated a basal dihedral angle of the rhombohedron larger than the theoretical one (75.03∘ against 66.4∘), which was explained by an admixture of microscopic striating terraces of {100} faces. Trigonal symmetry lowering of {100} leads to two inequivalent rhombohedra (prolate – elongated and oblate – flattened), and the occurrence of only prolate rhombohedra perpendicular to schistosity was explained by the possible action of an electric field.

Figure 2(a) Location of Madan Pb–Zn ore field. (b) Sources of studied samples in the ore field. Green stars: main ore deposits. Blue lines: main ore-controlling fault zones. Geology: 1 – Arda unit (migmatized gneisses), 2 – Madan allochthone (gneisses, amphibolites, marbles); 3 – Paleogene conglomerates, 4 – Eocene granitoid, and 5 – Asenitsa unit (para-metamorphic rocks). Simplified geological map, according to Vassileva et al. (2009).
The Madan Pb–Zn ore field is located in the Rhodope Massif (south Bulgaria), about 70 km to the south of Plovdiv (Fig. 2a), close to Greece (Vassileva et al., 2009 and 2010). Ore deposits are distributed in a 10×20 km area on the southeast flank of the Rhodope Massif. There are six main multi-kilometer-long ore veins (Fig. 2b), oriented NW–SE, cross-cutting metamorphic series (gneisses, amphibolites, micaschists, and marbles). There are three ore types: veins, stockworks, and skarns. Distal skarns are the result of a metasomatic process, through the interaction of acid solutions with marbles and gneiss (Hantsche et al., 2021). Replacement is incomplete, leading to the formation of large cavities with various well-crystallized minerals: galena, sphalerite, pyrite, chalcopyrite, quartz, and carbonates (Petrussenko, 1991).
Petrussenko (1991) lists 35 mines and ore deposits in the Madan ore field. Only five mines were open until recently (Vassileva et al., 2010). Three among them are well known to have provided the best mineral samples for museums and mineral collectors: Krushev Dol, Petrovitsa, and Gyudyurska (Fig. 2b). Other samples may be provided by the Deveti Septemvri (“9th of September”) and Borieva mines. In his mineralogical description, Petrussenko (1991) did not describe rhombohedral pyrite. Pyrite with peculiar morphology (whiskers, thin platelets) has been described by Bonev et al. (1985), but rhombohedral crystals were not observed either.
Studied rhombohedral crystals of pyrite (pyrite-R) were extracted from cavities by mineral dealers from Madan. Unfortunately, no field description of their occurrence is available. On the basis of more than 200 samples provided by several dealers, the majority clearly relates to pyrite-R. Often Madan is the only indication about their origin. When the name of the mine is given, Borieva is the most frequent, then Gyudyurska and more rarely Deveti Septemvri and Krushev Dol. Samples from Borieva appeared to be the most interesting, especially for the study of twinning.
The size of selected rhombohedral single crystals varies from 1 up to 6 cm. They have a fresh shine or are weakly tarnished. Accessory minerals occasionally associated with pyrite-R are millimeter-long cubic crystals of pyrite with striated faces (“triglyph” facies), dark Fe-rich sphalerite, galena, prismatic quartz, dolomite, fine chlorite, and traces of apatite. Sub-millimeter hexagonal flakes of graphite were frequently observed at the surface of pyrite-R crystals from Gyudyurska.
Sphalerite, galena, and cubic pyrite may be partly included in pyrite-R crystals, and crystals of cubic pyrite clearly disrupt the growth of pyrite-R crystals. Pyrite-R thus appears as a late-stage sulfide. In one case a late sub-centimeter cubic crystal of galena was observed as an overgrowth on a crystal of pyrite-R.
An X-ray powder diagram in ordinary conditions (analyst: P.-E. Petit), as well as SEM chemical analysis, did not indicate any significant difference relative to cubic pyrite. According to the following description of individual crystals and their various twinning, pyrite-R will be considered, unless a more detailed crystallographic study is conducted, pseudo-cubic trigonal pyrite, with point group symmetry .
4.1 Indexation of the rhombohedron
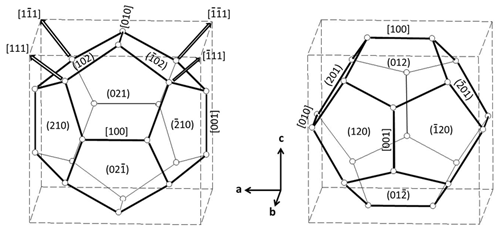
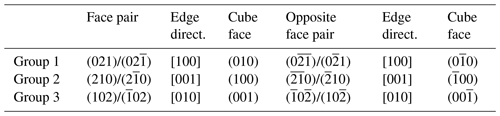
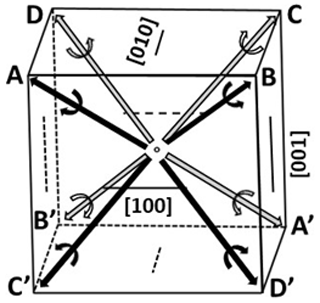
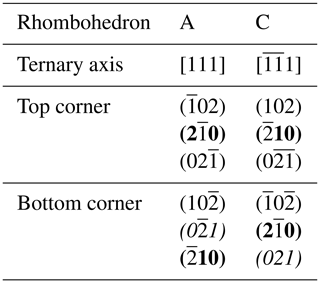
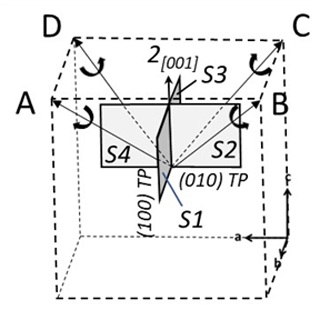
The rhombohedron is derived from the pyritohedron. As pyrite is hemihedral (cubic , there are two choices for the indexation of the faces of the pyritohedron (Fig. 3a and b). Imbrication of these two figures gives the well-known iron-cross penetration twin. Table 1 gives the list of the 12 faces of the form {201} of Fig. 3a. These faces form three groups related by ternary axis. In each group two faces in contact (matched faces) are related by a reflection about the {100} plane, and the two others are deduced by inversion.
Table 2Indexation of E faces (bold characters) of the rhombohedron with [111] chosen as the ternary axis, together with possible minor paired P faces, and intermediate cube faces.
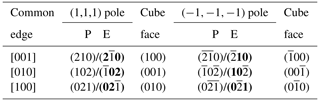
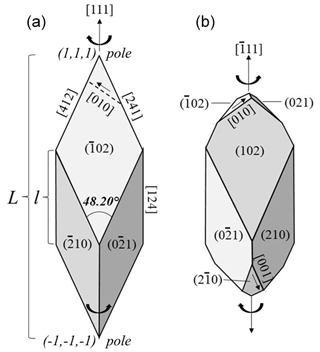
In Fig. 3a, the ternary axis corresponding to [111] can be selected as the only ternary axis surviving in pyrite-R. On this basis, the rhombohedron is obtained by suppression of the six (2×3) faces of the pyritohedron in contact with this ternary axis (“polar faces” P). The six remaining faces (“equatorial faces” E) form an elongated rhombohedron (Figs. 1 and 4a). Table 2 indicates the E faces (bold characters), the P faces, and the cube faces. The acute angle of the lozenge is 48.20∘ (Fig. 4a), and the acute dihedral angle of the rhombohedron is 66.42∘, as indicated by Jeremejew (1887). The ratio of the elongation L of the rhombohedron relative to its edge length l is . The P faces are generally present as additional minor faces in Madan crystals (Fig. 4b), as well as the faces of the cube between matched faces (Table 2). This induces a truncation of the two corners, with a significant decrease of the ratio.
4.2 Rhombohedral crystals from Madan
Figure 5a and b are two examples of well-developed rhombohedral crystals. The first crystal (Fig. 5a) comes from Gyudyurska. It shows numerous small cubes of pyrite (up to 3 mm), which sometimes block the growth of rhombohedron edges. Some faces of the rhombohedron are strongly striated, and the ratio is ∼2. This morphology is very close to that presented by Honma et al. (1987). The second crystal (Fig. 5b) comes from Borieva. Only two small crystals of cubic pyrite are visible. Faces of the cube show a better development, with minor {210} faces. The ratio is ∼1.7. Figure 6 schematizes this morphology.

Figure 5Two examples of rhombohedral crystals of pyrite from the Madan ore field. (a) Gyudyurska deposit (L: 3.3 cm) and (b) Borieva deposit (L: 2.8 cm).
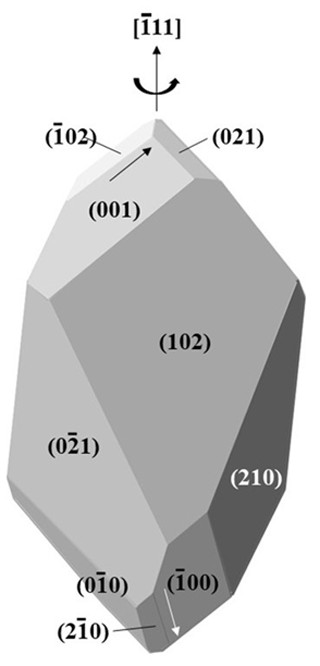
Figure 6Scheme of the crystal from Borieva (Fig. 5b). Combination of main E form, medium form {100}, and minor P form (orientation according to [11]). The arrows define the rotation direction of striation (top: counterclockwise, bottom: clockwise).
The geometric face form of the simple rhombohedron has eigensymmetry , which however is not a subgroup of pyrite point group . Point group is the common maximal subgroup of these two groups, which is eventually the eigensymmetry of these pyrite rhombohedra. This sample is therefore a rare example of a crystallographic face form whose eigensymmetry is lower than the corresponding geometric face form (Nespolo, 2015). Striations visible in Fig. 5 represent face edges parallel to the basal axes of the cubic unit cell. They are oblique relative to the two acute corners of the rhombohedron, which permits us to define a clockwise rotation for one corner and a counterclockwise rotation for the opposite (see arrows in Figs. 4 and 6). The presence of these striations explains the lower symmetry of the rhombohedra with respect to their geometric face forms, in the same way as they explain the merohedral symmetry of cubic pyrite.
5.1 Generalities
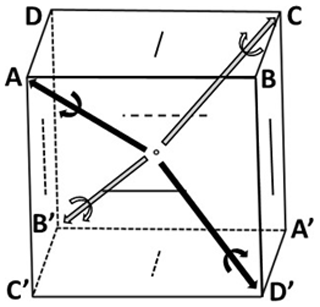
The only common twin of pyrite is the iron-cross twin, a penetration twin easily recognized when the two crystals are pyritohedra, with one crystal deduced from the other by a 90∘ rotation around [100] (see Fig. 3). Spinel twin, a contact twin with (111) acting as a twin plane, was rarely described (Goldschmidt and Nicol, 1904; Gaubert, 1928). Twins reported by Smolar (1913) were considered questionable by Pabst (1971). Contact twinning of pyrite was re-examined recently by Moëlo et al. (2023), who distinguished three types of contact twins and discussed the validity of the twin of the spinel type. In their recent study of pyrite with tetrahedral habit, Žorž et al. (2022) described two types of penetration twins, one by inversion, the second by a 180∘ rotation about one ternary axis of the tetrahedron. Up to now, only the iron-cross twin has been the subject of modern re-examination through transmission electron microscopy (TEM) study (Rečnik et al., 2016).
In Madan samples, visual inspection permitted us to quickly detect some crystals with re-entrant angles, characteristic of twinned samples. The collection of an increasing number of samples revealed several types of twinning. These twins, relatively simple, have been analyzed on the basis of the general principles of twinning. Considering a cubic lattice, they all fall in the category of merohedric twinning (Nespolo and Ferraris, 2000) because some of the symmetry operations, which are lost when cubic hemihedry of pyrite is replaced by the trigonal symmetry of pyrite-R (reflections and two-fold rotations), act as twin operations for the latter.
The main part of samples described here comes from the Borieva mine, where apparently the conditions of crystallization of pyrite-R were the most favorable for the nucleation and development of twins. Four twin types have been distinguished. Three correspond to contact twins, the last one to a penetration twin. Erratic twinning during crystal growth may give more complex, dissymmetric edifices.
5.2 Twin description method
The morphological characterization of a twin needs the description of the composition surface between twinned crystals and the determination of twin operation(s), which permits us to define a twin type. Here, whatever the twin type, observed faces of different constitutive pyrite crystals can be easily indexed on the basis of the same cubic unit cell, according to Fig. 3a. Correspondence between faces of twinned crystals permits us to establish the twin operations mapping the individuals of the twin, i.e., the chromatic operations of the twin point group (Nespolo, 2019). {100} is the unique composition plane.
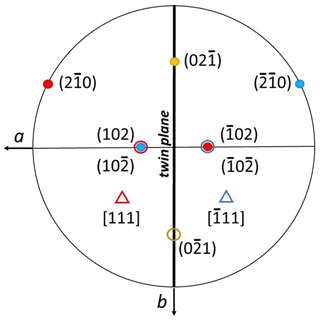
Figure 11Stereographic projection of MT type. Red color refers to A, blue color to B, and orange color to common faces. Circles: faces, triangles: ternary axes.
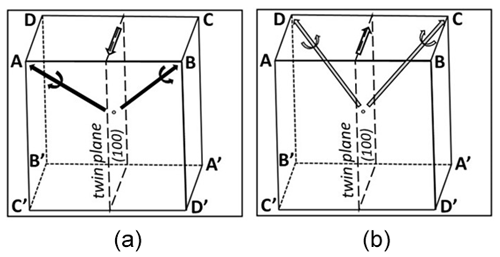
Figure 12Two symbolic schemes of reflection twin, from A + B or C + D pairs. The arrow on the (100) twin plane m determines the rotation of the hemi-rhombohedra (curved arrows).
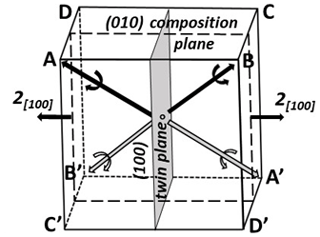
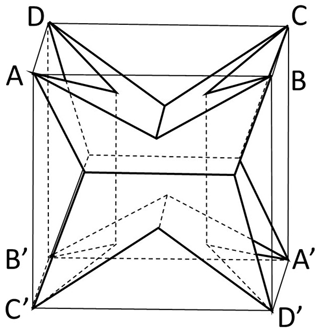
Each twin type has been symbolized taking into account the general scheme of Fig. 7. Each pair, AA′, BB′, etc., corresponds to one of the four possible rhombohedra. It is the sum of two hemi-rhombohedra, A + A′, B + B′, etc. Each hemi-rhombohedron has its own rotation direction, revealed by the striation direction determined by the segments on cube faces. A, C, B′, and D′ have a clockwise rotation, and A′, C′, B, and D have a counterclockwise rotation. A hemi-rhombohedron is simply a trigonal pyramid terminated by a pedion. As geometric face form, its eigensymmetry would be 3m, but in our sample we have crystallographic face forms with eigensymmetry 3.
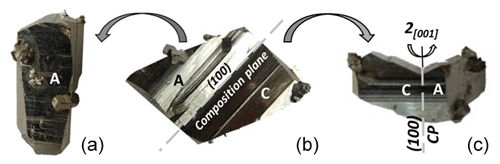
Figure 13Twin of rotation twin (type 2 – Borieva). (a) Long side (smooth face); (b) top view; and (c) short, striated side. CP: composition plane, 2[001]: two-fold twin axis along [001].
Considering a rhombohedral unit cell, AA′ rhombohedron relates to the same a, b, and c unit-cell vectors as the cubic unit cell. For the three other rhombohedra, (a′, b′, c′) correspond to (−a, b, c) (BB′), (−a, −b, c) (CC′), and (a, −b, c) (DD′).
5.3 Reflection twin (MT – type 1)
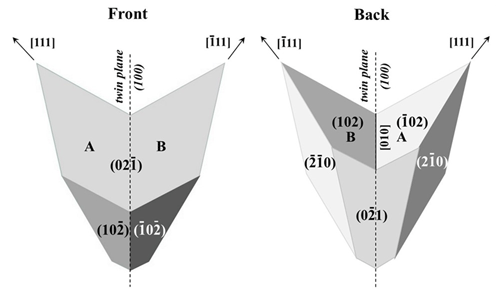
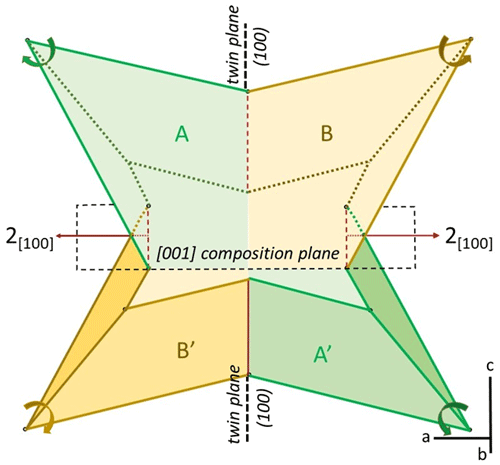
This type of twin is the most frequent one (a small percentage of collected samples). A small twin, quite complete ( cm – Fig. 8), from Borieva constitutes the best example. A re-entrant angle is clearly visible. It is a contact twin where the twin plane between A and B is parallel to the composition plane (100). The re-entrant angle is the complement of the angle of the dihedron between two paired faces of the pyritohedron (126.87∘).
Figure 9 is an ideal scheme of this twin type, built on the basis of the rhombohedron of Fig. 4a. This crystal can be cut in two halves (hemi-rhombohedra) by the (100) twin plane, part A with [111] as the three-fold axis, and part A′ in the opposite [] direction. Only A subsists in Fig. 9, twinned with B. Their ternary axes correspond to neighboring corners of the cube. Part B of the twin can be derived directly from A through reflection about the (100) twin plane, or indirectly through inversion (leading to A′), followed by an 180∘ rotation of A′ about the [100] twin axis.
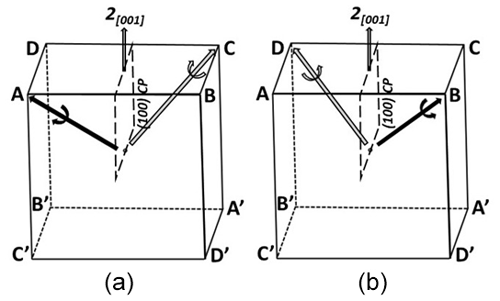
Figure 16Symbolic schemes of the rotation twin. (a) Clockwise sub-type A + C and (b) counterclockwise sub-type B + D.
Table 3Pyritohedron faces in the reflection twin (see Fig. 9). Bold characters: common main faces, italics: absent.
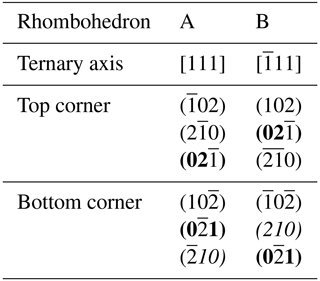
Table 3 lists the main faces of the two rhombohedra developed in this twin. A and B have the two faces (02 (front) and (01) (back) in common; these faces are invariant under the twin operation m(100) and are the largest faces of the two twinned individuals. The re-entrant dihedron is formed by small faces (02) (A) and (102) (B). A is of the clockwise type: streaks on the (02) face of A are parallel to the [010] direction of the re-entrant angle. Consequently, B is of the counterclockwise type. There are also two other lateral main faces, (20) (A) and 0) (B), and two minor faces at the bottom, (10 (A) and (0 (B). Faces (10) and (210) are lacking. Figure 10 is a more complex scheme, with six additional P faces and five {100} faces.
Figure 11 is the stereographic projection of the twin of Fig. 9. The (100) twin plane m is the only twin element. In the twin classification according to chromatic point groups (Nespolo, 2019), it corresponds to point group m′. Figure 12a symbolizes this MT type (A + B pair). Any other combination of two adjacent hemi-rhombohedra (edge connected: 12 possibilities) gives the same twin, for instance the C + D pair (Fig. 12b).
5.4 Rotation twin (RT – type 2)
Figure 13 gives an example of this second twin type. This sample ( cm) is well developed, with numerous small crystals (∼0.1 to 5 mm) of triglyph pyrite attached to it. The top view (Fig. 13b) shows a quite perfect diamond-shaped profile, while the lateral view of the short side (Fig. 13c) shows a pronounced re-entrant angle, identical to the re-entrant angle of twin type 1, which differentiates two crystals (A and C). Striations of the two short sides result from the combination of (021), (02, and (010) faces, and their symmetric ones, while the two long sides correspond to well-developed smooth (20) and (10) faces, with small (210) and (0) truncations, respectively.

Figure 19Incomplete crossed twin (∼4 cm – Borieva): (a) front view, (b) oblique view, and (c) right side.
This twin is also a contact twin, idealized in Fig. 14 with A and C hemi-rhombohedra. The composition plane is (100), and C is derived from A by a two-fold rotation around [001]. The ternary axes of A and C correspond to [111] and [1] of the cubic cell, respectively. They correspond to ternary axes of two opposite corners of the cube, with an angle of 109.47∘. Striations visible in Fig. 13b are parallel to the re-entrant angle. Contrary to twin type 1, twinned crystals have the same rotation direction, clockwise or counterclockwise, which defines two twin sub-types. It is clockwise for the sample of Fig. 13. One sub-type is derived from the other by the (100) reflection plane.

Figure 20Crossed twin (Borieva): oblique view (a) and scheme (b). Yellow line: limit of crystal C2. Small arrow: point of view of Fig. 21.
As the two-fold axis is contained in the composition plane, it corresponds to parallel hemitropy (Nespolo and Souvignier, 2017). According to Fig. 14, the only twin element is the two-fold axis 2[001]: it corresponds to chromatic point group 2′.
Table 4 lists the main faces of the two rhombohedra observed in this twin. Among the 12 possible faces, two are absent, four are common to the two crystals, and the ideal twin presents only eight faces. The two common faces (20) and (10) are smooth and well developed; they correspond to the large sides of the diamond-shaped profile (Fig. 13b). Figure 15 schematizes the more complex morphology encountered in natural twins, on the basis of the sample of Fig. 13. Figure 16 is the symbolic representation of the two sub-types of the rotation twin, clockwise and counterclockwise.
5.5 Crossed twin (CT – type 3)
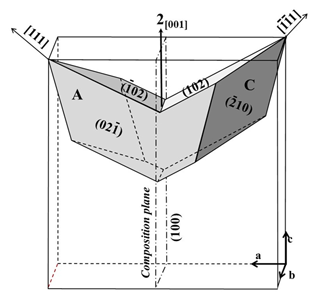
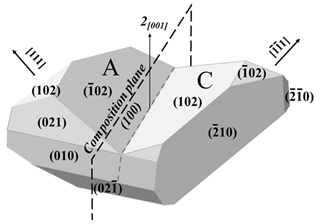
The combination of two hemi-rhombohedra gives two possible twin types, depending on whether they correspond to two adjacent or two opposite cube corners. The combination of two complete rhombohedra, instead, gives only one type of penetration twin, as represented ideally by Fig. 17. Here the BB′ rhombohedron is derived from AA′ through the (100) twin plane, as well as a two-fold rotation around [100]. Figure 18 gives the symbolic scheme of this CT type. The two individuals have a common symmetry center ; by adding the 2[100] twin axis (or the (100) twin plane), the twin corresponds to chromatic point group .
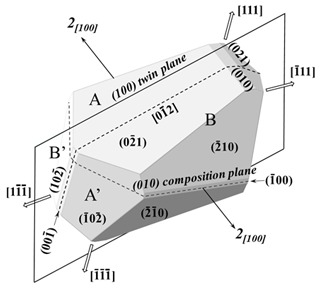
Figure 23Ideal scheme of the twin of Fig. 22. Dashed lines indicate the traces of the (100) twin plane and (010) composition plane.
Incomplete development of this twin type has been observed in two samples, corresponding to the dissymmetric association of one rhombohedron with a hemi-rhombohedron (Figs. 19 and 20). The front view of the first sample (Fig. 19a) indicates a reflection twin and the view of the right side (Fig. 19c) a clockwise rotation twin. The twin plane is (100), and [100] is the direction of the twin axis, with (010) as the composition plane.
The second twin (Fig. 20) is relatively large but very irregular: cm (mass: 70 g). This oblique view shows a smaller C crystal as an asymmetric triangular pyramid overcoming a large face of the second crystal AA′. A lateral view (Fig. 21) shows a strongly striated surface. The limit between the two crystals, irregular, is clearly visible, especially because there is no continuity between striations from one to the other crystal. It materializes the penetration between the two crystals.

Figure 25Simplified scheme of trapezoidal twin. (a) – front view, (b) – bottom view. Diamond: twin axis 2[001].
Some samples appear as dissymmetric flattened pyritohedra. The best example is the small sample ( cm) of Fig. 22. There are two large, well-developed smooth faces (each with its very small combined face at one of its extremities) that induce the crystal flattening. The four other sides, strongly striated, each correspond to the development of paired faces, two lateral large ones and two little ones. Intermediate, small cubic faces are also present. As all the faces of the pyritohedron are present, together with the faces of the cube, it resembles a distorted pyritohedron of cubic pyrite.
This dissymmetric pyritohedron would correspond to a complete crossed twin, according to the ideal scheme of Fig. 23, combining AA′ and BB′ rhombohedra. Twin elongation, as indicated by the elongation of the two large smooth faces (E type), corresponds to the direction [02]. (02 and (01) are the smooth faces. There is a (100) twin plane, which contains the elongation direction, and thus the median line of the large faces, as well as the middle of the edges between the two pairs of combined faces at the two extremities. There is also a twin axis, perpendicular to the (100) twin plane, through the middle of the two edges of the main lateral combined faces.
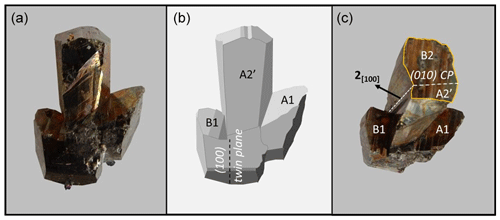
Figure 27“Trident” twin (Borieva). (a) Front view, (b) scheme of the front view, and (c) oblique view.
The lack of re-entrant angles corresponds to the development, during twin growth, of P faces, as (10) for B, paired with (0) for A′. Such a process of disappearance of a re-entrant angle is well known in other twinned minerals, for instance in Japan twins of quartz, which induces a flat triangular morphology (Grigor'ev and Jabin, 1975).
5.6 Trapezoidal twin (TT – type 4)
There is only one example of this twin (Fig. 24), with dimensions cm. Its front view shows a trapezoidal profile. There are two well-developed smooth lateral faces, (0) and (02, according to the ideal scheme of Fig. 25. The front view shows a quite symmetric morphology of the top and bottom surfaces, where the combinations of (210) and (20) faces form a double groove parallel to (010).
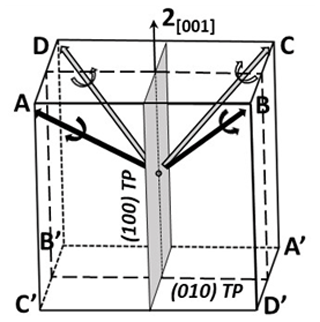
According to Fig. 25b, there is a second twin plane (100), perpendicular to the (010) twin plane of the reflection twin of type 1. This trapezoidal twin is a double-contact twin with two twin planes whose intersection gives a two-fold twin axis. It combines four hemi-rhombohedra, with their ternary axes at the four corners of a square. The (100) flattening of the twin would indicate that its growth was controlled by the main development of the (100) twin plane. Figure 26 symbolizes this twin type. The two twin planes and the common twin axis define the tetrachromatic point group (m(2)m(2)2(2))(4).
5.7 Erratic twinning
Some samples present an irregular morphology indicating erratic twinning. Fig. 27 shows a complex twin with a trident aspect. Its basal part corresponds to a reflection twin type (individuals A1 and B1). At the place of the re-entrant angle there is the development of an elongated twin of the rotation type (individuals A′2 and B2). While there is spatial continuity between A1 and A′2, B1 and B2 are disjoined. Apparently, the growth of this sample began as a reflection twin, followed by the development of the rotation twin. Other complex twin edifices, not detailed here, have rarely been encountered. These observations suggest that a new twin may appear during crystal growth, independently of the initial twin type.
6.1 Twin classification
The first crystals of pyrite with rhombohedral habitus were observed more than 160 years ago, and they have so far been considered simple morphological curiosities. The examination of numerous rhombohedral crystals of pyrite from the Madan ore field, as well as the characterization of their twinning, clearly proves that it corresponds to a pseudo-cubic trigonal pyrite variety (pyrite-R) of point group , not defined up to now. The different types of twinning observed (Table 5) are generated by symmetry operations present in cubic pyrite but absent in pyrite-R, which act as twin operations: {100} reflections and two-fold rotations). They all correspond to twinning by metric merohedry.
While in the classic iron-cross twin of cubic pyrite the twin point group corresponds to the cubic holohedry , the twin point groups of the various twin types of pyrite-R encountered in the Madan ore district are lower: monoclinic m′, 2′ or ', or orthorhombic (m(2)m(2)2(2))(4). The CT type involves whole rhombohedra, while the other types only involve hemi-rhombohedra. Otherwise, twinning may evolve during crystal growth to give complex edifices. On the basis of this twin classification, different crystallographic aspects can be examined.
6.2 Twin interface
Among various genetic categories of twins (Nespolo and Ferraris, 2004), twins of rhombohedral pyrite described here correspond to growth twins. In the nucleation process of a simple contact twin (here types 1 or 2), starting from a disordered medium (here a hydrothermal solution), the first step would probably be the formation of the twin interface (generally planar). This interface can be considered a very-few-atom-tick lamella (a single or a very small number of polyhedra), whose orientation is the composition plane. Such interface is often compared to a crystal defect. It seems better to consider it a diperiodic crystal (two free dimensions, the third with a finite width), acting as a support for the epitactic overgrowth of the two twinned individuals. The point group symmetry of this diperiodic crystal should match the point group symmetry of the twin.
In a reflection twin, its interface can be symbolized by a twin plane m with its indices as a subscript and a vector bisector of the ternary axes of the two hemi-rhombohedra. For instance, in Fig. 9, this interface will be noted as m(100)(b+c). Similarly, in a rotation twin, its interface can be symbolized by a two-fold twin axis 2 with the indices of its composition plane as a subscript and a vector within this plane parallel to the binary axis, with an index corresponding to the rotation, clockwise (C) or counterclockwise (AC). For instance, in Fig. 14, this interface will be noted as 2(100)cC.
In the crossed twin, the contact surface between the two rhombohedra is divided into four twin interface sectors, i.e., two for each interface type. From Fig. 17, one obtains Fig. 28 with the following sectors Sn: S1 m(100)(b+c), S2 , S3 2(100)aC, and S4 2(100)(−aAC). In the trapezoidal twin, there are also four twin interface sectors but of the same type: S1 m(100)(b+c), S2 , S3 , and S4 m(010)(a+c) (Fig. 29).
6.3 Polysynthetic twinning
In some twins, strong striation corresponds to the repetition of grooves (Fig. 24), which may correspond to polysynthetic twinning. The twin of Fig. 30 presents a zig-zag profile, which would correspond to the sequence A1–B–A2. Here, as in other twin samples, one observes a small shift between the trace of the re-entrant angle and the ridge on the opposite side. It indicates that the composition surface in such a contact twin is not exactly a plane. At the atomic scale, the composition surface of a twin is generally considered a variety of crystal defects. Ideally, in a contact twin, the growth of such a defect is constrained in two directions, which gives a composition plane, while in a penetration twin, there is no growth constraint (Kern, 1961; Nespolo and Moëlo, 2019), and the twin contact is a non-planar-surface (“rough surface” – see Fig. 21). The observed shift in contact twins may correspond to a constraint along only one direction, the groove direction. The composition surface would thus correspond to a “corrugated sheet”, with random undulations. Twin growth would be favored along the groove direction.
6.4 Cyclic cubic twinning
According to some observations, two cyclic tetrachromatic twins with cubic symmetry are possible, taking into account either four hemi-rhombohedra or four rhombohedra.
6.4.1 With four hemi-rhombohedra: CCT1 twin
The distorted rhombohedral crystal A of Fig. 31 (length: 5 cm, 75 g) shows a re-entrant angle on two of the three faces around its ternary axis. This corresponds to two clockwise rotation twins, A + C and A + D′, related through a 120∘ rotation around the ternary axis. C and D are poorly developed.
Theoretically, a second rotation would generate a third crystal B′, giving ideally a twin of four hemi-rhombohedra according to the four corners of a tetrahedron (cyclic cubic tetartohedral twin CCT1 – Fig. 32). It corresponds to twin point group (2(2)3(3,1))(4). There are two sub-types, clockwise (A + C + B′ + D′ – this figure) and counterclockwise (B + D + A′ + C′). The contact between individuals is composed of six distinct twin interfaces of the same type (for instance, 2(100)cC), each corresponding to a single rotation twin between two among the four constitutive hemi-rhombohedra. Such a CCT1 twin type has not been observed at Madan, but it could explain the pyrite tetrahedra described by Žorž et al. (2022).
6.4.2 With four rhombohedra: CCT2 twin
Another complex cubic twinning can be derived from the trapezoidal twin through the substitution of the four hemi-rhombohedra by four complete rhombohedra (CCT2 twin). It is symbolized by Fig. 7 in Sect. 5.2. It corresponds to twin point group (2 (all the symmetry operations lost with respect to the cubic hemihedral symmetry of pyrite appear here as twin operations). In each {100} twin plane, the twin interface is divided into four distinct sectors of the same interface type, for instance m(100)(b+c)], which gives a total of 12 sectors.

Figure 34Triglyph cubic pyrite with incurved faces from Ambas Aguas (Spain). Size: 1.5 cm (photo: F. Popa).
Figure 33 represents the ideal morphology of this twin. Some cubic crystals of pyrite from Ambas Aguas (Spain) present striated, strongly curved faces (Fig. 34). According to Grigor'ev and Jabin (1975), such a peculiar morphology relates to the category of split crystals. Here, it could be explained by a growth process initiated by this CCT2 twin type of trigonal pyrite.
6.5 Twin frequency
For a given mineral, the frequency of a twin type varies among deposits, and, when there are different twin types, these types generally have different frequencies. The main factor that favors one type above another is purely crystallographic, i.e., their relative degree of structural restoration through twin operations (Nespolo and Souvignier, 2015). But this rule cannot act between twin types 1 and 2, as these twins conduct to the same structural restoration: they would be equally probable. A chemical factor may favor one of these two twin types, as exemplified by the iron-cross twin, where, at the atom scale, the {110} twin boundary is Cu-rich (Rečnik et al., 2016).
Sulfide ores from the Madan ore field, especially those from the Borieva mine, provide a top sampling material for the characterization of rhombohedral pyrite as a new variety of pyrite, pseudo-cubic trigonal (pyrite-R), with various twin types by merohedry. Through careful X-ray single crystal study, Bayliss (1989) described another pseudo-cubic pyrite with orthorhombic symmetry, space group type Pca21.
Relative to ideal schemes, rhombohedral crystals as well their twins show growth defects which would need further detailed examinations. Face striation is more or less pronounced, even in a single crystal. Generally, it corresponds to the competition between the main E faces of the rhombohedron, its paired {210} P faces, and its intermediate cubic faces. But in other cases, it may be the trace of composition planes due to polysynthetic twinning. The distinction between these two types of striation is an open question. In addition, Madan sulfide ores provide various samples for future TEM study, following the work of Rečnik et al. (2016).
Twinning, observed for the first time at Borieva, is interesting not only from a crystallographic point of view but also from a crystal genetic one. The common formation of centimeter-scale rhombohedral crystals of pyrite as well as their twinning in the Madan ore field were probably subordinated to very peculiar and stable geochemical conditions during their growth. In situ observation of pyrite-R is necessary to fit its place in the paragenetic succession established by Vassileva et al. (2009b) at Madan, as well as to constrain geological and physical–chemical factors which permitted its formation. The late crystallization of pyrite-(R) would indicate a low temperature of formation. Moreover, reducing conditions are suggested by the association of graphite flakes at Gyudyurska.
In this study, based on a classic examination of crystal morphology, twinning of rhombohedral pyrite was analyzed supposing a cubic lattice and a trigonal crystal structure (twinning by metric merohedry). This hypothesis needs to be confirmed by precise crystal chemical examination through X-ray diffraction (study in progress), following the work of Bayliss (1989). Such an approach is a prerequisite to solve the question of the stability of pyrite-R relative to ordinary cubic pyrite.
The author has declared that there are no competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The main part of pyrite samples was obtained from mineral dealers Valentin Savov and Georgi Bozukov (Madan), as well as Christian Lolon (Cléguer, France). Careful review by Massimo Nespolo (Lorraine University, Nancy) and Emil Makovicky (Copenhagen University) permitted the author to greatly enhance the quality of the manuscript. The review process was meticulously supervised by Sergey Krivovichev (St. Petersburg State University). The author also appreciates the assistance of Pierre-Emmanuel Petit (IMN J. Rouxel, Nantes University, CNRS). Useful information was given to the author by Artem Oganov (Skolkovo Institute, Moscow), Cristian Biagoni (Pisa University), and Rossitsa Vassileva (Geological Institute, Sofia). Crystal drawing was facilitated using the software FACES© of Georges Favreau, who is sincerely thanked.
This paper was edited by Sergey Krivovichev and reviewed by Massimo Nespolo and Emil Makovicky.
Bayliss, P.: Crystal chemistry and crystallography of some minerals within the pyrite group, Amer. Mineral., 74, 1168–1176, 1989.
Bonev, I. I., Reiche, M., and Marinov, M.: Morphology, perfection and growth of natural pyrite whiskers and thin platelets, Phys. Chem. Minerals, 12, 223–232, 1985.
Gaubert, P.: Sur un cristal de pyrite, maclé suivant la loi des spinelles, Bull. Soc. fr. Minéral., 51, 211–212, 1928.
Goldschmidt, V.: Pyrite, in Atlas der Kristallformen, vol. 6, Winter Edit., Heidelberg, 1920.
Goldschmidt, V. and Nicol, W.: Spinellgesetz beim Pyrit und über Rangordnung der Zwillingsgesetze, Neues Jahr. Mineral., 2, 93–113, 1904.
Grigor'ev, D. P. and Jabin, A. G.: Ontogeny of Minerals, Nauka Edit., Moscow, 340 pp., 1975 (in Russian).
Hantsche, A. L., Kouzmanov, K., Milenkov, G., Vezzoni, S., Vassileva, R., Dini, A., Sheldrake, T., Laurent, O., and Guillong, M.: Metasomatism and cyclic skarn growth along lithological contacts: Physical and geochemical evidence from a distal Pb-Zn skarn, Lithos, 400–401, https://doi.org/10.1016/j.lithos.2021.106408, 2021.
Honma, H., Okamura, S., Sakakibara, Y., Nakata, M., and Inamori, J.: On pyrite with hemihedral symmetry of pentagonal dodecahedron from Chichibu mine, Saitama prefecture, Bull. Tokyo Gakugei Univ., Section IV, 39, 117–126, 1987.
Jeremejew, I. V.: Beschreibung einiger Mineralien, welche auf den Goldwäschereien der Ländereien der Orenburgischen Kosaken und Baschkiren gefunden werden [German translation: Th. Tschernyschew of Eremeyev, I. V., Neues Jahr. Min. Geol. Pal., 2, 256–266, 1889], Gornii Journal, 3, 263–306, 1887 (in Russian).
Kern, R.: Sur la formation des macles de croissance, Bull. Soc. Fr. Minéral. Cristallogr., 84, 292–311, 1961.
Moëlo, Y., Nespolo, M., and Farges, F.: Pyrite contact twins, Acta Cryst., 79, 32–45, https://doi.org/10.1107/S2052520622011714, 2023.
Nespolo, M.: The ash heap of crystallography: restoring forgotten basic knowledge, J. Appl. Crystallogr., 48, 1290–1298, 2015.
Nespolo, M.: The chromatic symmetry of twins and allotwins, Acta Cryst., 75, 551–573, 2019.
Nespolo, M. and Ferraris, G.: Twinning by syngonic and metric merohedry. Analysis, classification and effects on the diffraction pattern, Z. Kristallogr., 215, 77–81, 2000.
Nespolo, M. and Ferraris, G.: The oriented attachment mechanism in the formation of twins – a survey, Eur. J. Mineral., 16, 401–406, 2004.
Nespolo, M. and Moëlo, Y.: Structural interpretation of a new twin in staurolite from Coray, Brittany, France, Eur. J. Mineral., 31, 785–790, 2019.
Nespolo, M. and Souvignier, B.: Application of the crystallographic orbit to the study of twinned crystals, The example of marcasite, Cryst. Res. Technol., 50, 442–450, 2015.
Nespolo, M. and Souvignier, B.: Structural analysis of twins in feldspars. I. Carlsbad twinning, Eur. J. Mineral., 29, 939–947, 2017.
Oganov, A. R.: A find of rhombohedral crystals of pyrite, Zap. Vces. Miner. Obsch., 1, 65–68, 1996.
Palache, C., Berman, H., and Frondel, C.: The system of mineralogy, Vol. I: Elements, sulfides, sulfosalts, oxides, John Wiley & Sons Eds., New-York, 834 pp., 1944.
Petrussenko, S.: Minerals of the Madan ore field, Mineral. Rec., 22, 439–445, 1991.
Rečnik, A., Zavašnik, J., Jin, L., Čobić, A., and Daneu, N.: On the origin of “iron-cross” twin of pyrite from Mt. Katarina, Slovenia, Mineral. Mag., 80, 937–948, 2016.
Smolar, G.: Die Pyritzwillinge, Z. Kristallogr., 52, 460–500, 1913.
Vassileva, R. D., Atanassova, R., and Bonev, I. K.: A review of the morphological varieties of ore bodies in the Madan Pb-Zn deposits, Central Rhodopes, Bulgaria, Geoch. Mineral. Petr., Sofia, 47, 31–49, 2009a.
Vassileva, R., Atanassova, R., Kouzmanov, K., and Kerestedjian T.: Madan Pb-Zn deposits, Central Rhodopes, Bulgaria: mineralization stages and fluid inclusion microthermometry, Proc. XX ECROFI, University of Granada, 271–272, 2009b.
Vassileva, R. D., Atanassova, R., and Bonev, I. K.: Morphogenetic types of ore bodies, ore textures and crystallization mechanisms in the hydrothermal Madan deposits, Central Rhodopes, Scientific Annals, Proceedings of the XIX CBGA Congress, Thessaloniki, Greece, 99, 355–361, 2010.
Žorž, M., Voudouris, P., and Rieck, B.: Pyrite with lower cubic symmetry from Lavrion, Greece, Geologija, 65, 5–19, 2022.