Effect of Fe–Fe interactions and X-site vacancy ordering on the OH-stretching spectrum of foitite

The OH-stretching infrared absorption spectrum of a tourmaline sample close to the foitite end-member is interpreted in the light of the density functional theory (DFT) modeling of iron-bearing Y₃Z₆ clusters in tourmaline. The iron-bearing clusters reflect the Al-rich and Na-deficient character of foitite and contain either two Fe²⁺ and one Al³⁺ or one Fe²⁺ and two Al³⁺ ions at the Y sites. The clusters are embedded in a tourmaline host structure with dravite composition. For the iron dimer models, the structural and vibrational properties corresponding to the ferromagnetic (FM) or anti-ferromagnetic (AFM) arrangement of the iron spins and the effect of vacancy ordering along the [001] axis are considered. A significant difference in the relaxed structure of the FM and AFM clusters is observed, stemming from the electron delocalization and Fe–Fe bonding interactions in the FM cluster. These bonding interactions are not allowed in the AFM cluster. In this case, the valence electrons with opposite spins remain separately localized on the two Fe atoms. The AFM configuration is more stable than the FM one in the theoretical models, provided that the description of the on-site Coulomb repulsion in Fe(3d) orbitals is improved within the DFT + U framework. Based on the theoretical results, the two bands at 3630 and 3644 cm⁻¹ in the vibrational spectra of iron-rich and Na-deficient tourmalines are assigned to ^WOH groups associated with ^YFe${}_{\mathrm{2}}^{\mathrm{2}+}$^YAl³⁺ environments with an AFM coupling of Fe ions and surrounded by one and two vacant X sites, respectively. The two major ^VOH bands of the experimental spectrum are interpreted on the same basis, and these interpretations are extrapolated to Mn-bearing tourmalines.

1 Introduction

The OH-stretching modes of hydrous minerals lead to characteristic signals in their infrared or Raman spectra (Libowitzky and Beran, 2006). The high vibrational frequency and short correlation length of the related excitations support the use of OH-stretching vibrations as local probes of structural order and site occupancies in complex minerals (Hawthorne, 2016). This property is particularly useful for the study of solid solutions because the nature of neighboring cations affects the OH-stretching frequency. The OH-stretching spectra then reflect the cationic ordering in the investigated samples and provide important information about their thermodynamic properties (Hawthorne, 2016). In this approach, the experimental study of series of synthetic or natural samples along selected compositional joins can serve as a basis for the investigation of more complex samples. Experimental spectra are usually interpreted under the light of empirical relations between the OH-stretching frequency and microscopic parameters, such as the H-bond geometry (e.g., Libowitzky and Beran, 2006) or the sum of bond valences (e.g., Hawthorne, 2016; Bronzova et al., 2019).

However, this approach proves to be challenging for systems with a complexity level such that uncertainties already arise when interpreting the vibrational spectra of end-members. This is the case for the minerals belonging to the tourmaline supergroup. Tourmalines are complex borosilicates (Fig. 1) with the general formula XY₃Z₆(T₆O₁₈)(BO₃)₃V₃W, the most common ions (or vacancy) at each site being, for X, Na⁺, Ca²⁺, K⁺ and vacancy; for Y, Fe²⁺, Mg²⁺, Mn²⁺, Al³⁺, Li⁺, Fe³⁺ and Cr³⁺; for Z, Al³⁺, Fe³⁺, Mg²⁺ and Cr³⁺; for T, Si⁴⁺, Al³⁺ and B³⁺; for B, B³⁺; for V, OH⁻ and O²⁻; and for W, OH⁻, F⁻ and O²⁻ (Henry et al., 2011). Structural clusters comprising three equivalent octahedral Y and six equivalent octahedral Z sites can be identified in ideal tourmaline. These clusters with a 3-fold symmetry are the basic structural units that can be considered for the interpretation of the OH-stretching spectra of tourmaline (e.g., Bosi et al., 2016). The ^WOH group is coordinated to the three Y octahedral sites and points toward the X site. The three equivalent ^VOH groups are coordinated to one Y site and two Z sites and share a weak H bond with the O₅ oxygen bridging two tetrahedral sites (Gatta et al., 2014). Accordingly, the more intense ^VOH bands are usually observed at a lower frequency than the ^WOH bands (e.g., Watenphul et al., 2016; Berryman et al., 2015; Bosi et al., 2016). The presence of vacancies at the X site significantly decreases the ^WOH-stretching frequency with respect to their counterparts with the occupied X site. Even in samples close to end-member composition, the partial occupancy of the X site, the cationic inversion affecting the Y and Z octahedral sites, and the partial deprotonation of OH groups at the W site leads to significant uncertainties in the interpretation of the ^VOH- and ^WOH-stretching spectra. In this context, first-principles modeling methods represent an alternative way to relate the vibrational spectra to the atomic-scale environment of OH groups. Based on their theoretical modeling, the main bands in the vibrational spectra of dravite and Mg-foitite, two end-members of the tourmaline supergroup, have recently been assigned to specific cationic configurations and site occupancies, confirming the sensitivity of OH groups to their local environment (Fuchs et al., 2022). In addition, this study has revealed an effect of the vacancy ordering along the [001] axis on the ^WOH-stretching frequency. The ^WOH band associated with a ^YMg${}_{\mathrm{2}}^Y$Al configuration surrounded by two vacant X sites (^X□–^YMg^YMg^YAl–^WOH–^X□), as in the Mg-foitite end-member, is increased by 17 cm⁻¹ with respect to the equivalent configuration with a single vacant X site facing the ^WOH group (^XNa–^YMg^YMg^YAl–^WOH–^X□) in dravite.

Figure 1 View of the ideal tourmaline structure displaying the main crystal sites involved in a structural YZZ–YZZ–YZZ cluster. The vertical dashed line corresponds to the 3-fold axis parallel to the [001] direction of the hexagonal supercell. Three equivalent Y sites and six equivalent Z sites occur in the cluster. The X^a and X^b sites are equivalent by translational symmetry but occur at different distances from the ^WOH belonging to a given cluster.

Compared with Mg–Al tourmalines, Fe-bearing tourmalines, such as schorl and foitite with the nominal formula NaFe₃Al₆(Si₆O₁₈)(BO₃)₃OH₄ and □Fe₂Al₇(Si₆O₁₈)(BO₃)₃OH₄, respectively, correspond to a higher complexity level from both experimental and theoretical perspectives. The frequent occurrence of Fe³⁺ ions in experimental or natural samples increases the number of potential cationic configurations associated with OH groups (e.g., Bosi and Lucchesi, 2004). The importance of electronic correlation (e.g., Hsu et al., 2011) as well as potential metal–metal interactions (e.g., Sherman, 1987) also deserves special attention in the theoretical modeling of iron-bearing systems. Accordingly, the extrapolation of the band assignment proposed for the Mg–Al tourmalines (Fuchs et al., 2022) to Fe-bearing tourmalines might not be straightforward. However, iron-bearing tourmalines are important petrogenetic indicators due to their ubiquity and to their sensitivity to fO₂ conditions (e.g., Foit et al., 1989; Fuchs et al., 2002; Pieczka and Kraczka, 2004), which motivates a detailed study of their vibrational properties. Here, we analyze the infrared spectrum of a natural foitite sample close to the foitite end-member. Its low content in Mg²⁺, Fe³⁺ and alkali cations facilitates comparison with the theoretical properties of selected iron-bearing clusters in a model tourmaline structure. A revised interpretation of the OH-stretching bands in alkali-deficient ferrous tourmalines is then proposed.

2 Methods

2.1 Provenance, composition and FTIR analysis of the foitite sample

The LH12 sample belongs to a series of Fe-bearing tourmaline samples previously studied by Paulet et al. (1991) and Fuchs et al. (1995, 2002). It is has been collected from the core of the alteration system of Lincoln Hill in the Humboldt Range (Pershing County, Nevada). Hydrothermal alteration affected volcanic and volcano clastic piles that had accumulated in pull-apart-type basins. Foitite appears in heavily transformed zones in association with quartz and pyrophyllite (Al₂Si₄O₁₀(OH)₂). Based on Mössbauer spectroscopy, the LH12 sample only contains Fe²⁺ ions at the Y (86.5 %) and Z (13.5 %) site, which leads to the formula assuming full B and OH occupancies (Fuchs et al., 1995):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& \left({\square }_{\mathrm{0.81}}{\mathrm{Na}}_{\mathrm{0.19}}\right)\left({\mathrm{Mg}}_{\mathrm{0.05}}{\mathrm{Mn}}_{\mathrm{0.01}}{\mathrm{Ti}}_{\mathrm{0.01}}{\mathrm{Fe}}_{\mathrm{1.23}}^{\mathrm{2}+}{\mathrm{Al}}_{\mathrm{1.46}}\right)\\ & \left({\mathrm{Fe}}_{\mathrm{0.19}}^{\mathrm{2}+}{\mathrm{Al}}_{\mathrm{5.81}}\right)\left({\mathrm{Si}}_{\mathrm{5.96}}{\mathrm{Al}}_{\mathrm{0.04}}{\mathrm{O}}_{\mathrm{18}}\right){\left(B{\mathrm{O}}_{\mathrm{3}}\right)}_{\mathrm{3}}{\left(\mathrm{OH}\right)}_{\mathrm{4}}.\end{array}\end{array}$$

This sample is thus close to the foitite–schorl join, which is characterized by the alkali-defect type substitution (Foit and Rosenberg, 1977):

$$\begin{array}{}\text{(2)}& {}^X{M}^{+}{+}^Y{M}^{\mathrm{2}+}{=}^X\square {+}^Y{M}^{\mathrm{3}+},\end{array}$$

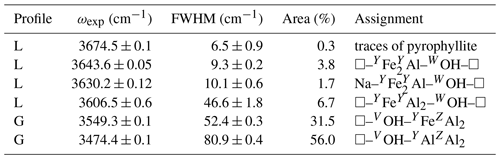
where in the present case M⁺, M²⁺ and M³⁺ stand for Na⁺, Fe²⁺ and Al³⁺, respectively. The Li content is below 200 ppm (Fuchs et al., 1995). The low amount of Mg and the lack of Fe³⁺ should facilitate the interpretation of its OH-stretching spectrum by limiting the number of relevant local configurations. The transmission powder infrared spectrum of the LH12 sample was recorded at room temperature on a pellet containing 1.5 and 300 mg of sample and KBr, respectively, using a Nicolet Magna 560 FTIR spectrometer with a resolution of 2 cm⁻¹. The OH-stretching spectrum was fitted using Fityk software (Wojdyr, 2010). Depending on the bands, Lorentzian or Gaussian profile shapes have been used (Table 1).

Table 1 Profile function, frequency (ω_exp), full width at half maximum (FWHM) and relative area of OH-stretching bands in the LH12 sample (Fig. 2).

L: Lorentzian; G: Gaussian.

2.2 Theoretical modeling

The theoretical properties of iron-bearing clusters in dravitic tourmaline have been investigated using density functional theory (DFT) with the generalized gradient approximation (GGA) to the exchange–correlation functional as proposed by Perdew, Burke and Ernzerhof (PBE) (Perdew et al., 1996). The modeling was done as in Fuchs et al. (2022) using a plane-wave and pseudo-potential scheme, as implemented in the PWscf and PHonon codes from the Quantum ESPRESSO package (Giannozzi et al., 2009; http://www.quantum-espresso.org, last access: 12 February 2023). The ionic cores were described by optimized norm-conserving pseudo-potentials from the SG15 ONCV library (Hamann, 2013; Schlipf and Gigy, 2015). The wave functions and the charge density were expanded in plane waves with 80 and 480 Ry cutoffs, respectively. Relaxation of atomic positions was performed until the residual forces on atoms were less than 10⁻⁴ Ry a.u.⁻¹.

The models of iron-bearing clusters (Table 2) have been obtained by selectively substituting Fe for one or two ^YMg atoms in specific $\mathrm{1}\times \mathrm{1}\times \mathrm{2}$ supercell configurations of Fuchs et al. (2022). Although being a significant simplification, the study of isolated iron-bearing clusters in Al–Mg tourmaline ensures a proper control of the magnetic properties of the system using spin-polarized calculations. The high-spin state has been assumed for the Fe²⁺ ions, and ferromagnetic (FM) order and anti-ferromagnetic (AFM) order have been considered for the iron dimers. The theoretical (super)cell parameters are identical to those previously used, which facilitates the comparison with the results of Fuchs et al. (2022). For the electrostatically charged models, the macroscopic neutrality of the periodic system was ensured by a compensating homogeneous background charge spread over the cell. Harmonic vibrational properties (atomic displacements and frequencies of the transverse optical modes at the Brillouin zone center) were calculated using the density functional perturbation theory (DFPT) (Baroni et al., 2001) as implemented in the PHonon code (Giannozzi et al., 2009). The OH-stretching frequencies have been determined by only considering the displacements of the oxygen and hydrogen atoms belonging to the OH groups of the Fe-bearing cluster as in Fuchs et al. (2022). Additional information on the theoretical approach is provided in the Supplement. Due to the approximations involved in the calculation, the theoretical frequencies can differ from their experimental counterparts by several dozens of wavenumbers (cm⁻¹). However, previous studies suggest that this difference is mostly systematic for a given mineral, making it possible to establish well-defined correlations between experimental and theoretical frequencies (e.g., Balan, 2020; Fuchs et al., 2022).

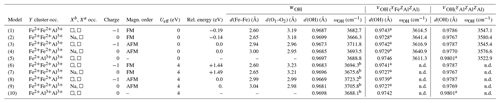
Table 2 Local configuration, relative energy, theoretical interatomic distances and OH-stretching frequencies (ω_OH) of iron-bearing clusters in tourmaline. The d(O₁–O₂) distance corresponds to the length of the edge shared by the Y octahedral sites occupied by iron atoms. Model structures are given as .cif files in the Supplement.

^a Two symmetric sites. ^b Frequencies obtained using finite differences. n.d.: not determined.

In addition, more realistic DFT + U calculations have been performed to improve the treatment of inter-electron repulsion in the partially occupied Fe(3d) orbitals. This approach was previously used for the modeling of iron pairs in beryl (Lin et al., 2013). In DFT + U calculations, an effective correction based on the Hubbard model of electron correlations in solids is introduced to account for imperfect cancellation of self-interaction between strongly localized 3d electrons. The correction, described by the U_eff parameter, removes spurious Coulomb repulsion of an electron with itself. It favors the localization of electrons and therefore integer occupancy of the atomic orbitals. In the present study, the U_eff value was set to 4 eV. It is in the range of the U_eff parameters self-consistently determined in various Fe-bearing minerals (2.9 to 4.9 eV) (Cococcioni and De Gironcoli, 2005; Hsu et al., 2011; Blanchard et al., 2008).

Although implemented in the PWscf code, the DFPT calculation of vibrational frequencies at the DFT + U level is prohibitively slow for large system sizes. Selected ^WOH-stretching frequencies were thus obtained using a finite-difference method (Balan et al., 2007). The total energy of the system was calculated for O and H displacements along the OH bond direction, while keeping the mass center of the OH group stationary. A total of eight displacements, symmetric with respect to the equilibrium position, were considered, corresponding to OH distance variations from −0.04 to 0.04 a.u. The total energy values were fitted using a fourth-order polynomial, and the harmonic OH-stretching frequency was obtained from the quadratic coefficient. Testing of the method on a standard GGA configuration led to a stretching frequency within 0.1 cm⁻¹ of that obtained using DFPT.

3 Results

3.1 The infrared spectrum of the LH12 sample

Two regions can be identified in the OH-stretching spectrum of tourmalines. Above 3600 cm⁻¹, the bands are usually ascribed to ^WOH groups, whereas the more intense signals observed below 3600 cm⁻¹ are related to ^VOH groups. However, both types of signal can overlap in the 3600–3620 cm⁻¹ region.

The FTIR spectrum of the LH12 sample (Fig. 2) displays two narrow bands at 3644 and 3630 cm⁻¹ related to ^WOH groups. Comparison with other samples from the same locality indicates that the weak narrow band at 3674 cm⁻¹ originates from trace amounts of pyrophyllite in the powder sample. The ^VOH groups produce two strong peaks at 3468 and 3546 cm⁻¹. The 3468 cm⁻¹ peak is asymmetric, with a significant broadening on its low-frequency side. The position of the broad contributions on its low-frequency tail was assessed from the local minima observed in the first derivative of the spectrum and was kept fixed during the fit of the spectrum. A satisfactory fit of the spectrum (Fig. 2) could then be achieved using six bands at 3137, 3270, 3343, 3407, 3474 and 3549 cm⁻¹ and three narrow bands at 3644, 3630 and 3674 cm⁻¹ (Table 1). A shoulder on the high-frequency side of the strong 3546 cm⁻¹ peak corresponds to an additional band at 3606 cm⁻¹ in the fit. Due to its overlap with the other bands, its parameters are however affected by a significant uncertainty. Note also that the positions (Table 1) of the two components corresponding to the two major peaks slightly differ from the peak maximum at 3468 and 3546 cm⁻¹. This difference can be ascribed to the constrained symmetric Gaussian shape adopted for these components.

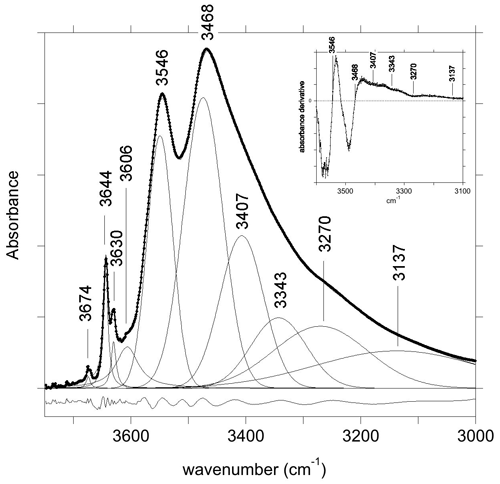
Figure 2 Powder infrared absorption spectrum of the LH12 sample in the OH-stretching range. The spectrum was decomposed into individual components (Table 1). The inset shows the first derivative spectrum that was used to assess the position of the four broader components accounting for the low-frequency tail of the broad peak at 3468 cm⁻¹. The residue reported at the bottom was arbitrarily shifted for clarity's sake.

As pointed out by Gonzalez-Carreño et al. (1988), the interpretation of the broad bands in the 3100–3400 cm⁻¹ range (Table 1) is not straightforward. In this low-frequency range, the tourmaline powder spectra can involve contributions related to anomalous dispersion effects (e.g., Prost, 1972), to traces of molecular water (Castañeda et al., 2000), and to low amounts of tetrahedral boron (Bosi et al., 2012; Kutzscbach et al., 2016; Bronzova et al., 2019) or aluminum (Nishio-Hamane et al., 2014; Bosi et al., 2022b). Accordingly, the four broad bands accounting for the low-frequency tail of the 3468 cm⁻¹ peak (Fig. 2) will not be further discussed in the present study.

3.2 Theoretical results

3.2.1 Structural and electronic properties of iron-bearing clusters in tourmaline

A series of iron-bearing clusters in tourmaline have been investigated (Table 2). They correspond to various schemes of Y-site occupancy and vacancy ordering and reflect the Al-rich and X-site-deficient character of foitite. The model with a local configuration closer to the foitite end-member, which has a fully vacant X site, consists in a cluster of two Fe atoms (Fe dimer) and one Al atom at the Y site surrounded by two vacant X sites along the c axis. As X sites are often partially occupied, an equivalent model with a single vacancy in the X site facing the ^WOH group (referred to as X^a, Fig. 1) has also been considered. In this case, the X site on the opposite side of the Y₃Z₆ cluster (referred to as X^b, Fig. 1) is occupied by Na. A third model consists in one Fe and two Al atoms at the Y site surrounded by two vacant X sites. All these models display a mirror symmetry, leading to two equivalent ^VOH groups in ^YFe^ZAl₂ environments for the ^YFe dimers and to two equivalent ^VOH groups in ^YAl^ZAl₂ environments for the ^YAl dimer (Table 2).

Both the FM and the AFM configurations of the ^YFe dimers have been considered. The results obtained with one or two vacant X sites are roughly similar (Table 2). The magnetic configuration has a significant effect on the structure of the iron dimers. Considering the Fe dimers with two vacant X sites, the Fe–Fe distance is 2.6 Å in the FM configuration and increases to 2.94 Å in the AFM configuration. The bond length of the ^WOH groups is shorter by more than 10⁻³ Å in the AFM configuration than in the FM one. In contrast, the magnetic coupling at the Y site has a negligible effect on the ^VOH bond length with variations <10⁻⁴ Å. At the GGA level, the FM configuration of the ^YFe dimer is found to be more stable than the AFM configuration by 0.19 eV. In the models with a single vacancy at the X site, similar variations in the Fe–Fe and OH distances are observed between the AFM and FM configurations (Table 2).

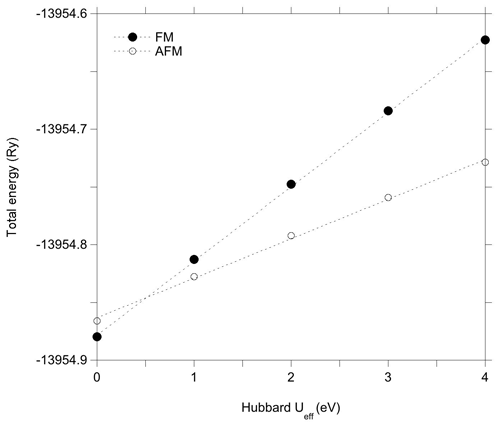
The Hubbard correction applied in DFT + U calculations has a moderate effect on the structure of the clusters (Table 2). Bond length variations in the ^WOH and ^VOH coordinated to iron atoms are smaller than 10⁻³ Å. For the ^VOH group solely coordinated to Al atoms, the variation is negligible (<10⁻⁴ Å). In the AFM-coupled iron dimers, the Fe–Fe distance increases by ∼ 0.04 Å. However, the Hubbard correction significantly affects the relative energy of the magnetic configurations, reversing the relative stability of the AFM and FM configurations. In the DFT + U calculation, the AFM configuration is systematically found to be more stable than the FM one, with an energy difference reaching 1.44 eV for U_eff=4 eV. Calculations using intermediate U_eff values of 1, 2 and 3 eV indicate that the energy difference between the two magnetic configurations is linearly related to the U_eff value (Fig. 3).

Figure 3 Total energy of the models with iron dimers and two vacancies reported as a function of the Hubbard U_eff parameter value. The anti-ferromagnetic (AFM) coupling is favored with respect to the ferromagnetic (FM) coupling in the more realistic U-corrected models.

3.2.2 Theoretical OH-stretching frequencies related to Fe-bearing clusters

The investigated clusters display significant variations in OH bond length which correlate with the related OH-stretching frequencies (Fig. 4). For the ^VOH group the distance–frequency relation matches that previously determined on theoretical models of dravite and Mg-foitite (Fuchs et al., 2022). For the ^WOH groups, the frequencies tend to be downshifted by 10 to 20 cm⁻¹ from the previously established relation. A minor splitting (∼ 1 cm⁻¹) occurs for the two symmetric ^VOH groups due to their weak vibrational coupling, as discussed by Fuchs et al. (2022). The average frequencies are reported in Table 2 and Fig. 4.

Figure 4 Relation between theoretical OH-stretching frequency (ω_OH) and OH bond length (d(OH)) (Table 2). The PBE and PBE + U values are reported. The dashed line corresponds to the correlation determined on the dravite and Mg-foitite models (Fuchs et al., 2022): ω_OH= 18 668 − 15 477 d(OH). Filled circles: ^WOH in ^YFe${}_{\mathrm{2}}^Y$Al environment with AFM configuration; filled squares: ^WOH in ^YFe${}_{\mathrm{2}}^Y$Al environment with FM configuration; triangle: ^WOH in ^YFe^YAl₂ configuration; diamonds: ^VOH groups; open circles: Mg-bearing clusters (Fuchs et al., 2022).

As in the Mg–Al system, the occupancy of the X site affects the vibrational frequencies of the ^WOH and ^YOH groups. The ^WOH frequency associated with the iron dimers surrounded by two vacancies is higher by 16 to 19 cm⁻¹ than that calculated when a Na atom occupies the X^b site (Fig. 1). The presence of a vacancy (instead of a Na atom) at the X^b site decreases the ^VOH frequency by 25 to 35 cm⁻¹ for the ^YFe^ZAl₂ and ^YAl^ZAl₂ environments (from ∼ 3640 to ∼ 3615 cm⁻¹ and from ∼ 3580 to ∼ 3545 cm⁻¹, respectively; Table 2). It is also noteworthy that the ^VOH in the ^YAl^ZAl₂ environment is affected by the presence of one or two Fe²⁺ ions in the Y₃ cluster. In contrast, the frequency of the ^VOH in the ^YFe^ZAl₂ environment is less affected (Table 2).

The effect of cationic vacancies on the ^VOH and ^WOH stretching can be qualitatively understood by considering that local electric fields acting on OH groups in solids can strongly affect their stretching frequency (e.g., Hermansson, 1991). From this perspective, the removal of the Na⁺ cation is equivalent to locating a negative charge at the X site. The electric field induced by the X^a vacancy is directed from O to H, resulting in a lengthening of the ^WOH group and significant vibrational frequency decrease, as observed between dravite and Mg-foitite (∼ 100 cm⁻¹; Fuchs et al., 2022). The presence of an X^b vacancy, more distant from the ^WOH group (Fig. 1), partly counterbalances the effect of the X^a vacancy, explaining why the ^WOH-stretching frequency depends on the vacancy ordering along the [001] axis. As only the longitudinal component of the electric field is effective in inducing a frequency shift (Hermansson, 1993), the X vacancies predominantly affect the ^WOH groups, which are located on the 3-fold structural axis (Fig. 1). Due to a more lateral configuration, the X^b vacancy has a weaker effect on the neighboring ^VOH groups but still decreases their stretching frequency.

When considering the magnetic configurations, the shorter ^WOH bond length in the AFM configuration (with respect to the FM one) increases the OH-stretching frequency by more than 27 cm⁻¹. In the DFT + U-corrected models, the ^WOH frequencies further increase by ∼ 10 cm⁻¹ for both the AFM and the FM configurations with respect to those obtained using the standard DFT (Table 2). Accordingly, the U correction does not significantly affect the difference in ^WOH-stretching frequencies, which mostly reflects the structural differences between the FM and AFM configurations. Thanks to the significant structural relaxation and frequency variation due to the Fe–Fe interactions, it is thus possible to distinguish the different magnetic configurations of Fe²⁺ pairs through their vibrational OH-stretching signature. Note that the effect of the U correction on the ^WOH-stretching frequency of the cluster with a single Fe atom is negligible (<1 cm⁻¹), reflecting the weakness of the OH bond length variation (∼ 10⁻⁴ Å, Table 2).

4 Discussion

4.1 Interplay of magnetic ordering and electronic structure in Fe–Fe clusters

The magnetic ordering of the iron dimers in tourmaline significantly affects their local structure. The shortening of the Fe–Fe distance, as well as concomitant lengthening of the O₁–O₂ distance along the edge shared by Fe-occupied octahedral sites (Table 2), is noteworthy. This suggests that the magnetic ordering exerts a strong influence on the electronic structure of the cluster, driving the structural relaxation.

The electronic structure of (Fe₂O₁₀)¹⁵⁻ dimers has previously been studied by Sherman (1987) to model the intervalent charge transfer between high-spin Fe²⁺ and Fe³⁺ ions in minerals. Fe²⁺–Fe³⁺ charge transfer is a common feature of iron-bearing minerals. In tourmaline, thermally activated transfers are attested by the detection of intervalent iron atoms in Mössbauer studies (e.g., Fuchs et al., 1995; Andreozzi et al., 2008). In high-spin iron ions, the minority-spin (β) 3d states are split off from the fully occupied majority-spin (α) states by the intra-atomic exchange interaction. The Fe(3d) β states of the dimer also occur at an energy significantly higher than the O(2p) states, favoring their localization and explaining why a molecular-type approach is more relevant to modeling the charge transfer than approaches related to band theory (Sherman, 1987). In the ground state of the FM configuration of the symmetric (Fe₂O₁₀)¹⁵⁻ dimer, the highest occupied molecular orbital (HOMO) results from an axial (σ) bonding interaction between two Fe(3d) β orbitals. Due to the FM order, the minority-spin electron can be delocalized over the two Fe atoms. In the AFM configuration, the minority spin of one Fe atom corresponds to the majority spin of the other. As the majority-spin states are fully occupied and occur at a lower energy than the minority-spin states, the delocalization of the minority-spin electron present on one Fe atom on the other one is not possible. Thus, the ground state of the AFM configuration corresponds to the localization of the minority-spin electron on a single Fe atom of the dimer, giving distinguishable Fe²⁺ and Fe³⁺ ions (Sherman, 1987).

In the present system (Fig. 5), the iron valence states occur at an energy ∼ 2 eV above the top of the valence band related to O(2p) states, as determined on the pristine dravite model of Fuchs et al. (2022). The ^YFe²⁺ dimers in tourmaline differ from the (Fe₂O₁₀)¹⁵⁻ dimer by significantly stronger site distortions, involving O atoms bonded to H, Al, Si or B atoms, and by the occurrence of the two minority-spin electrons related to the two Fe²⁺ ions (instead of one in the Fe²⁺–Fe³⁺ pairs). However, their calculated properties can be analyzed from a molecular perspective and a comparison can be drawn with those of the (Fe₂O₁₀)¹⁵⁻ dimer.

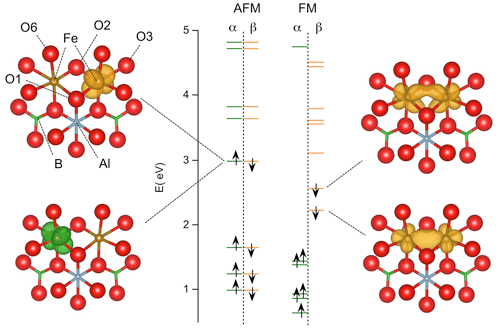
Figure 5 Energy levels of iron pairs in tourmaline calculated with the PBE functional (models 1 and 3, Table 2). The energy is reported with respect to that of the top of the valence band (O(2p) states) in the theoretical model of pristine dravite. The majority (α) and minority (β) spin states correspond to the green and orange bars, respectively. Isosurfaces corresponding to the spin-selected density of states of the two highest occupied spin orbitals are reported. Fe–Fe interaction in the FM configuration is attested by the electron delocalization over the two Fe atoms. In the AFM configuration, the electrons with opposite spin states are localized on each Fe atom.

The ground state of the FM configuration in tourmaline is noticeably consistent with that determined for the symmetric (Fe₂O₁₀)¹⁵⁻ dimer by Sherman (1987). In the present case, the lowest-energy state occupied by minority-spin electrons is a molecular orbital resulting from the axial interaction between two Fe(3d) orbitals (Fig. 5), similar to the 16a₁ state of the dimer. The other state, located just above and corresponding to the HOMO of the system, reveals a lateral interaction (mostly π) between two Fe(3d) orbitals (Fig. 5) similar to that observed in the 10b₁ state of the dimer (Sherman, 1987). In contrast, the electronic delocalization over the two Fe atoms is not possible in the AFM configuration, as discussed by Sherman (1987). Accordingly, the highest occupied states correspond to two degenerate Fe(3d) atomic orbitals with opposite spins localized on the adjacent Fe atoms (Fig. 5). In the FM configuration, the electronic delocalization over the two Fe atoms leads to a bonding interaction and explains the significant shrinking of the Fe–Fe distance in the relaxed structure compared with the AFM configuration in which no specific Fe–Fe interaction occurs.

In the light of these results, it is therefore possible to understand why the improved treatment of the on-site Coulomb repulsion in Fe(3d) orbitals reverses the relative stability of the AFM and FM configurations with respect to the standard DFT result, even for relatively low values of the U_eff parameter. As mentioned in the Methods section, the explicit inclusion of an on-site Hubbard U term for the Fe(3d) electrons represents a strong energy penalty for the delocalized FM solution compared to the already localized AFM one, overcoming the stabilization resulting from Fe–Fe covalent interactions even for low values of the U_eff parameter. Accordingly, the U correction favors the localized states with respect to the delocalized ones, explaining the relative stabilization of the localized AFM configuration with respect to more delocalized FM configuration for U_eff values as small as ∼ 0.5 eV (Fig. 3).

4.2 Assignment of OH-stretching bands in foitite

The infrared and Raman spectra of tourmaline usually display a series of bands in the 3300–3800 cm⁻¹ range typical of OH-stretching modes. The bands observed above 3620 cm⁻¹ are related to ^WOH groups, whereas those below 3600 cm⁻¹ are assigned to ^VOH groups. The ^VOH bands are generally stronger and broader than the ^WOH ones. In the LH12 foitite spectrum, a doublet related to the ^WOH groups is observed at 3630 and 3644 cm⁻¹, with a stronger intensity of the 3644 cm⁻¹ band. Consistently, a doublet at the same frequencies is observed in the Raman spectra of natural black tourmaline samples (Lensing-Burgdorf et al., 2017). In this series of samples, the relative intensity of the two bands is variable, with a stronger intensity of the 3644 cm⁻¹ component in the foitite samples (Lensing-Burgdorf et al., 2017). A similar doublet is observed in the Raman spectrum of the foitite sample (S44) studied by Watenphul et al. (2016). The polarized infrared spectrum of the schorl sample (T3) with partial X-site occupancy investigated by Bosi et al. (2015) displays a doublet at 3628 and 3645 cm⁻¹, with a stronger intensity of the 3628 cm⁻¹ band in this case. Two bands at 3632–3633 and 3644–3646 cm⁻¹ are also observed in the spectra of the Mn-bearing counterpart of the ferrous tourmalines. In the spectrum of the celleriite co-type, with about half occupancy of the X site, the two components have similar intensities (Bosi et al., 2022a). In the princivalleite sample, which has approximately one-third of the X sites vacant, the low-frequency component at 3632 cm⁻¹ is dominant (Bosi et al., 2022b).

The two bands at 3630 and 3644 cm⁻¹ are usually ascribed to ^WOH groups in ^YM^YAl₂ and ${}^Y{M}_{\mathrm{2}}^Y$Al (M denotes Fe²⁺ or Mn²⁺) environments, respectively. This assignment is however hardly reconciled with the more aluminous character of foitite (dominant contribution at ∼ 3644 cm⁻¹) with respect to schorl (dominant contribution at ∼ 3630 cm⁻¹). In addition, the 14 cm⁻¹ downshift related to the substitution of a trivalent for a divalent cation would be significantly weaker than that observed in Mg-foitite. In the Mg-foitite spectrum, the ^YMg^YAl₂ and ^YMg${}_{\mathrm{2}}^Y$Al bands are observed at 3619 and 3657 cm⁻¹, corresponding to a downshift of 38 cm⁻¹ (Berryman et al., 2016; Fuchs et al., 2022). In contrast, a smaller splitting is consistent with the frequency shift related to the occurrence of one or two vacancies sandwiching the Y₃Z₆ cluster along the [001] direction. When it is surrounded by two vacancies at the X site in synthetic Mg-foitite, the ^WOH group in a ^YMg${}_{\mathrm{2}}^Y$Al environment leads to a band at 3657 cm⁻¹, whereas it is observed at 3641 cm⁻¹ when it is associated with a single X^a vacancy in dravite, corresponding to a 16 cm⁻¹ shift. The effect of vacancy ordering on the ^WOH-stretching frequency in Fe-foitite is supported by the theoretical results obtained on iron-bearing clusters, which indicate a 16-to-19 cm⁻¹ shift between configurations with one or two X vacancies along the [001] direction (Table 2). Based on these theoretical results, the bands at 3630 and 3644 cm⁻¹ in the foitite spectrum can be ascribed to ^WOH groups in ^YFe${}_{\mathrm{2}}^Y$Al environments associated with one and two vacancies, respectively, at the X site. This interpretation is consistent with the relative variations in the two band intensities in Fe- or Mn-bearing tourmaline samples with different concentrations of X vacancies (Watenphul et al., 2016; Lensing-Burgdorf et al., 2017; Bosi et al., 2015, 2022a, b). It suggests that the relative intensity of these two bands could be used to determine the concentration of vacant X sites in tourmaline samples. Even though the ^WOH groups can suffer partial deprotonation in tourmaline, the relative intensity of the bands should reflect the probability that a vacancy occurs at the X^b site, which should be weakly affected by the protonation state of the more distant ^WO site. In the LH12 sample, the relative intensity of the 3430 and 3444 cm⁻¹ bands (Table 1) indicates that ∼ 70 % of the X sites are vacant. This value can be compared with the concentration of vacant X sites inferred from the chemical composition (81 %).

It can be noticed that the band related to ^WOH groups in a ^YFe${}_{\mathrm{2}}^Y$Al–^XNa environment and reported at 3726 cm⁻¹ in the Raman spectra of Watenphul et al. (2016) is not observed in the FTIR spectrum of the LH12 sample. Its absence could be related to a preferential deprotonation of the ^WOH sites facing an occupied X site (Watenphul et al., 2016) combined with the weaker infrared (IR) activity of OH groups vibrating at higher frequencies (e.g., Libowitzky and Rossman, 1997). This last assumption was ascertained on ideal Mg-foitite and dravite models, revealing that the corresponding ^WOH IR activity decreases from 1.2 to 0.4 (D Å⁻¹)² amu⁻¹ between Mg-foitite and dravite, respectively. In comparison, the Raman activity assessed at the local density approximation (LDA) level displays a relative variation in the opposite direction, increasing from 255 to 346 Å⁴ amu⁻¹ from Mg-foitite to dravite, which could favor the observation of ^YFe${}_{\mathrm{2}}^Y$Al–^XNa environments in the Raman spectra. The relative variations in the theoretical IR (6.5 and 5.7 (D Å⁻¹)² amu⁻¹) and Raman (491 and 464 Å⁴ amu⁻¹) activities of the ^VOH groups in Mg-foitite and dravite, respectively, suggest a weaker influence of the X-site occupancy on the properties of the ^VOH groups.

Comparing the theoretical frequencies determined for the iron-bearing clusters with their experimental counterparts in foitite (Fig. 6), the two experimental bands better match the frequencies determined for the ^YFe${}_{\mathrm{2}}^Y$Al environments in the AFM configuration. The corresponding theoretical overestimation of experimental frequencies by ∼ 75–80 cm⁻¹ is similar to that previously determined for dravite and Mg-foitite (Fuchs et al., 2022), while the ^WOH-stretching frequencies related to the FM configurations plot significantly out of the correlation (Fig. 6).

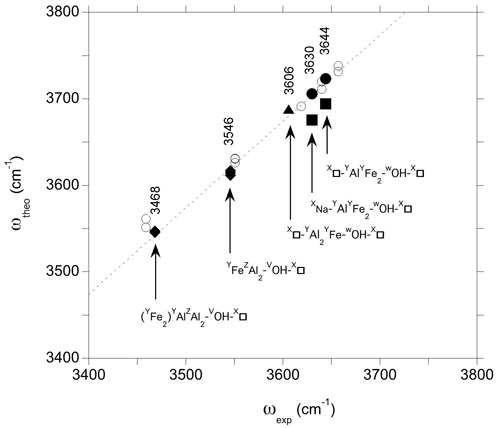
Figure 6 Relation between theoretical (ω_OH) and experimental (ω_exp) OH-stretching frequencies in foitite. The theoretical ^WOH and ^VOH frequencies are the PBE + U and PBE values, respectively (Table 2). Experimental frequencies (Table 1) are indicated. The dashed line corresponds to the equation ${\mathit{\omega }}_{\mathrm{OH}}={\mathit{\omega }}_{\exp }+\mathrm{75}$ cm⁻¹. Filled circles: ^WOH in ^YFe${}_{\mathrm{2}}^Y$Al environment with AFM configuration; filled squares ^WOH in ^YFe${}_{\mathrm{2}}^Y$Al environment with FM configuration; triangle: ^WOH in ^YFe^YAl₂ configuration; diamonds: ^VOH groups; open circles: Mg-bearing clusters (Fuchs et al., 2022).

The comparison of theoretical and experimental frequencies also supports the assignment of the band at 3606 cm⁻¹ (Fig. 6) to a ^WOH group in a ^YFe^YAl₂ environment associated with two vacancies. However, an overlapping contribution from ^VOH groups in this frequency range cannot be fully excluded (Fuchs et al., 2022). The strong band at 3546 cm⁻¹ can be assigned to the ^VOH group in a ^YFe^ZAl₂ environment associated with a vacant X^b site, whereas the ^VOH group in ^YAl^ZAl₂ environments leads to the broad peak with a maximum at 3468 cm⁻¹. These interpretations are similar to those given to the bands at 3551 and 3459 cm⁻¹ in Mg-foitite (Fuchs et al., 2022). As in Mg-foitite, the large width of the ^VOH bands indicates that they are most likely associated with more than a single local configuration of the ^VOH group. Assuming a 75 cm⁻¹ shift between theoretical and experimental frequencies, contributions related to ^VOH group in ^YFe^ZAl₂ and ^YAl^ZAl₂ environments with a Na-occupied X^b site are expected at ∼ 3566 and 3502 cm⁻¹, respectively, but they are not resolved in the infrared spectrum of the LH12 sample. Two bands are observed at 3570 and 3517 cm⁻¹ in the Raman spectrum of the S44 foitite sample reported by Watenphul et al. (2016), but the presence of Li in this sample precludes their straightforward assignment. The ^VOH groups are also sensitive to the occupancy of the other sites of the cluster through the induced structural relaxations. For example, the stretching of ^VOH groups in ^YAl^ZAl₂ environments is downshifted by more than 20 cm⁻¹ when the cluster contains a single Fe atom instead of two. Such a configuration could therefore contribute to the broadening of the ^VOH band on its low-frequency side (Fig. 2). Other configurations not explicitly considered in the theoretical models could also contribute to the ^VOH signals, such as those related to the partial inversion of Y- and Z-site occupancies as previously discussed for dravite and Mg-foitite (Fuchs et al., 2022).

Based on the observation that the stretching frequencies of OH groups coordinated to Mn²⁺ and to Fe²⁺ ions in the trioctahedral structure of talc are similar (Wilkins and Ito, 1967), the present results could also bring constraints for the interpretation of the celleriite spectrum (Bosi et al., 2022a). As discussed above, the two bands at 3633 and 3646 cm⁻¹ should correspond to ^WOH groups in ^YMn${}_{\mathrm{2}}^Y$Al environments associated with one and two vacant X sites, respectively. The band at 3604 cm⁻¹ is close to that observed at 3606 cm⁻¹ in foitite and likely related to ^WOH groups in a ^YMn^YAl₂ environment. The broader bands at 3487 and 3562 cm⁻¹ can be assigned to ^VOH groups in ^YAl^ZAl₂ and ^YMn^ZAl₂ environments, respectively. With the presence of a vacancy at the X^b site having a stronger effect on the ^VOH groups related to ^YAl^ZAl₂ environments than on those related to ^YM^ZAl₂ environments, the band at 3518 cm⁻¹ could be related to an ^YAl^ZAl₂ environment, pointing to an occupied X^b site. However, as for the foitite sample studied by Watenphul et al. (2016), vibrational contributions related to the presence of Li in this celleriite sample are also expected, which makes a straightforward assignment of the minor ^VOH bands more difficult.

5 Conclusions

We have theoretically analyzed the OH-stretching spectrum of foitite. A revised interpretation of the ^WOH bands at 3630 and 3644 cm⁻¹ is proposed, suggesting that the relative intensity of these two bands could be a sensitive probe of the vacancy concentration at the X site. In addition, significant structural differences related to the Fe–Fe magnetic coupling were observed in models with ^YFe²⁺ pairs. These differences can be traced back to the Fe–Fe bonding which occurs between edge-sharing octahedrally coordinated Fe²⁺ with a FM spin arrangement and is forbidden for an AFM order. The comparison of observed and predicted OH-stretching frequencies supports an AFM coupling of ^YFe²⁺ pairs in tourmaline, which is also found as the most stable solution in DFT + U.