A new clinopyroxene thermobarometer for mafic to intermediate magmatic systems

Clinopyroxene-only thermobarometry is one of the most practical tools to reconstruct crystallization pressures and temperatures of clinopyroxenes. Because it does not require any information of coexisting silicate melt or other co-crystallized mineral phases, it has been widely used to elucidate the physiochemical conditions of crystallizing magmas. However, previously calibrated clinopyroxene-only thermobarometers display low accuracy when being applied to mafic and intermediate magmatic systems. Hence, in this study, we present new empirical nonlinear barometric and thermometric models, which were formulated to improve the performance of clinopyroxene-only thermobarometry. Particularly, a total of 559 experimental runs conducted in the pressure range of 1 bar to 12 kbar have been used for calibration and validation of the new barometric and thermometric formulation. The superiority of our new models with respect to previous ones was confirmed by comparing their performance on 100 replications of calibration and validation, and the standard error of estimate (SEE) of the new barometer and thermometer are 1.66 kbar and 36.6 ^∘C, respectively. Although our new barometer and thermometer fail to reproduce the entire test dataset, which has not been used for calibration and validation, they still perform well on clinopyroxenes crystallized from subalkaline basic to intermediate magmas (i.e., basaltic, basalt-andesitic, dacitic magma systems). Thus, their applicability should be limited to basaltic, basalt-andesitic and dacitic magma systems. In a last step, we applied our new thermobarometer to several tholeiitic Icelandic eruptions and established magma storage conditions exhibiting a general consistency with phase equilibria experiments. Therefore, we propose that our new thermobarometer represents a powerful tool to reveal the crystallization conditions of clinopyroxene in mafic to intermediate magmas.

1 Introduction

The reconstruction of pre-eruptive magmatic temperatures (T) and pressures (P) (e.g., Putirka, 2008, 2018) is a fundamental topic in igneous petrology, volcanology, and geochemistry as (i) temperature and pressure strongly control the stabilities of solid phases and complementary liquid lines of descent in the course of magma differentiation and solidification (e.g., Thompson, 1974; Villiger et al., 2007; Botcharnikov et al., 2008a) and (ii) accurate estimation of both temperature and pressure provide a critical perspective for elucidating the storage of magma as well as its thermal state at depth (e.g., Ruprecht et al., 2012; Cadoux et al., 2014; Geiger et al., 2018; Eskandari et al., 2018). However, although several rigorous geothermobarometers have been calibrated based on thermodynamics and experimental data during the past decades, predicted P and T are not always satisfying, as reflected by large differences between calculated and experimental values (Fig. 1).

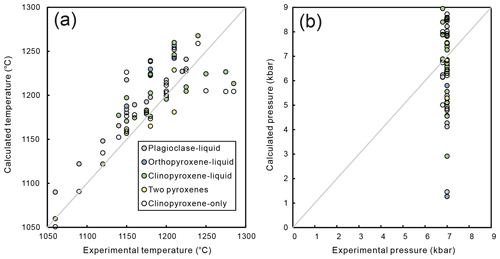
Figure 1 Comparison between experimental pressures and temperatures (data obtained at 6.8 and 7 kbar from the following studies: Husen et al., 2016; Médard et al., 2004; Villiger et al., 2007; Whitaker et al., 2007) and corresponding calculated conditions obtained using various geothermobarometric equations (Putirka, 2008). Note the relatively good agreement for temperatures but the incapability of the equations at predicting accurate pressures. The thermobarometers involved here are Eqs. (24a), (25a), (28a), (29a), (31), (33), (38), (32a), and (32d), respectively, from Putirka (2008). Calculations are performed by imposed experimental T or P if the model is T-dependent or P-dependent, respectively.

Clinopyroxene (Cpx) is commonly present in igneous rocks and exhibits large compositional variations, especially in intermediate to basic and ultrabasic systems. Various clinopyroxene-based thermobarometers have been established due to its compositional sensitivity to changes in magmatic temperature and pressure (e.g., Nimis, 1995; Putirka et al., 1996). Among them, the two-pyroxene, i.e., clinopyroxene and orthopyroxene (Opx), and the clinopyroxene-liquid thermobarometers are the most frequently used ones, and many recalibrations have been conducted to improve their precisions (e.g., Lindsley and Andersen, 1983; Mercier et al., 1984; Brey and Kohler, 1990; Anderson et al., 1993; Sack and Ghiorso, 1994; Putirka, 2008; Liang et al., 2013). However, due to additional magmatic processes such as magma mixing or mingling, the coexistence of two pyroxenes in natural rocks does not necessarily imply that they co-crystallized from the same magma even if Fe–Mg distribution indicates chemical equilibrium, limiting the applicability of the two-pyroxene geothermobarometer to natural rocks. Moreover, compositional zonation of pyroxene crystals commonly observed in magmatic rocks further complicates the application of pyroxene geothermobarometry to natural samples.

Since clinopyroxene is distinctively more common in igneous rocks compared to the coexistence of two pyroxenes, clinopyroxene-liquid thermobarometers have been more widely used. During the past decades, the clinopyroxene-liquid thermobarometer has been calibrated by several authors. Generally, these calibrations are predominantly based on site occupancy data, including Jd (NaAlSi₂O₆; jadeite)-liquid equilibria for barometery and Jd–DiHd (Ca(Mg, Fe)Si₂O₆; diopside-hedenbergite), CaTs (CaAlAlSiO₆; calcium-Tschermak)-DiHd exchange equilibria for thermometry (e.g., Putirka et al., 1996, 2003; Putirka, 2008; Neave and Putirka, 2017), and thermodynamical or empirical models (e.g., Massota et al., 2013; Liang et al., 2013; Brugman and Till, 2019). Nevertheless, it is quite difficult or even impossible to obtain the composition of the melt the clinopyroxene crystallized from in natural samples, and the sole application of Fe–Mg exchange as an indication of equilibrium could be problematic (Zellmer et al., 2014). Moreover, if magma mixing and mingling or fractional crystallization were involved in the corresponding samples (Putirka, 2008), the melt composition in equilibrium with the target clinopyroxene is almost impossible to constrain.

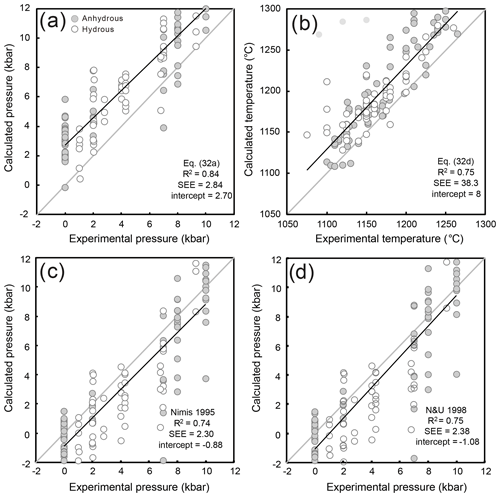
Figure 2 Test performed on published clinopyroxene-only barometers and thermometers with data from experiments carried out on basalts (Baker and Eggler, 1987; Tormey et al., 1987; Grove et al., 1992; Toplis and Carroll, 1995; Yang et al., 1996; Villiger et al., 2004, 2007; Berndt et al., 2005; Whitaker et al., 2007, 2008; Husen et al., 2016); 1 : 1 lines are shown in pale gray. Regression lines through the test dataset are shown in black. Experimental data of HK19.1 SV27, HK19.1 SV28, HK19.1 SV24, and HK19.1 SV25 from Villiger et al. (2007) were excluded from the regressions and are shown in pale gray. (a) Eq. (32a) from Putirka (2008), (b) Eq. (32d) from Putirka (2008). For both models, calculations were performed iteratively. (c) Cpx-only barometer of Nimis (1995) and (d) Cpx-only barometer of Nimis and Ulmer (1998).

Accordingly, to better constrain P and T conditions of magma storage, empirical Cpx-only thermobarometers have been developed and calibrated on experimental data during the last decades (e.g., Nimis, 1995; Nimis and Ulmer, 1998; Nimis, 1999; Nimis and Taylor, 2000; Putirka, 2008). However, these Cpx-only barometers (e.g., Nimis, 1995; Putirka, 2008) exhibit strong systematic errors possibly due to the paucity of experimental data at relevant crustal pressures (≤ 12 kbar) and the thermodynamic complexity of clinopyroxene stability. For instance, the model of Nimis (1995) systematically underestimates pressures for high-pressure experiments (Putirka, 2008), while Eq. (32a) of Putirka (2008) systematically overestimates pressure for experiments run at crustal pressure conditions (Fig. 2). Fortunately, extensive experimental work was conducted at crustal pressures on magmatic systems after 2008 (e.g., Botcharnikov et al., 2008b, 2015; Almeev et al., 2012, 2013a, b; Vetere et al., 2015; Webster et al., 2015; Husen et al., 2016; Erdmann and Koepke, 2016; Stechern et al., 2017; Koepke et al., 2018), providing the ideal basis and opportunity to improve and recalibrate existing clinopyroxene-based geothermobarometers.

In this study, we propose new Cpx-only thermometric and barometric models calibrated for basic to intermediate magmatic systems. A total of 559 experiments compiled from the literature were used for calibration and validation. In addition, we recalibrated and verified the previous Cpx-only barometric and thermometric models using the identical experimental dataset. Results from the validation process indicated that our new models perform better than the previous models. In a second step, 508 experiments from the literature that do not overlap with the calibration and validation dataset were selected to confirm the generalization ability of our models. Finally, we provide an immediate application of our new algorithms to natural clinopyroxenes from Iceland. The new thermometer and barometer result in magma storage temperature and pressure estimates comparable to the results of Neave and Putirka (2017).

2 Method

2.1 Experimental data

The data used for calibration and validation are from the following literature: Baker and Eggler (1987), Bartels et al. (1991), Berndt et al. (2005), Botcharnikov et al. (2008a), Bulatov et al. (2002), Di Carlo et al. (2006), Draper and Johnston (1992), Falloon et al. (2001), Feig et al. (2006), Gaetani and Grove (1998), Grove et al. (2003, 1992), Husen et al. (2016), Kelemen et al. (1990), Kinzler and Grove (1992), Kogiso and Hirschmann (2001), Laporte et al. (2004), Mahood and Baker (1986), Médard et al. (2004), Müntener et al. (2001), Pichavant et al. (2002), Pickering-Witter and Johnston (2000), Putirka et al. (1996), Schwab and Johnston (2001), Scoates et al. (2006), Sisson and Grove (1993), Thy et al. (2006, 1998), Toplis and Carroll (1995), Tormey et al. (1987), Villiger et al. (2007, 2004), Wasylenki et al. (2003), Whitaker et al. (2007, 2008), and Yang et al. (1996). These experimental data were subsequently filtered applying the following criteria: (1) the chemical composition of the coexisting melt has to be reported, and the SiO₂ content of the melt must be below 60 wt %; (2) experimental pressures are in the range of 1 bar to 12 kbar; (3) the Al^VI and Jd content of clinopyroxenes is higher than 0. The selected data cover a wide range of melt compositions, with most of them falling within the compositional fields of basalt and basaltic andesite according to the TAS (total alkalis versus silica) diagram (Fig. 3; N = 559).

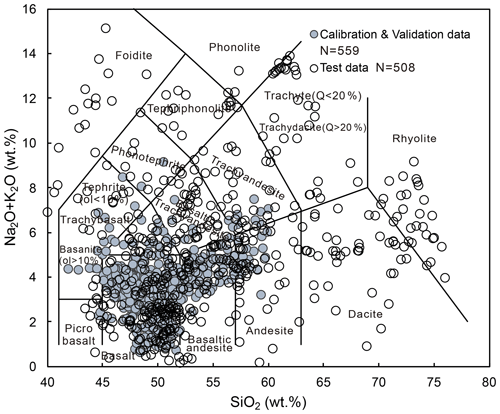
Figure 3 Total alkali versus silica diagram of melt compositions in equilibrium with clinopyroxenes utilized for calibration, validation, and testing. Blue circles refer to experimental data employed for calibration and validation; unfilled circles represent test data.

The dataset employed for testing our models for their generalization ability represents a subset of the global clinopyroxene dataset used in Neave and Putirka (2017). However, the experimental data that had previously been used for calibration and validation data were excluded. Experiments at pressures higher than 20 kbar and temperatures lower than 800 ^∘C were also removed. There was no further limitation for both melt and clinopyroxene compositions for the purpose of verifying the applicability of our new models to a wide range of pressures, temperatures, and melt compositions. Following the abovementioned criteria, 508 experimental runs were selected as test data. Further details concerning the calibration, validation, and test datasets are provided in Table S1 in the Supplement.

2.2 Models and regression strategy

The new nonlinear barometric model is described as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}P\left(\mathrm{kbar}\right)& =a\cdot \mathrm{NLT}\cdot \ln {\mathrm{Al}}^{\mathrm{VI}}+b\mathrm{Si}+c{\mathrm{Fe}}^{\mathrm{tot}}+d\mathrm{Mg}\\ & +e\mathrm{Ca}+f\mathrm{Na}+g,\end{array}\end{array}$$

where NLT is a nonlinear term that is only clinopyroxene-composition-dependent,

$$\mathrm{NLT}={\displaystyle \frac{{\mathit{\omega }}_{\mathrm{0}}{\mathrm{Al}}^{\mathrm{VI}}}{{\mathit{\omega }}_{\mathrm{0}}A{l}^{\mathrm{VI}}+{\mathit{\omega }}_{\mathrm{1}}\mathrm{Ti}+{\mathit{\omega }}_{\mathrm{2}}\mathrm{Cr}+{\mathit{\omega }}_{\mathrm{3}}{\mathrm{Fe}}^{\mathrm{tot}}+{\mathit{\omega }}_{\mathrm{4}}\mathrm{Mn}+{\mathit{\omega }}_{\mathrm{5}}\mathrm{Mg}}},$$

and a–g as well as ω_i represent parameters to be calibrated. Given that the activity of the Jd component (NaAl^VISi₂O₆) in clinopyroxene is strongly pressure sensitive (Putirka et al., 1996), the NLT, which is closely correlated with octahedral alumina contents (Al^VI), could also be pressure-dependent.

Since this function is differentiable with respect to its parameters, gradient descent is an efficient optimization method. Gradient descent represents an algorithmic tool to minimize an objective function (in this paper, the loss function) parameterized by the model's parameters by updating the parameters in the opposite direction of the gradient of the objective function with respect to the parameters. The learning rate determines the size of the steps undertaken to reach a minimum (Ruder, 2017). Thus, model parameters of Eq. (1) as well as NLT were determined by the gradient descent algorithm. We used the Adam algorithm (Kingma and Ba, 2017) of the PyTorch library to implement gradient descent (Paszke et al., 2019). The learning rate was set to 0.01, and the employed loss function was MSE (mean square error):

$$\mathrm{loss}={\displaystyle \frac{\mathrm{1}}{N}}\cdot {\sum }_{n=\mathrm{1}}^N{\left(y_n-{\widehat{y}}_n\right)}^{\mathrm{2}}.$$

The new thermometric model is described as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}T\left({}^{\circ }\mathrm{C}\right)& =\mathrm{100}\left[a\cdot \mathrm{NLT}+b\mathrm{Ti}+c\mathrm{Al}+d\mathrm{Mn}+e\mathrm{Mg}\right.\\ & \left.+f\mathrm{Ca}+g{\mathrm{Fe}}^{\mathrm{2}+}+h{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{wt}\mathit{\%}\right)+i\right],\end{array}\end{array}$$

where a–j are parameters to be calibrated by least square method, while the parameters of NLT have already been determined above in the barometric model. For comparison, we additionally recalibrated previously established barometric models (Nimis, 1995; Eqs. 32a and 32b in Putirka, 2008) applying the same dataset. The Cpx-only thermometric model of Putirka (2008) was adapted by adding a H₂O term and is referred to as Eq. (32dH) for the remainder of this contribution:

$$\begin{array}{}\text{(32dH)}& T\left({}^{\circ }\mathrm{C}\right)={\displaystyle \frac{\mathrm{93100}+\mathrm{544}P\left(\mathrm{kbar}\right)}{\begin{array}{c}a+b\mathrm{Ti}+c{\mathrm{Fe}}^{\mathrm{tot}}+d\left(\mathrm{Al}+\mathrm{Cr}-\mathrm{Na}-\mathrm{K}\right)\\ +e{\left[\ln \left(a_{\mathrm{En}}^{\mathrm{cpx}}\right)\right]}^{\mathrm{2}}+f{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}}},\end{array}$$

where the term $a_{\mathrm{En}}^{\mathrm{cpx}}$ was taken from Nimis and Taylor (2000): $a_{\mathrm{En}}^{\mathrm{cpx}}=(\mathrm{1}-\mathrm{Ca}-\mathrm{Na}-\mathrm{K})(\mathrm{1}-\mathrm{0.5}(\mathrm{Al}+\mathrm{Cr}+\mathrm{Na}+\mathrm{K}\left)\right)$.

For the above-introduced models, clinopyroxene components were determined using the procedures reported in Putirka (2008), assuming six oxygen anions per formula unit. The new models we present herein are empirical, and introduced parameters have no thermodynamic significance.

2.3 Division of calibration and validation data

For the purpose of equally splitting the data, the 559 experiments were firstly divided into 7 groups of 2 kbar intervals, where 1 bar experiments were assigned to a separate group. Then, for each group, one subset of the data (80 %) was used for calibration and the second one (20 %) for validation of predicted pressure and temperature conditions. The calibration and validation datasets were randomly assigned. After random segmentation of the entire dataset, the calibration data consisted of 444 experiments, and the validation dataset contained 115 experiments. To provide a robust performance estimation for each model, we performed n = 100 replications of the random splitting, calibration, and validation procedures and analyzed the general distribution of loss values. The goodness of the established models was evaluated with the loss value, which is related to the standard error of estimate (SEE) as follows:

$$\mathrm{SEE}=\sqrt{{\displaystyle \frac{n}{n-\mathrm{2}}}\cdot \mathrm{loss}}.$$

Consequently, we infer that the model with the lowest loss value represents the most suitable one. The codes used in this paper are available in the Supplement (Codes S1 and S2).

3 Results

3.1 Evaluation of different models

Figure 4a and b represent loss value frequency histograms for pressure estimations employing different models on the calibration and validation data. P32b (Eq. 32b in Putirka, 2008) exhibits the best performance for both calibration and validation data, with average loss values of 2.12 and 2.29, respectively. We herein used the average rather than the value of the highest frequency to illustrate the performance of the different models. We infer that the average is more representative, although in most cases the difference between the two is negligible. Equation (1) performs slightly worse, with loss values of 2.49 (calibration dataset) and 2.67 (validation dataset). Average loss values of the models P32a (Eq. 32a in Putirka, 2008) and Nimis (1995) range between 2.99 and 3.55. As a consequence, P32b is the best-performing barometric model investigated herein. However, the P32b and P32a models are T-dependent, and, in practice, it is almost impossible to obtain accurate temperature information from natural clinopyroxenes. Therefore, in most cases, calculations with both barometers should be performed iteratively. We performed calculations of P32b and P32a iteratively with equation P32dH used to constrain temperature for each repetition step, and results are also shown in Fig. 4b. Following this iterative procedure, the performance of both models drops significantly, with average loss values of 3.36 and 3.42 for calibration and validation data for P32b and even worse values for P32a (4.06 and 4.11). We assume that the intrinsic error in the P32dH algorithm was transferred to barometric calculations during the iterative process. In addition, the H₂O content of the coexisting melt, which is also difficult to constrain accurately, is implemented in P32b, introducing an additional error source. Consequently, we conclude that our newly calibrated barometer (Eq. 1) represents the best-performing algorithm of the ones investigated in this study.

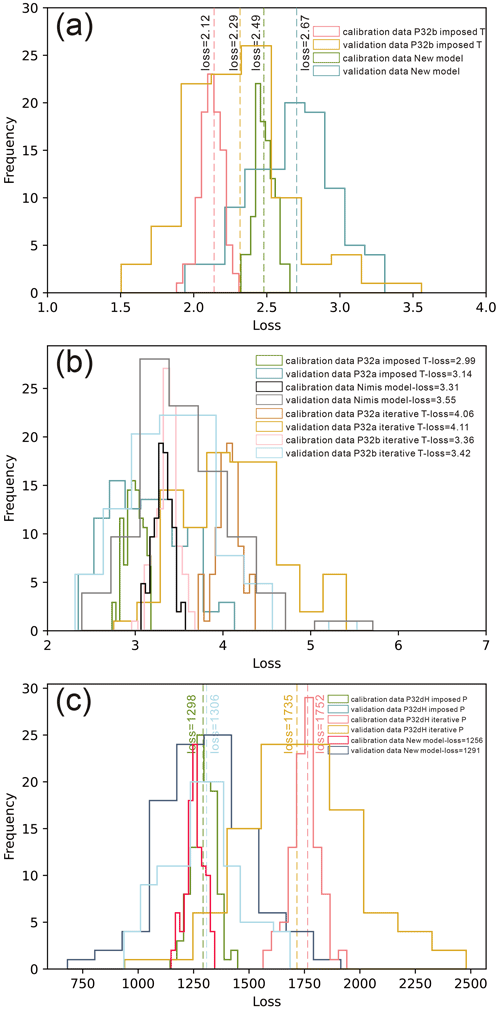
Figure 4 Loss value frequency distribution histogram for pressure and temperature estimations applying different models to the calibration and validation data: (a) comparison between our barometric model (Eq. 1) and P32b; (b) comparison between existing barometer models of P32a, P32b, and Nimis and Ulmer (1998); (c) comparison between our thermometric model (Eq. 2) and P32dH.

Equation (2) performs best for both calibration and validation data, with loss values of 1256 and 1291, respectively (Fig. 4c). In contrast, P32dH performs slightly worse, with loss values of 1298 and 1306, even though calculations were conducted imposing experimental pressure. In detail, the performance of P32dH drops significantly when combined with iterative calculations employing P32b, which is the most precise Cpx-only T-dependent barometric model, with loss values of 1752 and 1735. In summary, compared with previous Cpx-only thermobarometric models, our new algorithms (Eqs. 1 and 2) are the most precise and practical ones. However, it has to be pointed out that Eq. (2) contains a melt H₂O term, and caution should be taken upon its usage if the H₂O content of the coexisting residual melt has not been constrained reliably.

3.2 Calibration of the thermometric and barometric models

We selected one of the 100 replications' results as the new barometer and thermometer. The corresponding loss values of Eq. (1) are 2.49 (calibration data) and 2.65 (validation data) and thus comparable to the mean values of all replications (2.49 and 2.67; see Fig. 4). Calibration and validation results of the algorithms P32b and P32dH for the identical calibration and validation dataset are also reported (see below) to allow better comparison between the different models. Established parameters of the new models are reported in Tables 1 and 2. A spreadsheet for calculating temperatures and pressures is provided in Table S2.

Table 1 Parameters of NLT determined by descent algorithm.

Table 2 Parameters for thermometric and barometric models.

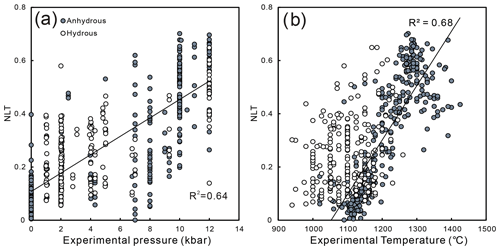
Figure 5 Experimental pressure and temperature–NLT (value of the nonlinear term) plots. Blue circles refer to anhydrous experiments, while white ones correspond to hydrous experiments. The solid lines are regression lines.

Although the parameters of NLT were determined by regression of Eq. (1), their values show strong correlation both with pressure and with temperature over the entire range of the calibration and validation data (Fig. 5). The R² score of T vs. NLT in anhydrous systems (0.68; only anhydrous experiments were considered) is even higher compared to the correlations between T and other compositional components of clinopyroxene (e.g., Mg and EnFs), thereby indicating that the temperature information is mainly stored in the NLT term of clinopyroxenes. This explains the good performance of Eq. (2) in reproducing experimental T.

Figure 6 Performance of our new barometer and P32b on the calibration and validation datasets: (a) and (b) are results for the calibration data; (c) and (d) are results for the validation data; results of iteratively calculated pressures of Eqs. (32a) and (32d) from Putirka (2008) for the calibration and validation data are shown in (e) and (f), respectively. Blue circles refer to anhydrous and unfilled ones to hydrous experimental data. The gray lines illustrate 1 : 1 trajectories, and the black ones represent regression lines.

Figure 6 illustrates the reproducibility of Eq. (1) and algorithm P32b with the calibration and validation data. P32b represents the best-performing model, with an R² score of 0.88 for both calibration and validation data, when experimental temperature is imposed during calculation. Equation (1) is slightly worse, with R² scores of 0.86. The intercepts of both barometers are distinctively smaller than their SEE, and established regression lines almost coincide with the 1 : 1 line, indicating that the two barometers do not have a systematic error over the entire pressure range investigated (1 bar–12 kbar). In addition, we tested the influence of melt H₂O contents on Eq. (1) by removing the hydrous experiments from the calibration and validation data. As a consequence, the R² score slightly improved to 0.90 for both datasets. Although the model itself does not contain a H₂O term, this influence of water contents in melt could be explained with the effect of water on the cell volume of clinopyroxene (Nimis and Ulmer, 1998). Nonetheless, we decided to remove the H₂O term in the final model as in most cases the improvement of the model via the addition of a H₂O term could not remedy the errors caused by imprecise estimations of melt H₂O contents. In addition, H₂O-free barometers are significantly more convenient to use in practice.

Furthermore, the mean standard error of estimate (SEE) between predicted and experimental conditions represents an even more solid indicator of the models' precision. The SEEs of Eq. (1) and P32b are 1.66 and 1.54 kbar, respectively. However, the performance of P32b drops significantly when pressure is iteratively calculated with P32dH, the P-dependent Cpx-only thermometer, with R² scores of 0.81 and 0.87 and a SEE of 1.87 and 1.88 kbar for calibration and validation data. In practice, given that equations P32b and P32dH are both H₂O-dependent, additional errors and uncertainties are introduced by imprecise estimations of melt H₂O contents. Consequently, we conclude that our new barometer (Eq. 1) represents the most practical and precise one among the Cpx-only barometers investigated herein when applied to natural samples.

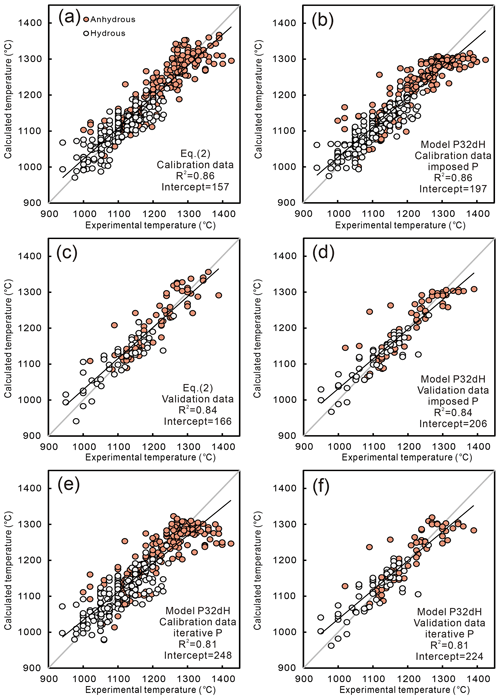
Figure 7 Performance of our new thermometer (Eq. 2) and P32dH on the calibration and validation datasets: (a) and (b) are results for the calibration data; (c) and (d) are results for the validation data; results of iteratively calculated temperatures using Eqs. (32a) and (32d) from Putirka (2008) on calibration and validation data are shown in (e) and (f). Orange circles refer to anhydrous experimental data, and unfilled circles correspond to hydrous experimental data. Gray lines illustrate 1 : 1 trajectories, and black lines represent regression lines.

Figure 7 reports the reproducibility of Eq. (2) and P32dH for the calibration and validation data. The new model (Eq. 2) shows the best reproducibility for both the calibration and validation dataset, with R² of 0.86 and 0.84, respectively, and a SEE of 36.6 ^∘C. P32dH performs slightly worse, with R² of 0.86 and 0.84, respectively, and a SEE of 36.8 ^∘C. Performing iterative calculation with P32b instead of imposing P also significantly diminishes the performance of P32dH, with R² of 0.81 for both datasets and a SEE of 42.4 ^∘C. However, it has to be noted that both thermometric models are H₂O-dependent, and thus caution must be taken when H₂O content of equilibrium melt cannot be constrained precisely.

3.3 Assessment of the effect of H₂O and fO₂

The effects of melt H₂O content and fO₂ on the performance of our new models are investigated by comparing the difference in the residuals (P_exp–P_calc, T_exp–T_calc) with melt H₂O content and fO₂. As shown in Fig. 8a and b, there are no obvious correlations between fO₂ and P_exp–P_calc as well as T_exp–T_calc (R² = 0.030 and 0.004, respectively). In principle, an enhanced incorporation of the aegirine component (Aeg; NaFe³⁺Si₂O₆) in clinopyroxene under oxidizing conditions could contribute to an overestimation of the jadeite (NaAlSi₂O₆; Jd) component (Blundy et al., 1995), resulting in specious estimation results for the Jd-in clinopyroxene barometer (Neave and Putirka, 2017). However, this does not impact our barometric and thermometric models as we made no assumptions concerning the Jd content in clinopyroxene proactively in our models.

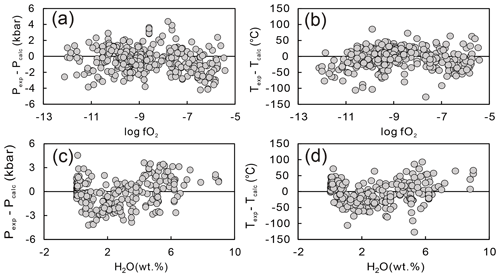
Figure 8 Comparison between P_exp–P_calc and T_exp–T_calc with melt H₂O content (wt %) oxygen fugacity (fO₂). For panels (a) and (b), only experimental data quantitatively reporting the oxygen fugacity conditions were used.

P_exp–P_calc and T_exp–T_calc are both weakly related to meltwater content for H₂O contents higher than 1 wt %, with R² of 0.29 and 0.21, respectively (Fig. 8c, d). As discussed earlier, it is unsurprising that residual P relates to melt H₂O contents since Eq. (1) does not contain a H₂O term. The effect of H₂O on the cell volume of clinopyroxene could slightly affect the pressure estimates. However, there is no obvious H₂O effect that significantly impacts the reproducibility of our new barometer for the calibration, validation, and test datasets (see below). Thus, we infer that the presence of water in the coexisting melt does not affect our new barometer's precision in practical application. Additionally, the poor correlation between T_exp–T_calc and H₂O has no significance because Eq. (2) contains a H₂O term, and the maximum T residual was not obtained from the melt with the highest H₂O content.

4 Discussion

4.1 Evaluating the new clinopyroxene-only thermobarometer

Although regression statistics provide important information concerning the performance of our new models, it is important to verify their reliability with an independent test dataset that has not been used before for calibration and validation.

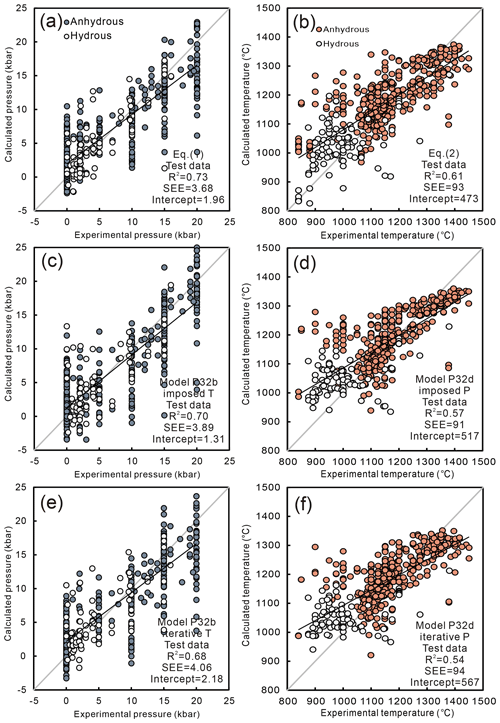
Figure 9 Performance of different algorithms on the test dataset. (a) Our new barometer (Eq. 1), (b) our new thermometer (Eq. 2), (c) P32b with imposed T, (d) P32dH with imposed P, (e, f) iterative calculation of P32b and P32dH. Blue and orange circles refer to anhydrous experimental data, while unfilled circles correspond to hydrous experiments. Gray lines illustrate 1 : 1 trajectories, and black lines represent regression lines.

The generalization ability of these thermobarometric models was verified by testing them on the global test dataset that has not been used previously for calibration and validation. Equation (1) performs slightly worse on the global dataset compared to the calibration and validation datasets (Fig. 9a; R² = 0.73, SEE = 3.68 kbar, intercept = 1.96 kbar). This mismatch cannot simply be attributed to the fact that some experiments in the test dataset were performed on magmas lying beyond the compositional range covered by the calibration dataset since conditions of experiments with dacitic and rhyolitic melt compositions (e.g., Martel et al., 1999; Patiño Douce, 1995; Patiño Douce and Beard, 1995; Prouteau and Scaillet, 2003) were well reproduced by Eq. (1). In detail, pressures of 15 and 20 kbar experiments are systematically underestimated, while pressures for the 1 atm data are systematically overestimated (Fig. 9a), and, consequently, we infer that the diminished performance of Eq. (1) for the test dataset mainly arises from calculations for these experimental data. The failure of our new barometer to satisfactorily reproduce high pressures could be due to the lack of high-pressure experiments in the calibration dataset. The overestimation of pressure for the 1 atm data, however, is probably due to some Na loss experienced by these experiments (Neave and Putirka, 2017). Additionally, pressures of experiments that were performed on basaltic, basaltic andesitic, and dacitic magma systems (e.g., Barclay and Carmichael, 2004; Bender et al., 1978; Falloon et al., 1999, 1997; Fram and Longhi, 1992; Grove et al., 1997; Kennedy et al., 1990; Martel et al., 1999) were well reproduced by Eq. (1), while pressures of experiments on phonolitic systems (Berndt et al., 2001) were systematically overestimated. Consequently, we propose that our new barometer is particularly suitable for clinopyroxene crystallized from subalkaline magmas. Likewise, model P32b exhibits a poor generalization ability for the entire test dataset when performing calculations with imposed experimental temperature (Fig. 9b; R² = 0.70, SEE = 3.89 kbar, intercept = 1.31 kbar). However, the SEE even slightly increases upon iterative calculations of P employing P32dH (Fig. 9e; R² = 0.68, SEE = 4.06 kbar, intercept = 2.18 kbar). Similar to Eq. (1), most of the errors arise from the experimental data at 1 atm as well as above 12 kbar. Thus, we propose that the calibration of a Cpx-only barometric model applicable to a wide pressure range without reducing accuracy and precision is rather unrealistic.

Similar to our barometer, also the new thermometer (Eq. 2) struggles to reasonably reproduce the entire test dataset (Fig. 9b; R² = 0.61, SEE = 93 ^∘C, intercept = 473 ^∘C). Most discrepancies can be attributed to the test data experiments with melt compositions out of the calibration range. For example, for experiments conducted on intermediate acidic systems (e.g., Berndt et al., 2001; Draper and Green, 1999; Patiño Douce, 1995; Patiño Douce and Beard, 1995; Springer and Seck, 1997), experimental temperatures are highly overestimated by Eq. (2) (140 ^∘C on average). However, the poor applicability of Eq. (2) to the entire test dataset is unsurprising given that temperature information is mainly stored in residual melt compositions (Petrelli et al., 2020). Nonetheless, similar to Eq. (1), the new thermometer successfully reproduces experimental temperatures of basaltic, basaltic andesitic, and dacitic systems (e.g., Barclay and Carmichael, 2004; Bender et al., 1978; Falloon et al., 1999, 1997; Fram and Longhi, 1992; Grove et al., 1997; Kennedy et al., 1990; Martel et al., 1999). The P32dH model could also not satisfactorily reproduce experimental temperatures of the entire test dataset (Fig. 8d; R² = 0.57, SEE = 91 ^∘C, intercept = 517 ^∘C), and its performance becomes even worse if calculations are performed iteratively in combination with P32b (Fig. 8f; R² = 0.54, SEE = 94 ^∘C, intercept = 567 ^∘C).

In summary, our new barometer (Eq. 1) and thermometer (Eq. 2) are both specifically suitable for basic to intermediate subalkaline magmatic systems. Although Eq. (1) has been shown to work well for magma compositions outside of the calibration and validation range (such as rhyolites), we still recommend being cautious when applying it to magmas far beyond basaltic, basaltic, andesitic, and dacitic compositions.

4.2 Application of the new models to Iceland volcanoes

The magmatic plumbing systems of tholeiitic eruptions from Iceland's rift zones have been broadly discussed in the past (e.g., Maclennan et al., 2001; Neave et al., 2013, 2015). Recently, Neave and Putirka (2017) recalibrated a new clinopyroxene-liquid barometer especially for tholeiitic basalts that was subsequently applied to a variety of Icelandic basalts to constrain their pre-eruptive magmatic storage conditions. In detail, compositions of liquids in equilibrium with measured clinopyroxenes were rigorously selected based on multiple-component equilibria (e.g., Fe–Mg, Ti, CaTs components).

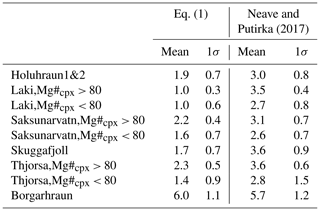
To test the applicability of our new thermobarometric models to natural clinopyroxenes, we applied our new barometer and thermometer to the same natural samples used by Neave and Putirka (2017). Results of our calculations as well as Neave and Putirka (2017) are summarized in Fig. 10 and Table 3. Although using an identical dataset, our new barometer and thermometer both returned systematically lower pressure and temperature estimates for the more evolved volcanoes (0–4 kbar) compared to Neave and Putirka (2017) (0–6 kbar). However, for the highly primitive Borgarhraun basalts, our new models as well as Neave and Putirka (2017) both resulted in higher pressure and temperature estimates, with 6.0 ± 1.1 kbar, 1244 ± 19 ^∘C for the former and 5.7 ± 1.2 kbar, 1234 ± 19 ^∘C for the latter. Accounting for the intrinsic errors in our new models (1.66 kbar and 36.6 ^∘C) and the algorithms calibrated by Neave and Putirka (2017) (1.4 kbar and 28.4 ^∘C), we conclude that the P–T estimates of both thermobarometers are actually covering identical ranges. Additionally, our barometer results for the Holuhraun eruption (1.9 ± 0.7 kbar) agree slightly better with independent estimates using the OPAM (olivine–plagioclase–augite–melt) barometer (2.1 ± 0.7 kbar; Hartley et al., 2018).

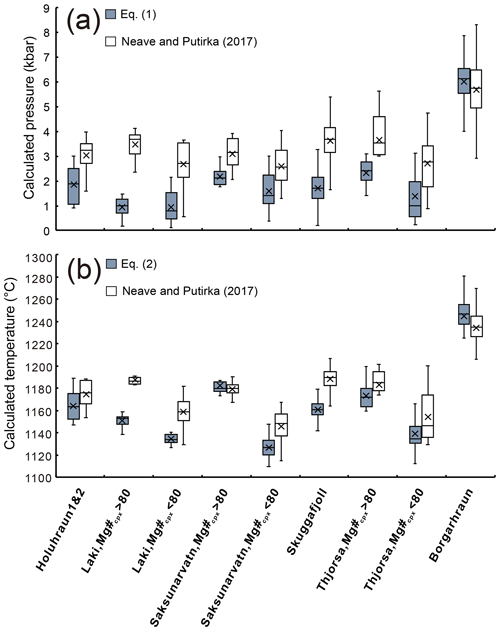
Figure 10 Box plots of crystallization pressures and temperatures calculated for the clinopyroxenes from Icelandic basalts. Blue boxes refer to results calculated with our new models, while unfilled ones were established with Neave and Putirka (2017). Horizontal lines in each box represent median numbers, and crosses correspond to averages.

Table 3 Comparison of barometric results between our new model (Eq. 1) and Neave and Putirka (2017).

To confirm the reliability of our new models' results for the Icelandic basalts, we further applied them to clinopyroxenes from experiments on the 2014–2015 Holuhraun lava by Neave et al. (2019). Barometric and thermometric calculations were performed for all experimental clinopyroxene data reported in Neave et al. (2019). For comparison, we additionally performed calculations for the same dataset by iteratively solving the barometer from Neave and Putirka (2017) and Eq. (33) from Putirka et al. (2003), where disequilibrium clinopyroxene compositions were previously eliminated based on multicomponent equilibrium analysis (DiHd, EnFs, CaTs, Fe–Mg). Calculation results are listed in Table S3 and summarized in Fig. 11. Although some disequilibrium clinopyroxene data were used for the calculations with our new barometer and thermometer, experimental pressures and temperatures were still well reproduced (e.g., those experimental pressures of 1 and 3 kbar, experimental temperature of 1160 ^∘C). In addition, maximum observed deviations between calculated and experimental P–T conditions (e.g., at 6 kbar or 1200 ^∘C) are still within 1 SEE of the new thermobarometric models, underlining the reproducibility of our new models. Moreover, the majority of established pressure and temperature estimates agree well with the results of the barometer from Neave and Putirka (2017) and Eq. (33) from Putirka et al. (2003) (Fig. 11). Consequently, our new thermobarometer resulted in robust and reliable P–T estimates for natural clinopyroxenes from Icelandic basalts. Performed calculations also confirm that our new models do not require any prior filtering of clinopyroxene data for disequilibrium. One possible reason for this feature is that clinopyroxenes approach chemical equilibrium from random directions, and averaging calculated pressures and temperatures eliminates potential errors caused by disequilibrium (Putirka et al., 2003; Putirka, 2008). Thus, we recommend averaging calculation results when applying our new barometer and thermometer to natural clinopyroxenes crystallized from (supposedly) similar P–T conditions.

Figure 11 Box plots of pressures and temperatures calculated for the experimental clinopyroxenes from Neave et al. (2019). Blue boxes and dots refer to results calculated with our new models, and green ones correspond to values established by iterative calculations with Eq. (1) from Neave and Putirka (2017) and Eq. (33) from Putirka (2008). Horizontal lines in each box represent median numbers, and crosses illustrate averages. Blue–green dotted lines correspond to experimental pressures or temperatures.

5 Conclusions

In this contribution, we calibrated new nonlinear Cpx-only barometric and thermometric models that are suitable for basic to intermediate magmatic systems in the pressure range of 1 bar to 12 kbar. Extensive comparisons between previous Cpx-only thermobarometers and our new algorithms were performed, confirming that our new models are the most practical as well as most accurate and precise ones currently available. However, our new thermobarometers revealed some limitations in applicability to the entire experimental test dataset but performed reasonably well for basaltic, basaltic andesitic, and dacitic systems. Consequently, we recommend to only apply our new barometric and thermometric formulations to basic to intermediate subalkaline magma systems.

The applicability of our barometer and thermometer to natural clinopyroxenes was verified by recalculating crystallization pressures and temperatures of Icelandic basalts. Calculated magma storage conditions employing our new models agreed well with previous estimates and conclusions from other studies. Moreover, our tests revealed that, in case calculation results are averaged, no filtering of clinopyroxene data for potential disequilibrium is required before applying our new models. Consequently, the new Cpx-only thermobarometer presented herein can be confidently used to estimate magmatic temperatures and pressures in basaltic and basalt-andesitic magmatic systems.