Structural, textural, and chemical controls on the OH stretching vibrations in serpentine-group minerals

The OH stretching vibrational properties of eight serpentine samples from veins of the New Caledonian ophiolite have been investigated by Fourier-transform infrared spectroscopy (FTIR) in the mid-infrared and near-infrared ranges and by Raman spectroscopy. The samples were selected for their monophasic composition (Lz: lizardite; Ctl: chrysotile; and Atg: antigorite) making them representative of the three serpentine species. Comparison of fundamental and overtone spectra allowed us to interpret most of the observed bands and to propose consistent spectral decomposition in individual components. The OH stretching bands related to intrinsic vibrational properties of the minerals are distinguished from those associated with chemical substitutions in octahedral sites (mainly Fe and Ni for Mg substitutions). Observations made on the most symmetric Lz are consistent with previous interpretations and underline the effect of macroscopic parameters on OH stretching bands in the FTIR spectra. The major importance of the distribution of OH bond lengths in the broadening of the vibrational signals of the less symmetric and more distorted Atg is confirmed. The combination of the three spectroscopic methods makes it possible to unravel the occurrence of two different types of interlayer OH environments in Ctl nanotubes. One corresponds to the features observed at 3684 and 7171 cm⁻¹ in the fundamental and overtone spectra, respectively, and is similar to the local OH environment observed in Lz. The other corresponds to broader signals observed at 3693 and 7200 cm⁻¹ in the fundamental and overtone spectra, respectively. It reflects a distribution of OH bond lengths likely related to local structural misfits between adjacent layers in the tubular structure of Ctl.

1 Introduction

Serpentine-group minerals are $\mathrm{Mg}/\mathrm{Fe}$ 1 : 1 layered silicates which play an essential role in the rheology of numerous geological settings where aqueous fluids interact with ultramafic rocks. They result from faulting and hydration of the oceanic crust and are generated through hydrothermal alteration of ultramafic silicates (mostly olivine and orthopyroxene) (e.g. Mével, 2003). Serpentines are formed at various pressures and temperatures during the unrolling of the oceanic crust from spreading ridges to subduction zones (Mével, 2003; Andreani et al., 2004, 2007; Deschamps et al., 2011). They can also form during the obduction of the oceanic crust onto continental formations, as reported for the ophiolite nappe of New Caledonia (Cluzel, 2001; Ulrich et al., 2010). Recent studies carried out on this ophiolite have shown that the low-grade hydrothermal alteration of serpentine veins, associated with the cooling and dismantling of the ophiolite nappe, is most likely at the origin of the Ni silicate ore deposits (also known as garnierites) of the island (Fritsch et al., 2016, 2019; Cathelineau et al., 2017). Minerals of these deposits include serpentine residues in variable proportions but also newly formed and highly hydrated Mg–Ni series of 2 : 1 layer silicates (mostly talc-like minerals and locally sepiolite).

The diversity of serpentine-group minerals combines variations in the curvature of 1 : 1 layers, defining the ideal members of this mineral group, and the incorporation of chemical impurities, mostly through cationic substitutions (Wicks and O'Hanley, 1988). The structural diversity is attributed to a lattice mismatch between the tetrahedral (T) and octahedral (O) sheets, which favours the curvature of the T–O layers leaving the smaller (T) inside and the larger (O) outside (Hurlbut and Klein, 1977). Curvature of the layers is optimal in chrysotile (Ctl), which occurs as bundles of nanotubes (Whittaker, 1956; Yada, 1967), while lizardite (Lz) presents flat layers (Wicks and O'Hanley, 1988). In polygonal and polyhedral serpentine, curved and flat sectors alternate in cylindrical or onion peel geometry, respectively (Baronnet and Devouard, 2005; Baronnet et al., 2007). Antigorite (Atg) displays a wavy corrugated layer structure resulting from the inversion of curvature in sectors of different lengths (Kunze, 1961). These inversions induce a slight Mg(OH)₂ depletion in Atg. It has been suggested that curvature changes among serpentine-group minerals are linked to slight variations in their crystal chemistry. Species with optimal curvature, i.e. Ctl, are often closer to the ideal formulae Mg₃Si₂O₅(OH)₄, while cationic impurities (e.g. Fe, Ni, and Al) would be required to stabilize the flat structure of Lz (Yariv and Heller-Kallai, 1975). However, such relationships between crystal structure and crystal chemistry have been debated for a long time (Page, 1968; Whittaker and Wicks, 1970) and were not supported by the synthesis of pure Mg lizardite that shows platy particles (Chernosky, 1975; Mondésir and Decarreau, 1987).

Vibrational spectroscopies are among the routine methods most frequently used in the characterization of serpentines. Raman spectroscopy has been shown to be a suitable technic for the discrimination of serpentine species (Lemaire, 2000; Rinaudo and Gastaldi, 2003; Auzende et al., 2004; Petriglieri et al., 2015, Cathelineau et al., 2015). Fourier-transform infrared (FTIR) spectroscopy (e.g. Luce, 1971; Farmer, 1974; Yariv and Heller-Kallai, 1975; Titulaer et al., 1993; Fuchs et al., 1998; Post and Borer, 2000; Falini et al., 2002; Foresti et al., 2005; Anbalagan et al., 2010; Basile et al., 2010) and near-infrared (NIR) spectroscopy (Reddy et al., 2009; Baron and Petit, 2016) are also sensitive to the variability in serpentine-group minerals. In addition, the combination of micro-FTIR and Raman spectroscopy has been successfully used to infer the dehydration mechanisms of Lz and Ctl (Trittschack et al., 2012; Trittschack and Grobéty, 2013).

These studies often focus on the characteristic bands related to OH stretching modes. These modes are almost uncoupled from the other vibrational modes occurring at significantly lower frequencies and are therefore considered as sensitive probes of local perturbations of the crystal structure. However, the contrasting properties of the two types of OH groups occurring in serpentines may complicate the interpretation of spectroscopic observations. The inner OH groups are linked to three octahedral cations (mainly Mg) and are stretched perpendicularly to the layers, pointing towards the centre of the six-fold ring of SiO₄ tetrahedra. The interlayer OH groups are located on top of the trioctahedral layer pointing to the O atoms of basal plane of the next T–O layer. Inner OH groups thus display a comparatively larger distance to their translational equivalents than interlayer OH groups. This minimizes the dipolar coupling between inner OH groups and explains that related stretching modes behave as isolated oscillators, leading to well-defined absorption bands in high-quality samples. As in talc (Wilkins and Ito, 1967; Petit et al., 2004a, b; Blanchard et al., 2018), the stretching frequency of inner OH groups in serpentine-group minerals is primarily controlled by the cationic occupancy of neighbouring octahedral sites (Baron and Petit, 2016). In contrast, the interlayer OH groups display more significant interactions, leading to the splitting of coupled vibrational modes and to long-range collective behaviour (Balan et al., 2002b; Prencipe et al., 2009). This adds some complexity to the vibrational spectra of serpentine-group minerals, and their identification and quantification in complex mineral assemblages, such as those observed in Ni silicate ores, may become challenging.

Detailed experimental investigations of the vibrational spectroscopic properties of representative serpentine samples are thus expected to document the sensitivity of OH stretching spectra to variations in their crystal structure (e.g. layer curvature, bond strength) and chemical composition. Here, we show how it is possible to disentangle the various parameters controlling the spectral shapes by combining transmission FTIR spectroscopy in the mid-infrared range, diffuse reflectance NIR spectroscopy, and Raman spectroscopy measurements on eight monophasic Lz, Ctl, and Atg samples from New Caledonian serpentine veins.

2 Materials and methods

The eight samples of serpentine selected for this study belong to a large set of un-mineralized and mineralized veins collected by Fritsch et al. (2016) in the saprock of thick Ni laterite deposits from New Caledonia. Their monophasic composition was cross-checked by Raman spectroscopy and high-resolution transmission electron microscopy (HR-TEM). Their habits and texture are illustrated in Fig. 2 of Fritsch et al. (2016). Samples of Lz belong to black serpentine veins of various thicknesses (1–400 mm) which crosscut the whole section of the ophiolite nappe. Only two samples made of predominant platelets of Lz (Lz1 and Lz2) could be isolated as the black serpentine veins may also comprise protoserpentine (smaller and less differentiated platelets), tubular-shaped Ctl and talc in variable proportions (Fritsch et al., 2016, 2019). The purity of the other serpentine veins may be linked to specific field patterns. Samples of Ctl (Ctl1, Ctl2, and Ctl3) belong to crack-infilling seals (superimposed rows of joint fibres, up to 50 mm of thickness) similar to those observed in oceanic environments (Ramsay, 1980; Andreani et al., 2004; Renard et al., 2005). High-temperature Atg samples (Atg1, Atg2, and Atg4) are from detachment faults of the saprock and are observed as coatings on wavy corrugated surfaces. Serpentine veins made of Atg or Ctl are commonly greenish brown. They are locally bleached (thin white coatings on fault walls) and closely associated with numerous grains (lenses) of magnetite. They are predominant at the basement of the ophiolite nappe in thrusting and shearing zones (Ulrich et al., 2010).

The samples were crushed, ground with agate pestle and mortar, and air-dried prior to chemical and mineralogical investigations. Chemical analyses of bulk samples were performed using a Perkin-Elmer 1100b atomic absorption spectrophotometer (AAS) after acid digestion of 1000 mg of a finely powdered aliquot in a high-pressure TFM Teflon™ vessel using an ETHOS 1600 Milestone microwave system.

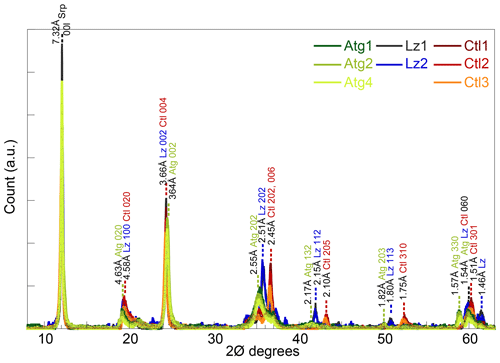
X-ray diffraction (XRD) was performed on randomly oriented powders of bulk samples, previously sieved at 50 µm, using a Bruker D8 Advance diffractometer equipped with LYNXEYE detector (Cu Kα radiation, 40 kV, 30 mA). Data were recorded in step-scan mode between 4 and 65^∘ 2θ with 0.016^∘ steps and counting 480 s per step. Peak position, peak intensity, and full width at half maximum (FWHM) of the basal reflections were determined with Fityk^® after background stripping. They were converted into coherent-scattering domain sizes (CSDS) in the c* direction (defined by the statistical range of number of layers: N) using the Scherrer equation.

Raman spectra were recorded on only three of the samples (Lz2, Ctl3, Atg2) using a Renishaw (Wotton-under-Edge, UK) inVia Reflex micro-spectrometer equipped with a 514 nm Spectra-Physics (20 mW) argon laser. The laser was focused on the powder sample using a DM LM Leica (Wetzlar, Germany) microscope with a 100× objective (NA = 0.90), and its power at the sample surface was set at 1 mW. To check the structural homogeneity of the sample, four spots of analysis with a beam size of ∼ 1 µm were selected and 10–20 spectra were accumulated for each spot in the static mode (3480 to 3922 cm⁻¹).

Mid-infrared (MIR) spectroscopy was performed in the transmission mode on pellets 2 cm in diameter and prepared with 1 mg of sample and 150 mg of KBr salt. The mixture was pressed for 5 min and dried overnight in an oven at 110 ^∘C. MIR spectra were collected with a Thermo Scientific Nicolet 760 FTIR spectrometer equipped with an EverGlo source, a KBr beam splitter, and a deuterated triglycine sulfate DTGS-KBr detector. The spectra were recorded over the 400–4000 cm⁻¹ range with a resolution of 4 cm⁻¹ and co-additions of 100 scans.

Near-infrared (NIR) spectroscopy was performed on powder samples without any dilution. NIR spectra were obtained using a Thermo Scientific Nicolet 6700 FT-IR spectrometer equipped with a white light source, a CaF₂ beam splitter, and a Thermo Scientific Smart NIR integrating sphere equipped with an internal InGaAs detector. Powder samples were analysed in diffuse-reflectance mode. The resulting NIR spectra are the sum of the 100 scans collected over the 3850–7500 cm⁻¹ range at a resolution of 4 cm⁻¹.

Spectroscopic signals in the OH stretching region of the Raman and MIR spectra (3750–3600 cm⁻¹), as well as in that of the NIR spectra (7300–6900 cm⁻¹), were decomposed into individual components using the Fityk^® programme (Wojdyr, 2010). No smoothing of the data was performed before fitting. The baseline was treated as a linear function, which was fitted together with the other components as recommended by Meier (2005). It is important to stress that it is not possible to a priori define a theoretical line shape in these spectra because of the occurrence of various inhomogeneous broadening causes. The observed bands can be considered as envelopes associated with distributions of frequencies. Decompositions were thus done using functions allowing for shape variations including asymmetry and Gaussian to Lorentzian character. The relaxation of the constraints related to the shape of individual components was counterbalanced by restricting the number of contributions to visible features, thus avoiding the introduction of contributions with unclear physical interpretations (see, for example, Meier, 2005; Brauns and Meier, 2008; Stancik and Brauns, 2008). Although the proposed decompositions are certainly not unique, they show that the proposed interpretations are not in contradiction with experimental observations and that they help to better define individual contributions. These proposed decompositions also ease the comparison of the various spectra recorded on a same sample.

Figure 1 Powder XRD patterns of the eight serpentine samples selected for this study (lizardite: Lz1, Lz2; chrysotile: Ctl1, Ctl2, Ctl3; antigorite: Atg1, Atg2, Atg4).

3 Results and discussion

3.1 Crystal chemistry of lizardite, chrysotile, and antigorite samples

The XRD peaks at d spacings of ∼ 7.32, 4.61, 3.65, and 1.54 Å of the eight samples (Fig. 1) are characteristic of trioctahedral 1 : 1 layer silicates of the serpentine mineral group (Bailey, 1969; Brindley and Wan, 1975; Wicks and O'Hanley, 1988). No crystalline phases other than serpentines could be identified on the XRD traces. The sharp and intense peaks of the basal reflections of the serpentine species (CSDS₀₀₁: 80–165 N) are consistent with large crystal sizes on HR-TEM images (Fritsch et al., 2016).

The three serpentine species (Atg, Ctl, and Lz) can be differentiated from the position of weaker peaks at ∼ 36, 42, and 51^∘ 2θ (Fritsch et al., 2016). Indeed, these peaks are present at slightly lower angles for Atg than Ctl, with an intermediate position for Lz (Fig. 1). For the most prominent peaks at ∼ 36^∘ 2θ, the 202 reflection is for instance at a d spacing of 2.55 Å for Atg, 2.45 Å for Ctl, and 2.51 Å for Lz. At high angles and on both sides of their common 060 reflection for trioctahedral layer silicates (1.54–1.51 Å), additional peaks are recognized at d spacings of 1.57 Å for Atg and 1.46 Å for Lz. According to d spacings reported in Wicks and O'Hanley (1988), the serpentine species belong to the 1T polytype for samples of Lz and 2M polytype (clinochrysotile) for samples of Ctl.

Table 1 Bulk chemical composition (weight, wt, oxide %) of the eight serpentine samples selected for this study (lizardite: Lz1, Lz2; chrysotile: Ctl1, Ctl2, Ctl3; antigorite: Atg1, Atg2, Atg4). In the table, p.h.f. signifies per half formula.

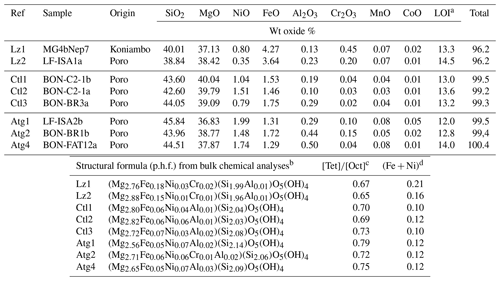
^a Loss of ignition. ^b In the given formulae, we assume Al is in tetrahedral sites when Si < 2 and Fe is totally reduced in octahedral sites. However, the occurrence of octahedral Fe³⁺ is not excluded notably to ensure the neutrality of the structure. ^c Molar cation ratio between tetrahedral and octahedral sites. ^d Molar content of transition elements (Fe, Ni) per half formula (p.h.f.).

The chemical composition of the eight samples (Table 1) indicates the presence of minor amounts of transition elements (mostly Fe and Ni) and aluminium, as well as a molar cation ratio between tetrahedral and octahedral sites ($\left[\mathrm{Tet}\right]/\left[\mathrm{Oct}\right]$) close to that expected for serpentine species (theoretical value of 0.67). Slight chemical changes can be noticed from the low to high temperature serpentines. The $\left[\mathrm{Tet}\right]/\left[\mathrm{Oct}\right]$ ratio increases from 0.65 to 0.79, and the content of transition elements (i.e. Fe + Ni) decreases significantly in Ctl and, to a lesser extent, in Atg. The higher $\left[\mathrm{Tet}\right]/\left[\mathrm{Oct}\right]$ ratio for Atg is consistent with the slight depletion of octahedral cations (or accumulation of silica) due to the inversion of the curved lath sectors. Table 1 shows in addition that Atg and, to a lesser extent, Ctl commonly have more Ni (and Al) and less Fe than Lz. Note that a correlated change in colour of the veins is also observed, grading from black for dominant Lz to dark or faint greenish brown for Ctl and Atg.

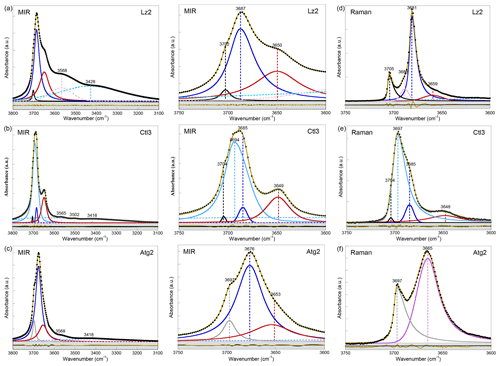
Figure 2 Left: MIR spectra of samples (a) Lz2, (b) Ctl3, and (c) Atg2 in the 3800–3100 cm⁻¹ range (OH and H₂O vibrations). Centre: enlarged view of the MIR OH stretching bands between 3750 and 3600 cm⁻¹ (see Appendix A, Fig. A2 for the complete set of samples). Right: Raman spectra of samples (d) Lz2, (e) Ctl3, and (f) Atg2 in the 3750–3600 cm⁻¹ range (OH stretching bands). The spectra have been decomposed into individual components using asymmetric Lorentzian–Gaussian functions. Black dots: experimental data. Solid brown line: best fit (residues in bottom grey box). Plain black and grey curves: inner OH stretching modes. Plain blue and red (or purple) curves: interlayer OH stretching modes. Dashed pink and light blue curves: H₂O vibration modes.

3.2 Vibrational spectroscopy of OH stretching modes in lizardite, antigorite, and chrysotile

Fundamental and first overtone OH stretching bands reported from MIR (Fig. 2a–c, see also Fig. A2), Raman (Fig. 2d–f), and NIR (Fig. 3a–c) investigations on the eight samples are consistent with those reported previously for trioctahedral 1 : 1 layer silicates of the serpentine group (e.g. Farmer and Russell, 1964; Auzende et al., 2004; Trittschack et al., 2012; Trittschack and Grobéty, 2013; Petriglieri et al., 2015). Position, width, and intensity of the bands in both the fundamental and overtone regions of vibrational spectra remain quite similar within each species of serpentine. By contrast, they may change significantly from one serpentine species to another, as well as from one spectroscopic technic to the other. In the following sections, the vibrational spectroscopic properties of OH stretching modes in Lz, Atg, and Ctl will be successively presented and discussed.

Table 2 Fundamental (1v) average frequency (w_e cm⁻¹) of OH stretching and H₂O vibration modes measured on decomposed MIR and Raman spectra in lizardite (Lz), chrysotile (Ctl), and antigorite (Atg) from serpentine (Srp) veins of the New Caledonian ophiolite. Reference of lizardite from Balan et al. (2002) is also given for comparison (Lz-ref).

Frequency (w_e) in bold: well-defined OH stretching peaks.
Assignment of the fundamental transitions:
(1) inner OH in Mg₃ and (*) Mg₂M configurations; (2) in-phase (A1 symmetry) and (3) out-of-phase (E symmetry) interlayer OH for Lz and Ctl (note that for Atg a clear-cut distinction cannot be made and bands (2) to (3) are simply related to interlayer OH groups);
(4), (5), and (6) weakly bound water with possible interference of OH stretching associated with octahedral trivalent cations for (4).

3.2.1 OH stretching modes in lizardite

The high symmetry of Lz facilitates the assignment of observed signals to specific vibrational modes. The FTIR OH stretching bands of Lz (Figs. 2a and A2a) have been interpreted in terms of vibrational modes for some time (e.g. Yariv and Heller-Kallai, 1975) with a later confirmation by theoretical studies (Balan et al., 2002b; Prencipe et al., 2009). Observations made of Lz samples can thus be considered as benchmarks for the interpretation of the spectra of other less symmetric serpentine species.

In the FTIR spectra of Lz (Figs. 2a, A2a, Table 2), the dominant OH stretching band attributed to the in-phase stretching (A₁ symmetry) of the interlayer OH groups is broad and asymmetric with a maximum at ∼ 3687 cm⁻¹ and a long tailing slope towards lower frequencies. The shoulder at higher frequency (∼ 3702 cm⁻¹) corresponds to the inner OH group, while the broader band at lower frequency (∼ 3652 cm⁻¹) is related to the degenerate out-of-phase stretching (E symmetry) of the interlayer OH groups. Two broad signals are also observed at lower frequencies at ∼ 3568 and ∼ 3428 cm⁻¹ (Fig. 2a). They are likely due to weakly bound water molecules (Falini et al., 2002) and/or occurrence of trivalent cations in the serpentine structure (Serna et al., 1979). Note that the presence of molecular water in all the investigated serpentine samples is attested by the H₂O bending mode absorption at 1635 cm⁻¹ in their FTIR spectra (not shown). The two broad signals are particularly intense in the two Lz samples (Fig. 2a). They overlap at higher frequency, with the sharper bands assigned to the OH stretching vibrations, and point to greater hydration of Lz, the low temperature serpentine species. It is worth reporting that the broad signal observed at ∼ 3568 cm⁻¹ has been previously observed on the spectrum of the reference Monte Fico lizardite and attributed to the presence of octahedral Fe²⁺ (e.g. Fuchs et al., 1998; Balan et al., 2002). However, the extent of the shift (119 cm⁻¹) with respect to the main signal assigned to the interlayer OH vibration at ∼ 3687 cm⁻¹ for Lz is inconsistent with the expected shift related to isovalent cationic substitutions (typically ∼ 14 cm⁻¹; Petit et al., 2004b). This signal is more likely related to the occurrence of structural trivalent cations and/or absorbed water molecules. Following the above analysis, the two Lz MIR spectra were fitted using five functions (Fig. 2a): three for the OH stretching modes (plain black, blue, and red curves) and two for the broad signals at lower frequency (dashed pink and light blue curves). To improve the agreement between model and experimental data, some degree of asymmetry was allowed to model the shape of the main band at 3687 cm⁻¹ (plain blue curve).

Table 3 First overtone (2v) average frequency (w_e cm⁻¹) of OH stretching modes measured on decomposed NIR spectra in lizardite (Lz), chrysotile (Ctl), and antigorite (Atg) from serpentine (Srp) veins of the New Caledonian ophiolite.

Frequency (w_e) in bold: well-defined OH stretching peaks.
^a Trace amount of talc detected in the sample from a weak peak at ∼ 7184 cm⁻¹ for inner OH in an Mg₃ configuration. ^b Anharmonicity parameter calculated for the inner OH (from MIR and NIR values displayed on Tables 2 and 3).
Assignment of the OH overtone transitions:
weak bands related to first excitation levels of coupled interlayer OH oscillators in (W2) Mg₃ and (W2_M) Mg₂M configurations (with M= Fe²⁺ or Ni²⁺);
stronger bands due to second excitation levels of uncoupled OH groups: (1) inner OH in (S1) Mg₃ and (S1_M) Mg₂M configurations and (2) interlayer OH in (S2) Mg₃ and (S2_M) Mg₂M configurations.

The OH stretching modes of Lz have both IR and Raman activity. The Raman spectrum of Lz2 (Fig. 2d) thus displays OH stretching bands similar to those observed on its FTIR counterpart registered in the MIR range (Fig. 2a). More specifically, the stretching band of inner OH groups in an Mg₃ environment is observed at nearly the same frequency (3705 cm⁻¹) as in MIR spectra (3702 cm⁻¹). The in-phase stretching of the interlayer OH groups still corresponds to the dominant band. This band is sharper and shifted towards a lower frequency from 3687 cm⁻¹ in MIR spectra to 3681 cm⁻¹ in the Raman spectrum of Lz2. Due to this shift, the inner OH band is clearly separated from the others observed at lower frequencies. On the low-frequency side of the dominant band, a shoulder centred at 3659 cm⁻¹ corresponds to the out-of-phase stretching of the interlayer OH group. The prominent Raman band at 3681 cm⁻¹ also displays on its high-frequency side a shoulder at 3688 cm⁻¹ (Fig. 2d). This latter contribution most likely corresponds to the stretching of inner OH groups in an Mg₂M environment (with M= Fe or Ni). Indeed, the relative position of this feature with respect to the inner OH band at 3705 cm⁻¹ corresponds to a downshift of 17 cm⁻¹, which is consistent with the effect of cationic occupancies on the stretching frequencies of inner OH groups in $\mathrm{Fe}/\mathrm{Mg}$ talc series (Petit et al., 2004a). Based on this analysis, the Lz2 Raman spectrum was fitted using five functions (Fig. 2d): two for the inner OH stretching modes in Mg₃ and Mg₂M configurations, respectively (plain black and pink curves), two others for the in-phase and out-of-phase interlayer OH (plain blue and red curves), and a last one for the contribution of water molecules at lower frequency (dashed light blue curve). As for MIR spectra, the main band for the in-phase interlayer OH was described using an asymmetric Lorentzian function with a more pronounced broadening on its low-frequency side (plain blue curve).

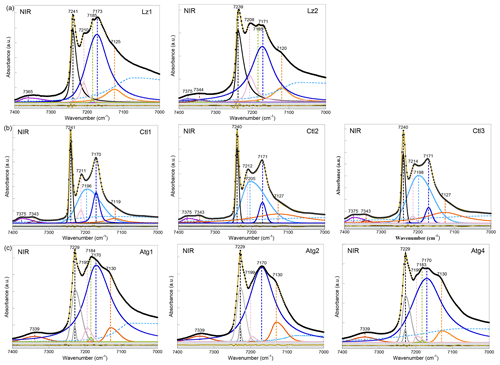
Figure 3 NIR spectra in the 7400–7000 cm⁻¹ range (first overtone region of OH stretching bands) of (a) lizardite (Lz1, Lz2), (b) chrysotile (Ctl1, Ctl2, Ctl3), and (c) antigorite (Atg1, Atg2, Atg4). The spectra have been decomposed into individual components using asymmetric Lorentzian–Gaussian functions. Black dots: experimental data. Solid brown line: best fit (residues in bottom grey box). Plain black, grey and pink curves: inner OH stretching modes. Plain blue and orange curves: interlayer OH stretching modes. Dashed light blue curve: H₂O vibration mode.

The differences observed between the FTIR and Raman spectra of Lz can be ascribed to the effect of various macroscopic parameters on the vibrational spectra. The intense band associated with the in-phase interlayer OH stretching mode is downshifted by 6 cm⁻¹ between the infrared and Raman spectra. Similar shifts have been previously reported for an OH stretching mode polarized perpendicularly to the layers in kaolinite-group minerals (Farmer, 1998, 2000). They arise from macroscopic electrostatic interactions and reflect the interplay between the size and shape of mineral particles and the different wavelengths of the exciting radiation (514 nm in Raman spectroscopy compared with ∼ 3 µm in IR spectroscopy) (Farmer, 1998, 2000; Balan et al., 2001, 2005). These effects also occur in Lz (Balan et al., 2002b) and can account for the systematic red shift of the main OH stretching band observed between the FTIR and Raman spectra. They also contribute to the broadening of absorption bands in real samples obtained by grinding, which display an uncontrolled diversity of particle shapes (e.g. Balan et al., 2008). In contrast, the weaker inner OH and the out-of-phase inter-layer OH stretching modes are almost unaffected by these electrostatic interactions and occur at nearly the same frequency in the FTIR and Raman spectra. It is noteworthy that a significant narrowing of the main OH stretching band occurs in the Raman spectrum (8 cm⁻¹) with respect to its FTIR counterpart (32 cm⁻¹). The distribution of particle sizes and their uneven repartition in the mineral KBr pellet has a pronounced broadening effect on the intense infrared absorption bands recorded in transmission geometry (Griffiths et al., 2018). This effect does not occur in the Raman measurements performed on pure powders, explaining the observation of a narrower intense signal in the Raman spectrum of Lz2.

The first OH-overtone region of the NIR spectra of Lz (Fig. 3a, Table 3) displays more complex spectral features than its fundamental FTIR (Fig. 2a) and Raman (Fig. 2d) counterparts. A series of well-defined peaks is observed between 7300 and 7000 cm⁻¹, corresponding to local transitions to the second excitation level of single OH oscillators, whereas the weaker signals between 7400 and 7300 cm⁻¹ involve the simultaneous transitions to the first excitation level of two interlayer OH oscillators (Balan et al., 2021a).

The sharp and intense signal observed at 7240 cm⁻¹ is ascribed to the stretching overtone of inner OH groups. The calculated anharmonicity parameter (Xanhar) of ∼ −82 cm⁻¹ (Table 3) is consistent with that determined by Petit et al. (2004b) and Baron and Petit (2016) on Mg–Ni series of 1 : 1 and 2 : 1 layer silicates (−85.6 cm⁻¹). The relatively sharp signal at ∼ 7209 cm⁻¹ is also assigned to inner OH groups, but it occurs in the vicinity of an octahedral coordinated divalent transition cation (Mg₂M environment, where M is Fe or Ni) (Balan et al., 2021a). Assuming an anharmonicity parameter similar to that calculated for the Mg₃ environment, the fundamental stretching signal corresponding to the overtone of inner OH groups in an Mg₂M environment (i.e. in serpentines of low chemical impurity) will then occur at ∼ 3688 cm⁻¹, superimposed on the band ascribed to the in-phase stretching of the interlayer OH in MIR spectra and consistent with the interpretation of the shoulder observed at this frequency in the Raman spectrum.

Compared with fundamental transitions, an interesting feature of the overtone transitions observed between 7000 and 7300 cm⁻¹ is a reduction in the band splitting related to the dipolar coupling of interlayer OH oscillators (Balan et al., 2021a). The smaller splitting is no longer resolved in the spectra but instead contributes to the broadening of the bands. A one-to-one assignment of the observed bands to specific atomic-scale environments is thus possible, as it is for the inner OH bands. The broad and predominant peak centred at ∼ 7172 cm⁻¹ is assigned to interlayer OH groups in an Mg₃ environment, while the weaker feature at ∼ 7123 cm⁻¹ corresponds to interlayer OH groups in an Mg₂M environment (Fig. 3a, Table 3). An additional weak, sharp band at ∼ 7184 cm⁻¹ in the Lz samples reveals minute amounts of talc. Flakes of talc have been locally identified under the microscope in the dense mesh pattern of the black serpentine veins (Fritsch et al., 2016, 2019). Finally, the weak features at high frequency appear as a single broad and asymmetric band centred at 7365 cm⁻¹ in sample Lz1 and a split band in sample Lz2, with a first component at high frequency (7375 cm⁻¹) and a second at slightly lower frequency (7344 cm⁻¹). Balan et al. (2021a) have ascribed the first component at 7375 cm⁻¹ to two-phonon transitions involving interlayer OH groups in an Mg₃ environment and have proposed that the second component at 7344 cm⁻¹ corresponds to similar transitions involving OH groups in an Mg₂M environment.

According to this analysis (Fig. 3a), the inner OH overtones of Lz were fitted using two functions for the Mg₃ and Mg₂M environments (black and pink curves). Two other functions were used to fit the overtones of interlayer OH groups in both kinds of environments (blue and orange curves), and a broad and asymmetric component was introduced to account for a signal of adsorbed water molecules at lower frequency (dashed light blue curve). The strong overlap between these components, however, introduces a high degree of uncertainty in the fit, and the width and shape parameters cannot be confidently extracted. Additionally, one or two functions were used to account for the weak features above 7300 cm⁻¹ in Lz1 and Lz2, respectively.

3.2.2 OH stretching modes in antigorite

Compared with Lz, Atg still displays a periodic structure but with a larger unit cell, lower symmetry, and more significant structural distortions (e.g. Grobéty, 2003; Capitani and Mellini, 2004; Capitani et al., 2009). These changes induce significant modifications on the vibrational spectra of Atg compared to those of Lz. The key role of structural distortions in the differences observed between the Atg and Lz FTIR spectra has been recently demonstrated by theoretical modelling of the FTIR spectrum of the m=17 antigorite polysome (Balan et al., 2021b). This is specifically the case with the broad and dominant OH stretching band (Figs. 2c, A2c, Table 2), which is observed at ∼ 3676 cm⁻¹. This band corresponds to a series of vibrational modes (45 modes in the m=17 polysome) involving the OH groups in interlayer configuration. Its width is related to the scattering of vibrational frequencies due to a distribution of OH bond lengths in the large and low-symmetry unit cell of Atg. The marked shoulder at 3697 cm⁻¹, on the high-frequency side of the main band, is attributed to inner OH vibrations, which also display some scattering of frequency but with a narrower distribution (Balan et al., 2021b). Accordingly, the MIR spectra of Atg (Fig. 2c) were fitted using three components for the inner and interlayer OH stretching (grey, blue, and red curves). As for Lz, the central band (blue curve) is dominant, large, and slightly asymmetric.

The Raman spectrum of Atg2 displays two broad and asymmetric bands, with a more pronounced broadening towards low frequencies (Fig. 2f). The inner OH stretching band is centred at 3697 cm⁻¹, at the same frequency as in MIR spectra (Table 2). In contrast, the dominant band ascribed to interlayer OH stretching is downshifted in the Raman spectrum by 11 cm⁻¹ with respect to its MIR counterpart. As for Lz, the inner OH band is thus more clearly separated from the interlayer OH band in the Raman spectrum due to the greater sensitivity of the more intense band to macroscopic electrostatic interactions (Balan et al., 2021b). The fitting of the Raman spectrum using two asymmetric components (grey and purple curves in Fig. 2f) confirms the larger width of the inner OH band in Atg (15 cm⁻¹) than in Lz (7 cm⁻¹). This width compares with the dispersion of inner OH frequencies (23 cm⁻¹) theoretically determined in the m=17 polysome antigorite (Balan et al., 2021b). The width of the main band is also similar in the MIR (33 cm⁻¹) and Raman (27 cm⁻¹) spectra, which is a further indication that the broadening of this band mostly arises from the structural distortions and distribution of interlayer OH bond lengths.

In agreement with the observations made on fundamental bands, the overtone spectra of Atg (Fig. 3c, Table 3) reveal a downshift of the inner OH frequency from 7240 cm⁻¹ in Lz to 7229 cm⁻¹. A weak shoulder is observed at ∼ 7199 cm⁻¹ (i.e. 30 cm⁻¹ below the inner OH band). Following the same reasoning as in Lz, it can be assigned to the stretching of inner OH in an Mg₂M environment. The broad and dominant band centred at 7170 cm⁻¹ most likely corresponds to interlayer OH in an Mg₃ environment, whereas the shoulder at 7130 cm⁻¹ can be ascribed to interlayer OH in an Mg₂M configuration, as in Lz. The small talc contribution at 7184 cm⁻¹ is also observed in the Atg1 and Atg4 samples. Spectral fitting was performed using similar components as for Lz (grey, pink, blue, and orange curves in Fig. 3c). However, the peculiar asymmetric shape of the band related to inner OH required the introduction of two components (grey curves) with similar frequencies but different widths. The larger component has a width of 30 cm⁻¹, which corresponds to twice that observed for the fundamental band determined from the Raman spectrum. This supports the interpretation of the larger width of the inner OH stretching band in Atg as reflecting a distribution of vibrational frequencies related to structural distortions. Note, however, that homogeneous broadening mechanisms may also contribute to the line-width difference between fundamental and overtone transitions (e.g. Jakob and Persson, 1998) and that further investigations would be required to better specify the homogeneous broadening contribution to the observed line widths.

3.2.3 OH stretching modes in chrysotile

Unlike Lz and Atg, the wrapping of TO layers to form nanotubes in Ctl breaks the crystal periodicity. It is thus not possible to interpret the spectra on the basis of accurate periodic models of vibrational properties similar to those obtained for Lz or Atg (Balan et al., 2002b, 2021b; Prencipe et al., 2009). In addition the strong overlap of vibrational bands precludes the use of a straightforward spectral fitting to identify individual components because the unicity of the solution is not granted. As a consequence, the proposed interpretations are grounded on a comparison of Ctl with Lz and Atg, considering in conjunction the three spectroscopic techniques.

The OH stretching bands recognized on the MIR spectra of Ctl (Figs. 2b, A2b, Table 2) are similar to those observed in Lz (Figs. 2a and A2a). The prominent band at ∼ 3685 cm⁻¹ and the weaker band at ∼ 3649 cm⁻¹ most likely correspond to the in-phase and out-of-phase stretching of the interlayer OH groups. However, both bands are narrower, and the contribution at lower frequency of broad signals attributed to bound water molecules and/or trivalent cations (Fig. 2b) is smaller than in Lz (Fig. 2a), leading to a greater resolution of the Ctl OH vibration modes. Note also that the Ctl spectra also display a weak contribution at ∼ 3502 cm⁻¹, which is not observed in the other serpentine samples. Two shoulders are observed on the high-frequency side of the prominent OH band at ∼ 3693 cm⁻¹ and 3704 cm⁻¹ (Fig. 2b). The signal at 3704 cm⁻¹ is equivalent to that reported in Lz and is therefore ascribed to the inner OH group, while the assignment of the 3693 cm⁻¹ feature will be discussed in the light of other observations. A very small variability in the position of these features is noticed from one sample to another, and the main spectral change is attributed to the relative intensity of the shoulder at 3693 cm⁻¹, which increases gradually from Ctl1 to Ctl2 and then Ctl3 (Fig. A2b).

The Raman spectrum of Ctl3 (Fig. 2e) displays similar bands to those reported by FTIR (Fig. 2b) but with different intensities. Contrary to what has been established for the Raman spectrum of Lz2, the main band remains broad. It is, however, centred at 3697 cm⁻¹, whereas a shoulder is observed at 3685 cm⁻¹, which is the frequency corresponding to the maximum of the FTIR band (Table 2). Due to these changes, the inner OH band at 3704 cm⁻¹ cannot be identified from a visual inspection of the Raman spectrum. These observations are consistent with the comparison of FTIR and Raman spectra reported in previous studies for Ctl (e.g. Farmer, 1974; Kloprogge et al., 1999; Auzende et al., 2004; Trittschack and Grobéty, 2013; Petriglieri et al., 2015; Tarling et al., 2018).

In the overtone spectra of Ctl (Fig. 3b), the sharp and intense signals observed at 7240 cm⁻¹ and ∼ 7212 cm⁻¹ correspond to the stretching of inner OH groups in Mg₃ and Mg₂M environments, respectively, as for Lz (Balan et al., 2021a). These features are narrower in Ctl than in the other serpentine samples. The strong peak centred at ∼ 7171 cm⁻¹ is assigned to interlayer OH groups in an Mg₃ environment, while the weaker feature at ∼ 7124 cm⁻¹ corresponds to interlayer OH groups in an Mg₂M environment (Table 3). However, the shape of the peak at 7171 cm⁻¹ is more complex in Ctl than in Lz with an inflexion on its high-frequency side which suggests the occurrence of two overlapping contributions: a sharper signal at ∼ 7171 cm⁻¹, a frequency similar to that observed in Lz, and a second broader signal at ∼ 7200 cm⁻¹ (Fig. 3b, Table 3). This second contribution significantly overlaps with the better-defined bands at 7171 and 7212 cm⁻¹. Finally the splitting of the weak features corresponding to simultaneous transitions involving coupled OH oscillators observed at high frequency is more apparent in the three Ctl samples than in the other serpentine samples. This splitting leads to two components at 7375 and 7343 cm⁻¹, similar to those observed in Lz2.

Although the above assignments account for most of the observed bands, several features observed in the present study, as well as in previous investigations, still require some explanations. Of particular interest is the assignment of the feature observed at ∼ 3693 cm⁻¹ in the FTIR spectra. As stated above, the stretching of inner OH groups most likely corresponds to the narrow bands observed at 3704 and 7240 cm⁻¹ in the fundamental FTIR and overtone NIR spectra, respectively. These frequencies coincide with those reported for Lz, indicating that the cylindrical distortion of the layers weakly affects their internal structure, as previously discussed by Balan et al. (2002a) for the Si–O stretching bands. Assuming similar OH bond anharmonicity ($X_{\mathrm{anhar}}=-\mathrm{84}$ cm⁻¹), the occurrence of a second inner OH stretching band at ω_OH=3693 cm⁻¹ should lead to an overtone contribution at ω_2OH=7218 cm⁻¹ (${\mathit{\omega }}_{\mathrm{2}\mathrm{OH}}=\mathrm{2}({\mathit{\omega }}_{\mathrm{OH}}+X_{\mathrm{anhar}})$). The assignment of the 3693 cm⁻¹ feature to an inner OH group is thus not supported by the NIR spectra, which do not reveal any contribution but rather display a local minimum at this frequency. Accordingly, this feature should be more likely related to interlayer OH groups.

Turning to the Raman spectrum, the apparent intensity increase observed at this frequency also requires an explanation because it is unlikely that a minor OH stretching band in the FTIR spectrum becomes dominant in the Raman spectrum in the absence of any specific symmetry reasons. As discussed above, the dominant band in the FTIR and Raman spectra of Lz is related to the same in-phase OH stretching mode, and the observed changes are mostly related to the different effect of macroscopic parameters, leading to a downshift and narrowing of this band in the Raman spectrum. Based on these observations, the narrowing of a broader band peaking at 3693 cm⁻¹ appears to be a more plausible explanation for the relative intensity variations of the 3693 and 3684 cm⁻¹ features between the FTIR and Raman spectra of Ctl. In fact, the Raman and FTIR spectra of Ctl3 can be decomposed using two components centred at ∼ 3693 cm⁻¹ and ∼ 3684 cm⁻¹ (light and dark blue curves in Fig. 2b and e). The width of the latter was fixed at the same value (10 cm⁻¹) in the two spectra, whereas the width of the former decreases from 28 to 16 cm⁻¹. The agreement between the decomposition result and the experimental data (see bottom grey boxes in Fig. 2b and e) indicates that this simple and physically plausible interpretation reconciles the observations made in FTIR and Raman spectroscopy. In this case, the absence of frequency downshift between the FTIR and Raman spectra can be explained by the diameter of Ctl nanotubes (typically <100 nm), which remains smaller than the wavelength of the exciting radiation in both the FTIR and Raman spectra. The present analysis is also supported by the high-pressure Raman spectroscopic studies of OH stretching bands in Ctl (Auzende et al., 2004; Mizukami et al., 2007). These studies consistently indicate the presence of a single inner OH band at 3701 cm⁻¹ characterized by a pressure dependence of 2 to 4.2 cm⁻¹ GPa⁻¹. In contrast, the other components identified at 3690 and 3683 cm⁻¹ by Mizukami et al. (2007) display larger pressure dependences of 13.1 and 9.4 cm⁻¹ GPa⁻¹, respectively, suggesting that both components correspond to interlayer OH groups.

Furthermore, the occurrence of two contributions related to interlayer OH groups in the FTIR and Raman spectra is consistent with the observations of the broader signal and narrower peak at 7200 and 7171 cm⁻¹, respectively, in the NIR spectra (light and dark blue curves in Fig. 3b). The narrower contribution at 3684 and 7171 cm⁻¹ (dark blue curve in Figs. 2b, e and 3b) is very similar to the vibrational pattern identified in Lz and should correspond to a similar arrangement of adjacent layers. The broader contribution at 3693 and 7200 cm⁻¹ (light blue curve in Figs. 2b, e and 3b) is more likely related to local misfits between adjacent TO layers inducing a scattering of OH bond length and stretching frequencies. These misfits can weaken the hydrogen bonding between interlayer OH groups and facing oxygens, causing an increase in the related OH stretching frequencies. Although the spatial localization of these two types of local environments in the Ctl nanotubes is not clearly established, the present interpretation is also consistent with the Raman spectra of chrysotile and polygonal serpentine reported by Petriglieri et al. (2015) and Tarling et al. (2018), which are characterized by a significantly more intense contribution of the 3684 cm⁻¹ component in the latter.

4 Conclusions

This study reveals the diversity of the OH stretching signals in the serpentine mineral group which renders their identification quite challenging in complex mineral assemblages such as those commonly reported in Ni silicate ores. Combining different spectroscopic technics on monophasic (or dominant) mineral phases leads to a consistent assignment of their vibration spectra in both the fundamental and overtone regions. The results highlight the great potential of NIR spectroscopy for better recognition of specific vibrational signals linked to the discrete occurrence of transition elements such as Fe and Ni in the octahedral sheet of serpentines. They also bring a basis for the decomposition of serpentine vibrational spectra in terms of physically meaningful components. Unfortunately, the overlap between the signals introduces a significant uncertainty in the fitting procedure, making it difficult to quantitatively infer the cationic distribution in the crystal structure from vibrational spectroscopic data.

Appendix A: FTIR spectra of lattice vibrations in lizardite, chrysotile, and antigorite samples

Here, we report and briefly discuss the FTIR spectra in the mid-IR range (1200–400 cm⁻¹) of the eight serpentine samples (Fig. A1). These spectra present major similarities with those reported by Farmer (1974) and Yariv and Heller-Kallai (1975). As for the OH stretching bands, they enable a discrimination of the serpentine species from each other. Assignment of the lattice bands is done according to the theoretical works of Balan et al. (2002b) and Prencipe et al. (2009) for Lz, Balan et al. (2002a) for Ctl, and Balan et al. (2021a) for Atg. The first series of bands in the 1200–800 cm⁻¹ range corresponds to the stretching modes of Si–O bonds (section I in Fig. A1). The band at ∼ 1082 cm⁻¹ (black curve in Fig. A1a) is due to the vibration of apical Si–O bonds (A1 symmetry), while the degenerate vibrations of basal Si–O bonds (E symmetry) lead to the intense band centred at ∼ 975 cm⁻¹ in Lz.

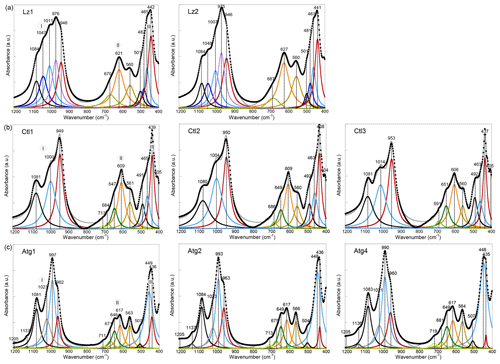
Figure A1 MIR spectra in the 1200–400 cm⁻¹ range (lattice transitions) of (a) lizardite (Lz1, Lz2), (b) chrysotile (Ctl1, Ct2, Ct3), and (c) antigorite (Atg1, Atg2, Atg4). The spectra have been decomposed into individual components using Lorentzian functions. Black dots: experimental data. Solid grey line: best fit. (I) Si–O stretching vibrations, (II) libration and hindered translation of OH groups, and (III) Si–O bending vibrations.

This broad and asymmetric signal displays several bumps or shoulders indicating the occurrence of several overlapping contributions (blue and red curves in Fig. A1a) likely due to chemical impurities, in particular with the occurrence of trivalent cations (e.g. Al³⁺) in tetrahedral sites (Yariv and Heller-Kallai, 1975). The peaks assigned to basal Si–O modes in the Ctl spectra (Fig. A1b) are identified at ∼ 950 cm⁻¹ for the most intense peak and at 1005 cm⁻¹ for the second peak. This second peak at ∼ 1005 cm⁻¹ is a diagnostic feature of the tubular morphology of Ctl particles and corresponds to an additional resonance of the dielectric function related to collective ionic charge excitations in multi-wall hollow nanotubes (Balan et al., 2002a).In Atg (Fig. A1c), the anisotropy related to the occurrence of tetrahedral reversals leads to the splitting of basal Si–O vibrations resulting in two bands centred at ∼ 995 and ∼ 962 cm⁻¹ (Balan et al., 2021a). The weaker bands at 1137 and 1205 cm⁻¹ are assigned to Si–O stretching in the eight- and six-membered silicate rings of the reversals.

Features reported in the 800–500 cm⁻¹ range (section II in Fig. A1) comprise a band at ∼ 565 cm⁻¹ (brown curve in Fig. A1), which is ascribed to the hindered translation of OH groups along a direction perpendicular to the layers, and a series of two or more vibrational bands at higher frequencies (orange and green curves in Fig. A1), associated with the libration of OH groups. The band ascribed to the hindered translation of OH groups is well-defined in Atg. For the other OH-libration bands that are reported at 606–627 cm⁻¹, it is also intense and present in all three serpentine species, whereas a pronounced asymmetry with several shoulders is observed at higher frequency increasing from Lz to Ctl and then Atg.

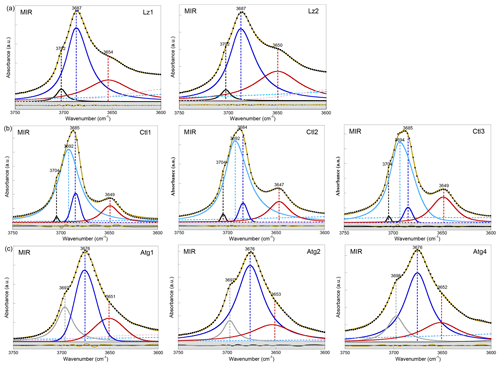
Figure A2 MIR spectra in the 3750–3600 cm⁻¹ range (first overtone region of OH stretching bands) of (a) lizardite (Lz1, Lz2), (b) chrysotile (Ctl1, Ctl2, Ctl3), and (c) antigorite (Atg1, Atg2, Atg4). The spectra have been decomposed into individual components using asymmetric Lorentzian–Gaussian functions. Black dots: experimental data. Solid brown line: best fit (residues in bottom grey box). Plain black and grey curves: inner OH stretching modes. Plain blue and red (or purple) curves: interlayer OH stretching modes. Dashed pink and light blue curves: H₂O vibration modes.

The series of bands in the 500–400 cm⁻¹ range (section III in Fig. A1) correspond to modes dominantly related to the bending of Si–O bonds and/or the deformation of MgO₆ octahedra, also involving contributions from hydrogen displacements (Balan et al., 2002b; Prencipe et al., 2009). As for the Si–O stretching vibrations, these bands also differ significantly from one serpentine species to another. A broad signal centred at ∼ 442 cm⁻¹ is observed in Lz, whereas contributions at 492 and 507 cm⁻¹ are more apparent in the Ctl and Atg spectra, respectively.