Low-temperature infrared spectrum and atomic-scale structure of hydrous defects in diopside

Hydrous defects in diopside (CaMgSi₂O₆) play an important role in the water budget of the Earth's mantle. Related OH-stretching modes lead to a variety of infrared absorption bands observed in natural or experimental samples. In the present study, we report new low-temperature infrared spectra of reference natural diopside samples in the OH-stretching range. In parallel, the structure and vibrational properties of a series of OH-bearing defects in diopside are theoretically determined at the density functional theory level. The infrared spectra make it possible to resolve additional bands in the region above 3600 cm⁻¹ and reveal that their anharmonic behavior differs from that of the bands at lower frequency. A comparison of theoretical results with experimental data makes it possible to propose atomic-scale geometries corresponding to observed OH-stretching bands. It confirms that the bands observed at 3620–3651 cm⁻¹ are related to M³⁺ ions substituted for Si in tetrahedral sites, while the 3420 cm⁻¹ band is associated with the Na⁺ for Ca²⁺ substitution. In both cases, H⁺ incorporation compensates the charge deficit due to the heterovalent substitution. The other major mechanism of water incorporation in diopside relates to the charge compensation of cationic vacancies, among which Ca vacancies play a central role. The 3357 cm⁻¹ band corresponds to doubly protonated Ca vacancies in pure diopside. In experimental diopside-bearing trivalent cations, the bands at 3432–3460 cm⁻¹ correspond to singly protonated Ca vacancies with a nearby octahedral M³⁺ ion, while the 3310 cm⁻¹ band likely involves a more remote charge compensation by M³⁺ ions. More complex defects associating Ca vacancies with tetrahedral M³⁺ and octahedral Ti⁴⁺ ions are proposed for the bands observed between 3500 and 3600 cm⁻¹ in natural diopside. The Fe²⁺ for Mg²⁺ and Fe²⁺ for Ca²⁺ substitutions are also found to affect nearby OH-bearing defects, causing a shift and broadening of OH stretching bands in chemically more complex diopside samples.

1 Introduction

Diopside is considered a major host of “water” in the upper mantle (e.g., Demouchy and Bolfan-Casanova, 2016) contributing to the Earth global budget of water. As in other nominally anhydrous minerals, water occurs as hydroxyl groups associated with cationic vacancies or chemical impurities, ensuring the electric neutrality of the defective crystal (e.g., Keppler and Smyth, 2006; Skogby, 2006). The occurrence of OH groups at low concentration in natural and experimental samples of diopside is attested by their characteristic OH stretching bands in Fourier-transform infrared (FTIR) spectra. Various bands differing in position and pleochroism have been identified and categorized. In pure diopside, the spectra display a prominent band observed at 3357 cm⁻¹ and ascribed to divalent cation vacancies compensated by two protons (Stalder and Ludwig, 2007; Sundvall et al., 2009; Purwin et al., 2009). At variance, natural samples, as well as experimental samples doped with chemical impurities, display a larger variety of signals. The spectra of diopside, containing trivalent cations and synthesized at 20 kbar under silica saturation, display two additional bands, one at 3310 cm⁻¹ and the other one observed between 3432 and 3462 cm⁻¹ depending on the nature of the trivalent impurity (Stalder and Ludwig, 2007). Band absorbances generally follow the order $E//\mathit{\gamma }\gg E//\mathit{\beta }\cong E//\mathit{\alpha }$, where α, β and γ correspond to the principal axes of the optic indicatrix and E denotes the polarization of the infrared beam. Under the same conditions, sodium-bearing samples display a band at 3428 cm⁻¹ with the absorbance order $E//\mathit{\beta }\cong E//\mathit{\alpha }\gg E//\mathit{\gamma }$ (Purwin et al., 2009). Al-bearing synthetic samples can also display an absorption band at 3650 cm⁻¹, as well as a doublet at ∼3450 and ∼3500 cm⁻¹, depending on the synthesis conditions (Gavrilenko et al., 2010). Absorption bands above 3600 cm⁻¹ have been reported in experimental Fe-bearing samples (Skogby, 1994) and natural samples (Ingrin et al., 1989; Johnson et al., 2002; Andrut et al., 2007). Their absorbance follows the order $E//\mathit{\beta }>E//\mathit{\alpha }\gg E//\mathit{\gamma }$, and they are usually ascribed to the coupled incorporation of trivalent cations and protons at the tetrahedral Si site (e.g., Beran, 1976; Skogby et al., 1990; Johnson et al., 2002; Bromiley et al., 2004; Gavrilenko et al., 2010). In natural samples, the origin of several bands observed between 3500 and 3600 cm⁻¹ is still debated (e.g., Yang et al., 2019; Azevedo-Vannson et al., 2020). These bands are prominent in uncommon spectra of upper-mantle xenoliths (Denis et al., 2015; Patkó et al., 2019; Azevedo-Vannson et al., 2020).

In the present study, we report new low-temperature infrared spectra of natural diopside samples previously investigated by Ingrin et al. (1989), Andrut et al. (2007), and Yang et al. (2019). In parallel, we use a quantum-mechanical modeling approach to investigate the structure and infrared spectroscopic properties of a series of OH-bearing defects in diopside. This approach has been previously used to interpret the infrared spectrum of OH defects in important silicate-group minerals (e.g., Wright, 2006; Balan et al., 2011, 2013, 2017; Blanchard et al., 2009, 2017; Ingrin et al., 2014; Jollands et al., 2020). Combining experimental observations and theoretical results provides important constraints to help unravel the atomic-scale structure of OH defects in diopside.

2 Methods

2.1 Low-temperature infrared spectroscopy

The samples are well-characterized gem-quality diopside crystals from Austria and Russia previously investigated by Ingrin et al. (1989), Andrut et al. (2007), and Yang et al. (2019). Their composition is close to the endmember composition: Ca_0.97Cr_0.01Mg_0.97Fe_0.04Al_0.01Si_1.99O₆ and Ca_0.99Mn_0.01Mg_0.94Fe_0.06Al_0.01Si_1.99O₆ for the Russian and Austrian samples, respectively. For the Russian sample, infrared transmission spectra have been recorded at a 2 cm⁻¹ resolution with 128 scans accumulated per spectrum using a cryogenic cell cooled with a liquid helium system and a Brucker FTS-IFS 66v spectrometer from Institut d'Astrophysique Spatiale (IAS), Orsay, France. For this analysis, unpolarized measurements were performed on two pieces of the same slice of the Russian diopside. One piece was heated in air at 1000 ^∘C for 320 h in order to remove all hydrogen present in the sample and was used to build reference spectra collected at the different temperatures. The reported spectra were then collected on the second untreated piece using the reference spectrum for background correction. For the Austrian sample, the spectra have been recorded at a resolution of 2 cm⁻¹ with 150 scans accumulated per spectrum using a Perkin Elmer GX2000 spectrometer. The temperature was monitored using a Linkam FTIR600 stage cooled with liquid nitrogen with ZnSe windows dedicated to infrared measurements, and the background was measured for each temperature through the cooling stage (Ingrin et al., 2013). A polynomial baseline was subtracted from the spectrum.

2.2 Theoretical modeling of OH defects

The properties of OH defects have been theoretically investigated within the density functional theory (DFT) framework using the PWscf code of the Quantum ESPRESSO package (Giannozzi et al., 2009; http://www.quantum-espresso.org, last access: 1 October 2020). The modeling scheme used the generalized gradient approximation (GGA) to the exchange-correlation functional as proposed by Perdew, Burke and Ernzerhof (PBE functional; Perdew et al., 1996), and periodic boundary conditions. The ionic cores were described using optimized norm-conserving Vanderbilt (ONCV) pseudopotentials (Hamann, 2013; Schlipf and Gygi, 2015) with a 80 Ry cutoff on the electronic wave functions, as in Balan et al. (2019) and Jollands et al. (2020). Structural properties of OH-bearing defects were determined using $\mathrm{1}\times \mathrm{1}\times \mathrm{2}$ diopside supercells (80 atoms) containing up to four hydrogen atoms. Brillouin zone sampling for the electronic integration was restricted to the Γ point. Unit-cell parameters of pure diopside (monoclinic, S.G. C2/c) were optimized at zero pressure (a=9.88 Å, b=9.02 Å, c=5.33 Å, β=106.5^∘) and were used without further relaxation to produce the OH-bearing supercells. As usually observed in DFT modeling of silicates performed at the GGA level, the theoretical cell lengths are overestimated with respect to those determined experimentally (a=9.745 Å, b=8.899 Å, c=5.251 Å, β=105.63^∘; Cameron et al., 1973). For all systems, the relaxation of atomic internal coordinates was performed until the residual forces were less than 10⁻⁴ Ry a.u.⁻¹. For models containing isolated paramagnetic cations (Ti³⁺, Cr³⁺, Fe³⁺, Fe²⁺), spin-polarized calculations have been performed imposing the high-spin state of the ion to the supercell.

The vibrational modes, the Born effective charge tensors and the electronic dielectric tensor were calculated at the Brillouin zone center (Γ point) using the linear response theory (Baroni et al., 2001) as implemented in the PHonon code (Giannozzi et al., 2009; http://www.quantum-espresso.org; last access: 1 October 2020). The high-frequency OH stretching modes that are decoupled from the other vibrational modes occurring at a significantly lower frequency can be accurately calculated by only considering the displacement of the oxygen and hydrogen atoms involved in OH groups (Balan et al., 2008). The complex low-frequency dielectric permittivity tensor has been calculated for each defect by adding only the ionic contributions related to the OH-stretching modes to the electronic permittivity tensor and using an arbitrary damping parameter of 4 cm⁻¹, accounting for the width of absorption bands (Balan et al., 2008). For a symmetry lower than orthorhombic, the orientation of the principal axes of the dielectric tensor of the pristine or defective crystal is not fully constrained by the crystal symmetry. The principal axes of the index and absorption tensors may thus differ, which complicates the straightforward computation of the infrared absorption spectrum (e.g., Sambridge et al., 2008). To circumvent this difficulty, the anisotropy of the electronic contribution to the dielectric tensor was neglected as this anisotropy marginally affects the value of the absorption coefficient. Infrared absorption coefficients were then computed for polarizations parallel to the axes of an orthogonal frame (uα, uβ, and uγ) chosen such that it approximately coincides with the experimentally determined principal axes of diopside optic indicatrix (e.g., Hess, 1949). The uβ orientation is parallel to the crystal b axis, and uγ forms an angle of 40^∘ with the c axis and uα an angle of 23.5^∘ with the a axis. In the following, uα, uβ and uγ refer to the theoretical axes, while α, β and γ refer to the experimental geometry.

3 Results

3.1 Low-temperature infrared spectra of diopside

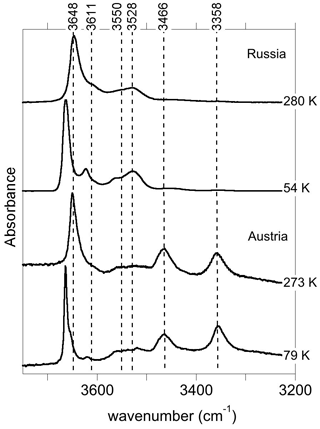
The infrared spectra of reference diopside samples (Fig. 1) display a series of well-resolved OH-stretching bands characteristic of OH defects in diopside (e.g., Ingrin et al., 1989; Andrut et al., 2003, 2007; Yang et al., 2019). An asymmetric band at 3646–3650 cm⁻¹ with a shoulder at ∼3611 cm⁻¹ is observed at near-ambient temperature in both samples. Two bands at 3528 and 3550 cm⁻¹ significantly contribute to the spectrum of the Russian sample, while their relative intensity is weaker in the Austrian sample. In contrast, the Austrian sample displays two additional bands at 3466 and 3358 cm⁻¹. The low-temperature spectra reveal that the behavior of bands above 3600 cm⁻¹ differs from that of the bands observed at lower frequency, although a narrowing is observed for all the bands. Moderate shifts are observed for the bands toward 3358 (−3 cm⁻¹), 3466 (<1 cm⁻¹), 3528 (<1 cm⁻¹) and 3550 cm⁻¹ (+7 cm⁻¹). In contrast, the band at 3646–3650 cm⁻¹ shifts to 3663 cm⁻¹, i.e., by +13–17 cm⁻¹, corresponding to a slope of ∼0.07 cm⁻¹ K⁻¹. The shoulder at ∼3611 cm⁻¹ leads to a well-resolved band at 3623 cm⁻¹ at low temperature (+8 cm⁻¹), and an additional component is revealed at 3655 cm⁻¹ in the Austrian sample. In the Russian sample, this additional component is not resolved but explains the asymmetry of the 3663 cm⁻¹ band. Note that the different recording temperature of the Russian (54 K) and Austrian (79 K) samples should not affect the relative position of the bands by more than 2 cm⁻¹.

Figure 1 Infrared absorption spectra of Russian and Austrian diopside samples recorded at near-ambient and low temperatures. Note the significant positive shift and narrowing of the bands observed at frequencies above 3600 cm⁻¹.

3.2 Theoretical models of OH defects

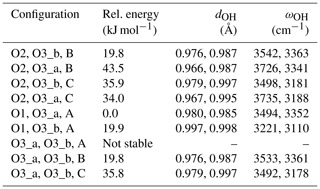
The structure of diopside (Fig. 2a) displays single chains of SiO₄ tetrahedra (T sites) parallel to the c axis. The Mg²⁺ cations sit in chains of edge-sharing octahedra (M1 sites) between the apices of the tetrahedra. The 8-fold coordinated Ca²⁺ cations occupy larger M2 sites forming chains between the bases of the tetrahedra. Both M1 and M2 sites are located on a 2-fold symmetry axis parallel to the [010] direction. Three nonequivalent oxygen atoms occur in the structure. The O1 oxygen corresponds to the apex of silicate tetrahedra and is connected to two M1 cations and one T cation. The O2 oxygen is linked to one T, one M1 and one M2 cation resulting in some degree of underbonding. In contrast, the O3 oxygen bridges two T cations and is slightly overbonded due to the proximity of the M2 cation. Starting configurations of neutral OH-bearing defects related to cation vacancies or chemical impurities have thus been constructed based on an educated guess assuming that protons are preferentially located in the proximity of the most severely underbonded oxygens. The theoretical properties of OH groups in relaxed models are summarized in Tables 1 and 2.

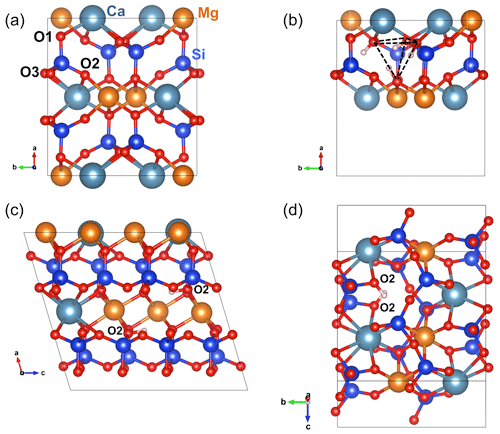
Figure 2 (a) Structure of diopside viewed along the [001] direction. (b) Structure of the (4H⁺)${}_{\mathrm{Si}}^{\times }$ defect in diopside viewed along the [001] direction (model 1, Table 1). (c) Structure of the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ defect in diopside viewed along the [010] direction (model 2, Table 1). Note the two O2–H groups lying in the (001) plane. (d) Structure of the (2H⁺)${}_{\mathrm{M}\mathrm{1}}^{\times }$ defect in diopside viewed along the [100] direction (model 4, Table 1). Atom colors – Si: blue; oxygen: red; Mg: orange; Ca: greyish blue; H: light pink.

Table 1 Theoretical properties of OH defects in diopside (structure files are provided in the Supplement).

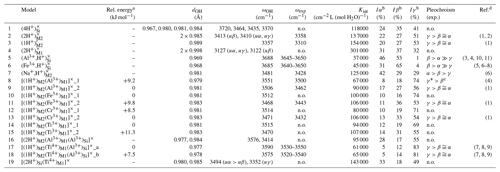
n.o.: not observed. ^a The relative energy is defined with respect to the most stable configuration of the model with the same stoichiometry. ^b Iα, Iβ, Iγ: relative absorbances for polarizations along uα ($u\mathit{\alpha }\wedge a=\mathrm{23.5}{}^{\circ }$), $u\mathit{\beta }(//b)$,
and uγ ($u\mathit{\gamma }\wedge c=\mathrm{40}$^∘). ^c γ^* is the direction perpendicular to β in the (100) plane. ^d (1) Stalder and Ludwig (2007); (2) Sundvall et al. (2009); (3) Andrut et al. (2007); (4) Gavrilenko et al. (2010); (5) Skogby (1994); (6) Purwin
et al. (2009); (7) Ingrin et al. (1989); (8) Skogby et al. (1990); (9) Shuai and Yang (2017); (10) Johnson et al. (2002); (11) Bromiley et al. (2004)

Table 2 Theoretical properties of selected defects with nearby isovalent substitutions (structure files are provided in the Supplement).

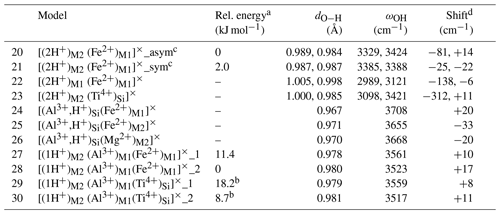
^a The relative energy is defined with respect to the most stable configuration of the model with the same stoichiometry. ^b Reference is model 17. ^c In the asymmetric configuration, the 2-fold site symmetry is broken, while it is preserved in the symmetric configuration. ^d The shift is calculated with respect to the related model without isovalent substitution (Table 1). For models displaying two close frequencies, the frequency of the (u,u) polarization has been considered.

3.2.1 OH-bearing defects driven by vacant or substituted tetrahedral sites

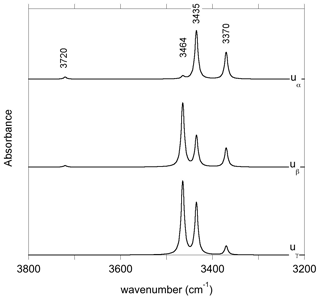
The charge compensation requirements related to the removal of a Si⁴⁺ cation from a T site can be ensured by the addition of four protons forming four hydroxyl groups associated with the vacant T site. In the relaxed configuration of the (4H⁺)${}_{\mathrm{Si}}^{\times }$ defect (model 1, Table 1, Fig. 2b), one of the OH group points out of the T site leading to a relatively short O–H distance and a high OH stretching frequency (3720 cm⁻¹). The three other OH groups form H bonds along the edges of the T site and lead to three vibrational modes between 3300 and 3500 cm⁻¹ involving the coupled motion of H atoms. The intensity of the bands at lower frequency is significantly stronger than that of the 3720 cm⁻¹ band (Fig. A1).

Another more complex mechanism ensuring the charge compensation of an Si vacancy can involve two protons and a nearby Ti⁴⁺ for Mg²⁺ substitution, leading to a [(2H⁺)_Si(Ti⁴⁺)_M1]^× stoichiometry. Among the potential configurations (Appendix B), the most stable one (model 19, Table 1) leads to stretching frequencies of 3352 and 3494 cm⁻¹ with dominant polarization along uγ and (uα>uβ), respectively. Tetrahedral sites in diopside are also commonly occupied by trivalent cations such as Al³⁺ and Fe³⁺. The M³⁺ for Si⁴⁺ substitution requires the addition of one proton to ensure the charge compensation, the underbonded O2 atom appearing to be the most favorable site for the proton location. A previous modeling of this defect using empirical potentials also proposed the O2 atom as the most favorable docking site for the proton in this coupled substitution scheme (Gatzemeier and Wright, 2006). The O2–H group in the relaxed (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ model (model 5, Table 1) forms a weak H bond with an O3 atom and displays a relatively short O2–H length (0.969 Å), leading to a stretching band at 3688 cm⁻¹. The band is strongly pleochroic with a very weak contribution for polarization parallel to uγ. The incorporation of a Fe³⁺ ion instead of Al³⁺ leads to a very similar geometry and almost identical vibrational properties (model 6, Table 1).

Additional models displaying trivalent cations in tetrahedral sites have been obtained by substituting the neighboring Ca²⁺ ion with a smaller Mg²⁺ or Fe²⁺ ion – [(Al³⁺,H⁺)_Si(Mg²⁺)_M2]^×, [(Al³⁺,H⁺)_Si(Fe²⁺)_M2]^×. The occurrence of Fe²⁺ ion in the M2 site of diopside has been reported by, for example, Andrut et al. (2003). Although the orientation of the O2–H group is similar to that observed in the (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ model, the modification of the local environment increases the O2–H distance by ∼0.002 Å and decreases the OH stretching frequency by 20 to 33 cm⁻¹ (models 25 and 26, Table 2). In contrast, the Fe²⁺ for Mg²⁺ substitution in the neighboring M1 site increases the OH stretching frequency by 20 cm⁻¹ (model 24, Table 2).

3.2.2 OH-bearing defects driven by vacancies or impurities in the M2 site

The charge compensation related to the removal of a Ca²⁺ cation from the M2 site can be ensured by the addition of two protons, preferentially on the two severely underbonded O2 oxygens. Locating the two hydrogen atoms on O1 atoms leads to a less stable configuration (by 75 kJ mol⁻¹), which does not confirm the preferred protonation of O1 atoms in M2 vacancies previously suggested by Gatzemeier and Wright (2006). After relaxation, the two symmetric O2–H groups of the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ model are nearly parallel to the c axis with a slight canting in the (100) plane (Fig. 2c). They share relatively long H bonds (2.14 Å) with the O1 atoms. Two stretching modes are observed at 3410 and 3413 cm⁻¹, with polarizations parallel and perpendicular to the b axis, respectively (model 2, Table 1).

Sodium incorporation in the M2 site of diopside is common and mostly due to the coupled Na⁺ for Ca²⁺ and Al³⁺ for Mg²⁺ substitutions (jadeite-type substitution). However, the charge compensation of the Na⁺ for Ca²⁺ substitution can also be ensured by the addition of a proton near the M2 site. In this case, and consistent with the findings of Gatzemeier and Wright (2006), the underbonded O2 atom was considered the favored site for the proton location. After relaxation (Fig. 3b), the corresponding model leads to a band at 3481 cm⁻¹ with the following pleochroism: $E//u\mathit{\alpha }>E//u\mathit{\beta }\approx E//u\mathit{\gamma }$ (model 7, Table 1).

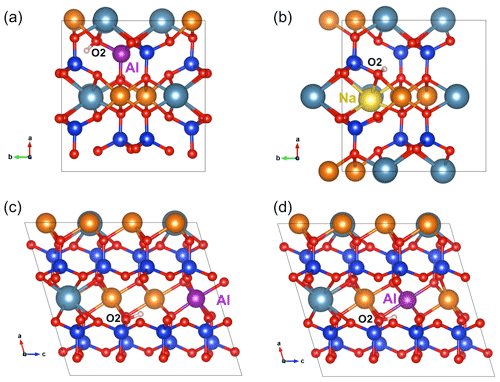
Figure 3 (a) Structure of (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect in diopside viewed along the [001] direction (model 5, Table 1). (b) Structure of the (Na⁺,H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ defect in diopside viewed along the [001] direction (model 7, Table 1). (c) Structure of the [(1H⁺)_M2(Al)_M1]^×_1 defect in diopside viewed along the [010] direction (model 8, Table 1). (d) Structure of the [(1H⁺)_M2(Al)_M1]^×_2 defect in diopside viewed along the [010] direction (model 9, Table 1). Atom colors are the same as in Fig. 2.

To complete the picture, a series of M2 vacancy models in which the charge compensation is only partially ensured by one H⁺ have been considered. In this case, several mechanisms can balance the remaining charge of the defect. Trivalent cations are commonly incorporated in the smaller octahedral M1 sites of diopside. The corresponding charge excess can contribute to the compensation of neighboring M2 vacancies. Models of M2 vacancies displaying a single OH group and associated with trivalent cations (Al³⁺, Fe³⁺, Cr³⁺ and Ti³⁺) in M1 sites have thus been considered (models 8–15, Table 1). Two cationic configurations occur depending on the relative position of the vacant M2 and substituted M1 sites. Not considering the proton location, the 2-fold symmetry of the M2 site is broken in configuration 1 (Fig. 3c), while it is preserved in configuration 2 (Fig. 3d). In the Al substituted models, configuration 2 is more stable than configuration 1 by ∼9 kJ mol⁻¹ (models 9 and 8, Table 1). Compared with configuration 1, configuration 2 displays a longer O2–H bond and a 45 cm⁻¹ lower stretching frequency. For a given configuration, the replacement of Al³⁺ by Fe³⁺, Cr³⁺ or Ti³⁺ cations decreases the O2–H frequency by ∼40 cm⁻¹. The vibrational and spectroscopic properties of the Cr³⁺- and Ti³⁺-bearing models are almost identical.

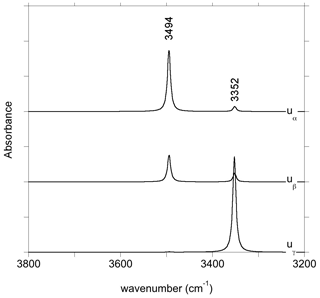
The charge neutrality of an M2 vacancy only displaying one H⁺ can also be ensured by an electrostatic countercharge homogeneously distributed over the volume of the supercell. This procedure is expected to mimic a more remote charge compensation mechanism, weakly affecting the local geometry of the defect. In the relaxed (1H⁺)${}_{\mathrm{Ca}}^{\prime }$ model, the orientation of the remaining O2–H group is similar to that observed for the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ configuration, but the O2–H bond is slightly longer, decreasing its stretching frequency to 3357 cm⁻¹ (model 3, Table 1).

More complex configurations modifying the local environment of M2 vacancies displaying two OH groups have also been investigated. The Tschermak substitution involves the coupled substitution of two Al³⁺ for one Si⁴⁺ and one Mg²⁺ ion, thus ensuring electrostatic neutrality. It is a common feature of Al-bearing pyroxenes (e.g., Deer et al., 1978). In this case, a relatively large number of cationic configurations can occur, depending on the relative locations of the vacant M2, tetrahedral Al and octahedral Al sites. Five M2 vacancy models with a Tschermak-type environment have been tested. In all the models, the 2-fold symmetry is broken leading to two OH groups with distinct spectroscopic properties. In the most stable configuration (model 16, Table 1), the length (0.984 Å) and stretching frequency (3414 cm⁻¹) of the OH group located between the two Al sites are similar to those determined for the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ model. In contrast, the O–H distance of the other group decreases to 0.977 Å, and its frequency increases to 3576 cm⁻¹. The other four models also displayed a splitting of the two OH stretching frequencies with one occurring in the 3425–3356 cm⁻¹ range and the other increasing to the 3510–3580 cm⁻¹ range. Similar to the Tschermak-type configurations, a series of M2 vacancy models displaying a tetrahedral Al³⁺ associated with a Ti⁴⁺ ion in a neighboring M1 site were investigated. In this case, only one OH group ensures a local electrostatic neutrality of the defect (Fig. 4). The two most stable configurations only differ by 7.5 kJ mol⁻¹ (models 17 and 18, Table 1). The O–H distances are still close to 0.977 Å leading to stretching frequencies of 3575 and 3590 cm⁻¹. Chemically equivalent models with inverted cationic configurations (models 29 and 30, Table 2), i.e., tetrahedral Ti⁴⁺ and octahedral Al³⁺, are not energetically favored and display stretching frequencies close to their counterparts with full Si occupancy – [(1H⁺)_M2(Al³⁺)_M1]^×_1 and [(1H⁺)_M2(Al³⁺)_M1]^×_2 (Table 1).

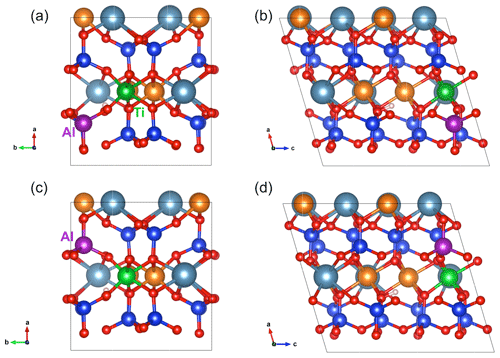
Figure 4 (a,b) Structure of [(2H⁺)_M2(Ti⁴⁺)_M1(Al³⁺)_Si]^×_a defect in diopside viewed along the [001] (a) and [010] (b) directions (model 17, Table 1). (c, d) Structure of [(2H⁺)_M2(Ti⁴⁺)_M1(Al³⁺)_Si]^×_b defect in diopside viewed along the [001] (c) and [010] (d) directions (model 18, Table 1). Atom colors are the same as in Fig. 2.

Finally, models displaying a Fe²⁺ for Mg²⁺ substitution in the vicinity of Ca vacancies have been examined (models 20 and 21, Table 2). In the [(2H⁺)_M2(Fe²⁺)_M1]^× model with asymmetric cationic configuration, the stretching frequency of the OH group in the coordination sphere of the Fe²⁺ cation increases by 14 cm⁻¹, while the other decreases by 81 cm⁻¹. In the symmetric configuration, the two OH frequencies decrease by 22–25 cm⁻¹. In this case, none of the OH groups are directly bonded to Fe²⁺.

3.2.3 OH-bearing defects driven by vacancies in the M1 site

The underbonding of oxygen atoms resulting from the removal of the central cation from an octahedral M1 site is significantly stronger for the two O2 atoms than for the other four O1 atoms. The relaxed (2H⁺)${}_{\mathrm{M}\mathrm{1}}^{\times }$ model (model 4, Table 1) displays two symmetric O2–H groups parallel to the (100) plane and forming hydrogen bonds with neighboring O1 atoms. This model leads to two stretching modes at 3122 and 3127 cm⁻¹ with polarizations parallel and perpendicular to the b axis, respectively. As for the vacant M2 site, additional models of M1 vacancies involving nearby cationic substitutions have also been explored. They will not be discussed in further detail here because their low stretching frequencies (<3200 cm⁻¹) do not seem to correspond to any experimental observation on diopside. For example, the Fe²⁺ for Mg²⁺ substitution in the neighboring M1 site leads to frequencies of 3121 and 2989 cm⁻¹ (model 22, Table 2).

4 Discussion: interpretation of experimental observations

4.1 General properties of OH-bearing defects in diopside

The observed correlations between the geometry, the stretching frequency and the infrared absorption coefficient of OH groups in diopside (Figs. 5 and 6) are consistent with previous studies performed at the same theoretical level (e.g., Balan et al., 2008, 2011) except for a frequency shift of $\sim +\mathrm{50}$ cm⁻¹ due to the use of different pseudopotentials. It is expected that the theoretical stretching frequencies obtained in the present study overestimate the frequencies experimentally observed at ambient temperature by typically 10 to 50 cm⁻¹, as observed in quartz (Jollands et al., 2020). A stronger overestimation, amounting to 125 cm⁻¹, has, however, been recently observed for OH defects in corundum (Balan, 2020). We will see in the following that the theoretical frequencies of OH defects in diopside are systematically upshifted by ∼50 cm⁻¹ compared to their experimental counterparts (Fig. 7).

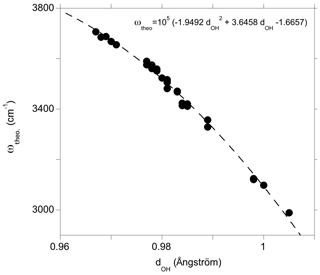
Figure 5 Theoretical OH-stretching frequency (ω_theo) as a function of the O–H distance (d_OH). The dotted line corresponds to a quadratic fit of the data serving as a guide for the eye.

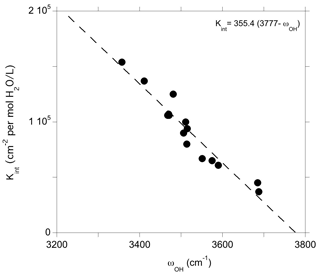
Figure 6 Theoretical integrated absorption coefficient (K_int) of OH stretching mode as a function of frequency (ω_OH). Models displaying multiple bands (models 1, 16 and 19, Table 1) or a frequency significantly lower than those experimentally observed (model 4, Table 1) have not been included in the figure.

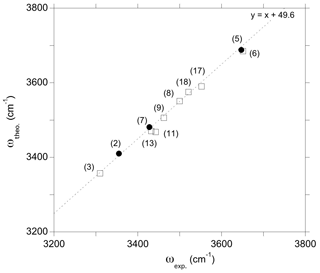
Figure 7 Theoretical stretching frequency of OH groups as a function of experimental frequency for the series of relevant models. The labels refer to the models of Table 1. The 1:1 correlation has been obtained only using models (5), (7) and (2) (full circles). Alignment of the other models (open squares) in this correlation supports the proposed interpretations (see text).

The relation between the stretching frequency and the infrared absorption coefficient of OH groups challenges the use of a single absorption coefficient value for water quantification in pyroxenes and supports the use of wavelength-dependent calibrations. Furthermore, the observed scattering of the data indicates that defects with relatively close stretching frequencies can display significantly different absorption coefficients. For example, the (Na⁺,H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ and [(1H⁺)_M2(Fe³⁺)_M1]^×_1 models (models 7 and 10, Table 1) are observed at 3481 and 3512 cm⁻¹ and display absorption coefficients of 125 000 and 100 000 cm⁻² L (mol H₂O)⁻¹, respectively. On the experimental side, significant differences of absorption coefficients have been reported for omphacite and augite by Katayama et al. (2006) and Bell et al. (1995) (83400 vs. 38300 cm⁻² L (mol H₂O)⁻¹, respectively) despite a moderate variation in average stretching frequencies (3475 vs. 3540 cm⁻¹, respectively). Accordingly, the present results suggest that improvements in water quantification would require a proper identification of the defects related to the observed bands and the establishment of proper site-specific OH absorption coefficients, as previously done, for example, for olivine (Kovács et al., 2010).

4.2 OH defects in pure diopside

Experimental spectra of OH-bearing synthetic diopside have been reported by Stalder and Ludwig (2007) and Sundvall et al. (2009). Under saturated silica conditions, the spectrum is dominated by a band at 3355 cm⁻¹ with absorbances following the order $E//\mathit{\gamma }>E//\mathit{\alpha }\approx E//\mathit{\beta }$. The properties of the observed band are thus consistent with those computed for the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ model at 3410 and 3413 cm⁻¹ (model 2, Table 1). Interestingly, the theoretical results indicate that the band observed for the $E//\mathit{\beta }$ polarization should be shifted by a few wavenumbers toward the high frequencies with respect to the bands observed for polarizations in the perpendicular plane. Although this minor shift can go unnoticed in experimental spectra recorded with a 4 cm⁻¹ resolution, this theoretical prediction could be tested in future experimental works.

A weak and broad band without clearly defined pleochroism can also occur at 3230 cm⁻¹ in the experimental spectra of pure diopside (Sundvall et al., 2009). However, it does not match any of the presently investigated models. In particular, it does not correspond to the properties of the (2H⁺)${}_{\mathrm{M}\mathrm{1}}^{\times }$ defects which should occur at significantly lower frequencies. It can also be noticed that lower frequencies are correlated to stronger absorption coefficients. Accordingly, it is unlikely that hydrous vacancies in the M1 site occur in significant proportions in pure diopside without being noticed. This observation is consistent with the previous conclusions made for enstatite that hydrous M vacancies are preferentially associated with the M2 site (Stalder et al., 2012; Balan et al., 2012).

Hydrogarnet-type defects corresponding to four hydroxyl groups located at a tetrahedral site have been reported and modeled in a number of orthosilicates such as garnet (e.g., Nobes et al., 2000, Geiger and Rossman, 2018), zircon (Nasdala et al., 2001., Balan et al., 2013) and forsterite (Lemaire et al., 2004; Berry et al., 2005; Balan et al., 2011, 2017). Based on the properties of the computed (4H⁺)${}_{\mathrm{Si}}^{\times }$ model (model  1, Table 1), this type of defect should lead to a weak band at high frequency (>3670 cm⁻¹) and a series of more intense bands in the 3300–3400 cm⁻¹ range. According to the current experimental spectra, it seems unlikely that hydrogarnet-type defects occur at significant concentration levels in pure diopside.

4.3 OH defects in Na-bearing synthetic diopside

Experimental spectra of Na-doped diopside have been studied by Purwin et al. (2009). Compared with those of pure diopside, they display a major band at 3428 cm⁻¹ with absorbances following the order $E//\mathit{\alpha }>E//\mathit{\beta }>E//\mathit{\gamma }$. The properties of this band are consistent with those determined for the band at 3481 cm⁻¹ of the (Na⁺,H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ model (model 7, Table 1), although the theoretical model leads to a slightly different pleochroism ($I\mathit{\alpha }>I\mathit{\beta }\cong I\mathit{\gamma }$). It can be noticed that the relative intensity of the Iα and Iγ components in the (a,c) plane depends on the angles between the optic and crystal axes, a parameter which is affected by the chemical variability of pyroxenes and can differ from one sample to the other (e.g., Hess, 1949). The present theoretical model supports the hydrogen incorporation mechanism proposed by Purwin et al. (2009).

4.4 OH defects associated with trivalent cations

Trivalent cations in diopside can occur in tetrahedral or octahedral M1 sites. Incorporation in the M1 sites is generally favored by high silica activity. In addition, strong crystal field stabilization precludes the occurrence of Cr³⁺ ions in tetrahedral sites. Accordingly, the main bands observed in the spectra reported by Stalder and Ludwig (2007) should reflect the preferential incorporation of trivalent cations in M1 sites. The position of the band observed at 3462, 3443 and 3432 cm⁻¹ depends on the nature of the trivalent cation: Al³⁺, Fe³⁺ and Cr³⁺, respectively. Its absorbance follows the order $E//\mathit{\gamma }\gg E//\mathit{\beta }\cong E//\mathit{\alpha }$, similar to that observed for the band related to the doubly protonated M2 vacancies. According to the present results, the bands between 3462 and 3432 cm⁻¹ can be assigned to an M2 vacancy displaying one OH group and a nearby trivalent cation occupying an M1 site in the less symmetric configuration ([(1H⁺)_M2(M³⁺)_M1]^×_2; models 9, 11 and 13, Table 1). For Al³⁺ and Cr³⁺, the relative shift of the theoretical frequencies (35 cm⁻¹) is consistent with the difference experimentally observed ($\mathrm{3462}-\mathrm{3432}=\mathrm{30}$ cm⁻¹). The agreement is less good for the Fe³⁺-bearing model, for which the other cationic configuration is also found to be more stable by 9 kJ mol⁻¹ and the experimentally observed band is at a frequency 10 cm⁻¹ higher than that observed for Cr³⁺. This lower agreement can most likely be ascribed to a lower performance of standard DFT calculations treating the Fe³⁺-bearing systems. Beside the signals related to the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ and [(1H⁺)_M2(M³⁺)_M1]^× defects, the spectra reported by Stalder and Ludwig (2007) in the presence of trivalent cations systematically display a band at 3310 cm⁻¹ with the same pleochroism. However, this band does not depend on the nature of the trivalent cation. The best match with a theoretical model is observed for the (1H)${}_{\mathrm{M}\mathrm{2}}^{\prime }$ model (model 3, Table 1), which involves a homogeneous charge compensation. Accordingly, this band could be related to isolated OH groups associated with M2 vacancies and involving a more remote compensation for the remaining electrostatic charge by the trivalent cations in octahedral sites.

At variance with those of Stalder and Ludwig (2007), the infrared spectra of Al³⁺-bearing diopside reported by, for example, Gavrilenko et al. (2010), display a band at 3650 cm⁻¹. This band also commonly occurs in natural diopside samples (e.g., Andrut et al., 2007; Johnson et al., 2002) and in one sample of Purwin et al. (2009) containing Fe³⁺. Its absorbance follows the order $E//\mathit{\beta }>E//\mathit{\alpha }\gg E//\mathit{\gamma }$. These observations are consistent with the properties determined for the (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ model but also with those of the (Fe³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect; the frequency shift between Al- and Fe-bearing defects is only 3 cm⁻¹ (models 5 and 6, Table 1). This confirms the interpretation previously proposed by Beran (1976) and Bromiley et al. (2004). A band with similar properties is observed at 3620 cm⁻¹ in Fe-bearing diopside (Skogby, 1994) and can also be ascribed to the (Fe³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect geometry. Compared with the observations of Purwin et al. (2009), the significantly lower (30 cm⁻¹) frequency of the band observed by Skogby (1994) may be explained by the fact that the Fe-bearing diopsides of Skogby (1994) also contain a fraction of Fe²⁺ ions in sites near the defect affecting the vibrational frequencies. For example, the presence of an Fe²⁺ ion in the nearby M2 site decreases the frequency of the (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect by 33 cm⁻¹ (model 25, Table 2), and a similar frequency lowering can be expected for the (Fe³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect even though a satisfactory theoretical modeling of systems containing magnetically coupled Fe ions could not be obtained. In contrast, an Fe²⁺ ion in the nearby M1 site should increase the vibrational frequency by 20 cm⁻¹ (model 24, Table 2). Based on these elements, the bands observed at 3663 and 3623 cm⁻¹ in the low-temperature infrared spectrum of the Austrian and Russian samples (Fig. 8) could be related to (M³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defects with Ca²⁺ (normal occupancy) and Fe²⁺ ions in the nearby M2 site, respectively; the substitution in the M2 site explains the shift of 40 cm⁻¹ between the two bands. The theoretical shift between the (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ or (Fe³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defects is very small (3 cm⁻¹) and consistent with presence of a component at 3655 cm⁻¹, which is only resolved in the low-temperature Austrian spectrum. Although uncertainties related to the modeling approach make it difficult to more precisely assign the two bands, the correlation observed between the Al content and the 3645 cm⁻¹ band (at ambient temperature) in a zoned diopside crystal from Austria (Andrut et al., 2003) suggests that the major component at 3663 cm⁻¹ in the low-temperature spectra is related to the (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect, while the minor component at 3655 cm⁻¹ would correspond to the (Fe³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect. Consistent with the proposed interpretation of the 3623 cm⁻¹ band, Andrut et al. (2003) also observed a significant partitioning of Fe²⁺ in the M2 site in the OH-rich region of the same zoned crystal.

Figure 8 Band assignment in the low-temperature infrared spectra of Russian and Austrian diopside samples.

Finally, a sample (Al-Di₉₇₆) investigated by Gavrilenko et al. (2010) displays a doublet at ∼3450 and ∼3500 cm⁻¹, the two components having the same pleochroic properties. As discussed above, the band at 3450 cm⁻¹ likely corresponds to the [(1H⁺)_M2(Al³⁺)_M1]^×_2 model (model 9, Table 1). Considering that the other [(1H⁺)_M2(Al³⁺)_M1]^×_1 model (model 8, Table 1), with a less symmetric cationic configuration, leads to a stretching frequency 45 cm⁻¹ higher, it is reasonable to ascribe the second component experimentally observed at 3500 cm⁻¹ by Gavrilenko et al. (2010) to this other configuration despite its slightly higher energy (∼9 kJ mol⁻¹).

Further constraints can be found by reporting theoretical frequencies as a function of experimental frequencies (Fig. 7). For OH groups not involved in strong H bonds, it is meaningful to assume that the discrepancy between theoretical and experimental frequencies can be roughly described by a constant shift corresponding to a 1:1 correlation slope. The frequency shift determined using only the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$, (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ and (Na⁺,H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ models (models 2, 5 and 7, Table 1), for which the clearest agreement between theory and experiment is observed, is ∼49 cm⁻¹ (Fig. 7). Thus, the alignment of the other more complex defects on the same trend further supports the interpretations given above.

It is also noteworthy that the bands associated with trivalent cations in tetrahedral sites display a different behavior as a function of temperature compared with those involving fully or partially protonated M2 vacancies. The significant narrowing and positive shift observed at low temperature for the bands above 3600 cm⁻¹ (Fig. 1) are similar to the anharmonic behavior observed for two OH-stretching bands in the infrared spectrum of forsterite (Ingrin et al., 2013, 2014; Balan et al., 2017). These two bands correspond to OH groups pointing out of a tetrahedral site and not significantly engaged in H bonds, one in the (4H⁺)${}_{\mathrm{Si}}^{\times }$ defect of forsterite (Balan et al., 2011) and the other in a more complex (B³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ defect (Ingrin et al., 2014). In the present case, the OH group also points out of a tetrahedral site and the O(H)…O distance involving the OH group associated with trivalent cations is 3.38 Å, close to the upper limit observed between weakly H-bonded and nonbonded OH entities (Libowitzky 1999; Libowitzky and Beran, 2006). By analogy with forsterite (Balan et al., 2017), the anharmonicity of some of the OH bands observed in the infrared spectra of diopside is thus likely related to the specificities of the atomic-scale environment of the related OH groups. Accordingly, the temperature-induced modifications of infrared spectra could help identify different local environments of OH groups in chemically more complex pyroxene samples.

4.5 OH defects related to bands between 3500 and 3600 cm⁻¹ in natural diopside

Beside the bands observed in experimental samples, natural diopside frequently displays spectra with a series of bands between 3500 and 3600 cm⁻¹: one or two bands observed between 3520 and 3550 cm⁻¹ (Skogby et al., 1990; Skogby, 2006; Shuai and Yang, 2017; Patkó et al., 2019) and a band at ∼3520 cm⁻¹, which is frequently associated with a band at a higher frequency around 3600 cm⁻¹ (Patkó et al., 2019; Azevedo-Vannson et al., 2020). It is difficult to propose an explanation for these bands solely based on the investigated series of relatively simple chemical models involving divalent or trivalent cations being substituted for Ca²⁺, Mg²⁺ or Si⁴⁺ ions. The occurrence of Al³⁺ in octahedral site hardly produces bands at high enough frequencies, whereas the frequency decrease (33 cm⁻¹) of the (Al³⁺,H⁺)${}_{\mathrm{Si}}^{\times }$ model related, for example, to the presence of a Mg²⁺ or Fe²⁺ ion in the nearby M2 site is too weak. Thus, chemically more complex models should be considered. The first series of models involved an M2 vacancy associated with a local Tschermak-type environment with a pair of Al³⁺ ions distributed over a tetrahedral and an M1 octahedral site. These models revealed that, although the stretching of the OH group linked to the Al atoms was observed at a frequency close to or lower than those of the (2H⁺)${}_{\mathrm{M}\mathrm{2}}^{\times }$ defect, the other group, pointing in the direction of the Al-bearing sites, displayed a frequency increase consistent with the occurrence of bands in the 3500–3600 cm⁻¹ frequency range. However, the paired nature of the OH groups associated with this model was not consistent with the observation that some spectra dominated by bands between 3500 and 3600 cm⁻¹ do not display bands in the 3350–3400 cm⁻¹ range (e.g., Yang et al., 2019). These observations thus suggest that these bands could be related to a similar environment but with a single OH group occurring in the vacant Ca site. In this case, the defect neutrality could be locally ensured by the presence of a tetravalent cation in the octahedral site, most likely Ti⁴⁺. Depending on the investigated samples, Ti⁴⁺ appears to be distributed between tetrahedral and octahedral sites in Al-bearing diopside (Quartieri et al., 1993). As a matter of fact, the corresponding most stable models lead to stretching frequencies 69 to 90 cm⁻¹ higher than those theoretically determined for the [(1H⁺)_M2(Al³⁺)_M1]^×_2 model (3506 cm⁻¹). Considering that the experimental frequency associated with the [(1H⁺)_M2(Al³⁺)_M1]^×_2 model is observed at 3462 cm⁻¹, experimental bands associated with the Ti-bearing models are expected to occur between 3531 and 3550 cm⁻¹, thus matching some of the frequencies frequently observed in natural samples (models 17 and 18, Table 1). Although the proposed environment is chemically complex and may seem to be unlikely at first sight, it is noteworthy that the main bands observed in natural olivine from xenolith samples are related to a complex hydrous defect involving an Si vacancy partially charge compensated by a Ti⁴⁺ ion substituted for Mg²⁺ in the M1 site (Walker et al., 2007; Balan et al., 2011). In the case of olivine, this configuration is allowed by the edge-sharing between the M1 octahedral and the tetrahedral site. Ti-associated defects have also been reported in metamorphic garnets (Reynes et al., 2020). In this case, the electrostatic neutrality of the Si vacancy is ensured by two protons located in the tetrahedral site and two Ti⁴⁺ for M³⁺ substitutions in neighboring sites. In the case of diopside, the T site only shares a corner with the M1 site, which is occupied by an M²⁺ cation. This geometry precludes an efficient charge compensation of the vacant T site by a single Ti⁴⁺ substitution in the octahedral site, as in the [(2H⁺)_Si(Ti⁴⁺)_M1]^× model, and would favor an association of Ti⁴⁺ ions with Ca vacancies. Observations of the corresponding spectra in xenolith samples having experienced dehydration processes (Patkó et al., 2019) or carbonatitic metasomatism (Azevedo-Vanson et al., 2020) suggest that these Ti-associated centers could have a greater stability than chemically more simple defects.

Finally, the band just below 3520 cm⁻¹ observed in some mantle diopsides by Patkó et al. (2019) and Azevedo-Vannson et al. (2020) could be explained by a defect of the type [(1H⁺)_M2(Al³⁺)_M1(Fe²⁺)_M1]^×_1, assuming that configuration 1 of the defect becomes energetically competitive compared to configuration 2 (models 27 and 28, Table 2). Above, we proposed model 1 of the [(1H⁺)_M2 (Al³⁺)_M1]^× defect (model 8, Table 1) to explain the band at 3500 cm⁻¹ observed in one of the synthetic Fe-free samples of Gavrilenko et al. (2010). Here again, it seems that configuration 1 remains competitive compared to configuration 2 when Mg²⁺ is replaced by Fe²⁺ in the M1 site near the defect. The co-occurrence of a band above 3450 cm⁻¹ that could be attributed to configuration 2 in the same sample confirms that both configurations could occur at the same time. The fundamental role of Fe²⁺ in explaining the shift toward the high frequencies observed in natural diopsides is also supported by the occurrence of these two bands in the Fe-rich samples synthesized in Skogby (1994; sample Di5).

5 Conclusions

A comparison of theoretical properties of OH-bearing defects in diopside with experimental data has confirmed previously proposed interpretations, providing a detailed picture of the defect geometry for the bands at 3647–3620 cm⁻¹ (associated with tetrahedral M³⁺ ions) the bands at 3460–3432 cm⁻¹ (associated with octahedral M³⁺ ions and singly protonated Ca vacancies), the 3420 cm⁻¹ band (associated with the Na⁺ for Ca²⁺ substitution), and the 3350 cm⁻¹ band (associated with doubly protonated Ca vacancies). A more tentative interpretation has been proposed for the 3300 cm⁻¹ band which is also likely associated with singly protonated Ca vacancies. For the bands between 3500 and 3600 cm⁻¹, frequently observed in natural diopside, more complex defects need to be considered. Defects involving singly protonated Ca vacancies associated with tetrahedral M³⁺ and octahedral Ti⁴⁺ ions, as well as frequency shifts due to the substitution of Fe²⁺ for Mg²⁺ ions in the vicinity of the above-mentioned defects, can be proposed. In addition, the chemical complexity of diopside, involving, for example, the common Fe²⁺ for Mg²⁺ or Na⁺ for Ca²⁺ substitutions, may not only shift but also broaden the bands.

Here, it can be noted that the assignment of the major bands observed on well-characterized pure or chemically doped synthetic samples appears to be quite robust in terms of frequency and polarization properties. This supports the strategy used to build the defect models, which is based on simple crystal-chemical considerations. However, it is not possible to fully rule out that other missing configurations or defects occur in natural samples. In this respect, the interplay between the occurrence of partial solid solutions, the presence of trace elements and the incorporation of OH groups cannot be tackled using only quantum-mechanical models which are intrinsically size-limited. In the same line, it could be hazardous to directly extrapolate the present results to pyroxenes with more complex chemical compositions, such as augite (Skogby, 2006) or omphacite (Koch-Müller et al., 2004; Katayama et al., 2006). These systems would deserve additional experimental and theoretical work, among which are low-temperature infrared spectroscopic measurements on experimental samples and advanced theoretical modelings enabling a more efficient sampling of the configurational space in large systems.

Appendix A

Figure A1 Theoretical infrared spectrum of the (4H)${}_{\mathrm{Si}}^{\times }$ defect.

Appendix B: Properties of [(2H⁺)_Si(Ti⁴⁺)_M1]^× defects

Here we investigate the various possible configurations of diopside defects with the [(2H⁺)_Si(Ti⁴⁺)_M1]^× stoichiometry, i.e., doubly protonated vacancies with nearby Ti⁴⁺ for Mg²⁺ substitutions. The tetrahedral coordination of the Si atom corresponds to one O1, one O2 and two O3 atoms. Experimental Si–O distances are 1.609 (Si–O1), 1.585 (Si–O2), and 1.665 and 1.687 Å for O3_a and O3_b, respectively (Cameron et al., 1973). Accordingly, the doubly protonated vacancy can display two among four, i.e., six, different schemes of proton fixation. In addition, the O1 and O2 atoms are coordinated to two and one Mg atoms, respectively. The O3 atom is not coordinated to Mg. In the following, the Mg atom linked to O2 is labeled A, while the Mg atoms at a distance of 2.061 and 2.137 Å of the O1 atom are labeled B and C, respectively. Assuming that O atoms cannot be simultaneously coordinated by an H⁺ and a Ti⁴⁺ ion, nine configurations of the defect can potentially occur, among which one (O1, O3_a, A) is significantly more stable than the others (Table B1). Note that the “O3_a, O3_b, A” configuration was not found to be stable, and the H atom migrates from O3_b to O1 leading to the “O1, O3_a, A” geometry.

Table B1 Properties of [(2H⁺)_Si(Ti⁴⁺)_M1]^× defects.

Figure B1 Theoretical infrared spectrum of the [(2H⁺)_Si(Ti⁴⁺)_M1]^× defect (configuration O1, O3_a, A).