Partitioning of chromium between garnet and clinopyroxene: first-principle modelling versus metamorphic assemblages

Understanding the geochemical behaviour of trace and minor elements in mineral assemblages is of primary importance to study small- and large-scale geological processes. Partition coefficients are frequently used to model the chemical evolution of minerals and fluids during melting and in metamorphic rocks of all grades. However, kinetic effects hampering equilibrium partitioning may invalidate the modelling. This study aims at calculating partition coefficients and testing their applicability in natural mineral assemblages, choosing Cr in garnet and clinopyroxene via exchange with Al as a case study. First-principle modelling has been combined with measurements and element mapping to estimate partition coefficients for Cr and the deviation from equilibrium. Results highlight the role of crystal chemistry over the strain field around point defects, controlling the dynamics of the Cr³⁺ = Al³⁺ exchange between clinopyroxene and garnet. Ab initio calculations allowed estimation of Cr partition coefficients between garnet and clinopyroxene, using a thermodynamic approach based on endmembers and mixing models simplified for trace element behaviour. The Cr³⁺ = Al³⁺ exchange reaction between garnet and the jadeite component of clinopyroxene depends on the grossular and pyrope content, with Cr preferentially incorporated into grossular over jadeite but preferentially incorporated into jadeite over pyrope. Comparison of predicted partition coefficients to measured concentrations in natural samples, together with element mapping, shows large disequilibrium. Cr-rich and Cr-poor sectors exhibit disequilibrium attributed to slow diffusivity of Cr during crystal growth and interface-coupled dissolution–precipitation, even for garnet–clinopyroxene assemblages crystallized around 850 ^∘C.

1 Introduction

Trace and minor elements have been used as tracers of many geological processes and understanding their geochemical behaviour is highly important to petrology. The distribution of trace elements – rare earth elements (REEs) in particular – gives information on the source material of lavas (e.g. Helmke, 1972, using REEs, Co, Hf and Cr on lunar basalts; Hofmann, 1988), on the evolution of magmas (e.g. Allègre et al., 1977; Shorttle et al., 2016), and on fluid–rock interactions during diagenesis and metamorphic conditions of all grades (Wigley et al., 2013; Boutoux et al., 2014). Numerous studies of the isotopic signature of trace elements also rely on partition coefficients with huge implications on our understanding of large- and small-scale processes through element fractionation (e.g. Chauvel et al., 2008; Pabst et al., 2012).

Trace and minor elements can also provide information on how equilibrium is reached or hampered in metamorphic rocks. For example, sectors locally enriched in trace elements and cross-cutting major element zoning have been described and interpreted as disequilibrium features in mineral assemblages up to granulite facies (e.g. Chernoff and Carlson, 1999; Martin, 2009; Kohn, 2014; Carlson et al., 2015). Trace and minor elements are also used to investigate diffusivity in minerals and associated timescales (John et al., 2012; Ague and Axler, 2016), constrain pressure–temperature–time paths, and study metasomatism (e.g. Hickmott and Shimizu, 1990; Rubatto and Hermann, 2003; Angiboust et al., 2014; Kohn, 2014). However, going beyond a qualitative description of kinetic features and quantifying the amount of disequilibrium shown by trace elements in a sample remains challenging.

The partitioning of trace and minor elements between minerals and/or fluids remains poorly constrained in many cases, on both theoretical and applied grounds (Albarède and Bottinga, 1972; Dubacq and Plunder, 2018). Studies of strain fields around defects and decoration provide a robust starting frame (e.g. Carpenter et al., 2009), and several approaches and thermodynamic formalisms are available (Wagner et al., 2017; Dubacq and Plunder, 2018). Unfortunately, the dependency of partition coefficients on composition is not trivial, and the vast number of solid solutions, even in common mineral assemblages, is daunting. The dependency on composition complicates applications as incorporation of small amounts of additional components to solid solutions may affect partitioning dramatically (e.g. Dubacq and Plunder, 2018, show that a 5 % addition of majorite in pyrope garnet increases the garnet–melt partition coefficient by orders of magnitude). Modelling approaches for the incorporation of trace elements in mineral structures are also challenged by the necessary large number of atoms in simulations, as for melts (e.g. Wagner et al., 2017). Despite this complexity, theoretical modelling provides in-depth understanding of defect incorporation in mineral structures, linking strain to energy differences independently of experimental petrology and measurements.

Chromium (Cr), regularly found in trivalent form in various concentrations in pelitic and mafic metamorphic rocks, has been chosen here as a proxy to bigger and more complex trivalent cations such as REEs. In Cr³⁺ form, the d shell of Cr is partially filled. The resulting electronic configuration, with smaller shells, is easier to model than that of REEs. The incorporation of Cr³⁺ in silicates is generally explained by the homovalent substitution ^YCr³⁺ = ^YAl³⁺, where octahedral sites are highly favoured for hosting Cr³⁺ as justified by the crystal field theory and shown by X-ray diffraction (XRD) studies (e.g. Burns, 1976; Ohashi, 1980; Langer and Andrut, 1996; Yang et al., 1999; Urusov and Taran, 2012).

The present study models the Cr³⁺ = Al³⁺ substitution with first-principle calculations in garnet and clinopyroxene with varying Cr³⁺ concentration, shedding light on the impact of crystal chemistry over strain, energy differences and partitioning. The environment of the exchange site plays a key role in strain accommodation during relaxation. Results are compared with measurements of the distribution of Cr in selected metamorphic rock samples of medium and high grade, highlighting disequilibrium features. Interface-coupled dissolution–precipitation appears to control the distribution of Cr due to its very low effective mobility.

2 Nomenclature, material and methods

2.1 Crystal chemistry and terminology

The garnet–clinopyroxene is a common assemblage appearing in varied conditions. It is typical of eclogite facies rocks when the clinopyroxene includes a significant jadeite component.

Silicate garnets belong to the $Ia\stackrel{\mathrm{‾}}{\mathrm{3}d}$ space group (e.g. Smyth and Bish, 1988). They are characterized by a variety of solid solutions, with the general formula X₃Y₂Si₃O₁₂, where X is the dodecahedral site (hosting divalent cations, mainly Fe²⁺, Mn²⁺, Mg²⁺, Ca²⁺) and Y the octahedral site (hosting trivalent cations, mainly Al³⁺, Cr³⁺, Fe³⁺; Geiger, 1999; Lacivita et al., 2015). ${\mathrm{SiO}}_{\mathrm{4}}^{\mathrm{4}-}$ tetrahedra are not bonded to each other and share corners with YO₆ octahedra, as shown in Fig. 1 for grossular (Ca₃Al₂Si₃O₁₂). Incorporation of Cr takes place in octahedra and is modelled as a Cr³⁺ = Al³⁺ exchange: uvarovite (Ca₃Cr₂Si₃O₁₂) is the calcic endmember of this binary solid solution Ca₃(Al_1−xCr_x)₂Si₃O₁₂ with grossular (Langer et al., 2004; Tsujimori and Liou, 2004). In magnesian garnet, pyrope (Mg₃Al₂Si₃O₁₂) forms a similar solid solution with knorringite (Mg₃Cr₂Si₃O₁₂).

Figure 1 Crystal structures of grossular and jadeite. Trivalent Cr³⁺ substitutes with Al³⁺ in ${\mathrm{AlO}}_{\mathrm{6}}^{\mathrm{9}-}$ octahedra in both minerals (Y site). The dodecahedral site (X) of grossular incorporates Ca²⁺ and that of jadeite Na⁺.

Clinopyroxene is a subgroup of pyroxene minerals. It is a monoclinic inosilicate with the C2∕c space group (Smyth and Bish, 1988). ${\mathrm{SiO}}_{\mathrm{4}}^{\mathrm{4}-}$ tetrahedra form simple chains connected by corners (Fig. 1). Clinopyroxene has the general formula M2M1Si₂O₆ where M1 and M2 are octahedral sites (with M2 frequently including Ca²⁺, Na⁺ and M1 Al³⁺, Cr³⁺, Fe³⁺, Mg²⁺). As in garnet, Cr is mostly incorporated in octahedral sites and modelled with the same Cr³⁺ = Al³⁺ exchange, defining a solid solution between kosmochlor (NaCrSi₂O₆) and an aluminous endmember such as jadeite (NaAlSi₂O₆; Tsujimori and Liou, 2004; Reznitsky et al., 2011; Secco et al., 2002). Mineral abbreviations in this article originate from Whitney and Evans (2010), except for knorringite (Kno). For results of modelling in solid solutions, abbreviations are built with a radical indicating the original defect-free mineral and a prefix with the incorporated element, such as CrGrs for Cr-doped grossular and AlUv for Al-doped uvarovite.

2.2 Ab initio modelling

2.2.1 Protocol

Ab initio modelling provides very precise estimations of energy, volume and strain in defect-bearing minerals, with potential for systematic studies of partitioning between minerals. Calculations have been performed on periodic crystals with the CRYSTAL17 program (Dovesi et al., 2005, 2018). CRYSTAL17 uses orbitals as a linear combination of Gaussian functions and computes ground state energy directly from the Hamiltonian, using quantum equations and approximations that allow solving Schrödinger's equation for multielectronic atoms (see Sherman, 2016). Complete technical description is given in Dovesi et al. (2018). The B3LYP density functional has been selected as it is simply implemented with a localized Gaussian basis set and has shown excellent agreement with experimental data, including vibrational spectroscopy (Pascale, 2004; De La Pierre and Belmonte, 2016; Sherman, 2016).

The Al³⁺ = Cr³⁺ substitution is simulated by directly replacing an Al³⁺ ion (ionic radius: 0.535 Å after Shannon, 1976) by a Cr³⁺ defect (ionic radius: 0.615 Å after Shannon, 1976) in aluminous endmembers or a Cr³⁺ ion by Al³⁺ in Cr-rich minerals. Structure relaxation triggers deformation around the defect, by altering interatomic distances and/or changing angles to stabilize the structure and decrease lattice energy (Urusov and Taran, 2012). For each structure, CRYSTAL17 first computes the ground state energy by energy minimization using an iterative self-consistent field method (Dovesi et al., 2018) until the energy difference between two cycles becomes less than 10⁻⁷ Ha. Chromium has been locked in ferromagnetic state during the first eight cycles in order to stabilize its spin and maintain electro-neutrality during the cycles. The whole crystal geometry is then optimized following a second iterative procedure, until convergence criteria are satisfied (arbitrary units of the software): maximum energy gradient (0.00045), RMS gradient (0.0003), maximum atom displacement (0.0018) and associated RMS (0.0012). Modelled optimized energies allow computation of a defect energy, which corresponds to the difference between the energetic state of the mineral with and without defect (e.g. Allan et al., 2003). The defect energy is expressed per mole of defect and sums the excess enthalpy of the mineral and the intrinsic energetic difference between Cr³⁺ and Al³⁺. The latter does not vary with mineral structure. Consequently, differences in the defect energies of garnet and clinopyroxene reflect differences in excess enthalpy, allowing us to access Gibbs energies of reactions and partition coefficients as detailed below.

Grossular–uvarovite, pyrope–knorringite and jadeite–kosmochlor solid solutions involve homovalent Al³⁺ = Cr³⁺ substitution in one site. Computations have first been made on primitive cells for endmembers. Then solid solutions are modelled by incorporating one defect in increasingly large cells, always starting from the endmember structure. Supercells have been used and are expressed using S_n, with n the volume factor between the primitive cell and the supercell. Larger supercells have more dilute defects, closer to trace element behaviour but with space group symmetry constraints released, allowing strain localization around the defect. The thermodynamics of non-ideal mixtures states that partition coefficients vary non-linearly with concentration, reaching a fixed value at the dilution limit – when elements behave as trace. This corresponds to the concentration where defects are sufficiently far from each other to not interact, so that defect energies stay constant with decreasing defect concentration. In this procedure, defect atoms are distributed homogeneously in the structure, as far apart from one another as possible, to reproduce the effect of a trace point defect. Ordering is not considered further, implying that computed structures for solid solutions far from endmembers (e.g. 50 % grossular 50 % uvarovite) are of little interest as their configuration is likely not that of equilibrium, which will be temperature dependent (see e.g. Dove et al., 1996). It is noted that defect energies have the dimension of enthalpy and do not vary with pressure and temperature. Therefore, vibrational contributions to the Gibbs energy of exchange reactions and partition coefficients are neglected as they largely cancel out in the exchange reaction, unlike differences in lattice enthalpies which are of larger magnitude.

2.2.2 Thermodynamic formalism

In this section, partitioning of Cr between garnet and clinopyroxene is presented with the grossular and jadeite endmembers. Similar equations are written for pyrope–knorringite and jadeite–kosmochlor binary solid solutions. The partition coefficient $D_{\mathrm{Cr}}^{\mathrm{Grs}/\mathrm{Jd}}$ quantifies the distribution of Cr³⁺ between grossular garnet and jadeite clinopyroxene at equilibrium. $D_{\mathrm{Cr}}^{\mathrm{Grs}/\mathrm{Jd}}$ is defined as

$$\begin{array}{}\text{(1)}& D_{\mathrm{Cr}}^{\mathrm{Grs}/\mathrm{Jd}}={\displaystyle \frac{x_{\mathrm{Cr}}^{\mathrm{Grs}}}{x_{\mathrm{Cr}}^{\mathrm{Jd}}}},\end{array}$$

where $x_{\mathrm{Cr}}^{\mathrm{Grs}}$ is the concentration of Cr in grossular and $x_{\mathrm{Cr}}^{\mathrm{Jd}}$ that of Cr in jadeite (e.g. Morse, 2015). Here concentrations are expressed from the number of moles of elements per formula unit using the usual O₁₂ anion basis for garnet and O₆ for clinopyroxene. Incorporation of Cr³⁺ into the mineral structure is modelled as an exchange reaction with a liquid L (e.g. a melt or supercritical aqueous fluid) as in Blundy and Wood (1994):

$$\begin{array}{}\text{(R1)}& {\displaystyle }& {\displaystyle }\mathrm{Grs}+{\mathrm{Cr}}^{\mathrm{3}+}\left(L\right)=\mathrm{CrGrs}+{\mathrm{Al}}^{\mathrm{3}+}\left(L\right),\text{(R2)}& {\displaystyle }& {\displaystyle }\mathrm{Jd}+{\mathrm{Cr}}^{\mathrm{3}+}\left(L\right)=\mathrm{CrJd}+{\mathrm{Al}}^{\mathrm{3}+}\left(L\right).\end{array}$$

The grossular–jadeite exchange is the difference between Reactions (R1) and (R2), yielding (see Dubacq and Plunder, 2018)

$$\begin{array}{}\text{(R3)}& \mathrm{Grs}+\mathrm{CrJd}=\mathrm{CrGrs}+\mathrm{Jd}.\end{array}$$

The standard Gibbs free energy of reaction ΔG_r^∘ is the difference between the energetic state of products and reactants in the exchange Reaction (R3). As defect energies U_d are the differences between mineral endmembers and their substituted counterparts (e.g. $U_{\mathrm{d}}^{\mathrm{Cr}/\mathrm{Grs}}=E_{\mathrm{CrGrs}}-E_{\mathrm{Grs}}$), ΔG_r^∘ is simply the difference in defect energies, such as for $\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{3}}$:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{3}}=U_{\mathrm{d}}^{\mathrm{Cr}/\mathrm{Grs}}-U_{\mathrm{d}}^{\mathrm{Cr}/\mathrm{Jd}}.\end{array}$$

The constant of reaction K is linked to temperature T, the gas constant R and $\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_i$. Therefore, K may be expressed as a function of defect energies:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}K={\displaystyle \frac{a_{\mathrm{Cr}}^{\mathrm{Grs}}\cdot a_{\mathrm{Al}}^{\mathrm{Jd}}}{a_{\mathrm{Cr}}^{\mathrm{Jd}}\cdot a_{\mathrm{Al}}^{\mathrm{Grs}}}}=& \exp \left({\displaystyle \frac{-\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{3}}}{RT}}\right)\\ & =\exp \left({\displaystyle \frac{-U_d^{\mathrm{Cr}/\mathrm{Grs}}+U_{\mathrm{d}}^{\mathrm{Cr}/\mathrm{Jd}}}{RT}}\right).\end{array}\end{array}$$

Assuming ideal mixing at trace concentrations, activities are assimilated to concentrations, yielding

$$\begin{array}{}\text{(4)}& K={\displaystyle \frac{x_{\mathrm{Cr}}^{\mathrm{Grs}}\cdot x_{\mathrm{Al}}^{\mathrm{Jd}}}{x_{\mathrm{Cr}}^{\mathrm{Jd}}\cdot x_{\mathrm{Al}}^{\mathrm{Grs}}}}={\displaystyle \frac{D_{\mathrm{Cr}}^{\mathrm{Grs}/\mathrm{Jd}}}{D_{\mathrm{Al}}^{\mathrm{Grs}/\mathrm{Jd}}}}.\end{array}$$

The partition coefficient $D_{\mathrm{Cr}}^{\mathrm{Grs}/\mathrm{Jd}}$ is obtained with

$$\begin{array}{}\text{(5)}& D_{\mathrm{Cr}}^{\mathrm{Grs}/\mathrm{Jd}}={\displaystyle \frac{x_{\mathrm{Al}}^{\mathrm{Grs}}}{x_{\mathrm{Al}}^{\mathrm{Jd}}}}\exp \left({\displaystyle \frac{-U_{\mathrm{d}}^{\mathrm{Cr}/\mathrm{Grs}}+U_{\mathrm{d}}^{\mathrm{Cr}/\mathrm{Jd}}}{RT}}\right),\end{array}$$

where defect energies are estimated with CRYSTAL17. The final set of reactions includes Cr exchange between grossular and jadeite (Reaction R3) and between pyrope and jadeite (Reaction R4) as well as the Al exchange reactions between uvarovite and kosmochlor (Reaction R5) and between knorringite and kosmochlor (Reaction R6):

$$\begin{array}{}\text{(R4)}& {\displaystyle }& {\displaystyle }\mathrm{Prp}+\mathrm{CrJd}=\mathrm{CrPrp}+\mathrm{Jd},\text{(R5)}& {\displaystyle }& {\displaystyle }\mathrm{Uv}+\mathrm{AlKos}=\mathrm{AlUv}+\mathrm{Kos},\text{(R6)}& {\displaystyle }& {\displaystyle }\mathrm{Kno}+\mathrm{AlKos}=\mathrm{AlKno}+\mathrm{Kos}.\end{array}$$

Equation (5) is also used for natural samples to estimate theoretical partition coefficients between garnet and pyroxene at the measured composition. In that case the value used for the defect energy is that of the endmembers weighted by their fraction, which is equivalent to applying an ideal mixing model for trace-element-doped endmembers. For simplicity, the Fe²⁺ component of garnet (almandine) has been attributed to Mg (pyrope), its closest equivalent in terms of cation size, possibly altering the calculated partition coefficient in favour of pyroxene.

2.3 Description of samples

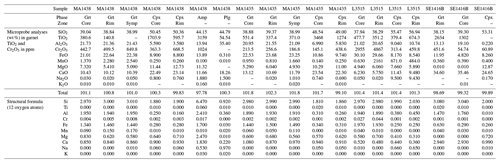
Four samples have been selected from research collections. Sample mineralogy and crystallization conditions are summarized in Table 1. Samples MA1435 and MA1438 originate from the metamorphic sole of the Mount Albert Ordovician ophiolitic massif (Quebec, Canada). Both are garnet–clinopyroxene-bearing mafic amphibolites named amphibolite du diable metamorphosed at granulite facies conditions along a clockwise pressure–temperature path (described by Dubacq et al., 2019). They are mainly composed of garnet porphyroblasts (30 %–40 %), clinopyroxene (30 %–40 %), green amphibole and plagioclase with minor epidote, quartz, rutile and Fe-oxides (Fig. 2e). Orthopyroxene is not present. Garnet rims show symplectitic textures with clinopyroxene, amphibole and/or plagioclase. Clinopyroxene size is comprised between hundreds of micrometres to 2 mm.

Table 1 Mineral occurrences in the samples and associated peak metamorphic conditions.

Figure 2 Optical microscope photographs of the samples. (a, b, c) Sample L3515, with veins highlighted. White rectangles show area selected for element mapping; (b) atoll garnets; (c) garnet and omphacite from the T2 vein. (d) Rodingite sample SE1416B: garnet crystals (with hydrogrossular-rich rim) surrounded by calcite. (e) Sample MA1438 with garnet–amphibole–clinopyroxene assemblage. The red box indicates the zone used for element mapping (Fig. 10a).

The L3515 sample (Fig. 2a) is a Fe–Ti-rich metagabbro from the eclogitic slice of Monte Viso, a meta-ophiolitic complex of the Western Alps, and has been described by Locatelli (2017). It has experienced successive fluid circulation events together with brecciation, recorded by veins and mineral assemblages with varying trace element content. This has been interpreted as progressive opening of the system with increasing contribution of serpentinite-derived fluids (Locatelli, 2017). About half of the thin section is constituted of metagabbro mylonitic clasts. In that zone, atoll garnets (50–300 µm) are very abundant (≈75 %) and associated with deep green omphacite – optically zoned – often smaller than 100 µm (≈15 %) and small amalgamated rutile grains (Fig. 2b). Omphacite is found as individual crystals and included in garnet. The sample shows also a small zone of eclogitic matrix mostly (>70 %) composed of omphacite crystals ranging between 800 µm and 1.5 mm, associated with garnet porphyroblasts containing omphacite and rutile inclusions. Apatite and lawsonite pseudomorphs are also observed in the matrix. Two types of veins, T1 and T2, are found: T1 is composed of abundant prismatic omphacite crystals up to 2.5 mm and lawsonite pseudomorphs. The T2 type contains garnet and omphacite (Fig. 2c).

Sample SE1416B originates from the garnet–clinopyroxene-bearing amphibolitic sole of the Semail ophiolite (Oman). This sample is a rodingite part of the series sampled and described by Soret et al. (2017). Rodingites are the product of hydrothermal alteration of the mafic rocks linked to devolatilization of marbles from the metamorphic sole. The sample SE1416B shows a rich diversity of minerals including wollastonite, calcite, clinopyroxene, garnet, titanite, apatite and epidote (Table 1). Clinopyroxene and calcite constitute more than 50 % of the sample. Variably sized garnet is present (≈15 %–20 % of the sample). Small garnets surrounded by large calcite crystals are locally observed with a rim enriched in hydrogrossular component (Fig. 2d).

2.4 Analytical techniques

Samples have been analysed by electron probe microanalyzer (EPMA) after optical microscopy. Analyses were carried out with Cameca SX50 and SX100 instruments at CAMPARIS (Sorbonne Université, Paris, France). Analytical conditions were tuned for low detection limits of Cr for point measurements in wavelength-dispersive spectroscopy (WDS) acquisition mode with 40 nA beam current, 20 keV acceleration voltage and three spectrometers analysing Cr, allowing an average detection limit of 120 ppm (for Cr). Albite (Na), diopside (Mg, Si, Ca), orthoclase (Al, K), Fe₂O₃ (Fe), MnTiO₃ (Mn, Ti) and Cr₂O₃ (Cr) were used for standardization of elements in brackets. For element maps, Cr has been measured with high beam current (299 nA) and a detection limit of about 25 ppm. Compositional maps were quantified with the manufacturer's software (with the PAP method of Pouchou and Pichoir, 1991, as for point measurements) and processed with in-house software. Structural formulae were calculated on the basis of 12 oxygen atoms for garnet and 6 oxygen atoms for clinopyroxene. Particular attention has been paid to avoiding micro-inclusions that can trap ions like Cr³⁺ (Yang and Rivers, 2001). Representative point analyses are provided in Table A1.

3 Results

3.1 Mineral structures and strain

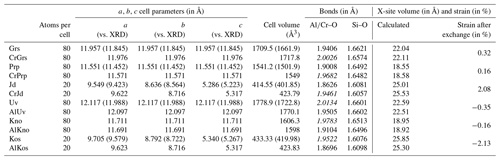
A list of computed cell parameters and volumes is given in Table 2 for endmembers; solid solutions with a Cr defect for CrGrs, CrPrp and CrJd; and the Cr-rich counterparts with Al defect AlUv, AlKno and AlKos. A synthetic table of the main computations carried out for all generated cells and supercells is also provided in the Supplement (Table S1). Experimental determinations from Smyth and McCormick (1995) are given for comparison. Overestimations of cell volumes by the B3LYP functional are observed but remain small. Deviations from XRD measurements are below 1.5 % for cell parameters and comprised between 2.6 % and 3.3 % for volumes. It is noteworthy that the formalism used for calculations of exchange reactions and partition coefficients will cancel out systematic errors.

Table 2 Cell parameters and volumes computed with CRYSTAL17 compared to data from Smyth and McCormick (1995) given in brackets. Al–O, Cr–O and Si–O bond lengths are also provided. Computed Cr-O bond lengths are given in italic.

The deformation ε of cation–oxygen bonds after incorporation of a Cr defect and relaxation of the structure has been computed from the initial (L_i, before defect incorporation) and final (L_f, with defect) interatomic distances:

$$\begin{array}{}\text{(6)}& \mathit{\epsilon }={\displaystyle \frac{L_{\mathrm{f}}-L_{\mathrm{i}}}{L_{\mathrm{i}}}}\cdot \mathrm{100}.\end{array}$$

Figure 3a shows the displacement of atoms around the defect after the Al³⁺ = Cr³⁺ exchange. Results are presented for the largest lattices of aluminous garnet endmembers only – grossular and pyrope – for readability. Computations in jadeite and chromiferous endmembers show similar variations with similar conclusions. Overall, a rapid non-linear decrease in the displacement is observed away from the Cr atom, reaching values below 0.01 Å about 5 Å away from the defect. This is consistent with relaxation being almost entirely accommodated over that distance. Deformation is shown in terms of bond strain (Fig. 3c) and angle variations (Fig. 3b). The strain patterns in all garnet types appear very similar with small differences, with strain being mostly accommodated by the two first neighbours. Greater strain is observed for pyroxene endmembers. Bond strain of pyrope, grossular and jadeite are compared (Fig. 3c) for primitive cell S₁ and quadruple supercell S₄. For both garnet types, Cr–O bonds undergo the strongest strain (about 3.5 % for pyrope and 3.2 % for grossular). The strain at about 10 Å – corresponding to the size of their primitive cell – is higher for S₁ than for S₄, highlighting interaction of defects. Small differences in relaxation are noted between and within mineral groups. Close to the defect (first four neighbours), pyrope shows more strain than grossular, in terms of bond lengths and angular strain (Fig. 3b): Cr–O–Si angle strain is almost twice larger in pyrope (≈1.6 %) than in grossular. In comparison, O–Si–O is more strained in Cr-rich jadeite – almost 1.0 %.

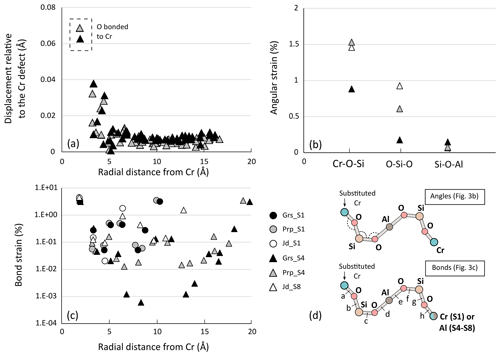
Figure 3 Computed strain in defect-doped minerals. Note that (c) is on a log scale; absolute values of bond strain are plotted. Triangles indicate supercells S₄ for garnets and S₈ for pyroxene, whereas circles are for smaller cells S₁. (a) Displacement of atoms in grossular and pyrope (in Å) as a function of the radial distance to the defect (located at 0 Å). (b) Angular strain (in %). Angles correspond respectively to Cr–O–Si, O–Si–O and Si–O–Al, as illustrated in (d). (c) Computed bond strain (in %) in primitive cells S₁ and supercells S₄ as a function of the radial distance from the Cr defect (in Å). (d) Sketch of angles and bonds strained after defect incorporation. Letters from “a” to “h” correspond to the successive bonds.

Figure 4 illustrates bond strains in jadeite and grossular in the vicinity of a Cr defect. Even though the exchange of Al³⁺ for the bigger ion Cr³⁺ induced stretching of the bonds directly linked to the defect, relaxation is also accommodated by shortening of neighbouring bonds. In grossular, bond strain is symmetric around the defect but not radial in the sense of continuum mechanics (Fig. 4a). Cr–O bonds are affected by stretching (≈3 %) and neighbouring Si–O bonds are shortened by about 0.3 %. Most of the deformation is accommodated by the first two neighbours of the defect. The chain structure of jadeite displays a more distributed and complex strain (Fig. 4b). Cr–O bonds are stretched up to about 4.5 %, not symmetrically. As for grossular, Cr³⁺ = Al³⁺ exchange also induced shortening of some Si–O and Al–O bonds.

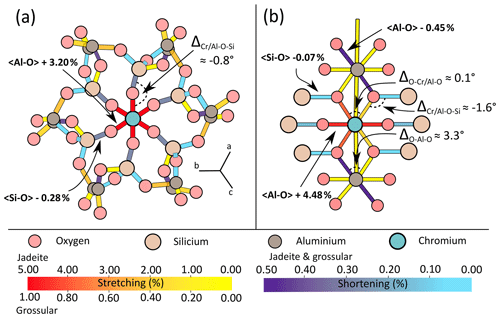
Figure 4 Bond strain in Cr-doped grossular and jadeite. Strain is expressed in percent (%), indicated for both minerals as stretching for positive values and shortening for negative values. (a) Bond strain in the grossular primitive cell after Cr³⁺ = Al³⁺ substitution. (b) Planar representation of chromium's local environment in jadeite after Cr³⁺ = Al³⁺ substitution.

Importantly, the replacement of Al by Cr in the octahedral site induces stretching of the adjacent dodecahedral site (Fig. 5 and Table 2). Cation–oxygen bonds in the dodecahedral site are more strained in CrPrp than in CrGrs (up to ≈1 % stretching and ≈0.5 % shortening). Overall, the Ca site (CrGrs) increases by 0.32 % when the Mg site (CrPrp) increases by 0.16 %, with both values being consistent with the cell volume increase after incorporation of Cr (Smyth and Bish, 1988, reported that the X site is 2.5 % smaller in grossular than in uvarovite). The Na site in jadeite is more strained than garnet sites with a volume increase of 2.1 % and up to 2 % bond stretching and 0.9 % compression.

Figure 5 Bond strain (in %) in the dodecahedral site neighbouring the defect site for Cr-doped pyrope (a), grossular (b) and jadeite (c). Strain is indicated in red for positive values (stretching) and blue for negative values (shortening). Oxygen atoms with bold circles are bonded to the Cr defect.

3.2 Energy and volume variations

Solid solutions between Al and Cr endmembers show increasing volume with Cr content, consistent with the bigger ionic radius of Cr³⁺ (Shannon, 1976). The increase is essentially linear. Excess volumes are not zero but are all small (Fig. 6a): up to about −0.03 cm³ p.f.u. for jadeite–kosmochlor (i.e. less than 0.05 % of the jadeite cell volume p.f.u.) and below about −0.03 cm³ p.f.u. for grossular–uvarovite and pyrope–knorringite (below about 0.03 % of cell volume p.f.u. in both cases). For garnet, the trend is slightly dissymmetric, with more variability observed near aluminous endmembers (low Cr content). Pyroxene excess volumes are generally negative and follow comparable trends. Excess enthalpies are also small, lower than 0.05 kJ mol⁻¹ p.f.u. Excess enthalpies tend to zero close to the endmembers, consistent with trace element behaviour and proper convergence of calculations during relaxation. The grossular–uvarovite solution has the largest excess enthalpy (Fig. 6b).

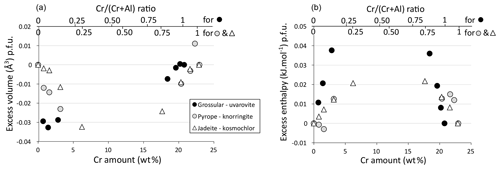
Figure 6 Excess quantities for garnet and clinopyroxene solid solutions as a function of the Cr amount. (a) Excess volume for jadeite–kosmochlor (Jd–Kos), grossular–uvarovite (Grs–Uv) and pyrope–knorringite (Prp–Kno) solid solutions. (b) Excess enthalpy for jadeite–kosmochlor (Jd–Kos), grossular–uvarovite (Grs–Uv) and pyrope–knorringite (Prp–Kno) solid solutions.

Small excess volumes show that the strain fields of defects do not interact and not an absence of strain. The volumes of the Y site (where defects are incorporated) and of their first neighbouring X site are provided in the Supplement (Table S1 and Fig. S1). Calculations for the largest lattices, where defects are most diluted, have the smallest excess volumes per formula unit but show the largest strain for the defect Y site. In Cr-doped grossular, this shows that relaxation takes place around the whole Cr defect site, itself relatively undeformed compared to the Cr site of uvarovite, and vice versa for Al incorporation in uvarovite. The volume of the X site is little affected, as some bonds are stretched, some bonds are shortened and polyhedra are tilted during strain accommodation (Figs. 4 and 5).

3.3 Theoretical partitioning of Cr

Figure 7 shows calculated defect energies along the binary solid solutions investigated. The difference between garnet and clinopyroxene defect energies – for the same Cr proportion, as shown on the X axis – gives the Gibbs free energy of the exchange reactions (Reactions R3, R4, R5, R6). Comparing results obtained for garnet supercells S₂ (1.4 wt % Cr in CrGrs, 1.6 wt % for CrPrp) and S₄ (0.7 wt % Cr in CrGrs, 0.8 wt % for CrPrp), defect energies stabilize around 1 wt % Cr. The Gibbs free energy of reaction is estimated from the largest supercells where Cr dilution is highest (S₄ for garnets and S₁₆ for clinopyroxene). The value for $\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{3}}$ (Grs–Jd exchange) is negative with $\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{3}}=-\mathrm{7}$ kJ mol⁻¹, whereas $\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{4}}$ (Prp–Jd exchange) is positive with $\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{4}}=\mathrm{22}$ kJ mol⁻¹. In other words, calculations show that at equilibrium Cr is more favourably incorporated in grossular than in jadeite and more favourably incorporated in jadeite than in pyrope, in agreement with estimations of Dubacq and Plunder (2018) and experimental trends of van Westrenen et al. (2003). The value of ΔG_r^∘₅ (Uv–Kos exchange) is positive with 8 kJ mol⁻¹, whereas that of $\mathrm{\Delta }{G}_{\mathrm{r}}{{}^{\circ }}_{\mathrm{6}}$ (Kno–Kos exchange) is negative with −25 kJ mol⁻¹. Al incorporation is therefore more favourable to the Mg-garnet chromiferous endmember than to the Ca-garnet chromiferous endmember.

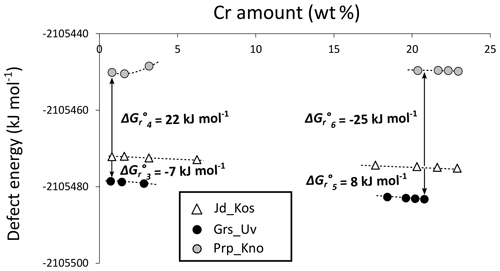
Figure 7 Computed defect energies (in kJ mol⁻¹) for garnet and clinopyroxene solid solutions as a function of the Cr amount (in wt %). The Gibbs free energy of reaction is given for each exchange reaction.

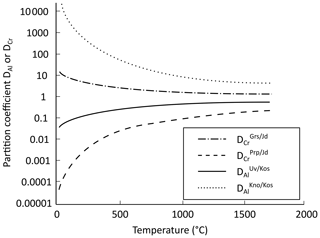
Figure 8 shows partition coefficients estimated using Eq. (5) as a function of temperature. The Cr partition coefficient for grossular–jadeite and Al partition coefficient for knorringite–kosmochlor are greater than 1, reflecting Cr partitioning in favour of Ca-garnet and Al partitioning in favour of Mg-garnet. On the contrary, Cr is predicted to partition in favour of jadeite for the pyrope–jadeite system, and Al is incorporated preferentially in kosmochlor for the uvarovite–kosmochlor system.

Figure 8 Evolution of calculated partition coefficients D^Grt∕Cpx of Cr and Al with temperature (in ^∘C) for grossular–jadeite, uvarovite–kosmochlor, pyrope–jadeite and knorringite–kosmochlor exchange reactions.

3.4 Distribution of Cr in natural samples

Figure 9 shows the composition of garnet and clinopyroxene in the four samples. In samples MA1435 and MA1438 (granulite-facies amphibolite), garnet is a solid solution with high and variable almandine (Alm ≈40 %–50 %) and grossular contents (Grs ≈27 %–40 %), as well as minor pyrope content of 20 %–30 % (Fig. 9a). The spessartine component is below 6 %. Estimated Fe³⁺ content is very low (≤0.1 a.p.f.u) and neglected thereafter. Zoning is observed for Fe, Mg and Mn, with generally increasing Mn and Fe from core to rims and decreasing Mg (Fig. 10a–e). Mn in symplectites increases toward the rim up to a maximum ring, followed by a thin Mn-poor and Ca-rich zone (Fig. 10d–e; see Dubacq et al., 2019, for details). The Al content varies within 1 wt % Al₂O₃ and is lower in Cr-rich zones (Fig. 10b and c). The Ca content decreases globally from core to rims and increases again in the symplectites (Fig. 10d). Clinopyroxene (Fig. 9b) is mainly of diopside type (XCa ≈0.5–0.7) with a small jadeite component (XAl =0.1–0.2). Radial zoning is observed for Al (from 6 wt % Al₂O₃ in crystal cores to about 3 wt % in rims, Fig. 10c). In garnet and clinopyroxene, Cr content is very heterogeneous with sector zoning and thin Cr-rich or Cr-poor stripes cross-cutting major element zoning and grain boundaries. Chromium content ranges from below the detection limit (<120 ppm) to more than 3000 ppm Cr₂O₃ in garnet and 700 ppm Cr₂O₃ in clinopyroxene. Cr-rich domains are mostly found in garnet, but Cr-rich zones also cross-cut grain boundaries and extend to the adjacent amphibole crystals (Fig. 10b). A negative correlation between Al and Cr is observed in some garnet crystals but not systematically. In garnet, Cr-rich zones are also Ca-rich in cores of amalgamated crystals. In clinopyroxene, Cr also displays sector and patchy zoning apparently unrelated to that of Al.

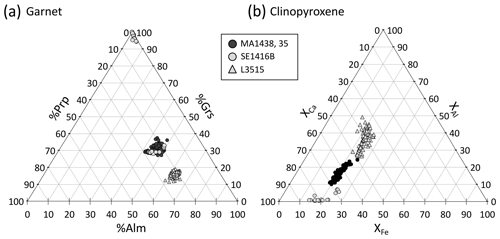
Figure 9 Garnet and clinopyroxene compositions for the present samples. (a) Garnet composition is shown as a function of grossular, pyrope and almandine content. (b) Clinopyroxene composition.

Figure 10 EPMA composition maps for MA1438. (a) Scanning electron microscope (SEM) image, (b) Cr₂O₃ map, (c) Al₂O₃ map, (d) CaO map and (e) MnO map correspond to the area highlighted in Fig. 2e. Stars indicate point analyses selected to estimate apparent partition coefficients reported in Table 3. (f) Microphotograph of zone 2. Corresponding compositional map for Cr₂O₃ (g) and Al₂O₃ (h) in garnet–clinopyroxene–amphibole.

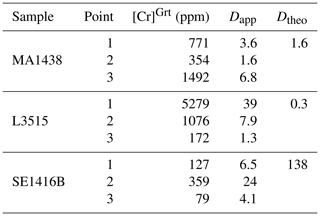
Table 3 Apparent (D_app) and computed (D_theo) partition coefficients of Cr between garnet and clinopyroxene for each sample.

Garnet in the L3515 samples is Fe-rich and Ca-poor (XAlm >60 %, XGrs <20 %, XSps <2 %, Fig. 9a). Radial zoning is observed for Mg and Mn, with increasing Mg (from ≈4.5 to 6.5 wt % MgO) and decreasing Mn (from 0.6 to 0.1 wt % MnO). Clinopyroxene displays two main compositions corresponding to cores and rims, as described by Locatelli (2017). Cores are of diopside type with CaO content between 10.1 and 15.6 wt % and MgO content between 6.4 and 9 wt %. The jadeite component increases from core to rim, from ≈8.5 to ≈10.3 wt % Al₂O₃ and from ≈8.6 to ≈9.6 wt % Na₂O (Fig. 11i and j). There is a marked negative correlation between Al and Cr, with Cr-rich, Al-poor sectors (Fig. 11). As for previous samples, Ca and Al display complex and patchy zoning. In Fig. 11g, the Cr-rich zone follows the garnet–clinopyroxene boundary. Alternations of thin Cr-rich and Cr-poor bands are also observed, with Cr- and Ca-enriched bands cross-cutting the radial zoning displayed by major elements (Fig. 11b and d). In clinopyroxene, Cr₂O₃ content reaches 0.4 wt % but is below the detection limit for other parts of the crystals (Fig. 11b and h). Positive and negative correlations between Al and Cr are found in this sample. Some Cr- and Al-poor zones are also Na-poor and Ca- and Mg-rich (Fig. 11h, i and j).

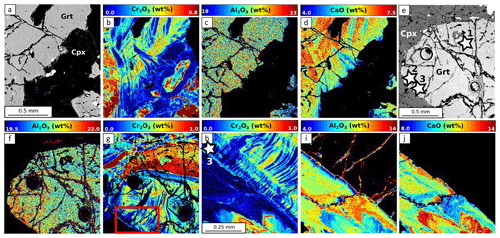
Figure 11 EPMA composition maps for L3515. The area imaged in (a) (SEM image) has been mapped for its Cr₂O₃ (b), Al₂O₃ (c) and CaO (d) content. Image (e) (SEM) shows the area mapped forAl₂O₃ (f) and Cr₂O₃ (g). Maps shown in (h) for Cr₂O₃, (i) for Al₂O₃ and (j)  for CaO are close-up maps of the area shown in red in (g). Stars indicate point analyses used to estimate apparent partition coefficients reported in Table 3. The NaO map (not shown) shows similar variations to that of Al₂O₃, as for MgO and CaO.

In sample SE1416B, garnet is Ca-rich and contains very little Mg (Fig. 9a). The Ca enrichment reflects incorporation of grossular – and to a smaller extent hydrogrossular – components. Radial, successive zoning patterns are found for all analysed elements (Fig. 12). Crystal cores are globally enriched in Al and Ca and are poor in Mn and Fe. The oscillation-like zone displays progressive Al and Ca decrease with Fe and Mn increase. The hydrogrossular component increases at the rim. Contrary to other samples, Cr shows successive zoning negatively correlated with Al. Clinopyroxene is of diopside type, with XCa ≥70 % (Fig. 9b). Epidote displays an allanite-rich core which decreases towards the rim enriched in pistacite component.

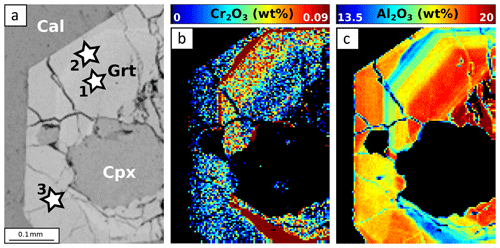
Figure 12 EPMA composition maps for SE1416B. Stars indicate point analyses used to estimate apparent partition coefficients reported in Table 3. (a) SEM image. (b) Composition map for Cr₂O₃ in garnet. (c) Composition map for Al₂O₃ in garnet.

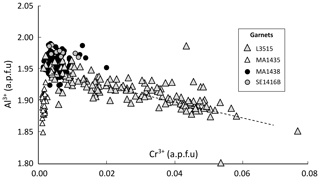
Figure 13 Cr–Al correlation graph for garnet in all samples. The dashed line shows 1:1 exchange of Cr³⁺ and Al³⁺. Element concentrations are expressed in atoms per formula unit (a.p.f.u.).

Figure 13c shows correlations between Cr³⁺ and Al³⁺ in garnet from all samples. In L3515, which has the highest concentration in Cr, a well-defined negative correlation is observed between Al and Cr, consistent with Cr³⁺ = Al³⁺ exchange. No trend is observed for the other samples as Cr is too diluted to significantly modify Al concentration.

Given the disparity of Cr concentrations in garnet of the four samples, apparent partition coefficients D_app have been estimated on selected garnet point analyses, as indicated by the stars in the figures. The amount of Cr in clinopyroxene has been considered homogeneous, excluding analyses from the most-Cr-rich sectors. Table 3 reports the obtained D_app, in comparison with the theoretical partition coefficient D_theo computed for each sample using Eq. (5).

4 Interpretations and implications

4.1 Chemical control on Cr partitioning and strain accommodation

The Al³⁺ = Cr³⁺ exchange is the preponderant mechanism for Cr³⁺ incorporation in garnet and clinopyroxene. However, concomitant cation exchange is possible. For garnet in the MA1535, MA1538 and L3515 samples, the coupled substitution ^VIIICa²⁺ + ^VICr³⁺ = ^VIIIMg²⁺ + ^VIAl³⁺ is observed in part of the samples, consistent with the positive correlation between Cr and Ca in composition maps (e.g. Fig. 11d). This mechanism was also proposed in previous studies (e.g. Wood and Kleppa, 1984; Griffin et al., 1999; Kopylova et al., 2000). It has been especially described in mantle rocks where it has been named “lherzolite trend” (Griffin et al., 1999). Similarly, Kopylova et al. (2000) proposed that the grossular component of garnet was dependent on Cr content, pressure and temperature in clinopyroxene-bearing xenoliths from Jericho kimberlite, Canada.

In garnet and pyroxene, neither strain nor displacement are radial around defects. Instead, some bonds neighbouring defects are stretched, some bonds are shortened and polyhedra are tilted. This is in opposition to the lattice strain model (Blundy and Wood, 1994, among many others) as discussed by Dubacq and Plunder (2018). The contrasted accommodation of strain in garnet and jadeite is easily explained by differences in their crystal structures. Garnets are rigid nesosilicates: strain is more localized and limited compared to jadeite. Polyhedral tilting is limited and bond length variations accommodate most of the strain in the vicinity of the defect. Jadeite is less rigid and densely packed than garnet, allowing more polyhedral tilting in addition to bond length variations.

Incorporation of Cr³⁺ mostly impacts the host octahedral site, but there is also strain in the dodecahedral site of the garnet and clinopyroxene endmembers. The X site expands due to Cr³⁺ incorporation, especially in grossular, in agreement with the positive correlation between Cr and Ca: presence of Ca in the X site may promote incorporation of Cr³⁺ by decreasing steric hindrance. Computed D_theo coefficients display systematic opposite behaviour when comparing pyrope with grossular, with Cr³⁺ preferentially incorporated in grossular over jadeite and preferentially incorporated in jadeite over pyrope. This confirms the correlated behaviour of Ca and Cr is not restricted to mantle rocks.

In clinopyroxene, coupled mechanisms may also be proposed in addition to the likely dominant Al³⁺ = Cr³⁺ substitution. Unfortunately, EPMA measurements do not evidence any, due to very low amount of Cr in pyroxene. The Tschermak-type substitution ^IVSi⁴⁺ + ^VIMg²⁺ = ^IVAl³⁺ + ^VICr³⁺ has been proposed, by Urusov and Taran (2012), where Cr³⁺ does not substitute with Al³⁺ but with octahedral Mg²⁺. Similar coupled exchanges involving Na⁺ may be proposed for clinopyroxene but are not observed here, yet Na⁺ likely plays a role in clinopyroxene similar to Ca²⁺ in garnet. The modelled joined expansion of the Na and Al sites after Cr incorporation explains easier incorporation of trace Cr in jadeitic clinopyroxene. Incorporation of Cr in the Mg site coupled with that of Na in the Ca site of diopside has not been modelled here but could be a mechanism worth investigating at low Cr concentrations.

It follows that concentration of defects may be of key importance for the computation of realistic partition coefficients. This has not been modelled here but it is noted that studies report clustered defect contents in natural crystals (Peterman et al., 2019; Seydoux-Guillaume et al., 2019).

4.2 Disequilibrium and role of kinetics

Composition maps provide clear evidence of Cr disequilibrium, and comparison of theoretical and apparent partition coefficients allow us to estimate its extent for each sample. The theoretical partition coefficient of 0.3 computed for the L3515 sample predicts a Cr partitioning in favour of clinopyroxene, which can be understood by the higher proportion jadeite in pyroxene and lower grossular content in garnet compared to the MA1438 and SE1416B samples. Apparent partition coefficients are hugely variable but generally much higher than the theoretical value. The Cr-rich sectors in garnet are drastically out of equilibrium with pyroxene, as for the Cr-poor garnet. Similarly, enriched patches in the MA1418 sample are out of equilibrium, showing preferential distribution in garnet. Some areas around the Cr-rich patches have Cr content consistent with equilibrium partitioning with clinopyroxene. As a result, Cr displays here only localized partitioning at equilibrium between garnet and clinopyroxene, despite the high temperature conditions (≈850 ^∘C) promoting diffusivity in metamorphic fluids, grain boundaries and intracrystalline diffusion. In the SE1416B sample, Cr partitioning is predicted to be largely in favour of garnet (D_theo=138). Although measurements show Cr is preferentially incorporated in garnet, concentrations are lower than predicted. This is partly due to the very low Cr content of clinopyroxene (close to or below the detection limit) complicating its measurement. Evolving composition of fluids during garnet growth is shown by changing Al and Cr content (Fig. 12). Equilibrium with included clinopyroxene has therefore probably not been maintained during the growth of garnet.

Compositional mapping of Cr-rich areas cross-cutting radial zoning of major elements can not be explained as a consequence of crystallization at equilibrium. The metamorphic reactions leading to crystallization of garnet and clinopyroxene are mediated by diffusion of cations in fluids and along grain boundaries, feeding the growing crystals. Evidence shows that the mobility of Cr was reduced during garnet growth in all samples but SE1416B (marble), with the effective diffusivity of Cr lower than the garnet growth rate: homogenization of Cr around the growing crystals was much slower than crystal growth. In this view, Cr-rich sectors are interpreted as the remnants of former Cr-rich phases – likely a phyllosilicate for elongated prismatic shapes seen in the L3515 sample (Fig. 11g–h). Martin (2009) provides similar interpretation from Cr and Y mapping in garnet. This argues for interface-coupled dissolution–precipitation, a kinetically controlled phenomenon reported in previous studies (e.g. the stunning maps of minor elements in garnet by Ague and Axler, 2016). Additional kinetics effects may be invoked (see Reznitsky et al., 2011; Kohn, 2014). In particular for clinopyroxene, some crystal faces may show higher apparent partition coefficients due to electrostatic effects (see Dowty, 1976). Electrostatic effects on crystal faces may generate zoning cross-cutting radial patterns, as observed by Van Hinsberg et al. (2006) for sectorial and hourglass zoning in tourmaline. Radial zoning of Cr in garnet attests to Cr mobility and may record evolving fluid composition (Angiboust et al., 2014). In this case, the use of equilibrium partition coefficients is justified; however, presence of sectorial zoning and interface-coupled dissolution–precipitation precludes equilibrium modelling.

Therefore, interpretation of Cr zoning should account for small-scale features showing disequilibrium, then local equilibrium crystallization (on a scale reflecting mineral assemblages), and lastly possible opening of the system via fluids.

5 Main conclusions

Combined ab initio modelling and mapping of the Cr³⁺ distribution in garnet and clinopyroxene allow detailed understanding of incorporation mechanisms effectively taking place in metamorphic rocks.

Ab initio modelling allows reproducing trace element behaviour for the Al³⁺ = Cr³⁺ substitution in garnet and clinopyroxene. Estimation of theoretical partition coefficients usefully combines with experimental petrology and measurements in natural rocks.

The Cr³⁺ = Al³⁺ exchange is not a function of cation radius differences only. The local environment of the exchange site and the structural differences between clinopyroxene and garnet play a role in strain accommodation, impacting the partitioning of Cr.

Kinetics is essential to explain Cr zoning in garnet and clinopyroxene, and departure from equilibrium may be estimated with observed deviation from theoretical partition coefficients. Slow crystalline diffusion, low diffusivity in fluids, and grain boundaries as well as electrostatic effects on crystal faces hamper reaching equilibrium.

Perspectives to this work include extension of the chemical system to divalent iron and application to other mineral assemblages. The results obtained here for Cr can probably be generalized to other relatively immobile trivalent trace elements such as Y (Martin, 2009) and other rare earths. Interface-coupled dissolution–precipitation in high-grade rocks (e.g. Ague and Axler, 2016) as well as electrostatic effects and clustering of defects are not in favour of using partition coefficients for geochemical modelling. Without going as far as Dowty (1976), who dismisses the use of clinopyroxene for thermobarometry on the ground of kinetic effects, measuring the distribution of trace elements when possible appears safer for correct interpretation.

Appendix A

Table A1 Representative EPMA analyses for garnet and clinopyroxene in samples MA1435, MA1438, L3515 and SE1416B. “Symp” stands for analyses made in symplectites; “–” denotes below the detection limit.