Structure and theoretical infrared spectra of OH defects in quartz

The infrared spectra of natural quartz, and synthetic quartz produced in conditions relevant to natural environments, generally contain some association of OH-stretching absorption bands at 3596, 3585, 3483, 3431, 3379 and 3313 cm⁻¹, and/or a broad band at ∼ 3400 cm⁻¹. In this study, a series of OH-bearing defects has been theoretically investigated from first principles within the density functional theory framework. The optimized structure, infrared spectroscopic properties and relative energy of defect configurations have been determined. Comparison with experimental observations enables the identification of atomic-scale configurations related to the experimentally observed OH-stretching bands. Consistent with previous interpretations, the results confirm the assignment of the bands at 3596 and 3483 cm⁻¹ to OH defects associated with B³⁺ substituting for Si⁴⁺ and to OH defects associated with Li⁺ cations located in the structural channels, respectively. They also confirm the assignment of the bands at 3313 and 3379 cm⁻¹ to OH associated with the Al³⁺-for-Si⁴⁺ substitution and, by implication, the previously given interpretation of the 3431 cm⁻¹ band in terms of Fermi resonance. The band at 3585 cm⁻¹ does not appear to be related to a hydrogarnet-type defect, as has been proposed previously, but potentially corresponds to isolated OH⁻ groups bridging two Si atoms, where the charge compensation is ensured by a nonlocal mechanism.

1 Introduction

The existence of hydrous defects in quartz is shown by the presence of infrared absorption bands related to OH-stretching vibrational modes (Kats, 1962; Aines and Rossman, 1984; Müller and Koch-Müller, 2009). These defects are known to modify some of the macroscopic physical–chemical properties of quartz, including its rheology and piezoelectric performance (e.g., Griggs and Blacic, 1965; Griggs et al., 1966; Mackwell and Paterson, 1985; Kronenberg et al., 1986; Cordier and Doukhan, 1991; Doukhan, 1995). The defects are also likely to provide pathways for diffusive hydrogen flux through quartz, by which quartz-hosted melt and fluid inclusions can be modified (Severs et al., 2007; Zajacz et al., 2009; Guo and Audétat, 2018; Myers et al., 2019) and OH contents of volcanic quartz can be modified before, during or post-eruption (Biró et al., 2016, 2017; Tollan et al. 2019). The infrared spectra of these defects can also be used to identify the provenance of detrital quartz in sands, sandstones and other siliciclastic materials (e.g., Stalder and Neuser, 2013; Stalder et al., 2017, 2019).

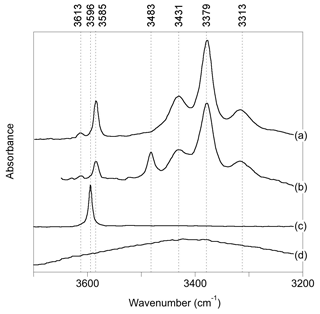
Figure 1 Experimental spectra of quartz samples displaying commonly observed OH-stretching bands (a): Stalder and Konzett (2012), sample pH32 (polarized E⊥[001]-E$\left|\right|$[001]); (b): Frigo et al. (2016), 10 % spodumene, 1.0 GPa (polarized E⊥[001]-E$\left|\right|$ [001]); (c) Thomas et al. (2009), B-doped quartz (unpolarized); (d) Potrafke et al. (2019), (polarized E$\left|\right|$[001]).

OH-stretching absorption bands at 3596, 3585, 3483, 3431, 3379 and 3313 cm⁻¹ dominate the infrared spectra of natural quartz samples and quartz grown at magmatic or hydrothermal conditions (Fig. 1). Most of these bands are polarized in the plane perpendicular to the quartz c axis. The band at 3585 cm⁻¹, which is observed following either synthesis in the pure quartz–water system (Stalder and Konzett, 2012) or deformation and/or annealing experiments using natural quartz (Rovetta et al., 1986, 1989), as well as in natural amethyst (Karampelas et al., 2005), has been proposed to be related to hydrogarnet-type defects, i.e., four protons associated with a vacant Si site (Stalder and Konzett, 2012). The bands at 3431, 3379 and 3313 cm⁻¹ are assigned to OH groups related to the substitution of Al³⁺ for Si⁴⁺, based on a correlation between Al and H (Kats, 1962), studies of paramagnetic defects by electron spin resonance following irradiation (Sibley et al., 1979; Halliburton et al., 1981) and their presence following synthesis in the quartz–albite system (Stalder and Konzett, 2012). Quartz synthesized in systems with elevated boron shows a band at 3596 cm⁻¹, thus assigned to OH associated with the B³⁺-for-Si⁴⁺ substitution (Staats and Kopp, 1974; Thomas et al., 2009; Baron et al., 2015). Finally, quartz samples produced in systems with high Li display a band at 3483 cm⁻¹, which is therefore associated with Li⁺ ions located in the structural channels of quartz (Kats, 1962; Frigo et al., 2016). This association is also supported by electro-diffusion “sweeping” experiments, whereby monovalent cations are passed through quartz by electrolysis, with infrared spectra measured before and after (e.g., Kats, 1962; Krefft, 1975).

In addition to OH-stretching bands related to OH defects, a broad and approximately isotropic band can be observed at around 3400 cm⁻¹ (Fig. 1; e.g., Potrafke et al., 2019). It is assigned to some form of defect with H₂O stoichiometry, which could be in the form of either clustered silanol groups or molecular H₂O (Aines and Rossman, 1984; Aines et al., 1984) but not liquid water, as shown by the lack of ice bands on cooling (Aines and Rossman, 1984).

Despite experimental constraints, the precise configuration of the OH-bearing structural defects in quartz remains elusive. Previous theoretical studies using quantum-mechanical modeling approaches have proposed stable models of OH-bearing defects in quartz (e.g., Lin et al., 1994; McConnell et al., 1995; Rosa et al., 2005), mostly focusing on their thermodynamic stability. Quantum-mechanical modeling tools can also be used to investigate the vibrational spectroscopic properties of models of OH defects that can be tested against experimental observations. This approach has been successfully used to interpret the infrared spectrum of OH defects in a number of silicate-group minerals (e.g., Blanchard et al., 2009, 2017; Balan et al., 2011, 2013, 2017; Ingrin et al., 2014). In the present study, we compute the theoretical infrared (IR) absorption spectrum of selected models of OH defects in quartz, focusing on OH defects potentially occurring in natural quartz. The comparison of theoretical and experimental data then provides important constraints to help unravel the nature of OH defects in quartz.

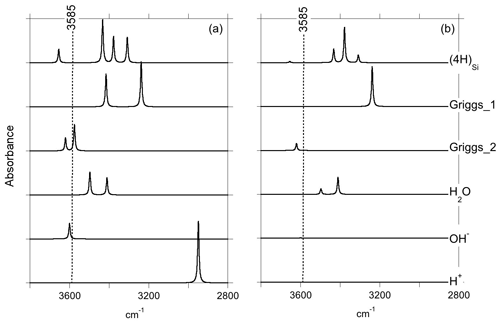
Figure 2 Theoretical IR absorption spectra of selected OH-bearing defects in the quartz–water system for polarizations perpendicular (a) and parallel (b) to the [001] direction. The position of the main IR band experimentally observed in the quartz–water system (Fig. 1) is indicated by the dotted line.

2 Methods

The properties of OH defects were theoretically investigated within the density functional theory (DFT) framework using the PWscf code of the Quantum Espresso package (Giannozzi et al., 2009; http://www.quantum-espresso.org, last access: 27 May 2020). The modeling scheme used the generalized gradient approximation (GGA) to the exchange–correlation functional as proposed by Perdew, Burke and Ernzerhof (PBE functional; Perdew et al., 1996) and periodic boundary conditions. The ionic cores were described using optimized norm-conserving Vanderbilt (ONCV) pseudopotentials (Hamann, 2013; Schlipf and Gygi, 2015). Cutoffs of 80 and 480 Ry on the electronic wave functions and charge density, respectively, were used as in Balan et al. (2019). Structural properties of α-quartz (SG P3₂21) were determined using its primitive cell (9 atoms), whereas $\mathrm{2}\times \mathrm{2}\times \mathrm{2}$ supercells (72 atoms) containing up to four hydrogen atoms were used to model the OH defects. Brillouin zone sampling for the electronic integration was performed using a $\mathrm{2}\times \mathrm{2}\times \mathrm{2}$ k-point grid for the quartz primitive cell and was restricted to the Γ point for the $\mathrm{2}\times \mathrm{2}\times \mathrm{2}$ supercells. Total energy convergence was verified to be better than 1 mRy per atom using a 120 Ry cutoff on the wave functions and a $\mathrm{3}\times \mathrm{3}\times \mathrm{3}$ k-point grid. Unit cell parameters of pure quartz were optimized at zero pressure and were used without further relaxation to build up the OH-bearing supercells. For all systems, the relaxation of atomic internal coordinates was performed until the residual forces were < 10⁻⁴ Ry a.u.⁻¹. As usually observed, the theoretical relaxed cell parameters of α-quartz (a=5.01 Å, c=5.51 Å) are overestimated with respect to their experimental counterparts (a=4.92 Å, c=5.41 Å; Levien et al., 1980), which is consistent with previous theoretical determinations at the DFT-GGA level (Hamann, 1996; Rosa et al., 2005; Méheut et al., 2007).

The vibrational modes, the Born effective charge tensors and the electronic dielectric tensor were calculated at the Brillouin zone center (Γ point), using the linear response theory (Baroni et al., 2001) as implemented in the PHonon code (Giannozzi et al., 2009; http://www.quantum-espresso.org, last access: 27 May 2020). The high-frequency OH-stretching modes, which are decoupled from the other vibrational modes occurring at much lower frequency, can be accurately calculated by only considering the displacement of the oxygen and hydrogen atoms involved in OH groups (Balan et al., 2008). The complex low-frequency dielectric permittivity tensor has been calculated for each defect by adding only the ionic contributions related to the OH-stretching modes to the electronic permittivity tensor and using an arbitrary damping parameter of 4 cm⁻¹, accounting for the width of absorption bands (Balan et al., 2001). The average dielectric tensor of the defective crystal was obtained by applying to the defect model the threefold rotation operations consistent with the crystal symmetry. The IR absorption spectrum for polarization perpendicular or parallel to the [001] direction was then calculated from the corresponding diagonal element of the average dielectric tensor (Figs. 2 and 3).

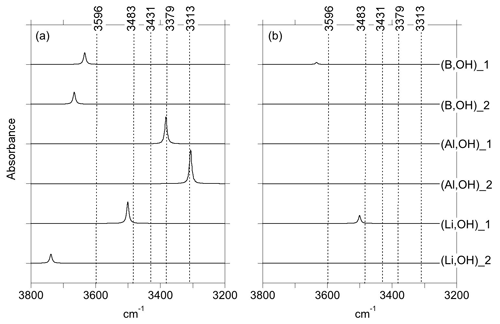
Figure 3 Theoretical IR absorption spectra of selected OH-bearing defects associated with chemical impurities for polarizations perpendicular (a) and parallel (b) to the [001] direction. The positions of the experimentally observed IR bands (Fig. 1) are indicated by the dotted lines.

It is noteworthy that the equivalent H₂O concentration of the models ranges between 0.6 and 2.5 wt %, which is significantly larger than concentrations observed in experimental and natural samples (usually < 500 ppm). The lowest defect concentration of periodic models is limited by the cell size that can be treated within an acceptable computational time. For OH defects in quartz, Rosa et al. (2005) found that a cell containing 36 atoms was large enough to minimize defect–defect interactions. The present use of a $\mathrm{2}\times \mathrm{2}\times \mathrm{2}$ supercell is thus expected to provide an accurate description of the local structure and vibrational properties of OH defects.

3 Results and discussion

3.1 OH defects in the pure quartz–water system

Two main hydrous defect types have been proposed in the pure SiO₂–H₂O system. The first is associated with 4 H⁺ charge-compensating a Si vacancy (e.g., Doukhan and Paterson, 1986; Stalder and Konzett, 2012). The second involves incorporating H₂O into the quartz structure by formation of silanol (Si–OH) groups (Brunner et al., 1961; Griggs and Blacic, 1965). In addition, a direct incorporation of H₂O molecules in structural channels has been proposed (Aines and Rossman, 1984).

Considering the first type, hydrous defects in nominally anhydrous silicates are often related to cationic vacancies (e.g., Keppler and Smyth, 2006). In silicates, the so-called hydrogarnet- or hydrogrossular-type defect ((4H)${}_{\text{Si}}^{\times }$) corresponds to the substitution of four protons for one Si⁴⁺ ion. Occurrence of this type of defect has been either reported or proposed in, for example, garnet (e.g., Nobes et al., 2000; Geiger and Rossman, 2018), zircon (Nasdala et al., 2001; Balan et al. 2013), forsterite (Lemaire et al., 2004; Berry et al., 2005; Balan et al., 2011, 2017; Padrón-Navarta et al., 2014) and ringwoodite (Blanchard et al., 2009). In quartz, a band at 3585 cm⁻¹ with polarization in the (001) plane, in samples experimentally synthesized in the quartz–water system, has been associated with the (4H)${}_{\text{Si}}^{\times }$ defect (Stalder and Konzett, 2012). This band also appears to be associated with a smaller band at 3613 cm⁻¹ (Fig. 4 of Stalder and Konzett, 2012).

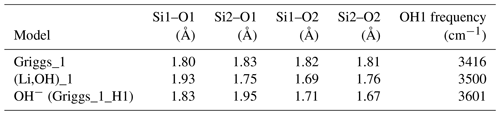
Table 1 Properties of OH-bearing defect models: OH bond length (d_OH), stretching frequency (ω_OH), integrated molar absorption coefficient (K_int) and relative energy (E_rel). Models that best match the properties of experimentally observed bands are in bold type.

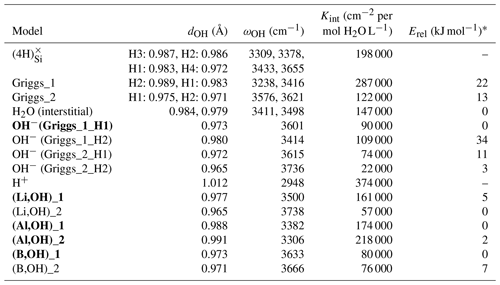
^* E_rel is the relative energy defined as the difference between the total energy of the model and that of most stable model with the same stoichiometry.

Figure 4 (a) Structure of the hydrogarnet ((4H)${}_{\text{Si}}^{\times }$) defect. Note the H bonds represented by the black plain lines. Those involving the H1, H2 and H3 atoms are oriented along the edges of the tetrahedral site. The OH4 group points out of the tetrahedral site. (b) Structure of interstitial H₂O. Note the weak bonding to a Si atom (doted line) and the H-bond pattern (black plain lines). In this and following figures, silicon atoms are in blue, oxygen atoms in red and hydrogen in light pink.

Optimization of the (4H)${}_{\text{Si}}^{\times }$ defect in quartz, starting from different initial guesses, can lead to various metastable configurations corresponding to different orientations of OH groups and H-bonding patterns. In the most stable configuration (Fig. 4; Table 1), the shortest OH group points outside the tetrahedral site formed by the four oxygens, whereas the three other OH groups point along the edges of the tetrahedron. A closed triangular configuration of these three OH groups, as determined by Rosa et al. (2005), has not been found to be stable. The (4H)${}_{\text{Si}}^{\times }$ defect leads to four OH-stretching bands. The shortest OH group vibrates at 3655 cm⁻¹ with polarization in the (001) plane, whereas the three other OH groups lead to three bands with frequencies ranging between 3300 and 3450 cm⁻¹ and significant contributions along the [001] direction (Fig. 2). Notwithstanding absolute differences in wavenumber between the computed bands and the observed band at 3585 cm⁻¹, the occurrence of four OH groups with different orientations in (4H)${}_{\text{Si}}^{\times }$ type defects cannot account for the observation by Stalder and Konzett (2012) of one main OH band in the (001) plane. This strongly challenges the attribution of the 3585 cm⁻¹ band experimentally observed in samples produced in the quartz–water system to (4H)${}_{\text{Si}}^{\times }$ defects. This also suggests that such a (4H)${}_{\text{Si}}^{\times }$ defect has potentially not been observed at all – to our knowledge no such spectra have been reported, although any 3300–3450 cm⁻¹ bands could be overwhelmed by bands associated with the Al³⁺-associated defect. Strong evidence a (4H)${}_{\text{Si}}^{\times }$ defect exists in olivine is provided both by the theoretical modeling of its infrared spectrum (Balan et al., 2011, 2017) and by the relative absorbance in the ∼ 3600 cm⁻¹ region between crystals synthesized in the presence of enstatite with high activity of silica (aSiO₂) versus periclase with low aSiO₂ (e.g., Lemaire et al., 2004). Clearly, such experiments cannot be conducted in the pure SiO₂ system. However, because the concentration of a defect containing four protons should increase with the fugacity of water (fH₂O) squared (Padrón-Navarta and Hermann, 2017), potentially, the presence or absence of such a defect could be determined by synthesizing quartz in the pure SiO₂ system at a range of pressures, working from the 2.0 GPa data point of Stalder and Konzett (2012).

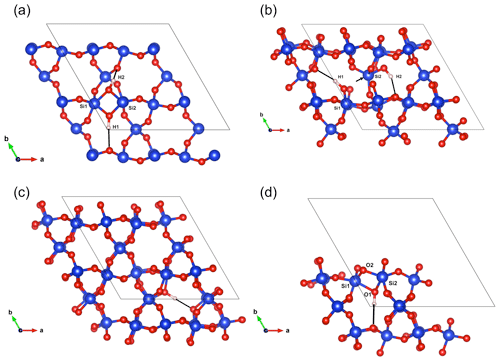
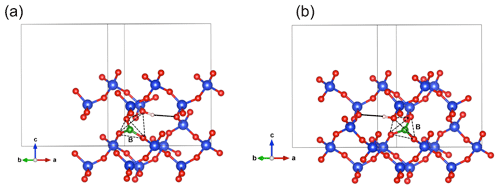
Figure 5 (a) Structure of the Griggs_1 defect. Note the asymmetric pair of OH groups bridging the fivefold coordinated Si1 and Si2 atoms. (b) Structure of the Griggs_2 defect. The arrow indicates the displacement of Si2 atom to an interstitial position. (c) Structure of the H⁺ defect. (d) Structure of the OH⁻ defect (Griggs_1_H1 model). The charge of the H⁺ and OH⁻ defects in (c) and (d) is compensated for by an electrostatic background homogeneously spread over the cell (see text).

The second class of OH-bearing defect that could occur in the quartz–water system results from the hydrolysis of a Si–O–Si bridge and dissociation of a water molecule forming two silanol (Si–OH) groups, i.e., generically Si–O–Si + H₂O = Si–OH + HO–Si (Brunner et al., 1961; Griggs and Blacic, 1965). The optimization of the “Griggs defect” leads to a structure almost identical to that previously determined by Rosa et al. (2005), with an asymmetric configuration involving the formation of two fivefold coordinated Si atoms and two OH bonds with different lengths (Griggs_1 model; Table 1; Fig. 5a). The shortest OH group lies in the (001) plane and forms a relatively long H bond (1.87 Å) across the channel of the quartz structure. The corresponding stretching frequency is computed at 3416 cm⁻¹. The other OH group forms a shorter H bond (1.60 Å) with an oxygen belonging to an adjacent silicate tetrahedron, resulting in a longer OH group canting with respect to the (001) plane. The related OH-stretching band is calculated at 3238 cm⁻¹ and displays contributions for polarizations perpendicular and parallel to the c axis (Fig. 2). The significant frequency difference between the experimental band at 3585 cm⁻¹ and the theoretical component at 3416 cm⁻¹ does not support the Griggs defect as a relevant model of the 3585 cm⁻¹ band. Concerning the low-frequency component, it should be also noted that bands at ∼ 3200 and 3300 cm⁻¹ are often present in quartz spectra, but these have been assigned to either Si–O overtones or combination vibrations of the quartz structure based on their insensitivity to annealing or H–D exchange (Kats, 1962), or to surficial OH (Biró et al., 2016). Furthermore, this Griggs_1 defect cannot be invoked to explain the broad H₂O band at ∼ 3400 cm⁻¹ – spectra including this band do not also include a second band at, or around, 3238 cm⁻¹. The lack of these bands, and by extension of the Griggs_1 defect, is consistent with its previously determined high formation energy (Rosa et al., 2005), which precludes its occurrence in quartz at thermodynamic equilibrium.

A different configuration of OH defects with the same stoichiometry as the Griggs_1 defect has also been determined in this study (Griggs_2 model). In this configuration, one of the Si atoms (Si2, Fig. 5b) occupies an adjacent interstitial site, increasing the distance separating the two silanol groups and preserving the fourfold coordination of Si atoms. The two OH groups display similar lengths and both form a H bond across a structural channel. The total energy of the Griggs_2 model is lower than that of the Griggs_1 configuration by 9 kJ mol⁻¹. An additional calculation involving a $\mathrm{3}\times \mathrm{3}\times \mathrm{3}$ supercell confirmed that the Griggs_2 configuration is more stable than the Griggs_1 configuration, although the energy difference reduces to 4 kJ mol⁻¹. The resulting theoretical infrared spectrum displays two bands at 3576 and 3621 cm⁻¹ with only the low-frequency band exclusively polarized in the (001) plane. This could be in line with the Stalder and Konzett (2012) observation, with a major band at 3585 cm⁻¹ and a minor band at 3613 cm⁻¹, although their data do not allow the polarization of the 3613 cm⁻¹ band to be determined. However, the difference in wavenumber between the two computed bands (45 cm⁻¹) is larger than the experimentally observed difference (28 cm⁻¹). In addition, each of the two bands of the Griggs_2 configuration is related to only one OH group, leading to comparable integrated intensities, with a ratio of the high-frequency band to the low-frequency band of ∼ 75 %.

Models including an interstitial water molecule have also been determined. The most stable model (Fig. 4b) is consistent with the previous findings of De Leeuw (2001) and Rosa et al. (2005). The water molecule displays a relatively long bond with a Si atom (dSi–O_W=2.10 Å), similar to that determined for water physisorption on silica clusters (Ma et al., 2005), and medium-strength H bonds (1.75 and 1.79 Å) with bridging oxygen atoms. This leads to a pair of OH bands at 3411 and 3498 cm⁻¹, with contributions perpendicular and parallel to the [001] direction (Fig. 2; Table 1). Although these bands could be broadened by anharmonic interactions with the host phonon bath and dynamical configurational disorder, isolated water molecules in quartz channels hardly account for the properties of the very broad isotropic signal observed at ∼ 3400 cm⁻¹ (Aines and Rossman, 1984).

Table 2 Inter-atomic distances and stretching frequencies of OH defects with double Si–O–Si bridges.

Taken together, none of these three defect types can explain the 3585 cm⁻¹ band observed by Stalder and Konzett (2012). In fact, a single OH band with a polarization in the (001) plane cannot be explained by any models of OH-bearing defects with a chemical composition ensuring a local electrostatic neutrality. Charge compensation of cationic vacancies in pure quartz involves the formation of four nonequivalent OH groups, whereas the dissociation of water molecules, and formation of a Griggs-type defect, leads to the formation of two nonequivalent OH groups. These observations suggest that a theoretical explanation of the 3585 cm⁻¹ band requires the local charge compensation constraint on the defect models to be relaxed and that models bearing H⁺- and OH⁻ should be treated separately. For such models, an electrostatic charge is uniformly spread over the supercell to ensure its neutrality, thus differing from models in which the charge compensation is ensured at the defect scale by explicit countercharges (coupled chemical substitutions or cationic vacancies). It can be noticed that a separate treatment of H⁺ and OH⁻ defects is in line with the experimental observation that hydrogen diffuses faster than oxygen in the quartz structure (e.g., Farver and Yund, 1991; Bachheimer, 1998; Kats, 1962).

The H⁺ model has been constructed by setting a hydrogen atom on a Si–O–Si bridge. The optimized configuration (Fig. 5c) displays an OH group bridging two Si atoms. In this configuration, the corresponding oxygen atom is significantly over-bonded, leading to a lengthening of the OH bond to 1.012 Å and reducing its stretching frequency to 2948 cm⁻¹.

Two OH⁻ models have been built by removing one of the two H atoms of the Griggs_1 model. Optimization of the models leads to strengthening of the Si–O–Si bridge, a lengthening of the distance between the Si atoms and the remaining OH group, and a related shortening of the OH bond (Table 2). The least stable configuration corresponds to the OH2 group of the Griggs_1 model. It leads to a band at 3414 cm⁻¹ and differs by 34 kJ mol⁻¹ from the other, precluding its significant occurrence at thermodynamic equilibrium. The most stable configuration (Fig. 5d) corresponds to the OH1 group of the Griggs_1 model. The corresponding OH group is parallel to the (001) plane and displays a theoretical stretching frequency of 3601 cm⁻¹. The spectroscopic properties of this model thus compare favorably with those of the OH-stretching band observed in samples synthesized in the quartz–water system and suggest that the 3585 cm⁻¹ band is related to isolated OH⁻ defects with a nonlocal charge compensation. Again, this could be tested experimentally by synthesizing quartz in the pure SiO₂–H₂O system as a function of fH₂O – the response of this proposed defect to changing fH₂O should be lower than that of a (4H)${}_{\text{Si}}^{\times }$ defect.

As with the Griggs_1 model, two OH⁻ models have also been built starting from the Griggs_2 structure, which displays a Si atom in an interstitial position and was found to be slightly more stable than the Griggs_1 configuration. After relaxation, the re-coordination of the dangling Si–O bond leads to the formation of fivefold Si atoms. When the OH group initially sits on the “interstitial” Si2 atom, it vibrates at 3736 cm⁻¹, whereas a lower frequency of 3615 cm⁻¹ is observed for the other model. These two models are less stable than the more stable one derived from the Griggs_1 structure, by 3 and 11 kJ mol⁻¹ (Table 1). The relative stability of these configurations was confirmed by additional calculations using a $\mathrm{3}\times \mathrm{3}\times \mathrm{3}$ supercell.

Therefore, according to our calculations, the most reasonable model explaining the band observed at 3585 cm⁻¹ corresponds to a OH group bridging two Si atoms already linked by an oxygen atom and pointing toward the center of a structural channel (Fig. 5d). In this case, the charge balance responsible for the 3585 cm⁻¹ band cannot be specifically identified but likely involves more remote charged species ensuring bulk electrostatic neutrality. This proposed configuration meets both the spectroscopic and relative stability criteria. In addition, the model is consistent with experimental observations of a high thermal stability of the 3585 cm⁻¹ band and a relatively high sensitivity to the exposure of quartz samples to ionizing radiations. Given that oxygen diffuses considerably more slowly than protons in quartz (e.g., Kats, 1962; Farver and Yund, 1991; Bachheimer, 1998), the radiation-induced dissociation of the OH group could be a potential mechanism leading to the formation of peroxy centers. Migration of protons could then contribute to the charge compensation of other defects related to impurities (Lipson and Kahan, 1985; Pankrath, 1991).

Figure 6 Structure of the (B,OH) defects. Note the location of the B atom on the face of the tetrahedral site. The OH group sits on the opposite corner and points outside of the tetrahedral site (shown by the dotted lines). (a) (B,OH)_1 model; (b) (B,OH)_2 model.

3.2 OH defects associated with chemical impurities

Compared with the chemically simple quartz–water system, the presence of chemical impurities leads to a larger variety of OH defects, as attested by their infrared-active stretching bands. However, the trace element population of quartz is relatively simple compared to other silicates, and the trace element content is generally on the order of tens of parts per million by weight. Cationic substitution is effectively limited to tetravalent (Ti⁴⁺, Ge⁴⁺), pentavalent (e.g., P⁵⁺) or trivalent cations (e.g., Al³⁺, Fe³⁺) replacing Si⁴⁺. Monovalent alkaline cations (Li⁺, Na⁺, K⁺) can be incorporated in channel sites, associated with anionic species (O²⁻, OH⁻) or with the abovementioned trivalent cations. Pertinent to this study, observed OH groups can thus be related to the charge compensation of trivalent cations or be associated with monovalent alkaline cations. The corresponding incorporation mechanisms will be referred to as the trivalent cation mechanism and the alkaline mechanism.

In the trivalent cation mechanism, hydrogen incorporation provides the charge balance, allowing substitution of a trivalent cation for a Si⁴⁺ cation. The substitution of boron or aluminum for silicon has been experimentally investigated and revealed a number of associated OH-stretching bands. Quartz samples grown in high-B systems display a characteristic band at 3596 cm⁻¹ that has been ascribed to a (B,OH) defect (Staats and Kopp, 1974; Thomas et al., 2009; Baron et al., 2015). This band has a dominant polarization in the (001) plane and a weaker contribution parallel to the [001] direction (Thomas et al., 2009; Baron et al., 2015). In the quartz–albite–water or granite–water systems, IR spectra of quartz display three bands polarized in the (001) plane and observed at 3313, 3379 and 3431 cm⁻¹ (Stalder and Konzett, 2012). It is noteworthy that deuteration experiments (two OD equivalents are observed instead of three OH bands; Kats, 1962) suggested that the 3379 and 3431 cm⁻¹ bands correspond to a single vibrational mode involved in a Fermi resonance with an overtone mode of the quartz structure.

Considering that the SiO₄ tetrahedron in quartz displays a twofold symmetry, two starting configurations have been considered for each substituted model. They correspond to the setting of one hydrogen atom in the vicinity of one of the two nonequivalent oxygen atoms belonging to the substituted tetrahedral site.

In both of the two optimized boron models, the boron atom moves toward one of the tetrahedron faces and adopts a threefold coordination, leaving the OH group at the opposite corner (Fig. 6a, b). A similar configuration of a hydroxylated defect associated with a boron atom for silicon substitution has previously been reported in olivine (Ingrin et al., 2014), and the defect geometry shares some similarities with the mixed carbonate–fluorine defect in apatite (Yi et al., 2013). The total energy of the two boron models differs by 7 kJ mol⁻¹ (Table 1). Theoretical OH-stretching spectra are computed at 3633 cm⁻¹ for the most stable configuration (B,OH)_1 and 3666 cm⁻¹ for the less stable one (B,OH)_2 (Fig. 3). Both are dominantly polarized in the (001) plane with a minor contribution along the [001] direction for the (B,OH)_1 model. The most stable configuration leads to the closer agreement with the experimental observation in terms of frequency and pleochroism. The (B,OH)_1 model is thus the preferred configuration explaining the 3596 cm⁻¹ band observed in quartz grown in the presence of tourmaline.

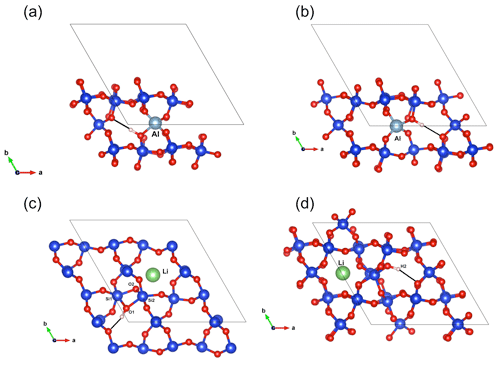
Figure 7 (a) Structure of the (Al,OH)_2 defect. (b) Structure of the (Al,OH)_1 defect. (c) Structure of the (Li,OH)_1 defect. (d) Structure of the (Li,OH)_2 defect.

As with the B-bearing models, two starting guesses were used for the two Al-bearing models. In these cases, the Al atom remains at the center of the tetrahedral site, and two configurations with similar energy are observed (Fig. 7a, b). They lead to two OH-stretching bands at 3306 and 3382 cm⁻¹ with a polarization in the (001) plane, closely matching the bands experimentally observed at 3313 and 3379 cm⁻¹. As proposed above and by Kats (1962), the missing 3431 cm⁻¹ band, which is always observed with the 3313 and 3379 cm⁻¹ bands, but not computed, is most likely related to a Fermi resonance.

Taken together, these calculations and observations explain why the B³⁺-associated defect has just one band where its Al³⁺ equivalent has three. The less symmetric configuration of the B³⁺ in the tetrahedron means that one location of the OH group is energetically preferred over the other location, leading to the observation of a single band for the B-associated defect in quartz. In contrast, the more regular environment of the fourfold-coordinated Al³⁺ ions leads to two OH configurations with similar energies and two related OH-stretching modes, one of them being observed as a pair of absorption bands due to its resonance with a quartz overtone.

In the alkaline mechanism, an alkaline cation located in a channel site counterbalances the negative charge excess related to the incorporation of OH⁻ groups. In this study, only Li⁺ cations have been considered, i.e., forming defects with the stoichiometry LiOH. Experimentally, the infrared spectrum of quartz samples grown in Li-bearing systems displays a characteristic band at 3483 cm⁻¹ (Baron et al., 2015; Frigo et al., 2016).

Models corresponding to a LiOH defect have been built by replacing one of the H atoms of the Griggs models with a Li atom. Optimized structures share some similarities with the models bearing OH⁻ in which the charge compensation was ensured by a homogeneous background. These similarities can be traced back to the weak efficiency of Li⁺ cations in locally compensating for the valence of dangling oxygen atoms, which re-coordinate to neighboring Si atoms. The two most stable models (Fig. 7c, d; Table 1), referred to as (Li,OH)_1 and (Li,OH)_2, correspond to the OH1 and OH2 groups of the Griggs_1 and Griggs_2 models, respectively. They display significantly different stretching frequencies at 3500 and 3738 cm⁻¹, respectively. Although the (Li,OH)_1 model is slightly less stable, its vibrational frequency is in much closer agreement with the experimental observation than the (Li,OH)_2 model (Fig. 3). It is thus the preferred model related to the band experimentally observed at 3483 cm⁻¹ in Li-bearing quartz samples.

Figure 8 Experimental vs. theoretical OH-stretching frequencies of defect models.

4 Concluding remarks

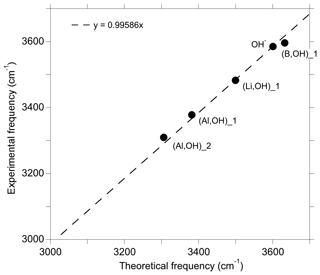
In the present study, we have theoretically determined the structure and the spectroscopic properties of a series of OH-bearing defects in quartz (Table 1). Among this series, five models have been related to experimentally observed bands, leading to interpretations of these bands in terms of atomic-scale configurations. It is however difficult to fully explore the configuration space related to the multiple potential orientation of OH groups toward more or less distant oxygen atoms. In addition, theoretical frequencies are systematically affected by a number of approximations, such as the neglecting of anharmonicity and the use of an approximate exchange–correlation functional. These approximations introduce some degree of uncertainty in the comparison of theory with experiment. It is thus noteworthy that the comparison of theoretical and experimental frequencies for the identified configurations follows a well-defined linear trend (Fig. 8). This suggests that the discrepancy between theory and experiment is dominated by the abovementioned systematic effects, which further supports our interpretations.

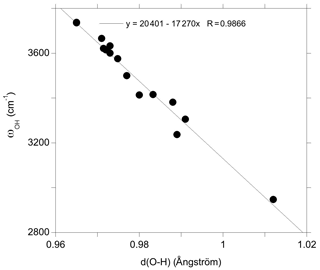
In addition, the investigated series of defects makes it possible to identify general trends explaining the variability of OH-stretching frequencies in quartz. As previously observed, the stretching frequency is almost linearly related to the O–H distance (Fig. 9), which is in turn controlled by local constraints of bond valence compensation (Brown, 2014). Comparing the structures related to the double Si–OH–Si bridges in the Griggs_1 defect (Fig. 5), the OH stretching frequency displays a systematic variation as a function of the nature of the charge compensation mechanism (Table 2). For the Griggs defect, the presence of a proton on each of the two bridging oxygen atoms leads to relatively long Si–O and OH bonds, corresponding to a relatively low stretching frequency at 3416 cm⁻¹. For the (Li,OH)_1 defect, the valence brought by the Li⁺ cation is smaller, leading to shorter Si–O2 bonds and a concomitantly longer Si–O1 bond. This induces a shortening of the OH1 bond and an increase in its stretching frequency to 3500 cm⁻¹. The effect is even more pronounced when the charge compensation is nonlocal, leading to a higher stretching frequency at 3601 cm⁻¹.

Figure 9 Theoretical OH-stretching frequencies of defect models vs. OH bond lengths.

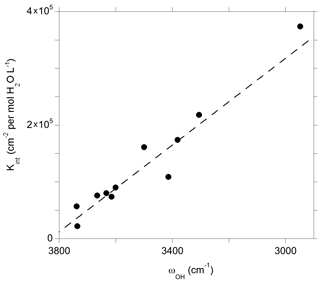
Figure 10 Theoretical integrated molar absorption coefficients (K_int) of defect models displaying a single OH group as a function of the corresponding OH-stretching frequency (ω_OH). The dashed line corresponds to the general trend of Balan et al. (2008) shifted by 50 cm⁻¹: $K_{\text{int}}=\mathrm{382}(\mathrm{3832}-{\mathit{\omega }}_{\text{OH}})$ (see text).

The theoretical infrared spectra also make it possible to examine the relation between the absorption coefficient and the OH-stretching frequency (Fig. 10). As previously observed, both quantities are linearly correlated and define a trend consistent with the general one obtained by Balan et al. (2008). Note that compared to this previous study, the OH-stretching frequencies obtained in the present study are shifted by ∼ 50 cm⁻¹ toward higher frequencies due to the use of the more accurate ONCV pseudopotentials, giving the general relationship $K_{\text{int}}=\mathrm{382}(\mathrm{3832}-{\mathit{\omega }}_{\text{OH}}$), where ω_OH is the OH-stretching wavenumber (dashed line in Fig. 10). The IR absorption of OH defects in quartz is comparatively stronger than those previously determined for the OH defects in Mg₂SiO₄ polymorphs, which is in line with experimental observations (Koch-Müller and Rhede, 2010). The consistence of the trend defined by OH defects in quartz with the general trend (Balan et al., 2008) sustains the use of a general wavenumber-dependent calibration (e.g., Paterson, 1982; Libowitzky and Rossman, 1997) to infer OH concentration in quartz from infrared spectra but does not support the use of a wavenumber-independent relationship as proposed by Thomas et al. (2009).