Crystal structure and elastic properties of parabreyite: a new high-pressure ring silicate in the CaSiO₃ system

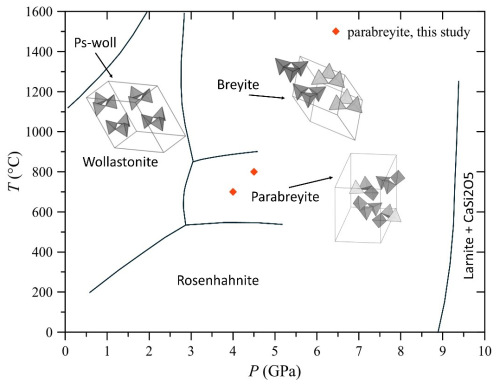
The CaSiO₃ system exhibits notable structural complexity, featuring different polymorphs and polytypes across various pressure (P) and temperature (T) conditions compatible with Earth's environments. Among these, the pseudowollastonite and breyite structures are characterized by the presence of threefold tetrahedral rings. In this study, we conducted multianvil syntheses in the pressure and temperature range 4–5 GPa and 600–800 °C to stabilize crystals of a new high-pressure polymorph reported by Chatterjee et al. (1984) and obtain structural information. The structure was solved by combining 3D electron diffraction (ED) and synchrotron single-crystal X-ray diffraction (SC-XRD). The new high-pressure polymorph, here referred to as parabreyite, features threefold tetrahedral rings, with a different configuration compared to breyite. Parabreyite is triclinic, $P\stackrel{\mathrm{‾}}{\mathrm{1}}$, with unit cell parameters a= 8.1911(10) Å, b= 9.3441(9) Å, c= 10.4604(10) Å, α= 73.901(8)°, β= 89.814(9)° and γ= 77.513(9)°. The bulk modulus, K₀= 90.7(5) GPa, was determined by an in situ SC-XRD experiment using a diamond anvil cell (DAC) in the pressure interval 0–10 GPa. Thermal expansion was also determined by low- and high-temperature SC-XRD measurements and resulted in a larger value compared to breyite. Additionally, we performed in situ synchrotron SC-XRD on synthetic pseudowollastonite in the pressure interval 0–14 GPa and did not observe any structural phase transition in this ring-type polymorph. We also report the differences between the Raman spectra of parabreyite and breyite to help with the in situ identification of these polymorphs. The threefold ring topology of parabreyite suggests a new configuration for high-density tetrahedra structures, with significant implications for the prediction of high-pressure sp³ carbonates.

1 Introduction

In recent years, the CaSiO₃ system has been extensively studied both experimentally and theoretically, as it represents one of the most abundant pure calcium silicates on our planet (Essene, 1974; Gasparik et al., 1994; Sueda et al., 2006; Belmonte et al., 2017; Milani et al., 2021; Sokolova et al., 2021). Despite having such a simple chemical composition, this system exhibits interesting structural complexity with a significant number of polymorphs and polytypes in the pressure–temperature space.

On the Earth's surface, CaSiO₃ polymorphs primarily result from contact metamorphism between calcium- and silicon-rich lithologies during reactions between calcite and quartz. In these scenarios, CaSiO₃ usually crystallizes as a mixture of triclinic wollastonite and monoclinic parawollastonite (wollastonite-2M), both characterized by silicon tetrahedra chains, with threefold tetrahedra periodicity (Hesse, 1984). The high-temperature polymorph pseudowollastonite is extremely rare in nature, since it requires direct crystallization above 1000 °C, but it is quite abundant in slag, cements and ceramic materials. This polymorph has a structure based on silicon tetrahedra forming threefold rings (Yang and Prewitt, 1999).

In the mantle, calcium silicate forms in magmatic and/or metamorphic contexts. Under upper mantle conditions, the high-pressure polymorph breyite has been widely identified as inclusions in diamonds (Joswig et al., 1999; Anzolini et al., 2016; Woodland et al., 2020/2021; Brenker et al., 2021). Its structure is also composed of threefold silicon tetrahedra rings, presenting a different topology compared to the one in the pseudowollastonite structure.

At higher pressures, the CaSiO₃ system dissociates into Ca₂SiO₄ larnite + CaSi₂O₅ titanite (Gasparik et al., 1994), which remain stable up to approximately 12 GPa, where they are replaced by the CaSiO₃ perovskite. The latter, representing the third most abundant phase in the lower mantle after bridgmanite (Mg,Fe)SiO₃ and Fe periclase (Mg,Fe)O, potentially stands as one of the most volumetrically abundant minerals of the whole Earth (Mattern et al., 2005; Irifune and Tsuchiya, 2015). This phase has been observed in only two natural samples, found as inclusions within diamonds. Its initial discovery was reported by Nestola et al. (2018), followed by a comprehensive characterization of another sample by Tschauner et al. (2021), which led to the approval of this mineral under the name davemaoite.

Experimental studies have shown that the CaSiO₃ system could be even more complex. Syntheses conducted in the CaO–Al₂O₃–SiO₂–H₂O (CASH) system (Chatterjee et al., 1984) have reported the presence of a potential new wollastonite polymorph, named wollastonite-IIm (woll-IIm), stable around 3.5 GPa and 700 °C, with a still-unknown crystal structure. The thermodynamic stability of this phase is also not fully constrained. Understanding the structural relationships and the boundary between breyite and this polymorph can help to determine the geological significance of these minerals in terms of P–T genesis conditions, especially for breyite included in diamonds.

In situ compressibility studies have further revealed that these structures can undergo multiple phase transitions induced by pressure, further increasing the number of different possible atomic arrangements between silicon tetrahedra and calcium polyhedra. Recently, Milani et al. (2021) carried out a comprehensive single-crystal in situ high-pressure study on triclinic wollastonite and breyite samples. They observed two phase transitions, both in wollastonite up to 22 GPa and in breyite up to 20 GPa, with the latter involving a reversible thermosalient effect (Skoko et al., 2010).

To add new crystallographic and thermodynamic data in the CaSiO₃ system, especially in the pressure range 0–9 GPa, we performed syntheses in the P–T range 0–5 GPa and 700–1200 °C. We present new experimental data and crystal structure determination by electron and X-ray diffraction of a new high-pressure polymorph, identified as woll-IIm (Chatterjee et al., 1984). The structure consists of a cyclosilicate, based on threefold tetrahedral rings, with a different topology compared to both breyite and pseudowollastonite. For comparison, Raman spectra for both breyite and the new high-pressure (HP) polymorph were also reported.

We also report single-crystal in situ compressibility and thermal expansion experiments on this new HP CaSiO₃ polymorph and new data on pseudowollastonite compressibility to complete the description of the thermoelastic behavior of these polymorphs in the CaSiO₃ system.

2 Materials and methods

2.1 Synthesis

High-pressure syntheses were performed with the multianvil apparatus available at the Department of Earth Sciences, University of Milan (DES-UM), starting from stoichiometric CaSiO₃ gel prepared following the procedure proposed by Hamilton and Henderson (1968). Two syntheses were conducted. The first synthesis (S1) was performed at 4 GPa and 700 °C, overlapping the conditions reported in the literature (Chatterjee et al., 1984). The gel used was calcinated at 1000 °C for 10 min. A standard MgO-octahedron with a 25 mm edge length (25 M assembly) with graphite furnace, an S-type thermocouple and a 3 mm diameter gold capsule were used. The second synthesis was performed with a similar experimental setup, at 4.5 GPa and 800 °C. For this synthesis, the gel used was not further calcinated. Excess of pure H₂O was added in all the experiments as a fluxing agent. Experimental details are listed in Table 1. Temperature is accurate to ± 20 °C, with no pressure correction for the e.m.f. of the thermocouple, and pressure uncertainties were assumed to be ± 3 % according to the accuracy of calibrant reactions (Fumagalli and Poli, 2005).

To obtain single crystals of pseudowollastonite, the procedure proposed by Yang and Prewitt (1999) was followed. A stoichiometric composition of CaSiO₃ (starting from CaCO₃ and SiO₂) was firstly decarbonated and successively melted at 1600 °C in a platinum crucible. The obtained glass was further heated at 1200 °C for 72 h, and single crystals of pseudowollastonite were synthesized (synthesis SX).

Table 1 Experimental details for syntheses.

2.2 Microprobe analysis

All the multianvil syntheses were analyzed by electron microprobe analysis (EMPA). Half of the capsules have been embedded in epoxy resin to obtain mounts suitable for the analysis. The mounts were then polished with ethanol to avoid chemical reaction with pure water. The chemical composition was determined by chemical microanalyses in wavelength-dispersive spectroscopy (EMPA-WDS) mode at DES-UM, using a Jeol 8200 instrument operating at 15 nA and 15 kV. The results of the analysis of different samples are reported in Table 2. Backscattered electron images are shown in Fig. 1a, b.

2.3 Electron diffraction

High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) images and 3D electron diffraction (3D ED) data were collected using a Zeiss Libra 120 Plus TEM, operating at 120 kV and equipped with a LaB₆ source, at the Center for Materials Interfaces of the Istituto Italiano di Tecnologia (IIT; Pontedera, Italy) and a Jeol JEM-F200 field emission gun, operating at 200 kV, at the Center for Instrument Sharing of the University of Pisa (CISUP; Pisa, Italy). The former is equipped with an omega filter, a single-electron Amsterdam Scientific Instruments (ASI) Timepix hybrid pixel detector (512×512 pixels) and a Bruker XFlash 6T-60 SDD detector for energy-dispersive X-ray spectroscopy (EDX). The latter is equipped with an ASI CheeTah hybrid single-electron detector (512×512 pixels). By inserting the smallest condenser aperture (5 µm for the Zeiss TEM, and 10 µm for the Jeol TEM) and defocusing the electron beam, a parallel beam (approx. 150 and 30 nm for Zeiss and Jeol, respectively) was used for ED data collection. We first located the candidate crystals for 3D ED in STEM mode (Fig. S1). Then, we performed the 3D ED experiments either in precession-assisted (PEDT) stepwise mode using the Zeiss TEM or in continuous (cRED) mode using the Jeol TEM (Gemmi and Lanza, 2019; Gemmi et al., 2019). Regardless of the chosen acquisition method, diffraction patterns were collected by the detector while tilting the selected crystals up to 120° under the electron beam. The data collected in cRED mode had an integration angle of 0.13°, while the PEDT data were collected with a precession semi-angle of 1°. The data used for structure solution were collected in PEDT.

Finally, PETS2 software was used for data reduction and unit cell determination, integration and merging (Palatinus et al., 2019). The reconstructed reciprocal volume from 3D ED data is displayed using VESTA software (Momma and Izumi, 2011). The structure was solved using SHELXT and refined with SHELXL (Sheldrick, 2015a, b) through the program Olex2 (Dolomanov et al., 2009).

2.4 X-ray diffraction analysis

Single crystals from S2 and SX were characterized with X-ray diffraction using the four-circle κ-geometry Rigaku XtaLAB Synergy diffractometer, available at DES-UM. The diffractometer is equipped with a PhotonJet (Mo) X-ray source, operating at 50 kV and 1 mA, with monochromatized Mo K_α radiation and with a hybrid pixel array detector located 62 mm from the sample position. X-ray diffraction data were indexed and integrated with CrysAlis RED software (Rigaku Oxford Diffraction, 2018). Structural refinement was handled with Jana2006 software (Petříček et al., 2014), and structural solution was performed with a charge-flipping algorithm, using Superflip software (Palatinus et al., 2007).

High-pressure in situ single-crystal diffraction experiments were then performed on the new HP CaSiO₃ polymorph and pseudowollastonite. A single crystal from S2 ($\mathrm{10}\times \mathrm{20}\times \mathrm{30}$ µm³) was loaded in a 600 µm culet membrane diamond anvil cell (DAC), with a stainless steel gasket and methanol–ethanol (4:1) as the pressure medium. X-ray data were collected up to 9.9 GPa and in decompression to assess whether hydrostatic conditions have been maintained during the experiment. A pseudowollastonite single crystal ($\mathrm{10}\times \mathrm{20}\times \mathrm{20}$ µm³) was loaded in a 300 µm culet BX90-type DAC (Kantor et al., 2012) with a rhenium gasket and neon as the pressure medium. A second pseudowollastonite single crystal ($\mathrm{20}\times \mathrm{25}\times \mathrm{30}$ µm³) was selected and loaded in a 600 µm culet DAC with methanol–ethanol (4:1) as the pressure medium. All the X-ray diffraction data were collected at the Xpress beamline at the Elettra synchrotron, Trieste, Italy (Lotti et al., 2020). During experiments, pressure was calibrated using ruby fluorescence (Mao et al., 1986).

Low- to high-temperature experiments were performed using a pre-tested single crystal of the HP CaSiO₃ phase placed in a quartz capillary with a diameter of 0.1 mm (Fig. S2) at the XRD1 beamline (Elettra synchrotron, Trieste, Italy). The low-temperature range 100–300 K was obtained with a liquid-nitrogen cryostat, while the high temperature, up to 766 K, was reached with a gas blower.

Diffraction data were handled as mentioned previously, and the obtained pressure–volume and temperature–volume data were then fitted with the Birch–Murnaghan equation of state (EoS; Birch, 1947) and the modified EoS from Holland and Powell (1998), respectively, using EosFit7-GUI software (Gonzales-Platas et al., 2016).

2.5 Micro-Raman spectroscopy

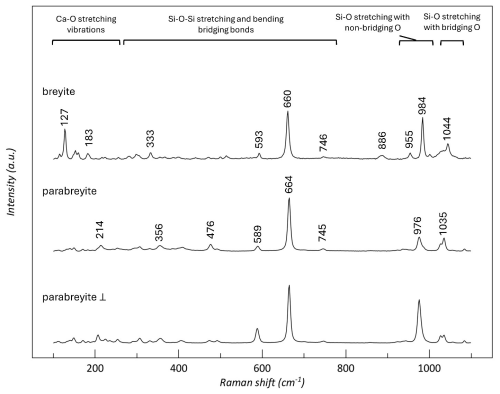
Micro-Raman spectra were collected with a Horiba LabRAM HR Evolution confocal micro-Raman spectrometer at the DES-UM equipped with ultra-low-frequency (ULF) filters. Laser light, excited with the 532 nm and 100 mW emission of a Nd:YAG laser source, was focused through a 100× objective (NA aperture of 0.9), giving a spot size of approximately 1 µm. The system was calibrated using a 520.7 cm⁻¹ line of a silicon wafer. Scattered light was collected in backscattering geometry, using a diffraction grating of 600 lines mm⁻¹ and a Peltier-cooled charge-coupled detector. To balance the signal-to-noise ratio, five accumulations of 60 s each with a 25 % reduced laser power were collected for parabreyite, and two perpendicularly polarized spectra were collected. All spectra were collected on the same samples analyzed with an electron microprobe. For comparison, we also measured the Raman spectrum of breyite, synthesized at 6 GPa and 1500 °C in a previous study (Milani et al., 2021). The breyite signal was collected with four accumulations of 20 s each with a 50 % laser power. In all the cases, the sample spot was visually examined under the microscope to ensure the absence of sample damage due to the laser irradiation.

3 Results and discussion

3.1 Microprobe

Average EMPA results for the different syntheses are reported in Table 2, while backscattered electron images are reported in Fig. 1a, b. In S1 (Fig. 1a), the run products consist of small crystals ranging from sub-micrometric to a size of 10–15 µm. The dark gray area, which covers the largest area of the image, has a CaSiO₃ composition. The lighter gray crystals present a Ca : Si ratio of 2:1, corresponding to the larnite composition. In this case, the total measured oxides sum to approximately 94 %, suggesting possible hydration for this phase. The chemical composition and textural features of this experimental product are quite similar to the ones reported by Németh et al. (2017) for synthesis performed at higher pressure. The synthesis S2 (Fig. 1b) consists of crystals with a 100 µm average size of CaSiO₃. Minor amounts of SiO₂ and CaCO₃ (darker crystals), likely resulting from the slight carbonation of the dried gel, are also present.

Figure 1 (a) Backscattered electron image of a portion of S1. (b) Backscattered electron image of a portion of S2.

Table 2 Average measured oxides in weight percent.

3.2 Electron and X-ray diffraction: crystal structure of parabreyite

The obtained crystals were studied by combining both electron and X-ray diffraction. Unit cell parameters and the volume of the measured crystals are reported in Table 3.

3D ED analysis of the lower-temperature synthesis (S1) revealed the presence of a heavily disordered phase with two well-defined unit cell parameters, a= 8.2 Å, c= 10.5 Å and β= 90°, and a strong streaking along the b^* reciprocal direction, which hampers a straightforward unit cell determination (Fig. 2). The crystals usually display an irregular crystal habit formed by thin sheets stacked along b^* (Fig. 2). If a semi-automatic indexing is carried out, PETS2.0 delivers an orthorhombic unit cell with b= 17.4 Å, which coincides with the cell proposed by Chatterjee et al. (1984) for their wollastonite-IIm phase. However, any attempt to solve the structure with the electron diffraction data extracted with this orthorhombic cell failed, suggesting that the cell is a result of the disorder, but the real underlying structure has a different geometry. To solve this mystery, we performed the peak search with a very high $I/\mathit{\sigma }$ ratio (> 15) with the aim to collect only the maxima along the streaking direction. Projected along special directions perpendicular to c^*, the peak table shows features characteristic of twinning (see Fig. 2 bottom right). In fact, the peaks could be indexed by two triclinic unit cells with a= 8.2 Å, b= 9.3 Å, c= 10.5 Å, α= 74°, β= 90° and γ= 77 Å, related by a 180° rotation along the b axis. The twinning occurs through reticular merohedry (Nespolo and Ferraris, 2004), with a fourfold orthorhombic super cell (a= 8.2 Å, b= 34.8 Å, c= 10.5 Å) being the twin lattice. Interestingly, a similar twinning, with different unit cell parameters, arises in the iodine salt of agomelatine (Skořepová et al., 2016), and it is widely described in Petříček et al. (2016). Therefore, in the case of the absence of disorder and the presence of two twinned individuals, the diffraction could be wrongly indexed with the fourfold orthorhombic cell. Structure solution attempts on single datasets failed since they were also affected by a low completeness (always below 60 %), in addition to the disorder and the twinning. We tried to improve the completeness by merging two datasets coming from two different crystals (still twinned), obtaining a final completeness of 62 % up to a resolution of 0.7 Å. With this dataset we could solve ab initio the crystal structure in space group $P\stackrel{\mathrm{‾}}{\mathrm{1}}$. Due to the low quality of the data, the kinematical refinement converges with a quite-high R value of 38 % (Table S1).

Table 3 Unit cell parameters of synthesized and natural CaSiO₃ polymorphs.

^* Unit cell parameters obtained by 3D electron diffraction.

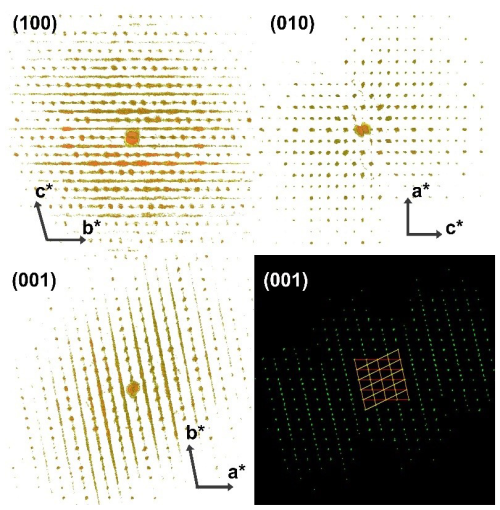
Figure 2 A 3D reconstruction of the reciprocal space obtained with 3D ED, viewed along the three main reciprocal directions. At the bottom right, the diffraction peaks detected with the high $I/\mathit{\sigma }$ strategy (displayed along the c^* direction) indexed with the two twinned cells.

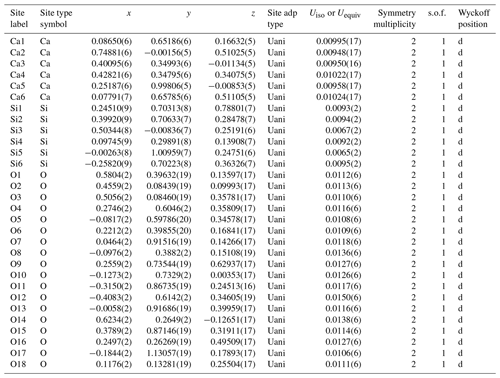
The second synthesis (S2), planned with a slightly larger water content and higher temperature to promote possible crystal growth, resulted in larger crystal domains. A few crystal grains suitable for single-crystal X-ray diffraction were successfully isolated. Some of them appeared twinned, but the diffraction spots were successfully indexed using the unit cell determined by 3D ED. After careful selection, single-crystal domains were also measured. X-ray diffraction analysis identified the unit cell parameters a= 8.1713(2) Å, b= 9.3318(2) Å, c= 10.4382(2) Å, α= 73.902(2)°, β= 89.8888(19)° and γ = 77.489(2)°, as well as vol = 745.14(3) ų, compatible with the S1 sample. The X-ray diffraction intensities allowed for the ab initio structure solution of this HP CaSiO₃ polymorph. The charge-flipping algorithm converged to a triclinic structure with space group $P\stackrel{\mathrm{‾}}{\mathrm{1}}$, corresponding to an R_obs value of 3.42 % and GOF_(all)= 1.53. Atomic coordinates and refinement details are reported in Table 4. Remarkably, the structural model coincides with the one derived by 3D ED. The two models compared using the COMPSTRU tools of the Bilbao crystallographic server (De La Flor et al., 2016) differ on average with 0.11 Å in their atomic positions.

Table 4 Atomic coordinates of parabreyite and statistical parameters of structure refinement. The abbreviations “adp” and “s.o.f.” signify atomic displacement parameter and site occupancy factor, respectively.

The crystal structure is characterized by a threefold tetrahedra ring configuration surrounded by distorted calcium polyhedra (Fig. 3), and it is similar to the structure of pseudowollastonite and breyite, which are stable at higher temperatures at low and high pressures, respectively (Fig. 4). According to its similar topology and pressure of occurrence, we propose naming the new polymorph parabreyite, following the nomenclature rules reported by Nickel and Grice (1998).

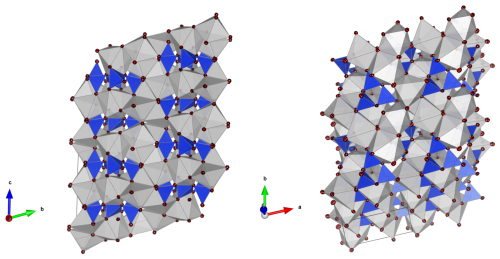
Figure 3 Representation of the parabreyite structure in two different orientations. The red spheres are oxygens, the silicon tetrahedra are in blue and gray polygons are Ca cation sites. The solid lines represent the dimensions of the unit cell. On the left, the structure is oriented to underline the stacking sequence along b^* (perpendicular to the $a--c$ plane).

However, from a structural perspective, the relative orientation of the silicon tetrahedra in breyite, parabreyite and pseudowollastonite is significantly different. As shown in Fig. 4, in the pseudowollastonite structure the tetrahedra rings have the outer edges pointing in almost the same direction, while in the breyite structure, one face of the three tetrahedra is nearly coplanar. In the parabreyite structure, two of the three tetrahedra point in almost the same direction, while the third one has the opposite orientation. In the $a--b$ plane, the orientation of adjacent rings alternates. The variation in the tetrahedra orientation has a clear effect on the density of these structures as well. Considering the measured unit cell parameters (Table 3), the calculated density of pseudowollastonite is ρ_pseudo= 2.92 g cm⁻³, and it is significantly lower than the density of the two high-pressure polymorphs, which is ρ_parabreyite= 3.11 and ρ_breyite= 3.08 g cm⁻³. For breyite, the density was obtained from the synthetic sample measured by Milani et al. (2021), which is consistent with the value ρ_breyite= 3.07 g cm⁻³ reported by Brenker et al. (2021) for the natural sample. Breyite and parabreyite share almost the same density also because of the presence of two different calcium sites in both structures. Specifically, they show a 1:2 ratio of larger eightfold coordinated sites and smaller sixfold distorted octahedral sites.

Figure 4 CaSiO₃ pressure–temperature stability field modified after Chatterjee et al. (1984). The syntheses presented in this study are reported along with the silicon tetrahedra framework of pseudowollastonite, breyite and parabreyite.

3.3 Micro-Raman spectroscopy

Micro-Raman spectra collected on synthetic breyite (synthesized in Milani et al., 2021) and parabreyite (this study) were interpreted according to literature studies on threefold ring CaSiO₃ structures (Richet et al., 1998; Brenker et al., 2021). As reported, the Raman shift region between 130 and 430 cm⁻¹ corresponds to the silicate network along with the Ca–O stretching vibration. The intermediate region between about 430 and 745 cm⁻¹ is probably related to the Si–O–Si stretching and bending bridging bonds. The higher frequencies, between 900 and 1000 cm⁻¹, represent Si–O stretching vibrations with non-bridging O atoms, while the peak at around 1040 cm⁻¹ corresponds to the Si–O stretching vibration with bridging O atoms. The Raman spectra of breyite and parabreyite are reported in Fig. 5. The spectra of breyite exhibit similar characteristics to those reported by Brenker et al. (2021), with slight variations that could be attributed to minor chemical differences. When comparing the spectra of breyite and parabreyite, the first noticeable distinction appears in the Ca–O region, where the peak of breyite at 127 cm⁻¹ is absent in the parabreyite structure. To verify that this feature is not related to a particular orientation of the parabreyite crystal, we collected the spectrum with a perpendicular polarization on the same crystal. Other spectra collected on crystals with different orientations did not show the occurrence of a peak in this region. In parabreyite, the dominant peak at around 660 cm⁻¹ is shifted to a higher Raman shift value, while the Si–O stretching region is characterized by different peak positions.

Figure 5 Raman spectra of parabreyite (this study) and breyite (synthesized in Milani et al., 2021).

3.4 Elastic behavior of parabreyite and pseudowollastonite

A single crystal of parabreyite was loaded in a diamond anvil cell to perform in situ high-pressure X-ray diffraction in the 0–10 GPa range. No discontinuity has been observed in the pressure interval investigated. The volume–pressure data were fitted using EoSFit-GUI software (Gonzales-Platas et al., 2016) with a second-order Birch–Murnaghan equation of state (BM2) due to horizontal Eulerian strain (f_e) vs. a normalized stress (F_e) plot (Angel et al., 2000) and a ${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}$ value of 0.56 (max ΔP = −0.15). The bulk modulus resulted in K₀= 90.6(5) GPa with Kp = 4 (implied value). The V₀ value was inferred from EoS extrapolation and is V₀= 746.6(2) ų. Data and the relative equation of state are plotted in Fig. 6 and detailed in Table S2.

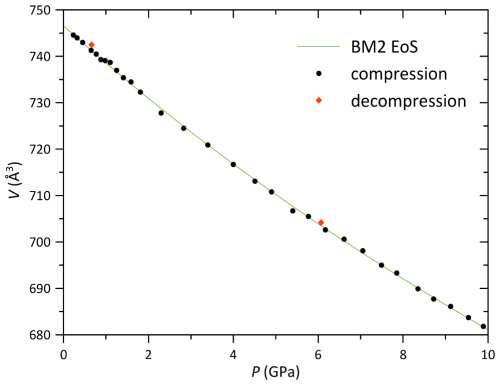
Figure 6 Parabreyite volume variation with pressure up to 9.89(5) GPa. The estimated standard deviation (e.s.d.) bars are smaller than the symbols.

The high-pressure behavior of pseudowollastonite has also been studied in the interval between 0 and 10.10(5) GPa, with DAC having 600 µm culet diamonds (psew_HP 600). Using the EoSFit7-GUI program (Gonzales-Platas et al., 2016), the Eulerian finite strain (f_e) vs. normalized stress (F_e) plot strongly suggests a third-order Birch–Murnaghan equation of state to fit the data, since it shows a positive slope. The bulk modulus resulted in K₀= 81(2) GPa, with Kp = 5.9(5) and Kpp = −0.12 (implied value). Least square fitting parameters are ${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}=$ 0.52 and maximum ΔP = 0.18. No phase transition has been observed in the interval analyzed. The second experiment was performed in the 0–13.64(5) GPa interval, with DAC having 300 µm culet diamonds (psew_HP 300). In this case, the F_e−f_e plot suggested a third-order Birch–Murnaghan equation of state that resulted in K₀= 76(3) GPa, with Kp = 6.6(7) and Kpp = −0.17 (implied value). Least square fitting parameters are ${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}=$ 4.31 and maximum delta pressure = 0.24. The obtained values are compatible with the experiment in the 600 µm culet DAC within 1σ. The bulk modulus obtained in this study is consistent with the value obtained by re-fitting the data published by Yang et al. (1999) with a second-order Birch–Murnaghan equation of state, which is K₀= 85(2) GPa (${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}=$ 4.53, maximum delta pressure = −0.14). Data are reported in Fig. 7, while the unit cell parameters for each pressure increment are reported in Table S3. The Eulerian finite strain (f_e) vs. normalized stress (F_e) plots for the different high-pressure runs are reported in Fig. S3.

3.5 Thermal expansion of parabreyite

One single crystal of parabreyite was measured in the temperature interval 100–766 K. No discontinuity or phase transition was observed in the studied interval. Unit cell parameters and volume obtained by X-ray diffraction are reported in Table S4. The volume–temperature data were fitted with the modified thermal equation of state by Holland and Powell (1998) to have a good fit for the low-temperature data as well. The obtained parameters are V₀= 752.570(13) ų, α₀= 5.21(5) and α₁= −0.83(4), with ${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}=$ 0.84. Data and the equation of state are reported in Fig. 8. For comparison, the same equation of state was used to fit the thermal expansion data available for breyite in the literature (Anzolini et al., 2016). The obtained values for breyite resulted in V₀= 376.41(3) ų, α₀= 4.55(13) and α₁= −0.95(19), with ${\mathit{\chi }}_{\mathrm{w}}^{\mathrm{2}}=$ 5.11. Within 1σ, the thermal expansion parameter α₀ of parabreyite is larger than the one of breyite.

4 Conclusions

The experiments conducted have highlighted the structural complexity of the CaSiO₃ system, despite its simple chemical composition. We report the stabilization and structural resolution of the new polymorph parabreyite, stable between at least 4.0–4.5 GPa and 700–800 °C, which further enriches the phase diagram of the CaSiO₃ system (Fig. 4). The temperature of the stability of parabreyite is slightly lower than that of the mantle geotherm. However, the different formation mechanisms proposed by Brenker et al. (2021) for breyite in the mantle do not limit the stabilization of this polymorph to specific pressure–temperature (P–T) conditions. Consequently, the formation of parabreyite at mantle conditions should not be excluded.

The in situ experiments allow for a comparison between the thermoelastic properties of the different threefold ring structures in the CaSiO₃ system. Despite their similar pressure occurrence, parabreyite and breyite exhibit a significantly different compressibility. In this study, we report a bulk modulus for parabreyite of K₀= 90.6(5) GPa, which is almost 15 % higher than the bulk modulus values reported in the literature for breyite, which are K₀= 78.6(13) GPa and K₀= 79(2) GPa (Anzolini et al., 2016 and Milani et al., 2021, respectively). Thus, breyite is more compressible than parabreyite. As mentioned previously, the two polymorphs also have a different thermal expansion coefficient, which is higher for parabreyite (α₀= 5.21(5), this study) than breyite (α₀= 4.55(13), Anzolini et al., 2016). Regarding pseudowollastonite, the low-pressure polymorph, we report a bulk modulus of K₀= 81(2) GPa, which is compatible with the value of K₀= 85(2) GPa reported by Young et al. (1999). Contrary to the findings reported in the literature (Lin et al., 2016), a phase transition of pseudowollastonite at 10 GPa was not observed. This discrepancy can be attributed to the fact that the methanol–ethanol–water mixture ($\mathrm{16}:\mathrm{3}:\mathrm{1}$ by volume) used by Lin et al. (2016) is no longer hydrostatic beyond 10 GPa. However, we observe that the equation of state (EoS) derived from the second run, which collected data over a broader pressure range (up to 13.64(5) GPa), yields a K₀ value of 76(3) GPa. This is slightly different from the value reported in the literature within a 1σ uncertainty. This discrepancy could be due to possible elastic softening, detectable only with a wider pressure range, which may indicate the onset of amorphization or an additional phase transition. These phenomena warrant further investigation at higher pressures.

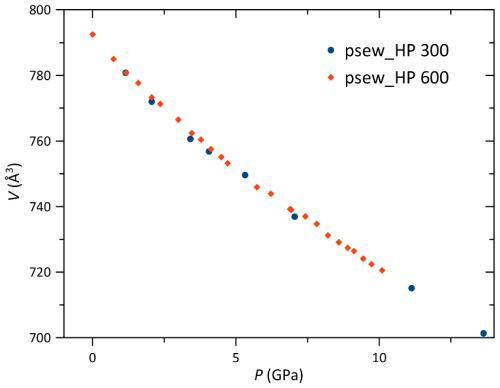
Figure 7 Pseudowollastonite volume variation with pressure in the 300 µm culet DAC (psew_HP 300) and 600 µm cullet DAC (psew_HP 600). The e.s.d. bars are smaller than the symbols.

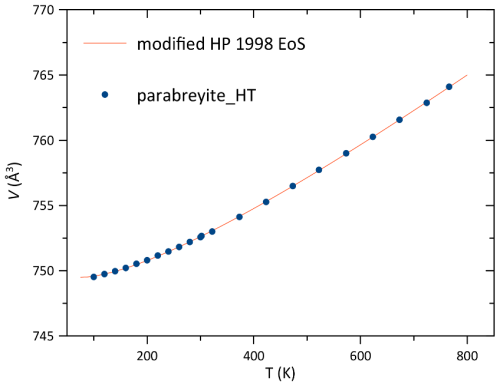
Figure 8 Parabreyite volume variation with temperature. The e.s.d. bars are smaller than the symbols.

From a crystallographic perspective, 3D ED was crucial in solving the structural puzzle of parabreyite. It was only through the preliminary structure determination obtained by 3D ED that single-crystal X-ray data could be successfully indexed, allowing the parabreyite structure to be refined with high accuracy.

The threefold ring structures of the CaSiO₃ polymorphs are significantly different when considering the relative orientation of the silica tetrahedra within the rings (see Fig. 4). The pseudowollastonite structure, with coaxial tetrahedra edges, has the same topology as other cyclosilicates, such as benitoite and wadeite (Zachariasen, 1933; Henshaw, 1955), while the breyite structure is analogous to the walstromite and margarosanite configuration (Freed and Peakor, 1967; Callegari and Boiocchi, 2016), with all the silicon tetrahedra pointing in the same direction. Interestingly, the parabreyite polymorph showed a third new topology, with two tetrahedra pointing in one direction and one in the opposite direction. This polymorph, like breyite, has two different large cation sites, suggesting a possible solid solution with larger elements (e.g., Ba as in walstromite). In situ high-pressure experiments on pseudowollastonite and parabreyite did not show a tendency towards the breyite structure, excluding the possibility of relating the different polymorphs through simple displacive processes. This was further confirmed by the quenchable nature of the phases studied.

The parabreyite structure and its relationship with breyite and pseudowollastonite may also suggest potential topologies for other tetrahedral ring structures in different classes of materials, such as high-pressure carbonates. Historically, germanate structures have been used as proxies to interpret high-pressure transformations in silicates (Ringwood and Major, 1967). Recent high-pressure studies on carbonates at megabar pressures have revealed topologies similar to those observed in cyclosilicates. For instance, magnesite-II (Chariton et al., 2020) and dolomite-IV (Merlini et al., 2017) feature threefold ring carbon sp³ tetrahedra with the same topology as breyite. Both theoretical and experimental studies have focused on pure compounds with stoichiometries corresponding to ambient pressure carbonate minerals. The similarity in density between parabreyite and breyite, along with their respective ring structures and stoichiometries involving larger and smaller cations, suggests that future investigations into carbonates might reveal new and unpredicted structures and stoichiometries.